文章信息
- 徐建伟, 徐青
- XU Jianwei, XU Qing
- 灌浆帷幕耐久性数值仿真分析
- Numerical simulation analysis of durability of grouting curtain
- 武汉大学学报(工学版), 2016, 49(2): 206-211
- Engineering Journal of Wuhan University, 2016, 49(2): 206-211
- http://dx.doi.org/10.14188/j.1671-8844.2016-02-008
-
文章历史
- 收稿日期: 2015-06-15
随着水工建筑物运行年龄的增长,其内部结构不断发生物理的和化学的变化.在我国,许多大坝已经或将逐步进入老龄期.因此,大坝的耐久性及服役寿命评估,将成为21世纪我国坝工界重要的研究课题[1],而防渗灌浆帷幕是大坝基础的关键组成部分,对灌浆帷幕耐久性的研究正越来越被人们重视.帷幕的耐久性,亦即帷幕的服役寿命,可采用帷幕防渗的有效年限来进行评估.帷幕在各类环境因素的作用下,随着运行时间的增长,帷幕中胶凝材料逐渐减少,当帷幕的渗透系数接近周围岩体时,我们判定帷幕失效.帷幕防渗效果的有效年限越长,帷幕的耐久性越高,而帷幕体防渗效果减弱受渗流场、化学场及溶质运移场等多场耦合作用的影响.随着水库的运行,大坝在上下游高水头差的长期作用下,渗透水流通过岩体的裂隙、断层等进入坝基.设置防渗帷幕可以降低坝基扬压力、减少渗漏、防止地层产生机械潜蚀等,保证坝基、坝肩的稳定.由于帷幕长期在渗透压力和一系列水化学的作用下,遭受侵蚀和损伤,水泥水化物(主要为Ca(OH)2 )溶出和分解,并不断被渗透水流带走,导致灌浆帷幕的微细观结构发生改变,从而使得帷幕的渗透性增大,又进一步使物理化学溶解、侵蚀加剧.帷幕体因此逐渐损失胶凝性和强度耐久性,从而造成帷幕体防渗性能的衰减.
近年来,大坝耐久性及服役寿命评估与坝基帷幕体的防渗耐久性问题得到广泛关注.中国不少研究者对此类问题的研究主要采用水文地球化学基本理论和方法,并成功将其应用于数值模拟分析.郑西来(1990)等[2]将岩-水作用线性规划模型应用于含水层系统;随后陈芸等[3]对岩-水作用线性规划模型进行了较深入的研究和运用.曾溅辉[4]于1993年比较系统地论述了地下水系统地球化学模拟的基本理论、方法应用、存在的问题及发展的方向;王锦国[5]等根据能量最小值原理,建立了坝基岩-水作用线性规划模型,并采用最优化求解方法得到岩-水作用中的化学反应程度及矿物溶解量;童海涛[6]等将随机方法引入坝基岩-水作用模拟中,根据地球热力学平衡原理和局部平衡假设,耦合岩-水作用的线性规划模型和Monte-Carlo方法,建立岩-水作用的随机模型,从其随机分布特征分析评价了岩-水作用对帷幕耐久性的影响.
为了研究灌浆帷幕防渗性能的衰减过程,本文将溶质运移的迁移-扩散模型、溶质在多孔介质中的溶解-沉淀模型与渗流模型耦合,建立3个模块的全耦合(直接耦合)模型[7-9],借助具有强大多物理场耦合分析功能的COMSOL Multiphysics[10]软件,建立数值分析模型,并采用有限单元法进行求解,得到可视化的帷幕体微细观结构随时间的变化过程及其耐久性评估的结果.
1 多物理场耦合基本模型 1.1 基本假定1) 坝基岩体为饱和等效连续介质,即只考虑固相和液相.
2) 地下水渗流服从Darcy定律,溶质扩散服从Fick定律.
3) 坝基区溶质浓度变化引起的地下水密度、粘性等物理特性的改变对渗流的影响忽略不计.
4) 不考虑溶质随地下水运移过程中与坝基区岩体发生的具体的离子化学反应,直接将其简化为源(或汇)项加入到偏微分方程中.
5) 地下水中溶质浓度的改变,全部由帷幕溶解扩散引起,不考虑坝基岩体溶解、沉淀所引起的变化.
6) 由于灌浆帷幕固体物质主要为Ca(OH)2,故假设帷幕体溶质全部为Ca2+,初始固相Ca(OH)2质量分数为1.
1.2 渗流模型坝基区为等效连续介质,地下水为饱和流,坝基地下水运动可以用以下渗流模型[11]来描述:
式中:Ss=ρgα1-θ+θβ,为单位贮存量;α为骨架颗粒的压缩性系数,一般取α=1~6×10-5cm2/kg; β为水的压缩性系数,一般取β=5×10-5cm2/kg;ρ为水的密度;θ为岩体的孔隙率;h为水头;t为时间;K为渗透系数张量;f0、f1、f2均为已知函数;Γ1、Γ2 分别为已知水头和已知流量边界;n为Γ2边界的外法线方向.
1.3 溶质运移模型渗入坝基的地下水溶液从上游向下游运动过程中,水溶液组分的运移及其岩-水化学反应引起的浓度变化可以用溶质运移模型[12]来描述:
式中:C为地下水溶液中溶质的浓度;F为溶质在多孔介质骨架中的质量分数;ρs为多孔介质的干密度;θ为介质孔隙率;u为地下水实际流速;D为水动力弥散系数张量;W为源(或汇)项;C0、C1、C2均为已知函数;A为已知浓度边界条件;B为已知溶质通量边界条件;n为B边界外法线方向;▽为微分算子.
弥散系数张量由下式给出:
式中:δ为Kronecker函数;aL为纵向弥散系数;aT为横向弥散系数;am为分子扩散系数;u为实际渗流速度;τ为多孔弯曲度;i、j分别表示坐标分量.
1.4 溶解-沉淀模型地下水流对帷幕体的侵蚀溶解作用[13]可用以下方程描述:
式中:Kd为分配系数;S为溶解吸附速率参数;F为固相溶质在多孔介质骨架中的质量分数;C为地下水溶液中溶质的浓度;F0、G0均为已知函数.
1.5 耦合模型帷幕体防渗及耐久性数值分析的多场全耦合模型,即将描述地下水运动过程的渗流模型、描述坝基地下水溶液溶质迁移扩散的溶质运移模型和描述地下水流对帷幕体侵蚀溶解的溶解-沉淀模型3个模型的控制方程联立求解.
本文采用多物理场耦合软件COMSOL Multiphysics建立坝基渗流场[14-15]、化学场及溶质运移场三场耦合的有限元数值模型,研究坝基帷幕在渗透力作用下,溶质的溶解-沉淀和迁移-扩散随时间的变化过程.确立全耦合模型后,需对模型控制方程的交叉耦合项和变量参数进行研究.本文考虑介质的渗透系数为时间和空间的函数,帷幕体在长期的地下渗水压力和水化学作用下,遭受不断的侵蚀溶解,胶凝材料减少,导致帷幕体孔隙率增加,渗透系数变大,而帷幕体渗透系数的增大又会导致渗透水流流速的变大及溶质运移过程的加快并加重化学浸蚀,形成一个相互影响的循环效果,最终导致帷幕的失效.
在流固耦合研究中,Louis(1974)根据一些坝基岩体钻孔压水试验的结果建立了渗透系数与正应力的经验公式[16]:
式中:σe为有效正应力,为研究点上的上覆岩层重量与孔隙水压力之差;K为岩体渗透系数;K0为σe=0时的渗透系数;α为经验系数,取决于岩石中的孔隙或裂隙状态.
本文类比渗透系数K与有效应力σe的经验公式,分析渗透系数随多孔介质中溶质的质量分数的变化关系,提出了如下渗透系数与多孔介质溶质质量分数的经验公式:
式中:F为固相溶质在多孔介质中的质量分数;K为多孔介质渗透系数;K1为F=1时的渗透系数;γ为经验系数,需通过试验确定.
2 应用算例 2.1 基本资料某混凝土重力坝坝高150 m,正常蓄水位高程445 m,下游水位高程345 m,坝底高程300 m、坝底宽105 m.坝基岩性以灰岩和白云岩为主,岩体渗透系数较为均匀,可视作各向同性.为增强防渗性能,在河床处设计深度100 m、厚5 m的灌浆帷幕.
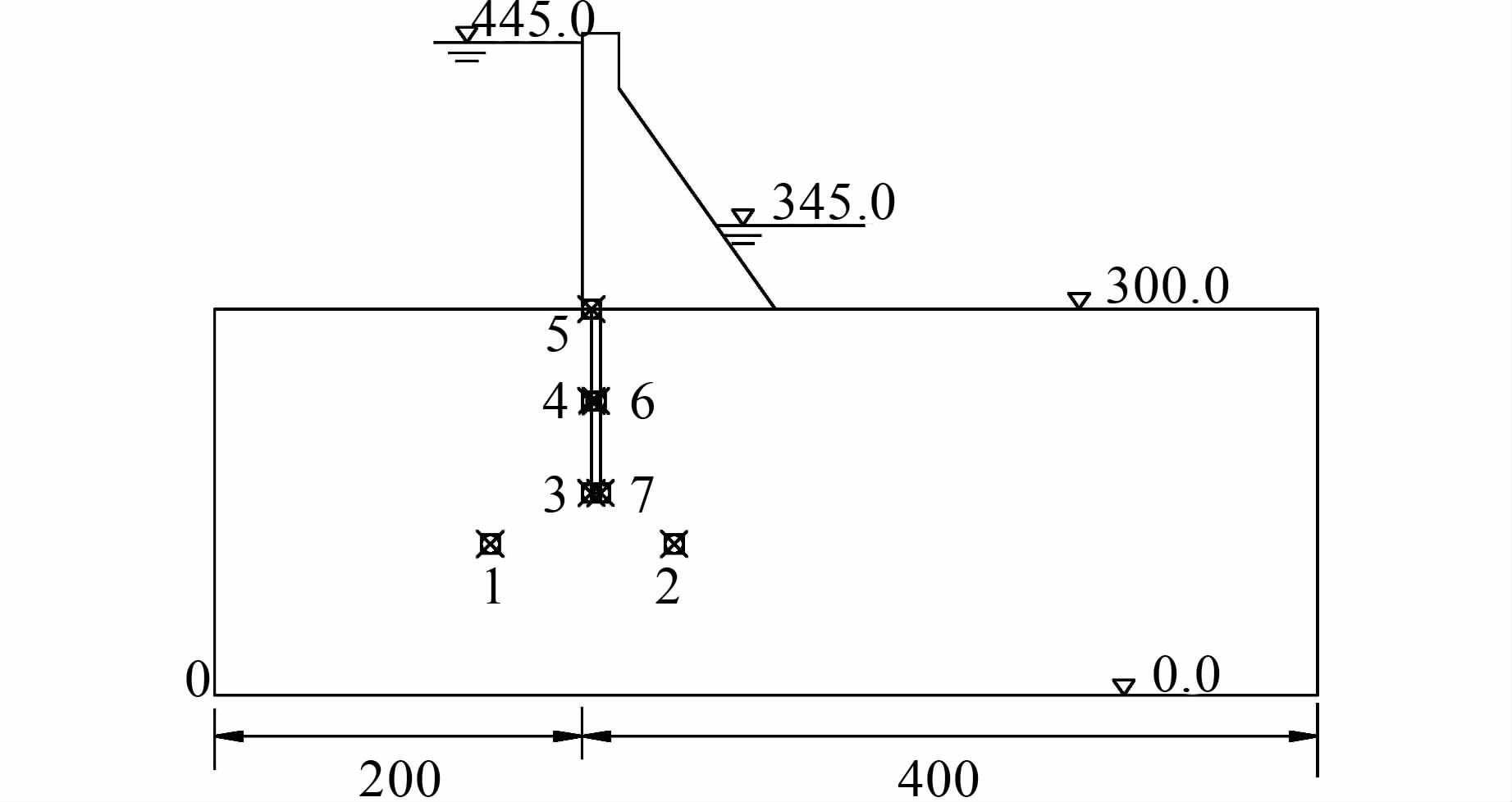
2.2 模型计算区域及参数的选定以坝基作为研究对象.研究区域:坝踵向上游延伸200 m,坝趾向下游延伸295 m,深度取2倍坝高.以坝基区域左下角0点为坐标原点,灌浆帷幕设置在距坝踵5 m处,如图 1所示,坝基水文地质参数如表 1所示.表 1中,ρs为多孔介质的干密度;K为坝基岩体渗透系数;θ1为坝基岩体孔隙率;θ2为帷幕孔隙率;μ为流体动力粘滞系数;C0为坝基区域初始钙离子浓度;F0为帷幕初始氢氧化钙质量分数;am为分子扩散系数;aL为纵向弥散系数;aT为横向弥散系数.
|
| 图 1 模型计算区域几何尺寸图(单位:m) Figure 1 Geometrical dimensions of model (unit:m) |
| ρs/ (kg·m3) | K/(m·s-1) | θ1 | θ2 | μ/(Pa·s) | C0/(kg·m-3) | F0 | am/(m2·s-1) | aL(m2·s-1) | aT (m2·s-1) |
| 2400 | 1×10-6 | 0.2 | 0.1 | 0.001 | 0 | 1 | 1×10-6 | 2.4×10-11 | 2×10-12 |
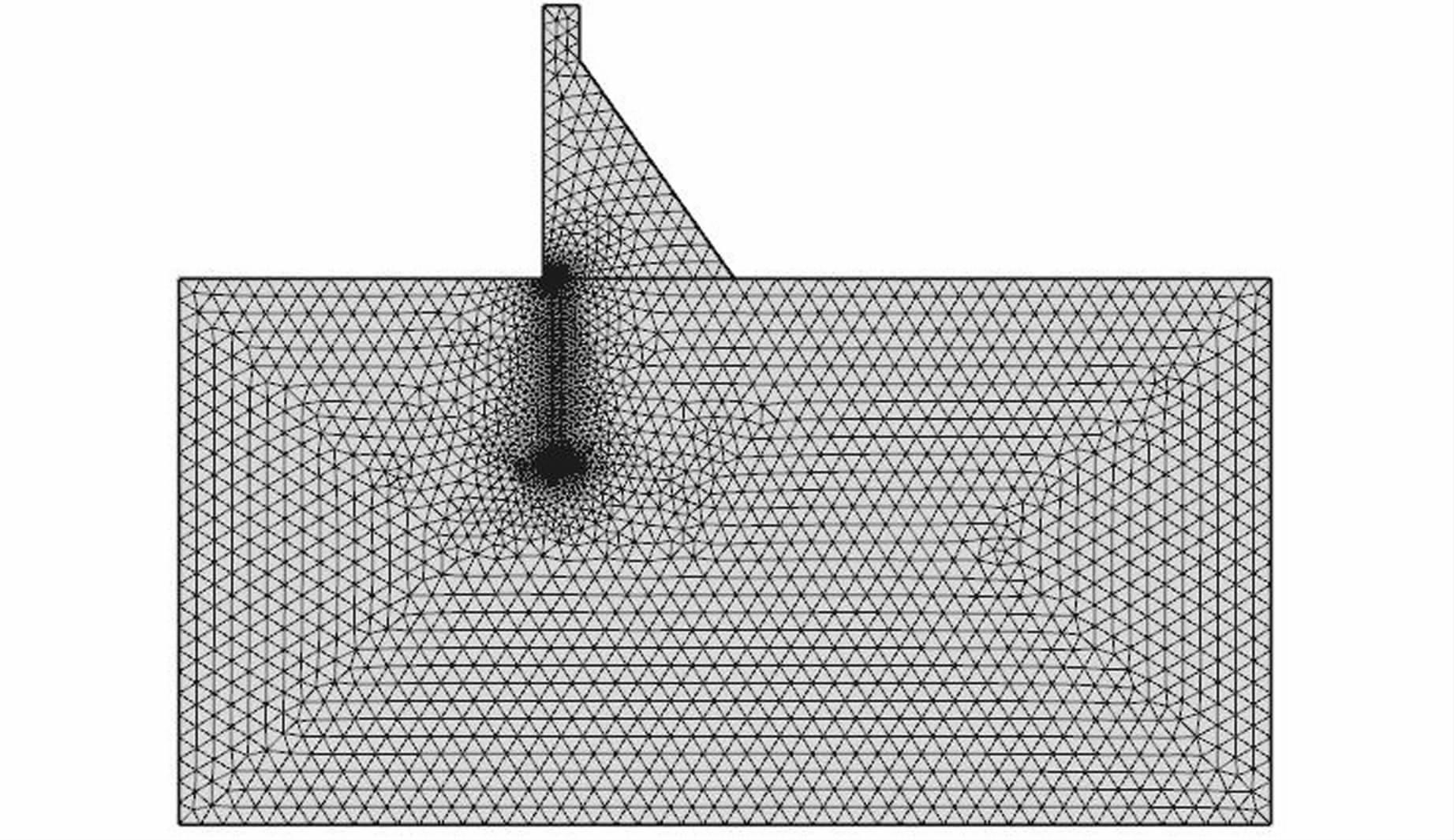
计算区域的模拟计算工作主要由计算区域的离散化和耦合模型的计算两个部分组成.首先对模型研究区进行网格剖分,并对边界区进行加密处理,共生成5 343个单元,其中边单元294个,端点单元16个,有限元网格如图 2所示.假定坝体完全不透水,不作为计算区域;帷幕体水化物全部为氢氧化钙.通过数值模拟,发现模拟区钙离子浓度变化在25 a后已趋于稳定,故以5 d为时间步长,25 a作为模拟的总时间进行模型的全耦合计算,模拟了帷幕体与地下水溶液之间物质交换在空间和时间上的变化过程,获得了坝基帷幕体防渗性能衰减的动态过程和规律,部分计算结果如图 3~8所示.
|
| 图 2 模型计算区域有限元网格图 Figure 2 Finite element mesh of model |

|
| 图 3 25 a时计算区域钙离子浓度分布及流速矢量图 Figure 3 Distribution of calciumion concentration and velocity vectogram after 25 years |
|
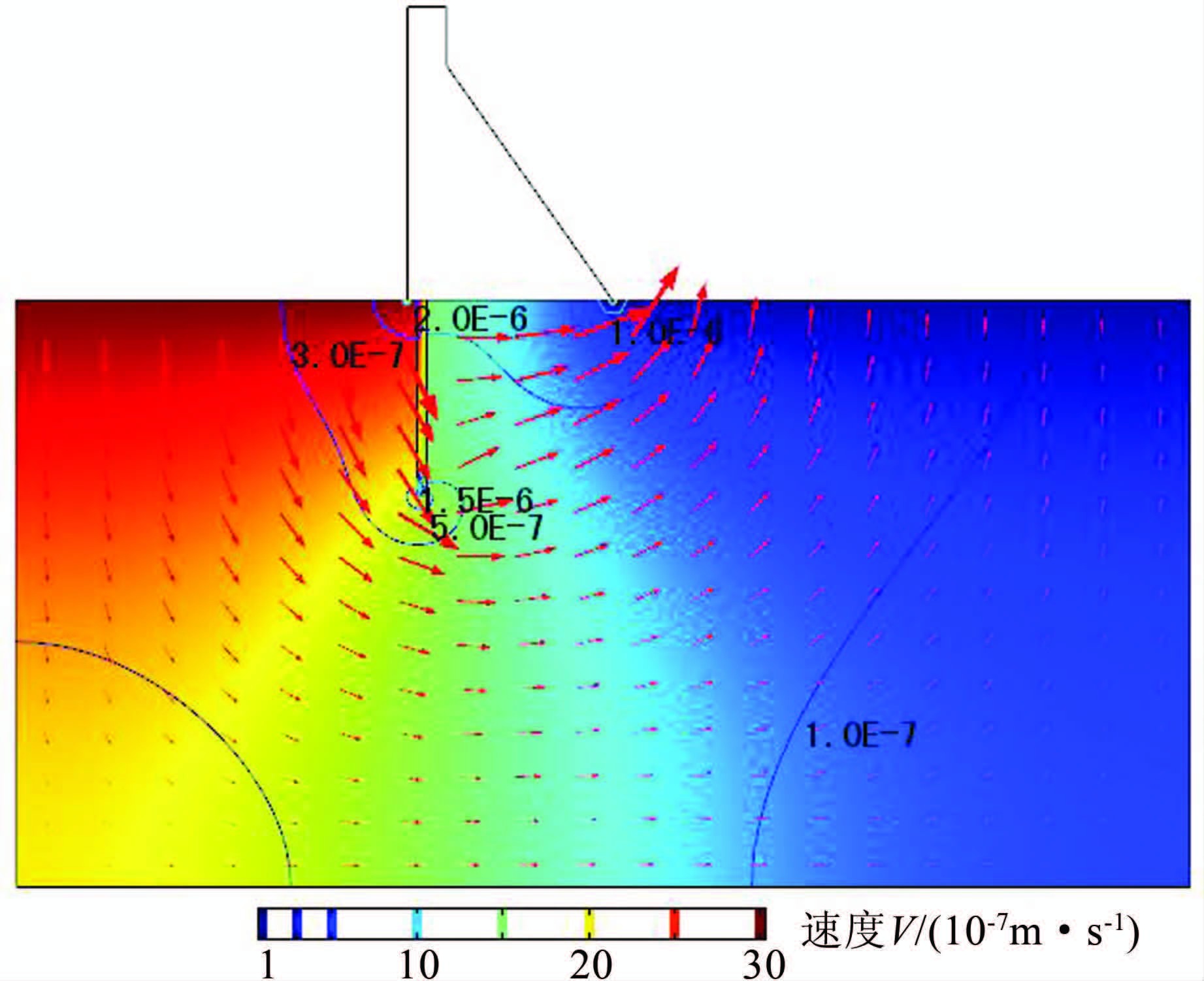
| 图 4 25年时计算区域流速绝对值分布图及流速矢量图 Figure 4 Distribution of velocity’s absolute velocities and velocity vectogram after 25 years |
|
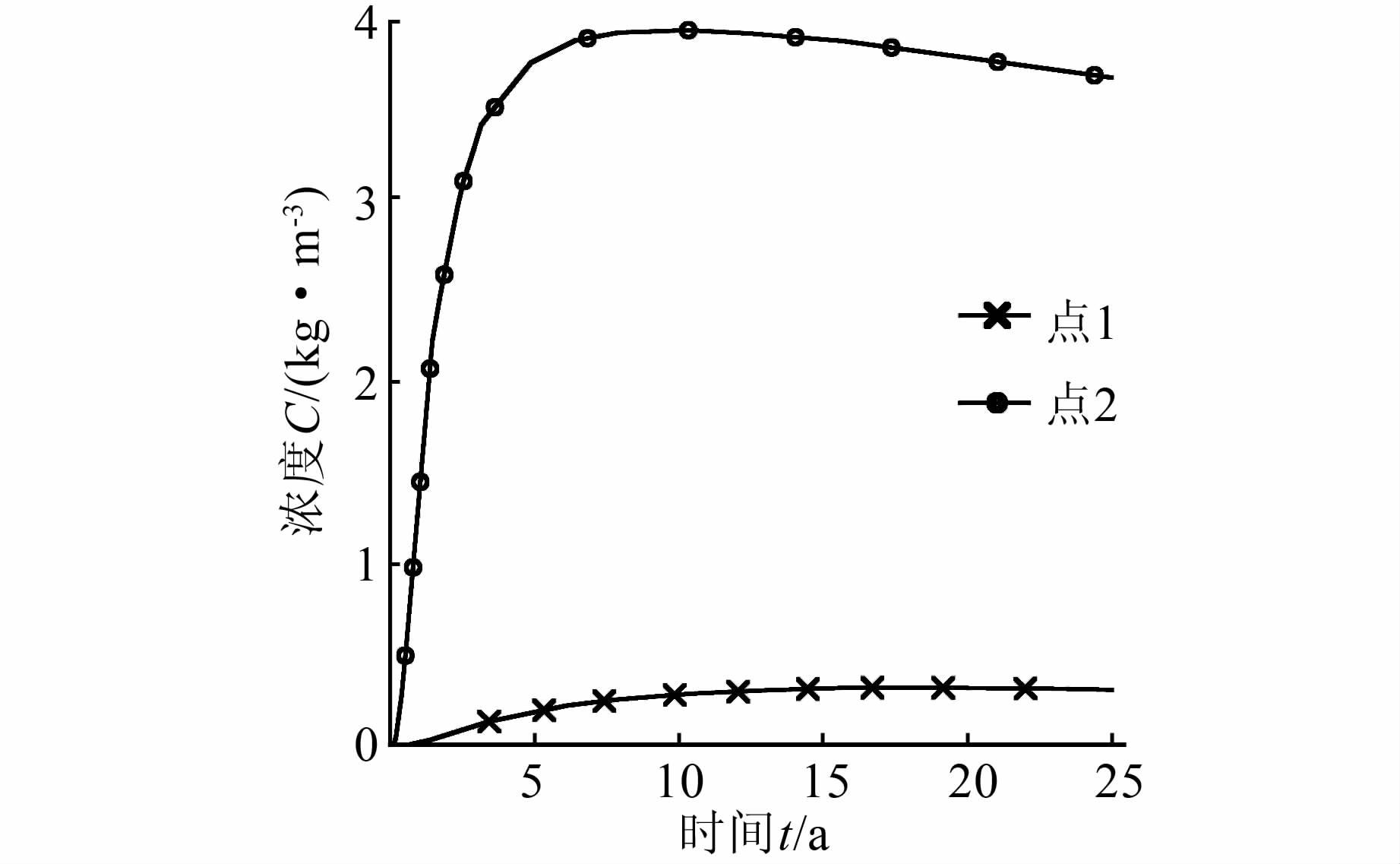
| 图 5 帷幕下方不同点处钙离子浓度变化 Figure 5 Calciumion concentration profile at various points under curtain |
|
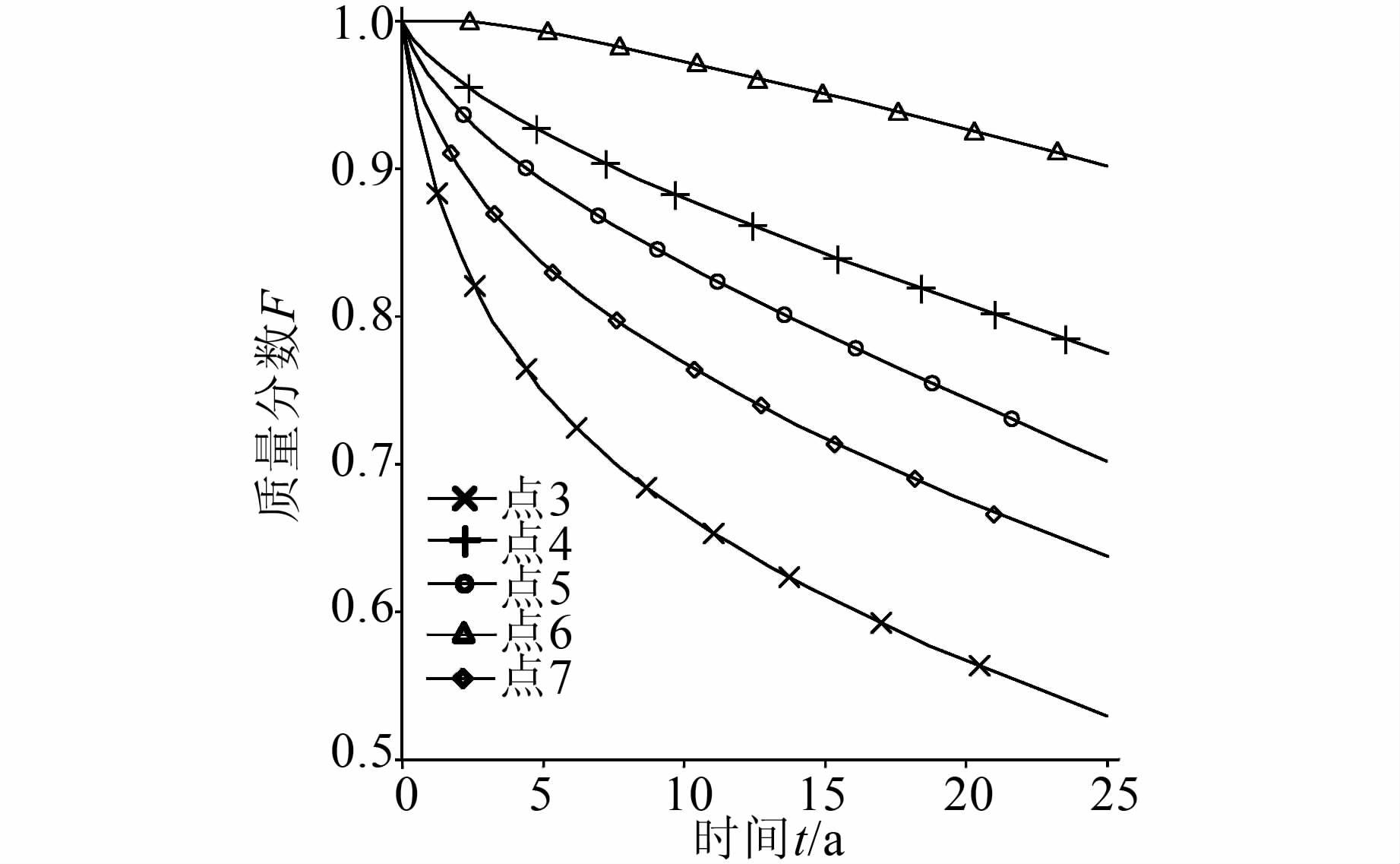
| 图 6 帷幕体不同点处氢氧化钙质量分数变化 Figure 6 Mass fraction profile of calcium hydroxide at various points of curtain |
|
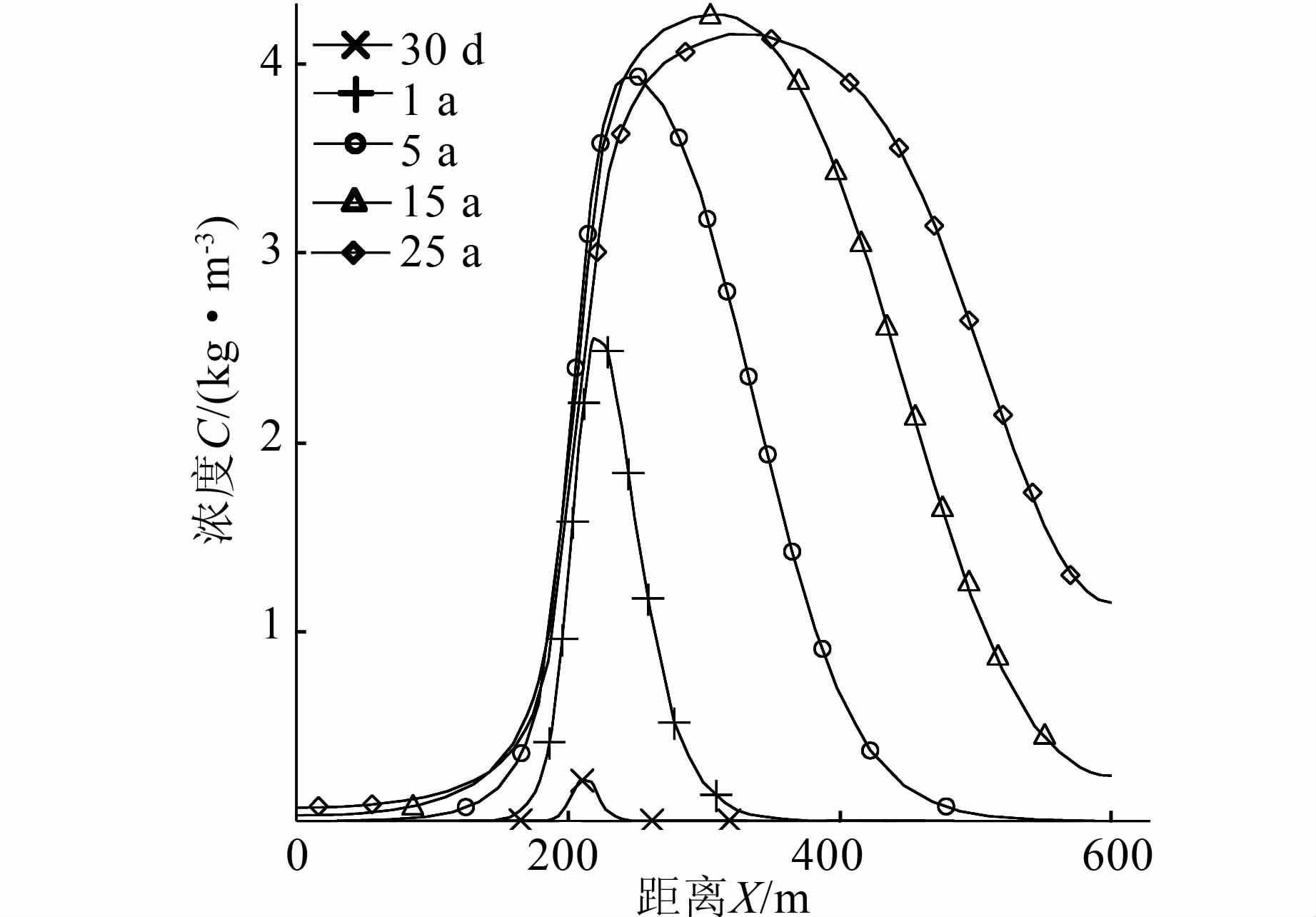
| 图 7 不同模拟时间后距帷幕底部50 m处顺河方向钙离子浓度分布图 Figure 7 Distribution of calciumion concentration with a distance of 50 m from the bottom of curtain after 30days,1,5,15 and 25 years |
|
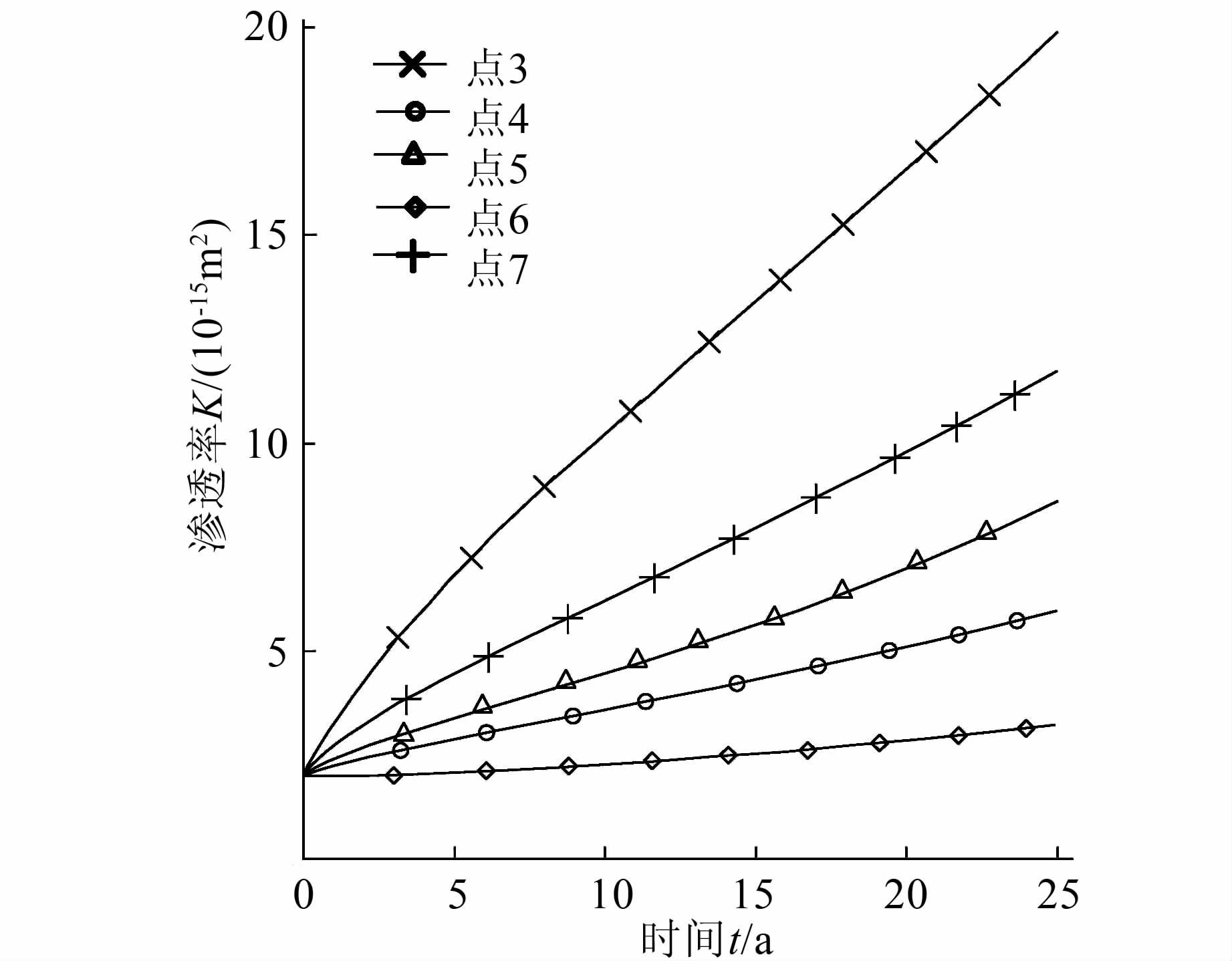
| 图 8 帷幕体不同点处渗透率变化 Figure 8 Permeability profile at various points of curtain |
从模拟计算结果可以看出以下几点:
1) 由图 3可知,溶解重点发生在帷幕底端,帷幕下游坝基ABCD区域钙离子浓度较高,在4 000~9 000 g/m3之间.图 5显示了帷幕下游处钙离子浓度的变化主要由对流引起,上游处钙离子浓度的变化主要由扩散引起,且对流作用强于扩散作用.实际地质环境中,在坝基钙离子浓度较高区域易形成沉淀带,从而堵塞排水孔,增大坝基扬压力,这一现象应予以重视.
2) 由于在帷幕底部及坝踵、坝趾处渗透坡降较大,从图 4可以看出,在这几处的地下水渗流速度较大,裂隙水压力在帷幕上游侧及帷幕底部较大.
3) 由图 6中帷幕不同点处氢氧化钙质量分数变化情况可以看出,帷幕体从外表面开始逐渐溶解,且不同部位的溶解程度不同,其中底部和上部的溶解量相对中部较大,且帷幕底部的溶蚀量要大于其顶部的溶蚀量,是帷幕体防渗能力衰减最快的区域;靠近坝基上游侧的帷幕溶蚀量要高于下游侧.这是由于帷幕孔隙压力随帷幕深度增加而逐渐增大,在帷幕底部、顶部,渗透水流速度较大,但帷幕底部渗流速度、渗透压力大于帷幕顶部;帷幕上游侧孔隙水压力大于下游侧.
4) 由图 6可知,坝基防渗帷幕中的钙类水化物(氢氧化钙)在大坝整个模拟运行期间始终处于溶解状态,并随着运行时间的增加,溶解量越来越大,达到 25 a时固体氢氧化钙质量分数最多减小至0.53,最大溶解量可达0.47;图 8渗透率变化曲线显示,运行25 a时,帷幕溶蚀量最大处的渗透率增大至2×10-14m2,是帷幕初始渗透率2×10-15m2的10倍(坝基渗透率取为1×10-13m2),说明帷幕体微细观结构发生了改变,抗渗性能衰减.
5) 为了进一步了解空间上模拟区域的钙离子浓度分布情况,研究了距帷幕体底端50 m处的浓度变化.图 7曲线显示了不同时段的钙离子浓度沿着顺河流方向先增大后减小,且在帷幕附近达到最大值,随着模拟时间的增长,帷幕逐渐溶解,钙离子浓度逐渐增大,且由于迁移扩散的作用钙浓度最大值位置有向下游偏移的趋势.
3 结论1) 本文采用数值方法研究帷幕体防渗性能衰减的动态过程,建立多物理场全耦合的模型,分析坝基帷幕在渗流场、化学场及溶质运移场多场耦合作用下,帷幕体在渗透力、溶解-沉淀和迁移-扩散过程中的侵蚀破坏规律.在地下水流长期的侵蚀、溶解作用下,帷幕逐渐地发生溶解侵蚀,渗透系数逐渐增大,随着时间的推移,帷幕防渗性能逐渐衰减,当衰减至与周围岩体渗透系数相近时,认为灌浆的抗渗作用消失,所经历的时间即作为帷幕的耐久性评价.
2) 耦合模型可以较真实地描述坝基物理化学特性的变化过程,由模拟结果获得了坝基不同部位、不同时刻帷幕-水之间的溶解侵蚀状况,由此可以定量判断帷幕渗透性和孔隙率的变化程度、防渗帷幕溶蚀失效的程度,推测帷幕正常工作的年限,坝基内可能发生沉淀地带及对坝基排水孔的影响.
3) 耦合模型输入所需的水文地质参数是保证模拟结果真实性的前提,帷幕体的渗透系数随固相溶质质量分数的变化关系中经验系数的确定尚需模型试验及现场监测资料的支撑,有待进一步完善.此外,耦合模型没有考虑具体的离子之间的化学反应,且坝基区岩体与地下水的反应也未计入模拟.
| [1] |
陈胜宏, 何真. 混凝土坝服役寿命仿真分析的研究现状与展望[J].
武汉大学学报(工学版), 2011, 44(3): 273–280.
Chen Shenghong, He Zhen. Status quo and prospect for simulation analysis of service life for concrete dam[J]. Engineering Journal of Wuhan University, 2011, 44(3): 273–280. |
| [2] |
郑西来, 刘洪俊. 山东氧化铝场地下水系统的环境地球化学反应模型[J].
地球化学, 1990(3): 270–276.
Zheng Xilai, Liu Hongjun. The environmental geochemical reaction model for the ground-water system in the dross dumping ground of Shandong alumina factory[J]. Geochimica, 1990(3): 270–276. |
| [3] |
陈芸, 高明. 水-岩作用模型及其在水-玄武岩反应中研究中的应用[J].
南京大学学报, 1994(1): 118–123.
Chen Yun, Gao Ming. A model for water-rock reactions and its application for the study of the mechanism of water-basalt reactions[J]. Journal of Nanjing University, 1994(1): 118–123. |
| [4] |
曾溅辉. 地下水地球化学模拟[J].
地质评论, 1993(6): 490–495.
Zeng Jianhui. Geochemical modeling of ground water[J]. Geological Review, 1993(6): 490–495. |
| [5] |
王锦国, 周志芳, 汤瑞凉. 水-岩作用的线性规划模型与应用研究——以溪洛渡水电工程为例[J].
水科学进展, 1999(2): 118–122.
Wang Jinguo, Zhou Zhifang, Tang Ruiliang. Research of linear programming model for water-rock reaction and its application hydroelectric project of Xiluodu as an example[J]. Advance in Water Science, 1999(2): 118–122. |
| [6] | 童海涛, 宋汉周. 水-岩作用系统的随机水文地球化学模拟[J]. 水科学进展, 2004, 15(2): 211–215. |
| [7] |
阿里木·吐尔逊.坝基老化岩-水-化学作用数值模拟研究[D]. 南京: 河海大学, 2005.
Alim Tursun. Numeric hydro-geo-chemical modeling of dam foundation aging[D].Nanjing: Hohai University, 2005. |
| [8] | Kulik D A. Thermodynamic concepts in modeling sorption at the mineral-water interface[J]. Rev. Mineral. Geochem, 2009, 70: 125–180. DOI:10.2138/rmg.2009.70.4 |
| [9] | Kolditz O, Bauer S, Bilke L, et al. OpenGeoSys: an open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media[J]. Environmental Earth Sciences, 2012, 67(2): 589–599. DOI:10.1007/s12665-012-1546-x |
| [10] | Multiphysics C. COMSOL Multiphysics User Guide (Version 4.3 a)[A]. COMSOL, AB, 2012. |
| [11] | Bear J. Dynamics of Fluids in Porous Media[M]. 2013. |
| [12] |
仵彦卿.
多孔介质渗流与污染物迁移数学模型[M]. 北京: 科学出版社, 2012.
Wu Yanqing. Mathematical Model of Flow and Contaminant Transport in Porous Media[M]. Beijing: Science Press, 2012. |
| [13] | Fesch C, Simon W, Haderlein S B, et al. Nonlinear sorption and nonequilibrium solute transport in aggregated porous media: Experiments, process identification and modeling[J]. Journal of Contaminant Hydrology, 1998, 31(3): 373–407. |
| [14] |
徐轶, 徐青. 基于COMSOL Multiphysics的渗流有限元分析[J].
武汉大学学报(工学版), 2014, 47(2): 165–170.
Xu Yi, Xu Qing. Finite element analysis of seepage based on COMSOL Multiphysics[J]. Engineering Journal of Wuhan University, 2014, 47(2): 165–170. |
| [15] |
喻建清, 徐青, 陈胜宏, 等. 复杂地质条件下渗流控制关键技术研究与应用[J].
水利学报, 2011, 47(2): 81–86.
Yu Jianqing, Xu Qing, Chen Shenghong, et al. Study and application of seepage control measures for complicated geological structure[J]. Journal of Hydraulic Engineering, 2011, 47(2): 81–86. |
| [16] | Louis C, Muller L. Rock hydraulics[C]// Rock Mechanics. Vienna: Springer-Verlag. 1974:299-387. |
 2016, Vol. 49
2016, Vol. 49




