文章信息
- 李彪, 徐礼华, 谷雨珊, 贾丽莉
- LI Biao, XU Lihua, GU Yushan, JIA Lili
- HCSA膨胀剂掺量对高强自密实混凝土性能影响研究
- Investigation on influence of HCSA expansive agent dosage on performance of high-strength self-compacting concrete
- 武汉大学学报 (工学版), 2017, 50(1): 90-96
- Engineering Journal of Wuhan University, 2017, 50(1): 90-96
- http://dx.doi.org/10.14188/j.1671-8844.2017-01-013
-
文章历史
- 收稿日期: 2016-05-23
2. 中建商品混凝土有限公司,湖北武汉 430072
2. China Construction Commercial Concrete Co., Ltd., Wuhan 430072, China
随着高强自密实混凝土的发展与应用,钢管核心混凝土质量难以保证,易出现脱空、蜂窝、麻面等工程问题[1-2]。如何解决这一问题,适应建筑业快速发展的需要,保证高层建筑钢管混凝土设计与施工质量成为亟待解决的问题。已有研究[3-4]表明,在混凝土中掺加膨胀剂配制自应力混凝土是解决这一难题的有效途径之一。
目前,国内外研究者分别从不同角度对自应力混凝土性能进行了研究,对进一步深入探讨自应力混凝土的作用机理和大力推动其工程应用起到了积极的促进作用。文献[5-6]利用静力平衡条件建立混凝土配筋率与限制膨胀率之间的关系,研究自应力混凝土膨胀规律。文献[3, 7-10]将混凝土自应力值与自由膨胀率和限制膨胀率联系起来,建立关系式,寻找能够满足给定条件的最佳膨胀剂掺量。文献[11-14]基于不同原理提出混凝土膨胀模型,得出混凝土膨胀变形随龄期的变化关系,为工程设计提供参考。但与此同时,值得注意的是,上述研究建立的混凝土膨胀模型较为复杂,物理意义并不十分明确,且研究的对象主要是采用自应力水泥、UEA或MgO系列膨胀剂配制的低强度混凝土,普遍存在膨胀速率慢、膨胀能低、膨胀稳定期长等工程问题,这与当前广泛使用的混凝土所具有早期强度高、脆性大等特性并不协调,因此在一定程度上限制了上述研究成果在工程实践中的进一步应用。
为解决这一问题,中国建筑材料科学研究院近年研制了一种爆鸣系列的HCSA混凝土膨胀剂,其膨胀能高、膨胀快、膨胀性能稳定,与减水剂、水泥等具有良好适应性,适用于配制高性能混凝土。赵顺增等[15-17]对该膨胀剂的性能、膨胀剂与化学外加剂及水泥适应性和膨胀剂对混凝土微结构的影响等进行了一系列研究,取得了相应研究成果,但对掺入HCSA膨胀剂的高强自密实混凝土膨胀模型及自应力值计算等内容则没有涉及,国内外对该领域的研究目前也基本处于空白。鉴于此,本文在自密实基体混凝土配合比的基础上,通过5种HCSA膨胀剂掺量的高强自密实混凝土性能试验,研究膨胀剂掺量对混凝土性能的影响,并基于试验结果,提出适用于掺HCSA膨胀剂的钢管约束条件下混凝土膨胀模型及自应力值计算公式。
1 试验设计 1.1 原材料及配合比水泥采用亚东P.O42.5普通硅酸盐水泥[18],其表观密度为3 010 kg/m3;矿物掺合料采用麻城I级粉煤灰、S95矿粉和微珠;细集料采用天然河砂,细度模数为2.7,表观密度为2 660 kg/m3;粗骨料采用级配良好的碎石,粒径为5~20 mm,表观密度为2 760 kg /m3。拌合水为洁净自来水。外加剂为聚羧酸高效减水剂。
在前期自密实混凝土配合比设计及膨胀剂砂浆试验结果的基础上,根据JGJ/T 178-2009《补偿收缩混凝土应用技术规程》[19]及GB 23439-2009《混凝土膨胀剂》[20]中关于单方混凝土膨胀剂用量的规定,本文试验通过在C60自密实混凝土中掺入质量分数(膨胀剂质量与胶凝材料总质量之比)为0%、6%、8%、10%、12%的HCSA膨胀剂,配制具有膨胀性能的自密实自应力高强混凝土(试件编号依次分别为H0、H1、H2、H3、H4),研究膨胀剂掺量对高强自密实混凝土性能的影响,设计试验配合比列于表 1。
| 编号 | 材料用量/(kg/m3) | 水胶比 | ||||||||
| 水泥 | 粉煤灰 | 矿粉 | 微珠 | 膨胀剂 | 河砂 | 碎石 | 水 | 减水剂 | ||
| H0 | 308 | 112 | 84 | 56 | — | 745 | 949 | 151 | 5.6 | 0.27 |
| H1 | 274 | 112 | 84 | 56 | 34 | 745 | 949 | 151 | 5.6 | 0.27 |
| H2 | 263 | 112 | 84 | 56 | 45 | 745 | 949 | 151 | 5.6 | 0.27 |
| H3 | 252 | 112 | 84 | 56 | 56 | 745 | 949 | 151 | 5.6 | 0.27 |
| H4 | 241 | 112 | 84 | 56 | 67 | 745 | 949 | 151 | 5.6 | 0.27 |
混凝土采用NJHS-60型双卧轴混凝土搅拌机拌和,考虑到掺入膨胀剂和减水剂等外加剂,适当延长了搅拌时间。混凝土抗压强度试验采用同批次每组9个边长为150 mm的标准立方体试块,标准养护条件下养护,测试其3、7及28 d立方体抗压强度。
混凝土自由膨胀变形测试试件的选择参照GB/T 50028-2009《普通混凝土长期性能和耐久性试验方法标准》[22]及GB 23439-2009《混凝土膨胀剂》规定,选择100 m x100 mm x515 mm棱柱体模具成型,并预先在试件中安装埋入式标靶和金属测头。混凝土浇筑时,预先在模具内铺设一层塑料薄膜,以减少水分的散失。在混凝土初凝后,用塑料薄膜和凡士林进行密封,终凝后拆模并进行测试。
混凝土自应力值测试在钢管约束条件下进行,试验设计3组12根直径为165 mm,厚度为4 mm,长度为600 mm的钢管。钢管底部预先焊有厚度为20 mm、边长为200 mm的方形钢板,以保证钢管直立稳定。试验中所用混凝土编号分别为H2、H3、H4(见表 1),钢管混凝土柱编号依次分别为G4-8、G4-10、G4-12。
1.3 测试方法依据JGJ/T 283-2012《自密实混凝土应用技术规程》,同时兼顾实用性和可操作性,混凝土拌和物工作性测试采用坍落度和扩展度2种方法。按GB/T 50081-2002《普通混凝土力学性能试验方法》进行立方体抗压强度测试。混凝土自由膨胀变形采用非接触收缩变形测试仪进行测试,如图 1。

|
| 图 1 自由膨胀率测试方法 Figure 1 Free expansion rate test method |
混凝土搅拌完成后迅速浇筑于钢管内,待其初凝后,用环氧树脂将钢管上端密封,避免与外界进行湿度交换。养护条件为自然养护。
试验采用电阻应变片测量钢管外壁环向应变和轴向应变,通过理论分析和计算得到混凝土的自应力值,具体分析过程如下[7]:
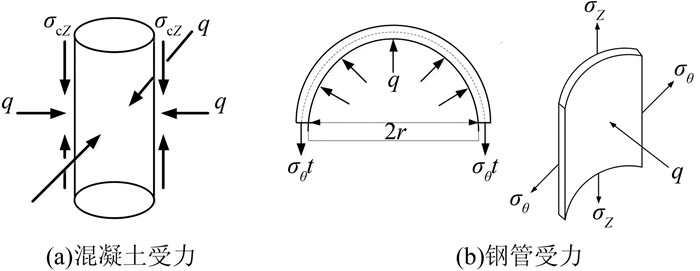
在混凝土产生一定膨胀变形的基础上,钢管混凝土中钢管及混凝土的受力分析如图 2。
|
| 图 2 钢管与混凝土受力示意图 Figure 2 Force diagram of steel tube and concrete |
由广义胡克定律可知:
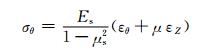 (1)
(1)
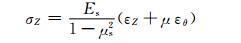 (2)
(2)
其中:σθ、σZ分别是钢管环向和轴向应力;εθ、εZ分别为实测环向和轴向应变;Es、μs分别是钢管的弹性模量和泊松比.
根据图 2所示,有:2σθ·t=2rq,解得核心混凝土径向压应力q为
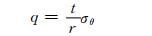 (3)
(3)
式中:r为钢管内半径;t为钢管壁厚.
根据轴向平衡条件As·σZ=Ac·σcZ,解得核心混凝土轴向压应力σcZ为
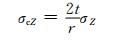 (4)
(4)
据以上分析,本文试验在钢管外壁垂直高度中部处焊贴轴向和环向应变片.具体测点布置如图 3.
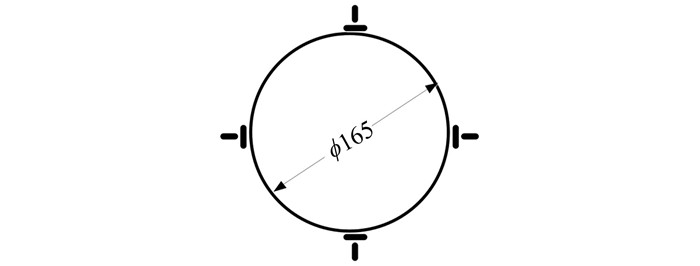
|
| 图 3 应变片测点布置平面图 Figure 3 Strain gauge measuring point layout plan |
不同膨胀剂掺量条件下,自密实自应力混凝土工作性及强度试验结果列于表 2.
| 编号 | 塌落度/扩展度 | R3/MPa | R7/MPa | R28/MPa |
| H0 | 260/575 | 39.6 | 55.0 | 71.2 |
| H1 | 255/570 | 40.4 | 54.1 | 68.4 |
| H2 | 260/590 | 38.5 | 49.2 | 65.6 |
| H3 | 260/580 | 37.6 | 45.0 | 65.2 |
| H4 | 265/580 | 28.8 | 42.6 | 63.0 |
| 注:R3、R7、R28分别为混凝土3、7、28 d立方体抗压强度. | ||||
由表 2可知,掺入膨胀剂的混凝土28 d立方体抗压强度均小于普通自密实混凝土组的立方体抗压强度;当膨胀剂掺量为6%时,混凝土早期抗压强度变化不大,H1组3 d抗压强度稍大于H0组的抗压强度.其原因在于:掺入膨胀剂使得混凝土内部产生一定膨胀损伤,混凝土28 d抗压强度下降;而当膨胀剂掺量较小时,膨胀剂水化产生少量的钙矾石可有效弥补混凝土内部因水化消耗而引起的孔隙,补偿混凝土的自收缩,有助于混凝土早期强度的提高.另外,当膨胀剂掺量大于8%时,混凝土早龄期强度发展缓慢,但后期强度发展较快,主要由于硬化后期膨胀剂水化较为完全,膨胀稳定,水泥石基体增大,强度快速发展;而由于此时膨胀剂掺量过多,膨胀变形过大,混凝土内部疏松,且其表面易产生裂纹,致使28 d抗压强度明显低于H0、H1、H2组的抗压强度.
2.2 自由膨胀率掺入膨胀剂的自密实混凝土自由膨胀变形测试在恒温20 ℃条件下进行,以避免外界温度变化对试验结果精度的影响,自由膨胀率随龄期变化试验结果绘于图 4.
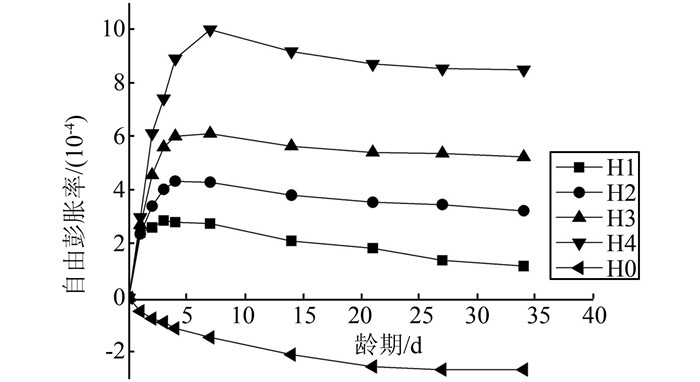
|
| 图 4 混凝土自由膨胀率随龄期变化曲线 Figure 4 Free expansion rate of concrete relations with age |
由图 4可知,随着膨胀剂掺量增加,混凝土自由膨胀率显著增大;混凝土的膨胀变形主要集中在水泥水化前期,大致7 d后,自由膨胀率达到峰值,因为膨胀剂的水化主要集中在混凝土硬化早期,此时混凝土中水分较多,水泥水化较为充分,自身产生的收缩不明显,混凝土的膨胀变形中扣除自收缩变形后,达到最大.随着龄期增加,混凝土自由膨胀率有一定程度的减小,主要因为混凝土中膨胀组分基本已水化完成,膨胀稳定,但混凝土毛细孔中的水分被水泥水化消耗,其内部湿度下降,自收缩严重,另外此阶段也有较小程度的徐变.当龄期达21 d以后,水泥水化已渐渐完成,收缩变形稳定,因此总的自由膨胀变形也趋于稳定.从图中可知,当膨胀剂掺量为6%时,混凝土在28 d时,膨胀变形几乎全被混凝土的自收缩抵消,因此,自应力混凝土中膨胀剂掺量应大于6%,才能产生一定程度的膨胀变形,在约束条件下产生初始自应力;当膨胀剂掺量为12%时,自由膨胀率可达9.96×10-4,混凝土膨胀性能较好.
2.3 钢管约束条件下混凝土自应力值将钢管环向及轴向应变测试值代入式 (3) 及式 (4),计算出在钢管约束条件下各龄期混凝土的自应力值,结果绘于图 5.
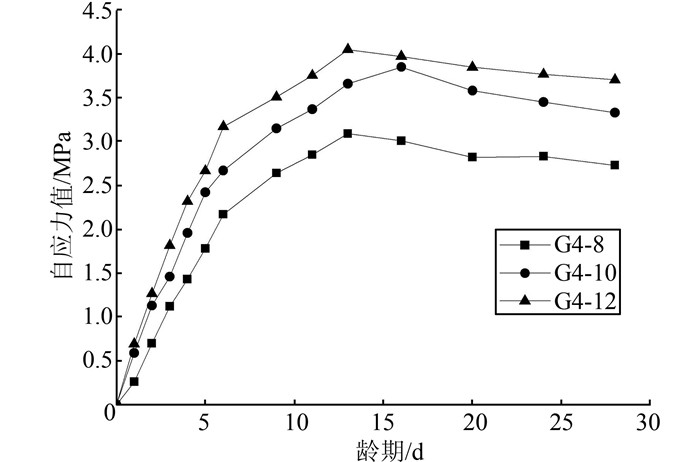
|
| 图 5 混凝土自应力值随龄期变化曲线 Figure 5 Self-stress value of concrete relations with age |
由图 5可知,在相同钢管约束条件下,不同膨胀剂掺量混凝土自应力值随龄期变化规律与自由膨胀率变化曲线类似,且随着膨胀剂掺量增加,混凝土自应力值逐渐增大.当膨胀剂掺量在8%~12%范围时,自应力值可达3.2~3.7 MPa.另外,7 d时混凝土自应力值已超过膨胀稳定时的85%,由此可再次证明膨胀剂水化主要集中在混凝土硬化早龄期.
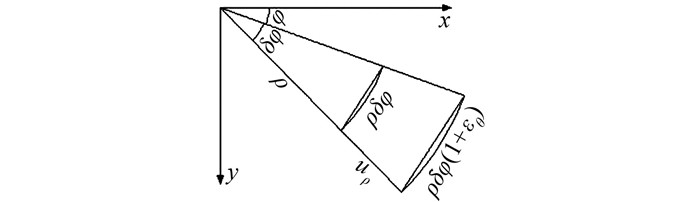
3 混凝土膨胀模型及计算 3.1 限制膨胀率计算利用弹性力学平面应变模型计算混凝土限制膨胀率.为简化计算,本文假设钢管与混凝土之间粘结良好,可共同变形;钢管与混凝土均在弹性范围内工作,计算简图如图 6.
|
| 图 6 平面应变问题计算简图 Figure 6 Plane strain problem calculation diagram |
由几何条件可得:
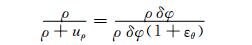 (5)
(5)
式中:uρ为钢管约束条件下混凝土径向位移.
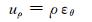 (6)
(6)
自应力混凝土限制膨胀率为混凝土膨胀后体积增量与初始体积之比:
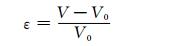 (7)
(7)
式中:V=π(ρ+uρ)2(1+εZ);V0=πρ2×1.化简得钢管约束条件下混凝土限制膨胀率为
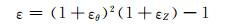 (8)
(8)
将试验测得的钢管表面环向和轴向应变代入式 (8) 中,计算混凝土的限制膨胀率,结果绘于图 7.
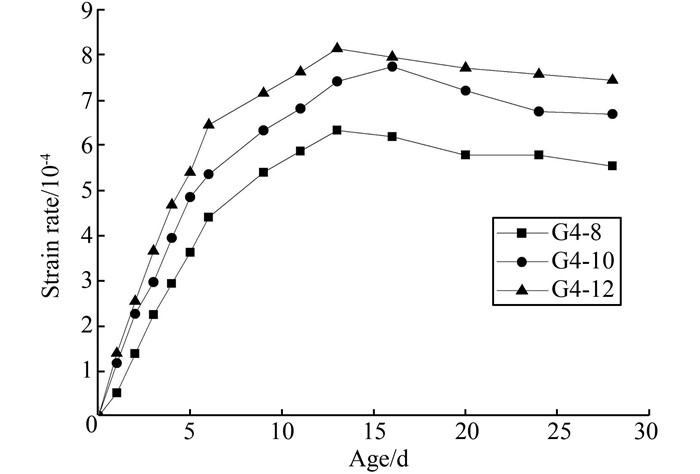
|
| 图 7 混凝土限制膨胀率 Figure 7 Confined expansion rate of concrete |
影响膨胀混凝土自应力值的因素有膨胀剂掺量、钢管约束条件、龄期、徐变、水胶比、温度等.对于本文试验,自应力值q远小于0.5fc(fc为混凝土立方体抗压强度实测值),混凝土徐变值很小,且混凝土养护及应变测试时间较短,徐变的影响可以忽略;膨胀剂水化主要集中在早龄期 (1~7 d),水化需水量充足,水化较为完全,且水胶比对于混凝土自应力值的影响不大,因此,水胶比对自应力值的影响可忽略不计;本文测试均在室内恒温条件下进行,环境温度引起的钢管与混凝土的相对膨胀率可忽略不计.因此,本文试验只考虑膨胀剂掺量、钢管约束条件和龄期3个因素水平对自应力值的影响,其因素表达式为
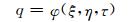 (9)
(9)
其中:ξ为钢管约束条件,与钢管本身的材料性质及尺寸有关;η为膨胀剂掺量,为膨胀剂与胶凝材料质量比;τ为龄期.
单向限制条件下有效自由膨胀变形和实测的限制膨胀变形随龄期的变化规律一般呈e指数关系,这一点被大量试验所证实[8].曲线的典型表达式为
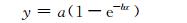 (10)
(10)
式中:a为描述不同膨胀剂掺量对终值膨胀率影响的参数;b为反映自应力混凝土膨胀率随龄期增长的模型参数.采用式 (10) 对图 7中混凝土限制膨胀率进行拟合,得到基本参数值.对比拟合结果,可见b值相差不大,忽略因试验中环境、测量等因素引起的误差,本文认为取其统计平均值0.2是合理的,将其代入式 (10) 再次拟合,可得基本参数a(修正值),结果列于表 3.
| 参数 | G4-8 | G4-10 | G4-12 |
| a/10-4 | 6.183 07 | 7.330 82 | 7.944 76 |
| b | 0.184 66 | 0.207 78 | 0.231 76 |
| a(修正值)/10-4 | 6.06 | 7.39 | 8.21 |
对表 3中参数a(修正值) 进行二次多项式拟合,可得:
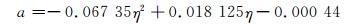 (11)
(11)
式中:η为膨胀剂掺量.当η=0时,a=-0.000 44×10-4,此时混凝土将发生体积收缩变形,因此是合理的.
3.3 自应力值计算弹性力学轴对称平面问题极坐标解答[22]:
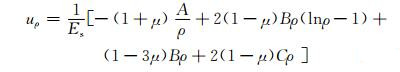 (12)
(12)
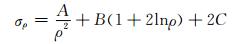 (13)
(13)
对式 (12),由位移单值连续条件可得:B=0.
对本文模型,(σρ)ρ=r=-q,(σρ)ρ=R=0,代入式 (13),可得:
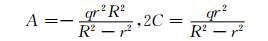 (14)
(14)
式中:q为混凝土自应力值;R、r分别为钢管外半径和内半径.
将式 (14) 结果代入式 (12) 中,可解得混凝土自应力值计算公式为
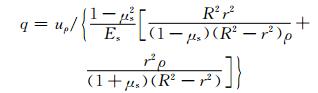 (15)
(15)
为验算式 (15) 的可靠性,将各参数试验值代入其中,计算出不同膨胀剂掺量条件下的混凝土自应力值,将其与试验值列于表 4.对表 4中数据进行统计分析可知,自应力值计算值与试验值之比为0.889 7,标准方差为0.005 7,吻合结果良好.
| 试件编号 | qt/MPa | qc/MPa | qc/qt |
| G4-8 | 2.65 | 2.37 | 0.894 |
| G4-10 | 3.33 | 2.95 | 0.886 |
| G4-12 | 3.70 | 3.29 | 0.889 |
通过掺入HCSA膨胀剂的高强自密实混凝土性能试验,深入分析了膨胀剂掺量对混凝土工作性、强度和膨胀性能的影响,并在钢管约束条件下进行混凝土自应力值测试,提出混凝土限制膨胀模型及自应力值计算公式.主要结论如下:
1) HCSA膨胀剂掺量对高强自密实混凝土工作性影响不大;当膨胀剂掺量大于6%时,随着膨胀剂掺量增加,混凝土28 d强度逐渐下降;当掺量为12%时,混凝土28 d立方体抗压强度为63 MPa,能够满足设计要求.
2) 当HCSA膨胀剂掺量在6%~12%范围内,混凝土膨胀变形随着膨胀剂掺量的增加逐渐增大;膨胀剂水化主要集中在混凝土硬化早龄期,自由膨胀变形于12~15 d范围内达到稳定.
3) 钢管约束条件下混凝土自应力值随膨胀剂掺量增加而逐渐增大;当膨胀剂掺量为8%~12%时,混凝土自应力值达3.2~3.7 MPa.
4) 基于弹性力学轴对称平面问题极坐标解答,提出钢管约束条件下混凝土膨胀率计算模型及自应力值计算公式,计算值与试验结果拟合良好,可供工程设计参考.
| [1] | Xu Lei, Huang Chengkui, Liu Yi. Expansive performance of self-stressing and self-compacting concrete confined with steel tube[J]. Journal of Wuhan University of Technology-Mater. Sci. Ed, 2007, 22(3): 341–342. |
| [2] | Albert K H Kwan, Wilson W S Fung. Shrinkage of high-strength concrete and high-flowability concrete[J]. HKIE Transactions, 2013, 17(3): 25–33. |
| [3] |
胡曙光, 丁庆军.
钢管混凝土[M]. 北京: 人民交通出版社, 2007: 47-84.
Hu Shuguang, Ding Qingjun. Concrete Filled Steel Tube[M]. Beijing: China Communication Press, 2007: 47-84. |
| [4] |
朱家荣.自应力钢管混凝土拱桥施工技术研究[D].重庆:重庆交通大学, 2010:17-30.
Zhu Jiarong. Research of construction about self-stress concrete-filled steel tube (SCFST) arch bridge[D]. Chongqing: Chongqing Jiaotong University, 2010: 17-30. |
| [5] | Chang Xu, Huang Chengkui, Zhang peng. Expansive behaviors of self-stressing concrete under different restraining conditions[J]. Journal of Wuhan University of Technology-Mater. Sci. Ed, 2011, 26(4): 783–785. |
| [6] | Sheikh Shamim A, O` Neill. Long-term behavior of expansive concrete drilled shafts[J]. Canadian Journal of Civil Engineering, 1986, 13(2): 213–217. |
| [7] |
尚作庆.钢管自应力自密实混凝土柱力学性能研究[D].大连:大连理工大学, 2007:35-46.
Shang Zuoqing. Experimental research on mechanical behavior of self-stressing and self-compacting concrete filled steel tube columns[D]. Dalian: Dalian University of Technology, 2007:35-46. |
| [8] |
徐磊.钢管自应力免振混凝土轴压柱设计理论研究[D].大连:大连理工大学, 2005:26-36.
Xu Lei. Research on the design theory for self-stressing and self-compacting concrete filled steel tube column under axial load[D]. Dalian: Dalian University of Technology, 2005: 26-36. |
| [9] |
赵洋.自应力钢管混凝土拱桥脱空与自应力检测技术研究[D].重庆:重庆交通大学, 2010: 63-69.
Zhao Yang. Study of cavity and self-stressing detection technology for self-stressing concrete filled steel tubular arch bridge[D].Chongqing: Chongqing Jiaotong University, 2010: 63-69. |
| [10] |
黄雅宁.自应力钢管混凝土设计理论研究[D].重庆:重庆交通大学, 2010: 23-30.
Huang Yaning. Study on design theory for self-stressing concrete filled steel tube[D]. Chongqing: Chongqing Jiaotong University, 2010: 23-30. |
| [11] |
朱伯芳. 微膨胀混凝土自生体积变形的增量型计算模型[J].
水力发电, 2003, 29(2): 20–23.
Zhu Baifang. Incremental type of computing model for the volume expansion of concrete with gentle volume expansion[J]. Water Power, 2003, 29(2): 20–23. |
| [12] |
杜宇, 蒋林华. 膨胀混凝土延迟膨胀损伤模型[J].
水利水电科技进展, 2010, 30(4): 4–7.
Du Yu, Jiang Linhua. Damage model for delay-expansion of expansive concrete[J]. Advances in Science and Technology of Water Resources, 2010, 30(4): 4–7. |
| [13] |
许补, 朱岳明. 基于水化度的MgO混凝土自生体积变形计算模型[J].
水利水电技术, 2008, 39(2): 22–25.
Xu Bu, Zhu Yueming. Computing model for autogenous volume deformation of MgO concrete based on degree of hydration[J]. Water Resources and Hydropower Engineering, 2008, 39(2): 22–25. |
| [14] |
罗冰, 沈成武, 郑舟军. 钢管混凝土膨胀率试验与测定分析[J].
交通科技, 2005(6): 86–88.
Luo Bing, Shen Chengwu, Zheng Zhoujun. Experiment and determining of dilate rate of micro-expansion concrete filled steel tube[J]. Transportation Science & Technology, 2005(6): 86–88. |
| [15] |
赵顺增, 刘立. HCSA高性能混凝土膨胀剂性能研究[J].
膨胀剂与膨胀混凝土, 2005(3): 3–8.
Zhao Shunzeng, Liu Li. Research on the performance of HCSA high performance concrete expansive agent[J]. Expansive Agent & Expansive Concrete, 2005(3): 3–8. |
| [16] |
赵顺增, 刘立. HCSA膨胀剂与化学外加剂、水泥的适应性研究[J].
膨胀剂与膨胀混凝土, 2006(2): 1–5.
Zhao Shunzeng, Liu Li. Study on the adaptation between HCSA expansive agent and chemical admixtures, cement[J]. Expansive Agent & Expansive Concrete, 2006(2): 1–5. |
| [17] |
赵顺增, 刘立. HCSA高性能混凝土膨胀剂及其应用[J].
膨胀剂与膨胀混凝土, 2012(4): 7–11.
Zhao Shunzeng, Liu Li. Performance and application of HCSA high performance concrete expansive agent[J]. Expansive Agent & Expansive Concrete, 2012(4): 7–11. |
| [18] | GB 175-2007通用硅酸盐水泥[S].北京:中国建筑工业出版社, 2007. GB 175-2007 General Purpose Portland Cement[S]. Beijing: China Building Industry Press, 2007. |
| [19] | JGJ/T 178-2009补偿收缩混凝土应用技术规程[S].北京:中国建筑工业出版社, 2009. JGJ/T 178-2009 Compensation Shrinkage Concrete Application Procedures[S]. Beijing: China Building Industry Press, 2009. |
| [20] | GB 23439-2009混凝土膨胀剂[S].北京:中国标准出版社, 2009. GB 23439-2009 Cement Expansive Material[S]. Beijing: China Building Industry Press, 2009. |
| [21] | GB/T 50082-2009普通混凝土长期力学性能试验方法标准[S].北京:中国建筑工业出版社, 2009. GB/T 50082-2009 Ordinary Concrete Mechanics Performance Test Method Standards for a Long Time[S]. Beijing: China Building Industry Press, 2009. |
| [22] |
徐芝纶.
弹性力学简明教程[M]. 第3版. 北京: 高等教育出版社, 2010.
Xu Zhilun. A Concise Course in Elasticity[M]. The third edition. Beijing: Higher Education Press, 2010. |
 2017, Vol. 50
2017, Vol. 50




