文章信息
- 刘树洁, 赖旭, 邹金, 王志伟
- LIU Shujie, LAI Xu, ZOU Jin, WANG Zhiwei
- 基于云模型理论的短期风速预测方法
- Cloud model based short-term wind speed prediction method
- 武汉大学学报 (工学版), 2017, 50(1): 69-74, 80
- Engineering Journal of Wuhan University, 2017, 50(1): 69-74, 80
- http://dx.doi.org/10.14188/j.1671-8844.2017-01-010
-
文章历史
- 收稿日期: 2016-04-13
2. 中国三峡建设管理有限公司,四川 成都 610000
2. China Three Gorges Projects Development Co., Ltd., Chengdu 610000, China
风速的随机性和波动性要求电力系统为风电提供足够的备用容量,以平衡其功率的实时变化.高精度的风速预测能有效减轻风电对电力系统的影响,也能提高风电场对风能的利用率.
风速预测的方法主要分为物理模型预测、统计模型预测以及人工智能预测等[1],预测误差一般在25%~40%之间[2].目前,国内外风速预测研究主要集中在时长为6 h以下的预测[3-8],这些方法虽然在超短期预测领域不断提高精度,却无法在预测时长上有所突破.这是由于随着预测时长的增加,风速的不确定性随之增加,如果在预测时长上要有所突破,同时保持预测精度,则必须要考虑风速变化的不确定性.因此,风速不确定性的描述方法成为风速预测的关键.
云模型是基于随机数学和模糊数学理论,统一刻画语言值中存在的随机性、模糊性及二者之间的关联性,用以描述定性概念和具体数值间的不确定性转换模型.由于云模型对不确定性的良好表达,自提出以来,该模型在智能控制、决策分析等领域已取得成功应用[9-11],近年来在电力系统状态估计、可靠性评估、电价预测等方向也有所应用[12-18].若将云模型描述不确定性的理论方法引入短期风速预测,在预测过程中将更能体现风速的不确定性.
本文从风速的不确定性角度出发,采用云模型对风速的不确定性进行描述,以此为基础对短期风速预测进行研究.首先选用模糊c聚类算法 (FCM) 对风速资料作聚类分析,将概念聚集为一些概念簇.然后根据云模型的理论建立两套云规则发生器,用两套规则发生器组合形成短期风速预测组合模型,预测24 h风速.
1 FCM聚类算法为了分析风速资料的特点和规律,在风速预测之前,首先应对风速资料进行聚类分析.风速资料聚类分析一方面要求每个类中的数据之间最大程度地相似,不同类中的数据最大程度地不同.另一方面,要求每个类的不确定性程度适中.故应从风速资料的本身特点出发,通过统计历史风速资料中的风速数据在按一定步长划分的各个区间中发生的频率来分析制定聚类的标准.
根据隶属度的取值范围,聚类方法可以分为传统的硬聚类和模糊聚类算法.模糊聚类中对隶属度没有非0即1的限制,有着更好的聚类效果与数据表达能力[19].考虑到风速的不确定性,故采用模糊聚类的方法.
在模糊聚类算法中广泛应用的是模糊c均值 (FCM) 聚类算法,它具有简单、高效、数据适应性强等特点[20].对给定的某一样本集X={xj, j=1, 2, …,n}⊆R,其FCM算法如下[19]:
1) 设定聚类个数c(1 < c < n) 和模糊指数m;令V=[vi,i=1, 2, …, c]为c个聚类中心向量构成的矩阵,初始化各类中心V(0);设置收敛的精度ε>0;令迭代次数k=0.
2) 计算样本点xj分别到聚类中心vi以及聚类中心vr的欧几里得距离dij与drj,r≠i:

3) 计算样本点xj属于第i类的隶属度:

4) 迭代得聚类中心矩阵V(k+1),令k=k+1:

重复上述步骤直到满足:

经过聚类分析,需构建有效的云模型挖掘风速资料的不确定性,实现风速预测.云模型是定性定量概念的转换模型,可实现定性概念与离散数据之间的不确定性转换.正态云模型用相互独立的一组参数共同表达一个定性概念的数字特征, 反映概念的不确定性.在正态分布函数与正态隶属函数基础上, 这组参数用期望Ex、熵En、超熵He 3个数字特征来表征[21].期望Ex指论域中云滴分布的数学期望,Ex也是样本空间中的点,是一个定性概念的最典型代表.熵En表示概念的可度量程度,反映了定性概念的不确定性, 表示在论域空间可以被定性概念接受的取值范围大小,即模糊度.超熵He表示熵的不确定度,它揭示了模糊性和随机性的关联.
2.1 前件云与后件云不确定性推理的基础是不确定性知识,通常使用如“if A then B”形式的定性规律来表达不确定性知识[22].其中,A和B分别为对应论域U1和U2的定性概念,A称为前件,B称为后件.前件云用以生成论域U1中定量值x属于定性概念的确定度μ.后件云用以生成论域U2中属于定性概念确定度为μ的定量值x.

|
| 图 1 一维云发生器 Figure 1 One-dimensional cloud generator |
输入:一维定性概念的数字特征 (Ex,En,He) 及定量x.
输出:定量值x属于定性概念的确定度μ.
后件云发生器如图 1(b), 具体算法如下:
输入:一维定性概念的数字特征 (Ex,En,He) 定量量值μ.
输出:满足确定度μ的定量值x.
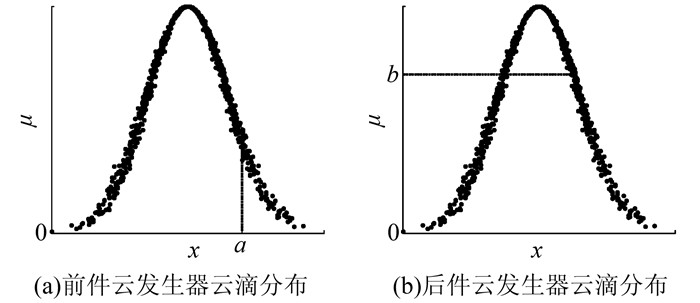
特定值a和μ通过前件云发生器生成的确定度构成的联合分布 (a,μ),如图 2(a)所示,所有云滴都分布在同一条直线x=a上.
特定确定度μ和通过后件云发生器生成的云滴构成的联合分布 (b,μ),如图 2(b)所示,所有云滴都分布在同一条直线μ=b上.
|
| 图 2 云滴的联合分布 Figure 2 Joint distribution of cloud drops |
将一个前件云发生器与一个后件云发生器相连接,则构造出单条件单规则发生器, 如图 3所示.

|
| 图 3 单条件规则发生器 Figure 3 Single condition rule generator |
单条件单规则发生器的具体算法如下[24]:
输入:前件的数字特征ExA, EnA, EeA及定量值xA,后件的数字特征ExB, EnB, EeB.
输出:满足确定度μ后件的定量值xB.
1) 生成以EnA为期望值、EeA为均方差的正态随机数E′nA;
2) 计算确定度:

3) 生成以EnB为期望值、EeB为均方差的正态随机数E′nB;
4) 若前件激活上升沿xA≤ExA,则后件同样激活上升沿此方向:

5) 若前件激活下降沿xA>ExA,则后件同样激活下降沿此方向:

风速变化除了与其前一时刻的风速存在联系,在一定时间内,风速还存在以日为基数的日变化.若仅考虑日变化规律,则体现的是风速在24 h内的整体变化趋势;若仅考虑邻近数据呈现出的某种当下的趋势,则体现的是局部风速变化的预测.单一考虑以上两者之一,都不能较完全地反映风速的变化规律.综合考虑两种规律,把邻近时刻风速体现的规律和历史风速反映的日变化规律加权组合,才能较准确地预测风速.故从风速序列挖掘以下两种时序规律:一是风速分钟级变化;二是风速的日变化规律.
将两种风速变化规律应用于正态云规则发生器中,形成风速预测机制.两套规则发生器产生的的云滴共同体现了分钟级和日变化两种规律.上述组合预测模型如图 4所示.

|
| 图 4 基于云模型的预测模型 Figure 4 Cloud model based prediction model |
利用上述组合云模型实现风速预测的具体步骤为:1) 由风速数据集聚类得到前件、后件.两种变化规律的风速数据集分别为测风间隔为15 min的风速时间序列以及历史资料中的某天某小时的风速序列.将不同的风速数据集聚类分析,并通过逆向规则发生器得到分类的风速定性概念.2) 运行前件云发生器,计算不同风速变化规律下激励x对于不同风速定性概念的隶属度μ.3) 运行不同规律下的规则发生器,得到相应的预测风速.4) 将两套规则发生器产生的云滴合成新的云滴群,这套云滴体现了两种风速变化的不确定性.5) 多次运行组合云模型,取其期望作为其确定的预测结果.
3 算例分析以甘肃某风电场实测风速资料为例.选取风电场2012年1月的测风数据,测风时间间隔是15 min.风速预测的起点是1月30日上午8:00,预测时长为24 h.将1月14日0:00到1月30日7:45的风速资料用于测风数据的规律挖掘,并以实测数据验证预测精度.风电场2012年1月14日0:00-2012年1月30日7:45的实测风速变化曲线见图 5.

|
| 图 5 甘肃某风电场风速变化曲线 Figure 5 Wind speed variation of a wind farm in Gansu Province |
根据图 5实测数据,统计得步长为0.2 m/s的风速频率分布曲线,见图 6.

|
| 图 6 风速频率分布图 Figure 6 Frequency distribution of the wind speed |
聚类分析时,预选聚类中心可参考图 6所示频率分布对应的局部最高点 (峰值),峰值越大,表示风速汇集越多,越能反映风速的定性概念.
采用FCM方法对图 5中的实测数据进行聚类分析,以所得到的一组风速数据集生成前件.由聚类所得数据在风速资料中对应的下一个15 min时刻的风速数据生成后件.通过逆向正态云发生器分别得到前件和后件云模型的数字特征,见表 1及表 2.
| 分组编号 | Ex | En | He |
| 1 | 0.656 3 | 0.501 7 | 0.193 2 |
| 2 | 2.041 9 | 0.385 0 | 0.141 8 |
| 3 | 3.192 0 | 0.382 7 | 0.122 3 |
| 4 | 4.298 0 | 0.328 5 | 0.127 4 |
| 5 | 5.004 1 | 0.201 4 | 0.085 5 |
| 6 | 5.456 4 | 0.163 4 | 0.056 1 |
| 7 | 6.041 7 | 0.257 1 | 0.077 5 |
| 8 | 7.112 3 | 0.395 9 | 0.124 1 |
| 9 | 8.563 8 | 0.591 3 | 0.222 0 |
| 10 | 10.726 0 | 0.956 5 | 0.357 9 |
| 分组编号 | Ex | En | He |
| 1 | 0.919 2 | 0.758 7 | 0.158 5 |
| 2 | 2.065 1 | 0.729 8 | 0.354 4 |
| 3 | 3.182 9 | 0.709 2 | 0.285 8 |
| 4 | 4.276 2 | 0.610 2 | 0.173 7 |
| 5 | 5.015 1 | 0.497 6 | 0.079 6 |
| 6 | 5.388 5 | 0.440 6 | 0.077 7 |
| 7 | 5.981 2 | 0.463 8 | 0.142 6 |
| 8 | 7.175 6 | 0.634 9 | 0.078 3 |
| 9 | 8.521 0 | 0.848 3 | 0.165 6 |
| 10 | 10.630 7 | 1.077 3 | 0.317 4 |
将此规律应用于单条件单规则发生器即形成分钟级变化规律的云模型规则发生器.
对于风速日变化规律,本文将每天同一时刻的风速数据组成的集合作为其历史风速资料,其处理过程和规则发生器生成过程与风速分钟级变化规律相同.以每天8时的数据为例,将每天8:00、8:15、8:30、8:45这4个时刻的数据集合经聚类、逆向规则发生器,得到前件、后件.日变化规律的云模型数字特征见表 3及表 4.
| 组别 | Ex | En | He |
| 1 | 0.463 6 | 0.360 1 | 0.119 1 |
| 2 | 1.885 7 | 0.559 5 | 0.079 0 |
| 3 | 3.771 3 | 0.599 0 | 0.136 3 |
| 4 | 5.297 3 | 0.454 8 | 0.170 0 |
| 5 | 7.393 8 | 0.778 4 | 0.215 4 |
| 组别 | Ex | En | He |
| 1 | 4.715 7 | 2.793 6 | 0.574 5 |
| 2 | 3.700 5 | 2.435 4 | 1.090 5 |
| 3 | 2.161 3 | 1.584 0 | 0.095 9 |
| 4 | 4.380 5 | 1.990 3 | 0.416 4 |
| 5 | 4.443 8 | 1.877 2 | 0.611 2 |
将日变化规律应用于单条件单规则发生器中即形成日变化规律的云模型规则发生器.
3.1 组合模型风速预测将日变化规律的云模型规则发生器和分钟级变化规律的云模型规则发生器产生的云滴组合形成新的云滴群.应用组合云模型10次,取其期望,得24 h的预测风速,预测结果与实测风速如图 7所示.为了便于分析比较,将本文采用组合云模型的预测结果和RBF[25]神经网络预测结果进行比较,对比结果见图 7.

|
| 图 7 24 h风速预测曲线 Figure 7 24 h wind speed forcasting curves |
对组合云模型的预测误差做频率分析,误差的频率分布直方图和累积频率分布直方图见图 8.

|
| 图 8 风速预测误差分布频率直方图 Figure 8 Error frequency histogram of predicted wind speed |
由图 8所示可知, 绝对误差小于0.5 m/s的预测风速出现概率有34.38%,绝对误差小于1 m/s的预测风速出现概率达66.68%,绝对误差小于1.5 m/s的预测风速出现概率达90.64%,绝对误差小于2 m/s的预测风速出现概率达97.94%.
预测误差的评价指标选择均方根误差 (root mean squared error,RMSE)、平均绝对误差 (mean absolute error,MAE) 以及平均绝对百分比误差 (mean absolute percentage error,MAPE).各误差评价指标的计算方法如下.
均方根误差 (RMSE):
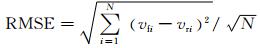 (1)
(1)
平均绝对误差 (MAE):
 (2)
(2)
平均绝对百分比误差 (MAPE):
 (3)
(3)
式中:vfi为第i时刻的预测风速值; vri为第i时刻的实测风速值.
组合云模型预测结果与RBF神经网络预测结果的误差评价指标见表 5.云模型的预测精度稍优于RBF神经网络.
| 预测方法 | RMSE/(m·s-1) | MAE/(m·s-1) | MAPE/% |
| 组合云模型 | 0.98 | 0.83 | 21.96 |
| RBF | 1.37 | 1.16 | 29.51 |
本文运用云模型对风速的不确定性进行描述.将风速变化中的分钟级变化规律和日变化规律作为云规则发生器,建立了短期风速预测的组合云模型,为短期风速预测提供了新的方法,该方法具有以下优势和特点:
1) 云模型预测方法可行.误差概率统计结果表明,预测误差基本呈正态分布,预测绝对误差小于2 m/s的预测点概率为97.94%.通过与RBF神经网络预测结果对比,组合模型24 h预测风速的误差评价指标均优于RBF神经网络,其均方根误差为0.98 m/s,平均绝对误差为0.83 m/s,平均绝对百分比误差为21.96%.证明该方法较适合短期风速预测.
2) 云模型的预测方法体现出了风速序列的不确定性.其预测结果为某一范围内小幅度波动的序列,用户可根据实际经验或其他信息辅助选择预测结果,也可取其期望作为确定的结果.
3) 云模型的扩展性好.可利用风速、风向、气温、气压等数据,将一维云模型规则发生器拓展为多维规则发生器,结合本文预测模型,有望提高云模型的预测精度.
| [1] | Foley A M, Leahy P G, Marvuglia A, et al. Current methods and advances in forecasting of wind power generation[J]. Renewable Energy, 2012, 37(1): 1–8. DOI:10.1016/j.renene.2011.05.033 |
| [2] |
刘烨, 卢小芬, 方瑞明, 等. 风力发电系统中风速预测方法综述[J].
电网与清洁能源, 2010(6): 62–66.
Liu Ye, Lu Xiaofen, Fang Ruiming, et al. A review on wind speed forecast methods in wind power system[J]. Power System and Clean Energy, 2010(6): 62–66. |
| [3] |
蔡凯, 谭伦农, 李春林, 等. 时间序列与神经网络法相结合的短期风速预测[J].
电网技术, 2008, 32(8): 82–85.
Cai Kai, Tan Lunnong, Li Chunlin, et al. Short-term wind speed forecasting combing time series and neural network method[J]. Power System Technology, 2008, 32(8): 82–85. |
| [4] |
潘迪夫, 刘辉, 李燕飞. 基于时间序列分析和卡尔曼滤波算法的风电场风速预测优化模型[J].
电网技术, 2008, 32(7): 82–86.
Pan Difu, Liu Hui, Li Yanfei. A wind speed forecasting optimization model for wind farms based on time series analysis and Kalman filter algorithm[J]. Power System Technology, 2008, 32(7): 82–86. |
| [5] |
杜颖, 卢继平, 李青, 等. 基于最小二乘支持向量机的风电场短期风速预测[J].
电网技术, 2008, 32(15): 62–66.
Du Ying, Lu Jiping, Li Qing, et al. Short-term wind speed forecasting of wind farm based on least square-support vector machine[J]. Power System Technology, 2008, 32(15): 62–66. |
| [6] |
杨琦, 张建华, 王向峰, 等. 基于小波-神经网络的风速及风力发电量预测[J].
电网技术, 2009, 33(17): 44–48.
Yang Qi, Zhang Jianhua, Wang Xiangfeng, et al. Wind speed and generated wind power forecast based on wavelet-neural network[J]. Power System Technology, 2009, 33(17): 44–48. |
| [7] |
王晓兰, 王明伟. 基于小波分解和最小二乘支持向量机的短期风速预测[J].
电网技术, 2010, 34(1): 179–184.
Wang Xiaolan, Wang Mingwei. Short-term wind speed forecasting based on wavelet decomposition and least square support vector machine[J]. Power System Technology, 2010, 34(1): 179–184. |
| [8] |
王辉, 刘达, 王继龙. 基于谱聚类和优化极端学习机的超短期风速预测[J].
电网技术, 2015, 39(5): 1307–1314.
Wang Hui, Liu Da, Wang Jilong. Ultra-short-term wind speed prediction based on spectral clustering and optimized extreme learning machine[J]. Power System Technology, 2015, 39(5): 1307–1314. |
| [9] |
张飞舟, 李德毅. 利用云模型实现智能控制倒立摆[J].
控制理论与应用, 2000, 17(4): 519–523.
Zhang Feizhou, Li Deyi. Intelligent control inverted pendulum with cloud models[J]. Control Theory and Applications, 2000, 17(4): 519–523. |
| [10] |
高键, 姜长生, 李众. 一种新的云模型控制器设计[J].
信息与控制, 2005, 34(2): 157–162.
Gao Jian, Jiang Changsheng, Li Zhong. A novel design of controller based on the cloud model[J]. Information and Control, 2005, 34(2): 157–162. |
| [11] |
赵彦博, 李超, 王维平, 等. 基于云模型的多属性决策方法适用性研究[J].
科学技术与工程, 2011, 11(35): 8767–8774.
Zhao Yanbo, Li Chao, Wang Weiping, et al. Robustness analysis of multi-attributes decision methods based on cloud model[J]. Science Technology and Engineering, 2011, 11(35): 8767–8774. |
| [12] |
钟清, 张文峰, 余南华, 等. 主动配电网谐波预测预警方法的研究[J].
电力系统保护与控制, 2014, 42(23): 50–56.
Zhong Qing, Zhang Wenfeng, Yu Nanhua, et al. Research on harmonic forecasting and warning of active distribution network[J]. Power System Protection and Control, 2014, 42(23): 50–56. |
| [13] |
王磊, 赵书强. 基于云模型的输电系统可靠性评估[J].
电网与清洁能源, 2010, 26(11): 19–23.
Wang Lei, Zhao Shuqiang. Reliability evaluation of transmission system based on cloud model[J]. Power System and Clean Energy, 2010, 26(11): 19–23. |
| [14] |
栗然, 崔天宝, 肖进永. 基于云模型的短期电价预测[J].
电网技术, 2009, 33(17): 185–190.
Li Ran, Cui Tianbao, Xiao Jinyong. Short-term electricity price forecasting based on cloud model[J]. Power System Technology, 2009, 33(17): 185–190. |
| [15] |
蔡国伟, 张斌, 王建元, 等. 云模型理论在互联电力系统负荷频率控制中的应用[J].
中国电机工程学报, 2015, 35(2): 353–358.
Cai Guowei, Zhang Bin, Wang Jianyuan, et al. Application of cloud model theory to the load frequency control in interconnected power systems[J]. Proceedings of the CSEE, 2015, 35(2): 353–358. |
| [16] |
杨薛明, 苑津莎, 王剑锋, 等. 基于云理论的配电网空间负荷预测方法研究[J].
中国电机工程学报, 2006, 26(6): 30–36.
Yang Xueming, Yuan Jinsha, Wang Jianfeng, et al. A new spatial forecasting method for distribution network based on cloud theory[J]. Proceedings of the CSEE, 2006, 26(6): 30–36. |
| [17] |
周明, 葛江北, 李庚银. 基于云模型的DFIG型风电场动态电压等值方法[J].
中国电机工程学报, 2015, 35(5): 1097–1105.
Zhou Ming, Ge Jiangbei, Li Genyin. Cloud model based DFIG wind farm dynamic voltage equivalence method[J]. Proceedings of the CSEE, 2015, 35(5): 1097–1105. |
| [18] |
李如琦, 凌武能. 基于云推理的短期风电功率预测模型[J].
电力系统保护与控制, 2012, 35(5): 1097–1105.
Li Ruqi, Ling Wuneng. Short-term wind power prediction model based on cloud reasoning[J]. Power System Protection and Control, 2012, 35(5): 1097–1105. |
| [19] |
曲福恒.
模糊聚类算法及应用[M]. 北京: 国防工业出版社, 2011: 7-66.
Qu Fuheng. Fuzzy Clustering Algorithm and Application[M]. Bejing: National Defense Industry Press, 2011: 7-66. |
| [20] | Xu R, Wunsch D. Survey of clustering algorithms[J]. Transactions on Neural Networks, 2005, 16(3): 645–678. DOI:10.1109/TNN.2005.845141 |
| [21] |
李德毅, 刘常昱. 论正态云模型的普适性[J].
中国工程科学, 2004, 6(8): 28–34.
Li Deyi, Liu Changyu. Study on the universality of the normal cloud model[J]. Engineering Science, 2004, 6(8): 28–34. |
| [22] |
代劲, 宋娟, 胡峰, 等.
云模型与文本挖掘[M]. 北京: 人民邮电出版社, 2013: 44-45.
Dai jing, Song Juan, Hu Feng, et al. Cloud Model and Text Mining[M]. Beijing: Posts and Telecom Press, 2013: 44-45. |
| [23] |
李德毅, 史雪梅, 孟海军. 隶属云和隶属云发生器[J].
计算机研究和发展, 1995, 32(6): 15–20.
Li Deyi, Shi Xuemei, Meng Haijun. Membership cloud and membership cloud generators[J]. Computer Research and Development, 1995, 32(6): 15–20. |
| [24] |
李德毅.
不确定性人工智能[M]. 北京: 国防工业出版社, 2005: 144-334.
Li Deyi. Artificial Intelligence with Uncertainty[M]. Bejing: National Defense Industry Press, 2005: 144-334. |
| [25] |
李文良, 卫志农, 孙国强, 等. 基于改进空间相关法和径向基神经网络的风电场短期风速分时预测模型[J].
电力自动化设备, 2009(6): 89–92.
Li Wenliang, Wei Zhinong, Sun Guoqiang, et al. Multi-interval wind speed forecast model based on improved spatial correlation and RBF neural network[J]. Electric Power Automation Equipment, 2009(6): 89–92. |
 2017, Vol. 50
2017, Vol. 50




