武汉大学学报(工学版)   2016, Vol. 49 Issue (6): 905-910

文章信息

邬晓光, 陈恒大, 郭飞, 姚丝思
WU Xiaoguang, CHEN Hengda, GUO Fei, YAO Sisi
独塔斜拉桥振动基频的实用估算公式
Practical estimation formula for vibration fundamental frequency of cable-stayed bridges with single tower
武汉大学学报(工学版), 2016, 49(6): 905-910
Engineering Journal of Wuhan University, 2016, 49(6): 905-910
http://dx.doi.org/10.14188/j.1671-8844.2016-06-018

文章历史

收稿日期: 2016-05-15
 Abstract              PDF               Figures               Tables
引用本文 0
邬晓光, 陈恒大, 郭飞, 姚丝思. 独塔斜拉桥振动基频的实用估算公式[J]. 武汉大学学报(工学版), 2016, 49(6): 905-910.
WU Xiaoguang, CHEN Hengda, GUO Fei, YAO Sisi. Practical estimation formula for vibration fundamental frequency of cable-stayed bridges with single tower[J]. Engineering Journal of Wuhan University, 2016, 49(6): 905-910.
独塔斜拉桥振动基频的实用估算公式
邬晓光1, 陈恒大1, 郭飞1,2, 姚丝思1     
1. 长安大学桥梁与隧道陕西省重点实验室，陕西 西安 710064;
 2. 浙江省交通规划设计研究院，浙江 杭州 310000
收稿日期: 2016-05-15
作者简介: 邬晓光（1961），男，教授、博导，研究方向为大跨度桥梁结构分析、施工控制、养护和维修加固，E-mail:740554100@qq.com.
基金项目: 国家自然科学基金项目（50908017）；中国电力建设股份有限公司科技专项资金项目（2014-38）；中央高校基本科研业务费专项资金项目（201493212002）.
摘要: 为方便计算独塔斜拉桥的振动基频，基于两跨独塔斜拉桥，应用Rayleigh法推导其竖弯振动基频公式，最后对此公式的可行性进行了算例验证，并讨论了该公式的适用对象及应用范围.研究结果表明：梁、塔及索截面形式对其竖弯振动频率没有影响，而支承条件对斜拉体系的竖弯频率影响较大；给出的基于能量法得到的纵飘基频计算值与有限元值误差能满足概念设计阶段的要求.
关键词： 桥梁工程     独塔斜拉桥     基频     估算     实用公式    
Practical estimation formula for vibration fundamental frequency of cable-stayed bridges with single tower
WU Xiaoguang1, CHEN Hengda1, GUO Fei1,2, YAO Sisi1     
1. Key Laboratory for Bridge and Tunnel of Shaanxi Province, Chang'an University, Xi'an 710064, China;
 2. Zhejiang Provincial Institute of Communications Planning, Design and Research, Hangzhou 310000, China
Abstract: In order to calculate fundamental frequency of the cable-stayed bridges with single tower conveniently, the cable-stayed bridges with single tower is taken as research object, a fundamental frequency formula for vertical vibration mode of cable-stayed bridges is derived by the Rayleigh method, and the concept of nominal unity mass anti-bending rigidity is introduced. Finally, the presented theoretical formula of fundamental frequency is validated by case study; and its suitabe objects and applicable range are discussed. The results indicate that the section types of the girder, tower and cable have no influence on the vertical frequency for vibration of cable-stayed bridges; but the supporting conditions have a great influence on vertical frequency of cable-stayed bridges. So it is necessary to consider the supporting conditions when calculating frequency.The fundamental frequency calculated by the recommended method has a little error compared with the finite element method results, which meets the requirement of conceptive design.
Key words: bridge engineering     cable-stayed bridges with inclined single tower     fundamental frequency     estimation     practical formula    

独塔斜拉桥作为一种新的结构形式，在概念设计阶段需要对其动力特性进行初步估算.《公路桥梁抗风设计规范》中的双塔斜拉桥的基频估算公式是以双塔漂浮体系为基础，采用数理统计方法拟合的经验公式，限于统计样本的数量，估算频率值与真实频率值可能存在较大差异.该公式是针对双塔漂浮体系而言，并未对其振动基频作出说明[1, 2, 3]；李国豪等提出采用单质点模型估算漂浮体系斜拉桥的基频，但是存在精算不高的问题[3]；袁万诚等针对文献[3]提出单质点模型计算精度不足的问题，提出双质点模型，用来估算一阶纵飘频率公式[4]；张永杨等根据主塔塔顶的抗推刚度与主梁的等效摆动刚度的差异，对文献[4]提出的估算公式进行修正[5]；文献[3, 6]采用Rayleigh法推导，将漂浮体系斜拉桥简化成多跨连续弹性地基梁模型，从而得到漂浮体系的频率估算公式；文献[7]将斜拉桥简化成多跨连续弹性地基梁模型，并对其进行修正；苗家武等考虑了主塔的偏位的影响，对文献[7]提出的估算公式进行修正[8]；文献[9-10]采用Rayleigh法推导了单跨悬索桥的近似竖弯基频表达式；文献[11-14]采用Rayleigh法推导了多塔悬索桥的竖弯频率，并对其进行修正；周勇军等针对高墩连续刚构桥这一特殊结构形式，利用Rayleigh法推导其纵飘基频的能量表达式[15].

综上所述，双塔漂浮体系的斜拉桥已有相关的竖弯基频近似计算公式，但是在诸多文献中均没有对独塔斜拉桥的竖弯基频近似计算公式进行讨论，对该结构的竖弯基频还停留在定性认识的基础上，其定量计算公式基本上处于盲区.虽然有限元法得到了广泛的应用，对此类桥梁来说，建模过程依然繁琐，不利于技术人员快速判断桥梁结构的振动特性.为此，本文对独塔斜拉桥的振动基频进行研究，采用Rayleigh法推导其竖弯基频估算实用公式，可供初步概念设计使用.

1 基于Rayleigh法的频率计算

根据能量守恒原理定律可得频率ωb的近似公式为

$\omega _{b}^{2}=\frac{{{U}_{\max }}}{{{T}_{\max }}}=\frac{\int_{0}^{l}{EI(x){{\left( {{\varphi }^{''}}(x) \right)}^{2}}dx}}{\int_{0}^{i}{m(x){{\varphi }^{2}}(x)dx}}$    (1)

其中：ωb为与此对应的频率；EI(x)、m(x)分别为弯曲刚度和质量分布值；φ(x)为满足桥梁位移边界条件的近似振型函数.

为方便表述，对下文中的符号作如下说明： EGIG、ETIT分别为加劲梁、主塔的抗弯刚度； η、ξ、ηci分别为加劲梁、主塔及拉索的振型函数； mG、mT、mci分别为加劲梁、主塔及拉索的线均布质量； Eci、Aci分别为拉索的弹性模量及截面面积； αci、Lci分别为拉索的水平倾角及长度.

1.1 结构体系的势能

斜拉体系在铅垂平面内发生一阶竖向振动时，其势能为加劲梁、主塔和拉索势能之和.

加劲梁的势能为

${{\mathsf{U}}_{1}}=\frac{1}{2}\int_{0}^{l}{{{E}_{G}}{{I}_{G}}}{{\left( \frac{{{d}^{2}}\eta }{d{{x}^{2}}} \right)}^{2}}dx$    (2)

主塔的势能为

${{U}_{2}}=\sum\limits_{i=1}^{n}{\left( \frac{1}{2}\int_{0}^{h_{Ti}^{{}}}{{{E}_{T}}{{I}_{T}}{{\left( \frac{{{d}^{2}}\xi }{d{{x}^{2}}} \right)}^{2}}dz} \right)}$    (3)

拉索在索力增量ΔF作用下，其弹性伸长量$\Delta {{L}_{ci}}=\frac{\Delta F}{{{E}_{ci}}{{A}_{ci}}}\bullet {{L}_{ci}}={{\eta }_{ci}}\bullet sin{{\alpha }_{ci}}$， 则可得

$\Delta F={{\eta }_{ci}}\frac{{{E}_{ci}}{{A}_{ci}}}{{{L}_{ci}}}sin{{\alpha }_{ci}}$

拉索的势能为

${{U}_{3}}=\frac{1}{2}\sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}\eta _{ci}^{2}\bullet {{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}$    (4)

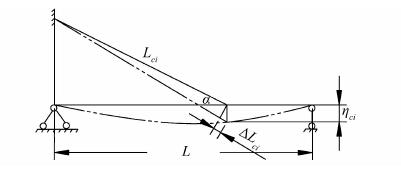
整体结构体系的振动使得拉索的倾角发生变化，索力也发生变化，索力的垂直分量的变化量为ΔFV≌ΔF·cosα·dα，拉索与主梁的变形协调如图 1所示.

图 1 拉索与主梁的变形协调 Figure 1 Deformation compatibility of cable and main girder
图选项

由几何关系

$d\alpha =\frac{\eta \cos {{\alpha }_{ci}}}{{{L}_{ci}}}$

于是

$\Delta {{F}_{V}}=\Delta F\bullet \frac{{{\cos }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}\bullet {{\eta }_{ci}}$

则拉索二次势能为

${{U}_{4}}=\frac{1}{2}\sum\limits_{i=1}^{n}{\Delta F\bullet \frac{{{\cos }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}\bullet \eta _{ci}^{2}}$    (5)

整个斜拉体系的势能为

$\begin{align} & U=\frac{1}{2}\left[ \int_{0}^{l}{{{E}_{G}}{{I}_{G}}}{{\left( \frac{{{d}^{2}}\eta }{d{{x}^{2}}} \right)}^{2}}dx+\sum\limits_{i=1}^{n}{\int_{0}^{{{h}_{Ti}}}{{{E}_{T}}{{I}_{T}}}{{\left( \frac{{{d}^{2}}\xi }{d{{x}^{2}}} \right)}^{2}}dz} \right. \\ & \left. +\sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}\eta _{ci}^{2}\bullet {{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}+\sum\limits_{c}^{n}{\Delta F\frac{{{\cos }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}\eta _{ci}^{2}} \right] \\ \end{align}$    (6)
1.2 结构体系的动能

斜拉体系在铅垂平面内发生一阶竖向振动时，其动能为加劲梁、斜拉索和主塔动能之和.

加劲梁的动能为

${{T}_{1}}=\frac{\omega _{b}^{2}}{2}\int_{0}^{l}{{{m}_{G}}{{\eta }^{2}}}dx$    (7)

斜拉索的动能为

${{T}_{2}}=\sum\limits_{i=1}^{n}{\frac{\omega _{b}^{2}}{6}{{m}_{ci}}\eta _{ci}^{2}{{L}_{ci}}}$    (8)

主塔的动能为

${{T}_{3}}=\frac{\omega _{b}^{2}}{2}\sum\limits_{i=1}^{n}{\int_{0}^{{{h}_{Ti}}}{{{m}_{T}}{{\xi }^{2}}}dz}$    (9)

则整个斜拉体系的动能为

$T=\frac{\omega _{b}^{2}}{2}\left( \int_{0}^{l}{{{m}_{G}}{{\eta }^{2}}}dx+\sum\limits_{i=1}^{n}{\frac{1}{3}{{m}_{c}}\eta _{ci}^{2}{{L}_{ci}}+\sum\limits_{i=1}^{n}{\int_{0}^{{{h}_{Ti}}}{{{m}_{T}}{{\xi }^{2}}}dz}} \right)$    (10)
1.3 斜拉体系的竖弯基频

将式(6)、式(10)代入式(1)，可得到斜拉体系的竖向振动频率的计算公式为

$\omega _{b}^{2}=\frac{\int_{0}^{l}{{{E}_{G}}{{I}_{G}}}{{\left( \frac{{{d}^{2}}\eta }{d{{x}^{2}}} \right)}^{2}}dx+\sum\limits_{i=1}^{n}{\int_{0}^{{{h}_{Ti}}}{{{E}_{T}}{{I}_{T}}}{{\left( \frac{{{d}^{2}}\xi }{d{{x}^{2}}} \right)}^{2}}dz}+\sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}\eta _{ci}^{2}\bullet {{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}+\sum\limits_{c}^{n}{\Delta F\frac{{{\cos }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}\eta _{ci}^{2}}}{\int_{0}^{l}{{{m}_{G}}{{\eta }^{2}}}dx+\sum\limits_{i=1}^{n}{\frac{1}{3}{{m}_{c}}\eta _{ci}^{2}{{L}_{ci}}+\sum\limits_{i=1}^{n}{\int_{0}^{{{h}_{Ti}}}{{{m}_{T}}{{\xi }^{2}}}dz}}}$    (11)

文献[3]指出，在结构的势能中，拉索的势能是主要的；加劲梁、主塔及拉索的二次能是次要的，可以忽略不计.结构动能中，主梁的动能是主要的，拉索、主塔的动能是次要的，可以忽略不计.于是，可得该结构的竖弯频率理论近似公式：

$\omega _{b}^{2}=\frac{\sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}\eta _{ci}^{2}\bullet {{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}}{\int_{0}^{l}{{{m}_{G}}{{\eta }^{2}}}dx}$    (12)

由式(12)分析可知，基频ωb仅与结构的计算参数Eci、Aci、MG和振型函数η(z，t)有关，与其他因素无关.为求解独塔斜拉桥的竖弯频率，首先应该获得其基本振型函数η(z，t).

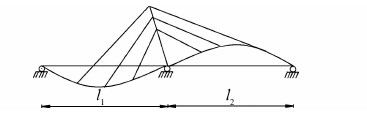
2 独塔斜拉桥竖弯基本振型

根据文献[3]及独塔斜拉桥的结构特点，可得到其1阶反对称和正对称的竖弯振型，如图 2、3所示.

图 2 1阶反对称竖弯振型 Figure 2 Mode shape of 1st asymmetric vertical vibration
图选项
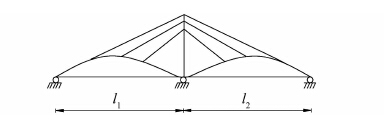
图 3 1阶正对称竖弯振型 Figure 3 Mode shape of 1st symmetric vertical vibration
图选项

由图 2、图 3分析可知，其振型函数η(x，t)与两跨连续梁竖向自由振动的振型函数η(x，t)类似.由于拉索和加劲梁满足变形协调条件，故只需确定满足边界条件的加劲梁的振型函数η(x，t)即可.由此只要找到能满足其竖向自由振动的振型函数η(x，t)，即可计算出独塔斜拉桥的1阶竖弯振动频率ωb.

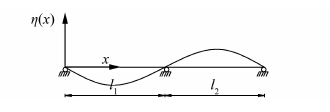
3 一阶反对称竖向弯曲频率计算公式

加劲梁一阶反对称的振型关于中间支座反对称，如图 4所示.

图 4 加劲梁1阶反对称竖弯振型 Figure 4 Mode shape of stiffening girder 1st asymmetric vertical vibration
图选项

对于满足1阶反对称竖弯自由振动，设其满足边界条件的加劲梁振型函数为

第1跨加劲梁振型曲线可表示为

${{\eta }_{1}}={{A}_{1}}\sin \frac{\pi x}{{{l}_{1}}}x\in (0{{l}_{1}})$    (13)

第2跨加劲梁振型曲线可表示为

${{\eta }_{2}}=-{{A}_{2}}\sin \frac{\pi x}{{{l}_{2}}}x\in (0{{l}_{2}})$    (14)

第1、2跨加劲梁振型曲线在桥塔处连续，即满足变形协调条件，可得η′1丨x=l1=η′2丨x=0，即

${{A}_{1}}\frac{\pi }{{{l}_{1}}}={{A}_{2}}\frac{\pi }{{{l}_{2}}}$    (15)

经简化可得

${{A}_{1}}={{A}_{2}}\frac{{{l}_{1}}}{{{l}_{2}}}=k{{A}_{2}}$    (16)
$\begin{align} & \sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}\eta _{ci}^{2}\bullet {{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}= \\ & A_{1}^{2}(\sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}{{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}{{\sin }^{2}}\frac{\text{ }\!\!\pi\!\!\text{ }x}{{{l}_{1}}}+\frac{1}{{{k}^{2}}} \\ & \sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}{{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}{{\sin }^{2}}\frac{\text{ }\!\!\pi\!\!\text{ }x}{{{l}_{2}}}) \\ \end{align}$    (17)
$\int_{0}^{l}{{{m}_{G}}{{\eta }^{2}}}dx=\frac{A_{1}^{2}}{2}({{m}_{G1}}{{l}_{1}}+\frac{1}{{{k}^{2}}}{{m}_{G2}}{{l}_{2}})$    (18)

将式(17)和式(18)代入式(12)可得

$\begin{align} & \omega _{b}^{2}=2\left( \sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}{{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}{{\sin }^{2}}\frac{\text{ }\!\!\pi\!\!\text{ }x}{{{l}_{1}}}+\frac{1}{{{k}^{2}}}\sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}{{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}{{\sin }^{2}}\frac{\text{ }\!\!\pi\!\!\text{ }x}{{{l}_{2}}} \right)/ \\ & \left( {{m}_{G1}}{{l}_{1}}+{{m}_{G2}}\frac{1}{{{k}^{2}}}{{l}_{2}} \right) \\ \end{align}$    (19)

若结构为对称布置时，式(19)可简化为

$\begin{align} & \omega _{b}^{2}= \\ & 2\frac{\sum\limits_{j=1}^{2}{\sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}{{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}{{\sin }^{2}}\frac{\pi x}{{{l}_{j}}}}}{\sum\limits_{j=1}^{2}{{{m}_{Gj}}{{l}_{j}}}} \\ \end{align}$    (20)
4 一阶正对称竖向弯曲频率计算公式

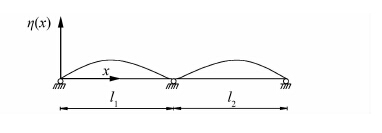
加劲梁一阶正对称的振型关于中间支座对称，如图 5所示.

图 5 加劲梁1阶正对称竖弯振型 Figure 5 Mode shape of stiffening girder 1st symmetric vertical vibration
图选项

对于满足1阶正对称竖弯自由振动，设其满足边界条件的加劲梁振型函数为

第1跨加劲梁振型曲线可表示为

${{\eta }_{1}}={{A}_{1}}\sin \frac{\theta x}{{{l}_{1}}}x\in (0{{l}_{1}})\theta =3.92$    (21)

第2跨加劲梁振型曲线可表示为

${{\eta }_{2}}={{A}_{2}}\sin \frac{\theta x}{{{l}_{2}}}x\in (0{{l}_{2}})\theta =3.92$    (22)

第1、2跨加劲梁振型曲线在桥塔处连续，即满足变形协调条件，可得η′1|x=l1=-η′2|x=0，即

${{A}_{1}}\frac{\cos \theta }{{{l}_{1}}}=\text{-}{{A}_{2}}\frac{1}{{{l}_{2}}}$    (23)

经简化可得

${{A}_{1}}=\text{-}{{A}_{2}}\frac{{{l}_{1}}}{{{l}_{2}}\cos \theta }=\text{-}\frac{k}{\cos \theta }{{A}_{2}}$    (24)

于是，可得

$\begin{align} & \sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}\eta _{ci}^{2}\bullet {{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}= \\ & A_{1}^{2}(\sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}{{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}{{\sin }^{2}}\frac{\theta x}{{{l}_{1}}}+ \\ & \frac{{{\cos }^{2}}\theta }{{{k}^{2}}}\sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}{{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}{{\sin }^{2}}\frac{\theta x}{{{l}_{2}}}) \\ \end{align}$    (25)
$\int_{0}^{l}{{{m}_{G}}{{\eta }^{2}}}dx=\frac{A_{1}^{2}}{2}({{m}_{G1}}{{l}_{1}}+\frac{{{\cos }^{2}}\theta }{{{k}^{2}}}{{m}_{G2}}{{l}_{2}})$    (26)

将式(25)和式(26)代入式(12)可得

$\begin{align} & \omega _{b}^{2}=2\sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}{{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}{{\sin }^{2}}\frac{\theta x}{{{l}_{1}}}+ \\ & \frac{{{\cos }^{2}}\theta }{{{k}^{2}}}\sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}{{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}{{\sin }^{2}}\frac{\theta x}{{{l}_{2}}}/ \\ & {{m}_{G1}}{{l}_{1}}+{{m}_{G2}}\frac{{{\cos }^{2}}\theta }{{{k}^{2}}}{{l}_{2}}\theta =3.92 \\ \end{align}$    (27)

若结构为对称布置时，l1/l2=k=1，式(27)可简化为

$\begin{align} & \omega _{b}^{2}=2\left( \sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}{{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}{{\sin }^{2}}\frac{\theta x}{{{l}_{1}}}+{{\cos }^{2}}\theta \sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}{{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}{{\sin }^{2}}\frac{\theta x}{{{l}_{2}}} \right)/ \\ & \left( {{m}_{G1}}{{l}_{1}}+{{\cos }^{2}}\theta {{m}_{G2}}{{l}_{2}} \right)\theta =3.92 \\ \end{align}$    (28)
5 算例验证

为验证文中解与有限元解的计算精度，下面以3座无辅助墩的独塔斜拉桥对上述公式加以验证，其中算例1、算例2和算例3的加劲梁截面形式均为π形截面，实桥结构计算参数如表 1所示.

表 1 实桥结构计算参数 Table 1 Structural parameters of real bridge
算例桥跨布置/mmG/(kg·m-1)$\sum\limits_{j=1}^{2}{\sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}}{{{L}_{ci}}}{{\sin }^{2}}\alpha }{{\sin }^{2}}\frac{\pi x}{{{l}_{j}}}}$/(N·m-1)$\sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}{{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}{{\sin }^{2}}\frac{\theta x}{{{l}_{1}}}+{{\cos }^{2}}\theta \sum\limits_{i=1}^{n}{\frac{{{E}_{ci}}{{A}_{ci}}{{\sin }^{2}}{{\alpha }_{ci}}}{{{L}_{ci}}}}{{\sin }^{2}}\frac{\theta x}{{{l}_{2}}}$/(N·m-1)
1149+14964 156.246.77×1072.15×108
2110+11062 586.118.29×1072.93×108
3170+17049 617.815.61×1071.71×108
表选项

将表 1中的计算参数分别代入式(20)、式(28)，可得上述3座实桥的振动基频计算结果，如表 2所示.

表 2 实桥一阶竖弯基频频率对比 Table 2 First fundamental frequency of comparison vertical vibration
算例ωb_AS/Hz有限元解/Hz文中解1/Hz文中解2/Hz误差1/%误差2/%
10.7160.8090.4240.7566.6011.50
20.9061.1000.5521.0395.6217.63
30.6830.7730.4080.7187.1111.64
注：误差1是文中解2与有限元解之间的误差；误差2是规范解与有限元解之间的误差.
表选项

由表 1、表 2分析可得，本文推导的竖弯基频能量表达式与有限元数值结果误差最大为7.11%，误差大小能满足概念设计阶段的要求.一阶反对称的估算值与有限元值之间的误差比一阶正对称的估算值与有限元值之间的误差相对要大，原因在于其振型函数更趋近于简支固端梁的振型函数.本文推导的纵飘竖弯基频能量表达式仅适用于塔梁固结、墩支承的独塔斜拉桥的竖弯频率估算，不适用于其他斜拉体系的竖弯频率估算.

6 结论

1) 主梁的支承条件对斜拉桥竖弯频率的影响较大，计算频率时不可忽视支承条件，应充分考虑支承条件.

2) 通过假设主梁的基本振型函数，推导了其一阶竖弯正对称和反对称的能量表达式，其结果与有限元数值结果吻合较好，可以适用于无辅助墩独塔斜拉桥竖弯频率初步概念设计阶段的估算中.

3) 本文竖弯频率实用计算公式仅适用于无辅助墩独塔斜拉体系，对其他体系斜拉桥应另做专门研究，《公路桥梁抗风设计规范》中的斜拉结构的竖向弯曲的基频估算公式不适用于塔梁固结、墩支承的独塔斜拉体系的竖弯频率的估算.

参考文献
[1] Ministry of Transportation of the People Republic of China. JTG/T D60-01-2004 Wind-resistant Design Specification for Highway Bridge[J]. Beijing: China Communications Press, 2004.
[2] 刘春华, 秦权. 桥梁结构固有频率的统计特征[J]. 中国公路学报, 1997, 10(4): 49–54.
Liu Chunhua, Qin Quan. Statistics of natural frequencies for bridge structures[J]. China Journal of Highway and Transport, 1997, 10(4): 49–54.
[3] 李国豪. 桥梁结构稳定与振动[M]. 北京: 中国铁道出版社, 2002.
Li Guohao. Stability and Vibration of Bridge Structures[M]. Beijing: China Railway Publishing House, 2002.
[4] 袁万诚, 闫冬. 斜拉桥纵飘频率简化计算方法[J]. 同济大学学报(自然科学版), 2005, 33(11): 1423–1427.
Yuan Wancheng, Yan Dong. Simplified calculational method of floating frequency for cable-stayed bridge[J]. Journal of Tongji University: Natural Science Edition, 2005, 33(11): 1423–1427.
[5] 张永杨.斜拉桥近似计算与结构体系研究[D]. 上海: 同济大学, 2010.
Zhang Yongyang. Approximate calculation and study of structural system in cable-stayed bridge [D].Shanghai: Tongji University, 2010. http://www.oalib.com/references/17048381
[6] 柳惠芬.斜拉桥的实用简化分析[D]. 上海: 同济大学, 1995.
Liu Huifen.Approximate calculation and study of structural system in cable-stayed bridge [D].Shanghai: Tongji University, 1995.
[7] Walther R. Cable Stayed Bridge[M]. 1999.
[8] 苗家武.超大跨斜拉桥设计理论研究[D]. 上海: 同济大学, 2006.
Miao Jiawu. Study for design theories of super-long cable-stayed bridge [D]. Shanghai: Tongji University, 2006. http://www.oalib.com/references/16928687
[9] 盛善定, 袁万城, 范立础. 悬索桥振动基频的实用估算公式[J]. 东北公路, 1996(1): 71–76.
Sheng Shanding, Yuan Wancheng, Fan Lichu. Practical estimation formula of vibration basic frequency of suspension bridge[J]. Northeast Highways, 1996(1): 71–76.
[10] 鞠小华, 廖海黎, 沈锐利. 对悬索桥对称竖弯基频近似公式的修正[J]. 土木工程学报, 2002, 2(1): 44–49.
Ju Xiaohua, Liao Haili, Shen Ruili. Modification on simplified formula of symmetric-vertical natural frequencies for suspension bridge[J]. China Civil Engineering Journal, 2002, 2(1): 44–49.
[11] 王本劲, 马如进, 陈艾荣. 多塔连跨悬索桥基频估算方法[J]. 结构工程师, 2011, 27(6): 54–58.
Wang Benjin, Ma Rujin, Chen Airong. Estimation of fundamental frequency of multi-pylon suspension bridge[J]. Structural Engineers, 2011, 27(6): 54–58.
[12] 王本劲, 马如进, 陈艾荣. 多塔连跨悬索桥基频估算实用公式[J]. 公路交通科技, 2012, 29(11): 58–62.
Wang Benjin, Ma Rujin, Chen Airong. Practical formula of fundamental frequency estimation for multi-pylon suspension bridge[J]. Journal of Highway and Transportation Research and Development, 2012, 29(11): 58–62.
[13] 张超, 黄群君, 许莉. 考虑主塔刚度影响的三塔自锚式悬索桥竖弯频率计算公式[J]. 长安大学学报(自然科学版), 2014, 34(6): 100–106.
Zhang Chao, Huang Qunjun, Xu Li. Frequency formulas for vertical vibration of three-tower self-anchored suspension bridge considering tower stiffness influence[J]. Journal of Chang'an University: Natural Science Edition, 2014, 34(6): 100–106.
[14] 姜洋.三塔悬索桥结构体系及施工过程关键问题研究[D]. 上海: 同济大学, 2014.
Jiang Yang. Study for structure system and process of construction for multi-tower suspension bridge [D]. Shanghai: Tongji University, 2014. http://www.cnki.com.cn/Article/CJFDTotal-SXJT201503025.htm
[15] 周勇军, 张晓栋, 宋一凡. 高墩连续刚构桥纵向振动基频的能量法计算公式[J]. 长安大学学报(自然科学版), 2013, 33(3): 100–106.
Zhou Yongjun, Zhang Xiaodong, Song Yifan. Calculation formula of longitude fundamental vibration frequency for continuous rigid frame bridge with higher pier based on energy method[J]. Journal of Chang'an University: Natural Science Edition, 2013, 33(3): 100–106.