武汉大学学报 (工学版)   2017, Vol. 50 Issue (1): 120-124

文章信息

孙志伟, 邬晓光
SUN Zhiwei, WU Xiaoguang
基于长期损失灰色预测的竖向预应力控制
Stress under anchor controlling in vertical prestress from long-term loss by gray prediction
武汉大学学报 (工学版), 2017, 50(1): 120-124
Engineering Journal of Wuhan University, 2017, 50(1): 120-124
http://dx.doi.org/10.14188/j.1671-8844.2017-01-018

文章历史

收稿日期: 2016-09-20
 Abstract              PDF               Figures               Tables
引用本文 0
孙志伟, 邬晓光. 基于长期损失灰色预测的竖向预应力控制[J]. 武汉大学学报(工学版), 2017, 50(1): 120-124.
SUN Zhiwei, WU Xiaoguang. Stress under anchor controlling in vertical prestress from long-term loss by gray prediction[J]. Engineering Journal of Wuhan University, 2017, 50(1): 120-124.
基于长期损失灰色预测的竖向预应力控制
孙志伟, 邬晓光     
长安大学公路学院，陕西 西安 710064
收稿日期：2016-09-20
作者简介：孙志伟 (1984-)，男，博士研究生，主要从事桥梁结构理论和桥梁维修加固研究，E-mail：120169927@qq.com.
通讯作者：邬晓光 (1961-)，男，教授、博士生导师，研究方向为大跨度桥梁结构分析、施工控制、养护和维修加固，E-mail：269728221@qq.com
基金项目：国家自然科学基金项目 (编号：50908017)；中央高校基本科研业务费专项资金项目 (编号：2014G3212002).
摘要：基于陕西省某连续刚构桥实桥监测系统采集到的桥梁有效竖向预应力长期变化数据，以实测数据作为初始序建立灰色系统理论预测模型GM (1, 1)，分析竖向预应力损失随时间的变化规律，进行时间非等步距残差修正，提出竖向预应力长期损失预测模型.采用该模型预测竖向预应力长期损失占控制张拉力的比例为7.92%，与实桥监测的7.8%~8.2%基本吻合，表明若采用公路桥规设计张拉力的0.6倍作为竖向预应力施工控制标准，将导致桥梁后期有效竖向预应力达不到要求.建议施工过程中锚下应力控制应充分考虑长期损失效应影响，压浆前锚下有效应力不小于设计张拉力0.7倍为宜.这为竖向预应力施工及无损检测提供了理论依据和参考，对PC混凝土箱梁竖向预应力体系应用发展具有重要的理论意义及实用价值.
关键词：桥梁工程    竖向预应力损失    灰色预测模型    锚下应力控制    
Stress under anchor controlling in vertical prestress from long-term loss by gray prediction
SUN Zhiwei, WU Xiaoguang     
College of Highway Engineering, Chang'an University, Xi'an 710064, China
Abstract: The paper based on the vertical prestress loss data of a concrete continuous rigid frame bridge collected by the real bridge monitoring system in Shaanxi province, establishes the grey theory forecasting model GM (1, 1) with the measured data as the initial order, analyzes the law of vertical prestress loss with time, and puts forward long-term vertical prestress loss prediction formula. Using this model to predict the long-term loss of vertical prestress accounted for 7.92% of the control tension; and it is consistent with the 7.8%-8.2% of the actual bridge monitoring basically. The results show that if using the design of the highway bridge gauge, 0.6 times of the tension forces, as vertical prestress construction control standard, will cause the late effective vertical prestress bridge can not meet the requirements.Based on the research outcomes, effective stress under anchor in vertical prestress construction should be more than 0.7 times of the designed stretch-draw force.The results provide a theoretical basis and reference for vertical prestress construction and NDE (nondestructive examination), and are of great importance of practical value for the application and development of vertical prestress system in prestressed concrete box-girder bridge.
Key words: bridge engineering     vertical prestress loss     grey forecast model     stress under anchor controlling    

竖向预应力体系是大跨径预应力混凝土连续 (刚构) 箱梁桥中至关重要的一部分，它能有效减小腹板主拉应力、防止开裂，关系到PC梁桥结构正常使用、耐久性甚至结构安全.但是，工程实践中由于各种因素影响，竖向预应力的应用并没有取得预期效果，腹板开裂现象没有得到遏制[1-3].

为了确保PC箱梁在施工过程中竖向预应力张拉力达到设计要求，最大程度降低PC箱梁腹板开裂风险，有效改善桥梁运营期的受力状态，最直接的途径就是箱梁施工过程中进行竖向预应力无损检测，测定实际张拉力，使竖向预应力张拉质量具有可控性，彻底解决人为因素引起的竖向预应力损失过大和失效的问题[4-6].目前，对于竖向预应力锚下有效应力控制标准研究仍为空白，普遍做法是参照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004) 中有效预应力折减系数0.6界定张拉效果是否合格[7].但是竖向预应力损失分为瞬时损失和长期损失两部分，长期损失伴随着桥梁结构全寿命周期一直存在，不可忽视，若仅以设计规范张拉力的0.6倍作为施工中控制标准，必然导致扣除长期损失后有效预应力小于规范要求，对腹板受力及防裂控制极其不利.

本文依托陕西省某连续刚构桥竖向预应力锚下有效应力长期监测数据，采用灰色预测理论建立竖向预应力长期损失GM (1, 1) 模型，探讨竖向预应力长期损失规律，并提出竖向预应力施工中锚下应力控制标准，为无损检测提供参考.

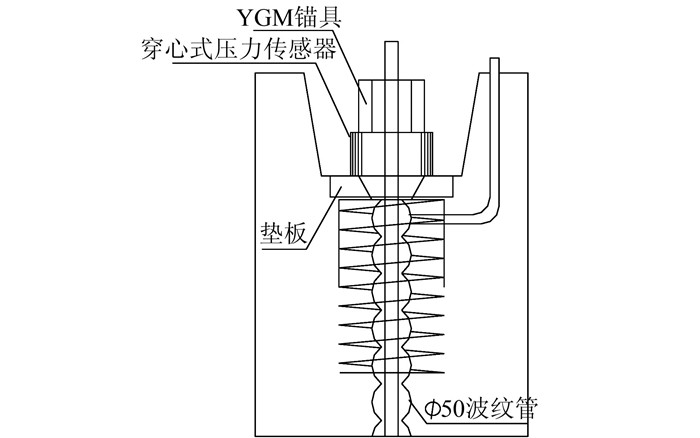
1 实桥监测系统建立 1.1 传感器布设方案

依托工程为某62.5+4×115+62.5 m预应力混凝土连续刚构桥，单箱单室，三向预应力体系，竖向预应力采用785 MPa的JL32精轧螺纹钢，箱梁腹板顺桥向间隔50 cm布置双排竖向预应力筋，上端张拉锚固，张拉力57 t.为了研究施工期间以及桥梁运营期间竖向预应力损失效应，探究损失规律，在每个T构4号块 (L/8)、8号块 (L/4)、跨中合龙段选取一侧腹板双排竖向预应力筋埋置穿心式压力传感器，如图 1~2所示.

图 1 传感器埋设位置示意图 Figure 1 Location of sensor
图选项
图 2 传感器埋设大样图 Figure 2 Position details of sensor
图选项
1.2 监测内容及结果

采集竖向预应力张拉全过程中传感器读数，以便于分析总结锚具回缩、混凝土压缩等引起的瞬时预应力损失.采集邻近竖向预应力张拉引起试验组预应力损失，验证已有理论研究成果.对竖向预应力张拉锚固后进行数据跟踪采集，分析竖向预应力损失时间效应.采集仪自带温度补偿系统，为了保证试验科学有效，试验竖向预应力筋张拉后7 d内，每天定时采集数据，7 d后每隔一天采集一次数据，之后随着预应力损失趋于稳定逐渐减小监测频率.

为了便于分析，对监测数据进行统计处理，把传感器测得相邻数据按时间优先原则做线性内插，把数列时间项调整为整数，并采用下式计算预应力损失率:

    (1)
    (2)

式中：Pl为竖向预应力损失；F为初始张拉力；N为实测压力值；P(i)为竖向预应力损失率.

将各传感器计算竖向预应力损失率平均值记为竖向预应力损失统计数据，如表 1所示.

表 1 竖向预应力平均损失率 Table 1 Percentage of average loss of vertical prestresses
天数 损失率/%
0 0
1 3.12
2 4.21
3 5.18
4 5.42
5 5.80
6 6.09
7 6.34
8 6.55
9 6.64
10 6.73
11 6.81
12 6.92
13 7.07
14 7.15
16 7.23
18 7.29
24 7.33
27 7.41
30 7.34
33 7.46
36 7.52
39 7.60
42 7.73
45 7.99
48 7.75
51 7.79
54 7.80
57 7.82
60 7.78
63 7.85
66 7.91
69 7.95
72 8.05
75 8.09
78 8.11
81 8.12
84 8.15
87 8.13
90 8.13
表选项
2 竖向预应力长期损失灰色预测模型

竖向预应力长期损失受锚具回缩、钢筋应力松弛、混凝土回弹、收缩徐变、温度等因素影响，将竖向预应力损失这一随时间变化的动态过程当作灰色过程，并利用灰色系统理论进行分析，建立灰色GM (1, 1) 预测模型对竖向预应力损失变化进行预测，无须过多追究引起其行为变化的原因，不必将系统行为与噪声行为加以分离[8-12]，不必处置竖向预应力损失这一复杂的过程，为长期损失预测找到了一条切实可行的建模途径.

2.1 灰色预测GM (1，1) 模型建立[13]

实桥监测系统采集的长期竖向预应力损失随时间变化曲线一般具有灰指数律特征，可以建立竖向预应力损失百分比序列对时间的一阶动态微分方程GM (1, 1) 模型.记初始竖向预应力损失序列为{P(i)(1)|i=1, 2, …, n}，对该序列进行递减计算，可以得到新序列{P(i)(0)|i=2, 3, …, n}，其中P(i)(0)=P(i)(1)－P(i－1)(1).记时间序列为{t(i)|i=2, 3, …, n}，对时间序列进行递减计算，得到新序列{t(i)(-1)|i=1, 2, …, n}，其中t(i)(－1)=t(i)－t(i－1).按照灰色系统理论的建模思路，得到一阶线性动态微分方程，记为GM (1, 1)：

    (3)

式中，参数a、b采用下式计算：

    (4)

其中：

    (5)
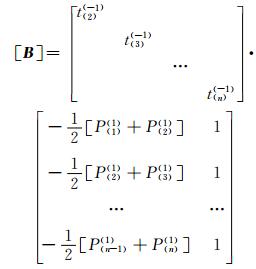    (6)

解方程 (3) 得到：

    (7)
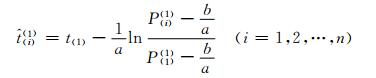    (8)

式 (7)、(8) 即为灰色理论GM (1, 1) 模型预测竖向预应力长期损失的计算公式，式 (7) 可计算任一时刻竖向预应力损失值，式 (8) 可预测达到某一竖向预应力损失值所需时间.

2.2 GM (1, 1) 残差修正模型

GM (1, 1) 模型一般要求时间步距等长，为提高精度，建立基于实测竖向预应力损失值与GM (1, 1) 预测值之差的非等步距修正模型.

对竖向预应力损失GM (1, 1) 模型预测值进行一次递减计算，得：

    (9)

预测值残差：

    (10)

预测值残差之和：

    (11)

按照竖向预应力损失率序列建模思路，得残差修正值：

    (12)

最终得到基于竖向预应力实测值与预测值之差的非等步距GM (1, 1) 修正预测模型：

    (13)

若预测模型不满足精度要求，可再对残差进行上述修正，直至满足要求.

2.3 实桥监测数据预测分析

按照上文建立竖向预应力灰色预测GM (1, 1) 模型，将表 1中统计数据作为GM (1, 1) 模型初始数据序列，求得参数a=0.271 6，b=2.110 7，aε=0.069，bε=0.010，如表 2.

表 2 GM (1, 1) 预测模型分析值 Table 2 Calculated value of GM (1, 1)
序号 t(i) 实测值P(i)(l) t(i)(－1) P(i)(0) 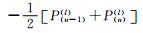预测值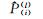 残差值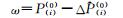 修正值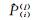
1 1 3.12 1 3.12 -1.56 1.85 1.27 1.86
2 2 4.21 1 1.09 -3.67 3.26 -0.32 3.28
3 3 5.18 1 0.97 -4.70 4.33 -0.10 4.36
4 4 5.42 1 0.24 -5.30 5.15 -0.58 5.18
5 5 5.80 1 0.38 -5.61 5.77 -0.24 5.82
6 6 6.09 1 0.29 -5.95 6.25 -0.19 6.30
7 7 6.34 1 0.25 -6.22 6.61 -0.11 6.67
… … … … … … … … …
34 75 8.09 3 0.04 -8.07 7.77 0.04 7.92
35 78 8.11 3 0.02 -8.10 7.77 0.02 7.92
36 81 8.12 3 0.01 -8.12 7.77 0.01 7.92
37 84 8.15 3 0.03 -8.14 7.77 0.03 7.92
38 87 8.13 3 -0.02 -8.14 7.77 -0.02 7.92
39 90 8.13 3 0 -8.13 7.77 0 7.92
表选项

最终求得竖向预应力损失长期预测修正模型为

    (14)

由于 (－7.77e－0.2716t－0.15e－0.0692t+7.92)=7.92，故经修正模型计算竖向预应力最终损失为初始张拉力的7.92%.

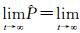
竖向预应力损失值、GM (1, 1) 模型预测值与修正的GM (1, 1) 模型预测值比较如图 3所示.

图 3 预测与实测竖向预应力损失值 Figure 3 Vertical prestress losses of prediction and test values
图选项
2.4 修正的GM (1，1) 模型精度检验

为了保证回归函数对竖向预应力长期损失预测的准确性，避免GM (1, 1) 修正模型产生过大误差，需要对修正模型进行精度检验.

残差方差：

    (15)

实测数据方差：

    (16)

后验差比值：

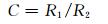    (17)

小误差概率：

    (18)

后验差、小误差概率可按表 3划分精度等级[14]，根据精度需要确定是否需要进行残差修正.

表 3 C、E的精度等级 Table 3 Accuracy levels of C and E
精度等级 优 良 可 差
E ＞0.95 ＞0.80 ＞0.70 ≤0.70
C ＜0.35 ＜0.50 ＜0.65 ≥0.65
表选项

经计算，R1=0.24，R2=1.32，C=0.18，E=0.97，精度等级满足要求.

对比可查竖向预应力实测损失值，统计见表 4.

表 4 国内大跨径连续箱梁桥竖向预应力损失实测值 Table 4 Vertical prestress loss measured values of long-span prestress concrete box girder bridge in China
桥梁名称 预应力损失值/kN 初始张拉力/kN 预应力损失百分比/%
沅水大桥[15] 40.2 516 7.80
株洲渌水大桥4号力筋[16] 43.0 628 6.85
株洲渌水大桥5号力筋[16] 55.0 695 7.91
陕西某连续刚构S1力筋 / / 8.80
陕西某连续刚构S2力筋 / / 9.20
表选项

数据表明，竖向预应力损失占初始张拉力比例波动较大，但是排除张拉工艺引起传力锚固时瞬时损失较大数据后，竖向预应力损失占初始张拉力百分比为7.8%~8.2%，与本文预测7.92%基本吻合.

3 结论

本文依据灰色系统理论，建立了大跨径连续箱梁桥竖向预应力损失值GM (1, 1) 模型和残差修正的非等步距GM (1, 1) 模型，经检验，预测值与实桥监测系统实测值拟合良好，表明这一方法具有相当的可靠性与准确性，可广泛应用于工程短期监测数据的长期预测分析.

影响竖向预应力损失的相关因素，诸如混凝土收缩徐变、钢筋应力松弛随时间推移逐渐减小，且各因素相互作用，叠加各因素单独引起预应力损失值与实际偏差较大，考虑钢筋松弛与时间关系为指数型函数，本文所建预测模型隐含指数模型，但为模型建立提供了一套合理系统的方法.

竖向预应力长期损失7.92%左右，而张拉锚固后前2天损失达4.0%，占总损失50%以上，7 d损失达6.5%，占总损失80%以上.《公路桥涵施工技术规范》(JTG/T F50-2011)7.9.1条关于后张法压浆及封锚规定：预应力筋张拉后，孔道应尽早压浆，在24 h内完成，否则应采取措施，确保力筋不出现锈蚀.故施工中竖向预应力锚下应力无损检测应在竖向预应力张拉完成后及时进行，建议压浆封锚前无损检测竖向预应力有效张拉力应充分考虑长期损失效应，张拉后锚下有效应力不小于设计张拉力的0.7倍为宜.

由于时间和传感器寿命有限，竖向预应力锚下实际应力仅采集到桥梁合龙后，但是桥梁二期铺装、运营过程中车辆动荷载、“潮汐现象”引起箱梁两腹板荷载不均匀分布都会对竖向预应力损失造成影响，值得进一步研究.

参考文献
[1] 交通部公路科学研究所.西部交通建设科技项目可行性研究报告:在用预应力连续箱梁、连续刚构桥箱梁开裂成因及处治技术研究[R], 2002.
Highway Science Research Institute of the Ministry of Communications.The feasibility study report of the western traffic construction science and technology project:In the study of cracking cause and treatment technology for prestressed concrete continuous box girder and rigid frame bridges[R], 2002.
[2] 施嘉.大跨径预应力混凝土连续刚构桥开裂成因分析研究[D].成都:西南交通大学, 2013.
Shi Jia.Study on the origin of cracking of long-span PC continuous rigid frame bridge[D].Chengdu:Southwest Jiaotong University, 2013.
[3] 陈妍如, 周水兴, 陈湛荣. 竖向预应力筋对连续刚构桥受力影响分析[J]. 重庆交通大学学报:自然科学版, 2008, 27(2): 173–176.
Chen Y R, Zhou X S, Chen Z R. Mechanic analysis on vertical prestressing bar to continuous rigid framed bridge[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2008, 27(2): 173–176.
[4] 于天来, 姜震. 连续刚构箱梁桥腹板开裂原因分析[J]. 中外公路, 2013, 33(2): 132–136.
Yu T L, Jiang Z. Analysis of the causes of cracks in the webs of continuous rigid box girder bridge[J]. Journal of China & Foreign Highway, 2013, 33(2): 132–136.
[5] 王玮玮.PC箱梁竖向预应力损失测试方法及应用技术研究[D].长沙:长沙理工大学, 2013.
Wang Weiwei.Research on the test methods of vertical prestressing losses and application technology in PC box girder[D].Changsha:Changsha University of Science & Technology, 2013.
[6] 周新波. 箱梁竖向预应力张拉力无损检测研究[J]. 山东大学学报 (工学版), 2013, 43(6): 77–94.
Zhou Xinbo. Non-destructive detection research of the box girder vertical prestressed tensile force[J]. Journal of Shandong University (Engineering Science), 2013, 43(6): 77–94.
[7] JTG D62-2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S].
JTG D62-2004 Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. http://www.oalib.com/references/16909281
[8] Deng J L. Negative power AGO in grey theory[J]. Journal of Grey System, 2001, 13(3): 1–6.
[9] Zhang Q S. Difference information entropy in grey theory[J]. Journal of Grey System, 2001, 13(2): 21–25.
[10] Song Z M, Wang Z D, Tong X J. Grey generating space on opposite accumulation[J]. Journal of Grey System, 2001, 13(4): 305–308.
[11] Song Z M, Xiao X P, Deng J L. The character of opposite direction AGO and class ratio[J]. Journal of Grey System, 2002, 14(1): 9–14.
[12] Deng J L. The Primary Methods of Grey Theory[M]. Wuhan: Huazhong University of Science and Technology Press, 2004: 26-34.
[13] 刘思峰, 谢乃明. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2013.
Liu Sifeng, Xie Naiming. Gray System Theory and Its Application[M]. Beijing: Science Press, 2013.
[14] 邓聚龙. 灰色控制系统[M]. 武汉: 华中理工大学出版社, 1988.
Deng J L. Gray Control System[M]. Wuhan: Huazhong University of Science and Technology Press, 1988.
[15] 黄伟群.竖向预应力长期损失的研究及施工与检测方法探索[D].湘潭:湖南科技大学, 2009.
Huang Weiqun.Research on the long-term loss and the method of construction & detection of vertical Prestress[D].Xiangtan:Hunan University of Science and Technology, 2009.
[16] 林鸣.预应力混凝土箱梁桥竖向预应力损失的研究[D].长沙:长沙理工大学, 2007.
Lin Ming.Research on vertical prestress losses in prestressed concrete box girder bridge[D].Changsha:Changsha University of Science & Technology, 2007.