文章信息
- 李亮, 褚雪松
- LI Liang, CHU Xuesong
- 考虑空间变异特性的土坡失稳模式比较分析
- Comparative analysis of failure mechanism for spatially variable slopes
- 武汉大学学报(工学版), 2016, 49(5): 690-695
- Engineering Journal of Wuhan University, 2016, 49(5): 690-695
- http://dx.doi.org/10.14188/j.1671-8844.2016-05-008
-
文章历史
- 收稿日期: 2016-04-01
边坡可靠度分析越来越受到国内外岩土工程业界的关注与重视,许多学者与工程技术人员都开展了相关的研究工作,得出了有意义的结论,为相关工程提供了技术保证,同时也丰富了边坡可靠度分析的方法与内涵[1-14].就目前研究的趋势来看,边坡确定性分析的极限平衡方法(Limit Equilibrium Method,LEM)以及强度折减方法均被用于边坡可靠度分析中.已有文献研究表明[15],对于确定性的边坡稳定分析,强度折减法和极限平衡方法能得到基本一致的安全系数,前者的优势在于无需进行滑动面形状的假定以及可以自动搜索并最终确定最危险的滑动范围,因此,边坡确定性分析时一般采用强度折减方法.若结合抽样次数较多的Monte-Carlo方法,应用强度折减法来进行边坡可靠度分析时,其巨大耗时往往会限制强度折减法在边坡可靠度分析中的应用.因此,为了节省计算时间,工程技术人员和业界研究学者会首先选择基于极限平衡方法和Monte-Carlo方法进行边坡可靠度分析.极限平衡方法和强度折减方法之间的对比研究,需要重视强度参数的空间变异特性,这一空间变异特性是土体材料固有的属性,在岩土工程业界得到了普遍认同[16].若考虑强度参数的空间变异特性之后,强度参数在边坡剖面内的分布趋于复杂,极限平衡方法和强度折减法相应的表现值得研究,本文正是着眼于这一问题,结合一土坡的短期稳定问题,利用一维随机场模拟了其不排水强度Su的空间变异特性,针对给定的随机场样本,分别应用极限平衡方法中的简化Bishop法、Morgenstern-Price法以及有限元(finite element method,FEM)强度折减法、有限差分(finite difference method,FDM)强度折减法进行了确定性分析,对比分析了其获得的安全系数以及失稳模式之间的差异,归纳总结得出了有意义的结论.
1 空间变异特性的随机场模拟土体材料强度参数的空间变异特性[17],就是不同位置上强度参数之间是相互区别又相互关联的.举例来说,若不考虑空间变异特性,则不同位置上强度参数是完全关联的(相同的);若空间变异特性无穷大,则不同位置上的强度参数之间是完全不同的.实际上,经过了不同的地质历史条件、沉积条件以后,土体材料强度参数之间的空间变异特性是介于以上两种特殊情况之间的.稳态随机场是最常用于模拟土体材料参数空间变异特性的手段之一,要构建一个稳态随机场,必须要确定某参数变量的均值、方差、自相似函数以及波动范围这4个参数.自相似函数和波动范围决定了材料参数变量空间变异特性的显著程度,一般来说,在其他条件相同的前提下,波动范围越大,空间变异特性越不显著,反之亦然.已有文献研究表明[8,9],自相似函数的不同对空间变异特性的描述有影响,在本文算例中,仅选取了一种最简单的指数型自相似函数来开展对比分析,即采用下式来确定位于点i和j的参数变量之间的相关系数ρij:
式中:dij为i和j两点之间的距离;λ为波动范围.在应用稳态随机场进行模拟之前,首先必须要对连续的随机场进行离散化,以便用于数值分析.以土体不排水强度Su为例,下文拟用竖直方向的一维稳态随机场模拟其空间变异特性,则连续的稳态随机场数学上可以表示为Su(h),经过离散后,可以表示为Su(k),k=1,2,…,n,此处,n为拟离散的水平土层数目,n的取值大小要由波动范围的大小以及敏感性分析来确定.已有研究表明[18]:离散之后的水平土层厚度Δh与波动范围λ的比值要控制在0.2以内,以便控制相对误差在10%以内.
2 边坡确定性分析方法边坡确定性分析是边坡可靠度分析的前提和基础,边坡可靠度分析中的极限状态函数一般是通过安全系数来构建的.目前一般认为边坡沿某一滑动面滑动的安全系数<1,即认为边坡沿该滑动面失稳;等于1时,边坡沿该滑动面处于极限状态;>1时,则认为边坡沿该滑动面处于可靠状态.当边坡的各种输入参数确定以后,可以选择使用极限平衡方法或者有限元强度折减法或者有限差分强度折减法来计算相应的稳定安全系数.在本文的算例中,选用加拿大Rocscience旗下的Slide 5.0中的简化Bishop法、Morgenstern-Price法以及Spencer法来进行边坡确定性安全系数的计算,此外还选用Rocscience旗下的Phase2.0有限元计算软件和Itasca旗下的FLAC软件,并结合强度折减法进行边坡稳定安全系数的计算.
当一维稳态随机场Su(h)中的均值、方差、自相似函数以及波动范围确定之后,可以用协方差分解方法产生一系列样本,即Sui(j)(j=1,2,…,n; i=1,2,…,N,其中,N为产生的样本系列数目).针对产生的每一系列样本值,分别将Sui(j)视为第j土层的Su值,来确定边坡的输入参数,最后分别采用以上3种计算策略来求解相应的边坡稳定安全系数,并记录其相应的滑动面位置(Slide5.0)以及滑动带的范围(Phase2.0和FLAC).汇总并归纳、对比分析了N系列样本值下,3种计算策略得到的安全系数以及滑动面或者滑动带范围.
3 算例分析 3.1 概述本文考虑一典型土坡的稳定性问题,如图 1所示,该土坡高度10 m,坡角45°,土的密度为2 000 kg/m3,暂不考虑其随机变异特性,即视其为一确定值.为评价该土坡的短期稳定性问题,土的不排水强度Su具有较大的变异特性,设其均值为40 kPa,标准差为12 kPa,符合对数正态分布,将该土坡在垂直方向均匀离散为12个水平土层,即Δh=1 m,n=12.采用公式(1)所示的指数型自相似函数,波动范围λ假定为5、10 m以及+∞.这样,Δh/λ限定在0.2以下.每一λ值下,利用Cholesky分解法随机生成N=10个系列样本值,将每一系列的样本值视为12个土层的Su值,再利用Slide5.0、Phase2.0、FLAC进行边坡短期稳定性分析,求得其安全系数与滑动面或者滑动带范围.需要注意的是,在进行有限元强度折减法或者有限差分强度折减法计算时,需要确定土的弹性模量和泊松比.根据文献[19],本文取E=100 MPa,泊松比v=0.3.此外,在应用Phase2.0和FLAC进行计算安全系数时,网格尺寸对计算结果有一定的影响,必须在计算之前首先进行网格尺寸敏感性分析,即先采用比较稀疏的网格计算,然后逐步加密网格,直至计算得到的安全系数与前一网格尺寸下结果相差不大或者满足一定的容许误差为止.限于篇幅,在此不再列出敏感性分析的具体结果,经最终计算分析,Phase2.0采用21 860个单元来离散图 1所示的土坡几何模型,FLAC采用19 675个单元来离散.本文算例分析是基于Phase2.0和FLAC中内置的强度折减模块进行的.
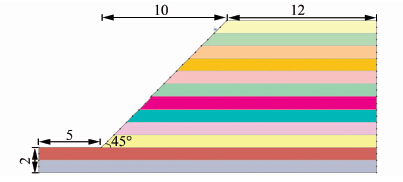
|
| 图 1 土坡的几何尺寸(单位:m) Figure 1 Geometry of soil slope (unit:m) |
将λ=5、10 m,+∞三种情况下计算得到的30组安全系数进行了汇总,以Phase2.0计算得到的安全系数作为基准,分别将简化Bishop法、Morgenstern-Price法、Spencer法、有限差分强度折减法与基准值进行了对比分析,比较结果如图 2所示.

|
| 图 2 安全系数对比 Figure 2 Comparison of Factor of safety |
由图 2可见,有限元计算方法得到的30个安全系数与有限差分法得到的安全系数之间呈现出高度的相关性,线性回归拟合的相关系数为0.999;有限元方法与简化Bishop法得到的安全系数之间也呈现出较高的相关性,相关系数为0.996.如图 2(c),有限元方法与Morgenstern-Price方法得到的安全系数之间呈现出相对较弱的相关性,其相关系数为0.87.对比发现,在确保网格尺寸对计算结果最小影响的前提下,有限元强度折减法与有限差分强度折减法得到的安全系数是一致的,简化Bishop法得到的安全系数与有限元强度折减法所得结果呈现出很强的相关性,线性回归拟合的相关系数达到0.996,这说明对于本文算题而言,尽管简化Bishop法适用于圆弧滑动面,但是其安全系数与有限元法具有可比性.然而,Morgenstern-Price法所得的安全系数与有限元法所得结果具有明显的不一致趋势,尽管其线性拟合的相关系数也有0.87之多.究其原因在于:Morgenstern-Price法在计算过程中,由于涉及到较多、复杂的迭代过程,有些可行滑动面的安全系数无法求出,导致搜索算法陷入局部最小,从而无法找到最小安全系数.Spencer法计算得到的安全系数与有限元法结果之间也呈现出较明显的分散性.因此,当应用Morgenstern-Price法和Spencer法进行最小安全系数搜索时,要变换不同的搜索算法,可以尝试应用不连续飞行粒子群算法[20]、和声搜索算法[21,22]来进行.
接着以波动范围λ=5 m为例,图 3对3种计算方法得到的失稳模式(包括滑动面以及滑动范围)进行了对比,由于有限元强度折减法和有限差分强度折减法得到的失稳模式是以塑性应变云图形式表示的,而极限平衡方法得到的失稳模式却是一条曲线,因此在判断几种方法所得到的失稳模式是否吻合时,需要加入读者的主观判断.如果极限平衡方法所得的曲线完全落入强度折减法得到的云图里面,即可认为是两种失稳模式吻合较好.从图 3对比来看,有限元以及有限差分强度折减法得到的塑性应变云图基本一致.就简化Bishop法得到的滑动面来看,除第7、第10个样本值外,简化Bishop法的曲线与强度折减法的塑性应变云图均相吻合;然而就Mor-genstern-Price和Spencer法而言,仅仅在第8个样本值下与强度折减法塑性应变云图吻合较好,反映出这两种极限平衡方法在搜索最小安全系数过程陷入局部最优,无法找到全局最小的安全系数以及失稳模式.另外,在第7、第10个样本值下,强度折减法得到了复合失稳模式,两个失稳模式在滑入端重合,在坡面的滑出端分离.非常有趣的是,在第7个样本值下简化Bishop法和Morgenstern-Price法得到的滑动面分别相应于复合失稳模式中的一个.但是,对于第10个样本值而言,简化Bishop法和Morgenstern-Price法的滑动面均相应于其中的一个失稳模式.

|
| 图 3 有限元法、有限差分法以及极限平衡方法所得失稳模式对比图(λ=5 m) Figure 3 Summary of FS and FM for FEM,FDM,and LEM procedures at λ=5 m |
Taylor研究指出[23],对于均质土坡短期稳定问题,坡角是否>53°可以作为判别浅层与深层滑坡的标准.对于均质边坡而言,坡角>53°一般发生浅层滑坡(滑出端经过坡脚),而坡角<53°则发生深层失稳(滑动面与坡底相切).当考虑土体材料的空间变异特性之后,上述判断标准已经不再适用.从图 3可以发现,本例中的坡角为45°,在第3、5、8、10样本值下,出现了浅层失稳,而在第1、2、4、6、10样本值下,出现了深层失稳,在第7个样本值下出现了浅层和深层复合失稳模式.可见,在考虑土体材料空间变异特性之后,边坡的失稳模式划分标准趋于复杂,仅仅通过坡角大小无法刻画.
图 4给出了波动范围为+∞时(即不考虑土体材料空间变异特性)几种方法得到的失稳模式对比图.由于不考虑空间变异特性,12个水平土层的Su值相同,相应问题变为均质土坡问题.由图 4可见,几种方法所得失稳模式基本吻合,而且出现深层失稳,这与Taylor划分标准吻合.由于为均质土坡问题,尽管安全系数不同,10个样本值下每次计算得到的滑动面或者滑动范围都是一致的.
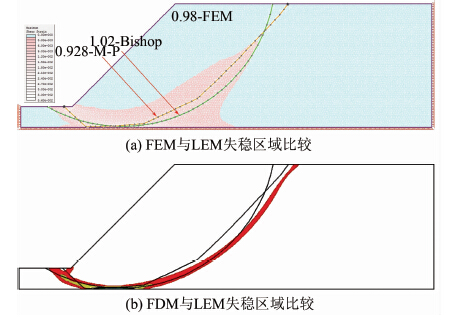
|
| 图 4 有限元法、有限差分法以及极限平衡方法所得 失稳模式对比图(λ=+∞) Figure 4 Summary of FS and FM for FEM,FDM,and LEM procedures at λ=+∞ |
考虑土体材料强度参数的空间变异特性之后,边坡稳定分析常用的数值手段是否适用值得探讨.本文通过一个简单的典型土坡算例,应用一维稳态随机场模拟了其在竖直方向的空间变异特性.分别利用Phase2.0、FLAC以及Slide 5.0数值分析软件对每个样本值下的安全系数以及失稳模式进行了计算,对比分析了不同波动范围下(不同的空间变异特性程度)几种数值计算方法结果之间的异同.
1) 在消除网格尺寸影响后,有限元强度折减法与有限差分强度折减法所得的安全系数与失稳模式一致.
2) 极限平衡方法中的简化Bishop法所得安全系数与强度折减法结果具有高度的相关性,线性拟合回归的相关系数接近1.0;除边坡发生复合失稳模式以外,简化Bishop法所得失稳模式与强度折减法相吻合.
3) 极限平衡方法中的Morgenstern-Price法和Spencer法虽然较之于简化Bishop法更加严谨,但是由于计算过程中所需的复杂迭代步骤导致搜索过程陷入局部最小,从而无法找到最优的安全系数和失稳模式,在考虑空间变异特性的边坡可靠度分析中,尽量避免使用.
4) 考虑土体材料参数空间变异特性之后,判断边坡发生浅层与深层失稳模式的标准趋于复杂化,不能仅仅通过坡角来判断.
| [1] |
李典庆, 周创兵, 陈益峰, 等. 边坡可靠度分析的随机响应面法及程序实现[J].
岩石力学与工程学报, 2010, 29(8): 1513–1523.
Li Dianqing, Zhou Chuangbing, Chen Yifeng, et al. Reliability analysis of slope using stochastic response surface method and code implementation[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1513–1523. |
| [2] |
陈昌富, 朱剑锋, 龚晓南. 基于响应面法和Morgenstern-Price法土坡可靠度计算方法[J].
工程力学, 2008, 25(10): 166–172.
Chen Changfu, Zhu Jianfeng, Gong Xiaonan. Calculation method of earth slope reliability based on response surface method and Morgenstern-Price procedure[J]. Engineering Mechanics, 2008, 25(10): 166–172. |
| [3] | Christian J. Geotechnical Engineering reliability: How well do we know what we are doing?[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(10): 985–1003. DOI:10.1061/(ASCE)1090-0241(2004)130:10(985) |
| [4] | Zhu H, Griffiths D V, Fenton G A, Zhang L M. Undrained failure mechanisms of slopes in random soil[J]. Engineering Geology, 2015, 191: 31–35. DOI:10.1016/j.enggeo.2015.03.009 |
| [5] | Wang Y, Cao Z, Au S K. Practical reliability analysis of slope stability by advanced Monte Carlo simulations in a spreadsheet[J]. Canadian Geotechnical Journal, 2011, 48(1): 162–172. DOI:10.1139/T10-044 |
| [6] | Ji J, Liao H J, Low B K. Modeling 2-D spatial variation in slope reliability analysis using interpolated autocorrelations[J]. Computers and Geotechnics, 2012, 40: 135–146. DOI:10.1016/j.compgeo.2011.11.002 |
| [7] | Ji J, Low B K. Stratified response surfaces for system probabilistic evaluation of slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(11): 1398–1406. DOI:10.1061/(ASCE)GT.1943-5606.0000711 |
| [8] | Jiang S H, Li D Q, Zhang L M, Zhou C B. Slope reliability analysis considering spatially variable shear strength parameters using a non-intrusive stochastic finite element method[J]. Engineering Geology, 2014, 168: 120–128. DOI:10.1016/j.enggeo.2013.11.006 |
| [9] | Li D Q, Xiao T, Cao Z J, Zhou C B, Zhang L M. Enhancement of random finite element method in reliability analysis and risk assessment of soil slopes using Subset Simulation[J]. Landslides, 2016, 13(2): 293–303. DOI:10.1007/s10346-015-0569-2 |
| [10] | Li L, Wang Y, Cao Z J, Chu X S. Risk de-aggregation and system reliability analysis of slope stability using representative slip surfaces[J]. Computers and Geotechnics, 2013, 53: 95–105. DOI:10.1016/j.compgeo.2013.05.004 |
| [11] | Li L, Wang Y, Cao Z J. Probabilistic slope stability analysis by risk aggregation[J]. Engineering Geology, 2014, 176: 57–65. DOI:10.1016/j.enggeo.2014.04.010 |
| [12] | Li L, Chu X S. Multiple response surfaces for slope reliability analysis[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(2): 175–192. DOI:10.1002/nag.v39.2 |
| [13] | Li L, Chu X S. Comparative study on response surfaces for reliability analysis of spatially variable soil slope[J]. China Ocean Engineering, 2015, 29(1): 81–90. DOI:10.1007/s13344-015-0006-2 |
| [14] | Chu X S, Li L, Wang Y J. Slope reliability analysis using length-based representative slip surfaces[J]. Arabian Journal of Geosciences, 2015, 8(11): 9065–9078. DOI:10.1007/s12517-015-1905-5 |
| [15] | Phoon K K, Kulhawy F H. Characterization of geotechnical variability[J]. Canadian Geotechnical Journal, 1999, 36(4): 612–624. DOI:10.1139/t99-038 |
| [16] |
赵尚毅, 郑颖人, 时卫民, 等. 用有限元强度折减法求边坡稳定安全系数[J].
岩土工程学报, 2002, 24(3): 343–346.
Zhao Shangyi, Zheng Yingren, Shi Weimin, et al. Analysis of safety factor of slope by strength reduction FEM[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(3): 343–346. |
| [17] | Vanmarcke E H. Probabilistic modeling of soil profiles[J]. Journal of the Geotechnical Engineering Division, ASCE, 1977, 103(11): 1227–1246. |
| [18] | Li L, Chu X S. Effect of 2-D random field discretization on failure probability and failure mechanism in probabilistic slope stability[J]. Geotechnical and Geological Engineering, 2016, 34(2): 437–447. DOI:10.1007/s10706-015-9955-8 |
| [19] | Tabarroki M, Ahmad F, Banaki R, Jha S K, Ching J Y. Determining the factors of safety of spatially variable slopes modeled by random fields[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(12): 2082–2095. DOI:10.1061/(ASCE)GT.1943-5606.0000955 |
| [20] | Li L, Yu G M, Chen Z Y, Chu X S. Discontinuous flying particle swarm optimization algorithm and its application to slope stability analysis[J]. Journal of Central South University of Technology, 2010, 17(4): 852–856. DOI:10.1007/s11771-010-0566-5 |
| [21] | Li L, Chu X S. An improved particle swarm optimization algorithm with harmony strategy for the location of critical slip surface of slopes[J]. China Ocean Engineering, 2011, 25(2): 357–364. DOI:10.1007/s13344-011-0030-9 |
| [22] | Li L, Cheng Y M, Chu X S. A new approach to the determination of the critical slip surfaces of slopes[J]. China Ocean Engineering, 2013, 27(1): 51–64. DOI:10.1007/s13344-013-0005-0 |
| [23] | Taylor D W. Stability of earth slopes[J]. Journal of the Boston Society of Civil Engineers, 1937, 24(3): 337–386. |
 2016, Vol. 49
2016, Vol. 49



