武汉大学学报(工学版)   2016, Vol. 49 Issue (4): 527-532

文章信息

王越, 梅亚东, 鲍正风, 孔艳君, 员江斌
WANG Yue, MEI Yadong, BAO Zhengfeng, KONG yanjun, YUN Jiangbin
不同调峰方式下三峡-葛洲坝梯级电站期望效益模型及应用
Application of expected benefit model in Three Gorges cascade hydropower stations with different peak shaving modes
武汉大学学报(工学版), 2016, 49(4): 527-532
Engineering Journal of Wuhan University, 2016, 49(4): 527-532
http://dx.doi.org/10.14188/j.1671-8844.2016-04-008

文章历史

收稿日期: 2015-04-26
 Abstract              PDF               Figures               Tables
引用本文 0
王越, 梅亚东, 鲍正风, 孔艳君, 员江斌. 不同调峰方式下三峡-葛洲坝梯级电站期望效益模型及应用[J]. 武汉大学学报(工学版), 2016, 49(4): 527-532.
WANG Yue, MEI Yadong, BAO Zhengfeng, KONG yanjun, YUN Jiangbin. Application of expected benefit model in Three Gorges cascade hydropower stations with different peak shaving modes[J]. Engineering Journal of Wuhan University, 2016, 49(4): 527-532.
不同调峰方式下三峡-葛洲坝梯级电站期望效益模型及应用
王越1,4, 梅亚东1,2, 鲍正风3, 孔艳君1,2, 员江斌1,2     
1. 武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072;
 2. 武汉大学水资源安全保障湖北省协同创新中心，湖北 武汉 430072;
 3. 中国长江电力股份有限公司三峡水利枢纽梯级调度通信中心，湖北 宜昌 443133;
 4. 中国水电建设集团国际工程有限公司，北京 100048
收稿日期: 2015-04-26
作者简介: 王越（1990-），男，硕士研究生，研究方向为水资源系统规划及管理，E-mail：wy1615@whu.edu.cn.
通讯作者: 梅亚东（1963-），男，教授，研究方向为水资源系统规划及管理，E-mail：ydmei@whu.edu.cn
基金项目: 国家自然科学基金重点项目（编号：51239004）；国家自然科学基金面上项目（编号：51479140）.
摘要: 考虑水电站参与调峰对时段平均出力的限制要求，结合实际电站的典型日出力过程与峰荷分布规律，以水电站的最大出力为随机变量，基于该随机变量服从指数分布的假设，以总调峰效益期望最大为目标，建立了长江三峡-葛洲坝梯级水电站长期优化调度模型，详细分析了三峡-葛洲坝电站单峰调峰、双峰调峰和逐月调峰3种调峰运行方式，计算了相应的分布参数和发电量.计算结果表明：该模型能在长期优化调度中更好地体现电力系统对水电的调峰需求，3种调峰方式运行下三峡-葛洲坝梯级多年平均电量分别是1 080、1 055、1 079亿kW·h，梯级调峰损失电量分别为9.9、34.6、9.5亿kW·h.
关键词： 三峡梯级     期望函数     调峰运行方式     水库调度     指数分布    
Application of expected benefit model in Three Gorges cascade hydropower stations with different peak shaving modes
WANG Yue1,4, MEI Yadong1,2, BAO Zhengfeng3, KONG yanjun1,2, YUN Jiangbin1,2     
1. State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China;
 2. Hubei Provincial Collaborative Innovation Center for Water Resources Security, Wuhan University, Wuhan 430072，China;
 3. Three Gorges Cascade Dispatching & Communication Center of China Yangtze River Power Co. Ltd，Yichang 443133，China;
 4. Sino Hydro Corporation Limited，Beijing 100048，China
Abstract: To meet peak shaving demand under the large-scale power grid platform in the long-term operation，hydropower stations’ average output needs to be controlled. This paper takes the maximum output of hydropower as a random variable, and based on the hypothesis that the variable follows exponential distributions, a long-term optimization model of the maximum peak shaving expectation for the Three Gorges cascade hydropower stations is established. This paper analyzes three peak-shaving modes for hydropower stations：i.e. single-peak curve, double-peak curve and setting the monthly limit value of output. And then, the corresponding distribution parameters are calculated. A case study of the Three Gorges cascade hydropower stations shows that the model of the maximum peak shaving expectation is effective in improving the peak regulation capacity. The hydropower generations of cascade reservoirs in three peak-shaving modes are 108, 105.5 and 107.9 TW·h; while the electricity loss caused by peak-shaving are 990, 3460 and 950 GW·h respectively.
Key words: Three Gorges cascade     expectation function     operation mode of peak shaving     optimal regulation     exponential distribution    

水电机组启停迅速、运行灵活，且水库一般都有调节能力，因而水电站在电网中多承担调峰、调频任务，即预留一定可用水量在用电高峰时段发电，最大限度地代替其他电站的工作容量，使余留给系统其他电站的负荷尽量平稳，从而有效减轻系统调峰压力，改善供电质量，达到减少整个电力系统燃料消耗的目的，保证电网的安全、稳定、经济运行[1, 2].

水电长期调峰任务要求控制水电站各时段的平均出力在某个出力限值以下，该出力限值应小于该时段的预想出力.这也是预留一定的调峰容量以便在高峰时投入的结果.针对水电长期调峰优化问题，目前主要有2种研究途径：1)通过出力约束即给定单站和系统的平均出力限制范围[3]；2)以调峰效益为目标建立优化模型[4].陈毕胜[5]、王金文[6]和武新宇[7]等分别从长期调峰效益最大、短期调峰电量最大以及长期典型日调峰电量最大对水电站调峰能力进行深入研究，何光宇[8]、何莉[9]和吴正佳[10]等针对三峡梯级水电站群构建了以调峰为目标的优化调度模型，并根据问题特点对传统算法进行改进，结合实例取得了较好的计算结果.已有研究对于考虑调峰限制下的水电站时段最大出力的确定方法：1)用装机容量乘以调峰系数取固定值，这种方法具有经验性，并且不能考虑到实际电站的典型日出力过程；2)将其假设为服从出力区间上均匀分布的随机变量[11]，使得最大出力在区间范围内等可能出现，这也与实际峰荷分布规律不甚相符.针对以上问题，为了兼顾长时期各时段调峰能力，文章以水电站的最大出力为随机变量，基于该随机变量服从指数分布的假设建立以效益期望值最大为目标的数学模型，并结合实际电站典型日负荷过程确定参数值，在不同调峰方式下进行计算分析.

1 调峰期望数学模型

文献[12]提出水电站调峰效益期望函数，该函数中用EB表示水电站单时段出力效益B的期望值.

1) 设调峰要求限制的水电站单时段出力上限为x，其概率密度函数为

$f(x)>0,x\in [{{N}_{\text{p}}},{{N}_{\text{y}}}],且满足\int_{{{N}_{p}}}^{{{N}_{y}}}{f(x)}dx=1$    (1)

式中：Np为调峰限制出力的最小可能值；Ny为水电站的装机容量(或预想出力).

则可求得该时段水电站出力效益B的期望值为

${{E}_{B}}=\int_{{{N}_{p}}}^{{{N}_{y}}}{Nf(x)}dx$    (2)

当N≤Np时：

${{E}_{B}}=\int_{{{N}_{p}}}^{{{N}_{y}}}{Nf(x)}dx=N\int_{N_{p}^{{}}}^{{{N}_{y}}}{f(x)}dx=N$    (3)

当Np＜N≤Ny时：

${{E}_{B}}=\int_{{{N}_{p}}}^{{{N}_{y}}}{\min \left( N,x \right)f(x)}dx=N-\int_{N_{p}^{{}}}^{N}{\left( N-x \right)}f(x)dx$    (4)

由式(2)~(4)可知，效益期望函数的物理意义是当时段出力小于Np时，水电站不会受调峰要求的影响，其发电效益就是N，当时段出力超过Np时，式(4)中减去部分即为受调峰出力限制下效益损失的期望值.

文献[12]中假定f(x)服从均匀分布.考虑到调峰要求限制的电站最大出力在[Np,Ny]范围内并非均匀分布，而是x越大，概率密度越小，因此假设x服从[Np,Ny]上的指数分布，并探讨该过程下调峰运行方式对水电站发电量的影响，其概率密度函数为

$f(x)=\left\{ \begin{align} & \lambda {{e}^{-\lambda x}}x>0 \\ & 0x\le 0 \\ \end{align} \right.$    (5)

将式(5) 代入式(4)中，由分部积分公式整理后，进一步得到单个电站时段调峰效益期望值表达式：

${E_B} = \left\{ {\begin{array}{*{20}{l}} N&,&{N \le {N_p}}\\ {N - \frac{1}{\lambda }{e^{ - \lambda N}} + ({N_p} - N + \frac{1}{\lambda }){e^{ - \lambda {N_p}}}}&,&{N \ge {N_p}} \end{array}} \right.$    (6)

λ为指数分布特征值，受到不同调峰方式影响，可利用矩法估计确定，$\hat{\lambda }=1/E,E$为实际电站典型日出力过程中调峰限制出力值的期望，在出力单位MW下求得.

1.1 目标函数

在满足综合利用前提下，以梯级电站总调峰效益期望最大为目标，优化梯级水电站长期调度方式，目标函数表达式为

$\max \sum\limits_{t=1}^{T}{\sum\limits_{j=1}^{m}{E\left[ B_{t}^{j}(N_{t}^{j}) \right]}}\cdot \Delta t$    (7)

式中：t为时段编号；j为水电站编号；m为系统中电站个数，T表示时段个数；Δt为计算时段小时数；E[Btj(Ntj)]表示系统中第j个水电站t时段调峰效益期望函数.式(7)中单个水电站时段调峰的出力效益E[Btj(Ntj)]按式(6)计算.

为满足水电站设计保证率要求，当时段出力低于保证出力时，引入如下“罚函数”：

$\left\{ \begin{array}{*{35}{l}} N_{t}^{\prime j}=N_{t}^{j}-\sigma A{{\left( N_{b}^{j}-N_{t}^{j} \right)}^{a}} \\ A,a>0 \\ \sigma =\left\{ \begin{align} &0\text{ }N_{t}^{j}\ge N_{b}^{j} \\ &1\text{ }N_{t}^{j}＜N_{b}^{j} \\ \end{align} \right. \\ \end{array} \right.$    (8)

式中：N′tj为惩罚后的名义出力；Nbj为对应水电站的保证出力；A、a为非负罚系数.引入罚函数后，将式(8)代入式(7)计算出力效益期望值.

1.2 约束条件

1) 水量平衡约束：

${{V}_{t+1,j}}={{V}_{t,j}}+({{Q}^{I}}_{t,j}-{{Q}^{O}}_{t,j})\cdot {{\tau }_{t}}$    (9)

式中：Vt,j、Vt+1,j分别为第j水电站第t时段初、末的水库蓄水量；QI，t,j、QO,t,j分别表示第j水电站第t时段平均入库和出库流量；τt表示换算系数.

2) 上下游水电站间水量联系：

${{Q}^{I}}_{t,j}={{Q}^{O}}_{t,j-1}+{{Q}^{J}}_{t,j}$    (10)

式中: QJ,t,j为第j水电站t时段扣除上游相邻水电站出流后的区间来水流量.

3) 水库水位限制：

$Z_{_{t+1,j}}^{\min }\le {{Z}_{t+1,j}}\le Z_{_{t+1,j}}^{\max }$    (11)

式中：minZt+1,j为第j水电站水库第t时段末允许消落水位的下限；maxZt+1,j表示第j水电站水库第t时段末允许蓄水的水位上限，在汛期、非汛期分别对应为汛限水位和正常蓄水位.

4) 水库下泄流量约束：

$Q_{_{t,j}}^{\min }\le {{q}_{t,j}}\le Q_{_{t,j}}^{\max }$    (12)

式中：maxQt,j、minQt,j分别表示第j水电站水库第t时段下泄流量的上下限，上限取决于电站过水能力和水库泄洪能力，下限则根据下游综合利用要求确定(灌溉、航运、生态等).

5) 水电站出力限制：

$P_{_{t,j}}^{\min }\le N_{t}^{j}\le P_{_{t,j}}^{\max }$    (13)

式中：maxPt,j、minPt,j分别表示第j个水电站t时段水电站出力的上下限，取决于机组额定出力、受阻容量及调峰等要求.

6) 边界条件：

${{Z}_{1,j}}={{Z}_{c,j}},{{Z}_{T+1,j}}={{Z}_{e,j}}$    (14)

式中：Zc,j、Ze,j分别为第j水电站调度期初、末的水库蓄水位.

2 不同调峰运行方式分析 2.1 调峰曲线模式

电站在系统中的日运行方式对其调峰能力有一定影响，并决定了长期调度中水电站考虑调峰限制下的时段最大出力值.目前三峡电站的日调节运行主要模式可分为单峰模式和双峰模式[13]，结合三峡梯调中心提供的三峡、葛洲坝电站典型日调峰出力过程，对2种调峰模式分析如下.

1) 单峰模式：日出力过程线为单峰单谷形状，如图 1、2所示，在单峰模式下，9:00~21:00为高峰时段，其他时段为低谷时段，峰谷负荷时间各占1/2.

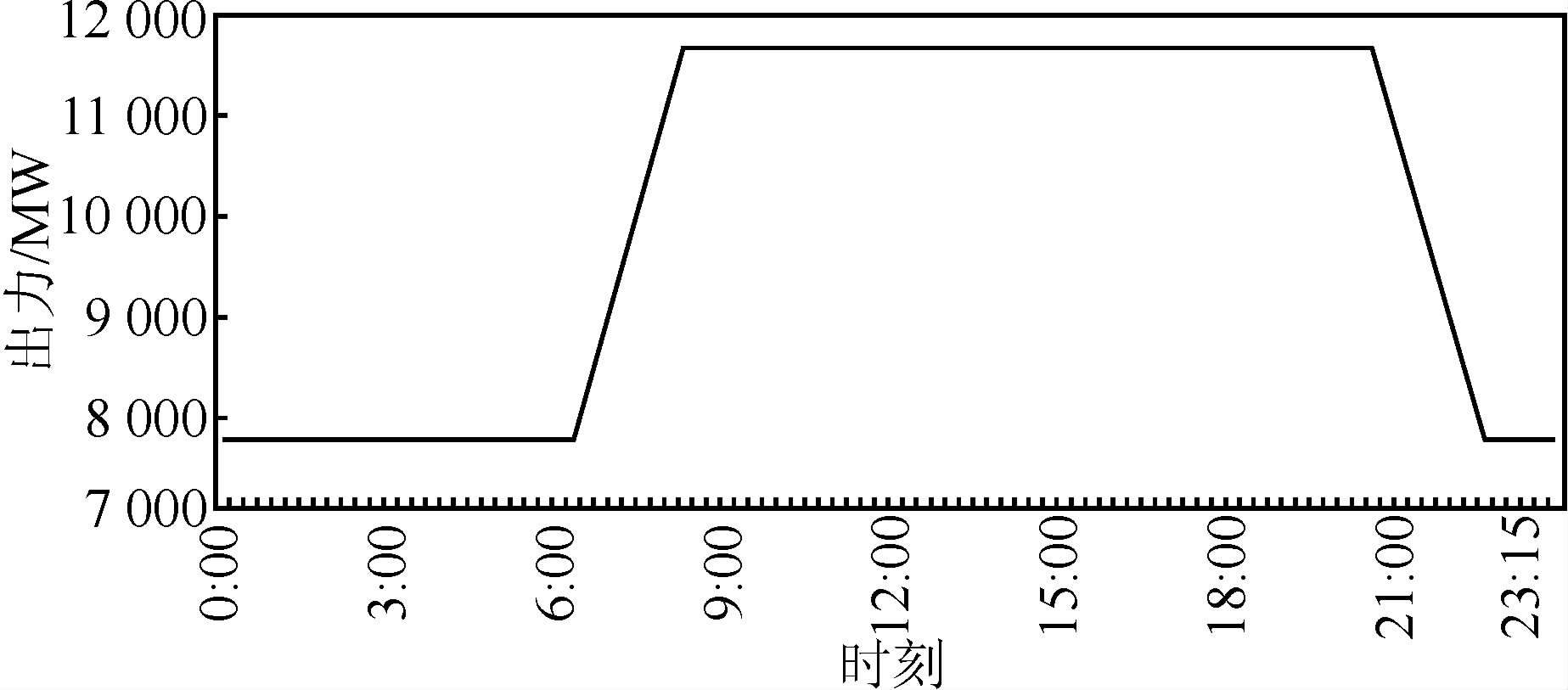
图 1 三峡电站单峰模式典型日调峰出力过程(时段：15 min) Figure 1 Typical daily load curve of Three Gorges hydropower plant in single-peak mode
图选项
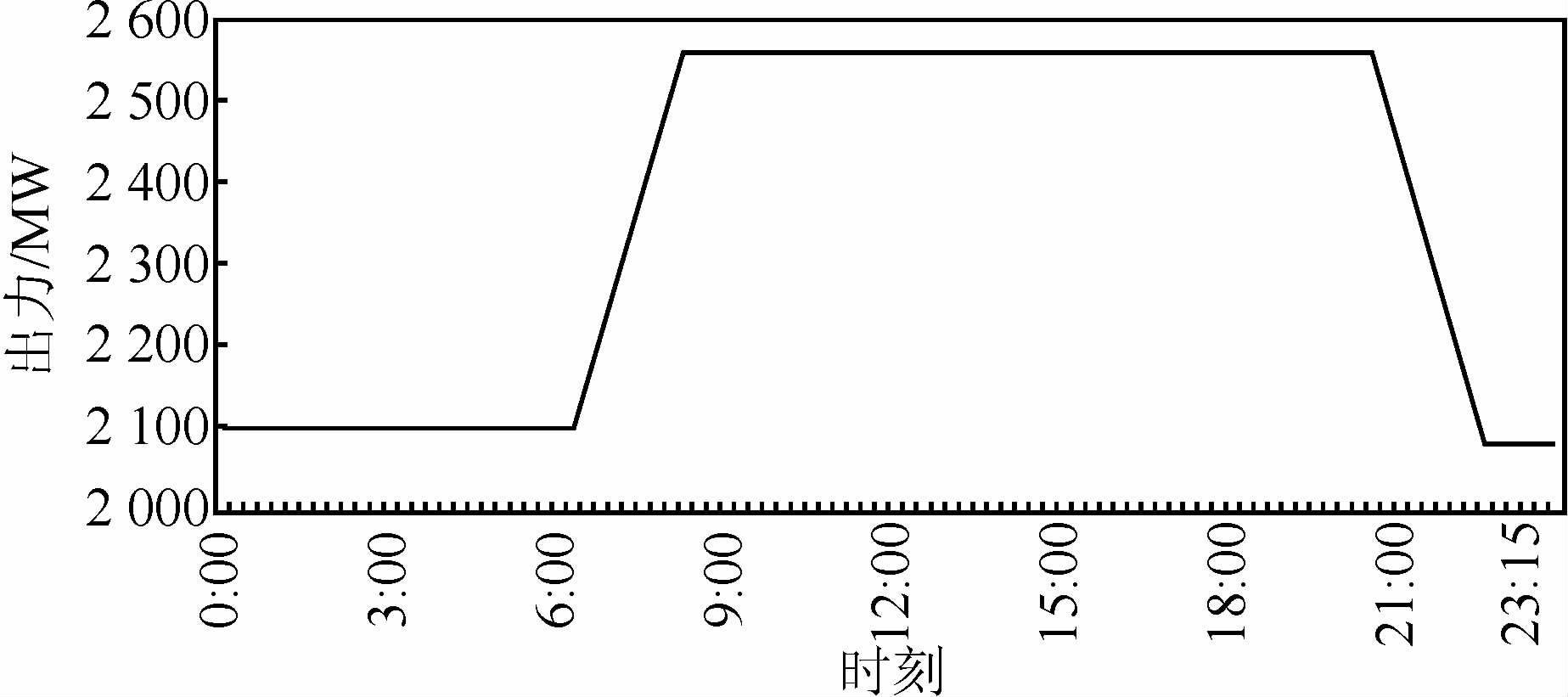
图 2 葛洲坝电站单峰模式典型日调峰出力过程(时段：15min) Figure 2 Typical daily load curve of GZB hydropower plant in single-peak mode
图选项

三峡电站在不同的日平均来流下，调节能力不同，图 1中三峡电站日均出力10 080 MW，日均出库流量13 400 m3/s，这个流量下日调峰量在3 000~4 000 MW；图 2为与图 1同一天过程下葛洲坝电站的日调峰负荷曲线，日均出力2 400 MW，作为反调节水库，葛洲坝电站调峰能力有限，在三峡电站调峰时，只需要合理利用反调节库容进行反调节，削减三峡调峰引起的不稳定流，适应航运的需要即可，基本日调峰量在400~500 MW左右.

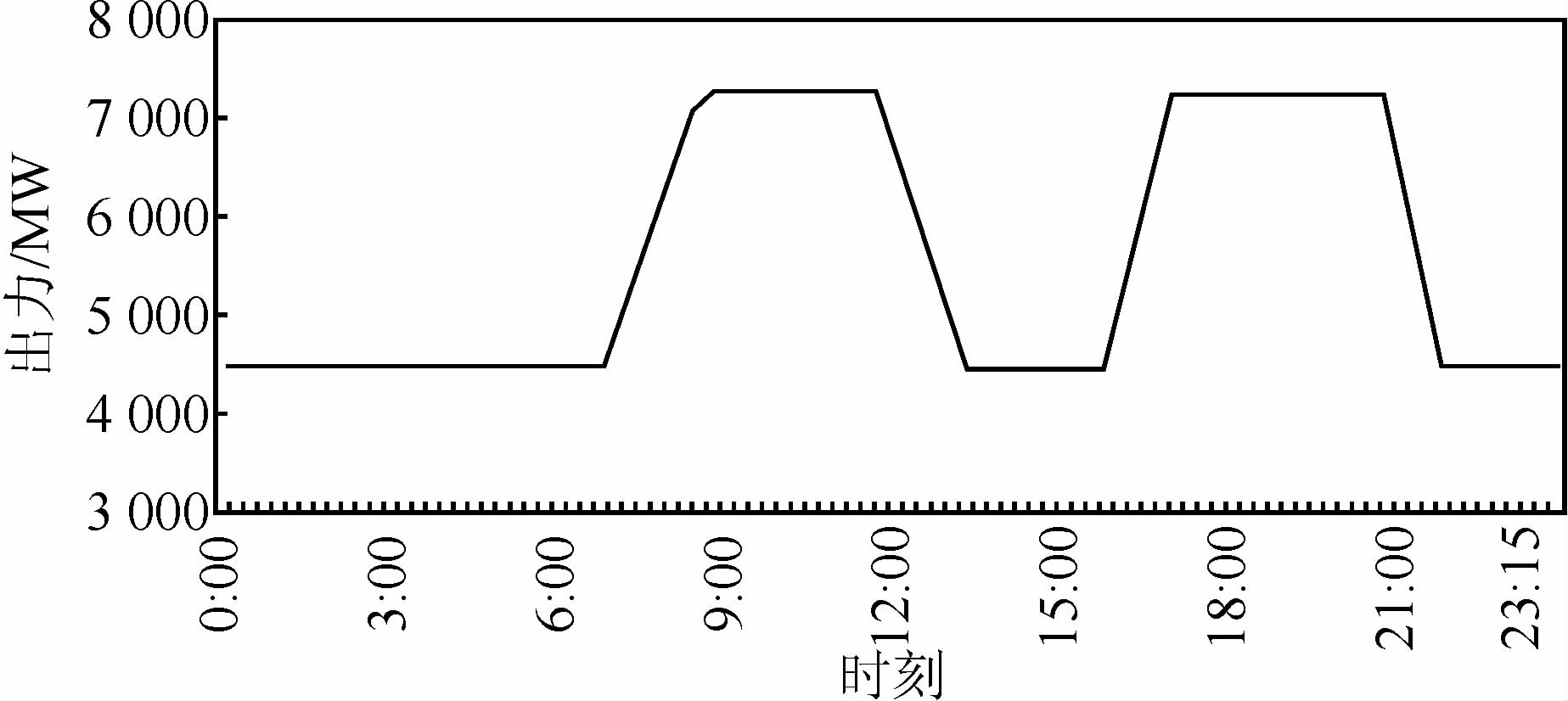
2) 双峰模式：日出力过程线为双峰形状(又称马鞍形状)，如图 3所示，即一日内8:00~12:00为早峰时段，18:00~22:00为晚峰时段，负荷低谷出现在23:00~次日7:00，其他时段为腰荷时段，峰谷腰负荷时间各占1/3.

图 3 三峡水电站双峰模式下典型日调峰出力过程(时段：15 min) Figure 3 Typical daily load curve of Three Gorges hydropower plant in double-peak mode
图选项

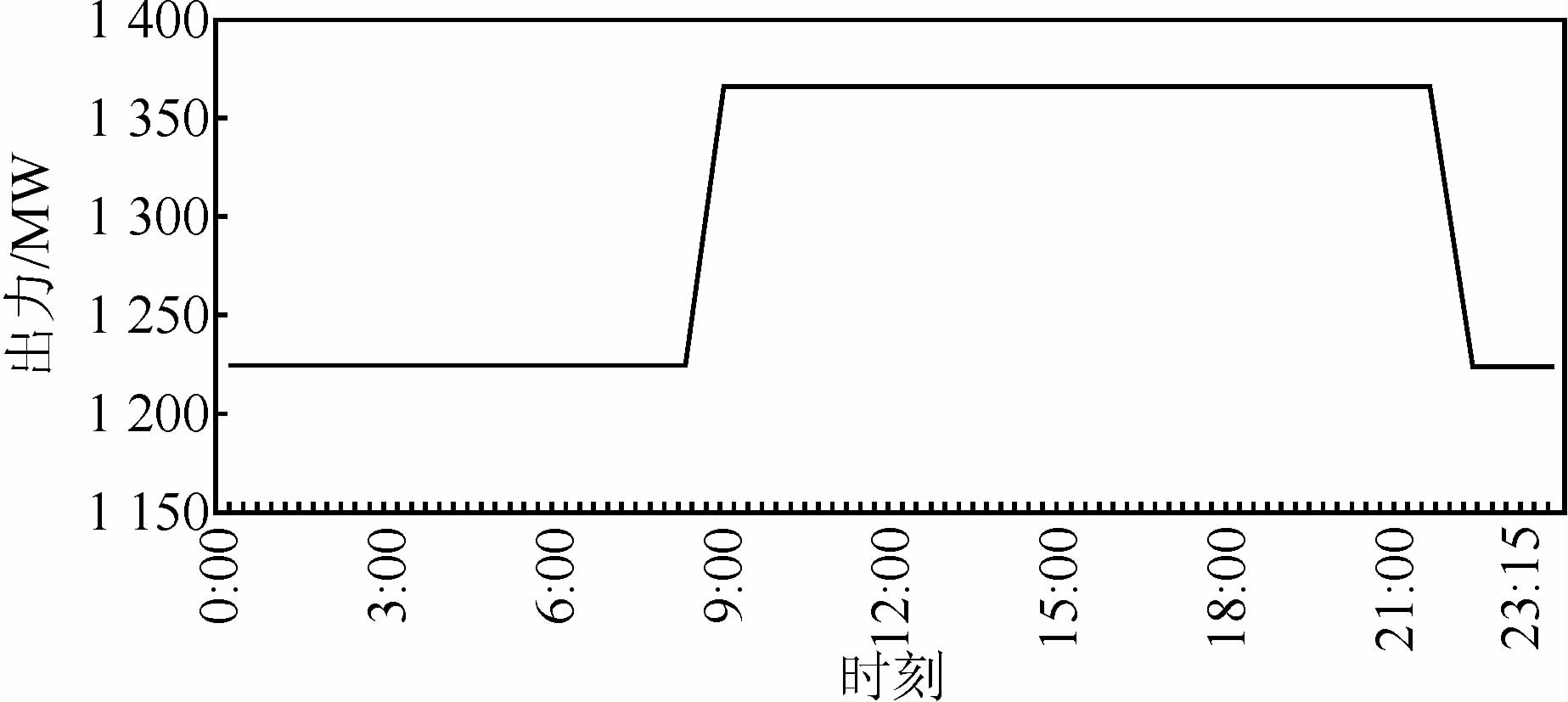
图 3中三峡电站日均出库流量6 000 m3/s，日均出力5 520 MW，同一天葛洲坝出力过程相对简单(图 4)，与单峰模式下相比差别不大，日均出力1 300 MW，并没有出现双峰的过程.

图 4 葛洲坝电站在三峡电站双峰下日出力过程(时段：15 min) Figure 4 Typical daily load curve of GZB hydropower plant in double-peak mode
图选项
2.2 不同调峰方式下参数确定

对于模型式(8)中的参数λ，不同的调峰运行方式下取值不同，计算如下3种调峰方式下的参数λ值.

方式1：根据单峰模式曲线下的电站日出力过程确定.

方式2：根据双峰模式曲线下的电站日出力过程确定.

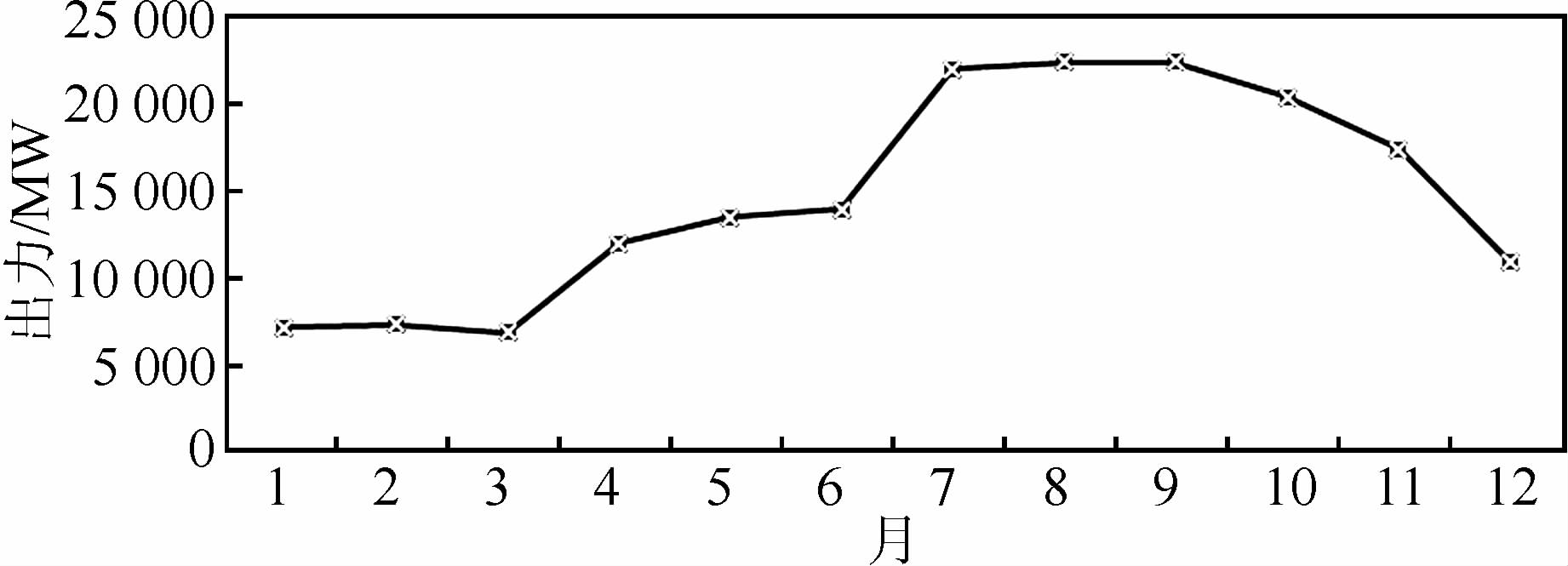
方式3：考虑电站各月来水流量不同导致出力大小的差异，结合三峡电站实际年份各月份参与调峰最大出力过程图(图 5)，取各月不同的调峰限制出力Np约束计算电站调峰能力，葛洲坝不单独考虑，以装机容量为上限.

图 5 三峡电站2014年各月平均调峰限制出力最大值 Figure 5 The monthly limit value of Three Gorges hydropower plant’s output in 2014
图选项

综上，求解其调峰限制出力值与参数λ，如表 1、2所示.

表 1 三峡、葛洲坝调峰模型参数值 Table 1 Distribution parameters of the cascaded reservoirs
电站参数/MW 单峰 双峰
Ny N>p N>p/MW λ(×10-4) N>p/MW λ(×10-4)
三峡 22 500 4 990 11 700 1.4 7 200 1.17
葛洲坝 2 940 1 040 2 560 1 370
表选项
表 2 三峡、葛洲坝逐月限制调峰方式下模型λ值(×10-4) Table 2 Distribution parameters of the cascaded reservoirs
月份
123456789101112
三峡
葛洲坝		 1.96 1.93 2.02 1.33 1.21 1.18 0.8 0.78 0.78 0.85 0.98 1.43
表选项
2.3 求解方法

对于多阶段决策的水电站群优化调度问题，通常采用动态规划方法求解.当水库数目较少时(2~5个水库)，使用动态规划方法可得到全局最优值[14].文章研究对象为1库2站梯级，可直接采用动态规划方法进行模型求解，求解步骤参照文献[15, 16].

2.4 结果分析

针对长江干流三峡、葛洲坝梯级水电站，选用1960-2009年共计49 a的径流资料，以月为计算时段，采用动态规划求解方法对建立的模型进行优化计算，得到优化调度结果(表 3).

表 3 不同运行方式下多年平均发电量比较 Table 3 Results of optimal operation

参数		 不考虑调峰 单峰调峰 双峰调峰 逐月修正
三峡/亿kW·h 908 899 881 900
葛洲坝/亿kW·h 181 181 174 180
梯级发电量/亿kW·h 1 089 1 080 1 055 1 080
三峡调峰损失电量/亿kW·h 9.7 26.9 8.11
葛洲坝调峰损失电量/亿kW·h 0.23 7.7 1.36
梯级总调峰损失电量/亿kW·h 9.93 34.6 9.47
梯级历时保证率/% 96.9 97.2 97 96.7
表选项

从表 3可见，不考虑调峰的实际电站优化调度总年平均发电量为1 089亿kW·h，在调峰期望效益最大模型计算下调度期内年均发电量分别为单峰模式1 080亿kW·h、双峰模式1 055亿kW·h、逐月调峰模式1 080亿kW·h；3种调峰模式下三峡电站因调峰损失的电量分别占不考虑调峰时三峡电站年均发电量的1.07%、2.96%、0.89%，葛洲坝电站在不同调峰模式下损失的电量分别占不考虑调峰时葛洲坝电站年均发电量的0.1%、4%、1%.

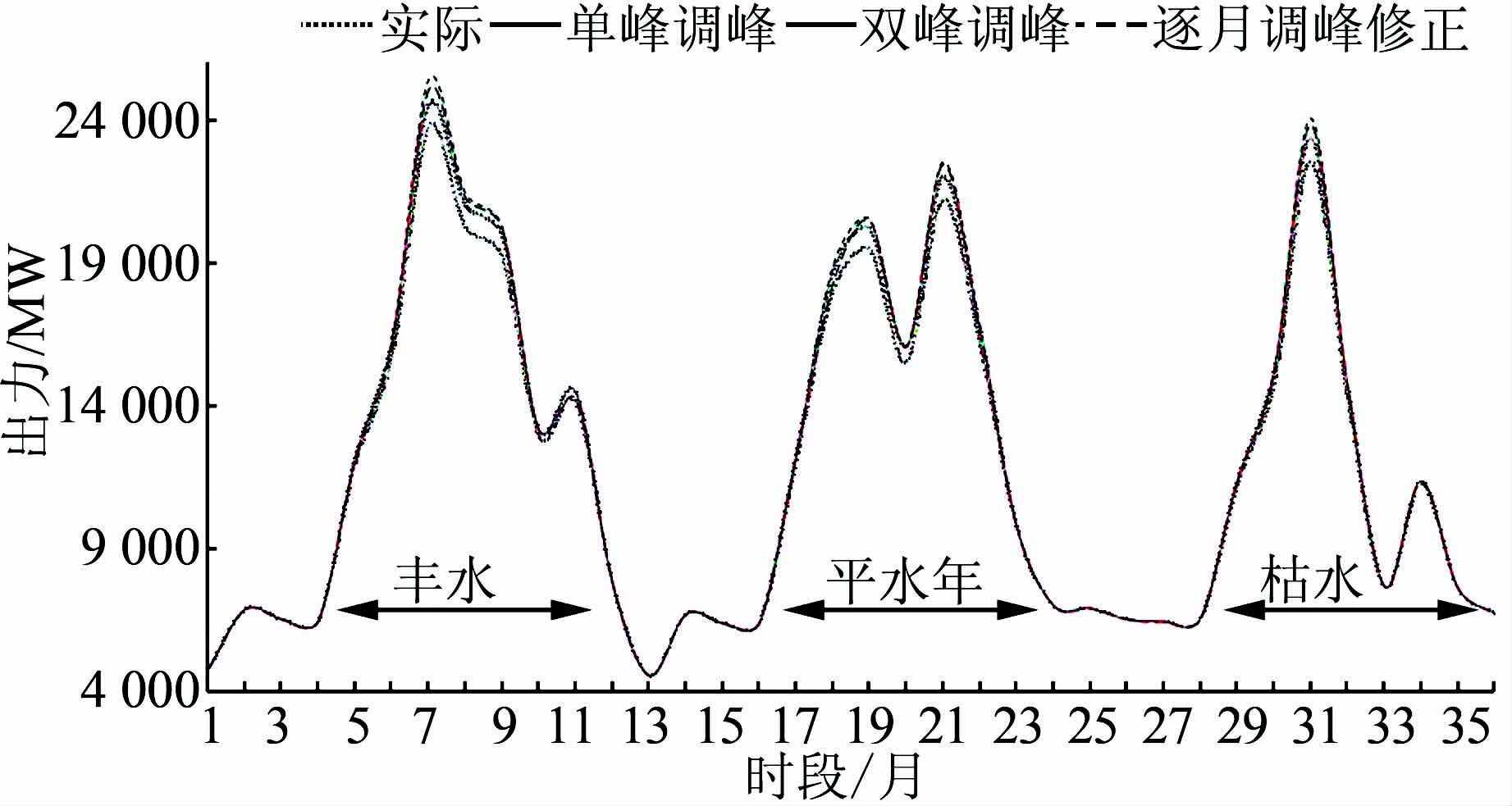
图 6为三峡-葛洲坝梯级电站典型年(丰、平、枯)下的时段出力过程，可以看出，几种调峰模式下各时段的出力值均未超过不考虑调峰的时段出力值，这与模型中期望效益函数特性是相符的；两电站都分别在兼顾保证率的情况下增加了调峰出力，虽然发电量有所损失，但可以更好地在长期调度中为水电站参与调峰预留出调峰容量.若考虑到峰谷电价的差异，可为系统创造更大的经济效益.

图 6 不同调峰模式典型年下梯级电站时段出力过程 Figure 6 Output figure of Three Gorges cascade hydropower stations in different peak-shaving modes
图选项

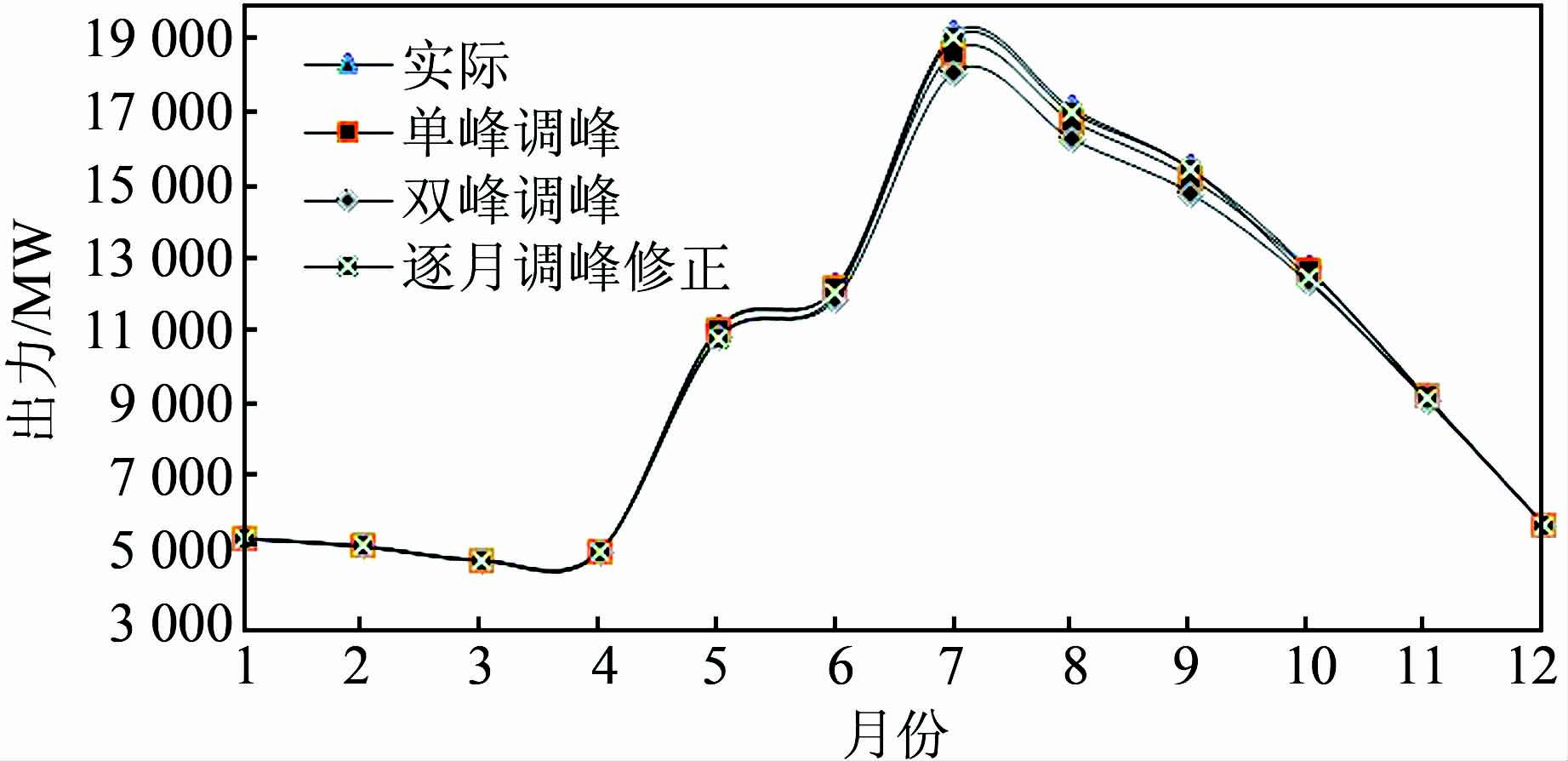
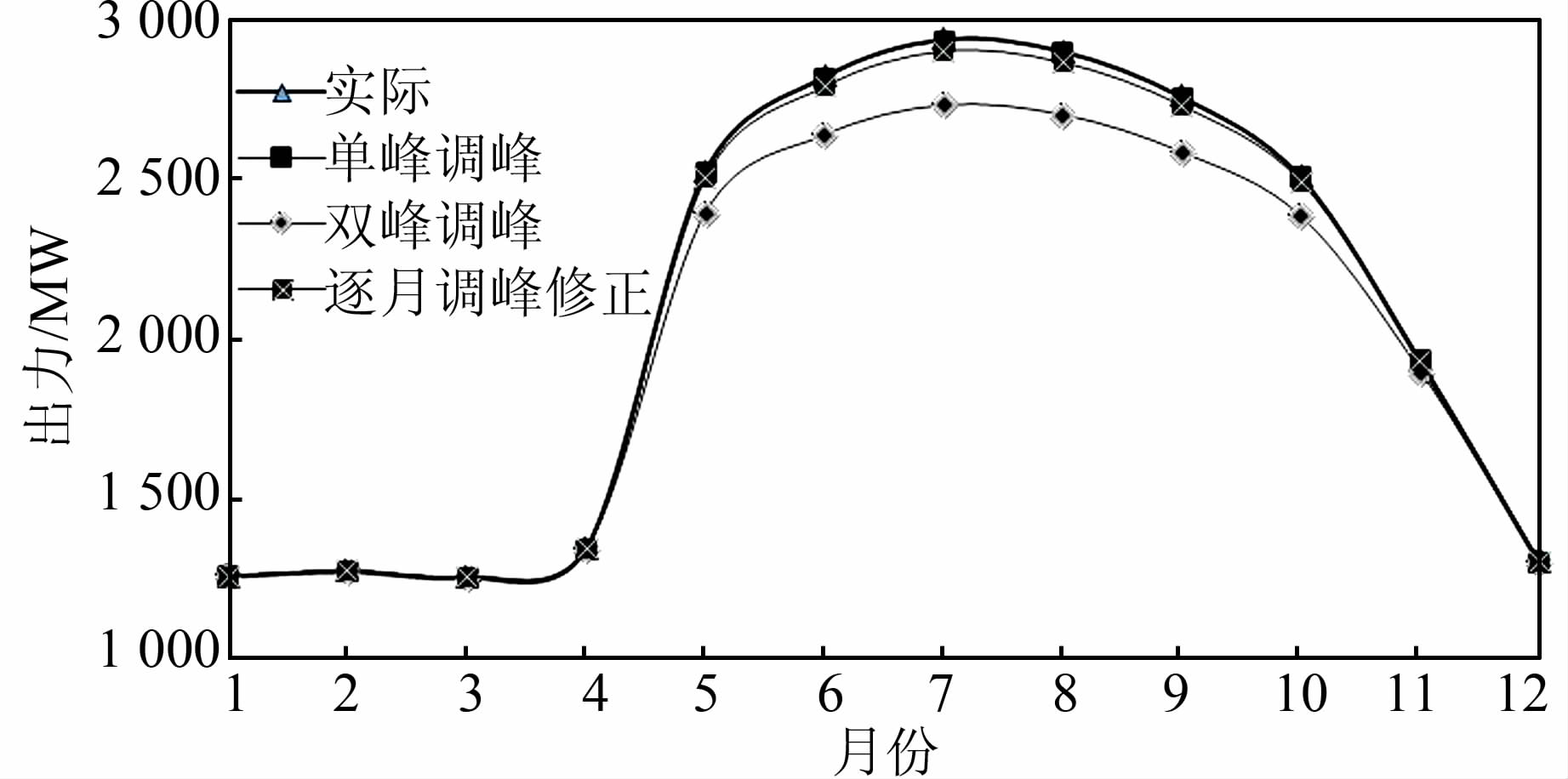
图 7、8表明：期望效益模型下三峡梯级调峰容量在5-10月增加明显；3种调峰模式下多年平均各月出力值为单峰模式下最大，逐月调峰其次，双峰模式下最小，模型通过对调峰限制出力的概率分布定义实现了电网系统对水电站调峰的控制要求：即预留一定的调峰出力空间，同时考虑调峰的水电站发电效益包括电量效益和调峰效益.在枯水期来水少，时段出力基本达不到限制最大出力，则此时优化策略趋向发电量最大，不受调峰影响，如11月-次年4月；丰水期下使出力均匀，保证各时段能有调峰预留前提下追求发电量最大，如5-10月.

图 7 不同调峰模式下三峡电站多年平均各月出力值 Figure 7 Monthly mean output figure of Three Gorges hydropower station in different peak-shaving modes
图选项
图 8 不同调峰模式下葛洲坝电站多年平均各月出力值 Figure 8 Monthly mean output figure of GZB hydropower station in different peak-shaving modes
图选项

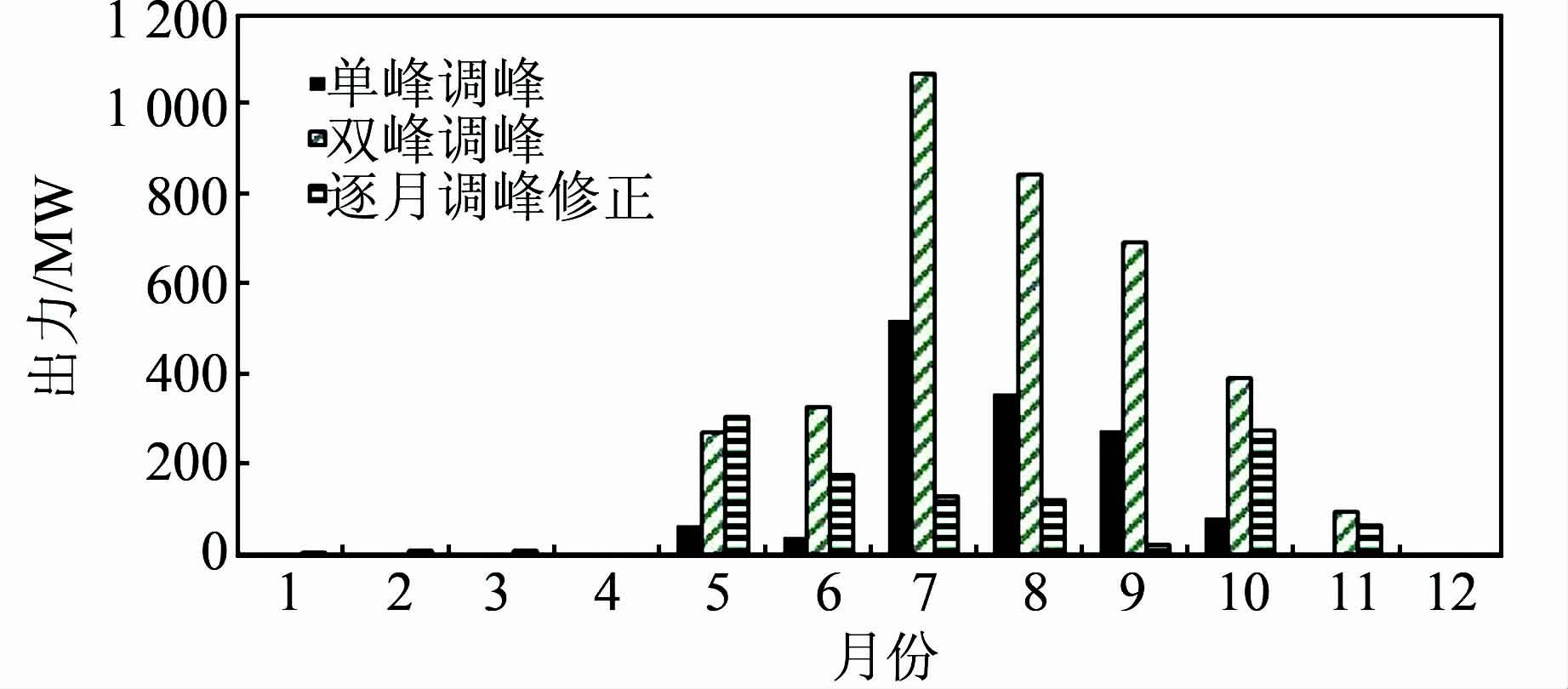
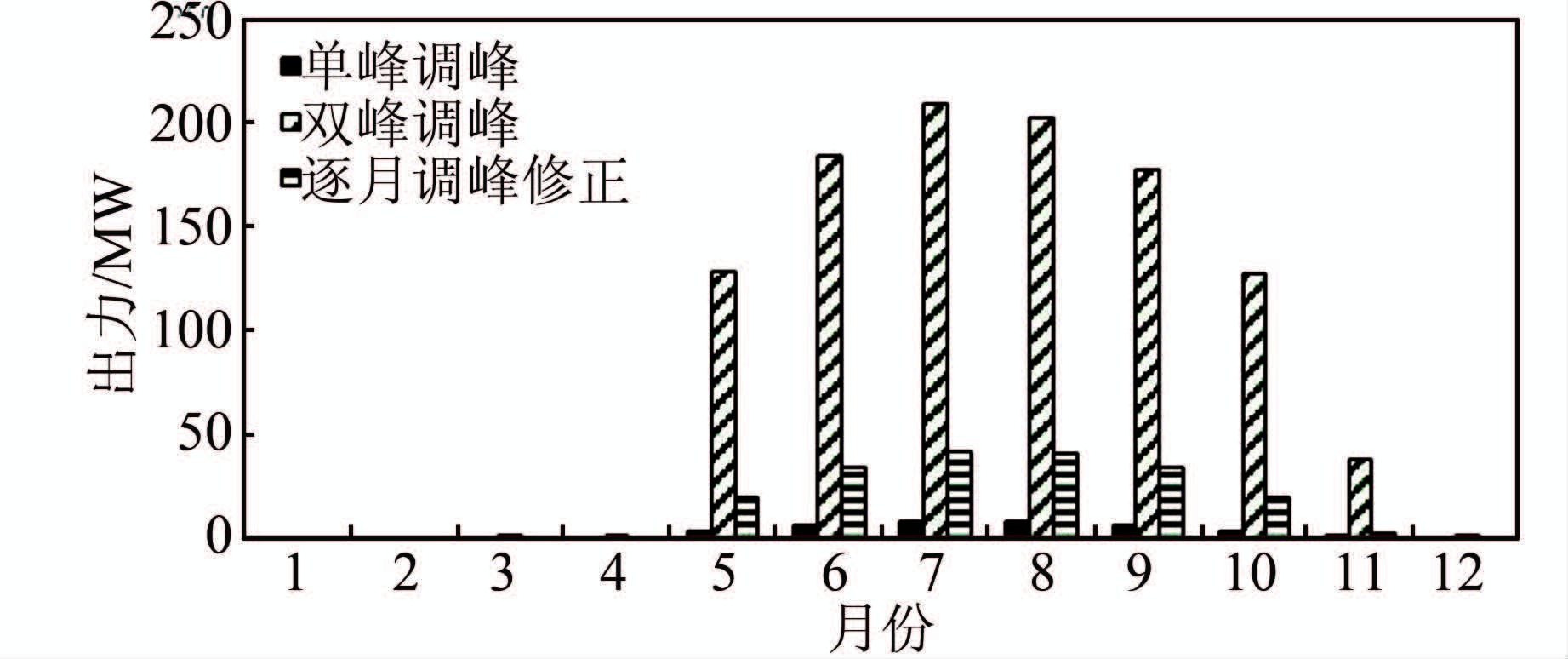
图 9、10显示，3种调峰模式下多年平均各月调峰增量为双峰模式下最大，逐月调峰其次，单峰模式下最小.三峡电站调峰有一定规律性，但在年或者月计划中并未给定调峰量，要根据实时水位和来水情况确定调峰.一般枯水期11月至次年3、4月，来水少，除非水库利用库容变动水位增加调峰量，电站基本不会参与调峰.5-6月集中消落期汛期受水位日变幅的限制，调峰增量也必须控制在300 MW左右，7-9月三峡水库出入库平衡控制，但是来水量级的大小使得调峰有一定不确定性，调峰增量较大的就是7、8月的汛期以及9月中旬到10月的蓄水期，此期间三峡电站月均调峰增量在400~1 100 MW级，葛洲坝电站作为反调峰电站，其月均调峰增量一般在80~200 MW级.

图 9 不同调峰模式下三峡电站多年平均各月增加调峰出力值 Figure 9 Monthly mean added output figure of Three Gorges hydropower plant in different peak-shaving modes
图选项
图 10 不同调峰模式下葛洲坝电站多年平均各月增加调峰出力值 Figure 10 Monthly mean added output figure of GZB hydropower plant in different peak-shaving modes
图选项
3 结语

以三峡梯级水电站为研究对象，建立了考虑保证出力要求的梯级总调峰效益期望最大的长期优化调度模型，对不同调峰方式下发电量及调峰损失电量进行了比较分析，为水电站长期调度中更好预留调峰容量提供了参考依据.实例研究表明：调峰期望效益最大模型能够在长期优化调度能更好地体现电力系统对水电长期调度的调峰需求，但由于电站实际日运行数据资料有限，对调峰要求水电站最大出力的分布规律的进一步验证还不充分.此外，如何将长期预留调峰容量和短期实时分配结合起来，更好发挥其调峰效益来适应电力市场环境，还需进一步探讨，另外本文仅以发电量作为目标，也没有考虑电价因素的影响.

参考文献
[1] Yang C J, Jackson R B. Opportunities and barriers to pumped-hydro energy storage in the United States[J]. Renewable & Sustainable Energy Reviews, 2011, 15(1): 839–844.
[2] Oudalov A, Cherkaoui R, Beguin A. Sizing and optimal operation of battery energy storage system for peak shaving application[J]. 2007 IEEE Lausanne Powertech, VOLS 1-5, 2007: 621–625.
[3] 温权, 张士军, 张勇传. 葛洲坝隔河岩联合调峰长期优化调度[J]. 华中理工大学学报, 1999(2): 56–58.
Wen Quan, Zhang Shijun, Zhang Yongchuan. The combined adjusting and optimal dispatch of Gezhouba and Geheyan Power Plants[J]. Journal of Huazhong University of Science and Technology, 1999(2): 56–58.
[4] 李彬艳. 水电站长期调峰初步研究[D]. 武汉:华中科技大学, 2007.
Li Binyan. Preliminary research on long-term peak regulation of the hydropower plant[D]. Wuhan: Huazhong University of Science and Technology, 2007.
[5] 陈毕胜, 李承军. 水库长期优化调度发电效益最大模型探讨[J]. 水电能源科学, 2004(3): 51–52.
Chen Bisheng, Li Chengjun. Study of long-term hydro optimal dispatching model of reservoir[J]. Water Resources and Power, 2004(3): 51–52.
[6] 王金文, 范习辉, 张勇传, 等. 大规模水电系统短期调峰电量最大模型及其求解[J]. 电力系统自动化, 2003(15): 29–34.
Wang Jinwen, Fan Xihui, Zhang Yongchuan, et al. Short-term generation scheduling for the peak-energy maximization of large-scale hydropower systems[J]. Automation of Electric Power Systems, 2003(15): 29–34.
[7] 武新宇, 程春田, 李刚, 等. 水电站群长期典型日调峰电量最大模型研究[J]. 水利学报, 2012(3): 363–371.
Wu Xinyu, Cheng Chuntian, Li Gang, et al. Research on long term typical day peak load regulation energy maximization model for hydropower systems[J]. Journal of Hydraulic Engineering, 2012(3): 363–371.
[8] 何光宇, 王稹, 裴哲义, 等. 三峡电力系统调峰问题的研究[J]. 电网技术, 2003(10): 12–16.
He Guangyu, Wang Zhen, Pei Zheyi, et al. Peak-load dispatching of Three Gorges power system[J]. Power System Technology, 2003(10): 12–16.
[9] 何莉, 伍永刚, 张勇传, 等. 梯级水电站短期调峰运行方式研究[J]. 水力发电, 2006(5): 71–73.
He Li, Wu Yonggang, Zhang Yongchuan, et al. Research on peak modulation modes of short-term scheduling for cascade hydropower stations[J]. Water Power, 2006(5): 71–73.
[10] 吴正佳, 周建中, 杨俊杰, 等. 调峰容量效益最大的梯级电站优化调度[J]. 水力发电, 2007(1): 74–76.
Wu Zhengjia, Zhou Jianzhong, Yang Junjie, et al. Optimal regulation for maximization of peak-energy capacity benefits in cascade hydropower stations[J]. Water Power, 2007(1): 74–76.
[11] 段文辉, 梅亚东, 陈立华, 等. 金沙江干流梯级水电站水库群长期优化调度[J]. 水电自动化与大坝监测, 2007(1): 17–20.
Duan Wenhui, Mei Yadong, Chen Lihua, et al. Long-term optimal operation of cascade hydropower plants on Jinshajiang River[J]. Hydropower Automation and Dam Monitoring, 2007(1): 17–20.
[12] 李承军, 马寅午, 张勇传. 水电站调峰效益期望模型初探[J]. 水电能源科学, 1997(4): 18–22.
Li Chengjun, Ma Yinwu, Zhang Yongchuan. Primary study on mathematic model of peak load hydroelectric plant[J]. Water Resources and Power, 1997(4): 18–22.
[13] 张滔滔, 胡晓勇. 三峡水电站调峰运用探析[J]. 水利水电技术, 2012(9): 99–102.
Zhang Taotao, Hu Xiaoyong. Analysis of peak-load regulating operation of Three Gorges Hydropower Station[J]. Water Resources and Hydropower Engineering, 2012(9): 99–102.
[14] Labadie J W. Optimal operation of multireservoir systems: State-of-the-art review[J]. Journal of Water Resources Planning And Management-ASCE, 2004, 130(2): 93–111. DOI:10.1061/(ASCE)0733-9496(2004)130:2(93)
[15] 陈森林. 水电站水库运行与调度[M]. 北京: 中国电力出版社, 2008.
Chen Senlin. Operation for Hydropower Plant and Reservoir[M]. Beijing: China Electric Power Press, 2008.
[16] 梅亚东, 熊莹, 陈立华. 梯级水库综合利用调度的动态规划方法研究[J]. 水力发电学报, 2007(2): 1–4.
Mei Yadong, Xiong Ying, Chen Lihua. A dynamic programming method for multi-purpose operation of cascade reservoirs[J]. Journal of Hydroelectric Engineering, 2007(2): 1–4.