武汉大学学报(工学版)   2016, Vol. 49 Issue (3): 372-377

文章信息

傅少君, 袁稳沉
FU Shaojun, YUAN Wenchen
基于有限元法的拱坝温度荷载简化公式
Simplified formula for temperature loads on arch dams based on FEM
武汉大学学报(工学版), 2016, 49(3): 372-377
Engineering Journal of Wuhan University, 2016, 49(3): 372-377
http://dx.doi.org/10.14188/j.1671-8844.2016-03-009

文章历史

收稿日期: 2015-12-26
 Abstract              PDF               Figures               Tables
引用本文 0
傅少君, 袁稳沉. 基于有限元法的拱坝温度荷载简化公式[J]. 武汉大学学报(工学版), 2016, 49(3): 372-377.
FU Shaojun, YUAN Wenchen. Simplified formula for temperature loads on arch dams based on FEM[J]. Engineering Journal of Wuhan University, 2016, 49(3): 372-377.
基于有限元法的拱坝温度荷载简化公式
傅少君, 袁稳沉     
武汉大学土木建筑工程学院，湖北 武汉 430072
收稿日期: 2015-12-26
作者简介: 傅少君（1969-），男，博士，教授、博士生导师，研究方向为工程数值计算与分析,E-mail:shaojunfu69@vip.sina.com.
通讯作者: 袁稳沉（1991-），男，硕士研究生，研究方向为工程数值计算与分析,E-mail：yuanwenchen@yeah.net
基金项目: 国家自然科学基金资助项目（编号：51579194）.
摘要: 现行《混凝土拱坝设计规范》（SL 282-2003）关于拱梁分载法温度荷载的简化公式尚不能很好地考虑拱坝的导温系数和水温边界，以至拱坝表面温度应力的计算误差较大并影响温控防裂措施.以小湾水电站高拱坝工程为依托，在全坝段、全过程三维有限元仿真反馈分析成果的基础上，分析了拱坝温度场时空分布规律，论证了解析解与数值解的一致性以及解析解的适用范围；应用复变函数法和傅里叶变换法，建立了拱梁分载法温度荷载的简化公式.算例结果表明，该简化公式计算温度荷载的精度有明显提高，因其可以较好地考虑混凝土导温系数和水温边界影响.
关键词： 拱坝     有限单元法     温度荷载     简化公式     拱梁分载法    
Simplified formula for temperature loads on arch dams based on FEM
FU Shaojun, YUAN Wenchen     
School of Civil and Architectural Engineering, Wuhan University, Wuhan 430072, China
Abstract: Now, the simplified formula of temperature load in the current Design specification for concrete arch dams (SL 282-2003) for the arch cantilever method did not take coefficient of thermal conductivity and water temperature boundaries into account perfectly, the error caused by which when calculating thermal stresses near the arch dam surface is so big that it influenced temperature control and anti-cracking measurements. Therefore, taking Xiaowan high arch dam as an engineering background, basing on the back-analysis simulation results considering the overall construction process and whole dam range finite element mesh, the time-space distribution laws of temperature filed in the arch dam was analyzed; the consistency between the analytic solutions and numerical results is proved; and the application scope of the analytic solutions is presented. Using the function of complex variable method and the Fourier transform, a new simplified formula of temperature load for concrete arch dam is established, which could be applied in the arch cantilever method. The better precision of the simplified formula is presented. A case study results show that the simplified formula has better precision due to considering better conductivity coefficient and water temperature boundaries when calculating temperature load.
Key words: arch dam     finite element method     temperature load     simplified formula     arch cantilever method    

假定拱坝上下游侧环境温度均以1年为周期作周期性变化，则水温和气温函数可用傅里叶级数表示[1].由于热传导方程是线性微分方程[2]，因此可应用叠加原理将运行期温度场分解为稳定温度场和变化温度场.前者由上下游边界条件中的常数项(年平均温度)确定，后者由边界条件中的简谐项确定.于是：

$T(x)={{T}_{1}}(x)+{{T}_{2}}(x)$    (1)

式中：T1(x)为稳定温度场；T2(x)为变化温度场.

${{T}_{1}}(x)=\frac{{{T}_{DM}}+{{T}_{UM}}}{2}+\frac{{{T}_{DM}}-{{T}_{UM}}}{L}x$    (2)

其中:TUM、TDM分别为上、下游表面年平均温度,℃.

对于T2(x)的求解，当坝体厚度大于20 m时，可简化为对半无限平板温度场问题的求解[3~4].求解一维热传导问题常用的方法有分离变量法和拉普拉斯变换法[5]，特别地，对于各点温度随着时间作简谐变化的准稳定温度场，还可用复变函数法[6~7].拱坝设计规范(SL 282-2003)(后简称“规范”)中采用的是复变函数法[8].规范中，半无限平板边界条件为

$\left\{ \begin{matrix} T=A\sin \left[ \frac{2\pi }{P}\left( \tau -{{\tau }_{0}}-\varepsilon \right) \right],\text{ }\left( x=0 \right) \\ T=0,\text{ }\left( x=\infty \right) \\ \end{matrix} \right.$

其解析解为

$T\left( {x}',\tau \right)=A{{e}^{-{x}'\sqrt{\frac{\pi }{aP}}}}\sin \left( \frac{2\pi }{P}\left( \tau -{{\tau }_{0}}-\varepsilon \right)-{x}'\sqrt{\frac{\pi }{aP}} \right)$    (3)

式中：P为温度变化周期(取P=365 d);A为表面温度变幅，℃;a为混凝土导温系数，m2/d；x′坐标以半无限板边界为原点.对于拱坝的上、下游侧，将其各自边界条件进行傅里叶变换可得相应的解.

将所有温度边界转换成傅里叶级数，将所有简谐项对应的解叠加即可得到解析解T2x′,τ.将T1(x)、T2(x)相加即求得了坝体厚度方向温度场T(x).

朱伯芳院士用三维有限元法模拟结果验证了上述坝体厚度方向温度场的解析解[3]，并根据解析解提出了拱坝温度荷载的简化公式[9]，其思路如下.

根据平截面假设[10]，拱坝内厚度方向温度场T(x)可分解为3部分，即平均温度Tm、等效温差Td、非线性温差Tn，分别计算如下[10~11]：

${{T}_{m}}=\frac{1}{L}\int_{-\frac{L}{2}}^{\frac{L}{2}}{T(x)dx}$    (4)
${{T}_{d}}=\frac{12}{{{L}^{2}}}\int_{-\frac{L}{2}}^{\frac{L}{2}}{T(x)xdx}$    (5)
${{T}_{n}}=T(x)-{{T}_{m}}(x)-{{{T}_{d}}(x)x}/{L}\;$    (6)

式中：x为沿坝体厚度方向的坐标,m，以坝体中线为原点，以下游方向为正方向；L为坝体厚度，m；T(x)为坝体厚度方向x处的温度，℃.

朱伯芳院士建议，拱坝温度荷载可以按下式计算[1, 8]：

$\left\{ \begin{matrix} {{T}_{m}}={{T}_{m1}}+{{T}_{m2}}-{{T}_{m0}} \\ {{T}_{d}}={{T}_{d1}}+{{T}_{d2}}-{{T}_{d0}} \\ \end{matrix} \right.$    (7)

式中：Tm0、Td0为封拱时坝体的平均温度和等效温差；Tm1、Td1是与拱坝运行期年稳定温度场T1(x)相对应的平均温度和等效温差；Tm2、Td2是与坝体变化温度场T2(x)相对应的平均温度和等效温差.

我国现行拱坝设计规范(SL 282-2003)采用此建议作了如下的规定：采用拱梁分载法计算温度应力时温度荷载只考虑坝体断面平均温度Tm和等效线性温差Td[8].

在实际应用中，简化公式存在3方面不足：1) 由表面水温计算各深度水温的公式[10]与实际水温边界条件有较大出入，计算结果将因此产生较大的差异.2) 该简化公式中不包含混凝土导温系数，只适于混凝土导温系数为0.1 m2/d的情况，而混凝土导温系数对温度荷载的影响很大.3) 该简化公式建立在一维温度场解析解的基础上，本文将证明当坝体较厚时，坝体温度场与一维温度场解析解有较大的差距.

为了解决问题3)，清华大学麦家煊考虑了二维热传导的影响，推导了拱坝温度场的二维和三维的解析解[4].但理论解非常复杂，不适于在工程应用.

本文以小湾拱坝工程为依托，以三维有限元全过程、全坝段温度场仿真结果及坝体实测值为基本依据[12~14]，研究解析解的适用范围，并在解析解的基础上建立拱坝的温度荷载简化公式，以期为拱梁分载法温度荷载计算提供一条更为准确、科学、实用的途径.

2 小湾拱坝运行期温度场分析 2.1 小湾拱坝温度场三维有限元模拟

小湾拱坝温度场分析的基本参数、有限元模型及分析成果详见文献[12~14].水温边界条件采用实测值(图 1).上游气温为

$T=19.784+7.54\times \sin \left[ \frac{2\pi }{365}\left( \tau -120 \right) \right]$    (8)
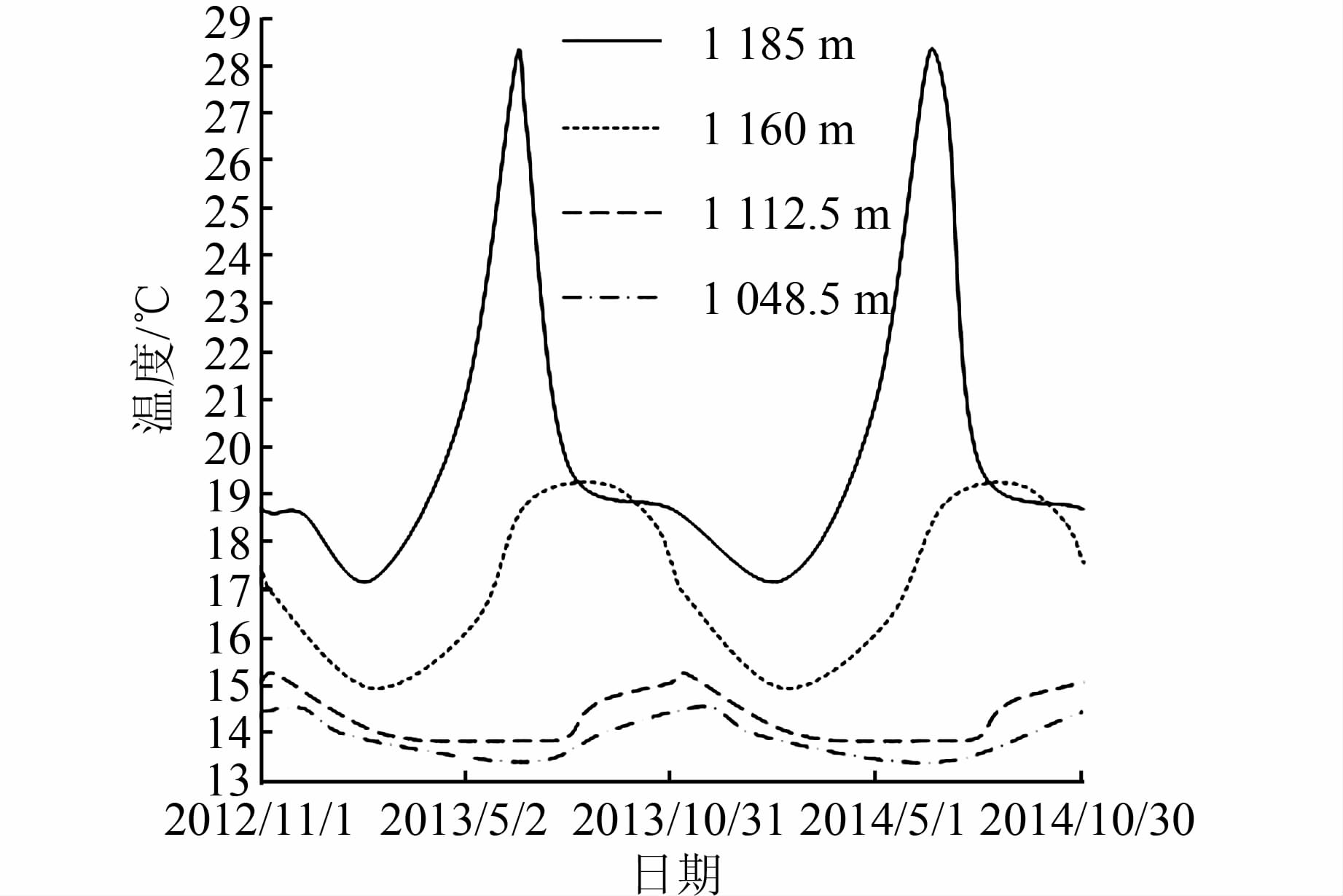
图 1 库水温度监测值 Figure 1 Measured values of water temperature
图选项

下游气温为

$T=22.5+3\times \sin \left[ \frac{2\pi }{365}\left( \tau -120 \right) \right]$    (9)

其中：τ为距起算时间2005年12月13日的天数.

1185、1 160、1 112.5、1 048.5 m高程的实际水温年变幅分别为5.5、2.15、0.62、0.56 ℃，用文献[1]中的水温计算公式计算结果分别为5.76、3.67、1.56、0.49 ℃.与实际水温年变幅相比，由文献[2]中的水温计算公式得到的水温年变幅的平均误差为59.9%，最大误差为151.6%，由此可见，若采用该计算公式估算水温将产生较大的误差.

小湾拱坝在5个典型断面布置了温度测点.图 2是15号坝段C4-A15-T-51测点温度实测值与仿真计算值的历程曲线.

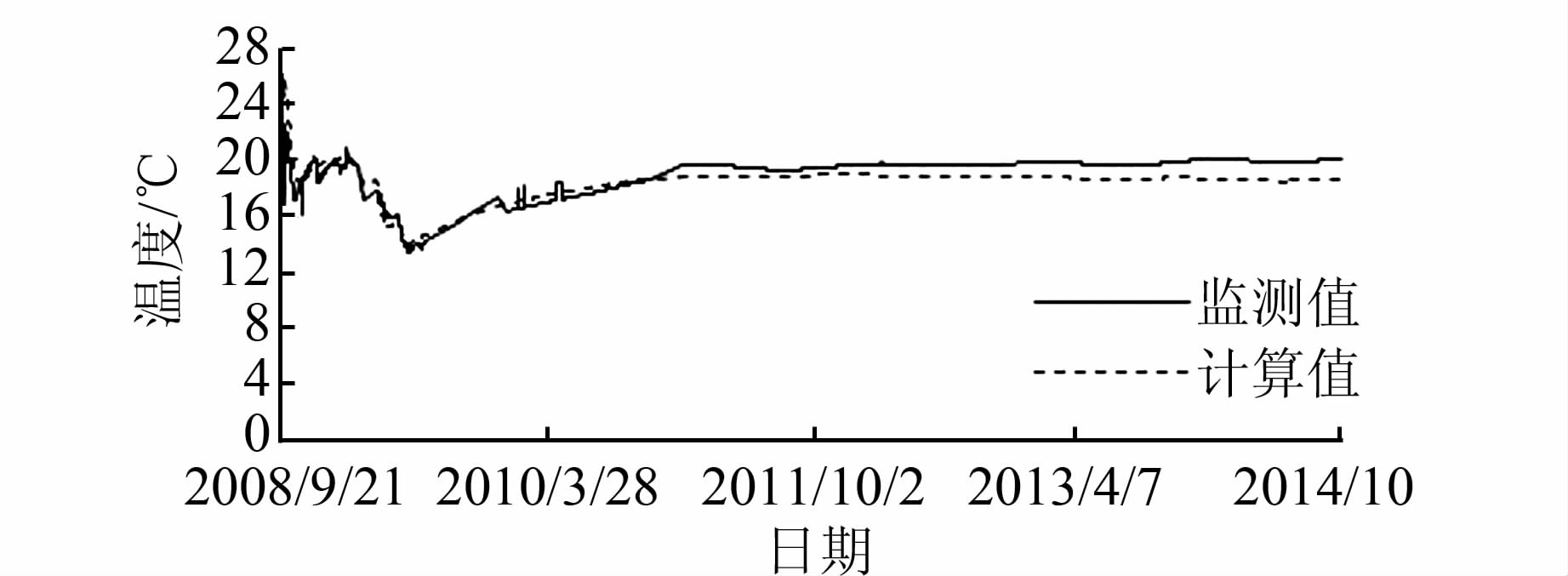
图 2 温度历程曲线(1 160.4 m高程，距上游面10.1 m) Figure 2 Temperature history of a typical monitored point
图选项

由图 2可知仿真计算值与监测值总体上相差1～3 ℃；对于坝体内部温度稳定后的测点，仿真计算值与监测值的差别都在3 ℃以内.说明仿真计算结果较好地反映了坝体实际温度场随时间变化过程及空间上的分布规律[12, 13].

图 3是有限元模拟计算得到的某断面在2014年2月15日和8月15日的温度等值线图.

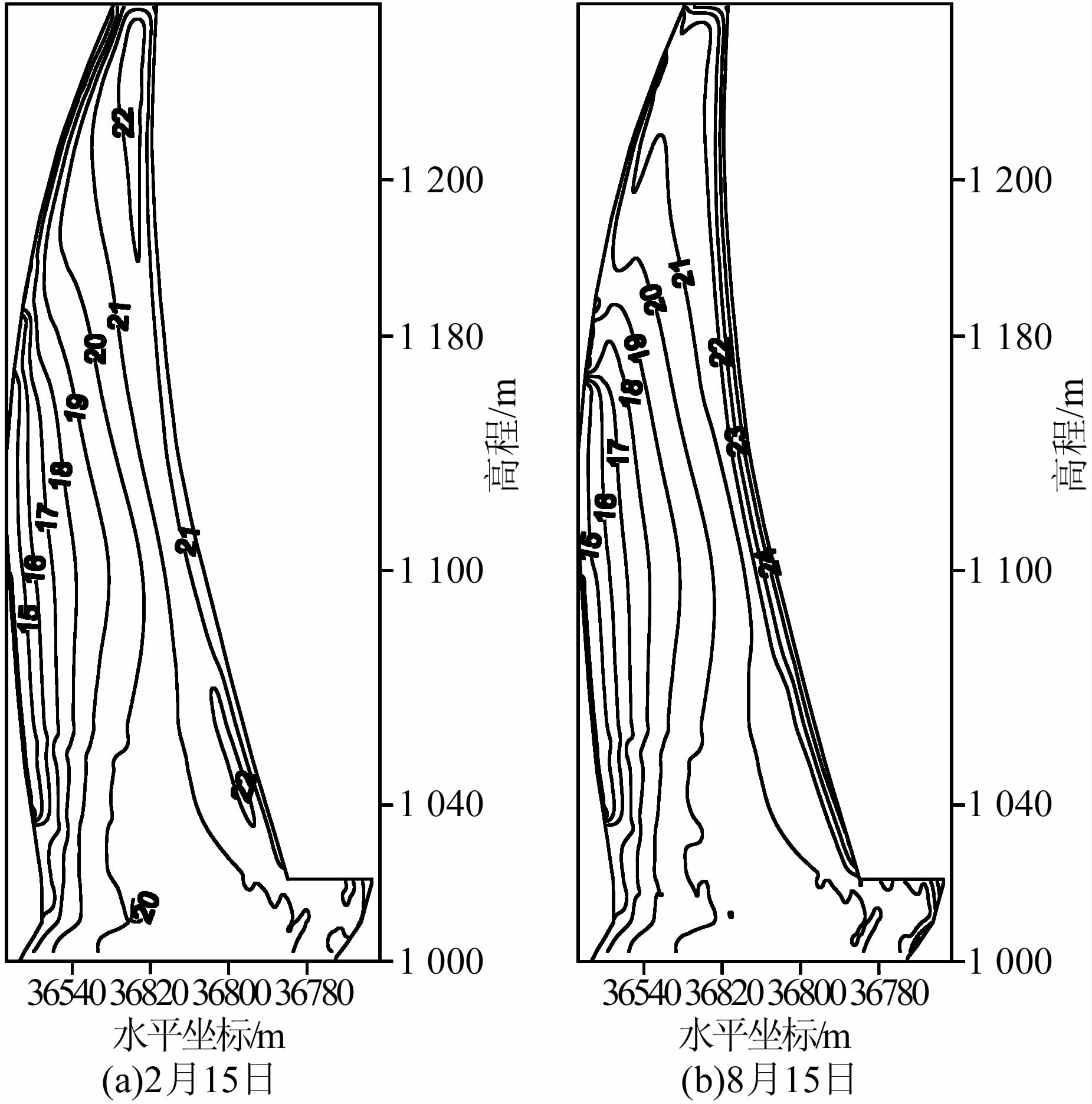
图 3 横断面温度等值线(单位：℃) Figure 3 Temperature contour maps on a typical transverse section (unit:℃)
图选项

考察图 3可知：

1) 图(a)与(b)中1 200 m高程以下的17~21 ℃等温线形状非常相近，这是由于厚度较大，坝体内部受外界温度变化影响较小，为稳定温度场.

2) 1 100~1 200 m高程厚度方向的稳定温度场梯度比较均匀.

3) 在1 100 m高程以下，上游侧厚度方向的温度梯度随深度逐渐增大，这反映了深处水温较低；坝体内部厚度方向的温度梯度随深度逐渐减小，这反映了坝基附近因受到地热影响而温度较高.该范围内厚度方向的稳定温度场梯度不均匀，若将此高程的温度场求解简化为半无限平板温度场问题将产生较大的误差.

2.2 温度场的解析解与有限元模拟值对比分析

通常温度荷载组合最不利时刻在2月中旬和8月中旬[11].用式(4)~(6)计算温度荷载最不利时刻各高程温度场解析解，并与数值仿真值比较(如图 4和5所示)，以上游侧表面为坐标原点.1 200 m高程由于离水面很近，水温和气温相位差小，所以6月中旬的温升较大，因此对6月中旬的结果进行计算比较.

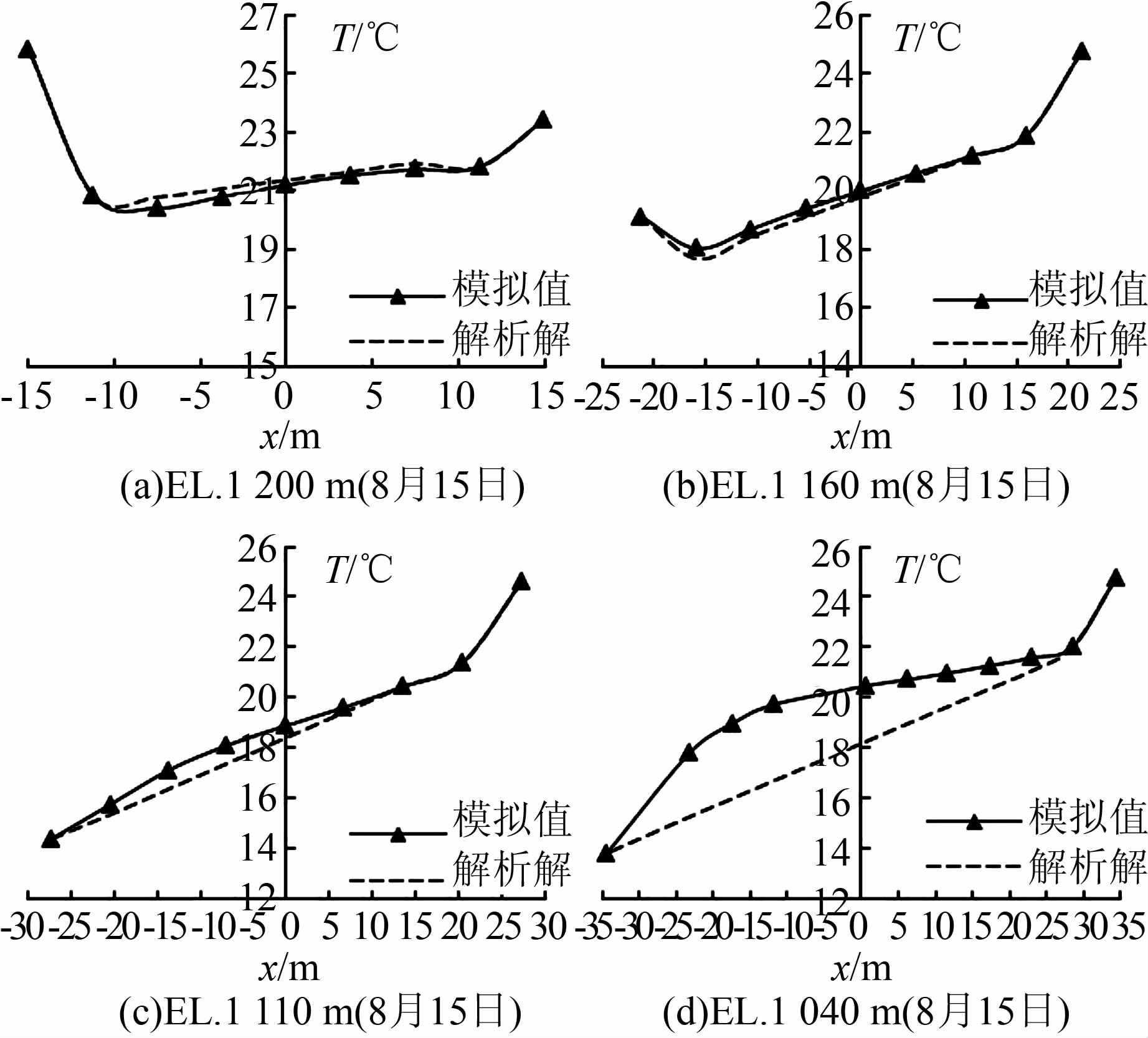
图 4 温升时各高程处的温度 Figure 4 Temperature distributions on several typical elevations in temperature-rise period
图选项
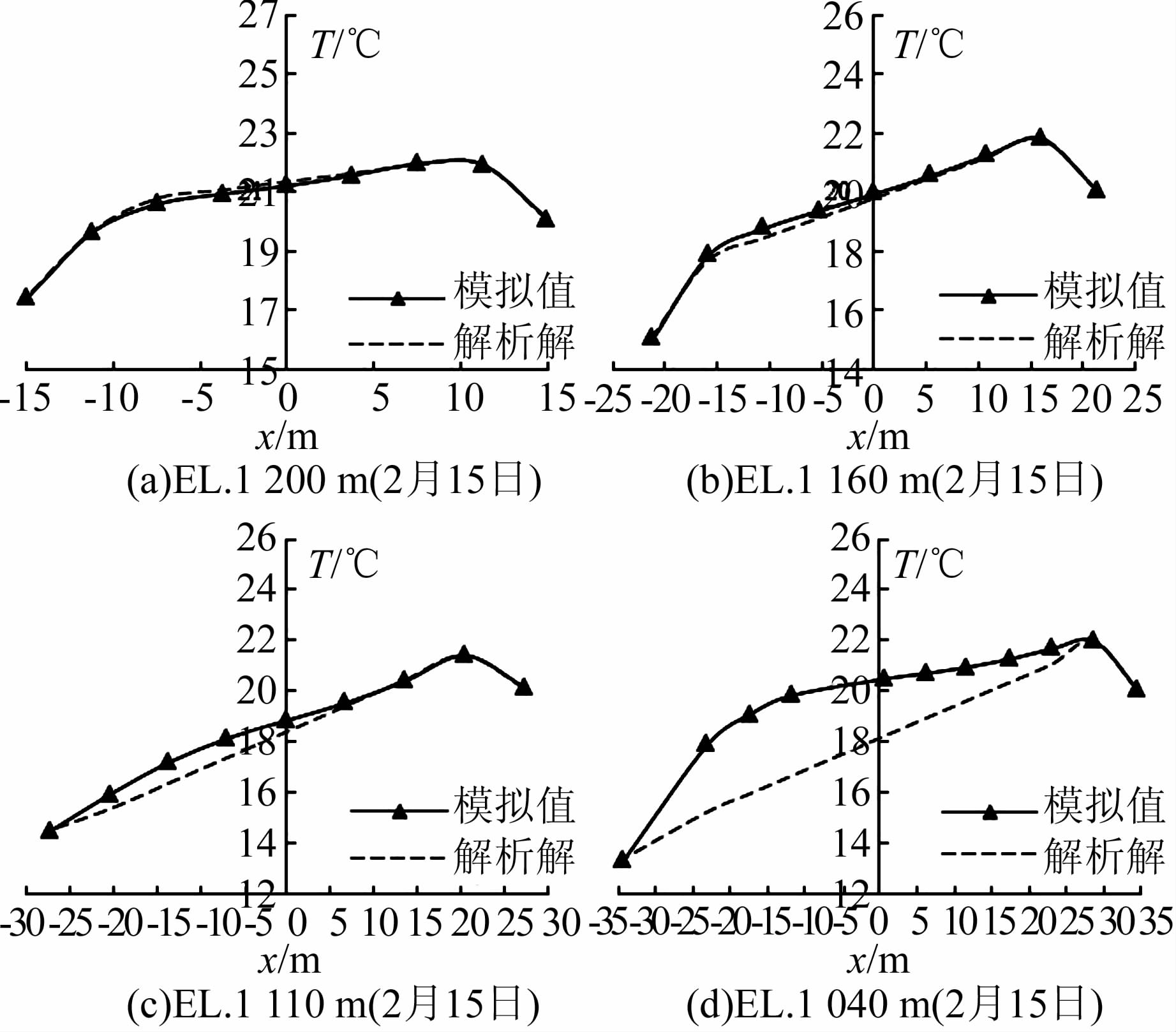
图 5 温降时各高程处的温度 Figure 5 Temperature distributions on several typical elevations in temperature-drop period
图选项

综合分析计算结果可知：

1) 1 110 m及以上高程，解析解与数值仿真值非常吻合，稳定温度场曲线为一条斜率近似为(TDM－TUM)/L的直线；1 040 m高程厚度方向温度场的解析解与数值仿真值差别较大，数值仿真值整体大于理论温度，最大差值为3.08 ℃，这是由于坝基附近受到了地热影响，若仍将问题简化为半无限平板温度场问题将产生较大的误差，即对于此高程，解析解不再适用.

2) 在最不利时刻，各高程上下游侧环境温度影响深度内(以下简称影响深度)的温度梯度近似为常值.

3) 环境温度对上、下游侧的影响深度均小于10 m.

4) 解析解与数值仿真值曲线在影响深度内几乎重合；混凝土表面温度变幅与环境温度年变幅完全一致，因此在计算年温度场解析解时，可假定混凝土表面温度等于环境温度.

3 温度荷载简化公式推导 3.1 简化公式的推导

根据2.2节得到的各高程坝厚方向温度场的4个特征，温度曲线可简化为由三段直线组成的折线分布图.由此得到基本思路：对于变化温度场，将上下游两侧影响深度内的温度曲线简化为直线；然后将简化后的T2(x)与T1(x)叠加得到T(x)；最后，据此建立计算温度荷载的简化公式.

在上下游侧环境温度影响深度内的变化温度场T2(x)简化为线性函数的过程中，应要求其平均温度保持不变，即要求简化函数在坝体厚度范围内积分值保持不变.

根据文献[15]，对于相同的温度边界，影响深度由混凝土的导温系数决定，而对于大部分混凝土，按0.1A考虑的年变化影响深度不会超过10 m.先考虑上游侧，将式(6)在 0~10 m内积分.记(2π/P)·(τ－τ0－ε)=b，积分值为

$\frac{A}{2}\sqrt{\frac{365a}{\pi }}\left[ \sin b-\cos b-{{e}^{{{x}_{2}}}}\left( \sin ({{x}_{2}}+b \right)-\cos ({{x}_{2}}+b) \right]$

其中

${{x}_{2}}=-10\sqrt{\pi /\left( aP \right)}$    (10)

将之记为S，则所求简化直线在x轴上的截距为

$\begin{align} & l\left( a,\tau \right)=\frac{2S}{A\sin b}=\sqrt{\frac{365a}{\pi }}\times \\ & \frac{\sin b-\cos b-{{e}^{{{x}_{2}}}}\left( \sin ({{x}_{2}}+b \right)-\cos ({{x}_{2}}+b)}{\sin b} \\ \end{align}$    (11)

其中:l即为最不利时刻变化温度场简化函数在x轴上的截距，反映了荷载最不利时刻的影响深度，其值见表 1.

表 1 l(a,τ)值 Table 1 Values of l(a,τ) from Eq. (11)
a/
(m2·d-1)/		 $l\left( a,\frac{P}{4}-45d \right)$
/m		 $l\left( a,\frac{P}{4}-30d \right)$
/m		 $l\left( a,\frac{P}{4}-15d \right)$
/m		 $l\left( a,\frac{P}{4} \right)$
/m		 $l\left( a,\frac{P}{4}+15d \right)$
/m		 $l\left( a,\frac{P}{4}+30d \right)$
/m		 $l\left( a,\frac{P}{4}+45d \right)$
/m		 $l\left( a,\frac{P}{4}+60d \right)$
/m		 $l\left( a,\frac{P}{4}+75d \right)$
/m
0.100
0.080
0.072
0.060 		0.150
0.036
0.007
-0.014		 1.608
1.342
1.240
1.105		 2.686
2.307
2.152
1.933		 3.623
3.146
2.945
2.652		 4.561
3.986
3.738
3.371		 5.638
4.951
4.650
4.199		 7.096
6.257
5.884
5.318		 9.571
8.473
7.977
7.218		 15.976
14.210
13.397
12.135
表选项

对边界条件进行傅里叶变换，根据第一个简谐函数项的相位τ，在表 1中查得相应的l值；根据2.2节结论4)，坝体上下游表面温度可直接取环境温度.由此可得到最不利时刻的变化温度场T2(x)简化函数:

$\begin{align} & {{T}_{2}}\left( x \right)= \\ & \left\{ \begin{matrix} {{T}_{U}}-{{T}_{UM}}-\frac{{{T}_{U}}-{{T}_{UM}}}{{{l}_{U}}}x\text{ }\left( \text{x}＜{{l}_{U}} \right) \\ {{T}_{D}}-{{T}_{DM}}-\frac{{{T}_{D}}-{{T}_{DM}}}{{{l}_{D}}}\left( x-L \right)\left( \text{x}>\text{L-}{{l}_{D}} \right) \\ \end{matrix} \right. \\ \end{align}$    (12)

式中：TU、TD分别为最不利时刻上、下游边界温度；lU、lD分别为最不利时刻上、下游的l值.

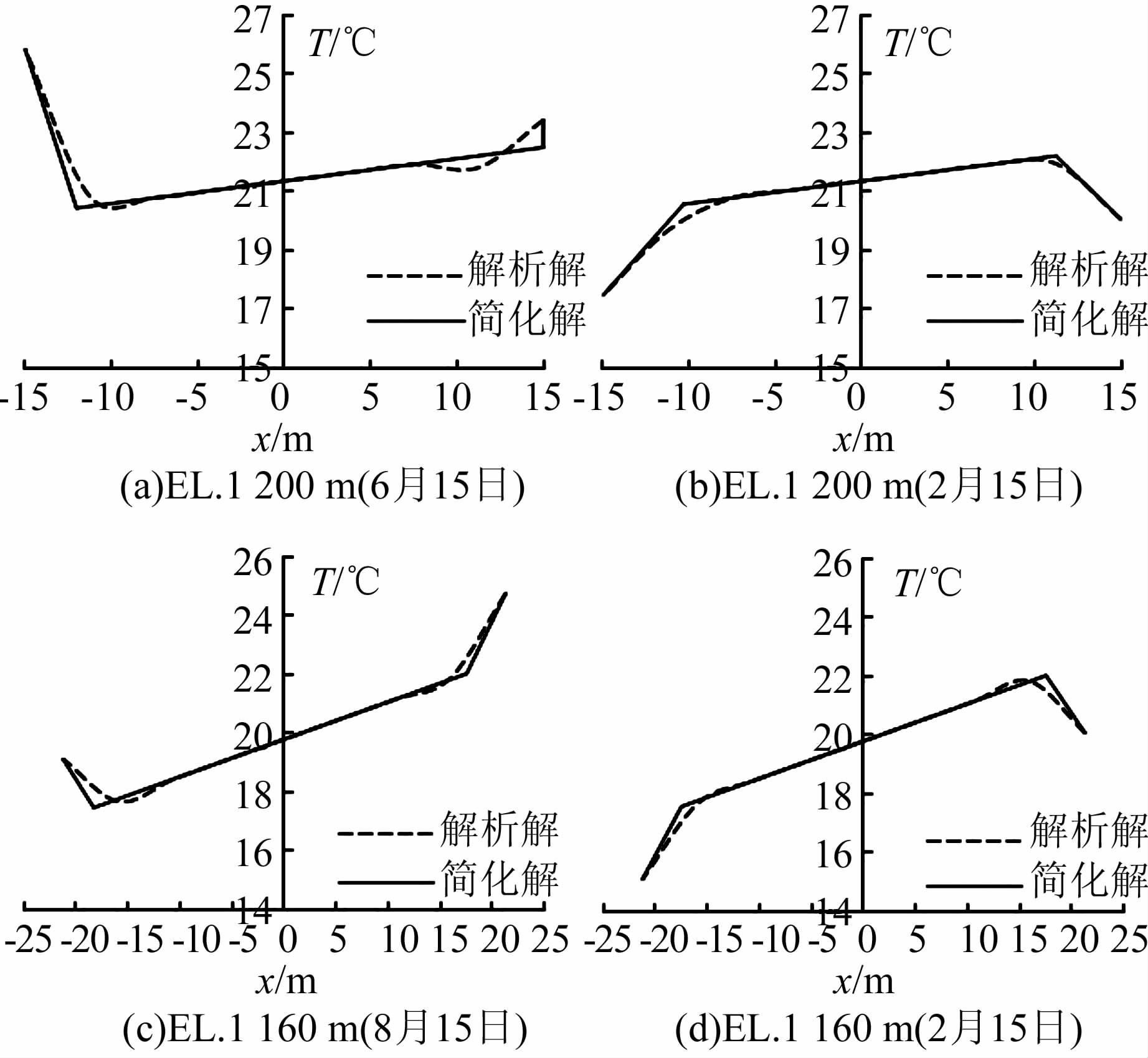
由式(4)、(5)及(12)得到简化的厚度方向温度分布简化解，并与解析解进行对比(如图 6所示).

图 6 温度场解析解与简化解 Figure 6 Analytic solutions and the simplified solutions of temperature field
图选项

由式(1)~(2)及上述简化方法可得Tm2和Td2的简化公式：

$\left\{ \begin{matrix} {{T}_{m2}}={\left[ \frac{\left( {{T}_{U}}-{{T}_{UM}} \right){{l}_{U}}}{2}+\frac{\left( {{T}_{D}}-{{T}_{DM}} \right){{l}_{D}}}{2} \right]}/{L}\; \\ {{T}_{d2}}=\frac{12}{{{L}^{2}}}\left[ \frac{\left( {{T}_{D}}-{{T}_{DM}} \right){{l}_{D}}}{2}\frac{L-{{l}_{D}}}{2}+\frac{\left( {{T}_{U}}-{{T}_{UM}} \right){{l}_{U}}}{2}\frac{L-{{l}_{U}}}{2} \right] \\ \end{matrix} \right.$    (13)
3.2 算例验证

为了验证该方法的有效性，将式(13)简化计算方法得到的Td2、Tm2与解析法、规范(SL 282-2003)的简化公式法的结果进行比较，见表 2.

表 2 Td2、Tm2的解析法、式(13)和规范简化公式计算结果 Table 2 Td2，Tm2 from analytic method,equations (13) andsimplified formula in design specification
高程/ m 日期 Td2 Tm2
解析解 式(13) 规范简化法 解析解 式(13) 规范简化法
12002014-02-150.320.290.72 -0.568 -0.518 -0.547
1200 2014-06-15 -1.74 -1.50 -0.72 0.338 0.277 0.547
1160 2014-02-15 -0.09 -0.10 -0.42 -0.351 -0.300 -0.248
1160 2014-08-15 0.16 0.15 0.42 0.314 0.267 0.248
表选项

由表 1可见，导温系数与影响深度正相关.

同时也可以发现，导温系数对影响深度的影响很敏感.例如，在τ－τ0=P/4时，规范中简化公式采用的导温系数为0.100 m2/d，其对应的l值比小湾拱坝混凝土实际导温系数0.071 78 m2/d所对应的l值大23.0%.

影响深度的误差将反映在厚度方向的温度场上，并最终反映在温度荷载结果中.因此，若简单地将混凝土导温系数假定为恒值0.100 m2/d，得到的温度荷载将产生较大的误差.

由表 2可见，以基于解析解计算所得的Td2为基准，式(13)计算结果的平均误差为10.1%，最大误差为13.8%，规范简化公式计算结果的平均误差为178.2%，最大误差为366.7%.

以基于解析解计算所得的Tm2为基准，式(13)计算结果的平均误差为14.0%，最大误差为18.0%；规范简化公式计算结果的平均误差为29.0%，最大误差为61.8%.

总的来说，本文提出的简化公式有着更高的精确度.

4 结论

以小湾拱坝仿真反馈分析温度场为基础，将温度场的仿真结果与解析解进行比较，分析了解析解的适用范围；基于解析方法思路建立了坝体厚度大于20 m情况下的拱梁分载法温度荷载简化公式；该简化公式适用于混凝土导温系数不同的拱坝，且可在计算中引入各高程不同的水温边界，而规范(SL 282-2003)的简化公式不能考虑各深度的实测边界温度因而精确度稍差.

对于一定高程下的坝基部位，因受到地热的影响，其厚度方向的温度场不能简化为半无限平板问题来求解.地热的具体影响深度还需要进一步研究.

参考文献
[1] 朱伯芳. 拱坝温度荷载计算方法的改进[J]. 水利水电技术, 2006, 37(12): 19–22.
Zhu Bofang. Improvement of method for computing temperature loads on arch dams[J]. Water Resources and Hydropower Engineering, 2006, 37(12): 19–22.
[2] Holman J P. Heat Transfer[M]. 10th ed. Beijing: China Machine Press,, 2011: 1-3.
[3] 杨波, 朱伯芳. 拱坝运行期非线性温差应力分析[J]. 水利水电技术, 2003, 34(6): 24–26.
Yang Bo, Zhu Bofang. Analysis of nonlinear temperature loads on arch dams[J]. Water Resources and Hydropower Engineering, 2003, 34(6): 24–26.
[4] 麦家煊. 拱坝温度场和温度荷载的计算(I)[J]. 水利学报, 1981(6): 30–45.
Mai Jiaxuan. Computation of temperature field and temperature loads on arch dams[J]. Journal of Hydraulic Engineering, 1981(6): 30–45.
[5] 王明新. 数学物理方程[M]. 北京: 清华大学出版社, 2009: 23-51.
Wang Mingxin. Mathematical Physics Equation[M]. Beijing: :Tsinghua University Press, 2009: 23-51.
[6] Carslaw H S, Jaeger J C. Conduction of Heat in Solids[M]. 2nd ed. Oxford: Oxford University Press, 1986.
[7] 雷柯夫AB. 热传导理论[M]. 北京: 高等教育出版社, 1955.
Lakoff A B. Heat Transfer[M]. Beijing: Higher Education Press, 1955.
[8] SL 282-2003 混凝土拱坝设计规范[S]. 北京:中国水利水电出版社,2003.
SL 282-2003 Design Specification for Concrete Arch Dams[S]. Beijing:China Water Power Press,2003.
[9] 朱伯芳. 论拱坝的温度荷载[J]. 水力发电, 1984, 23(9): 23–29.
Zhu Bofang. Temperature loads on arch dams[J]. Journal of Hydroelectric Engineering, 1984, 23(9): 23–29.
[10] 孙训芳, 方孝淑, 关来泰. 材料力学[M]. 北京: 高等教育出版社, 2009: 14-15.
Sun Xunfang, Fang Xiaoshu, Guan Laitai. Material Mechanics[M]. Beijing: Higher Education Press, 2009: 14-15.
[11] 黎展眉. 拱坝温度荷载与温度应力的考虑[J]. 水利水电科技进展, 2001, 21(5): 9–11.
Li Zhanmei. Consideration of temperature loads and temperature stress on arch dams[J]. Advances in Science and Technology of Water Resources, 2001, 21(5): 9–11.
[12] 邱焕峰, 蒋媛媛, 傅少君, 等. 小湾拱坝施工过程温度场仿真分析[J]. 武汉大学学报(工学版), 2010, 43(6): 723–726.
Qiu Huanfeng, Jiang Yuanyuan, Fu Shaojun, et al. Simulation analysis of temperature field in Xiaowan arch dam construction[J]. Engineering Journal of Wuhan University, 2010, 43(6): 723–726.
[13] 傅少君, 张石虎, 解敏, 等. 混凝土拱坝温控的动态分析理论与实践[J]. 岩石力学与工程学报, 2012, 31(1): 113–122.
Fu Shaojun, Zhang Shihu, Xie Min, et al. Dynamic analysis theory and practice for temperature control and cracking prevention of concrete arch dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(1): 113–122.
[14] 周华, 傅少君, 王国进, 陈胜宏. 小湾拱坝施工期温度场动态跟踪仿真[J]. 武汉大学学报(工学版), 2009, 42(1): 77–81.
Zhou Hua, Fu Shaojun, Wang Guojin, Chen Shenhong. Dynamic tracking simulation analysis of temperature field of Xiaowan arch dam during construction period[J]. Engineering Journal of Wuhan University, 2009, 42(1): 77–81.
[15] 朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京: 中国电力出版社, 1999: 67-70.
Zhu Bofang. Thermal Stresses and Temperature Control of Mass Concrete[M]. Beijing: Water Resources and Electric Power Press, 1999: 67-70.