文章信息
- 张琪, 杜志叶, 王振东, 杨知非
- ZHANG Qi, DU Zhiye, WANG Zhendong, YANG Zhifei
- 基于有限元的单芯XLPE电缆电感计算研究
- Research on calculating inductance of a single core XLPE cable based on finite elements
- 武汉大学学报(工学版), 2017, 50(3): 390-394
- Engineering Journal of Wuhan University, 2017, 50(3): 390-394
- http://dx.doi.org/10.14188/j.1671-8844.2017-03-011
-
文章历史
- 收稿日期: 2016-05-14
随着电网的不断发展和城市电网规划改造的需要,我国电力电缆线路在电力系统中的使用量正逐年上升,尤其是高压交联聚乙烯(XLPE)绝缘电缆在电网中所占的比重日益增长,城区110 kV线路大量采用交联聚乙烯电缆[1-3].而电力电缆线路电气参数的计算在电力系统中有着极其重要的作用,参数的准确性是研究电力电缆各种电气特性的重要基础,因此必须正确认识和掌握电缆线路的参数特点[4-5].
电缆的电感值在电力系统分析中起着重要作用,如计算电缆的损耗及谐振等,现在大多数计算方法都是针对直线电缆的电感值计算,而对于弯曲电缆的电感计算研究较少,常规经验公式只能计算特定形状导线的电缆,而电缆实际敷设过程中弯曲形状可能不是很规则,公式能应用的范围有限,故可采用仿真的方法进行计算.电感的计算需要分析电缆的磁场情况,本文基于电磁场分析大型仿真软件Ansys,利用有限元分析的方法,以110 kV的单芯XLPE电缆为例,分别对直线电缆及弯曲电缆的磁场及电感值进行计算分析.
1 电缆概况及参数研究用的110 kV单芯XLPE电缆型号为YJLW03 110 1×1000,电缆的截面图如图 1所示,由内而外分别是芯线、内半导体层、绝缘层、外半导体层、屏蔽层和护套.电缆各层所用材料及尺寸参数如表 1所示,线芯及金属屏蔽层的电阻率是查资料所得,其他各层均可以作为绝缘材料来处理,电阻率取值均为1×e14,该型号电缆各层均没有非线性铁磁材料,因此相对磁导率取值均为1.

|
| 图 1 单芯电缆结构图 Figure 1 Structure of a single core XLPE cable |
| 位置 | 材料 | 厚度 /mm |
电阻率 /(Ω·m) |
相对磁 导率 |
| 线芯 | 铜 | 19.7 | 1.724 1×e-8 | 1 |
| 内半导体层 | 半导体 | 1.5 | 1×e14 | 1 |
| XLPE绝缘层 | 交联聚乙烯 | 16 | 1×e14 | 1 |
| 外半导体层 | 半导体 | 1.5 | 1×e14 | 1 |
| 金属屏蔽层 | 铝 | 2.2 | 2.84×e-8 | 1 |
| PVC外皮 | PVC | 4.5 | 1×e14 | 1 |
直线电缆的电感值与电缆的长度呈线性关系,为了简化计算可以采用2D模型来代替3D模型对直线电缆进行仿真.电缆电感值会随频率变化而发生改变,但是在低频条件下趋肤效应不明显,且常用的是工频条件下的交流电感值,故以50 Hz频率下的谐波磁场仿真为例进行计算.
2.1 仿真求解根据电缆的结构图在Ansys中建立电缆的2D模型,通过Ansys中的谐波磁场求解来计算工频电感,选用plane53单元进行有限元分析,模型建立后首先将每个圆分成4部分,然后采用映射剖分的方式进行剖分,剖分后的模型如图 2所示,可以看出剖分的网格还比较规则,Ansys中计算时需要在模型外加一个空气边界,正常情况下分析电缆的磁场分布时空气边界取5倍模型大小就足够,但是为了使计算出的电感值更准确,此处空气边界取半径为10 m的圆,在电缆线芯中加载交流电流I,设置边界处的矢量磁势AZ为0后进行求解.

|
| 图 2 电缆2D模型剖分图 Figure 2 2D subdivision model of cable |
仿真得出电缆的磁感应强度B的云图分布如图 3所示,从图中可以看出电缆的磁场强度先逐渐变大,到导线芯边界处达到最大值,然后再逐渐变小,直到空气边界处接近于0,而且云图颜色层次分明,说明网格剖分较好,计算结果较为准确.

|
| 图 3 2D模型磁感应强度分布 Figure 3 Magnetic induction intensity of 2D model |
利用电压电流法计算出50 Hz频率下单位长度电缆的电感值.电压电流法的原理是先求出单位长度电缆两端的电压,再用电缆两端的电压除以电缆中加载的电流就可以计算出电缆的阻抗值,阻抗实部即为电阻值,虚部即为感抗值,然后根据感抗值和频率即可求出电感值.计算出电缆线芯单位长度的电感值为L=1.286 3e-6H.
2.2 公式计算可用公式来验证仿真计算结果,圆截面直线电缆电感计算公式如下:

式中:R2=10 m,为空气边界半径;R1=0.019 7 m,为电缆线芯半径.计算结果为L=1.295 9e-6H,Ansys仿真软件计算结果与公式计算结果误差 < 1%.
仿真结果与公式计算结果的对比说明,通过Ansys建模利用有限元分析的方法可以比较准确地计算出直导线的电感值.
3 弯曲电缆电感计算电缆在敷设过程中不可能一直呈直线敷设,根据实际情况电缆在敷设时有可能弯曲,如需要避让障碍物等,此时电缆需要转向.根据我国交流220 kV及以下城市电力电缆线路主要设计要求的电力行业标准DT/L5221-2005可知:在隧道内110 kV及以上的电缆,应该按照电缆的热伸缩量作蛇形敷设设计以吸收电缆线路热胀冷缩量.在电缆线路局部地段,把电缆敷设成圆弧形,如设在排管管道两端的工井处,用以吸收来自排管中的电缆热伸缩量,如设在大跨距的桥梁上,用以吸收由于桥梁主体热伸缩引起的电缆伸缩量.
在弯曲敷设的情况下电缆的磁场分布会发生变化,与直线电缆磁场分布不同,会影响电缆的电感值.因此有必要计算电缆在弯曲敷设时的电感值,但是常规经验公式只能计算某些特殊弯曲形状导线的电感值,公式计算范围不够广泛,而在工程实际中,电缆弯曲形状多种多样,利用仿真建模的方式可以便捷地计算任意形状的电缆电感值.
3.1 公式计算关于弯曲电缆电感影响因素较多,与导线轴的形状尺寸、截面形状等因素都有关.线性导线的自感可以表示为
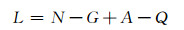
式中:N表示一个量,只与导线轴的形状和尺寸有关,而与导线截面的形状与尺寸及电流在截面上的分布无关;G、A和Q为与导线截面的形状与尺寸及电流在截面上的分布有关的量.
通常,差值A-Q与差值N-G相比甚小,可以忽略,因此一般近似认为

对于弯曲成圆弧的导线:

在直流和低频下:
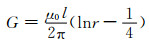
式中:R为圆弧弯曲的半径;θ为与导线长度对应的圆心角;I表示一个量,对应不同的θ角I值也不同[15].查电感计算手册可知,θ=180°时,对应的I=0.916 0;θ=360°时,对应的I=0.
故可以推出半圆形弯曲导线的电感计算公式为

闭合圆环导线电感计算公式为
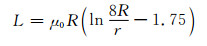
根据电力行业标准DT/L5221-2005可知,任何方式敷设的电缆,在垂直、水平转向部位和电缆热伸缩部位以及蛇形弧部位的弯曲半径,都有所规定,其中66 kV以上的单芯交联聚乙烯绝缘电缆允许的最小弯曲半径为20D,D为电缆的外径.本文中选择的单芯电缆的20倍外径约为2 m.
取弯曲半径R=2 m,电缆中导体半径r=0.019 7 m,将数据代入公式分别计算得到半圆形弯曲导线的电感值为L1=6.354 4e-6H,半圆弯曲导线单位长度的电感值为1.011 3e-6H.闭合圆环导线的电感值为L2=1.244 0e-5H,闭合圆环导线单位长度电感值为9.899 5e-7.与相同长度直线电缆电感值相比,半圆形电缆电感值与直导线电感值相差-21.96%,闭合圆环导线电感值与直导线电感值相差-23.61%,闭合圆环导线单位长度电感值比半圆形导线单位长度电感值小.计算结果说明弯曲电缆的电感值较小,且弯曲程度越大,单位长度电感值越小.
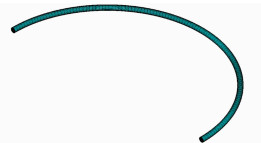
3.2 仿真计算为了验证上节中公式计算结果,在Ansys中建立半圆形弯曲电缆模型进行仿真,将仿真计算结果与公式计算结果进行对比.弯曲电缆与直线电缆不同,不能采用2D模型进行计算,需要建立3D模型,半圆形电缆模型如图 4所示,选用Solid97单元进行分析,计算时在模型外加一个立方体边界,电流流入和流出端加磁通平行边界条件,其他各个面的边界条件为磁势AX、AY、AZ都等于0,加载50 Hz交流电流后进行求解.
|
| 图 4 半圆弯曲电缆模型 Figure 4 Model of semicircular cable |
同样利用电压电流法计算弯曲电缆的电感,仿真计算出半圆形电缆的电感值L=6.115 6e-6H,与公式计算结果对比,误差为3.76%,产生误差的原因可能是模型剖分不够精细,软件计算产生误差.公式与仿真计算两者的误差在5%以内,可以认为在误差允许范围内,仿真计算结果正确,说明了利用有限元分析的方法计算弯曲电缆电感值是可行的.
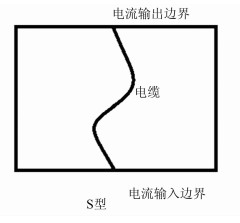
4 工程实例计算工程实际中为了吸收电缆线路热胀冷缩量电缆常作蛇形敷设设计,示意图如图 5所示,此时无法利用经验公式进行计算,因此可以利用本文提出的有限元分析方法,在Ansys中进行建模仿真计算.
|
| 图 5 电缆敷设示意图 Figure 5 Schematic diagram of cable lying |
根据示意图在Ansys中建立电缆的模型,电缆的弯曲部分半径也取2 m,电缆总长度为15.73 m,建模的过程中为了使剖分的网格比较规则、计算结果更加准确,采用拉伸的方式进行建模,先建立电缆二维截面图的模型,对面采用映射剖分的方式进行剖分,然后将剖分好的面沿着电缆弯曲的轴线进行带网格拉伸,面网格就拉伸成体网格,剖分好的模型如图 6所示,从图中可以看出模型的网格比较规则.同样在电缆外加一个立方体边界进行仿真计算,边界条件设置好后,加载50 Hz交流电流来计算它们的工频交流电感值.

|
| 图 6 蛇形弯曲电缆模型 Figure 6 Model of snake bended cable |
计算出蛇形电缆的电感值为L=1.702 4e-5H,此时单位长度电缆的电感值为1.082 3e-6.与同样长度的直导线电感值进行对比,两者相差-7.56%,蛇形敷设的电缆电感值也比直导线电感值小.
5 结论本文通过对110 kV单芯XLPE电缆进行建模,采用有限元计算的方法进行仿真获得直线电缆及弯曲电缆的电感值,并将计算结果进行了对比,可以说明有限元计算的方法适用于各种不同形状的电缆,能准确计算出电缆的电感值.弯曲电缆由于电缆形状的改变,磁场分布会发生变化,电感值也会改变,与直线电缆相比,单位长度弯曲电缆的电感值比单位长度直线电缆的电感值小,而且弯曲程度越大,电感值越小.
| [1] |
李红雷, 张丽, 张莉华. 交联聚乙烯电缆在线监测与检测[J].
中国电力, 2010, 43(12): 31–34.
Li Honglei, Zhang Li, Li Lihua. Online monitoring and detection techniques of XLPE cables[J]. Electric Power, 2010, 43(12): 31–34. DOI:10.3969/j.issn.1004-9649.2010.12.008 |
| [2] |
曹晓珑, 刘英, 钟力生, 等. 从2010国际大电网会议看电力电缆技术的发展现状和趋势[J].
高电压技术, 2010, 36(12): 3078–3083.
Cao Xiaolong, Liu Ying, Zhong Lisheng, et al. Power cabletechnology status and trends seeing from 2010 CIGRE conference[J]. High Voltage Engineering, 2010, 36(12): 3078–3083. |
| [3] |
胡春江, 王锋, 温定筠, 等. XLPE电缆局部放电在线检测技术现状[J].
电网技术, 2014, 38(Sup.1): 33–38.
Hu Chunjiang, Wang Feng, Wen Dingjun, et al. Development of partial discharge online detection system for high-voltage XLPE cable[J]. Power System Technology, 2014, 38(Sup.1): 33–38. |
| [4] |
唐忠, 高巍. 单芯XLPE电缆分布参数的研究与计算[J].
华东电力, 2014, 42(3): 534–540.
Tang Zhong, Gao Wei. Calculation and research of single-core XLPE power cable distribution parameters[J]. East China Electric Power, 2014, 42(3): 534–540. |
| [5] |
毛为民. 电力电缆相序阻抗计算与分析[J].
供用电, 2002, 19(4): 24–25.
Mao Weimin. Calculation and analysis of sequence impedance for power cable lines[J]. Distribution & Utilization, 2002, 19(4): 24–25. |
| [6] |
徐政, 钱洁. 电缆电气参数不同计算方法及其比较[J].
高电压技术, 2013, 39(3): 689–697.
Xu Zheng, Qian Jie. Comparison of different methods for calculating electrical parameters of power cables[J]. High Voltage Engineering, 2013, 39(3): 689–697. |
| [7] |
唐庆华, 刘宝成, 杨洪, 等. 高压电缆金属护套的接地方式对线路参数的影响[J].
电线电缆, 2009(2): 43–46.
Tang Qinghua, Liu Baocheng, Yang Hong, et al. Effect of the earthing method of the metal sheath in HV cables on line parameters[J]. Electric Wire & Cable, 2009(2): 43–46. |
| [8] |
邓星, 蒙绍新, 尹项根, 等. 多回并联电缆线路参数的不对称性分析[J].
高电压技术, 2010, 36(12): 3119–3124.
Deng Xing, Meng Shaoxin, Yin Xianggen, et al. Analysis of asymmetry of sequence parameters for parallel multi-circuit cables[J]. High Voltage Engineering, 2010, 36(12): 3119–3124. |
| [9] |
李长益, 丁伟. 高压电缆护层连接方式对线路参数的影响[J].
江苏电机工程, 2003, 22(6): 22–23.
Li Changyi, Ding Wei. Effect of sheath connection form of high voltage cable to line parameters[J]. Jiangsu Electrical Engineering, 2003, 22(6): 22–23. |
| [10] |
林晓宇, 张小敏. 电力电缆线路参数现场测量与分析[J].
电线电缆, 2008(3): 42–44.
Lin Xiaoyu, Zhang Xiaomin. Field measurement and analysis of power cable parameters[J]. Electric Wire & Cable, 2008(3): 42–44. |
| [11] |
陆家榆, 袁建生, 马信山. 地下隧道中电力电缆的线路阻抗矩阵相序阻抗矩阵和参数的分析[J].
电网技术, 1998, 22(9): 5–8.
Lu Jiayu, Yuan Jiansheng, Ma Xinshan. Analysis of matrix line impedance, matrix phase sequence imped ance and parameters of power cables in underground tunnels[J]. Power System Technology, 1998, 22(9): 5–8. |
| [12] |
王晓彤, 项祖涛, 班连庚, 等. 500 kV电缆线路工频参数的计算与分析[J].
电网技术, 2013, 37(8): 2310–2315.
Wang Xiaotong, Xiang Zutao, Ban Liangeng, et al. Calculation and analysis of power-frequency parameters for 500 kV cable lines[J]. Power System Technology, 2013, 37(8): 2310–2315. |
| [13] |
钱洁. 电力电缆电气参数及电气特性研究[D]. 杭州: 浙江大学, 2013.
Qian Jie. Study on electrical parameter calculation method and electrical characteristics of power cables[D]. Hangzhou:Zhejiang University, 2013. |
| [14] |
冯慈璋, 马西奎.
工程电磁场导论[M]. 北京: 高等教育出版社, 2013.
Feng Cizhang, Ma Xikui. Introduction to Engineering Electromagnetic Field[M]. Beijing: Higher Education Press, 2013. |
| [15] |
п. л. 卡兰塔罗夫, л. A. 采伊特林. 电感计算手册[M]. 陈汤铭, 刘保安, 罗应立, 译. 北京: 机械工业出版社, 1992.
Кадантаровп л, Цейтлин л A. Inductance Calculation Handbook[M].Translated by Chen Tangming, Liu Baoan, Luo Yingli, translated.Beijing:China Machine Press, 1992. |
 2017, Vol. 50
2017, Vol. 50



