文章信息
- 龚田牛, 卢亦焱
- GONG Tianniu, LU Yiyan
- 圆钢管混凝土构件抗弯性能数值分析与承载力计算
- Numerical analysis of concrete filled circular steel tube under bending load and its calculating method
- 武汉大学学报(工学版), 2018, 51(5): 422-425
- Engineering Journal of Wuhan University, 2018, 51(5): 422-425
- http://dx.doi.org/10.14188/j.1671-8844.2018-05-008
-
文章历史
- 收稿日期: 2017-02-28
2. 武汉大学土木建筑工程学院,湖北 武汉 430072
2. School of Civil and Architectural Engineering, Wuhan University, Wuhan 430072, China
钢管混凝土结构充分发挥钢管和混凝土两种材料的作用,具有强度高、延性好、耐疲劳和抗冲击等优点[1-3].近十几年来,钢管混凝土结构正越来越多地应用于高层与超高层建筑、拱桥与组合桥梁、大型工业厂房、地基桩等结构.钢管混凝土由于其力学特性适宜应用于轴压构件和小偏压构件.实际工程中的结构柱一般处于压弯状态,当结构柱的轴力较小而水平荷载较大时,可近似认为处于纯弯状态.另外钢管混凝土构件的纯弯性能是研究其压弯性能的基础,因此,有必要对钢管混凝土构件的纯弯性能进行深入研究.目前钢管混凝土构件抗弯承载力计算主要有数值计算方法[4, 5]和基于内力平衡的简化计算方法[6, 7].前者通过对数值计算结果的回归分析得出反映外套钢管对核心混凝土约束作用的弯矩提高系数,后者基于内力平衡理论,推导出钢管混凝土构件抗弯承载力计算公式.抗弯承载力计算值和试验值均吻合较好,且偏于保守.
本文根据考虑强化的理想弹塑性钢材本构关系和约束核心混凝土本构关系,对圆形截面钢管混凝土进行截面划分,采用数值方法计算了圆形钢管混凝土构件的弯矩-曲率关系曲线,通过拟合得出截面中性轴位置的计算方法;基于截面内力平衡理论推导出钢管混凝土构件的抗弯承载力计算公式,并与试验结果进行对比,公式计算结果和试验结果吻合较好,该公式形式简单,力学概念清晰,可以有效计算圆形钢管混凝土构件的抗弯承载力.
1 数值计算 1.1 本构关系由钢管混凝土构件纯弯试验[8-12]可知,在达到极限状态时,截面中性轴上移,受压区由于核心混凝土的膨胀,钢管处于拉-压受力状态,其屈服强度低于单向受力屈服强度,取受压屈服强度fyt=0.89fy[13],同时考虑钢材受拉时具有强化段,强化段的模量值Es1=0.01Es,εs=10εy.混凝土采用文献[4]提出的钢管约束混凝土本构关系.
1.2 计算假定与过程根据试验研究结果,在计算钢管混凝土受弯构件中性轴位置时作以下假定:
1) 截面在弯曲过程中符合平截面假定;
2) 忽略剪力对截面变形的影响;
3) 不考虑混凝土的抗拉强度;
4) 钢管和混凝土无相对滑移.
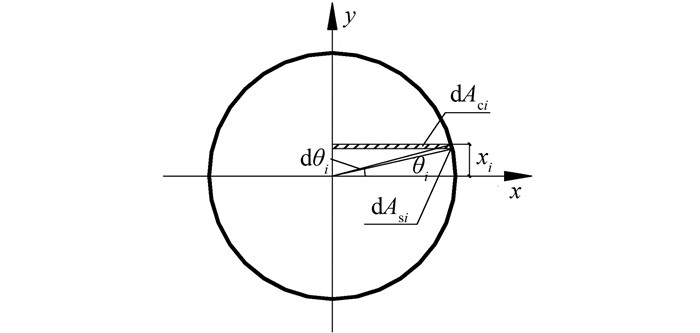
在对钢管混凝土受弯构件进行全过程数值分析时,应对其截面进行单元划分.如图 1所示,将钢管沿圆周方向划分为n等份,这样钢管每部分对应的圆心角dθ和面积dAsi以及混凝土面积dAci分别为
|
| 图 1 截面划分 Figure 1 Cross-section division |
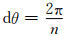 (1)
(1)
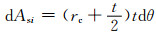 (2)
(2)
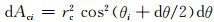 (3)
(3)
式中:rc为钢管内径;t为钢管壁厚.
由假设(1)可知,截面任意条带中心点的应变为
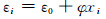 (4)
(4)
式中:ε0为截面形心处应变;xi为条带中心至截面形心轴的距离.
在划分完单元、确定每个单元的位置和应变以后,可由材料相应的本构关系求得其对应的应力,这样就可求得截面的轴力和弯矩:
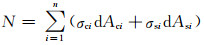 (5)
(5)
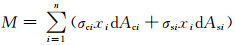 (6)
(6)
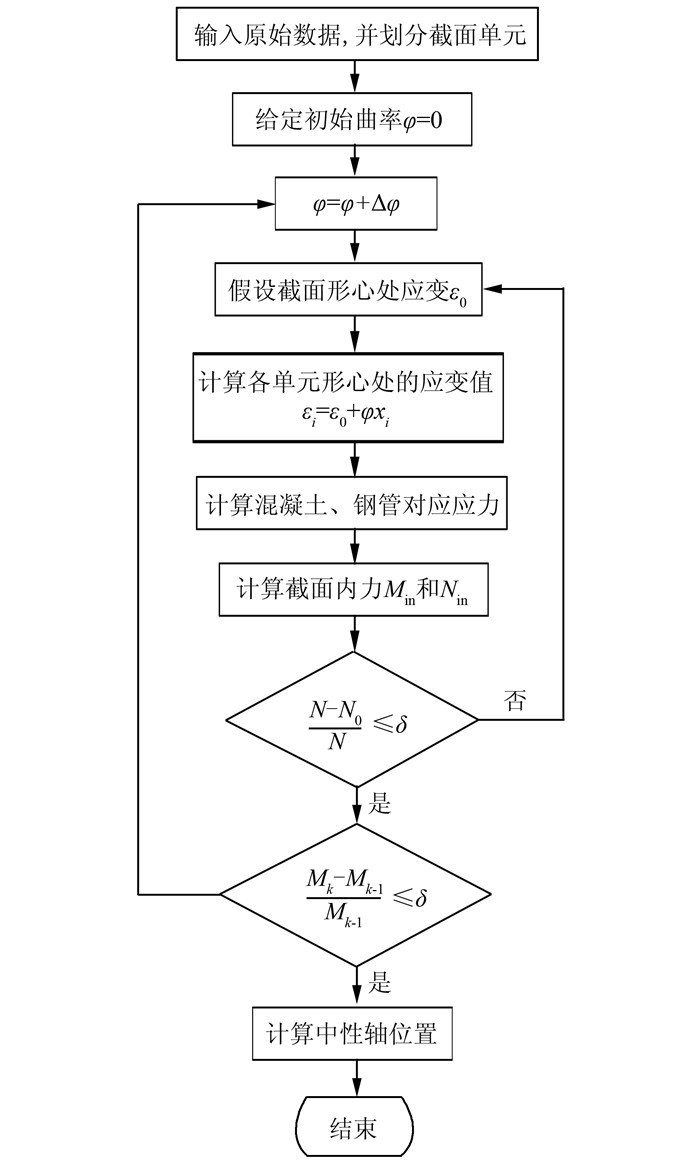
中性轴位置计算步骤如下:1)给定初始曲率φ,并假设截面形心处的应变为ε0;2)计算各个单元中心处对应的应变,根据材料本构关系计算出其对应的应力;3)根据式(5)、(6)计算截面内弯矩Min和轴力Nin;4)判断求得的Nin、Min是否满足平衡条件,否则调整ε0值,直到满意为止,得到M-φ曲线上一点;5)增加曲率,φ=φ+Δφ,重复第2~4步工作,得到M-φ曲线上下一点,如此反复迭代,即可获得M-φ全过程曲线.当弯矩的变化小于某一限值时,即认为构件达到极限承载力,由式(4)计算出极限状态时的中性轴位置.其计算框图如图 2所示.
|
| 图 2 计算框图 Figure 2 Calculation diagram |
文献[4]将钢管和混凝土同时考虑,其组合强度用抗压强度指标fscy表示,本文在推导钢管混凝土构件抗弯承载力时也将受压区钢管和混凝土统一考虑,其应力均达到fscy,忽略混凝土的抗拉强度,受拉区钢管应力取其屈服强度.
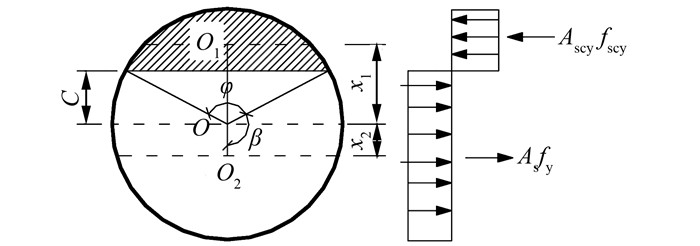
钢管混凝土构件受弯极限状态的应力分布如图 3所示,由截面内力平衡可得:
|
| 图 3 应力分布 Figure 3 Stress distribution |
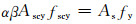 (7)
(7)
式中:α、β为等效圆形应力图系数[14, 15],可近似按混凝土规范取值;Ascy为受压区面积;fscy为抗压强度指标;As、fy为受拉区钢管面积及其强度.
由力矩平衡得:
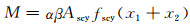 (8)
(8)
式中:x1为受压区混凝土重心到截面圆心的距离;x2为受拉区钢管重心到截面圆心的距离.
受压区混凝土为弓形,受拉区钢管为圆弧形,由几何知识可知:
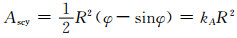 (9)
(9)
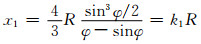 (10)
(10)
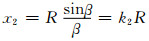 (11)
(11)
由式(8)~(11)可得出圆钢管混凝土柱的抗弯承载力简化计算公式:
 (12)
(12)
式中:k为截面系数,k=kA(k1+k2);kA为受压混凝土面积系数;k1为受压混凝土距离系数;k2为受拉钢管距离系数.
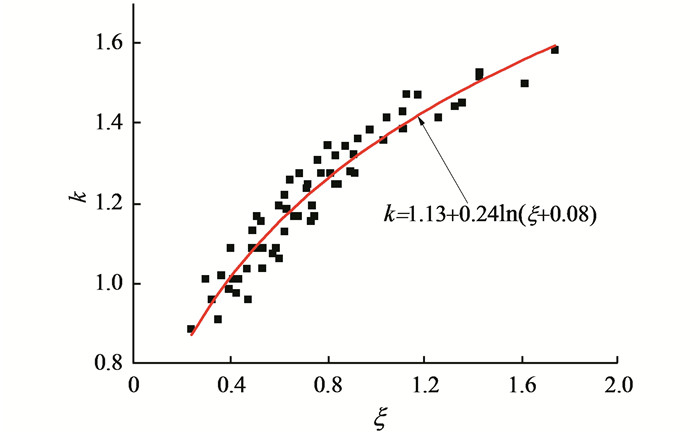
通过对不同参数的试件进行计算(钢管壁厚为2~8 mm,钢管屈服强度为235~420 MPa,核心混凝土强度为C30~C80),发现k可表示为套箍系数ξ的函数,如图 4所示.通过回归分析,k的表达式为
|
| 图 4 参数拟合 Figure 4 Parameters fitting |
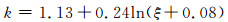 (13)
(13)
综上所述,本文提出圆钢管混凝土构件纯弯承载力计算公式,相应表达式为
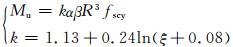 (14)
(14)
采用式(14)对相关文献试验数据[4, 8]进行了对比分析,表 1为圆钢管混凝土构件抗弯承载力计算值与试验值的对比情况,比值的平均值为0.875,均方差为0.091,可见二者吻合较好,提出的计算公式可以较精确地计算圆钢管混凝土构件的抗弯承载力,总体上偏于安全.分析原因是因为在计算中性轴位置的时候,并没有考虑钢管与混凝土的套箍效应,实际混凝土应变值要偏大很多.
| 编号 | D×t/(mm×mm) | fy/MPa | fck/MPa | Mt/(kN·m) | Mu//(kN·m) | Mu/Mt |
| 1 | 89×4.50 | 304 | 59.0 | 13.70 | 11.26 | 0.822 |
| 2 | 108×4.50 | 264 | 62.0 | 20.38 | 16.59 | 0.814 |
| 3 | 133×4.50 | 333 | 62.0 | 39.52 | 31.49 | 0.797 |
| 4 | 159×1.65 | 333 | 59.0 | 59.22 | 47.22 | 0.797 |
| 5 | 152×1.65 | 262 | 65.5 | 19.90 | 18.90 | 0.950 |
| 6 | 152×1.65 | 262 | 65.5 | 17.90 | 18.90 | 1.056 |
| 7 | 152×1.65 | 262 | 65.5 | 20.80 | 18.90 | 0.908 |
| 8 | 152×1.65 | 262 | 65.5 | 19.00 | 18.90 | 0.995 |
| 9 | 300×6.23 | 436 | 48.1 | 365.50 | 292.66 | 0.801 |
| 10 | 300×5.65 | 403 | 49.6 | 327.30 | 261.87 | 0.800 |
| 11 | 300×6.16 | 406 | 52.0 | 321.10 | 282.93 | 0.881 |
| 注:D、t为钢管外径和壁厚;fy为钢管屈服强度;fck为混凝土抗压强度标准值;Mt为抗弯承载力试验值;Mu为抗弯承载力公式计算值. | ||||||
1) 根据考虑强化的弹塑性钢材本构关系和约束核心混凝土本构关系,采用条带法计算了圆形截面钢管混凝土构件的弯矩-曲率关系曲线,通过拟合得出截面中性轴位置的计算方法.
2) 基于截面内力平衡理论推导出圆钢管混凝土构件的抗弯承载力计算公式,并与试验结果进行对比,公式计算结果和试验结果吻合较好,该公式可以有效地计算圆钢管混凝土构件的抗弯承载力,总体上偏于安全.
| [1] | Manojkumar V C, Mattur C N, Kulkarnib S M. Axial strength of circular concrete. Axial strength of circular concrete.filled steel tube columns.DOE approach[J]. Journal of Constructional Steel Research, 2010, 66(10): 1248–1260. DOI:10.1016/j.jcsr.2010.04.006 |
| [2] | Chunga K, Parkb S, Choib S. Material effect for predicting the fire resistance of concrete.filleds quare steel tube column under constant axial load[J]. Journal of Constructional Steel Research, 2008, 64(12): 1505–1515. DOI:10.1016/j.jcsr.2008.01.002 |
| [3] | Denavit, Mark D, Hajjar, et al. Nonlinear seismic analysis of circular concrete filled steel tube members and frames[J]. Journal of Structural Engineering, 2012, 138(9): 1089–1098. DOI:10.1061/(ASCE)ST.1943-541X.0000544 |
| [4] |
韩林海.
钢管混凝土结构——理论与实践[M]. 北京: 科学出版社, 2007.
Han Linhai. Concrete Filled Steel Tube Structure—Theory and Practice[M]. Beijing: Science Press, 2007. |
| [5] |
钟善桐.
钢管混凝土结构[M]. 第3版. 北京: 清华大学出版社, 2003.
Zhong Shantong. The Concrete.Filled Steel Tubular Structures[M]. 3rd edition. Beijing: Tsinghua University Press, 2003. |
| [6] |
臧华, 刘钊, 涂永明. 计算圆钢管混凝土构件抗弯承载力的新方法[J].
武汉理工大学学报, 2009, 31(17): 96–98.
Zang Hua, Liu Zhao, Tu Yongming. A new method for predicting ultimate flexural capacity of concrete.filled circular steel tubes[J]. Journal of Wuhan University of Technology, 2009, 31(17): 96–98. DOI:10.3963/j.issn.1671-4431.2009.17.027 |
| [7] |
黄宏, 张安哥. 圆钢管混凝土抗弯承载力的计算[J].
华东交通大学学报, 2008, 25(1): 1–3.
Huang Hong, Zhang Ange. The calculation of flexural capacity of concrete.filled circular steel tubes[J]. Jour nal of East China Jiaotong University, 2008, 25(1): 1–3. |
| [8] |
王庆利, 董志峰, 高建志. 圆截面钢管混凝土受弯构件试验研究[J].
四川建筑科学研究, 2007, 33(3): 9–12.
Wang Qingli, Dong Zhifeng, Gao Jianzhi. Experimental study on concrete filled circular steel tubular flexural members[J]. Sichuan Building Science, 2007, 33(3): 9–12. |
| [9] |
蔺海晓, 常旭, 黄承逵, 等. 钢管自应力混凝土抗弯性能研究[J].
河南理工大学学报(自然科学版), 2009, 28(3): 357–362.
Lin Haixiao, Chang Xu, Huang Chenkui, et al. Study on the mechanical performance of self. stressing concrete.filled steel tube short column under cure bending[J]. Journal of Henan Polytechnic University (Natural Science), 2009, 28(3): 357–362. |
| [10] |
吉伯海, 胡正清, 陈甲树, 等. 圆钢管轻集料混凝土构件抗弯性能的试验研究[J].
土木工程学报, 2007, 40(8): 35–40.
Ji Bohai, Hu Zhengqing, Chen Jiashu, et al. An experimental study on the behavior of lightweight aggregate concrete filled circular steel tubes under pure bending load[J]. China Civil Engineering Journal, 2007, 40(8): 35–40. |
| [11] |
丁发兴, 余志武. 圆钢管自密实混凝土纯弯力学性能[J].
交通运输工程学报, 2006, 6(1): 63–78.
Ding Faxing, Yu Zhiwu. Pure bending properties of self.compacting concrete filled circular steel tube[J]. Journal of Traffic and Transportation Engineering, 2006, 6(1): 63–78. |
| [12] |
高金东, 刘清, 何原野, 等. 圆钢管自密实混凝土梁的抗弯承载力研究[J].
混凝土, 2014(5): 35–40.
Gao Jindong, Liu Qing, He Yuanye, et al. Research on bending capacity of self.compacting concrete filled circle steel tubular beam[J]. Concrete, 2014(5): 35–40. |
| [13] | Architectural Institute of Japan (AIJ). Recommendations for Design and Construction of Concrete Filled Steel Tubular Structures[S]. Architectural Institute of Japan (AIJ), Tokyo, Japan, 1997. |
| [14] |
朱莉萍, 熊杰. 圆形截面偏心受压构件的等效应力图形设计方法[J].
工业建筑, 2001, 31(5): 75–77.
Zhu Liping, Xiong Jie. A design method of eccentrically compressed round.section memberwith equivalent stress figure[J]. Industrial Construction, 2001, 31(5): 75–77. |
| [15] |
王庆华, 熊志斌. 钢筋混凝土截面等效矩形应力图系数的计算[J].
南昌工程学院学报, 2011, 30(6): 58–61.
Wang Qinghua, Xiong Zhibin. Calculation of equivalent rectangular stress block coefficients of reinforced concrete section[J]. Journal of Nanchang Institute of Technology, 2011, 30(6): 58–61. |
 2018, Vol. 51
2018, Vol. 51




