文章信息
- 肖惠民
- XIAO Huimin
- 基于数值波浪水槽的波力直驱水轮机前导流口体型优选
- Configuration selection of front guide inlet for direct driving turbine based on numerical wave tank
- 武汉大学学报 (工学版), 2017, 50(1): 125-128
- Engineering Journal of Wuhan University, 2017, 50(1): 125-128
- http://dx.doi.org/10.14188/j.1671-8844.2017-01-019
-
文章历史
- 收稿日期: 2016-04-23
2. 武汉大学水力机械过渡过程教育部重点实验室,湖北 武汉 430072
2. Key Laboratory of Transients in Hydraulic Machinery of Ministry of Education, Wuhan University, Wuhan 430072, China
近几十年来,海洋能开发利用技术取得了快速发展,工程师们研发了各种波浪能、潮汐能、海流能以及温差能发电系统,建成若干试验电站,并进入商业化运营[1].本文涉及的波力直驱水轮机为一种新式的波浪能转换装置,由波浪直接驱动水轮机,集波浪能俘获和转换于一体,具有宽广的高效率区,对水头变化的适应性强,启动性能好[2].
波力直驱水轮机的前导流口是俘获波浪能的关键部件,其体型对整个波能转换装置的俘获宽度比及发电效益具有重要的影响.本文基于计算流体动力学技术,对波力直驱水轮机不同体型前导流口的水力特性进行了研究,考察了3种体型前导流口对水轮机流量、波浪俘获能力等的影响.文中根据物理水槽的造波原理,在FLUENT流动计算软件中通过设定造波板的运动规律模拟了三维规则波.
1 波力直驱水轮机结构及前导流口体型波力直驱水轮机如图 1所示,主要由前导流口、转轮、固定导流叶片、轮毂和蓄水池等组成.前导流口将波浪收集到水轮机中,后蓄水池可储存流过水轮机的水流.在一个波周期内,水流流入、流出水轮机形成往复水流,且水流驱动转轮朝同一方向旋转.该波力直驱水轮机既可以是近岸固定型的,也可以是海上漂浮型的.固定型的可安装在近海或近岸水域的挡水处,如防波堤内.
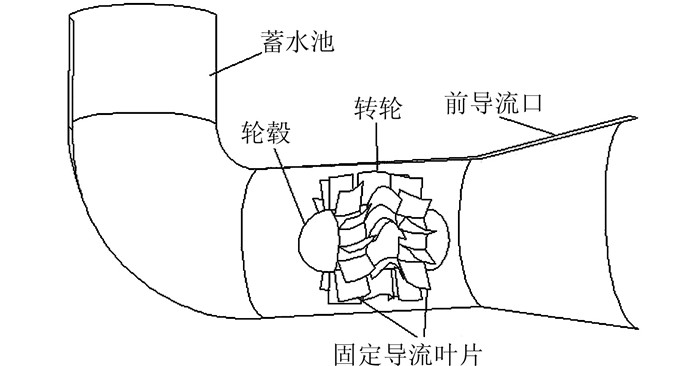
|
| 图 1 波力直驱水轮机示意图 Figure 1 Schematic diagram of wave direct driving turbine |
前导流口的水力设计应保证导流口前及其内部具有良好流态,水力损失小,整个波能转换装置具有高的俘获宽度比,提高发电效益.本文对3种不同的导流口体型进行了比较研究,相应体型如图 2所示.转轮外径0.3 m;前导流口长0.5 m,进出口直径分别为0.5、0.3 m;体型2圆弧半径为1.3 m;体型3双圆弧半径均为0.65 m.
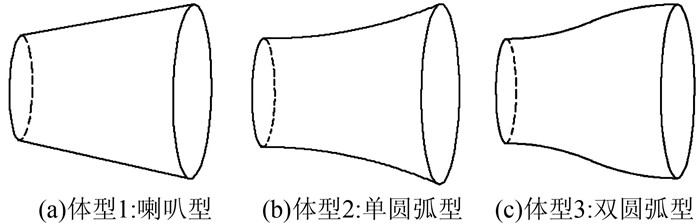
|
| 图 2 前导流口体型 Figure 2 Front guide inlet configuration |
随着计算流体动力学技术的发展,通过建立数值波浪水槽来进行数值仿真实验已在水波动力学领域得到广泛应用[3-6].与传统物模试验相比,数值波浪水槽具有成本低、不受尺寸限制、易于改造、无触点流场测量、可获得较详细的流场信息等优点.
本文基于不可压缩黏性流体的N-S方程和标准k-ε湍流模型,采用VOF (Volume of Fluid) 方法追踪自由面,利用FLUENT及其二次开发功能建立了可有效模拟线性波的三维数值波浪水槽.
2.1 控制方程二维数值波浪水槽的控制方程为以速度和压力为变量的不可压缩黏性流体的二维N-S方程和连续性方程:
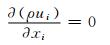 (1)
(1)
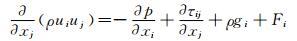 (2)
(2)
式中:τij为雷诺应力项,由标准k-ε紊流模型计算得到.
标准k-ε紊流模型:
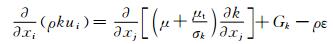 (3)
(3)
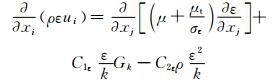 (4)
(4)
式中:C1ε=1.44;C2ε=1.92;Cμ=0.09;σk=1.0;σε=1.0.
自由面的追踪采用VOF法.VOF法引进了体积分数αq,用于表示第q种流体在网格单元内所占的体积比率.αq=0时表示单元内没有第q相流体;αq=1时表示单元内全部为第q相流体;0 < αq < 1时表示该单元为交界面单元.对于水波问题,由于只有气液两相,故q=1或2.αq满足方程:
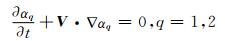 (5)
(5)
及约束方程:
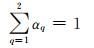 (6)
(6)
动边界造波是一种仿物理造波方法,通过造波边界的周期性往复运动模拟实际造波机的运动.
根据线性造波机理论[7-8],对于平衡位置在原点、冲程为S0、角频率为ω(周期为T) 的推板式造波机,推板简谐运动的速度为
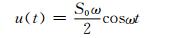 (7)
(7)
推板运动将产生一定周期和波高的波浪,并向外传播.根据势流理论[9],在水深为h的波浪水槽中,距离造波板较远的x处产生的波面可表示为
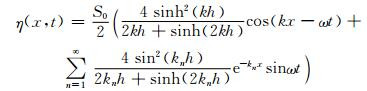 (8)
(8)
式中,波数k满足方程:
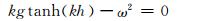 (9)
(9)
而kn为方程:
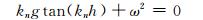 (10)
(10)
的第n个根.式 (8) 中第1项为造波板生成的行进波,而第2项为非传播波,代表局部扰动,它随着离开造波板距离的增加而以指数形式衰减,在离开造波板约3倍水深后,即可忽略.
造波板的冲程S0与目标波波高H有如下关系:
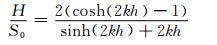 (11)
(11)
计算域如图 3所示,包括三维数值水槽和简化后的波力直驱水轮机.为减少计算量,水轮机部分未带导叶和转轮,仅包含了过流通道.三维数值波浪水槽长度为15.0 m,宽度为1.0 m,高度为1.05 m,造波板位于水槽的最左端 (y=0.0 m处).
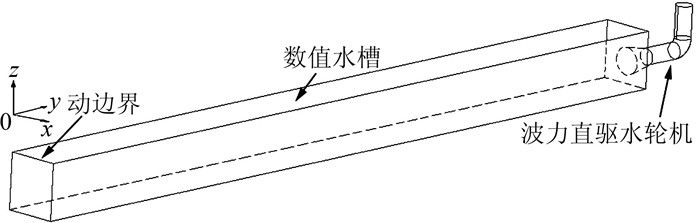
|
| 图 3 计算区域 Figure 3 Computational domain |
造波边界设为壁面,并运用动网格 (Dynamic Mesh) 技术中的动态层 (Dynamic Layering) 方法处理该活动边界问题.水槽和蓄水池顶部为压力出口边界条件.近壁处理采用标准壁面函数.
数值水槽采用六面体网格,为了能够更为精细地捕捉自由水面,在水气交界面处对网格进行了局部加密,单元格长0.05 m、宽0.05 m、高0.025 m,如图 4.整个计算区域共划分了约17.3万个单元格.

|
| 图 4 自由水面网格加密 Figure 4 Free water surface grid refinement |
方程压力项采用PRESTO!格式,其他项采用二阶迎风差分格式.采用PISO算法,实现压力和速度变量的分离求解.迭代控制精度ε=0.001,每步计算最大迭代步数30次.
4 计算结果及分析 4.1 计算工况根据我国近海波况,波浪的输入参数为:水深h=0.85 m,造波推板冲程S0=0.062 m,运动周期T=2.5 s.将上述参数代入式 (7),并通过UDF程序赋给动边界.计算时间步长为0.001 25 s.
4.2 波浪形态分析受造波板的影响,波面运动在最初的几个运动周期内较不稳定,8个周期后基本达到稳定,水槽中形成一列稳定、呈周期性变化的行波列 (图 5).即使在距造波板较近的位置如y=0.3 m处,波面的运动情况也较为稳定.图 6~8分别为y=0.3 m、y=6.558 m、y=14.9 m处的波形.

|
| 图 5 数值水槽纵剖面波形图 Figure 5 Wave pattern along numerical wave tank |
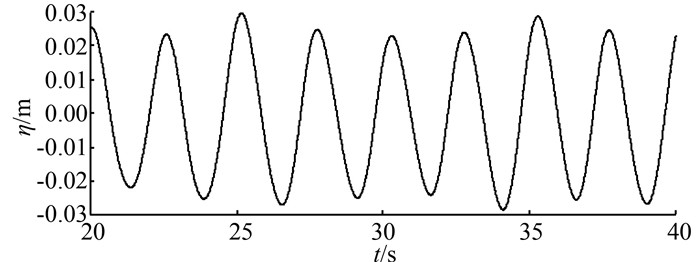
|
| 图 6 y=0.3 m处波形图 Figure 6 Wave profile at y=0.3 m |
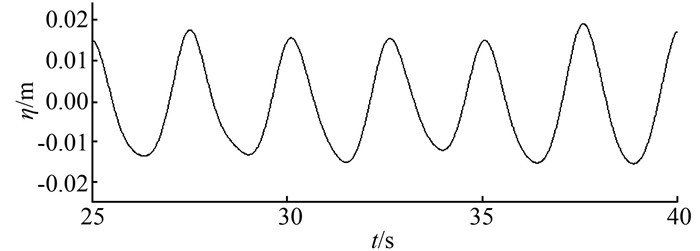
|
| 图 7 y=6.558 m处波形图 Figure 7 Wave profile at y=6.558 m |
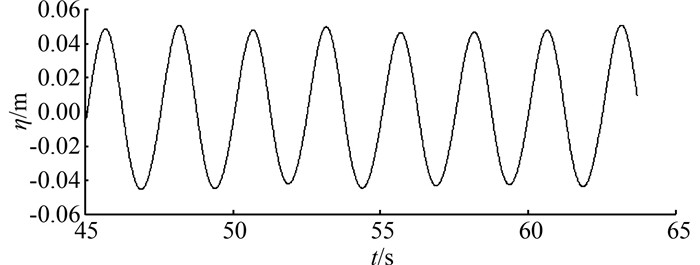
|
| 图 8 y=14.9 m处驻波波形图 Figure 8 Wave profile at y=14.9 m |
如图 6~8所示,波形因受到非线性作用的影响,波峰和波谷出现了不对称现象.且随着离造波板的距离的增大,波面幅值逐渐变小,即存在波幅沿程衰减的现象,这是波浪运动中非传播项及流体的粘性作用造成的.
在水槽右端、前导流口进口处,壁面产生的反射波将与入射波叠加,产生线性驻波,波幅约为原入射波波幅的2倍,如图 8所示.随着离壁面距离的增大,反射波逐步衰减,对入射波的干扰也逐步减小.
通过模拟计算得到的波浪周期和波长的统计结果如表 1所示,从表中可以看出,平均周期和平均波长与理论值相对误差均较小.
| 波浪周期T0/s | 波浪周期计算值T/s | 波浪周期相对误差/% | 波长理论值λ0/m | 波长计算值λ/m | 波长相对误差/% |
| 2.5 | 2.505 | 0.2 | 6.558 | 6.597 | 0.6 |
3种体型导流口的主要性能指标如表 2所示.由表可见,导流口体型对波力直驱水轮机的性能有直接的影响,即体型不同时,蓄水池涌浪高度、过机流量、系统俘获宽度比均有差别.体型1(喇叭型) 的3个指标均优于另外两种体型,性能最佳;体型2(单圆弧型) 各项指标相对较差;体型3(双圆弧型) 性能与体型1接近,居中.
| 导流口体型 | 蓄水池涌浪高度ΔZ/m | 过机流量Q/(m3·s-1) | 俘获宽度比ηc |
| 体型1 | 0.378 | 0.021 | 4.93 |
| 体型2 | 0.334 | 0.019 | 3.85 |
| 体型3 | 0.358 | 0.020 | 4.42 |
体型1后蓄水池自由表面波动情况、水轮机流量变化情况如图 9~10所示,波形与水槽中的波浪波形相一致.
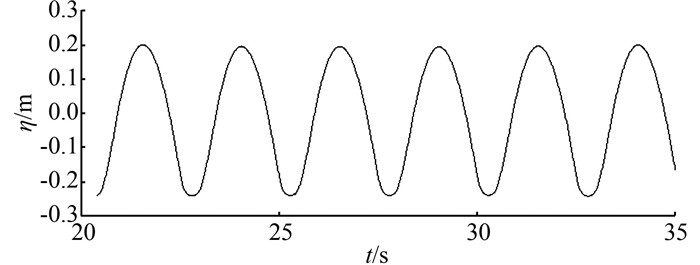
|
| 图 9 体型1后蓄水池涌浪波形图 Figure 9 Wave profile in rear reservoir matching first type front guide inlet |
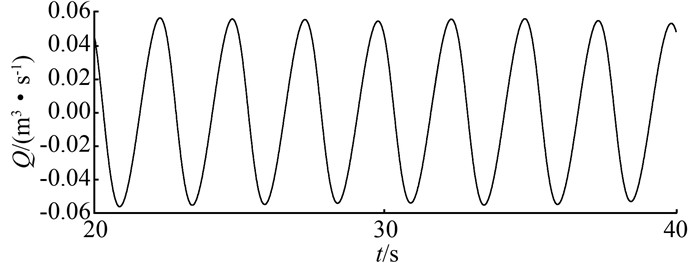
|
| 图 10 体型1过机流量变化曲线图 Figure 10 Discharge curve of first type front guide inlet |
俘获宽度比ηc为波浪能转换装置俘获的能量ET与其迎波宽度内的波浪能EW之比.在同样的波况下,俘获宽度比ηc越高,代表着波力直驱水轮机俘获波浪能的能力越强,其发电效益也越好.俘获宽度比ηc按下式计算:
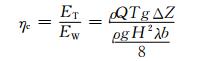 (12)
(12)
式中:ET为一个周期内波力直驱水轮机内水流所获得的势能;b为波力直驱水轮机前导流口的迎波宽度,0.5 m.
5 结论1) 基于FLUETN软件的动边界造波可在有限的计算时间内产生稳定的行波波列,并能生成驻波,且该方法产生的波形和线性理论结果相吻合.通过改变造波板的相关参数,还可根据需要获得不同波高、周期和波长的数值波浪.
2) 计算表明,导流口体型对波力直驱水轮机的性能有直接的影响,不同的导流口体型水轮机蓄水池涌浪高度、流量、俘获宽度比均有差别.喇叭型导流口性能指标优于另外两种体型,其俘获波浪能的能力更高,水轮机的发电效益将更好.
3) 为减少计算量,本文对水轮机进行了简化,后续将采用本文的模拟方法开展带完整水轮机的水轮机性能预估及过流部件的优化设计工作,以获得更为精准、全面的研究成果.
| [1] |
游亚戈, 李伟, 刘伟民, 等. 海洋能发电技术的发展现状与前景[J].
电力系统自动化, 2010, 34(14): 1–12.
You Yage, Li Wei, Liu Weimin, et al. Development status and perspective of marine energy conversion systems[J]. Automation of Electric Power Systems, 2010, 34(14): 1–12. |
| [2] |
肖惠民, 于波. 基于计算流体动力学的波力直驱式水轮机性能研究[J].
武汉大学学报 (工学版), 2014, 47(2): 207–210.
Xiao Huimin, Yu Bo. Analysis of performance of wave direct driving turbine based on computational fluid dynamics[J]. Engineering Journal of Wuhan University, 2014, 47(2): 207–210. |
| [3] |
刘加海, 杨永全, 张洪雨, 等. 二维数值水槽波浪生成过程及波浪形态分析[J].
四川大学学报 (工程科学版), 2004, 36(6): 28–31.
Liu Jiahai, Yang Yongquan, Zhang Hongyu, et al. Making waves in 2-D numerical flume and feature analysis of the numerical waves[J]. Journal of Sichuan University (Engineering Science Edition), 2004, 36(6): 28–31. |
| [4] |
李胜忠.基于FLUENT的二维数值波浪水槽研究[D].哈尔滨:哈尔滨工程大学, 2006.
Li Shengzhong. Study on 2-D numerical wave tank based on the software fluent[D]. Harbin: Harbin Institute of Technology, 2006. |
| [5] |
李凌, 林兆伟, 尤云祥, 等. 基于动量源方法的黏性流数值波浪水槽[J].
水动力学研究与进展 (A辑), 2007, 22(1): 76–82.
Li Ling, Lin Zhaowei, You Yunxiang, et al. The numerical wave flume of the viscous fluid based on the momentum source method[J]. Chinese Journal of Hydrodynamics, 2007, 22(1): 76–82. |
| [6] |
董志, 詹杰民. 基于VOF方法的数值波浪水槽以及造波、消波方法研究[J].
水动力学研究与进展 (A辑), 2009, 24(1): 15–21.
Dong Zhi, Zhan Jiemin. Comparison of existing methods for wave generating and absorbing in VOF-based numerical tank[J]. Chinese Journal of Hydrodynamics, 2009, 24(1): 15–21. |
| [7] | Ursell F, Dean R G, Yu Y S. Forced small-amplitude water waves: a comparison of theory and experiment[J]. J. Fluid Mechanics, 1960, 7(1): 33–52. DOI:10.1017/S0022112060000037 |
| [8] | Dean R G. Water Wave Mechanics for Engineers and Scientists[M]. New Jersey: Prentice-Hall Inc., 1984: 170-186. |
| [9] |
王永学. 无反射造波数值波浪水槽[J].
水动力学研究与进展 (A辑), 1994, 9(2): 205–214.
Wang Yongxue. Numerical wave channel with absorbing wave-maker[J]. Chinese Journal of Hydrodynamics, 1994, 9(2): 205–214. |
 2017, Vol. 50
2017, Vol. 50



