基于形状记忆合金的自复位摩擦耗能支撑滞回性能

文章信息

胡晓斌, 刘坤, 高良慧

HU Xiaobin, LIU Kun, GAO Lianghui

Hysteresis performance of self-centering friction damping braces based on shape memory alloy

武汉大学学报(工学版), 2016, 49(6): 860-865

Engineering Journal of Wuhan University, 2016, 49(6): 860-865

http://dx.doi.org/10.14188/j.1671-8844.2016-06-011

文章历史

收稿日期: 2015-11-10

Abstract

PDF

Figures

Tables

引用本文

胡晓斌, 刘坤, 高良慧. 基于形状记忆合金的自复位摩擦耗能支撑滞回性能[J]. 武汉大学学报(工学版), 2016, 49(6): 860-865. 复制到剪切板

HU Xiaobin, LIU Kun, GAO Lianghui. Hysteresis performance of self-centering friction damping braces based on shape memory alloy[J]. Engineering Journal of Wuhan University, 2016, 49(6): 860-865. 复制到剪切板

基于形状记忆合金的自复位摩擦耗能支撑滞回性能

胡晓斌¹, 刘坤¹, 高良慧²

1. 武汉大学土木建筑工程学院，湖北武汉 430072;
2. 湖北省宜昌宜洋置业有限公司，湖北宜昌 443005

收稿日期: 2015-11-10

作者简介: 胡晓斌(1979-)，男，博士，副教授，主要从事结构抗震研究，E-mail: newhxb@126.com.

摘要: 针对基于形状记忆合金(SMA)的自复位摩擦耗能支撑，提出了简化分析模型，研究了其在往复荷载作用下的滞回性能.首先通过理论推导，得出了往复荷载作用下自复位摩擦耗能支撑的力-位移曲线，提出了简化的滞回模型，然后通过参数分析研究了各参数对其滞回性能的影响.结果表明：自复位摩擦耗能支撑在卸载后存在一定的残余位移，其大小仅与阻尼器元件摩擦力及SMA元件奥氏体弹性刚度有关；自复位摩擦耗能支撑的滞回性能可采用修正的FS (Flag-shaped)模型来描述；SMA元件屈服力及耗能参数对自复位摩擦耗能支撑的滞回性能影响较大，奥氏体弹性刚度及屈服后刚度系数影响较小；增加阻尼器元件的摩擦力，可显著增强自复位摩擦耗能支撑的耗能能力，但会产生残余位移.

关键词：自复位摩擦耗能支撑滞回性能形状记忆合金摩擦阻尼器滞回模型

Hysteresis performance of self-centering friction damping braces based on shape memory alloy

HU Xiaobin¹, LIU Kun¹, GAO Lianghui²

1. School of Civil and Architectural Engineering, Wuhan University, Wuhan 430072, China;
2. Hubei Yichang Yiyang Estate Co.,Ltd., Yichang 443005, China

Abstract: A simplified analysis model is proposed for the self-centering friction damping brace (SFDB) based on shape memory alloy (SMA); and then its hysteresis performance under reversal loading is studied. By way of theoretical derivation, the force vs. displacement curve of the SFDB subjected to reversal loading is obtained and the simplified hysteresis model of the SFDB is proposed. Based on the above work, the influences of parameters on the hysteresis performance of the SFDB are analyzed parametrically. It is indicated that certain residual displacement occurs upon unloading of the SFDB, the magnitude of which are only related to the friction of the damper component and the austenite elastic stiffness of the SMA component; and the hysteresis performance of the SFDB can be described by the modified Flag shaped(FS) model. The yield force and energy dissipation parameter of the SMA component have a great impact on the hysteresis performance of the SFDB; while the effects of the austenite elastic stiffness and post-yield stiffness ratio are relatively small. The energy dissipation capacity of the SFDB can be significantly enhanced by increasing the friction of the damper component whereas it yields some residual displacement.

Key words: self-centering friction damping braces hysteresis performance shape memory alloy friction damper hysteresis model

自复位(self-centering)结构近年来引起了研究者和工程技术人员的高度重视.与传统的抗震结构不同的是，自复位结构卸载后变形能完全或基本恢复.在强震作用下，自复位结构基本不产生残余变形，震后不需或经少量的维修即可恢复正常使用^[1-4].从实现的途径来讲，自复位结构或构件可分为2类: 一类基于墙或梁柱节点的摇摆响应，如自复位墙或自复位框架结构；一类基于形状记忆合金(shaped memory alloy，简称SMA)的超弹性性能，如自复位耗能支撑.

自复位耗能支撑主要由3部分组成: 连接件、SMA和阻尼器，其中，连接件用来安装SMA，并连接至主体结构，SMA用来实现自复位性能，阻尼器用来增强支撑的耗能能力.由于摩擦阻尼器较易制作，且耗能性能稳定，因此在自复位耗能支撑中得到了广泛的应用.部分研究者^[5-11]研制了不同构造形式的自复位摩擦耗能支撑(self-centering friction damping brace，简称SFDB)，并对其力学及抗震性能开展深入研究.Zhu等^{[7, 8]}通过循环加载试验研究了Ni-Ti合金的超弹性性能，建立了单轴本构方程，并研制了基于Ni-Ti合金的自复位摩擦耗能支撑，然后将其应用于结构减震.研究表明自复位摩擦耗能支撑与屈曲约束支撑的减震效果相当，但前者的残余变形小很多.钱辉、任文杰等^{[9, 10]} 研制了一种形状记忆合金-摩擦复合阻尼器，并通过试验和数值模拟对其力学性能进行研究.张纪刚等^[11]对传统的Pall摩擦阻尼支撑体系进行改进，提出一种PFD-SMA(pall-typed frictional damper，简称PFD)支撑体系，并通过非线性时程分析表明在钢框架结构中采用PFD-SMA体系能有效降低结构的地震响应，同时结构具有自复位功能.

值得注意的是，上述大部分研究均基于特定的构造形式，采用试验或数值模拟的方法研究自复位摩擦耗能支撑的力学和抗震性能，而在理论层面上的研究则较少涉及.基于此，针对基于SMA的自复位摩擦耗能支撑，首先建立一般意义上的简化分析模型，然后通过理论推导，研究其在往复荷载作用下的滞回性能，并分析不同参数对其滞回性能的影响.

1 自复位摩擦耗能支撑的简化分析模型

不同的研究者针对基于SMA的自复位摩擦耗能支撑提出了不同的构造方法，图 1(a)所示即为一种典型的构造形式^[8].尽管构造方法不同，自复位摩擦耗能支撑均可视为SMA元件与阻尼器元件的并联，其简化分析模型如图 1(b)所示.

图 1 自复位摩擦耗能支撑简化分析模型 Figure 1 Simplified analytical model of SFDB

图选项

1.1 SMA元件的恢复力模型

SMA元件的恢复力模型采用FS(Flag-shaped)模型^[1]近似描述，如图 2(a)所示.其中:k_a、f_ys、d_y分别表示SMA元件奥氏体弹性刚度、屈服力及屈服位移;α_s表示屈服后刚度系数;β_s表示耗能参数;d_m表示SMA元件奥氏体完全转变成马氏体时的位移;k_m表示马氏体弹性刚度.可以看出，该模型需要6个参数才能完全确定下来.值得注意的是，上述参数是建立在构件层次上的，可方便地由SMA元件材料性质及几何尺寸求得.

1.2 阻尼器元件的恢复力模型

阻尼器元件的恢复力模型如图 2(b)所示，其中f_f表示摩擦力.可以看出: 当位移增大时(即速度大于0时)，摩擦力为f_f；当位移减小时(即速度小于0时)，摩擦力为-f_f；当速度反向时，摩擦力存在突变，其变化为2f_f.

图 2 各元件恢复力模型 Figure 2 Hysteresis models of each component

图选项

2 往复荷载作用下自复位摩擦耗能支撑受力分析

采用前节所述的简化模型，本节对往复荷载作用下的自复位摩擦耗能支撑进行受力分析，且假定受拉为正.为简化起见，仅考虑典型的滞回环，且只考虑受拉的情况.设卸载点位移为d_u，由图 2(a)可知，分析时需要考虑2种不同的情况: 1) 卸载点位移位于d_y和d_m之间，即d_y≤d_u≤d_m；2) 卸载点位移大于d_m，即d_u>d_m.

2.1 卸载点(d_u)在SMA屈服临界点(d_y)与奥氏

体完全转变成马氏体临界点(d_m)之间共定义7个特征点，其特征及相应的位移如表 1所示.分别利用SMA元件及阻尼器元件的恢复力模型，可求出各特征点位移对应的力，将各特征点依次连接起来，即得自复位摩擦耗能支撑的力-位移曲线，如图 3(c)所示.可以看出，当自复位摩擦耗能支撑完全卸载后，存在一定的残余位移.

表 1 特征点定义及相应的位移(d_y≤d_u≤d_m) Table 1 Definition of characteristic points and the corresponding displacements (d_y≤d_u≤d_m)

点号	特征	位移
1	阻尼器元件开始滑动	0
2	SMA元件奥氏体开始向马氏体转变	d_y
3	卸载点	d_u
4	阻尼器元件摩擦力反向	d_u
5	卸载至下平台	d_u-βd_y
6	SMA元件马氏体全部转变成奥氏体	(1-β)d_y
7	自复位摩擦耗能支撑复位	0

表选项

图 3 自复位摩擦耗能支撑典型滞回曲线(d_y≤d_u≤d_m) Figure 3 Typical hysteresis curve of the SFDB (d_y≤d_u≤d_m)

图选项

假定图 3(c)中6点位于横轴上方，则

${{f}_{ys}}-\beta {{f}_{ys}}-{{f}_{f}}>0$ (1)

可得

${{f}_{f}}＜1-\beta {{f}_{ys}}$ (2)

将6、7点连接起来，相交横轴于6′点，其横坐标即为残余位移d_r，易求出

${{d}_{r}}=\frac{{{f}_{f}}}{{{k}_{a}}}$ (3)

可以看出，残余位移的大小仅与阻尼器元件摩擦力及SMA元件奥氏体弹性刚度有关，当阻尼器元件摩擦力越大、SMA元件奥氏体弹性刚度越小时，其残余位移越大.

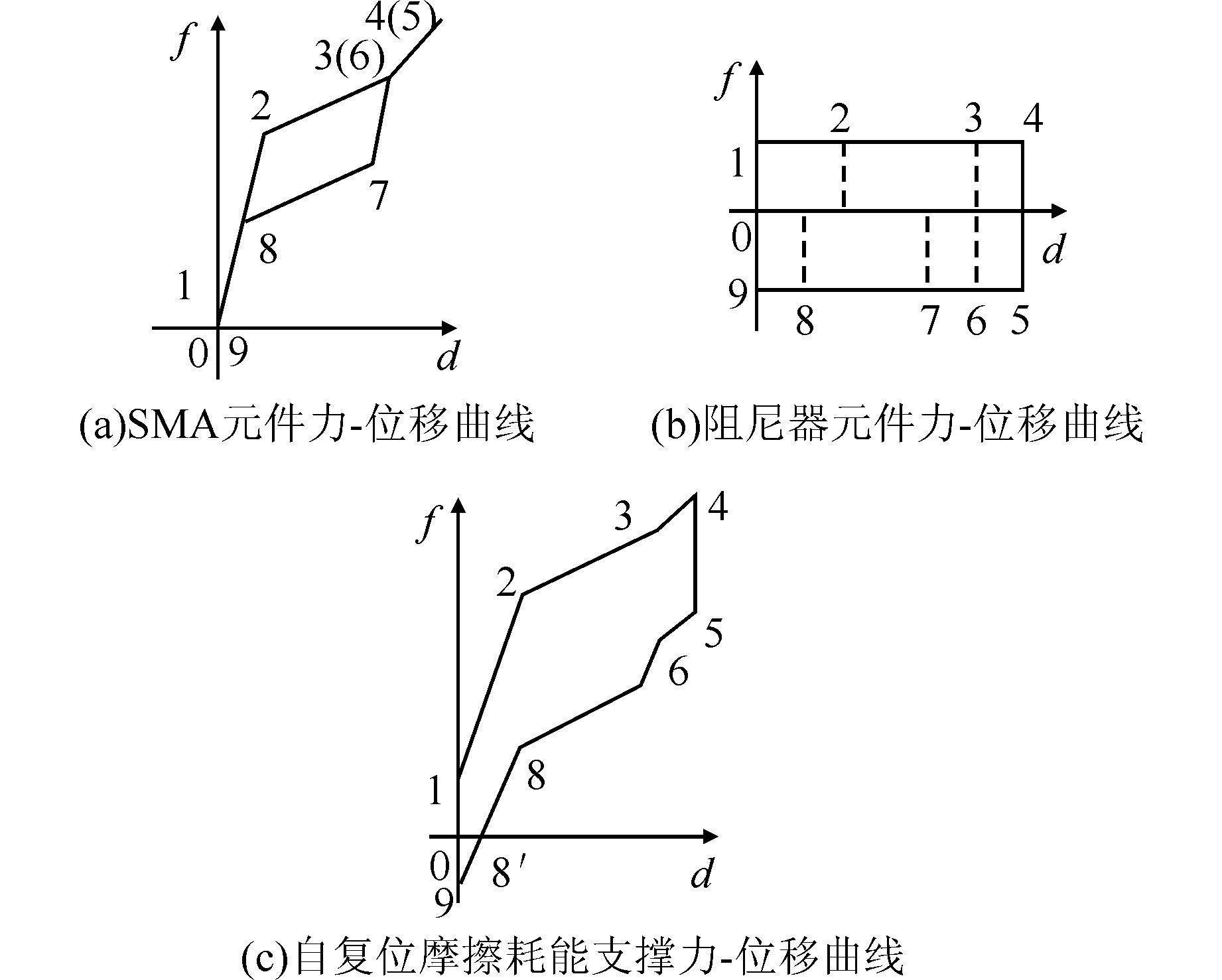
2.2 卸载点(d_u)在奥氏体完全转变成马氏体临界点(d_m)之后

定义9个特征点，其特征及相应的位移如表 2所示.分别利用SMA元件及阻尼器元件的恢复力模型，可求出各特征点位移对应的力，将各特征点依次连接起来，即得自复位摩擦耗能支撑的力-位移曲线，如图 4(c)所示.可以看出，当自复位摩擦耗能支撑完全卸载后，也存在一定的残余位移.

图 4 自复位摩擦耗能支撑典型滞回曲线(d_u>d_m) Figure 4 Typical hysteresis curve of SFDB (d_u>d_m)

图选项

表 2 特征点定义及相应的位移(d_u>d_m) Table 2 Definition of characteristic points and corresponding displacements (d_u>d_m)

点号	特征	位移
1	阻尼器元件开始滑动	0
2	SMA元件奥氏体开始向马氏体转变	d_y
3	SMA元件奥氏体完全转变成马氏体	d_m
4	卸载点	d_u
5	阻尼器元件摩擦力反向	d_u
6	SMA元件马氏体开始向奥氏体转变	d_m
7	卸载至下平台	d_m-βd_y
8	SMA元件马氏体完全转变成奥氏体	(1-β)d_y
9	自复位摩擦耗能支撑复位	0

表选项

假定图 4(c)中8点位于横轴上方，则

${{f}_{ys}}-\beta {{f}_{ys}}-{{f}_{f}}>0$ (4)

可得

${{f}_{f}} ＜1-\beta {{f}_{ys}}$ (5)

将8、9点连接起来，相交横轴于8′点，其横坐标即为残余位移d_r，易求出

${{d}_{r}}=\frac{{{f}_{f}}}{{{k}_{a}}}$ (6)

可见，式(4) ~(6) 与式(1) ~(3) 完全相同.

3 自复位摩擦耗能支撑简化滞回模型

为简化起见，仅考虑第1种卸载情况.由图 3(c)可知，自复位摩擦耗能支撑的滞回曲线为“旗形”，但存在一定的残余位移，因此可采用修正的FS(Flag-shaped)模型进行描述^[12]，如图 5粗实线所示，其中f_y 表示屈服力，k_e表示弹性刚度，α表示屈服后刚度系数，β为耗能参数，d_r为残余位移.

图 5 自复位摩擦耗能支撑简化滞回模型 Figure 5 Simplified hysteresis model of SFDB

图选项

为得出修正FS模型的参数，采用如下做法(图 5): 连接0、2两点，过4点作直线02的平行线分别交直线23和65的延长线于a、b两点，过6′点作直线02的平行线交直线56的延长线于c点.由几何关系，可得

${{f}_{y}}={{f}_{2}}$ (7)

${{k}_{e}}=\frac{{{f}_{2}}}{{{d}_{2}}}$ (8)

$\alpha =\frac{{{f}_{3}}-{{f}_{2}}}{{{d}_{3}}-{{d}_{2}}}/{{k}_{e}}$ (9)

$\beta =\frac{{{f}_{a}}-{{f}_{b}}}{{{f}_{2}}}$ (10)

其中，f₂、d₂分别表示2点的力和位移，其余类推.

由式(7) ~(10) ，代入各点的力和位移可得

${{f}_{y}}={{f}_{ys}}+{{f}_{f}}~$ (11)

${{k}_{e}}=\frac{{{k}_{a}}({{f}_{ys}}+{{f}_{f}})}{{{f}_{ys}}}$ (12)

$\alpha =\frac{{{f}_{ys}}}{{{f}_{ys}}+{{f}_{f}}}{{\alpha }_{s}}$ (13)

$\beta =\frac{(1-{{\alpha }_{s}}){{\beta }_{s}}{{f}_{ys}}+2{{f}_{f}}}{{{f}_{ys}}+{{f}_{f}}-{{\alpha }_{s}}{{f}_{ys}}}$ (14)

此外，d_r由式(3) 或式(6) 给出.

可以看出，当f_f=0时，即没有阻尼器元件时，由式(11) ~(14) 、式(3) 可得

${{f}_{y}}={{f}_{ys}}$ (15)

${{k}_{e}}={{k}_{a}}$ (16)

$\alpha ={{\alpha }_{s}}$ (17)

$\beta ={{\beta }_{s}}$ (18)

${{d}_{r}}=0$ (19)

此时，修正FS模型退化为FS模型.

4 自复位摩擦耗能支撑滞回性能参数分析

在前述研究的基础上，本节进一步通过参数分析，分别考察SMA元件及阻尼器元件设计参数对自复位摩擦耗能支撑滞回性能的影响.各参数取值如表 3所示，此外，假设卸载位移d_u=15 mm，且仅考虑第1种卸载情况.

表 3 分析参数取值 Table 3 Values of analysis parameters

参数		值
SMA元件	k_a/(kN·mm^-1)	1.606	1.823	2.040	2.257	2.474
	f_ys/kN	3.7	4.2	4.7	5.2	5.7
	α_s	0.012	0.014	0.016	0.018	0.020
	β_s	0.206	0.276	0.351	0.429	0.511
阻尼器元件	f_f/kN	0	0.4	0.8	1.2	1.6

表选项

为量化自复位摩擦耗能支撑的耗能能力，定义等效粘滞阻尼比:

${{h}_{e}}=\frac{1}{2\pi }\frac{{{S}_{1\tilde{\ }66}}\prime }{{{S}_{\Delta }}_{033\prime }~}$ (20)

式中: S_1~66′表示图 3(c)中1~6及6′点与坐标轴围成的多边形面积，S_Δ_033′表示由原点、3及3′点围成的三角形面积.

4.1 SMA元件参数的影响

1) SMA元件奥氏体弹性刚度

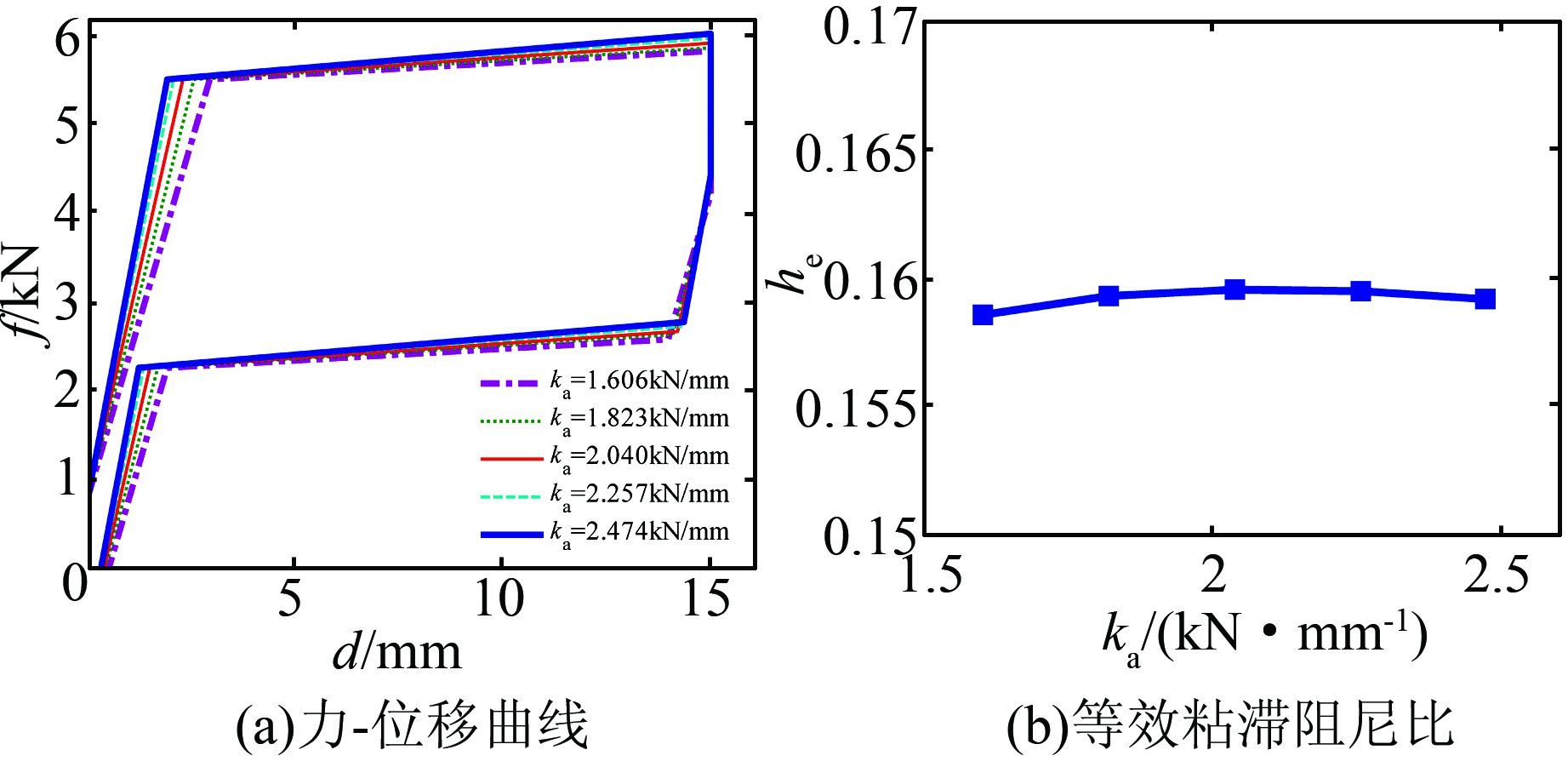
k_a按照表 3取值，其余参数固定，分别为: f_ys= 4.7 kN，α_s=0.016，β_s=0. 351，f_f =0.8 kN.图 6为计算所得的自复位摩擦耗能支撑力-位移曲线和相应的等效粘滞阻尼比，可以看出: 1) 当k_a增加时，力-位移曲线变化不大，等效粘滞阻尼比也变化不大，表明k_a对自复位摩擦耗能支撑的滞回性能影响不大.2) 随着k_a的增加，自复位摩擦耗能支撑的残余位移减小.

图 6 SMA元件奥氏体弹性刚度的影响 Figure 6 Effect of austenitic elastic stiffness of SMA component

图选项

2) SMA元件屈服力

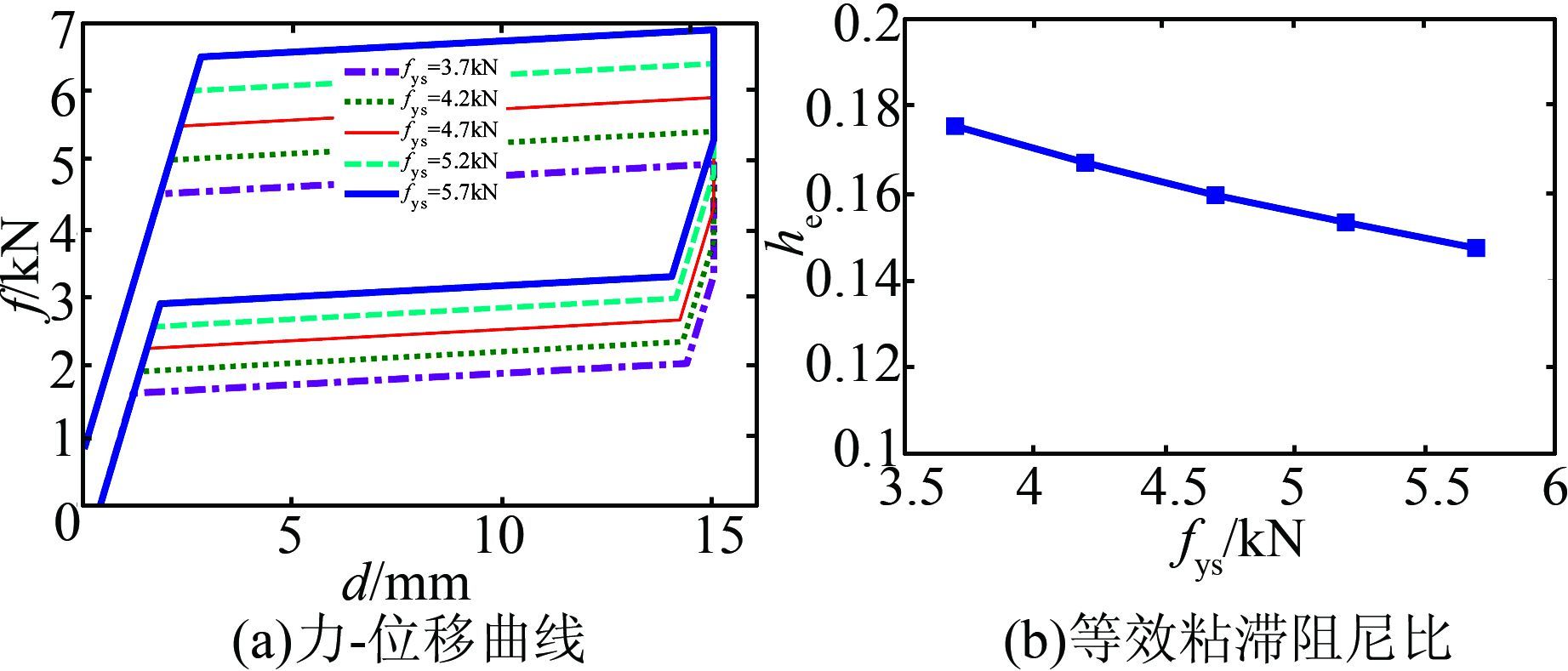
f_y_s按照表 3取值，其余参数固定，分别为: k_a = 2.040 kN/mm，α_s=0.016，β_s=0.351，f_f=0.8 kN.图 7分别为计算所得的自复位摩擦耗能支撑力-位移曲线和相应的等效粘滞阻尼比，可以看出: 1) 当f_ys增加时，力-位移曲线沿纵轴向上平移，相应的等效粘滞阻尼比减小，表明自复位摩擦耗能支撑的耗能能力减弱；2) 随着f_ys的增加，自复位摩擦耗能支撑的残余位移保持不变.

图 7 SMA元件屈服力的影响 Figure 7 Effect of yield force of SMA component

图选项

3) SMA元件屈服后刚度

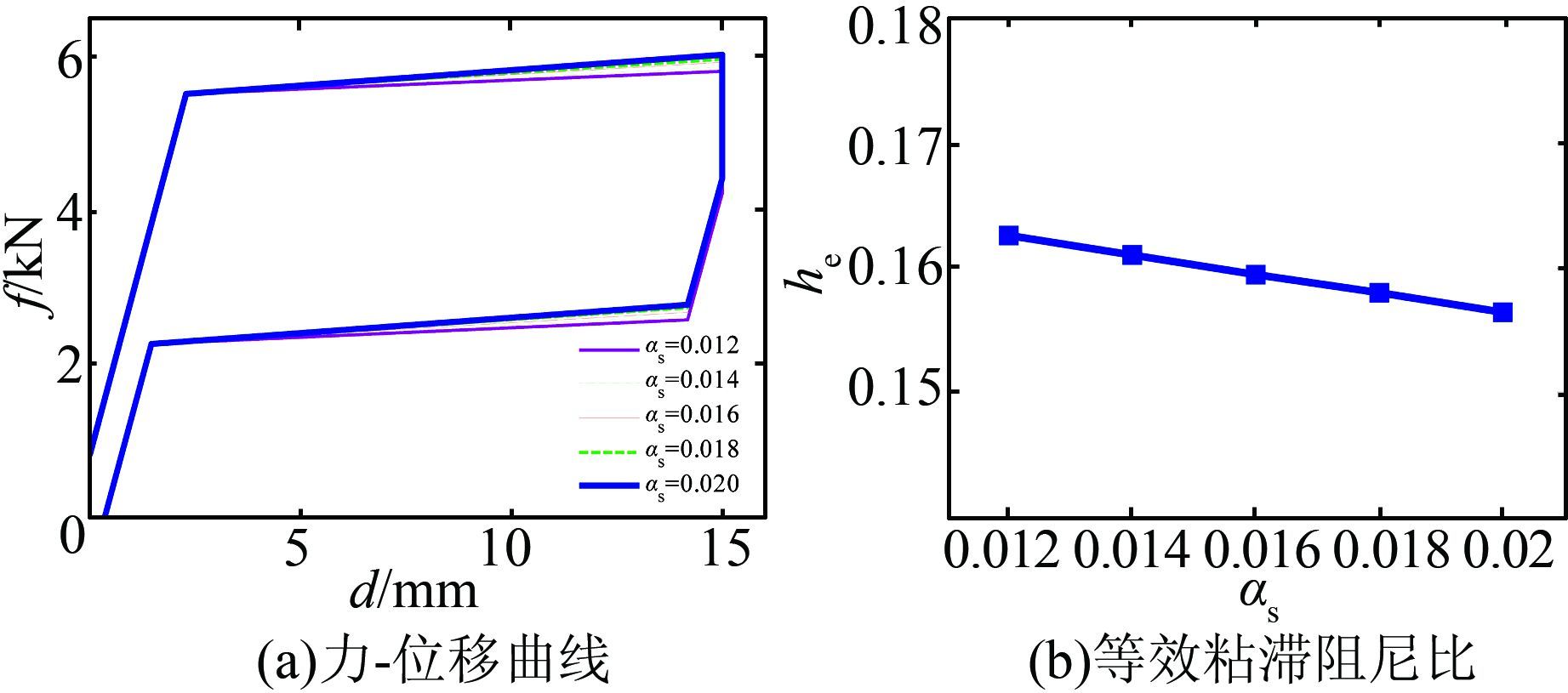
α_s按照表 3取值，其余参数固定，分别为: k_a= 2.040 kN/mm，f_ys= 4.7 kN，β_s=0.351，f_f =0.8 kN.图 8分别为计算所得的自复位摩擦耗能支撑力-位移曲线和相应的等效粘滞阻尼比，可以看出: 1) 当α_s增加时，力-位移曲线变化不大，等效粘滞阻尼比减小但不明显，表明α_s对自复位摩擦耗能支撑的耗能能力影响不大；2) 当α_s增加时，自复位摩擦耗能支撑的残余位移保持不变.

图 8 SMA元件屈服后刚度的影响 Figure 8 Effect of post-yield stiffness of SMA component

图选项

4) SMA元件耗能参数

β_s取值参照表 3，其余参数固定，分别为k_a=2.040 kN/mm，f_ys= 4.7 kN，α_s=0.016，f_f =0.8 kN.图 9为计算所得的自复位摩擦耗能支撑力-位移曲线和相应的等效粘滞阻尼比，可以看出: 1) 当β_s增加时，力-位移曲线沿纵轴负向扩展，相应的等效粘滞阻尼比也增加，表明自复位摩擦耗能支撑的耗能能力增强;2) 当β_s增加时，自复位摩擦耗能支撑的残余位移保持不变.

图 9 SMA元件耗能参数的影响 Figure 9 Effect of energy dissipation parameter of SMA component

图选项

4.2 阻尼器元件参数的影响

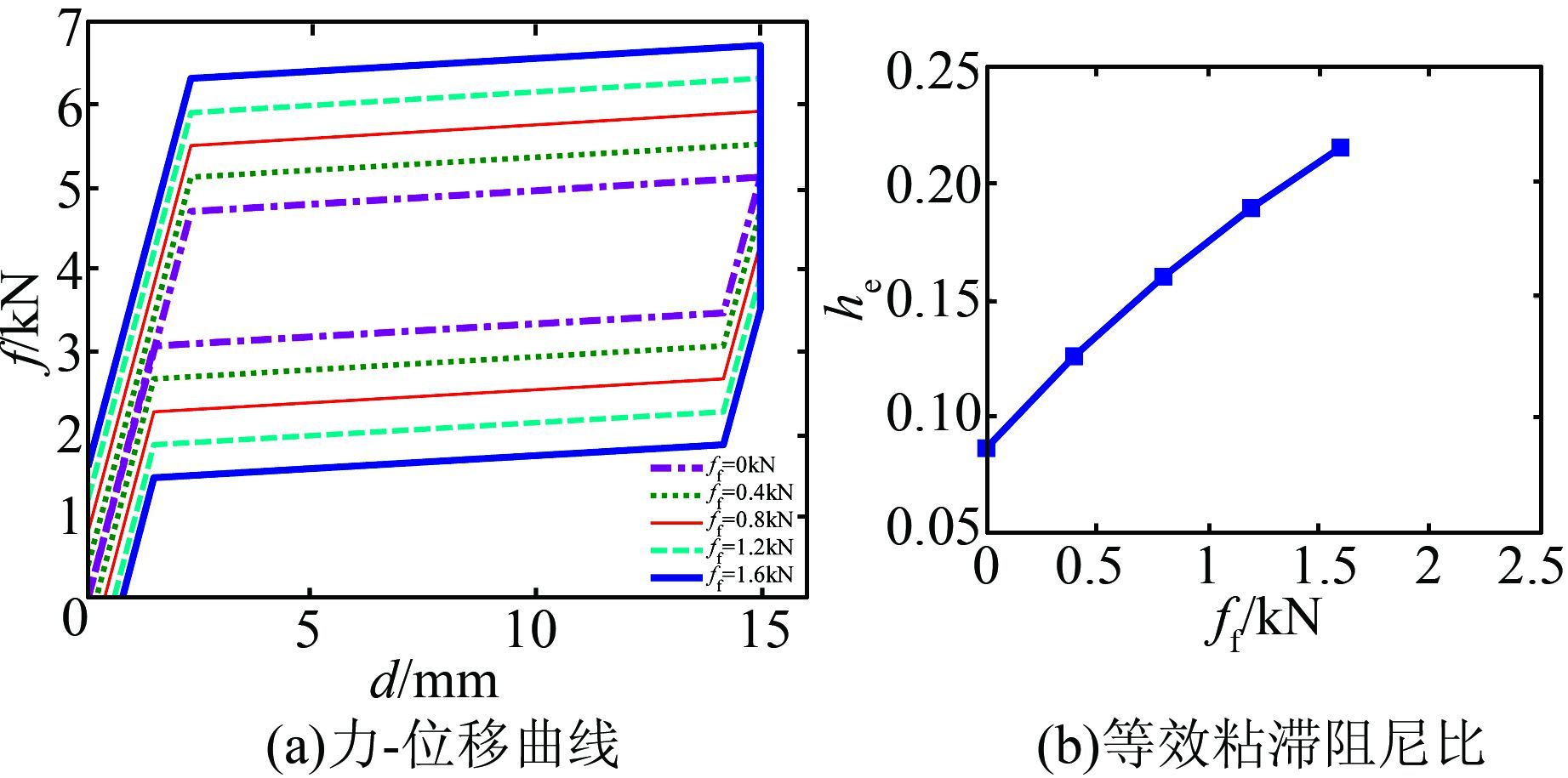
f_f取值如表 3所示，其余参数固定，分别为k_a= 2.040 kN/mm，f_ys= 4.7 kN，α_s=0.016，β_s=0.351.图 10分别为计算所得的自复位摩擦耗能支撑力-位移曲线和相应的等效粘滞阻尼比，可以看出: 1) 当f_f增加时，力-位移曲线沿纵轴向外扩展，相应的等效粘滞阻尼比明显变大，表明通过增加阻尼器元件的摩擦力，可以显著增强自复位摩擦耗能支撑的耗能能力.2) 当f_f增加时，自复位摩擦耗能支撑的残余位移变大.

图 10 阻尼器元件摩擦力的影响 Figure 10 Effect of friction force of damper component

图选项

5 结论

针对基于SMA的自复位摩擦耗能支撑，首先建立了一般意义上的简化分析模型，然后通过理论推导和参数分析研究了自复位摩擦耗能支撑在往复荷载作用下的滞回性能.

1) 自复位摩擦耗能支撑完全卸载后存在一定的残余位移，其滞回性能可用考虑残余位移的修正FS模型描述.

2) SMA元件屈服力及耗能参数对自复位摩擦耗能支撑的滞回性能影响较大，奥氏体弹性刚度及屈服后刚度系数影响较小.

3) 阻尼器元件可显著增强自复位摩擦耗能支撑的耗能能力，但会产生残余位移.

参考文献

[1]	Christopoulos C, Filiatrault A E, Folz B. Seismic response of self-centering hysteretic SDOF systems[J]. Earthquake Engineering and Structural Dynamics, 2002, 31(5): 1131–1150. DOI:10.1002/(ISSN)1096-9845

[2]	Seo C Y, Sause R. Ductility demands on self-centering systems under earthquake loading[J]. ACI Structural Journal, 2005, 102(2): 275–285.

[3]	潘振华, 潘鹏, 邱法维, 等. 具有自复位能力的钢结构体系研究[J]. 土木工程学报, 2010, 43(Sup): 403–410. Pan Zhenhua, Pan Peng, Qiu Fawei, et al. Analysis of self-centering steel structures’ development[J]. China Civil Engineering Journal, 2010, 43(Sup): 403–410.

[4]	周颖, 吕西林. 摇摆结构及自复位结构研究综述[J]. 建筑结构学报, 2011, 32(9): 1–10. Zhou Ying, Lü Xilin. State-of-the-art on rocking and self-centering structures[J]. Journal of Building Structures, 2011, 32(9): 1–10.

[5]	Dolce M, Cardone D, Marnetto R. Implementation and testing of passive control devices based on shape memory alloys[J]. Earthquake Engineering and Structural Dynamics, 2000, 29: 945–968. DOI:10.1002/(ISSN)1096-9845

[6]	Dolce M, Cardone D, Ponzo F C, et al. Shaking table tests on reinforced concrete frames without and with passive control systems[J]. Earthquake Engineering and Structural Dynamics, 2005, 34: 1687–1717. DOI:10.1002/(ISSN)1096-9845

[7]	Zhu S, Zhang Y. Seismic behavior of self-centering braced frame buildings with reusable hysteretic damping brace[J]. Earthquake Engineering and Structural Dynamics, 2007, 36: 1329–1346. DOI:10.1002/(ISSN)1096-9845

[8]	Zhu S, Zhang Y. Seismic analysis of concentrically braced frame systems with self-centering friction damping braces[J]. Journal of Structural Engineering, 2008, 134(1): 121–131. DOI:10.1061/(ASCE)0733-9445(2008)134:1(121)

[9]	钱辉, 李宏男, 任文杰, 等. 形状记忆合金复合摩擦阻尼器设计及试验研究[J]. 建筑结构学报, 2011(9): 58–64. Qian Hui, Li Hongnan, Ren Wenjie, et al. Experimental investigation of an innovative hybrid shape memory alloys friction damper[J]. Journal of Building Structures, 2011(9): 58–64.

[10]	任文杰, 王利强, 马志成, 等. 形状记忆合金-摩擦复合阻尼器力学性能研究[J]. 建筑结构学报, 2013, 34(2): 83–90. Ren Wenjie, Wang Liqiang, Ma Zhicheng, et al. Investigation on mechanical behavior of innovative shape memory alloy-friction damper[J]. Journal of Building Structures, 2013, 34(2): 83–90.

[11]	张纪刚, 卢爱贞. PFD-SMA支撑体系的抗震性能[J]. 中南大学学报, 2011(10): 3157–3163. Zhang Jigang, Lu Aizhen. Hysteretic behavior of advanced PFD-SMA frictional damping brace system[J]. Journal of Central South University (Science and Technology), 2011(10): 3157–3163.

[12]	Hu X, Zhang Y. Ductility demand of partially self-centering structures under seismic loading: SDOF systems[J]. Earthquake and Structures, 2013, 4(4): 365–381. DOI:10.12989/eas.2013.4.4.365