武汉大学学报(工学版)   2016, Vol. 49 Issue (6): 824-830

文章信息

文喜雨, 苏凯, 周亚峰
WEN Xiyu, SU Kai, ZHOU Yafeng
高压水工隧洞透水衬砌设计方法与理论研究
Research of pervious lining design and theory for high pressure hydraulic tunnel
武汉大学学报(工学版), 2016, 49(6): 824-830
Engineering Journal of Wuhan University, 2016, 49(6): 824-830
http://dx.doi.org/10.14188/j.1671-8844.2016-06-005

文章历史

收稿日期: 2015-06-17
 Abstract              PDF               Figures               Tables
引用本文 0
文喜雨, 苏凯, 周亚峰. 高压水工隧洞透水衬砌设计方法与理论研究[J]. 武汉大学学报(工学版), 2016, 49(6): 824-830.
WEN Xiyu, SU Kai, ZHOU Yafeng. Research of pervious lining design and theory for high pressure hydraulic tunnel[J]. Engineering Journal of Wuhan University, 2016, 49(6): 824-830.
高压水工隧洞透水衬砌设计方法与理论研究
文喜雨, 苏凯, 周亚峰     
武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072
收稿日期: 2015-06-17
作者简介: 文喜雨(1993-)，女，硕士研究生，研究方向为地下工程与压力管道，E-mail：whuwxy_2013@163.com.
通讯作者: 苏凯(1977-)，男，博士， 副教授，主要从事地下工程与压力管道的科研与教学工作， E-mail：suker8044@163.com
基金项目: 国家自然科学基金资助项目(编号：51179140, 51579194).
摘要: 基于高压隧洞透水衬砌理论，考虑了钢筋应变不均匀系数ψ1和裂缝间混凝土应变不均匀系数ψ2对配筋计算的影响，讨论了透水衬砌的设计方法，给出了使用透水衬砌理论进行工程设计的基本步骤，最后结合工程实例量化分析了考虑应变不均匀系数ψ1、ψ2影响的钢筋应力与渗流量变化特征.计算结果表明，ψ1、ψ2对钢筋应力和单位管长渗流 量均有明显影响，且前者的影响大于后者，同等配筋条件下的钢筋应力差别主要来源于ψ1，但当配筋率减小到一定程度时(小于0.4%)，ψ1、ψ2对渗流量的影响可以忽略；同时，随着钢筋应力的逐渐增加，ψ1、ψ2的影响逐渐减小，且在钢筋应力达到某一较大数值后(如ψ1=1.0时，120 MPa)，由于钢筋的作用得以充分发挥，ψ2的影响基本可以忽略.
关键词： 水工隧洞     透水衬砌     应变不均匀系数     钢筋应力     渗流量    
Research of pervious lining design and theory for high pressure hydraulic tunnel
WEN Xiyu, SU Kai, ZHOU Yafeng     
State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China
Abstract: Based on the pervious lining theory for high pressure tunnel, the influences of the reinforcing steel bar strain nonuniformity coefficient ψ1 and the strain nonuniformity coefficient of concrete between cracks ψ2 on the reinforcement computation are taken into account in the design of pervious lining. In addition, the basic design steps based on the pervious lining theory are presented. Finally, considering the strain nonuniformity coefficient ψ1&ψ2, the change characteristics of reinforcing steel stresses and seepage flow are analyzed with an actual case study. The results show that the ψ1 and ψ2 have obvious effects on reinforcing steel stresses and seepage flow; and the influence of the former is greater. Moreover, the differences of reinforcing steel stresses under the same reinforcement mainly result from ψ1. As the reinforcement ratio decreases to some degree (less than 0.4%), the influences of both ψ1 and ψ2 on seepage flow can be neglected. Meanwhile, the effects of ψ1 and ψ2 decrease with the increasing of the reinforcing steel stresses; and when the stress level of reinforcing steel is beyond a certain value (such as ψ1=1.0, 120 MPa), the influence of ψ2 could be neglected since the steel bar can play the role adequately.
Key words: hydraulic tunnel     pervious lining     strain nonuniformity coefficient     reinforcing steel stress     seepage flow    

随着水电工程的发展重心向西南地区转移，高压水工隧洞日益增多，在隧洞设计时，透水衬砌理论逐渐取代传统的面力理论[1-2]，成为现今衬砌设计的主流计算理论.1980年，张有天等指出隧洞水荷载的作用方式是场力[3]；1985年，张有天等再次提出隧洞设计应考虑衬砌和围岩有条件的联合工作[4]；1986年，A J Schleiss研究了传统“隧洞静力学”理论的适用性，并提出了新的透水隧洞设计标准[5]；1991年，曹克明等着重研究了体力理论下，衬砌与围岩脱开的条件以及此条件下衬砌的应力计算和限裂设计[6]；1997年，A J Schleiss考虑了衬砌的透水性以及应力场和渗流场的相互作用，提出了一种新的压力隧洞透水衬砌计算方法[7]；2005年，苏凯等推导了基于透水衬砌理论的弹性力学计算公式，并用水工隧洞设计规范和非线性有限元法进行了复核[8]；2009年，李新星等提出了一种基于体力理论进行衬砌结构透水设计的有限元计算方法[9]；2010年，苏凯等再次对透水衬砌理论进行研究，引入了钢筋和混凝土的应变不均匀系数来计算裂缝宽度[10].

目前透水衬砌理论已经逐步为人们所认可，但当前的研究重点只停留在对透水衬砌理论的研究分析和衬砌结构计算方法的探讨上，在此基础上，未曾有人研究钢筋和混凝土的应变不均匀性对结构计算的影响.而实际上，由于钢筋与混凝土的粘结作用在裂缝处和裂缝间相差较大，二者的拉应变也将呈现较大的不均匀性[11]，计算时，应变不均匀系数的取值将在一定程度上影响隧洞衬砌设计结果，而其具体的影响程度还需要进一步的研究.因此，本文在前人研究的基础上，回顾了透水衬砌基本理论，考虑了钢筋应变不均匀系数和裂缝间混凝土应变不均匀系数，给出了详细的透水衬砌计算方法，研究了应变不均匀系数的影响.

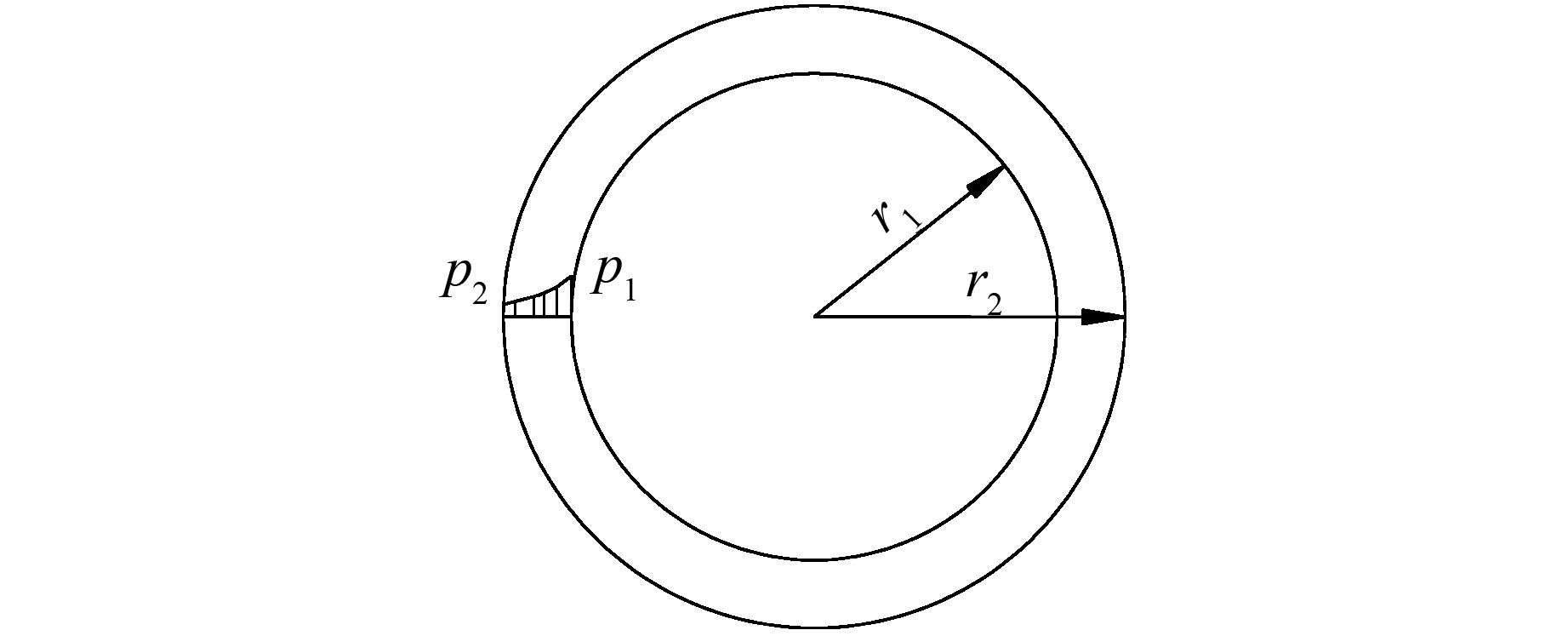
1 基本理论 1.1 透水衬砌理论模型

针对圆形有压隧洞，建立厚壁圆筒模型进行简化计算，在文献[6]的基础上，对透水衬砌理论的经典计算公式进行了详细推导，得出衬砌开裂前后厚壁圆筒上任一点的渗透水压力、径向应力、环向应力和径向位移的表达式.假定衬砌和围岩均为各向同性材料，并认为衬砌开裂前，水压力在衬砌和围岩内沿半径方向呈对数分布；衬砌开裂后，水压力在衬砌内呈线性分布，在围岩内呈对数分布[12]，计算简图如图 1所示, 具体表达式如表 1所示.其中: r1、r2分别为内、外半径；r为任一点至圆心的距离；p1、p2分别为内、外壁承受的渗透水压力；t为厚度参数，t=r2/r1；E为弹性模量；μ为泊松比.

图 1 厚壁圆筒模型计算简图 Figure 1 Thick-walled cylinder model
图选项
表 1 厚壁圆筒模型应力、位移表达式 Table 1 Stress and displacement of thick-walled cylinder model
工作状态物理量表达式
衬砌未开裂渗透水压力$p=\frac{{{p}_{2}}\left( \ln r-\ln {{r}_{1}} \right)+{{p}_{1}}\left( \ln {{r}_{2}}-\ln r \right)}{\ln {{r}_{2}}-\ln {{r}_{1}}}$
径向应力${{\sigma }_{r}}=\frac{{{p}_{1}}-{{p}_{2}}}{2\left( 1-\mu \right)}\left( \frac{\ln \frac{{{r}_{2}}}{r}}{\ln t}+\frac{1-\frac{{{r}_{2}}^{2}}{{{r}^{2}}}}{{{t}^{2}}-1} \right)$
环向应力${{u}_{r}}=\frac{r\left( {{p}_{1}}-{{p}_{2}} \right)\left( 1+\mu \right)}{2E\left( 1-\mu \right)}\left[ \frac{\left( 1-2\mu \right)\left( \ln \frac{{{r}_{2}}}{r}+1-\mu \right)}{\ln t}+\frac{1-2\mu +\frac{{{r}_{2}}^{2}}{{{r}^{2}}}}{{{t}^{2}}-1} \right]$
径向位移${{u}_{r}}=\frac{r\left( {{p}_{1}}-{{p}_{2}} \right)\left( 1+\mu \right)}{2E\left( 1-\mu \right)}\left[ \frac{\left( 1-2\mu \right)\left( \ln \frac{{{r}_{2}}}{r}+1-\mu \right)}{\ln t}+\frac{1-2\mu +\frac{{{r}_{2}}^{2}}{{{r}^{2}}}}{{{t}^{2}}-1} \right]$
衬砌已开裂渗透水压力$p=\frac{{{p}_{2}}\left( r-{{r}_{1}} \right)+{{p}_{1}}\left( {{r}_{2}}-r \right)}{{{r}_{2}}-{{r}_{1}}}$
径向应力${{\sigma }_{r}}=\frac{\left( 2-\mu \right)\left( {{p}_{1}}-{{p}_{2}} \right)}{3\left( 1-\mu \right)}\left( \frac{1-\frac{{{r}_{2}}^{2}}{{{r}^{2}}}}{{{t}^{2}}-1}+\frac{{{r}_{2}}-r}{{{r}_{2}}-{{r}_{1}}} \right)$
环向应力${{\sigma }_{\theta }}=\frac{\left( 2-\mu \right)\left( {{p}_{1}}-{{p}_{2}} \right)}{3\left( 1-\mu \right)}\left( \frac{1+\frac{{{r}_{2}}^{2}}{{{r}^{2}}}}{{{t}^{2}}-1}+\frac{{{r}_{2}}}{{{r}_{2}}-{{r}_{1}}}-\frac{\left( 1+\mu \right)r}{\left( {{r}_{2}}-{{r}_{1}} \right)\left( 2-\mu \right)} \right)$
径向位移${{u}_{r}}=\frac{r\left( {{p}_{1}}-{{p}_{2}} \right)\left( 1+\mu \right)\left( 2-\mu \right)}{3E\left( 1-\mu \right)}\left[ \frac{\left( 1-2\mu \right)\left[ \left( 2-\mu \right){{r}_{2}}-r \right]}{\left( {{r}_{2}}-{{r}_{1}} \right)\left( 2-\mu \right)}+\frac{1-2\mu +\frac{{{r}_{2}}^{2}}{{{r}^{2}}}}{{{t}^{2}}-1} \right]$
表选项
1.2 应变不均匀系数

由实测资料和计算分析得知，钢筋混凝土衬砌在高内水压力作用下不可避免地将会发生开裂[13-14].对于已开裂的隧洞衬砌，裂缝处的水荷载几乎全部由钢筋承担，钢筋的应变较大；裂缝间的水荷载由钢筋和混凝土共同承担，钢筋和混凝土的应变均较小，沿着隧洞环向钢筋和混凝土的拉应变表现出明显的不均匀性.

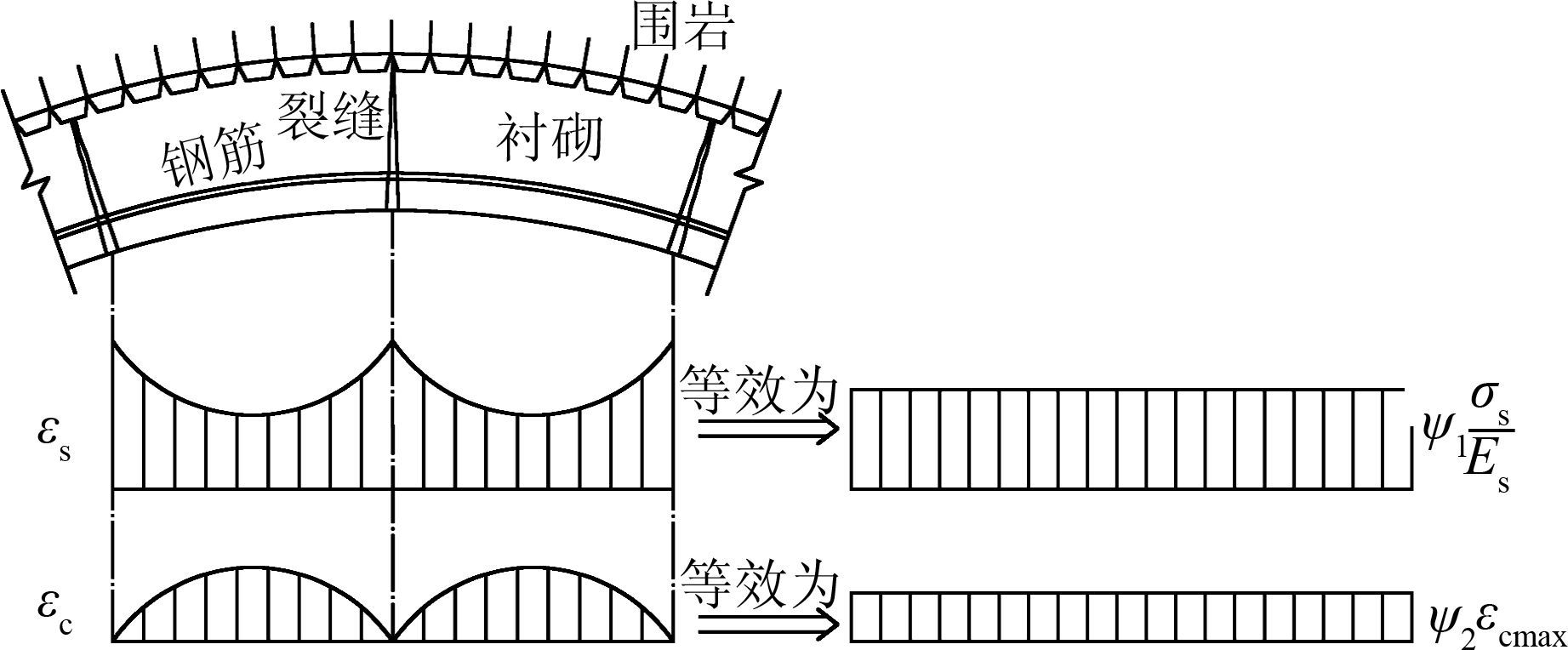
为使计算结果更加简便而又不失准确性，本文根据环向钢筋总伸长量相等的原则，将不均匀的钢筋应变等效为均布应变，通过钢筋应变不均匀系数ψ1来反映.同理，本文使用混凝土应变不均匀系数ψ2将相邻裂缝间的混凝土不均匀应变等效为均布应变，详见图 2所示.其中: εs为钢筋各断面的拉应变；εc为裂缝间混凝土各断面的拉应变；σs为裂缝处的钢筋应力，MPa；Es为钢筋的弹性模量，MPa；εcmax为混凝土的极限拉应变，取εmax=10-4.从图 2看出，ψ1(或ψ2)值越大，则钢筋(或混凝土)应变分布越均匀.

图 2 不均匀系数等效示意图 Figure 2 Equivalent nonuniformity coefficient sketch
图选项
2 透水衬砌计算方法 2.1 计算思路

对水工隧洞进行透水衬砌设计和程序编制时，按以下计算思路进行:

1) 根据比较衬砌开裂荷载与内水压力，判断衬砌的工作状态；

2) 计算不同衬砌工作状态下，衬砌外内壁的渗透水压力之比N；

3) 计算衬砌和围岩脱离的临界状态下的N*，判断衬砌和围岩的联合承载状态；

4) 计算不同配筋方案下的钢筋应力、最大裂缝宽度和单位管长渗流量；

5) 优选配筋方案.

2.2 具体步骤

1) 判断隧洞衬砌是否开裂

按式(1) 计算衬砌开裂的临界荷载，并与隧洞承受的内水压力p1比较: 若p裂 ＜p1，说明衬砌开裂，应按开裂后的计算公式进行衬砌配筋设计；若p裂>p1，说明衬砌没有开裂，应按衬砌未开裂时的计算公式进行衬砌设计:

${{p}_{裂}}={[{{R}_{L}}]}/{\left( \frac{\left( 1-N \right)\left( 1+{{C}_{4}} \right)}{1-{{\mu }_{c}}}-\frac{2{{t}^{2}}}{{{t}^{2}}-1}\frac{{{C}_{2}}{{C}_{4}}-\left( {{C}_{1}}+{{C}_{2}}{{C}_{4}} \right)N}{{{C}_{1}}+{{C}_{2}}{{C}_{3}}} \right)}\;$    (1)

式中:${{C}_{1}}=\frac{1+{{\mu }_{r}}}{{{E}_{r}}},{{C}_{2}}=\frac{1+{{\mu }_{c}}}{{{E}_{c}}},{{C}_{3}}=1-2{{\mu }_{c}}+\frac{2-2{{\mu }_{c}}}{{{t}^{2}}-1},{{C}_{4}}=\frac{1-2{{\mu }_{c}}}{2\ln t}+\frac{1}{{{t}^{2}}-1},N=\frac{{{p}_{2}}}{{{p}_{1}}},$[RL]为混凝土设计抗拉强度，MPa；Er、Ec分别为围岩、衬砌的弹性模量，MPa；μr、μc为围岩、衬砌的泊松比.

2) 计算衬砌外内壁水压力之比N

如果衬砌未开裂，则N直接由水流连续条件求得:

$N=\frac{{{K}_{c}}\ln \frac{R}{{{r}_{2}}}}{{{K}_{c}}\ln \frac{R}{{{r}_{2}}}+{{K}_{r}}\ln \frac{{{r}_{2}}}{{{r}_{1}}}}$    (2)

式中: Kr、Kc分别为围岩、衬砌的渗透系数，m/s；R为围岩的渗透半径，m.

如果衬砌开裂，流经未开裂衬砌混凝土的流量远小于流经衬砌裂缝的流量，因此在计算衬砌外壁流出的流量时，不能简单使用衬砌未开裂时的流量公式，而应采用裂隙岩体立方定理[15].最终根据水流连续条件(衬砌外表面流出流量等于围岩内表面流入流量)[16-17]，得出N的迭代计算式为

$\frac{\pi g}{192\upsilon {{\gamma }_{w}}}\frac{{{r}_{s}}{{K}_{w}}^{2}}{{{A}_{s}}^{3}{{E}_{s}}}\frac{{{p}_{1}}^{3}{{\left( 1-N \right)}^{3}}{{\left( {{r}_{1}}+{{r}_{2}} \right)}^{2}}}{{{r}_{2}}-{{r}_{1}}}\left( {{\psi }_{1}}{{p}_{1}}\left( 1-N \right)\left( {{r}_{1}}+{{r}_{2}} \right)-2{{A}_{s}}{{E}_{s}}{{\psi }_{2}}{{\varepsilon }_{c\max }} \right)=2\pi {{K}_{r}}\frac{N{{p}_{1}}}{{{\gamma }_{w}}\left( \ln R-\ln {{r}_{2}} \right)}$    (3)

式中:${{K}_{w}}=\frac{2.08}{{{E}_{s}}}\left( 3c+\frac{0.10d}{{{\rho }_{te}}} \right)$；υ为水的运动粘度，取为1.308×10-6m2/s；γw为水的重度，N/m3；rs为环向钢筋重心到隧洞中心线的距离，m；As为受拉区纵向钢筋截面面积，mm2；c为最外层纵向受拉钢筋外边缘与受拉区底边的距离，mm；d为钢筋直径，mm；ρte为纵向受拉钢筋的有效配筋率.

3) 判断衬砌和围岩是否联合承载

本文假定衬砌和围岩间的粘结力为零[18]，即当衬砌和围岩间的相互作用力为零时，衬砌和围岩相互脱离，不再联合承载[19].经公式推导，得出衬砌外内壁渗透水压力之比N*的表达式:

①衬砌未开裂，即p1 ＜p裂时:

${{N}^{*}}=\frac{{{C}_{2}}{{C}_{4}}}{{{C}_{1}}+{{C}_{2}}{{C}_{4}}}$    (4)

②衬砌开裂后，即p1>p裂时:

${{N}^{*}}=\frac{{{C}_{2}}{{C}_{5}}}{{{C}_{1}}+{{C}_{2}}{{C}_{5}}}$    (5)

式中:${{C}_{5}}=\frac{1-2{{\mu }_{c}}}{3\left( 1-{1}/{t}\; \right)}+\frac{2\left( 2\text{-}{{\mu }_{c}} \right)}{3\left( {{t}^{2}}-1 \right)}$.

通过N和N*的大小，可以判断衬砌和围岩的联合承载状态: 若N＜N*，衬砌和围岩间的相互作用力为压力，二者联合承载；若N>N*，衬砌和围岩间的相互作用力为零，说明二者相互脱离，不再联合承载.

4) 确定配筋方案

对于已开裂的衬砌，将式(3) 计算得出的N值分别代入式(6) ~(9) ，可求出裂缝处的钢筋应力、最大裂缝宽度[20]、裂缝条数、单位管长渗流量等物理量的数值:

钢筋应力:

${{\sigma }_{\text{s}}}=\frac{{{p}_{1}}\left( 1-N \right)\left( {{r}_{1}}+{{r}_{2}} \right)}{2{{A}_{s}}}$    (6)

最大裂缝宽度:

${{w}_{\max }}=2.08\frac{{{\sigma }_{s}}}{{{E}_{s}}}\left( 3c+\frac{0.10d}{{{\rho }_{te}}} \right)$    (7)

裂缝条数:

$n=\frac{2\pi {{r}_{s}}\left( \frac{{{\psi }_{1}}{{\sigma }_{s}}}{{{E}_{s}}}-{{\psi }_{2}}{{\varepsilon }_{c\max }} \right)}{\frac{{{w}_{\max }}}{2}}$    (8)

单位管长渗流量:

$Q=2\pi {{K}_{r}}\frac{N{{p}_{1}}}{{{\gamma }_{w}}\left( \ln R-\ln {{r}_{2}} \right)}$    (9)

最后，根据安全性和经济性原则，确定配筋方案，本文取最大裂缝宽度为0.25 mm，以此筛选出所有满足安全性要求的配筋方案，再按配筋率最小和渗流量最小的原则确定最优的配筋方案.

3 算例 3.1 基本资料

某水电工程装机容量为1 500 MW，其引水隧洞断面形式为圆形，隧洞内径为5.80 m，内水压力为1.028 MPa.隧洞采用钢筋混凝土衬砌: 衬砌厚度为60 cm，衬砌混凝土采用C25混凝土，其泊松比和渗透系数分别为0.167和1×10-9 m/s；围岩类别为Ⅲ类，变形模量为7 GPa，泊松比和渗透系数分别为0.25和4×10-6 m/s.

3.2 初步计算结果

首先取ψ1=ψ2=1.0，进行不同配筋方案下的透水衬砌设计，配筋方案和计算结果如表 2所示.

从表 2可以看出: 在不同配筋方案下，N均大于0.95，说明围岩承担的水压力占95%以上，围岩为主要的承载结构；配筋率越小，工程初期成本越低，但单位管长的渗流量越高，则后期运行时水流损失越大，因此在优选配筋方案时，需要综合考虑配筋率和渗流损失两方面因素进行选择.

表 2 配筋方案(ψ1=ψ2=1.0) Table 2 Reinforcement schemes(ψ1=ψ2=1.0)
配筋方案配筋率/%衬砌外内壁水压力之比N衬砌围岩是否脱离钢筋应力σs/MPa最大裂缝宽度wmax/mm单位管长渗流量Q/(10-3m3·(s·m)-1)
4Φ32mm0.530.951脱离95.9000.2481.087 5
5Φ28mm0.510.951脱离99.2190.2441.088 0
6Φ25mm0.490.952脱离102.1550.2421.088 9
7Φ20mm0.360.960脱离113.3210.2501.098 3
表选项
3.3 应变不均匀系数敏感性分析

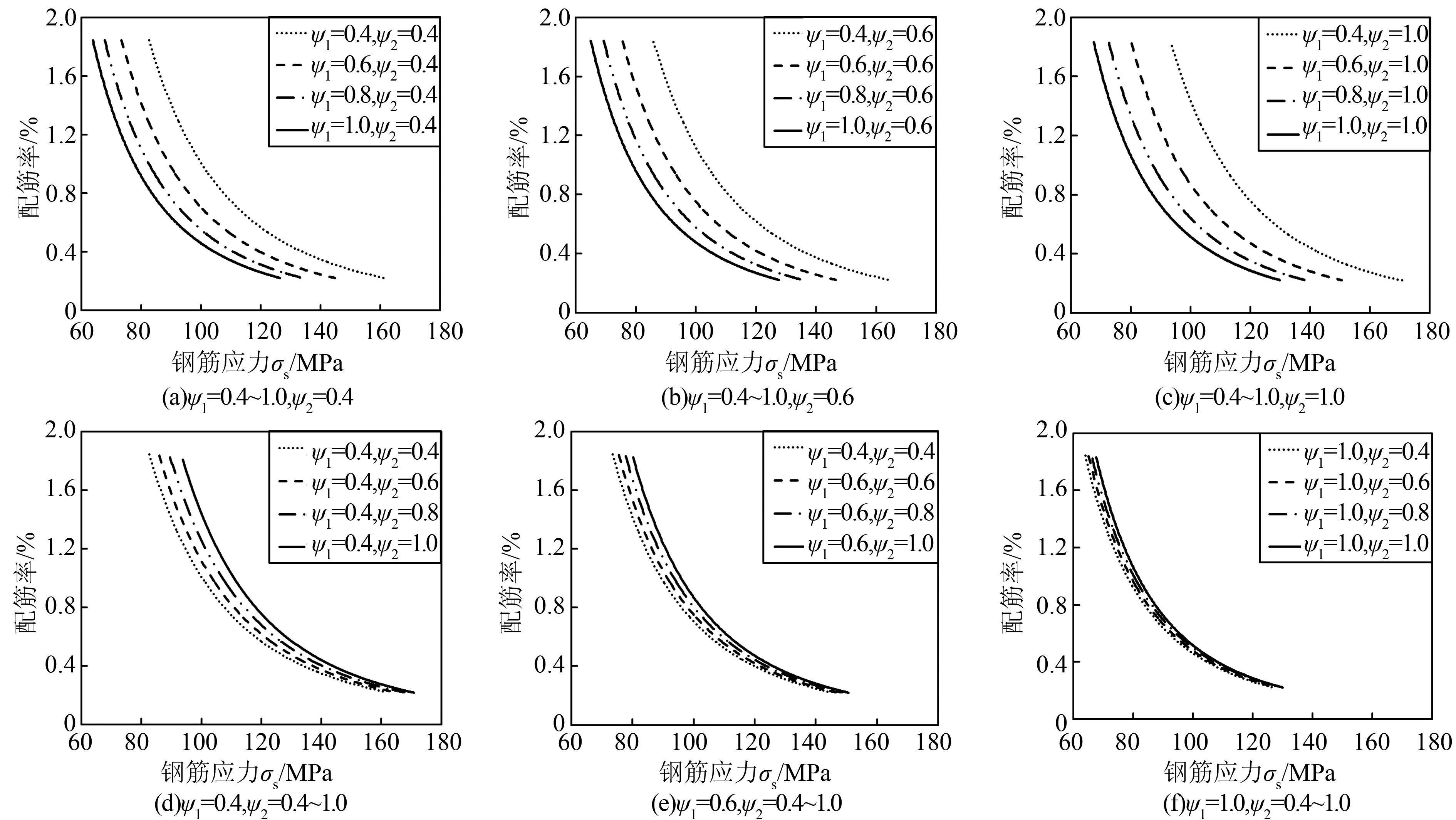
为了定量研究钢筋应变不均匀系数ψ1和裂缝间混凝土应变不均匀系数ψ2的影响，分别取ψ2(或ψ1)为定值0.4、0.6、1.0，ψ1(或ψ2)由0.4逐步增加至1.0，计算不同配筋方案下，每组(ψ1，ψ2)对应的衬砌裂缝处的钢筋应力，绘制配筋率-钢筋应力关系曲线图，如图 3所示.同时，取ψ2(或ψ1)为1.0，ψ2(或ψ1)由0.4逐步增加至1.0，计算不同配筋方案下，每组(ψ1，ψ2)对应的单位管长渗流量，绘制配筋率-单位管长渗流量关系曲线图，如图 4、图 4(b)所示，取ψ1、ψ2同时由0.4逐步增加至1.0，计算结果如图 4(c)所示.

从图 3(a)~(c)可知，ψ1的变化对配筋计算的影响较大.ψ1增大时，配筋率-钢筋应力曲线近乎向横坐标轴正方向平行移动.例如，配筋率为0.4%，ψ1由0.4增加至1.0时，钢筋应力从142.1 MPa逐渐减小至106.8 MPa，减小幅度达到24.84%.由此看出，钢筋应变不均匀系数ψ1对配筋计算的影响不容忽视.

从图 3(d)~(f)可知，ψ2的变化对配筋计算影响相对较小.例如，配筋率为0.4%，ψ2由0.4增加至1.0时，计算得到的钢筋应力从103.3 MPa逐渐增大至106.8 MPa，增加幅度仅为3.39%.同时，当钢筋应力大于某一较大数值时，不同ψ2值对应的配筋率-钢筋应力曲线有相互重合的趋势.当ψ1=0.4、0.6、1.0时，该数值分别为160、140、120 MPa，说明钢筋应力较大时，钢筋的作用得以充分发挥，此时可以不考虑混凝土的应变不均匀性，直接取ψ2=1.0.对比图 3(a)~(f)可以发现，配筋率和钢筋应力对ψ1的敏感性远大于对ψ2的敏感性，且ψ1和ψ2对配筋率和钢筋应力的影响效果刚好相反.

图 3 配筋率与钢筋应力关系曲线 Figure 3 Reinforcement ratio versus reinforcing steel stress for different nonuniformity coefficients
图选项

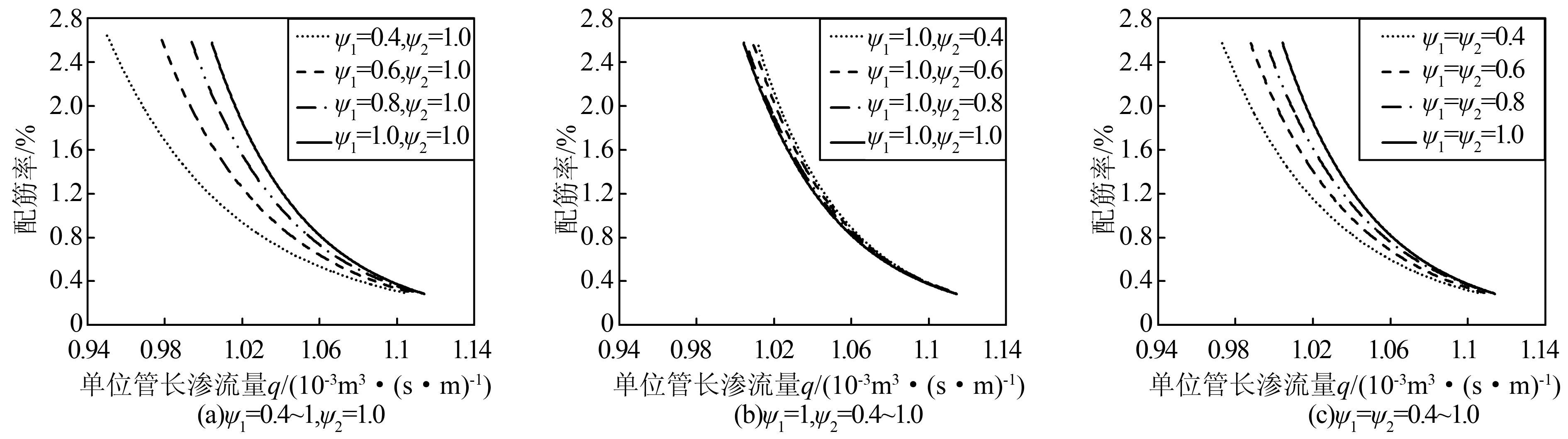
从图 4(a)可知，ψ1的变化对单位管长渗流量的影响较大，当配筋率为0.4%，ψ1由0.4增加至1.0时，单位管长渗流量从1.080×10-3m3/(s·m)增至1.096×10-3m3/(s·m)，增加了1.48%；而当配筋率为1.2%，ψ1由0.4增至1.0时，单位管长渗流量从1.002×10-3m3/(s·m)增至1.040×10-3m3/(s·m)，增加了3.79%.由此看出，配筋率一定时，ψ1越大，单位管长渗流量越大；同时，配筋率越大，ψ1对渗流量的影响越大.

从图 4(b)可知，ψ2的变化对单位管长渗流量的影响相对ψ1的影响较小，当配筋率为0.4%，ψ2由0.4增加至1.0时，单位管长渗流量从1.098×10-3m3/(s·m)减至1.096×10-3m3/(s·m)，减小了0.18%；当配筋率为1.2%，ψ1由0.4增加至1.0时，单位管长渗流量从1.045×10-3m3/(s·m)减至1.040×10-3m3/(s·m)，减小了0.48%.由此看出，配筋率一定时，随着ψ2的增加，单位管长渗流量略有减少，但总体而言，数值变化不大.

对比图 4、(b)和(c)可知，配筋率较低时，ψ1和ψ2对渗流量的影响较小，且整体而言ψ1的影响大于ψ2.

图 4 配筋率与单位管长渗流量关系曲线 Figure 4 Reinforcement ratio versus inflow per unit length of tunnel for different nonuniformity coefficients
图选项

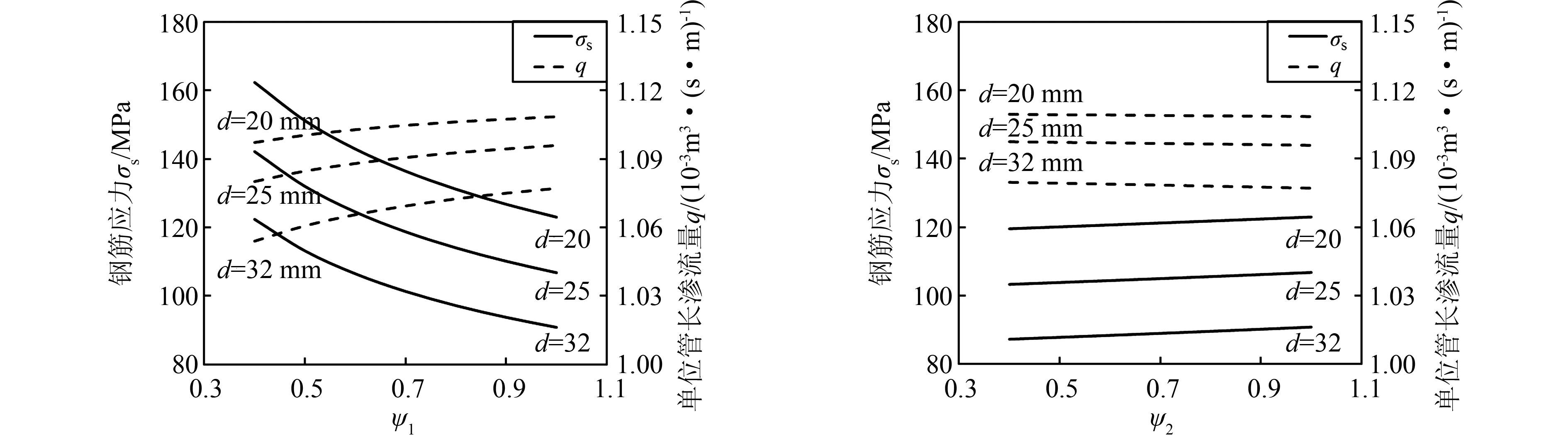
观察图 3和图 4可以发现，当配筋率一定、ψ1增加、ψ2不变时，钢筋应力减小，渗流量增加；ψ2增加，ψ1不变时，钢筋应力增加，单位管长渗流量减少.为了进一步分析配筋面积一定时钢筋应力与渗流量的变化规律，本文取配筋方案为5Φ20mm、5Φ25mm、5Φ32mm进行对比计算，详见图 5.其中:d为钢筋直径，mm.

图 5 一定配筋条件下的σs与q变化曲线 Figure 5 Steel stress versus inflow per unit length of tunnel for determined reinforcements
图选项

从图 5可知，配筋方案一定，ψ1增加时，钢筋应力呈现较大幅度的减小趋势，单位管长渗流量逐渐增加，但增幅较小，例如，当d=20 mm，ψ1由0.4增至1.0时，钢筋应力从162.3 MPa减小至123.0 MPa，减小了24.21%，而单位管长渗流量从1.097×10-3 m3/(s·m)增至1.108×10-3 m3/(s·m)，增加了1.00%.在ψ1一定，钢筋用量增加时，钢筋应力和单位管长渗流量均逐渐减小，例如，当ψ1=0.6，每米布置的钢筋根数不变，直径d由20 mm增至32 mm时，钢筋应力从142.9 MPa减小至106.5 MPa，减小了25.47%，单位管长渗流量从1.103×10-3 m3/(s·m)减小至1.066×10-3 m3/(s·m)，减小了3.35%.从图 5(b)可知，配筋方案一定，ψ2增加时，钢筋应力的增加趋势和单位管长渗流量的减少趋势均较缓慢，且渗流量几乎保持不变.当ψ2一定，钢筋用量增加时，钢筋应力和单位管长渗流量均逐渐减小，例如，当ψ2=0.6，每米布置的钢筋根数不变，直径d由20 mm增至32 mm时，钢筋应力从120.7 MPa减小至88.4 MPa，减小了26.76%，单位管长渗流量从1.109×10-3 m3/(s·m)减小至1.079×10-3 m3/(s·m)，减小了2.70%.比较图 5(a)、(b)可知，钢筋应力σs和单位管长渗流量q对ψ1的敏感性明显大于对ψ2的敏感性，且在保持钢筋间距不变化时，增加钢筋直径对控制钢筋应力和渗流量有较为明显的效果.

4 结论

在透水衬砌理论的基础上，结合工程实际定量分析了钢筋应变不均匀系数和裂缝间混凝土应变不均匀系数对钢筋应力和单位管长渗流量的影响，得出以下结论:

1) 钢筋应变不均匀系数ψ1和裂缝间混凝土应变不均匀系数ψ2对钢筋应力和单位管长渗流量的影响明显，且ψ1的影响大于ψ2的影响.

2) 在配筋方案相同的情况下，ψ1减小或ψ2增大时，钢筋应力增大，单位管长渗流量减小.当配筋率减小到一定程度时(小于0.4%)，ψ1、ψ2对渗流量的影响可以忽略.

3) 随着钢筋应力的逐渐增加，应变不均匀系数ψ1和ψ2的影响逐渐减小，在钢筋应力达到某一较大数值后(如ψ1=1.0时，120 MPa)，裂缝间混凝土应变不均匀系数ψ2的影响基本可以忽略，同等配筋条件下的钢筋应力差别主要来源于钢筋应变不均匀系数ψ1.

参考文献
[1] Simanjuntak T, Marence M, Mynett A E, Schleiss A. Mechanical-hydraulic interaction in the lining cracking process of pressure tunnels[J]. The International Journal on Hydropower & Dams, 2013, 20(EPFL-ARTICLE-189872): 112–119.
[2] Simanjuntak T D Y F, Marence M, Mynett A E, Schleiss A J. Pressure tunnels in non-uniform in situ stress conditions[J]. Tunnelling and Underground Space Technology, 2014, 42: 227–236. DOI:10.1016/j.tust.2014.03.006
[3] 张有天, 张武功. 隧洞水荷载的静力计算[J]. 水利学报, 1980(3): 52–62.
Zhang Youtian, Zhang Wugong. The static structure calculation of water loads on hydraulic tunnel[J]. Journal of Hydraulic Engineering, 1980(3): 52–62.
[4] 张有天, 张武功, 王镭. 再论隧洞水荷载的静力计算[J]. 水利学报, 1985, 3(3): 22–32.
Zhang Youtian, Zhang Wugong, Wang Lei. The second discussion of static structure calculation of water loads on hydraulic tunnel[J]. Journal of Hydraulic Engineering, 1985, 3(3): 22–32.
[5] Schleiss A J. Design of pervious pressure tunnels[J]. Water Power and Dam Construction, 1986, 38(5): 21–26.
[6] 曹克明, 刘世明. 高内水压力作用下隧洞钢筋混凝土衬砌设计理论的探讨[J]. 华东水电技术, 1991(3): 1–18.
Cao Keming, Liu Shiming. The discussion of design theory on hydraulic tunnel reinforced concrete lining under high water load[J]. East China Water Resources and Hydropower Engineering, 1991(3): 1–18.
[7] Schleiss A J. Design of reinforced concrete linings of pressure tunnels and shafts[J]. Hydropower & Dams, 1997, 3: 88–94.
[8] 苏凯, 伍鹤皋, 韩前龙. 高压透水隧洞工作机理探讨[J]. 水利水电技术, 2005(6): 61–64.
Su Kai, Wu Hegao, Han Qianlong. Discussion on working mechanism of high-pressure pervious tunnel[J]. Water Resources and Hydropower Engineering, 2005(6): 61–64.
[9] 李新星, 蔡永昌, 庄晓莹, 等. 高压引水隧洞衬砌的透水设计研究[J]. 岩土力学, 2009, 30(5): 1403–1408.
Li Xinxing, Cai Yongchang, Zhuang Xiaoying, et al. Design of permeable lining for high pressure hydraulic tunnel[J]. Rock and Soil Mechanics, 2009, 30(5): 1403–1408.
[10] Su Kai, Wu Hegao. Analysis of hydro-mechanical interaction to pervious pressure tunnel[C]// Asia-Pacific Power and Energy Engineering Conference 2010, Chengdu, China.
[11] Zhou Y, Su K, Wu H. Hydro-mechanical interaction analysis of high pressure hydraulic tunnel[J]. Tunnelling & Underground Space Technology, 2015, 47: 28–34.
[12] 苏凯, 伍鹤皋, 周创兵. 内水压力下水工隧洞衬砌与围岩承载特性研究[J]. 岩土力学, 2010, 31(8): 2407–2412.
Su Kai, Wu Hegao, Zhou Chuangbing. Study of combined bearing characteristics of lining and surrounding rock for hydraulic tunnel under internal water pressure[J]. Rock and Soil Mechanics, 2010, 31(8): 2407–2412.
[13] 侯靖, 胡敏云. 水工高压隧洞结构设计中若干问题的讨论[J]. 水利学报, 2001(7): 36–40.
Hou Jing, Hu Minyun. Discussion on some problems in design of high pressure tunnel for hydro projects[J]. Journal of Hydraulic Engineering, 2001(7): 36–40.
[14] Olumide B A. Numerical coupling of stress and seepage in the design of pressure tunnel under high internal water pressure[J]. International Journal of Engineering and Technology, 2013, 3(3): 235–244.
[15] 苏凯, 伍鹤皋. 水工隧洞内水外渗耦合分析[J]. 岩土力学, 2009, 30(4): 1147–1152.
Su Kai, Wu Hegao. Analysis of hydro-mechanical interaction in hydraulic tunnel with inner water exosmosis[J]. Rock and Soil Mechanics, 2009, 30(4): 1147–1152.
[16] Su K, Li Y. Design of pressure tunnel with reinforcement concrete lining under consolidation grouting[J]. Advanced Materials Research, 2012, 446-449: 2731–2735.
[17] Fernández G. Behavior of pressure tunnels and guidelines for liner design[J]. Journal of Geotechnical Engineering, 1994, 120(10): 1768–1791. DOI:10.1061/(ASCE)0733-9410(1994)120:10(1768)
[18] 伍鹤皋, 尚斌, 苏凯. 高压隧洞透水衬砌结构研究[J]. 武汉大学学报(工学版), 2011, 44(3): 321–325.
Wu Hegao, Shang Bin, Su Kai. Research of permeable linings structure for high pressure tunnel[J]. Engineering Journal of Wuhan University, 2011, 44(3): 321–325.
[19] 苏凯, 陈梦然, 程宵, 等. 基于有条件联合承载机理的导流隧洞衬砌安全与加固措施研究[J]. 水利水电技术, 2013, 44(9): 57–60.
Su Kai, Chen Mengran, Cheng Xiao, et al. Study on lining safety and strengthening measures for diversion tunnel based on conditional combined load-bearing mechanism[J]. Water Resources and Hydropower Engineering, 2013, 44(9): 57–60.
[20] 丁旭柳, 伍鹤皋, 朱忠华. 钢筋混凝土压力隧洞裂缝宽度计算方法的探讨[J]. 武汉大学学报(工学版), 2001, 34(2): 24–27.
Ding Xuliu, Wu Hegao, Zhu Zhonghua. Study on computational method of crack width of reinforced concrete pressure tunnels[J]. Engineering Journal of Wuhan University, 2001, 34(2): 24–27.