文章信息
- 章琰天, 陶劲松, 陈宇航, 沈顺群
- ZHANG Yantian, TAO Jingsong, CHEN Yuhang, SHEN Shunqun
- 含分布式电源的配电网合解环操作安全性分析
- Security analysis of operation of loop closing or opening in distribution network with distributed generations
- 武汉大学学报(工学版), 2016, 49(6): 930-936
- Engineering Journal of Wuhan University, 2016, 49(6): 930-936
- http://dx.doi.org/10.14188/j.1671-8844.2016-06-022
-
文章历史
- 收稿日期: 2015-12-17
2. 国网湖北神农架林区供电公司,湖北 神农架林区 442400
2. State Grid Hubei Shennongjia Branch,Shennongjia, 442400,China
随着我国社会的快速发展,用户对供电质量的要求逐渐提高,这就需要配电网的管理和运行更加稳定、合理、高效.我国城市多数的配电网都已经是以“闭环设计、开环运行”方式供电[1].当下配电网改造和升级以及越来越多的分布式电源加入到电网中,双端供电甚至是多端供电的模式越来越常见,如果在配电网利用已有的联络开关进行合解环操作,就能提高分布式电源运行的稳定性以及配电网供电的可靠性,使得配电网的运行更加高效和可靠.但是在含分布式电源的配电网合环过程中,线路、电气设备和分布式电源都会受到暂态过电压的冲击,这可能会使线路变形、设备绝缘损坏,某些情况下会造成继电保护误动作,导致合环操作失败[2].在本文中主要研究配电网合解环操作中的合环操作.
文献[1-3]主要通过稳态和暂态的潮流计算来判断是否能合解环.文献[4]分析了电网络中相角的扰动对于系统电压的影响.文献[5]认为合环暂态电流主要与合环电压幅值差与电压相角差有关.文献[6-8]论述了含有分布式电源的电网络的结构变化会使得潮流分布和线路电压产生相应变化.文献[9-11]研究了城市配电网合解环倒负载的相角差,但是其研究中没有分析分布式电源对电网合环操作产生的影响.文献[12]主要是通过计算合环点两侧电压判断能否合解环,但是对合环以后的网络结构变化以及在新结构下分布发电对电网的潮流影响缺乏详尽的论述.
这些研究主要针对独立配电网的合环过程,很少提及分布式电源对合环过程的影响,本文通过分析含多种类型分布式电源的配电网计划性合环操作过程,建立等效合环模型,推算出合环过程中的冲击电压和电流.利用软件PSCAD/EMTDC仿真并与推算结果比较,以验证理论的有效性和准确性.在此基础上,研究了分布式电源的容量、类型和距离对合环电压、时间和相角差的影响,为提高含分布式电源的配电网合解环操作的安全性提供理论依据.
1 合环成功的条件配电网合环过程中产生的暂态过电流使继电保护器动作是配电网合环操作失败的主要原因[13].由文献[10]分析可得,合环后的稳态电流由合环前的稳态电流与合环环流叠加组成.Ic表示合环环流,I表示合环时出现的冲击电流,Imax表示线路的最大容许载流量,μ表示合环前线路中电流有效值与其最大容许载流量之比,一般取0<μ<1.则有
即
从文献[12]可知,合环暂态过程中非周期分量的衰减时间Tt一般小于线路首端的电流保护Ⅱ段延时时间的整定值,这个值t一般可以取0.5 s,所以合环暂态过程只对瞬时电流保护器有影响,当瞬时速断保护定值I1op1的整定满足:
即
电流速断保护整定值大多数情况都能满足式(4),那么表示合环电流的非周期分量衰减时间比电流保护整定时间短,配电网合环电流的非周期分量在衰减过程中不会对合环操作产生影响.因此安全合环的条件可以简化为:合环后线路中稳态电流有效值小于线路的最大容许载流量[14].
2 线路仿真 2.1 DG模型本文使用的分布式电源是基于不同控制方式的水轮同步发电机,其模块主要由3部分组成,即同步发电机、交流发电机矫正励磁系统以及合成水轮控制器.
2.1.1 同步发电机在PSCAD仿真中,同步发电机模型及其参数的设置有两种形式,分别为发电机等效电路模式和发电机数学模型模式.本文采用后者.发电机数学模型分为两部分,即发电机转子运动方程及定子电压方程.不同发电机模型的转子运动方程基本相同,一般可表示为
其中:TJ为同步发电机的转子机械惯性时间常数,代表转子的转动惯量;ω0为发电机转子的额定电角速度;Tm、Te、Td分别为原动机输出的机械转矩、发电机内部电枢反应产生的电磁转矩以及转子转动过程产生的阻尼转矩.
同步发电机的定子电压方程为
其中:Ud、Uq分别为定子电压;ω为发电机转速,它决定发电机实际频率;Ra和Id、Iq分别表示定子绕组阻抗和定子d轴上电流、定子q轴上电流.d-q轴上的磁链分别由ψd和ψq表示,在本文使用的PSCAD同步发电机模型里,采用的两绕组转子模型,其磁链方程为
对应的二阶电压平衡方程:
其中:e′q、e′d为发电机次暂态电动势;Efq称为空载电动势,在本模型中,Efq的值与励磁电压Uf近似相等,所以Efq值由励磁控制器决定和控制.
2.1.2 励磁装置分布式发电单元主要有两种控制模式:1)恒功率控制模式(Unit Output Power Control,UPC),该模式是设定电源功率参考值,使发电机输出的功率恒定;2)馈线流量控制模式(Feeder Flow Control ,FFC),该模式通过调节发电机的输出功率使馈线上的有功功率保持不变[15].馈线流量控制(FFC)主要应用于风力发电机中,所以本文涉及的两种控制模式分别为恒功率控制模式(UPC)和无控制(NO)模式.UPC模式励磁系统工作原理为:励磁器将同步发电机的励磁电压作为控制量,同步发电机定子的端电压和定子电流作为反馈信号.通过反馈函数的计算来改变发电机的励磁电流,保证同步发电机的输出在一定范围内保持稳定.同时在闭环控制器中添加延迟函数仿真不同的反应时间,以模拟不同类型的同步电机的励磁系统.
2.1.3 机械液压控制器当外部负荷变化等原因引起发电机电压、频率扰动时,电机的转速也会随之改变,将这些信号传输到控制器中,通过调整水轮机进水阀门的方位,改变输出电压和发电机机械转矩的大小,使同步发电机端电压、频率以及输入有功稳定.两种不同模式的水轮机控制流程图如图 1、图 2所示.
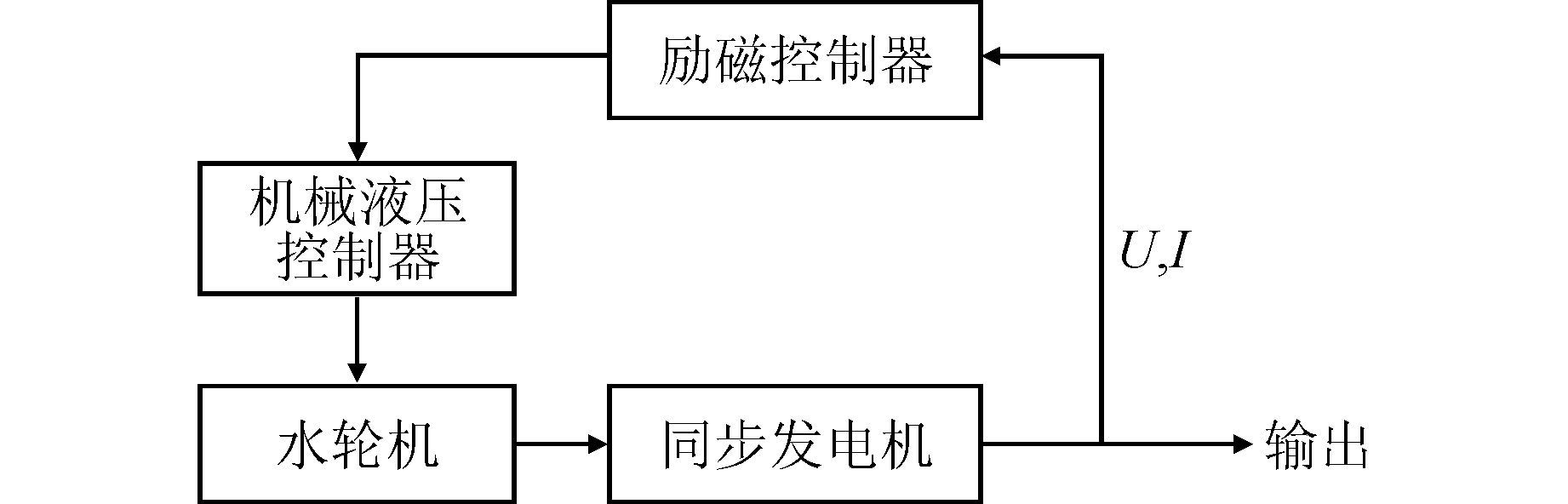
|
| 图 1 UPC模式的水轮机模型 Figure 1 UPC mode water turbine model |

|
| 图 2 NO模式的水轮机模型 Figure 2 NO mode water turbine model |
图 3是某供电公司110 kV配电环网的典型线路.在该网络中,配电变压器接有小型水力发电机组,本文仿真分析了含有两种不同控制模式的小型水力发电机的配电网合环过程.通过调取配电网与发电机组的历史数据,使用PSCAD/EMTPC仿真软件搭建系统模型,仿真分析配电网合环的物理特性.
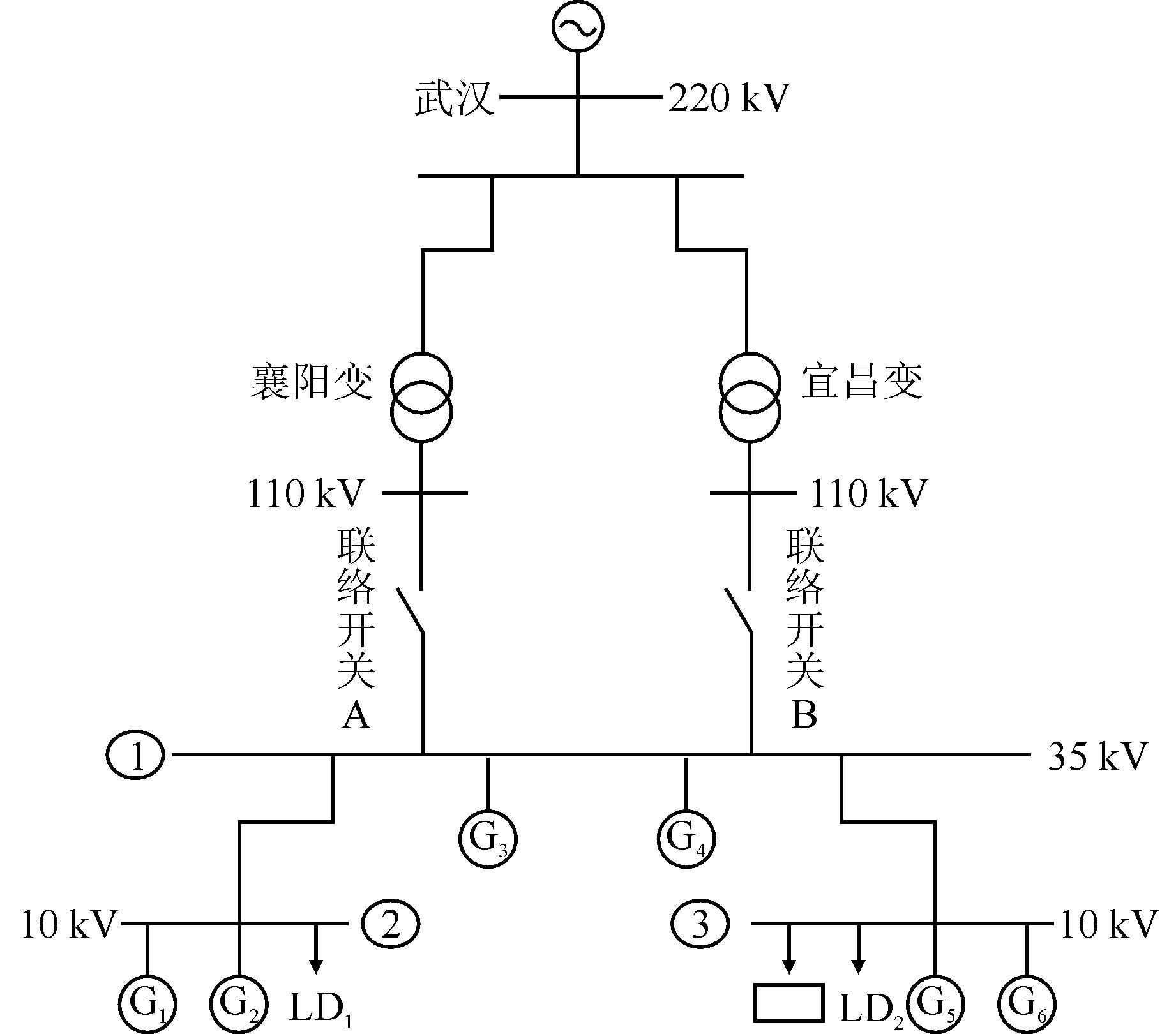
|
| 图 3 某供电公司的配电网系统 Figure 3 Distribution network system of a certain power supply company |
在该系统中,各个分布式电源的控制模式和容量如表 1所示.
| DG序号 | 控制方式 | 容量/MVA |
| 1 | UPC | 1.5 |
| 2 | UPC | 3.0 |
| 3 | UPC | 3.0 |
| 4 | UPC | 1.5 |
| 5 | UPC | 1.0 |
| 6 | NO | 1.0 |
母线1与母线2间距是5.304km,阻抗是0.583 4+j2.026 Ω;母线1与母线3间距是20 km,阻抗是2.4+j4.46 Ω.SLD1=1.2+j0.544 MVA,SLD2=2.1+j1.328 MVA.
发电机与主网的初始设定相角都是0°,无相角差.联络开关A和联络开关B的初始状态分别是闭合、断开,在t=0.2s时,将联络开关B的初始状态变为闭合.因为甲地-乙地-丁地线路(线路A)与甲地-丙地-丁地(线路B)长度不同,会在开关B的两端产生相角差.通过改变线路长度,获取在不同相角差下输电线路上的暂态电压.
利用文献[16]中对配电网的潮流计算方法,得到不同相角差下的合环暂态线电压大小,其与仿真值比较的结果如图 4所示.
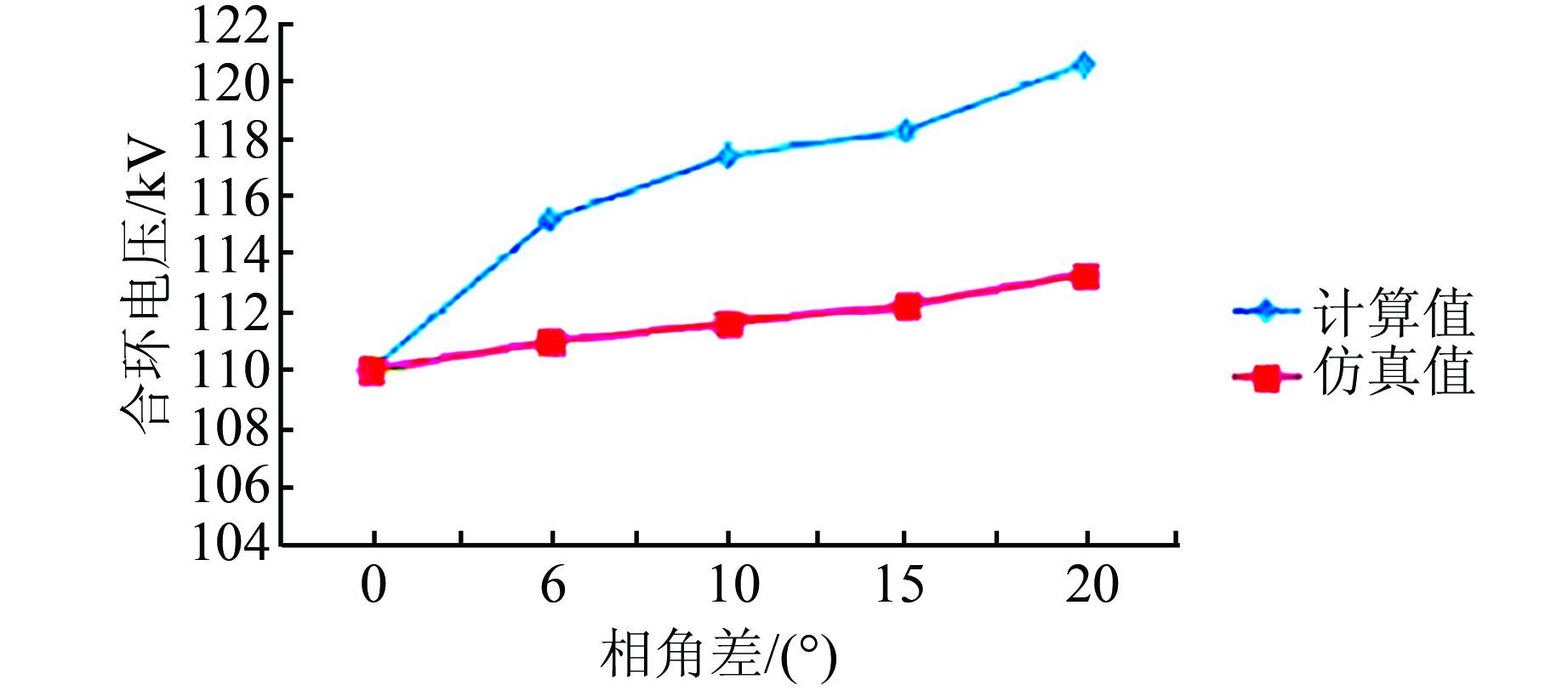
|
| 图 4 合环电压的计算值与仿真值的比较 Figure 4 Comparison of calculated values and simulation values of closing loop voltage |
图 4中计算值与仿真值有一定的偏差,这是因为在仿真过程中,为了使得分布式电源的输出波形尽量稳定,搭建分布式电源模型时,在其端口处串联了电抗器.但是二者的趋势大致相同,也能验证模型的正确性.
当合环相角差为10°时,合环过程中母线相电压和线电流的暂态波形分别如图 5、图 6所示.
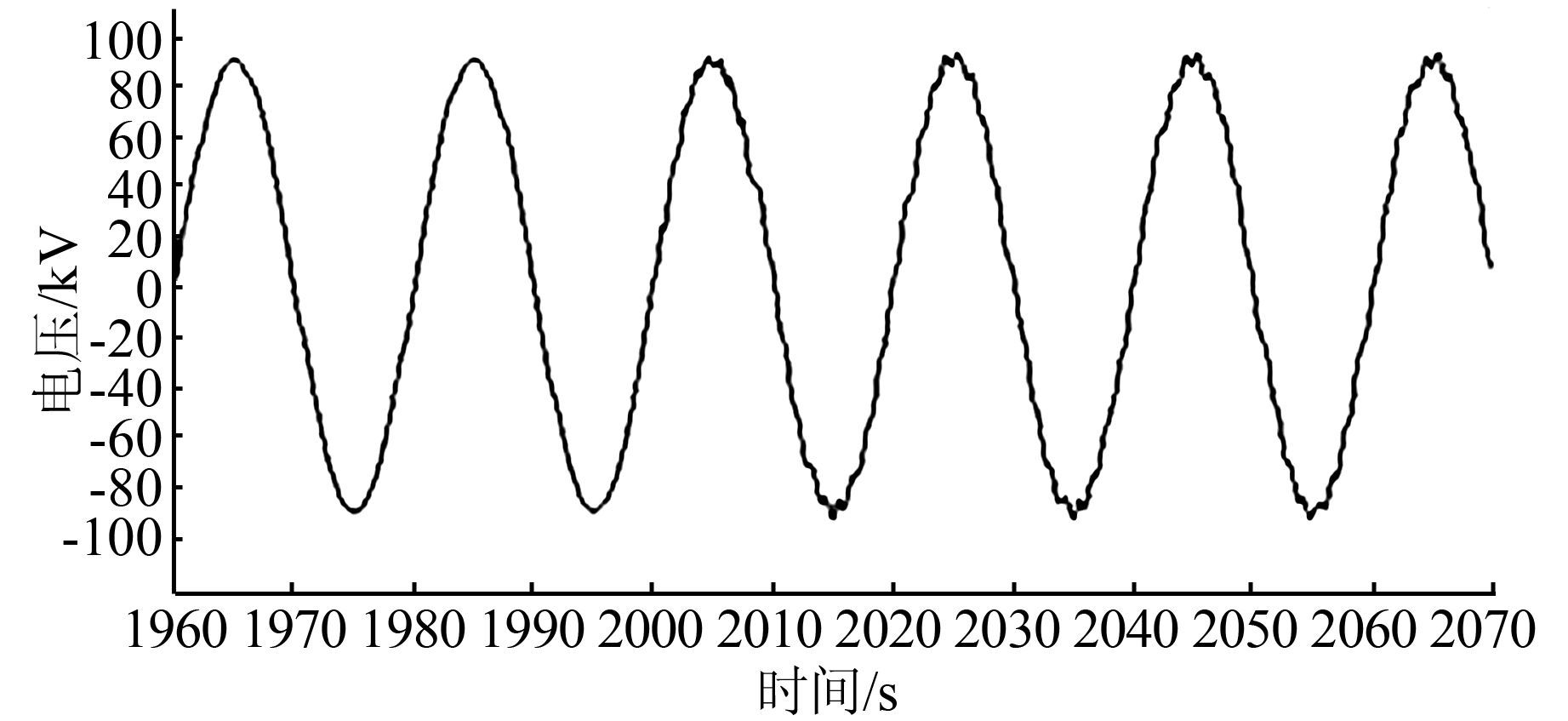
|
| 图 5 合环过程中母线暂态相电压波形 Figure 5 Bus transient phase voltage waveform during loop closing course |
|
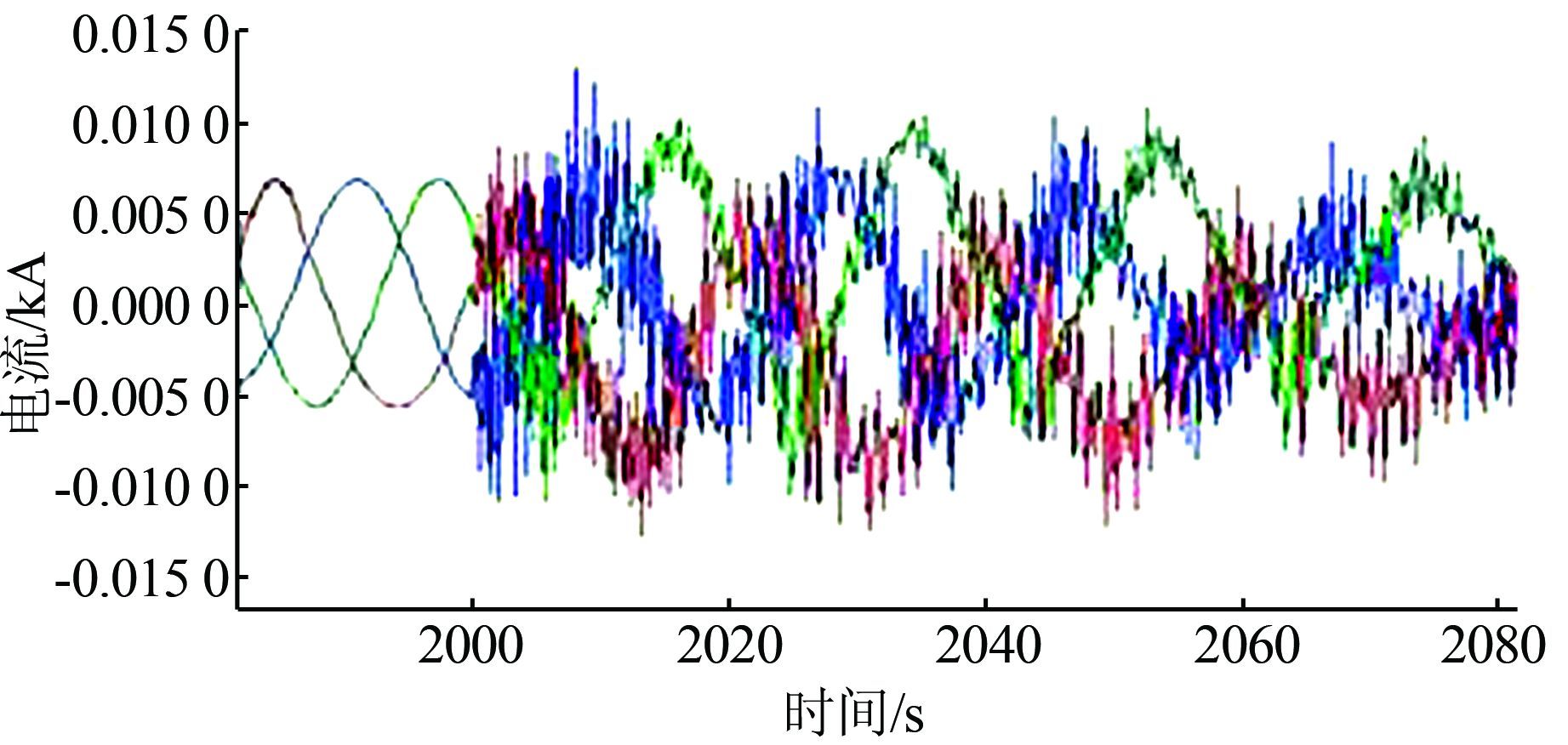
| 图 6 合环过程中母线暂态电流波形 Figure 6 Bus transient current waveform during loop closing course |
由波形可知在暂态过程中产生了冲击电压和冲击电流.在图 3所示环网结构下,仅在母线2上单独接入不同控制方式的分布式发电机,合环过程中的电压暂态波形分别如图 7、8所示.
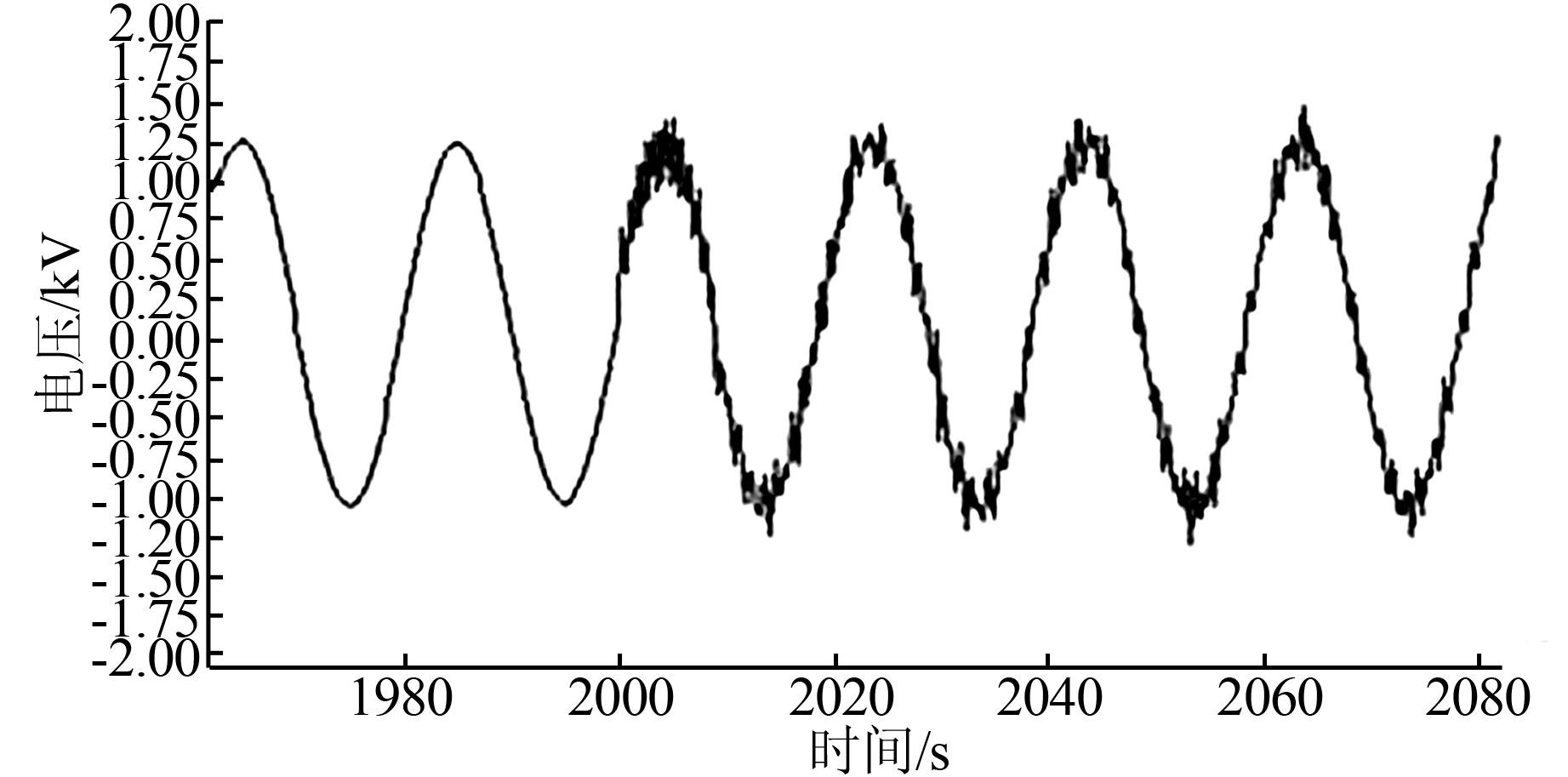
|
| 图 7 基于UPC控制发电单元相电压暂态波形 Figure 7 Transient phase voltage waveform basing on UPC control generating unit |
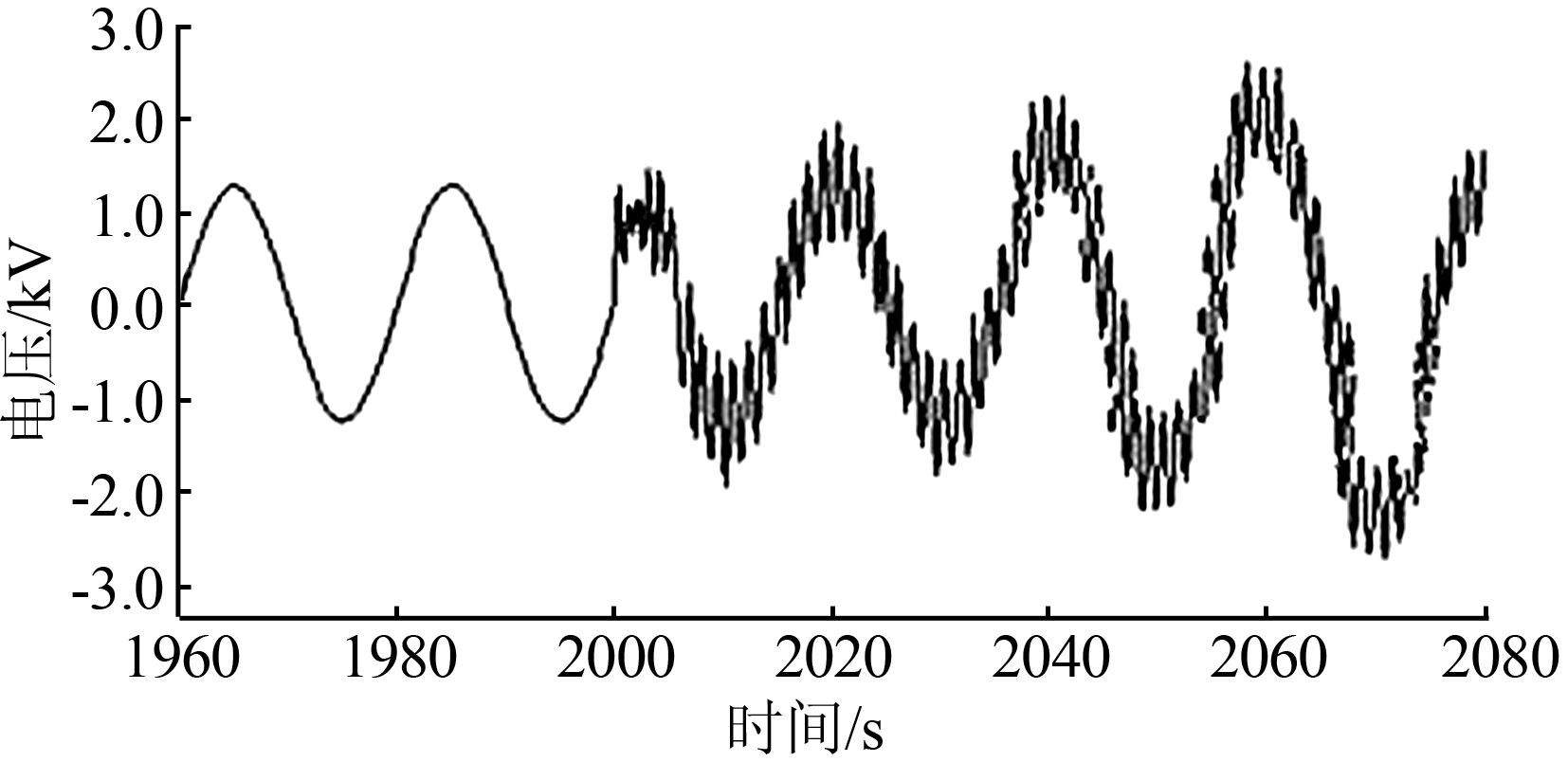
|
| 图 8 基于NO控制发电单元相电压暂态波形 Figure 8 Transient phase voltage waveform basing on NO control generating unit |
由图 7、8可知,UPC控制的分布式发电单元的端口电压基本处于稳定状态,而对于NO控制的分布式发电单元,则出现了端口电压升高的现象,这说明UPC控制的分布式发电单元的稳定性要优于NO控制的分布式发电单元.
利用文献[17]中的计算方法,在合环相角差为10°时,比较线路和分布式电源单元的继电保护的整定和合环环流,可以发现环流能躲过电流Ⅰ、Ⅱ段保护,但是环流会使电流Ⅲ段保护动作,考虑到Ⅲ段保护的整定时间为1.5s,必须在这个时间内完成合环、解环的操作,才能使继电保护不动作.因此人工操作是不可能完成的,可以考虑安装具有快速合解环功能的备自投装置.对于采用UPC控制模式的分布式发电单元,能躲过电流Ⅰ、Ⅱ、Ⅲ段保护,而采用NO控制模式的分布式发电单元,会使Ⅰ段保护装置动作.配电网合环电压与合环相角差的关系如图 9所示.
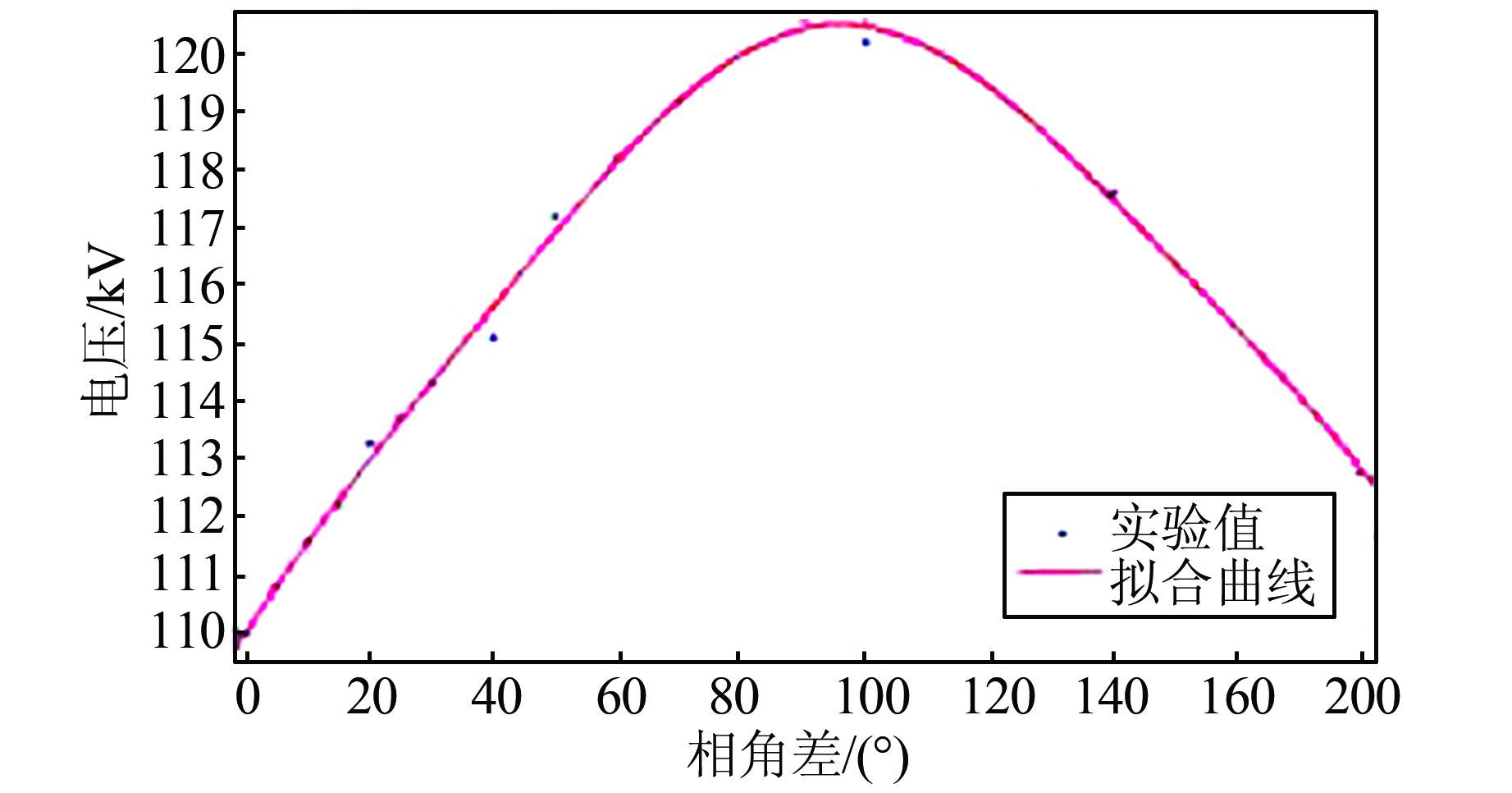
|
| 图 9 合环相角差与合环电压的关系图 Figure 9 Relation graph between phase angle difference and voltage of closing loop |
由图 9可知,随着相角差的增加,产生的冲击电压和冲击电流都在不断增大,当相角差为90°时,产生的冲击电压到达1.2Un.
3 分布式电源对配电网合环操作的影响以图 3系统为例,分别调整系统中分布式电源的条件,观察不同条件下分布式电源对配电网合环电压的影响.从文献[15]中可知合环暂态电流主要与合环电压幅值差与电压相角差有关,合环前系统处在稳定运行状态,合环暂态电流主要取决于合环操作过程中产生的过电压,所有合环成功与否主要取决于合环电压值的大小.下文主要讨论分布式电源对合环操作电压的影响.
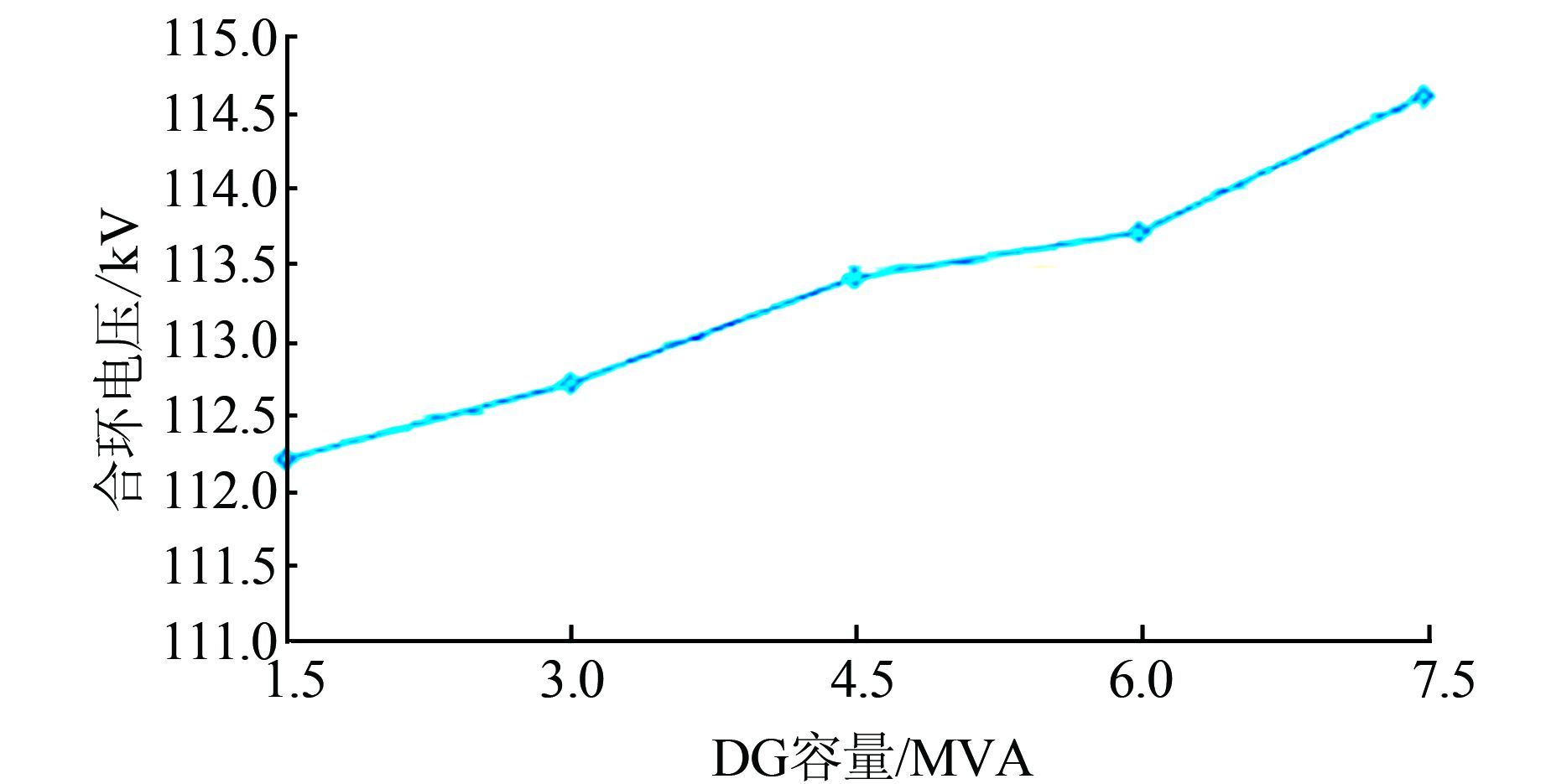
3.1 DG的容量对合环电压的影响改变接入配电网中分布式电源DG1容量的大小,在合环角度为15°时,合环电压有效值如图 10所示.
|
| 图 10 DG容量对合环电压的影响图 Figure 10 Influence graph of DG volume on voltage of closing loop |
由图 10可知,随着分布式电源的容量不断增加,合环电压值也会随之增加.因为增加分布式电源的容量,使得在合环过程中因为励磁控制的延迟而产生的额外功率变大,所以在相同相角差下的合环暂态过电压会不断升高.
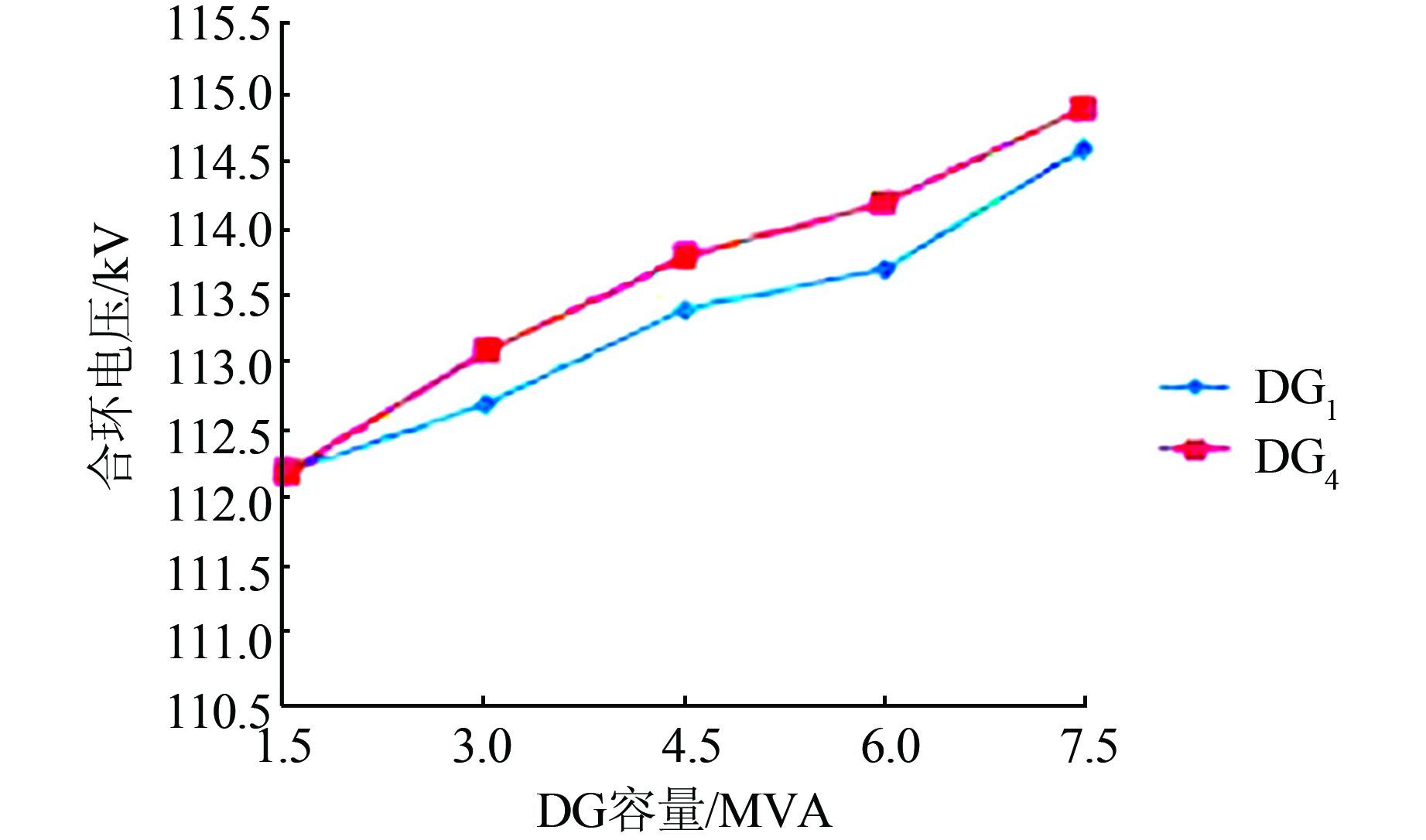
3.2 不同位置DG的容量对合环电压的影响分别改变接入配电网的分布式电源DG1、DG4的容量,在合环角度为15°时,合环电压有效值如图 11所示.
|
| 图 11 DG位置对合环电压的影响图 Figure 11 Influence graph of DG position on voltage of closing loop |
由图 11可知,越靠近合环点处的分布式电源的容量变化对合环过程中电压影响越大,这是由于系统合环操作使系统的拓扑结构由网状变成环形状,DG的容量变化使配电网潮流重新分配.
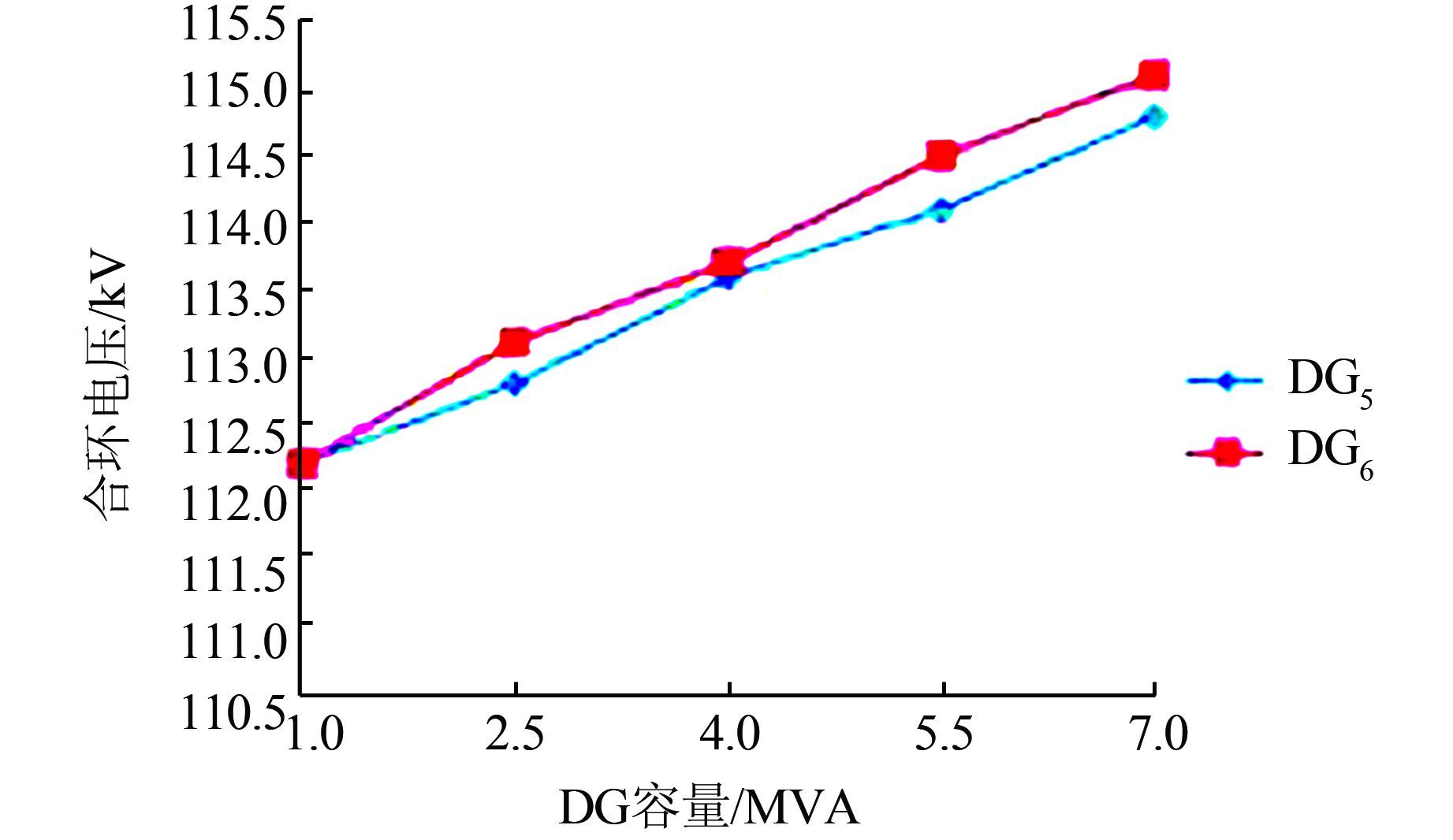
3.3 不同类型DG的容量对合环电压的影响分别改变接入配电网的分布式电源DG5、DG6的容量,在合环角度为15°时,合环电压有效值如图 12所示.
|
| 图 12 DG类型对合环电压的影响图 Figure 12 Influence graph of DG type on voltage of closing loop |
由图 12可知,当分布式电源容量变大时,励磁调节系统差的分布式电源对合环电压的扰动会大于励磁调节系统稍好的分布式电源.这是由于前者在合环过程中维持自身稳定性的能力差,导致了合环电压值升高.
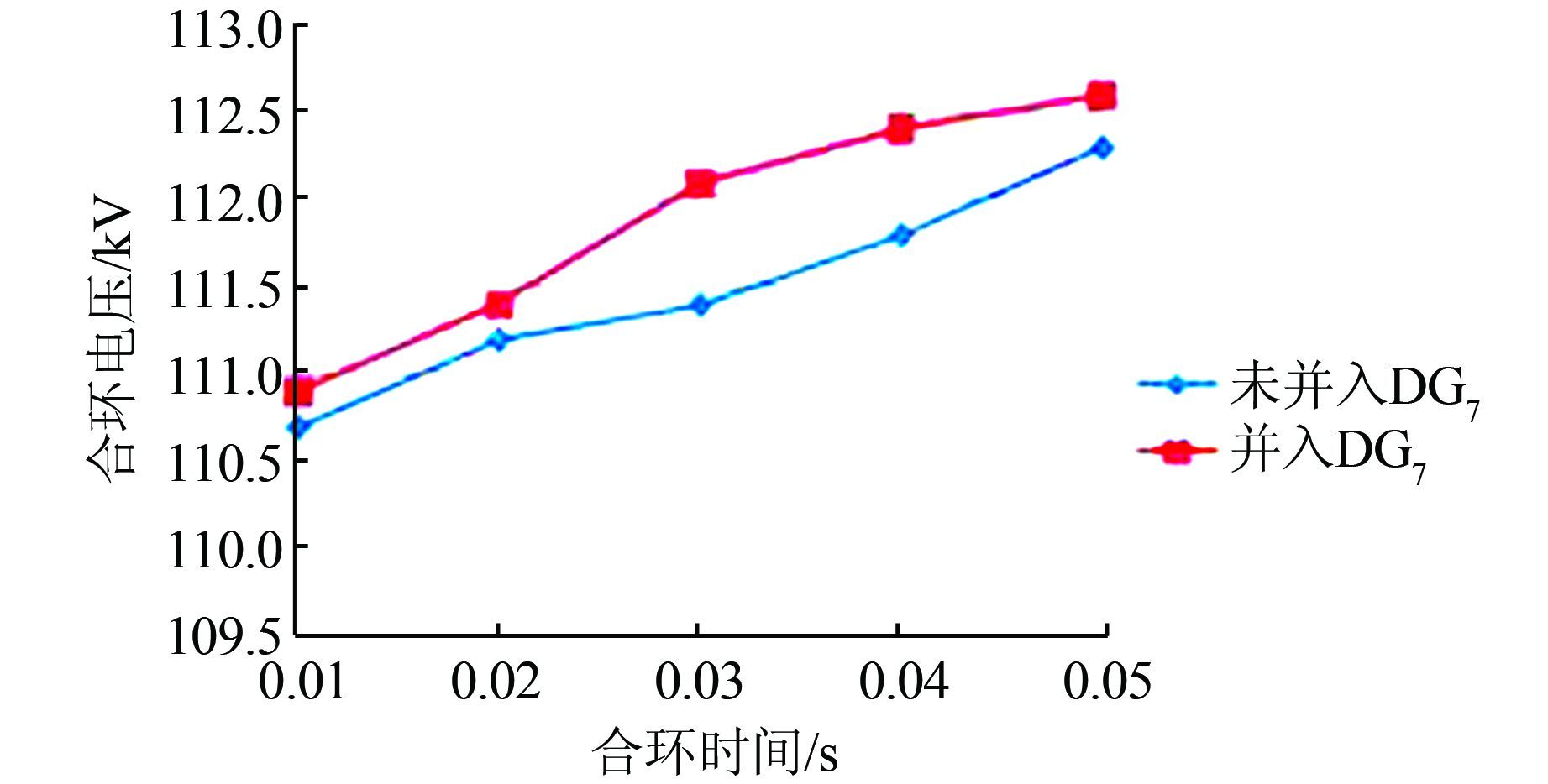
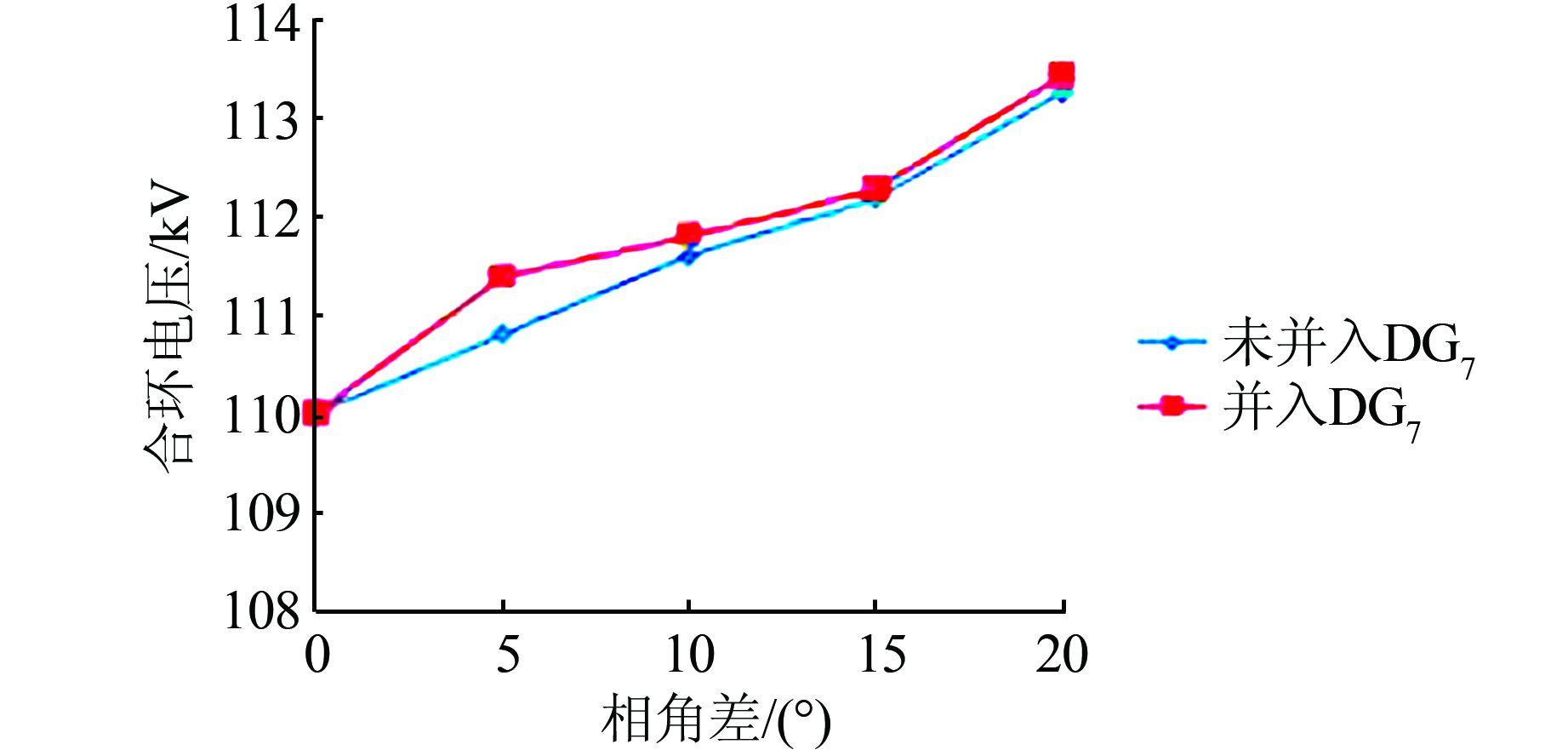
3.4 DG容量对合环时间与合环相角差的影响在图 3系统的位置7处,加入一台UPC控制的分布式电源DG7,其容量为1 MVA.当合环角度为5°时,观察合环时间对合环电压的影响.接着改变合环相角差,观察对其合环电压的影响.
由图 13、14可知,在相同合环时间或合环相角差下,合环电压随着分布式电源容量的增加而不断增大.
|
| 图 13 DG容量对合环时间的影响图 Figure 13 Influence graph of DG volume on loop closing time |
|
| 图 14 DG容量对合环相角的影响图 Figure 14 Influence graph of DG volume on phase angle of closing loop |
通过对分布式电源(DG)的容量大小、距离合环点的远近、合环时间的长短与合环冲击电压关系的分析,进而对系统的继电保护整定值重新设置,就能在保证系统安全和电能质量的前提下,尽量使合环相角差范围扩大,这将更有利于系统的安全和经济性运行.
4 结论配电网中含有分布式电源时,由于合环时潮流分布发生了改变,相角差不再仅仅局限于20°,而是应该根据线路继电保护装置的整定值进行重新计算,并且配合以下一种或者几种方法来减小合环电压,达到可以合环的安全电压值:
1) 含分布式电压的配电网合环过程中,随着分布式电源的容量不断增加,相同合环时间或者相角差下的合环电压越来越大,所以在合环操作过程中,需要依靠快速合解环功能的投切装置来缩短操作时间,降低合环过程中的电压.
2) 含分布式电源的配电网中,靠近合环点或者励磁系统不先进的分布式电源对于合环电压的影响要远远大于远离合环点或者励磁系统比较先进的分布式电源,前者应该优先引入电抗器或者是储能设备,来降低其对合环电压的影响.
3) 合解环操作时,为了达到增加合环相角差或者是降低合环冲击电压的目的,保证合环的成功,可以优先考虑解列大容量、励磁控制系统不先进或者靠近合环点的分布式电源.
4) 配电网规划分布式电源时,应该尽量少引入励磁控制调节比较差或者不含励磁控制调节的分布式电源.对于已经引入励磁控制调节比较差或者不含励磁控制调节的分布式电源的配电网,在选择合解环点时应当尽量远离这类分布式电源并且在合解环操作前降低其输出功率甚至可以提前解列.
5) 配电网中引入新的分布式电源前,需要通过计算对分布式电源的容量、类型、位置进行计算规划,这样有利于使配电网的安全性和经济性达到最优.
本文通过研究分布式电源对配电网合环操作的影响,对不同情况下的合环操作提出合理的决策和执行方案,为改进含分布式电源的配电网合环操作的安全性和经济性提供理论依据.
| [1] |
肖白, 邢文洋, 穆钢, 等. 城市中压配电网合环电流分析[J].
东北电力大学学报, 2013, 33(1): 84–88.
Xiao Bai, Xing Wenyang, Mu Gang, et al. Analysis of the closing loop current for urban medium-voltage distribution networks[J]. Journal of Northeast Dianli University, 2013, 33(1): 84–88. |
| [2] |
刘健, 孙泉, 张小庆, 张志华. 配电网合环分析与合环条件判断[J].
电力系统自动化, 2014, 38(11): 130–135.
Liu Jian, Sun Quan, Zhang Xiaoqing, Zhang Zhihua. Analysis and criteria for loop closing operation for distribution grids[J]. Automation of Electric Power Systems, 2014, 38(11): 130–135. |
| [3] |
苑捷. 配电网合环操作的研究[J].
陕西电力, 2007, 35(4): 36–39.
Yuan Jie. Research on loop closing operation in distribution network[J]. Shaanxi Electric Power, 2007, 35(4): 36–39. |
| [4] |
甘国晓, 王主丁, 李瑞, 等. 电网合环冲击电流计算方法及其简化计算公式[J].
电力系统自动化, 2014, 38(20): 115–120.
Gan Guoxiao, Wang Zhuding, Li Rui, et al. Methods and simplified formulas for calculating surge current from loop closing in distribution networks[J]. Automation of Electric Power System, 2014, 38(20): 115–120. |
| [5] |
汲亚飞, 赵江河. 辐射型配电网合环稳态电流计算方法研究[J].
电力系统保护与控制, 2009, 37(12): 15–19.
Ji Yafei, Zhao Jianghe. Calculation of the loop closing steady-state current in radial power distribution network[J]. Power System Protection and Contorl, 2009, 37(12): 15–19. |
| [6] | Srinivasa Rao R, Narasimham SVL, Ramalinga RAju M, et al. Distribution network reconfiguration using genetic algorithms with sequential encoding:subtractive and additive approaches[J]. IEEE Transactions on Power System, 2011, 26(3): 1080–1088. DOI:10.1109/IDAMS.2010.2076839 |
| [7] | Anderson P M, Farmer R G. History of the power system dynamic performance committee 1967-2007. .Available:http://ewh.ieee.org/soc/pes/psdpc/. |
| [8] | IEEE/CIGRE Joint Task Force on Stability Terms and Definitions. Definition and classification of power system stability[J]. IEEE Transactions on Power System, 2004, 19(2): 1387–1401. |
| [9] |
连鸿波, 顾振中, 余浩茹, 等. 10 kV配电网合环倒负荷研究[J].
华东电力, 2012, 40(6): 1045–1049.
Lian Hongbo, Gu Zhenzhong, Yu Haoru, et al. Closed loop load transfer in 10 kV distribution network[J]. East China Electric Power, 2012, 40(6): 1045–1049. |
| [10] |
郭雪丽, 齐昌宵, 史洪彬. 关于城市配网合环操作的研究[J].
电气应用, 2012, 31(23): 18–24.
Guo Xueli, Qi Changxiao, Shi Hongbin. Research on loop closing operation in distribution netwok[J]. Electrotechnical Application, 2012, 31(23): 18–24. |
| [11] |
李江华. 浅析10 kV配网合环产生环流的原因及预防措施[J].
电网技术, 2006, 30(sup.): 199–201.
Li Jianghua. Simple analysis of the reason and protective step of 10 kV distribution network causing circumfluence[J]. Power System Technology, 2006, 30(sup.): 199–201. |
| [12] |
邹俊雄, 周冠波, 付轲, 等. 10 kV配网合环转电计算模型与试验分析[J].
电力系统保护与控制, 2010, 38(8): 144–148.
Zou Junxiong, Zhou Guanbo, Fu Ke, et al. Electromagnetic loop closing calculation model and experimental analysis of 10 kV distribution network[J]. Power System Protection and Control, 2010, 38(8): 144–148. |
| [13] |
夏翔, 周昱甬, 邱伟成. 地区弱电磁环网合环潮流探讨[J].
继电器, 2004, 32(23): 28–31.
Xia Xiang, Zhou Yuyong, Qiu Weicheng. Power flow analysis of closing interconnection switches for weakly meshed networks in regional grid[J]. Relay, 2004, 32(23): 28–31. |
| [14] |
郑瑞晨, 李晓柯, 李祥发. 配电网合环冲击电流的暂态过程分析与仿真[J].
机电工程, 2010, 27(5): 68–70.
Zhen Ruichen, Li Xiaoke, Li Xiangfa. Transient analysis and simulation of surge current due to closing loop in distribution Network[J]. Journal of Mechanical and Electrical Engineering, 2010, 27(5): 68–70. |
| [15] | Lasseter R H.“Control and design of microgrid components,”PSERC final project reports .http://www.pserc.org/cgi-pserc/getbig/publicatio/reports/2006report/lasseter_microgridcontrol_final_project_report.pdf. |
| [16] |
房静静, 吉兴全, 高鹏, 等. 分布式电源的配电网合环短路电流分析[J].
山东科技大学学报, 2013, 32(2): 103–108.
Fang Jingjing, Ji Xingquan, Gao Peng, et al. Analysis of loop-closing short-circuit current with distributed generation combination in distribution network[J]. Journal of Shandong University of Science and Technongy, 2013, 32(2): 103–108. |
| [17] |
邬溢生. 10 kV 配电网络合环转供电操作的可行性分析及实际应用[J].
中国新技术新产品, 2013, 20(10): 159–160.
Wu Yisheng. Feasibility analysis and real application of closing loop operation of 10 kV distribution network[J]. China New Technologies and Products, 2013, 20(10): 159–160. |
 2016, Vol. 49
2016, Vol. 49




