武汉大学学报(工学版)   2016, Vol. 49 Issue (4): 487-491

文章信息

高兴, 刘士和, 王之婳
GAO Xing, LIU Shihe, WANG Zhihua
圆管中湍旋流的精细模拟与总流机械能损失
Refined simulation of turbulent swirling pipe flow and investigation into mechanical energy loss of total flow
武汉大学学报(工学版), 2016, 49(4): 487-491
Engineering Journal of Wuhan University, 2016, 49(4): 487-491
http://dx.doi.org/10.14188/j.1671-8844.2016-04-002

文章历史

收稿日期: 2016-03-20
 Abstract              PDF               Figures               Tables
引用本文 0
高兴, 刘士和, 王之婳. 圆管中湍旋流的精细模拟与总流机械能损失[J]. 武汉大学学报(工学版), 2016, 49(4): 487-491.
GAO Xing, LIU Shihe, WANG Zhihua. Refined simulation of turbulent swirling pipe flow and investigation into mechanical energy loss of total flow[J]. Engineering Journal of Wuhan University, 2016, 49(4): 487-491.
圆管中湍旋流的精细模拟与总流机械能损失
高兴1, 刘士和1, 王之婳2     
1. 武汉大学水利水电学院，湖北 武汉 430072;
 2. 同济大学，上海 200092
收稿日期: 2016-03-20
作者简介: 高兴（1990-），男，硕士研究生，主要从事水力学及河流动力学研究，E-mail: whugaoxing@163.com.
通讯作者: 刘士和（1962-），男，教授，博士生导师，主要从事水力学及河流动力学研究，E-mail:shihe3086@163.com
基金项目: 水利部公益性行业科技专项经费（编号：201101005）.
摘要: 湍旋流广泛存在于自然界与工程实际中，其流动特性及机械能损失的研究具有很高的理论意义与工程价值.通过开发数值旋流生成装置，采用雷诺应力模式封闭雷诺时均方程及有针对性的网格布置，实现了对圆管中湍旋流的三维精细模拟.计算成果表明：1）湍旋流的旋流数沿程呈分段指数衰减，其衰减系数有随雷诺数的增加而减小的趋势；2）湍旋流的切向时均流速沿径向的变化在旋流数较大时可近似用组合涡的速度分布来描述；3）与一般恒定均匀圆管湍流的总流机械能损失系数相比，带有旋流的圆管湍流的总流机械能损失系数要普遍大于前者，且旋流数越大，总流机械能损失系数越大.
关键词： 湍旋流     数值模拟     机械能损失    
Refined simulation of turbulent swirling pipe flow and investigation into mechanical energy loss of total flow
GAO Xing1, LIU Shihe1, WANG Zhihua2     
1. School of Water Resources and Hydropower, Wuhan University, Wuhan 430072, China;
 2.  Tongji University，Shanghai 200092，China
Abstract: The turbulent swirling flow is common in nature and engineering practice. The investigation on the flow characteristics and mechanical energy loss of turbulent swirling flow is of great theoretical significance and engineering value. A refined three-dimensional simulation of the swirling flow in a circular tube is conducted by developing a numerical swirl generating device, using Reynolds stress model to close Reynolds equation and targeted grid layout. The calculation results show that: 1) The swirl number of turbulent swirling flow which stands for the swirl intensity decreases along the pipe, which can be described by a segmented exponential formula. Besides, the decay factor decreases with the increase of Reynolds number generally. 2) The radial distribution of mean tangential velocity in the swirling flow can be roughly approximated with the velocity distribution of the compound vortex when the swirl number is large. 3) Compared to the steady uniform pipe flow, the mechanical energy loss coefficient of turbulent swirling flow is generally larger and even larger with the swirl number increasing.
Key words: turbulent swirling flow     numerical simulation     mechanical energy loss    

旋流是一种特殊的流动，且基本上呈湍流状态.旋风分离器、强化传热管、水力旋流器、水轮机尾水管等装置中均有旋流的身影；水利工程中利用旋流排沙、排螺、泄洪消能等也取得了不错的效果.研究旋流的流动特性不仅具有较高的工程价值，更能够加深人们对其流动机理与流动特性的认识.根据旋流产生装置及速度分布的不同，人们一般将其分为3类：曲线流动、旋转流动和涡旋流动[1].曲线流动利用静止边界的弯曲度，如弯管、螺旋槽纹管等来产生旋流；旋转流动借助旋转装置产生旋流[2]；涡旋流动则采用切向进流、或在进口段安装导叶片[3]等来产生旋流，由于旋流强度沿程衰减，这种流动也常被称为衰减旋流.

对旋流特性已分别采用实验研究和数值模拟开展过大量的研究工作.从实验研究成果来看，Kitoh[3]等人对旋流管沿程各断面上的切向流速、轴向流速沿径向的变化进行了实测，获得了旋流数沿程呈指数衰减等概念性认识.从数值模拟成果来看，Gibson等[4]、Hirai等[5]分别采用雷诺应力模型封闭雷诺时均方程，对旋流喷射和两同心圆柱体间的旋流进行模拟.总体上来看，现阶段的数值模拟主要针对旋转流动及涡旋流动，特别是对旋转蜂窝型管道产生的旋流[6, 7]和进口段安装导叶片产生的涡流[8]，且模拟范围多局限在长直管道中，进口条件则由实验成果提供，对进口段的数值旋流生成装置尚未开展过研究；现阶段数值模拟还多限于简化的二维轴对称模拟[6~9]，鲜有对圆管中湍旋流的三维数值模拟成果.此外，尚未对旋流运动的总流机械能损失进行过研究.有鉴于此，本文进行以下探究：1)开发数值旋流生成装置，采用雷诺应力模式封闭雷诺时均方程，采用结构化网格剖分计算区域，对圆管内的湍旋流进行三维精细模拟，并对不同雷诺数条件下旋流数(表征旋流强度)的沿程衰减等进行了分析；2)根据前述精细模拟成果，采用最新提出的总流机械能损失计算式对圆管中湍旋流的总流机械能损失进行计算，得到总流机械能损失系数随雷诺数与旋流数的变化特性.

1 数学模型与计算 1.1 控制方程

采用雷诺时均方程描述圆管中湍旋流的运动,控制方程中的连续方程与运动方程：

$\frac{\partial \overline{{{u}_{i}}}}{\partial {{x}_{i}}}=0$    (1)
$\frac{\partial \overline{{{u}_{i}}}}{\partial t}+\frac{\partial (\overline{{{u}_{i}}}\overline{{{u}_{j}}})}{\partial {{x}_{j}}}={{f}_{i}}-\frac{1}{\rho }\frac{\partial \overline{p}}{\partial {{x}_{i}}}+\upsilon \frac{{{\partial }^{2}}\overline{{{u}_{i}}}}{\partial {{x}_{j}}\partial {{x}_{j}}}+\frac{\partial }{\partial {{x}_{j}}}(-\overline{u_{i}^{'}u_{j}^{'}})$    (2)

式中：$\overline{{{u}_{i}}}$、$\overline{p}$分别为时均流速和时均压强；ρ、ν为水体密度与运动粘性系数；$-\overline{u_{i}^{'}u_{j}^{'}}$为雷诺应力，为一待封闭项.考虑到雷诺应力模式可以反映流线曲率、旋转湍流中非局部效应等的影响，与其他模式相比能更好地预测复杂湍流，因此采用该模式封闭雷诺时均方程，雷诺应力的控制方程为

$\begin{align} & \frac{\partial \overline{{{u}_{i}}^{'}{{u}_{j}}^{'}}}{\partial t}+\overline{{{u}_{m}}}\frac{\partial \overline{{{u}_{i}}^{'}{{u}_{j}}^{'}}}{\partial {{x}_{m}}}=\frac{\partial }{\partial {{x}_{m}}}({{C}_{s}}\frac{{{k}^{2}}}{\varepsilon }\frac{\partial \overline{{{u}_{i}}^{'}{{u}_{j}}^{'}}}{\partial {{x}_{m}}}+\nu \frac{\partial \overline{{{u}_{i}}^{'}{{u}_{j}}^{'}}}{\partial {{x}_{m}}})+{{G}_{ij}}-\frac{2}{3}\varepsilon {{\delta }_{ij}} \\ & -{{C}_{1}}\frac{\varepsilon }{k}(\overline{{{u}_{i}}^{'}{{u}_{j}}^{'}}-\frac{2}{3}k{{\delta }_{ij}})-{{C}_{2}}({{G}_{ij}}-\frac{2}{3}{{G}_{k}}{{\delta }_{ij}}) \\ \end{align}$    (3)

式中：${{G}_{ij}}=-\left( \overline{u_{i}^{'}u_{m}^{'}}\frac{\partial \overline{{{u}_{j}}}}{\partial {{x}_{m}}}+\overline{u_{j}^{'}u_{m}^{'}}\frac{\partial \overline{{{u}_{i}}}}{\partial {{x}_{m}}} \right)$；湍动能k与湍动能耗散率ε的控制方程为

$\left\{ \begin{array}{*{35}{l}} \frac{\partial k}{\partial t}+\overline{{{u}_{j}}}\frac{\partial k}{\partial {{x}_{j}}}={{G}_{k}}+\frac{\partial }{\partial {{x}_{j}}}((\nu +\frac{{{\nu }_{t}}}{{{\sigma }_{k}}})\frac{\partial k}{\partial {{x}_{j}}})-\varepsilon \\ \frac{\partial \varepsilon }{\partial t}+\overline{{{u}_{j}}}\frac{\partial \varepsilon }{\partial {{x}_{j}}}={{C}_{\varepsilon 1}}\frac{\varepsilon }{k}{{G}_{k}}+\frac{\partial }{\partial {{x}_{j}}}((\nu +\frac{{{\nu }_{t}}}{{{\sigma }_{\varepsilon }}})\frac{\partial \varepsilon }{\partial {{x}_{j}}})-{{C}_{\varepsilon 2}}\frac{{{\varepsilon }^{2}}}{k} \\ \end{array} \right.$    (4)

式中：${{G}_{k}}=-\overline{u_{i}^{'}u_{j}^{'}}\frac{\partial \overline{{{u}_{i}}}}{\partial {{x}_{j}}}$为湍动能产生项；C1、C2、Cs及Cε1、Cε2、σk、σε均为经验系数，其取值详见文献[10].

1.2 控制方程的离散

采用有限体积法离散控制方程，其中对流项采用QUICK格式[11]，此格式用于六面体时具有3阶精度，用于混合网格或四面体时具有2阶精度；扩散项采用基于节点的格林-高斯法(Green-Gauss node-based)，其求解更精确，能最小化伪扩散；压强项采用PRESTO格式，该格式对于高旋流、压强急剧变化或流线剧烈弯曲的复杂流动计算效果更好.压强-速度耦合采用SIMPLEC方法，其收敛性较优.

1.3 边界条件

进口边界为均匀来流，在其上给出速度分布；出口边界按照充分发展流动考虑.

1.4 关键问题的处理

在数值计算中，采用非平衡壁函数反映壁面对流动的作用.其他关键问题的处理包括数值旋流生成装置的开发与网格的剖分.

1.4.1 数值旋流生成装置的开发

类似Kitoh[3]等人的实验装置，采用径向导叶片通过数值方法来生成旋流，相关装置见图 1.其工作原理为：水流从进口段流入，受固壁作用只能沿导叶片间的流道流动，沿轴向的流线因此发生弯曲，水体获得切向速度，进而生成旋流并进入管段.

图 1 数值旋流生成装置总图(单位：mm) Figure 1 Sketch of numerical swirling flow generating device (unit:mm)
图选项

数值旋流生成装置为1个长200 mm、内径140 mm的圆筒，内部设置有1个起旋装置.该装置由24片平直导叶片组成，其呈放射状布置于圆盘上，翼弦长65 mm，叶片安装角取为60°(图 2).当安装角为0°时，管道中的流动即为常见的无螺旋的湍管流.为保持水流运动平稳，在圆盘中间还设置1个锥台形的整流元件，其高32 mm，底面半径为60 mm.

图 2 起旋装置 Figure 2 Swirl generator
图选项
1.4.2 计算网格

为实现对圆管中湍旋流的精细模拟，对数值旋流生成装置与管段的网格生成进行了细致处理，见图 3.数值旋流生成装置由于结构复杂，导叶及其附近采用四面体网格，其贴体性较好，其余部分则采用结构化网格；管段是标准的圆柱体，通过对起始断面进行分割，分块生成结构化网格，其方法为：考虑到近壁区物理量梯度很大[12]，采用边界层网格；与无螺旋的湍管流相比，湍旋流(有螺旋的湍管流)在管轴中心附近的速度变化较为剧烈，因此需对网格进行加密处理.起始断面剖分完成后，采用Cooper方法，沿圆柱的轴向扫掠即可生成全柱体的网格，其均为质量较高的六面体网格，相对于四面体网格，网格数量少，计算效率高，收敛速度会更快.

图 3 网格布置图 Figure 3 Grid layout
图选项
1.5 验证计算

Kitoh[3]等较为系统地实测了湍旋流时均流速等物理量，本文采用其实验成果进行验证计算.图 4给出离进口距离x/d分别为5.7、19和25.7的3个轴向位置处轴向时均流速、切向时均流速沿断面分布的计算成果与实测成果的比较.由图可知，两者基本一致.

图 4 验证计算结果 Figure 4 Verification results
图选项
2 湍旋流运动的精细模拟

采用前述数学模型分别对雷诺数在5×104～1.2×105范围内共7个工况的湍旋流进行模拟计算.下面根据计算成果就旋流数与时均流场的特性进行分析.

2.1 旋流数

在工程实际中，常需了解旋流强度的沿程衰减过程，但采用何种参数来表征旋流强度，则是早期研究的难点之一，不少早期研究者曾采用旋流装置的几何参数，如旋流片的H/D或进口导叶片的安装角，这明显不利于不同实验成果之间的比较.随后人们提出了无量纲角动量通量参数，也即旋流数Ω，其不仅具有确定的物理意义，也具有普适性.旋流数的定义为[13]

$\Omega =2\pi \rho \int_{0}^{{{r}_{0}}}{\overline{{{u}_{z}}}}\overline{{{u}_{\theta }}}{{r}^{2}}dr/\rho \pi r_{0}^{3}U_{_{m}}^{2}$    (5)

式中：$\overline{{{u}_{z}}}$、$\overline{{{u}_{\theta }}}$、Um分别是轴向时均流速、切向时均流速与合速度；r和r0分别为径向距离和管径；ρ为水体密度.

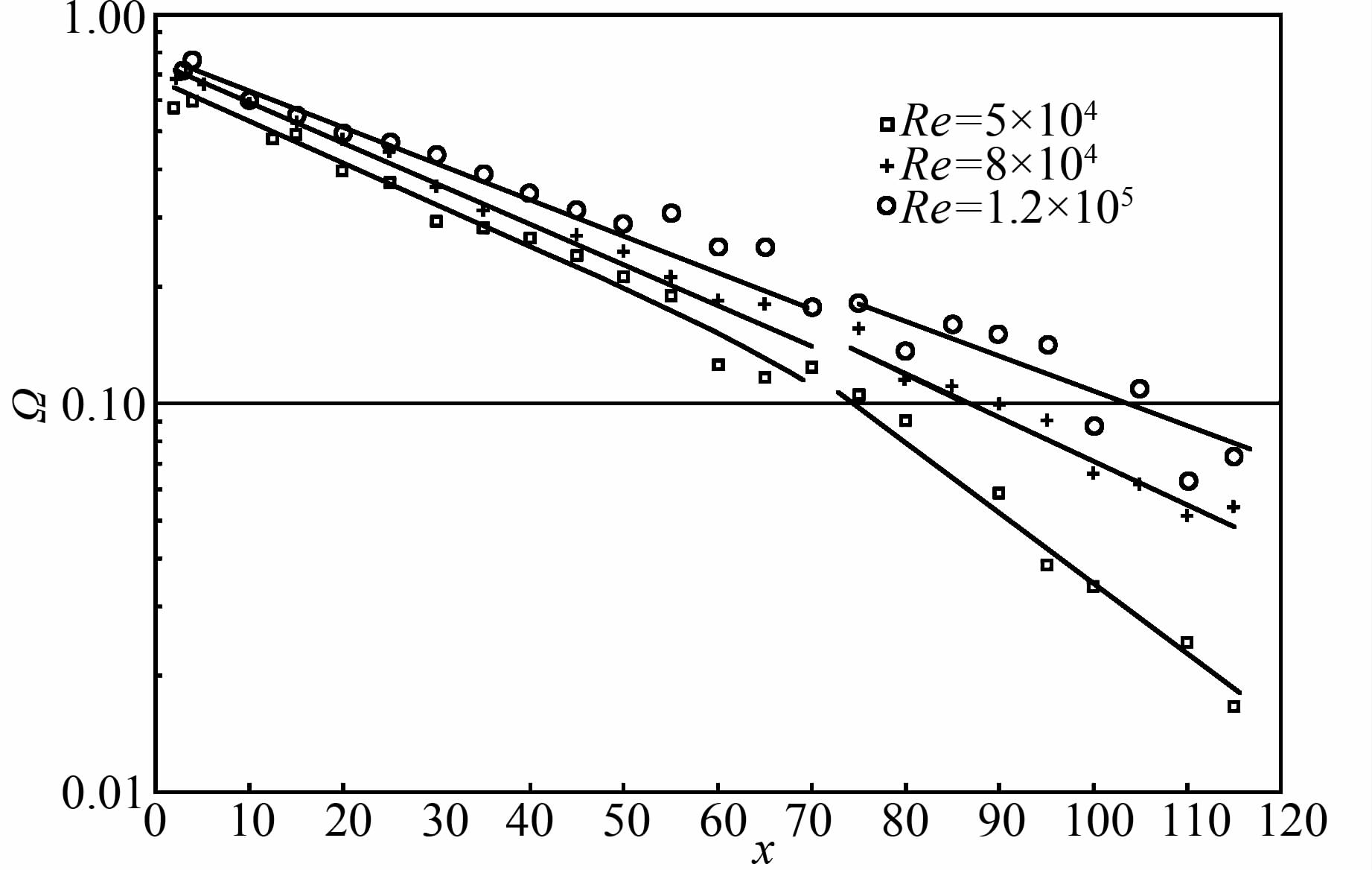
在一般的平直管道中，由于壁面摩擦其旋流强度总是沿程衰减的，图 5给出了不同雷诺数下旋流数的沿程衰减情况.由图可知：1)旋流数大致以分段指数形式沿程衰减，分界点在Ω=0.1～0.3，当Re=5×104时，分界点处Ω=0.1，这与Kitoh[3]的实验结果基本一致；但雷诺数越大，分界点处的特征旋流数亦随之增大.2)如以$\Omega ={{\Omega }_{0}}\exp (-\alpha \frac{x}{d})$来表示旋流数的沿程变化，式中α将为衰减系数，则α随雷诺数的增加而减小.

图 5 不同雷诺数下旋流数Ω的沿程变化 Figure 5 Variation of swirl number under different Reynolds numbers
图选项
2.2 时均流速

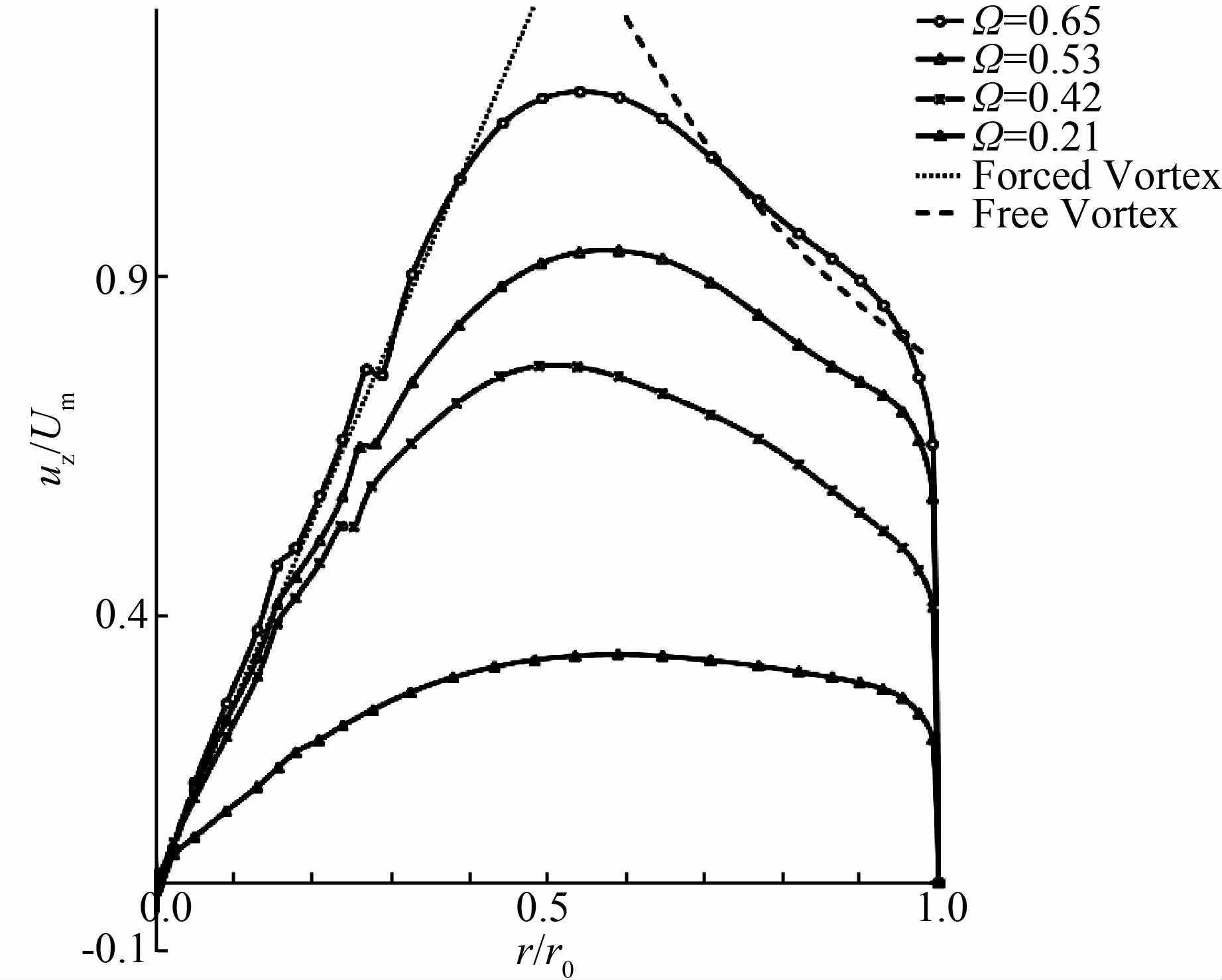
与轴向、切向时均流速相比，管内旋流的径向时均流速极小，几乎可以忽略.因此在研究旋流时均流速分布时，人们通常只关心轴向时均流速和切向时均流速，尤其是切向时均流速在流场中的分布特征.Kitoh[3]将切向时均流速沿径向细分为核心区、环形区和近壁区3个区，并将环形区和核心区的时均流速分布近似用自由涡和强迫涡运动来表征.图 6给出了几个不同轴向位置处切向时均流速沿径向的变化，并同时给出了兰金(Rankine)组合涡(强迫涡和自由涡的组合)的切向流速分布，由图可知：1)当旋流数较大时，除了交汇点附近外，组合涡的速度分布特性与计算成果较为吻合；2)随着旋流数的减小，核心区和环形区的分界逐渐变得模糊.

图 6 Re=1.0×105切向速度沿径向分布 Figure 6 Radial distribution of tangential velocity for Re=1.0×105
图选项
3 圆管中湍旋流的总流机械能损失

在水力学中，人们均采用伯努利方程来描述能量(机械能)的沿程变化，由于该方程系以重力场中理想不可压缩流体恒定流沿流线的伯努利积分为基础，通过经验修正来得到，其既无法直接考虑紊动的影响，也给不出能量损失的显式表达式，以至于在衡量旋流消能效果时，不得不通过试验研究来确定能量损失.笔者曾直接从粘性不可压缩流体运动的控制方程出发，得到了新的总流机械能方程及总流机械能损失显式表达式，解决了以上问题.得到的总流机械能损失hw的计算式为[14, 15]

$\rho gQ{{h}_{w}}=\iiint\limits_{V}{\left[ 2\mu \overline{{{s}_{ij}}}-\rho \overline{u_{i}^{'}u_{j}^{'}} \right]\overline{{{s}_{ij}}}dV}$    (6)

式中：Q、g、μ分别为流量、重力加速度与水体的动力粘性系数；$\overline{{{s}_{ij}}}$为时均变形速度张量.

根据前述精细模拟成果计算出总流机械能损失，采用达西-威斯巴赫公式估算总流机械能损失系数λ，并用不存在旋流的圆管湍流的总流机械能损失系数将带有旋流的圆管湍流的总流机械能损失系数(采用Blasius公式${{\lambda }_{0}}\text{=}\frac{0.3164}{{{\operatorname{Re}}^{0.25}}}$估算)归一化，其成果见图 7，相应的拟合关系式为

$\lambda (\operatorname{Re},\Omega )=0.3164\frac{\exp (\beta \Omega )}{{{\operatorname{Re}}^{0.25}}}$    (7)
图 7 λ/λ0随Ω的变化 Figure 7 Variation of λ/λ0 with Ω
图选项

式中，β为常数，本文中β=2.85.

由式(7)可知：带有旋流的圆管湍流的总流机械能损失系数要普遍大于不存在旋流的圆管湍流的总流机械能损失系数且旋流度越大，前者的总流机械能损失系数也越大.

3 结论

1) 圆管中湍旋流的旋流度沿程呈分段指数衰减，衰减系数有随雷诺数的增加而减小的趋势；其切向时均流速沿径向的变化在旋流数较大时可近似用组合涡的速度分布来描述，随着旋流数的减小强迫涡引起的速度分布将逐渐占优.

2) 与不存在旋流的一般圆管湍流的总流机械能损失系数相比，带有旋流的圆管湍流的总流机械能损失系数也随雷诺数的增加而减小，但后者要普遍高于前者，且旋流数越大，相应的总流机械能损失系数也越大.

参考文献
[1] Mehmet Yilmaz, Omer Comakli, Sinan Yapici, et al. Heat transfer and friction characteristics in decaying swirl flow generated by different radial guide vane swirl generators[J]. Energy Conversion and Management, 2003, 44(2): 283–300. DOI:10.1016/S0196-8904(02)00053-5
[2] Binnie A M. Experiments on the slow swirling flow of a viscous liquid through a tube[J]. The Quarterly Journal of Mechanics and Applied Mathematics, 1957, 10(3): 276–290. DOI:10.1093/qjmam/10.3.276
[3] Osami Kitoh. Experimental study of turbulent swirling flow in a straight pipe[J]. Journal of Fluid Mechanics, 1991, 225: 445–479. DOI:10.1017/S0022112091002124
[4] Gibson M M, Younis B A. Calculation of swirling jets with a Reynolds stress closure[J]. Physics of Fluids (1958-1988), 1986, 29(1): 38–48.
[5] Hirai S, Takachi T, Tanaka K, et al. Effect of swirl on the turbulent transport of momentum in a concentric annular with a rotating cylinder[J]. Trans. JSME. B, 1987, 53: 432.
[6] Najafi A F, Saidi M H, Sadeghipour M S, et al. Numerical analysis of turbulent swirling decay pipe flow[J]. International Communications in Heat and Mass Transfer, 2005, 32(5): 627–638. DOI:10.1016/j.icheatmasstransfer.2004.10.014
[7] Andrew Escue, Jie Cui. Comparison of turbulence models in simulating swirling pipe flows[J]. Applied Mathematical Modelling, 2010, 34(10): 2840–2849. DOI:10.1016/j.apm.2009.12.018
[8] Najafi A F, Mousavian S M, Amini K. Numerical investigations on swirl intensity decay rate for turbulent swirling flow in a fixed pipe[J]. International Journal of Mechanical Sciences, 2011, 53(10): 801–811. DOI:10.1016/j.ijmecsci.2011.06.011
[9] 李会雄, 周芳德, 陈学俊. 管内湍流旋流的数值计算[J]. 应用力学学报, 1994(2): 19–24.
Li Huixiong, Zhou Fangde, Chen Xuejun. Numerical calculation of turbulent swirling flow in a straight pipe[J]. Chinese Journal of Applied Mechanics, 1994(2): 19–24.
[10] 刘士和, 刘江, 罗秋实, 等. 工程湍流[M]. 北京: 科学出版社, 2011: 70-80.
Liu Shihe, Liu Jiang, Luo Qiushi, et al. Engineering Turbulence[M]. Beijing: Science Press, 2011: 70-80.
[11] Wang J, Priestman G H, Tippetts J R. Modeling of strongly swirling flows in a complex geometry using unstructured meshes[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2006, 16(8): 910–926.
[12] Ahmadvand M, Najafi A F, Shahidinejad S. An experimental study and CFD analysis towards heat transfer and fluid flow characteristics of decaying swirl pipe flow generated by axial vanes[J]. Meccanica, 2010, 45(1): 111–129. DOI:10.1007/s11012-009-9228-9
[13] Yajnik K S, Subbaiah M V. Experiments on swirling turbulent flows. Part 1. Similarity in swirling flows[J]. Journal of Fluid Mechanics, 1973, 60(04): 665–687. DOI:10.1017/S0022112073000406
[14] Liu Shihe, Xue Jiao, Fan Min. The calculation of mechanical energy loss for incompressible steady pipe flow of homogeneous fluid[J]. Journal of Hydrodynamics, Ser. B, 2013, 25(6): 912–918. DOI:10.1016/S1001-6058(13)60440-0
[15] 薛娇, 刘士和. 管流与明渠流层流的总流机械能损失及机械能损失计算[J]. 水动力学研究与进展A辑, 2016, 31(1): 9–14.
Xue Jiao, Liu Shihe. The mechanical energy equation and the calculation of mechanical energy loss for total laminar flow in pipes and open channels[J]. Chinese Journal of Hydrodynamics, 2016, 31(1): 9–14.