文章信息
- 陈瑞瑞, 张海林
- CHEN Ruirui, ZHANG Hailin
- 基于Ricean因子的无人机自适应MIMO通信方案
- Ricean factor based adaptive MIMO scheme for unmanned aerial vehicle
- 武汉大学学报(工学版), 2017, 50(3): 460-464
- Engineering Journal of Wuhan University, 2017, 50(3): 460-464
- http://dx.doi.org/10.14188/j.1671-8844.2017-03-022
-
文章历史
- 收稿日期: 2016-01-04
随着无人机应用的日益广泛,如何提升通信容量已成为无人机发展所面临的主要问题.而MIMO技术可以在相同带宽下成倍地提高通信容量[1].因此,如何将MIMO技术应用于无人机来提高通信容量已成为近年来的一个研究热点.文献[2]研究了无人机地空通信场景下如何通过合理配置天线间距以实现无人机的MIMO通信.文献[3, 4]表明,在较高相关性的MIMO信道下,波束赋形技术(beamforming, BF)可以获得较高的通信容量.而在散射分量丰富的MIMO信道下,空分复用技术(spatial multiplexing, SM)可以获得较高的通信容量[5].因此,在信道相关性变化较大时,相较于固定的传输方案,采用基于BF和SM的自适应MIMO方案会获得较大的容量提升[6, 7].而无人机在整个飞行过程中会随通信环境的不同而引起较大的Ricean因子变化[8].
因此,为了在低复杂度条件下提升无人机通信容量,本文提出了一种基于Ricean因子的自适应MIMO通信方案.该方案可以根据不同通信环境下的Ricean因子自适应切换MIMO通信方式,从而提高无人机通信容量.相较于最优MIMO方案,自适应方案降低了复杂度.本文将主要研究无人机的途中飞行场景.
1 系统模型及无人机信道特点 1.1 系统模型研究无人机环境下的MIMO通信,其发射天线数和接收天线数分别为Nt和Nr.接收信号可以表示为
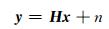 (1)
(1)
式中:y∈CNr×1,表示接收信号向量;H∈CNr×Nt,表示无人机MIMO信道矩阵;x∈CNt×1,表示发射信号向量;n∈CNr×1,表示均值为0的加性高斯白噪声,且ξ{nnH}=σn2INr,σn2表示噪声功率,INr表示Nr×Nr的单位矩阵.
无人机MIMO信道由视距路径和非视距路径组成,其信道矩阵H可以表示为
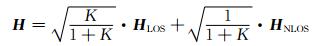 (2)
(2)
式中:HLOS和HNLOS分别表示H的视距(LOS)分量和非视距(NLOS)分量,K表示莱斯(Ricean)因子.K取值越大表明信道的相关性越强,反之则独立性越强.
1.2 无人机信道特点无人机通信地面站通常采用定向高增益的测控天线,故无人机和地面站之间会存在较强的LOS分量.同时,无人机信道也存在着由于不同传播路径所引起的NLOS分量.因此,我们将无人机信道看作Ricean信道是合理的.
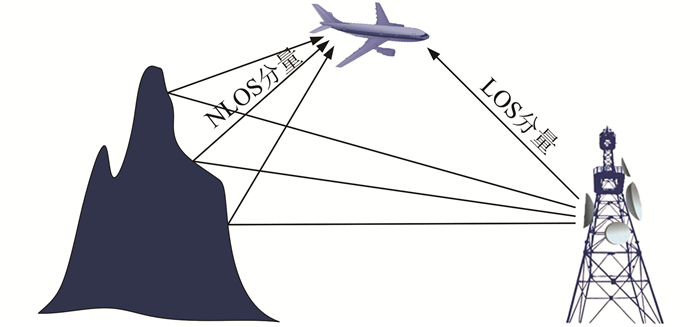
无人机通信信道和无人机的飞行状态紧密相关.根据无人机的飞行状态可以将信道分为两种不同的场景:途中飞行场景和任务执行场景.本文主要讨论途中飞行场景,如图 1所示.
|
| 图 1 途中飞行场景 Figure 1 En-route scenarios |
途中飞行场景是指无人机从地面站向任务地点飞行和返回的过程.在这一场景下,LOS分量可以近似认为和无人机的飞行方向是在同一个方向或者是反方向上.文献[8]表明,由于其他地貌或物体散射所引起的NLOS分量的波束宽度可看作3.5°并在此角度范围内均匀分布,且在途中飞行场景下,Ricean因子K的取值范围为2~20 dB.
2 无人机MIMO通信方案 2.1 无人机MIMO通信的最优方案无人机MIMO通信的遍历容量可以用C来表示.C的表达式可以写为
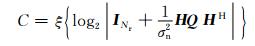 (3)
(3)
式中:Q是发射信号的协方差矩阵;ξ(·)表示求数学期望;|·|和(·)HHξ分别表示求一个矩阵的行列式和共轭转置.对无人机MIMO信道进行奇异值分解可得:H=UΣVH.相似地,发射信号的协方差矩阵Q也可以分解为:Q=VΛqVH,其中Λq为功率对角矩阵.在一定的功率限制下tr(Λq)=Pt,可获得最大容量的传输方案为
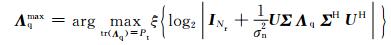 (4)
(4)
式中:tr(·)表示矩阵的迹.从公式(4) 可以看出,最优的功率分配方案可以在所有满足功率限制的输入信号方案中进行选择.也可以很清楚地看到最优传输方案是由信道矩阵的特征值所决定的.因此,对于给定的信道矩阵H,Λqmax需要在整个满足功率限制tr(Λq)=Pt的可行传输方案中进行最优化的选择.然而,因为这一最优化过程有着较高的复杂度,故在实际的无人机通信中是不容易实现的.因此,我们采用BF和SM两种技术的自适应切换方案来降低复杂度.下面我们对这两种技术分别进行分析.
2.2 BF和SM方案的容量对于BF技术来说,输入信号的协方差矩阵可以由下式表示:
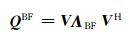 (5)
(5)
式中:ΛBF=diag(0…, Pt, …, 0), 是一个对角矩阵,Pt是唯一的一个非零的对角元素.将公式(5) 以及ΛBF代入公式(3), 我们可以获得BF的遍历容量表达式:
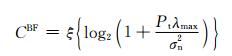 (6)
(6)
其中:λmax为矩阵HHH的最大特征值,其对应着状态最好的子信道.
要注意到对于BF传输方案,在接收端我们采用最大比合并法(MRC).
对于SM技术来说,发射信号的协方差矩阵为QSM=(Pt/Nt)·INt.SM技术的遍历容量如下式所示:
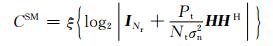 (7)
(7)
在本文中,我们运用线性接收机接收SM方案发送的信号,此时无人机MIMO信道可以看做Nt个平行的子信道.因此,公式(7) 也可以写作
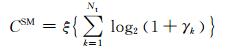 (8)
(8)
式中:γk为第k个子信道的条件性后处理信噪比.在本文中,我们考虑Nt≤Nr时的迫零检测线性接收机.γk由下式给定:
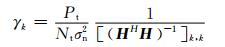 (9)
(9)
式中:[·]k, k为矩阵的第k个对角元素.
2.3 BF与SM的容量交点通过比较公式(6) 和(7),我们可以看出:BF技术更适用于较高相关性的无人机通信信道,而SM方案在独立信道下的性能会更好.为了从数学上更好地解释无人机信道相关性对于BF和SM方案的性能影响,我们将推导出BF和SM方案的容量交点.为了便于处理,我们运用瞬时信道容量公式来完成交点的推导.因此,我们给出BF和SM方案的瞬时信道容量:
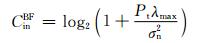 (10)
(10)
和
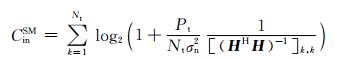 (11)
(11)
简洁起见,定义G=HHH,ρ=Pt/σn2.运用恒等式[G-1]k, k=|Gkk|/|G|,Gkk为矩阵G去掉第k行第k列后所留下的矩阵.因此,公式(11) 可以改写为
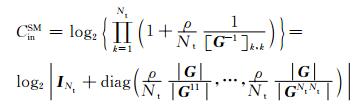 (12)
(12)
基于行列式的拓展[9],可以进一步将公式(12) 转化为
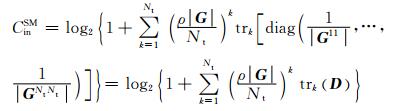 (13)
(13)
式中:D=diag(|G11|-1, |G22|-1, …, |GNtNt|-1);trk(D)表示矩阵D的所有k阶主子式之和.然后,通过求解等式CinBF=CinSM,我们可以获得交点的表达式为
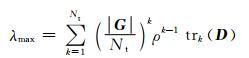 (14)
(14)
公式(14) 给出了理论上的BF与SM方案容量交点处所对应的信道最大特征值λmax.我们定义矩阵HHH的实际最大特征值为λmaxpr.如果λmaxpr>λmax,我们选择BF传输方案,否则我们选择SM传输方案.
基于以上分析我们可以给出一个无人机自适应MIMO通信方案:
步骤1:通过公式(14) 建立一个K值与信噪比所对应交点的查找表.
步骤2:由估计出的K值通过步骤1建立的查找表找到其所对应的交点处的信噪比.
步骤3:判断接收机所获得的信噪比是否大于交点处的信噪比.若大于就选择SM传输方案,否则选择BF传输方案.
3 复杂度分析本节将对公式(4) 所对应的最优MIMO传输方案和本文所提出的自适应MIMO方案进行复杂度的对比分析.为了分析复杂度,我们将ω定义为实数计算复杂度的一个基本单元.加法和减法的复杂度为2ω,乘法和除法的计算复杂度为6ω.
由公式(4) 可以看出,最优MIMO传输方案需要进行矩阵的奇异值分解.由于受到无人机通信系统规模的限制,无人机MIMO信道矩阵一般为维数较小的稠密矩阵.根据文献[9],计算稠密矩阵奇异值的最好方法为先进行Hessenberg化简,然后采用隐式QR分解算法.因此,最优MIMO传输方案的复杂度为
1) 矩阵HHH的计算复杂度为(8NtNr2-2Nr2)ω;
2) 奇异值分解:矩阵的Hessenberg化简需要(4Nr3/3)ω的复杂度,而隐式QR分解算法的计算复杂度为62Nr2ω;
3) 根据计算出的奇异值搜素最优传输方案需要Nrω的计算复杂度.
因此,最优传输方案的总复杂度为
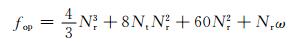 (15)
(15)
本文所提出的自适应方案先将K值与信噪比所对应的交点存储起来建立一个查找表.在无人机通信时,自适应方案会基于查找表选择通信方式,其复杂度主要由查找表的精确度所决定.例如,在途中飞行场景下,Ricean因子K的取值范围为2~20 dB.我们预存储180个K值所对应的信噪比交点值,则K值的精确度为0.1 dB.因此,将K值的个数定义为X并且K值在[2, 20]区间上均匀分布,则自适应方案的复杂度为
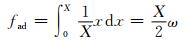 (16)
(16)
图 2给出了发射和接收天线数相等情况下,最优方案和自适应方案复杂度随天线数的变化.从图 2可以看出,当天线数为3时,最优传输方案的复杂度已达到103级,计算量很大.而自适应方案的复杂度是由K值的精确度所决定的,与天线数无关.当X为360时,K值的精确度为0.05 dB,已经非常精确了.而此时自适应方案的复杂度为102级,比最优方案降低了一个数量级.因此,相较于最优传输方案,本文所提出的自适应方案降低了计算复杂度.
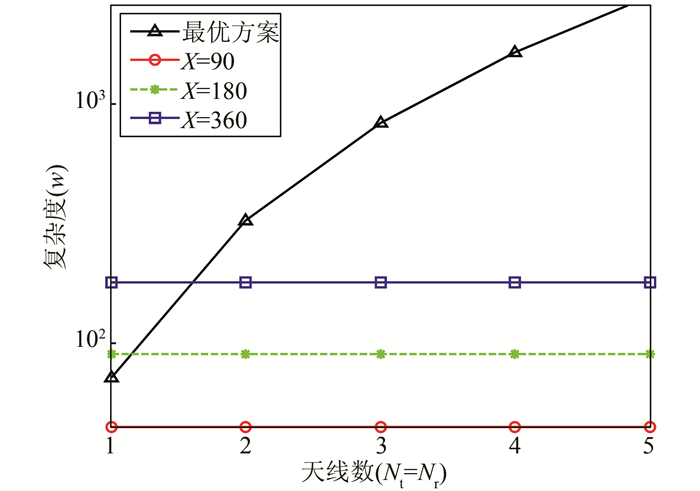
|
| 图 2 最优方案与自适应方案的复杂度分析 Figure 2 Complexity analysis of optimal and adaptive schemes |
本节首先通过仿真验证了BF与SM容量交点的存在,然后给出了在不同K值的Ricean信道下的自适应MIMO方案相较于传统单发单收(SISO)方案的容量对比.仿真分析中,我们设Nt=Nr=4,信道的NLOS分量HNLOS服从瑞利分布,信道噪声n服从均值为0且方差为1的高斯分布.
图 3给出了在K=5 dB的无人机Ricean信道下,BF与SM所获得的容量随信噪比的变化曲线.由图 3可以清晰地看到:随着信噪比的增加SM的性能逐渐超越了BF的性能,并在信噪比为16.7 dB处存在一个交点,这就充分证明了我们以上的分析.为了对比,我们在图 3中也给出了公式(4) 的最优容量曲线.同时也要注意到信噪比较大时,SM与最优容量之间的差距是可以通过更高复杂度的线性接收机来进一步减小的.但是本文所提出的基于BF与SM的自适应方案更加适合无人机通信,既能大幅度提升无人机通信的容量,同时也保证了实现的低复杂度.
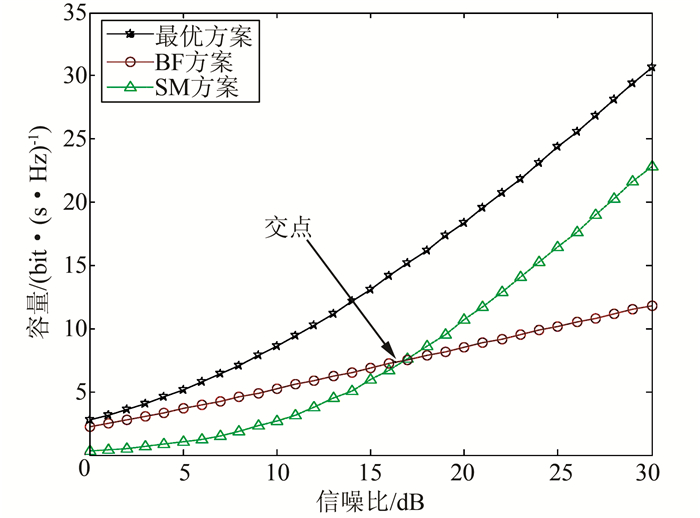
|
| 图 3 在无人机Ricean信道下BF、SM和最优方案所得到的容量 Figure 3 The capacity of BF, SM and the optimal scheme in the UAV Ricean channel |
为了直观地显示BF与SM交点随K的变化,基于交点公式(14) 我们给出了不同K值所对应的交点的变化曲线.
由图 4我们可以看出,BF与SM方案的容量交点是随着K值的增加而不断变大的,这与公式(14) 一致.K值的增大使得最大特征值λmax也增大,因此要想让SM的性能超越BF就需要更大的信噪比.
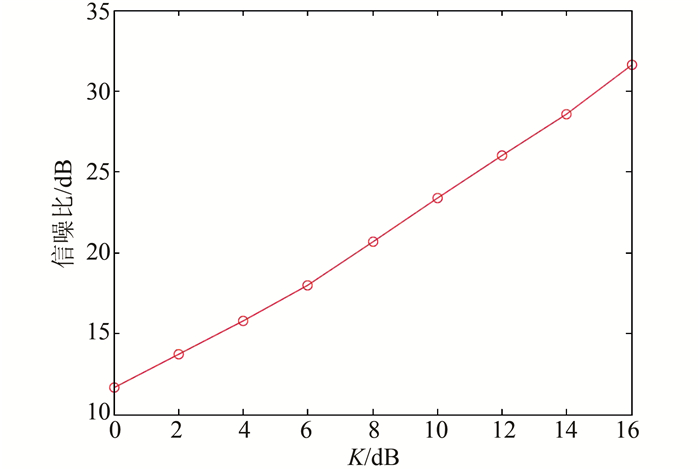
|
| 图 4 BF和SM容量交点 Figure 4 Crossing points of BF and SM capacity curves |
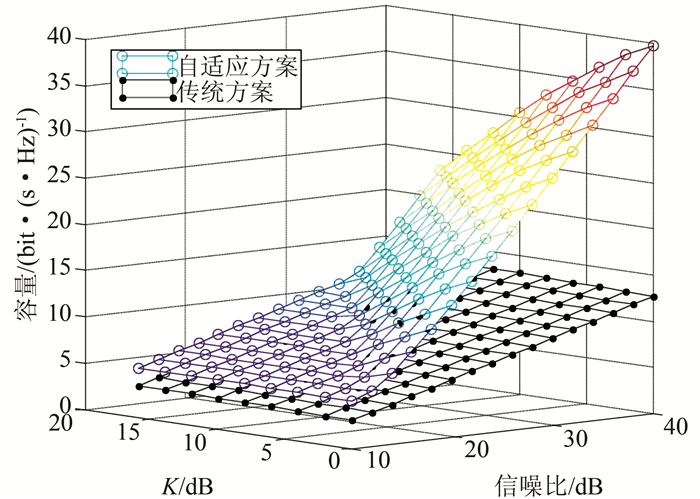
图 5给出了自适应MIMO方案与传统SISO方案的无人机通信性能对比图.从图中可以看出所提出的无人机自适应MIMO方案相较于传统SISO方案的性能优势.在较低信噪比时,较强的噪声干扰导致自适应方案的优势并不明显.但在高信噪比时,自适应方案的容量极大地超过了传统方案.
|
| 图 5 自适应方案与传统方案的性能对比 Figure 5 Comparison between adaptive and traditional schemes |
为了进一步提升无人机的通信容量,本文提出了一种基于Ricean因子的无人机自适应MIMO通信方案.所提出的方案利用了BF和SM两种主要MIMO通信技术,通过Ricean因子实现了BF与SM的自适应切换.相较于传统的无人机通信方案,该方案提升了无人机通信的容量,且在高信噪比时容量提升显著.而与最优MIMO方案相比,所提出的自适应MIMO方案降低了实现复杂度.
| [1] |
陈健, 李佳龙, 阔永红. AF-MIMO系统机会中继选择算法[J].
吉林大学学报(工学版), 2014, 44(6): 1818–1824.
Chen Jian, Li Jialong, Kuo Yonghong. Opportunistic relay selection algorithm for AF-MIMO system[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(6): 1818–1824. |
| [2] | Michailidis E T, Theofilakos P, Kanatas A G. Three-dimensional modeling and simulation of MIMO mobile-to-mobile via stratospheric relay fading channels[J]. IEEE Trans. Veh. Technol, 2013, 62(5): 2014–2030. DOI:10.1109/TVT.2012.2236691 |
| [3] | Taesang Yoo, Goldsmith A. On the optimality of multiantenna broadcast scheduling using zero-forcing beamforming[J]. IEEE J. Sel. Areas. Commun., 2006, 24(3): 528–541. DOI:10.1109/JSAC.2005.862421 |
| [4] | Jong Yeol Ryu, Wan Choi, Dong In Kim, Robert Schober. Beamforming for cooperative retransmission via user relaying in multiple-antenna cellular systems[J]. IEEE Trans.on Wireless Communication, 2015, 14(2): 854–869. DOI:10.1109/TWC.2014.2361136 |
| [5] | Heath R W, Love D J. Multimode antenna selection for spatial multiplexing systems with linear receivers[J]. IEEE Trans. Signal Processing, 2005, 53(8): 3042–3056. DOI:10.1109/TSP.2005.851109 |
| [6] |
李钊, 杨家玮, 姚俊良, 韩维佳. 一种空间相关信道收发联合自适应MIMO传输方法[J].
西安电子科技大学学报:自然科学版, 2009, 36(4): 590–595.
Li Zhao, Yang Jiawei, Yao Junliang, Han Weijia. Transmitter-receiver combined adaptive MIMO transmission scheme for spatially correlated channels[J]. Journal of Xidian University:Natural Science, 2009, 36(4): 590–595. |
| [7] | Forenza A, McKay M R, Pandharipande A, Heath R W, Collings I B. Adaptive MIMO transmission for exploiting the capacity of spatially correlated channels[J]. IEEE Trans. Veh. Technol, 2007, 56(2): 619–629. DOI:10.1109/TVT.2007.891427 |
| [8] | Haas Erik. Aeronautical channel modeling[J]. IEEE Trans. Veh. Technol, 2002, 51(2): 254–264. DOI:10.1109/25.994803 |
| [9] | Watkins D S. Fundamentals of Matrix Computations[M]. 2nd ed. J. Wiley and S. Inc, Eds. Wiley-Interscience, 2002. |
 2017, Vol. 50
2017, Vol. 50



