武汉大学学报(工学版)   2016, Vol. 49 Issue (1): 132-136

文章信息

熊轩, 王选择, 杨练根, 翟中生, 邬文俊, 范宜艳
XIONG Xuan, WANG Xuanze, YANG Liangen, ZHAI Zhongsheng, WU Wenjun, FAN Yiyan
基于激光干涉的三自由度测量系统的理论分析
Theoretical analysis of measurement system of three degrees of freedom based on laser interferometer
武汉大学学报(工学版), 2016, 49(1): 132-136
Engineering Journal of Wuhan University, 2016, 49(1): 132-136
http://dx.doi.org/10.14188/j.1671-8844.2016-01-023

文章历史

收稿日期: 2015-05-16
 Abstract              PDF               Figures               Tables
引用本文 0
熊轩, 王选择, 杨练根, 翟中生, 邬文俊, 范宜艳. 基于激光干涉的三自由度测量系统的理论分析[J]. 武汉大学学报(工学版), 2016, 49(1): 132-136.
XIONG Xuan, WANG Xuanze, YANG Liangen, ZHAI Zhongsheng, WU Wenjun, FAN Yiyan. Theoretical analysis of measurement system of three degrees of freedom based on laser interferometer[J]. Engineering Journal of Wuhan University, 2016, 49(1): 132-136.
基于激光干涉的三自由度测量系统的理论分析
熊轩1, 王选择1,2, 杨练根1,2, 翟中生1,2, 邬文俊1,2, 范宜艳1,2     
1. 湖北工业大学机械工程学院，湖北 武汉 430068;
 2. 湖北工业大学湖北省现代制造质量工程重点实验室，湖北 武汉 430068
收稿日期: 2015-05-16
作者简介: 熊轩(1989-)，男，硕士研究生，专业方向为光电技术，E-mail:152358024@qq.com.
摘要: 为了克服激光沿原光路返回产生激光回馈效应的影响，提出了一种以组合三反射镜为目标载体的三自由度测量方法，即三平面镜组合方法.它不同于平面镜或角隅棱镜作为目标镜的方法，既能使反射光线与原光线错开一定距离，保证反射光不会沿原光路返回，又能使反射光线保留目标测量对象的偏转信息.在实际测量过程中，一方面由于测量位移范围较小，测量光束与参考光束在测量过程中错开很小，不会影响干涉条纹的产生.另一方面考虑工作台偏转角度一般很小，对干涉条纹形状的影响不会造成对干涉条纹计数的破坏.实验应用结果表明，该方法适用于运动位移与偏转角度的三自由度同步测量.
关键词： 激光干涉     三自由度     位移与角度测量     条纹计数    
Theoretical analysis of measurement system of three degrees of freedom based on laser interferometer
XIONG Xuan1, WANG Xuanze1,2, YANG Liangen1,2, ZHAI Zhongsheng1,2, WU Wenjun1,2, FAN Yiyan1,2     
1. School of Mechanical Engineering, Hubei University of Technology, Wuhan 430068, China;
 2. Hubei Key Laboratory of Manufacture Quality Engineering, Hubei University of Technology, Wuhan 430068, China
Abstract: In order to prevent the laser from turning back to the original optical path, which may result in the feedback effect of laser, this paper presents a measurement method of three degrees of freedom based on three combined mirrors as the target carrier. This system also known as three-mirror combination method. Unlike those conventional method of using a mirror or a corner cube mirror as the target, the three-mirror method can shifted outgoing light to the incident light at a distance and keep the deflection information of outgoing light on the measurement target. On the one hand, in the process of the measurement, there is a small staggered distance between the measuring beam and the reference beam during actual measurement due to a relatively narrow measuring range of displacement, which would not affect the generation of interference fringes; on the other hand, considering the small deflecting angle of the workbench, the influence on the shapes of interference fringes would not do damage to their counting.This method is suitable for simultaneous measurement in multi-degree of freedom of displacement and deflection angle.
Key words: laser interferometer     three degrees of freedom     displacement and angle measurement     fringe counting    

随着现代科技的发展，机械加工对各项几何参数的测量精度要求越来越高.直线度与偏摆量作为形状误差的要素之一，直接影响零件的加工制造精度与测量精度，因而研究与设计对工作台角偏与线偏的实时在线测量方法具有重要意义.在精密加工、产品制造、定位导航等工业领域，高精度的角度测量方法具有重要意义.其中有自准直的方法[1]，主要通过面阵CCD反射回来光电的位置信息，得到目标的二维偏转角度.由于位置信息通过光强重心的计算得到，其精度与CCD分辨率相关，且对光路要求十分严格.为此，本文以微角度、微位移测量为目的，基于迈克尔逊干涉原理，在前期对干涉条纹形状识别的基础上[2]，提出了一种基于干涉条纹形状与三反射镜的组合测量光路，用于微小偏转角度条件下如导轨、微动台等的三自由度精密测量，实现包括直线度、偏摆量与线位移的同步测量.

三反射镜设计的目的在于，与平面镜相比[3, 4]，由于反射回来的光路发生了改变，不会导致反射光再次进入激光器而出现回馈现象，影响干涉质量.与角锥棱镜、直角棱镜相比[5-7]，能够测量除位移以外的两个角度偏转量，同时被测对象的另外两个方向上的平动不影响反射光线，能够保证与参考光重合.与光隔相比[1]，能够减少高昂的生产成本.

干涉条纹利用四象限光电探测器接收，经光电接收与转换电路获取四路光电信号.四路光电信号分成两组，采用椭圆拟合方法，分别计算它们之间的相位差[3]，从而得到反映条纹形状的方向与宽度参数，进一步应用偏转角与形状参数的关系模型，计算偏转角度[1].在进行条纹形状识别的同时，可以利用探测器形成的两组差分信号进行细分辨向，达到对光程差计算的目的[8-12].一般而言，差分信号的相位差约为90°，理论上这个相差在0~180°范围内变化均满足计数要求，为了可靠地细分辨向，实际应该在30°~150°范围内变化.

本文中系统以被测目标的六自由度的偏摆与位移进行分析，在探讨了干涉系统在避开返回光束方向改进的基础上，主要分析光路的数学模型，从理论上论证了在一定测量范围内利用干涉条纹形状与光程差同步测量的方法，进行三自由度测量的可行性.

1 光路设计 1.1 整体测量光路的设计

激光的干涉系统原理如图 1：氦氖激光器发出均匀的激光光斑，经一个偏振分光镜，其中的一束光直接透射到一个带有凹槽的三面镜上，作为测量光束；另一束光经过分光镜的反射射入到带有压电陶瓷的直角棱镜上，作为参考光束.两束光分别进行反射后汇聚在四象限的光电探测器上，形成一明一暗的干涉条纹.目标镜固定在被测工作台上，随工作台一起运动.在工作台位移出现改变时可引起条纹的移动，而工作台的角度发生改变时，形成干涉的两束光的夹角也会相应改变，致使干涉条纹的水平方向的角度、条纹之间的宽度出现变化.

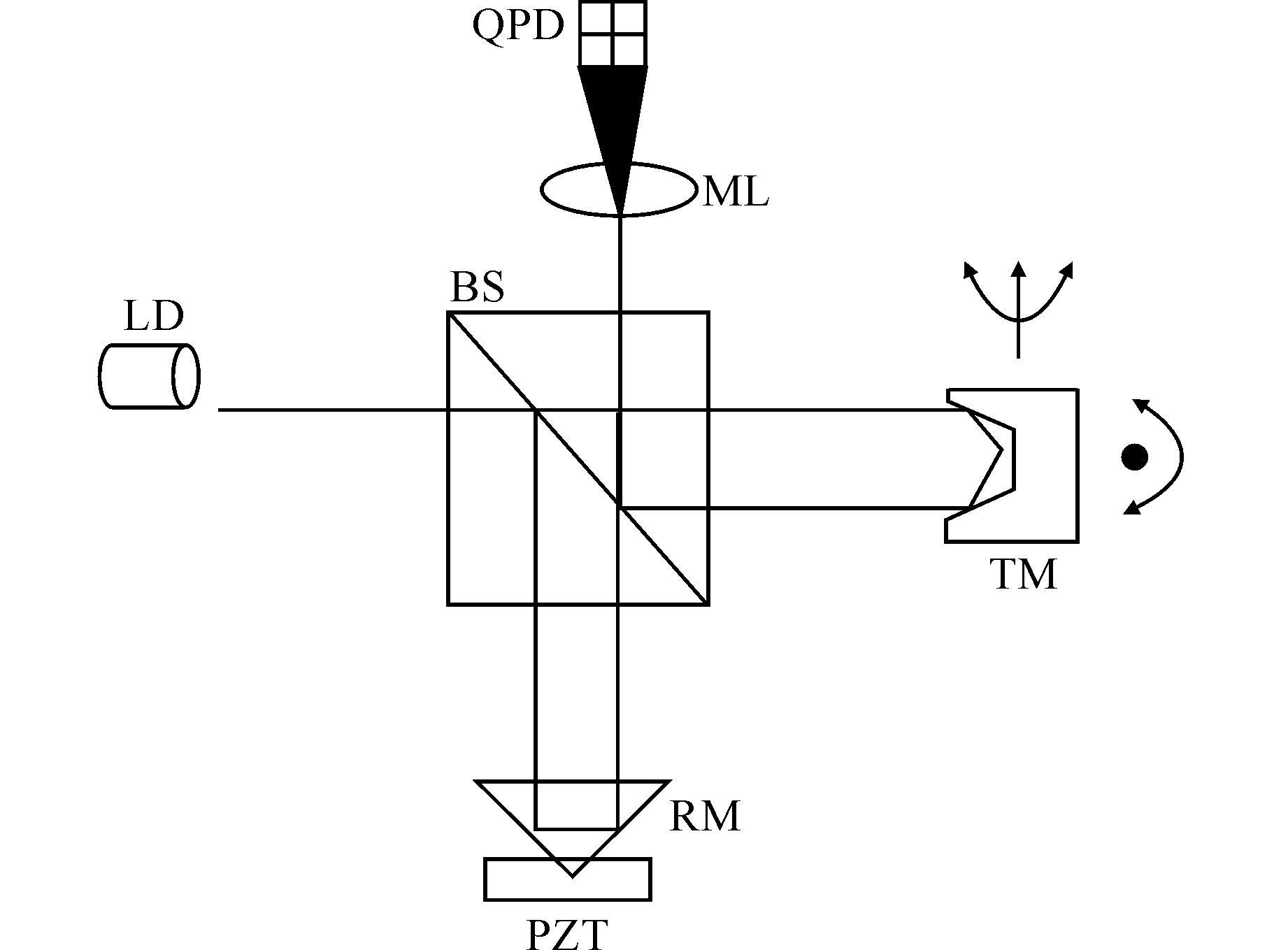
图 1 激光干涉原理示意图 Figure 1 Laser interferometer measurement system
图选项

此方法对仪器和设备的要求较低，通过使用扩束镜对干涉条纹进行放大，不但无需像自准直仪法那样对光斑实施严格的准直，而且对干涉条纹的形状大小也并没有过高要求，无需对环境的光强进行严格隔离.此测量方式所需处置的信号较为简单，仅需1个四象限的光电管，实施光电的转换，规避自准直仪内用CCD处置速度较慢的缺陷.实验证明，此方法优点在于简化处理结构，缩小体积,减少元件的使用量，减小成本.

该激光干涉系统主要是利用目标镜三个自由度的改变导致光束光程的变化这一原理达到测量工作台的目的.干涉条纹的形状与光程差存在一定的理论联系[2]，而工作台位移和角度的变化会引起光程差的改变.利用压电陶瓷作为动态干涉条纹的调制方法，将四象限接收器应用到干涉条纹的信号接收过程中来，并经过系统软件的算法设计，实现对模拟信号的转换，采用椭圆拟合方法实现对条纹宽度和位置的识别，从而可以得出工作台的角度和位移变化量的计算.图 2所示为整体实施方案系统框图.

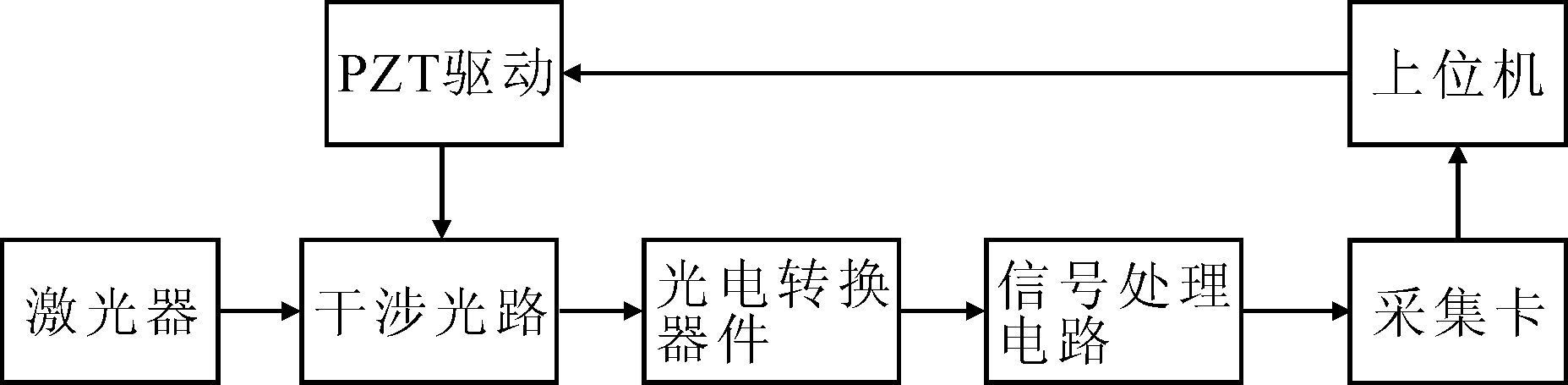
图 2 整体实施方案系统框图 Figure 2 Frame diagram of whole measuring system
图选项
1.2 三反射目标镜的设计

常规的平面镜同样可以实现直线度与偏摆量的测量，但测量过程中需要添加一个光隔阻断激光回馈对光源的干扰，这样不但增加了制作成本，同时对条纹接收的清晰度也会产生一定的影响，因此需要设计一个无回馈的激光测量系统.

通过用图 3所示的凹槽式三面镜改变反射光束，让参考镜反射光线与原光线错开一定距离，从而达到反射光束不沿原光路返回的目的.为了实现设计效果，通过计算，三面镜的两个夹角相等，且取120°时为最佳.

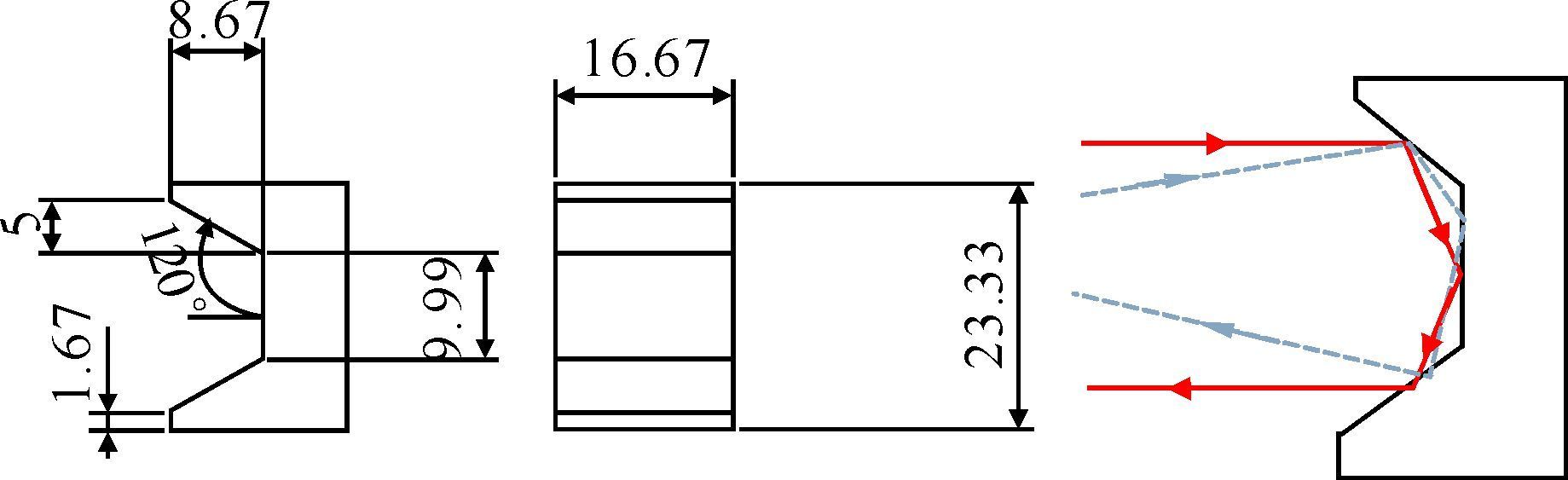
图 3 三反射镜设计图(单位：mm) Figure 3 Design of three objective mirrors (unit:mm)
图选项

通过公式推导，可以得出出射光线与入射光线关于水平对称变化，当入射光线垂直于三反射镜的中间面时，入射光与出射光平行，从而达到了在平面镜上所呈现的效果，实现设计目的.

2 光路的分析计算与理论推导

干涉系统在测量过程中，当目标镜发生变化时，对光程差影响程序不一致，因此，需要建立起光束方向、光程的空间矢量模型.

如图 1所示的光路中反射测量光束方向、光程与目标镜运动之间存在一定的几何关系.为了分析这种几何关系，首先运用向量方法建立光路方向方程.在假设入射光的方向向量为d1，3个面的法向量分别为n1、n2、n3的条件下，运用下式直接求解3次反射后光线的方向向量d2、d3、d4，由此可以得出光路方向的变化结果. 该光线向量反射公式为

${{d}_{2}}={{d}_{1}}-2{{d}_{1}}\centerdot n\centerdot n$    (1)

第二步建立光程差与目标镜空间运动姿态的关系向量模型.如图 4所示，在假设目标镜初始位置垂直于水平面的条件下，对入射光与出射光以水平方向截取一段，截取的两点为p1、p5,3个反射点分别为p2、p3、p4.然后在目标镜中间面的竖直方向做线段o1、o3,点o2为中点，同时设为空间直角坐标系的中点.点o1、o3分别在组合镜3个面的两两公共端.通过o1、d1、n1以及直线与平面交点公式可以推出p2的坐标,同理可求得点p3、p4、p5.对5个点求模得到光程L1.

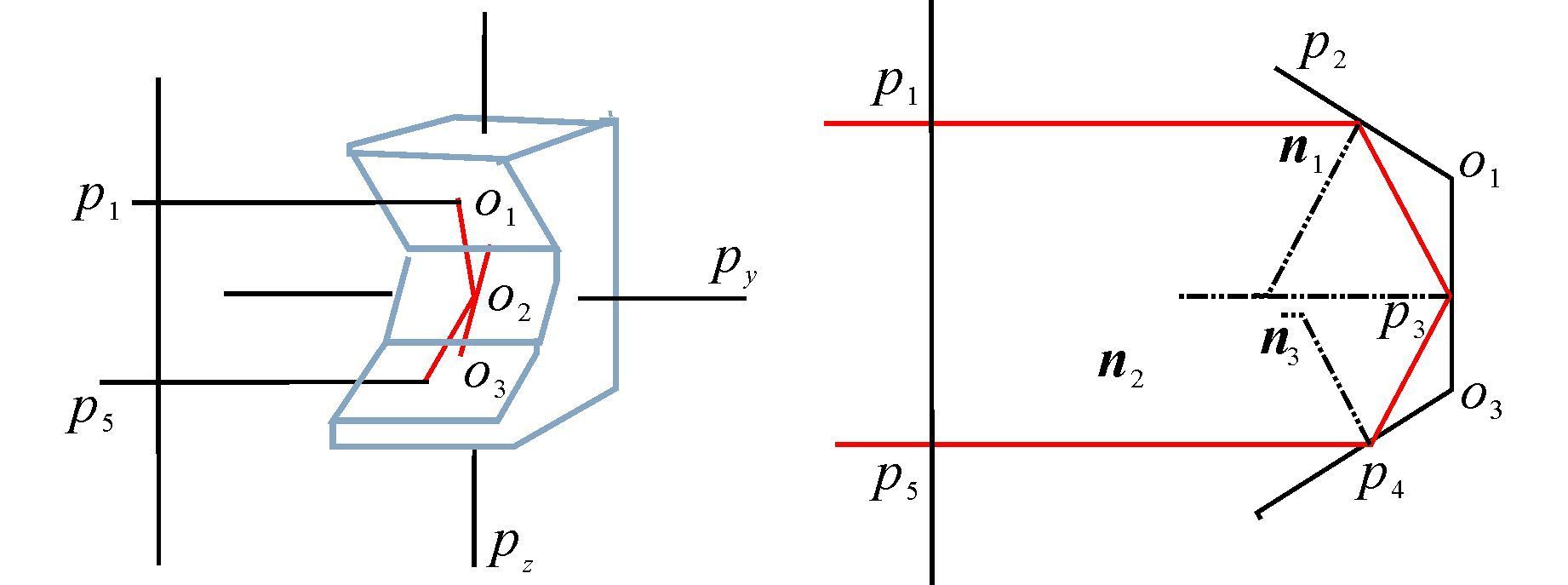
图 4 光程差与目标镜空间运动姿态关系 Figure 4 Relationship between optical path difference and spatial moving posture of target mirror
图选项

直线与平面交点公式为

${{p}_{2}}={{p}_{1}}+\frac{\left( {{o}_{1}}-{{p}_{1}} \right)\bullet {{n}_{1}}}{{{d}_{1}}\bullet {{n}_{1}}}{{d}_{1}}$    (2)

在此基础上，分别对目标镜六自由度的位移与偏转进行理论推导，假设目标镜在一个坐标轴上的位移为a,很容易得到变化后的o1、o3点的坐标，通过o点的变化可以得到位移后的光程L2.再假设目标镜在一个坐标轴旋转α角，通过向量绕轴旋转公式以及点绕轴旋转公式得到旋转后的3个法向量以及o1、o3的坐标.再由此推出旋转后光程L3.最后分别得出3个轴上位移与偏转的光程差变化.

向量绕轴旋转公式：

$\begin{align} & n_{1}^{'}={{n}_{1}}\bullet {{d}_{y}}\bullet {{d}_{y}}+({{n}_{1}}-{{n}_{1}}\bullet {{d}_{y}}\bullet {{d}_{y}})\times \\ & {{d}_{y}}\bullet \sin \theta +({{n}_{1}}-{{n}_{1}}\bullet {{d}_{y}}\bullet {{d}_{y}})\bullet \cos \theta \\ \end{align}$    (3)

点绕轴旋转公式为

$o_{1}^{'}={{o}_{2}}+\left( {{o}_{1}}-{{o}_{2}} \right)\cdot \cos \theta +({{o}_{1}}-{{o}_{2}})\times {{d}_{y}}\cdot \sin \theta $    (4)
3 仿真计算

利用Matlab对所建立的模型进行仿真.图 5(a)-(c)中，横坐标表示目标镜分别随x、y、z 3个轴方向的位移，假设步长为0.1 mm，而纵坐标表示与之对应的光程.当目标价绕y、z两轴旋转时，光程的变化量相等，且呈单调递增增加；当目标镜绕x轴旋转时光程没有变化.

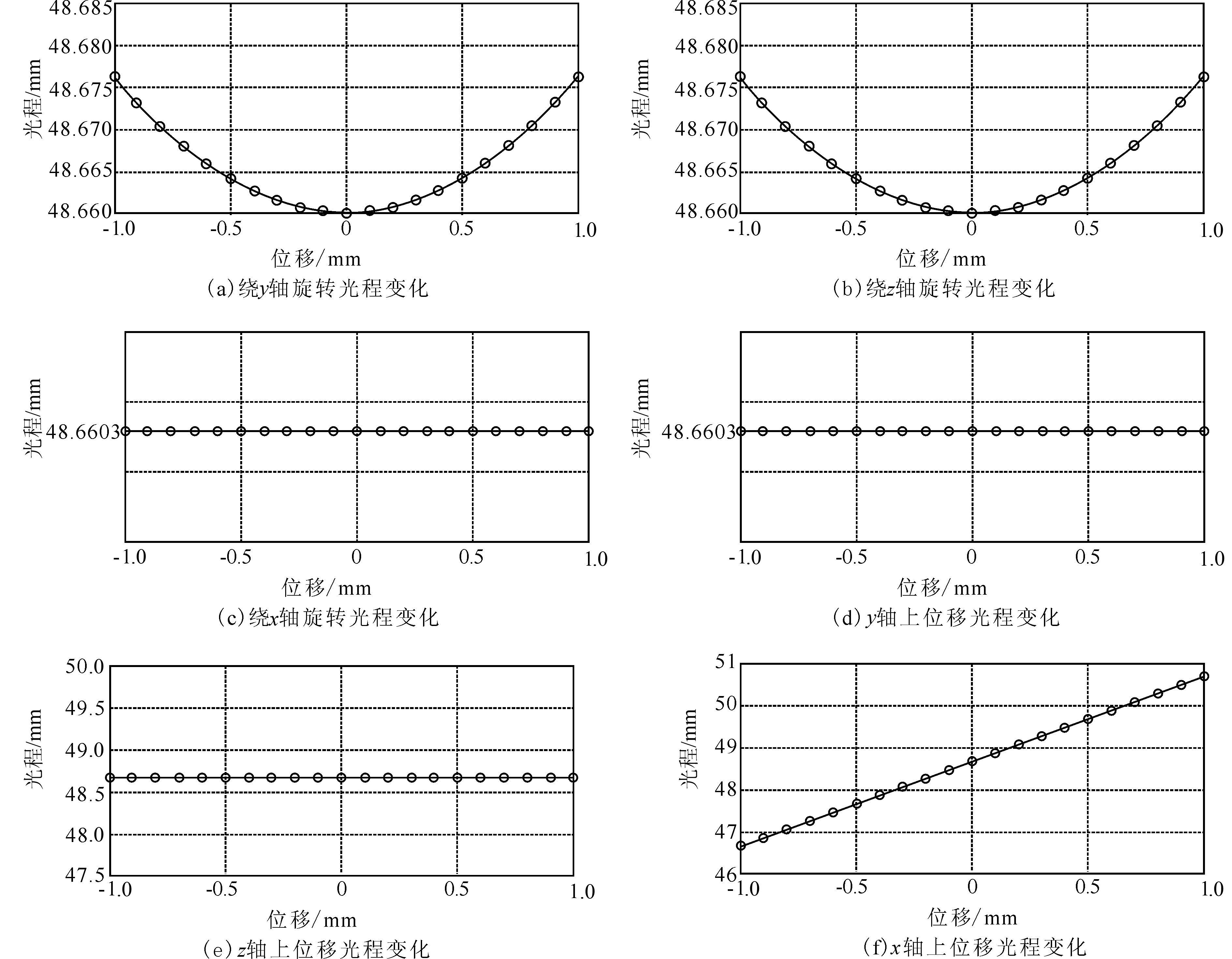
图 5 基于Matlab的六自由度仿真计算 Figure 5 Six degrees of freedom simulation calculation based on Matlab
图选项

图 5(d)-(f)中，横坐标分别表示目标镜分别随x、y、z 3个轴方向的角度偏转范围，假设步长为0.1°，而纵坐标表示与之对应的光程.当目标镜在y、z两轴方向位移时，光程没有变化；当目标镜在x轴方向位移时，光程的变化呈线性递增或递减.

通过仿真计算，表明设计系统能够实现3个单位空间向量的偏摆角度与运动位移的同步测量，且具有较高的测量精度.同时，计算表明在x轴的旋转和y、z方向的位移对光程的改变没有影响.因此得出了三自由度测量系统.

4 结论

本文在激光干涉测量系统的基础上，提出了一套能够消除回馈干扰的激光测量系统.该测量系统能够实现多个自由度偏转及位移的测量.通过公式的推导，可以分析光路在测量过程中光程的变化，进而影响干涉角度及条纹宽度.最后，通过实验采样，验证了本文提出的相关设计的准确性和可行性，该干涉测量系统能较好地实现工作台角偏与线偏的测量.

参考文献
[1] 蔡盛, 梁爽, 丁振勇, 等. 基于莫尔条纹的自准直测角方法研究[J]. 光电子·激光, 2008, 19(10): 1375–1377.
Cai Sheng, Liang Shuang, Ding Zhenyong, et al. Auto-collimation angular measurement method based on Moire fringe[J]. Journal of Optoelectronics·Laser, 2008, 19(10): 1375–1377.
[2] 王选择, 翟中生, 钟毓宁, 等. 应用动态调制与干涉条纹形状测量二维角度[J]. 光学精密工程, 2014(2): 274–280.
Wang Xuanze, Zhai Zhongsheng, Zhong Yuning, et al. Measurement of two-dimension angle using dynamic modulation and interference fringe shape[J]. Optics and Precision Engineering, 2014(2): 274–280.
[3] 周浩, 王选择, 翟中生, 等. 基于圆形四象限光电探测器的条纹形状识别方法研究[J]. 中国激光, 2012(7): 181–187.
Zhou Hao, Wang Xuanze, Zhai Zhongsheng, et al. Research on fringe shape recognition methods based on circular four-quadrant photoelectric detector[J]. Chinese Journal of Lasers, 2012(7): 181–187.
[4] 王淑珍, 谢铁邦, 常素萍, 等. 四象限光电探测器用于表面形貌测量的研究[J]. 中国机械工程, 2008, 19(19): 2348–2351.
Wang Shuzhen, Xie Tiebang, Chang Suping, et al. Study on four-quadrant photoelectric detector in surface topography measurement[J]. China Mechanical Engineering, 2008, 19(19): 2348–2351.
[5] 匡萃方, 冯其波, 刘斌. 角锥棱镜用于激光直线度测量的特性分析[J]. 光学技术, 2005, 31(2): 282–285.
Kuang Cuifang, Feng Qibo, Liu Bin. Analyzing characteristic of the cube corner retroreflector applied to laser straightness measurement[J]. Optical Technique, 2005, 31(2): 282–285.
[6] 魏若飞. 激光合成波长纳米位移测量干涉仪的准直方法研究[J]. 浙江理工大学学报, 2011, 28(4): 525–528.
Wei Ruofei. Study on alignment method of a laser synthetic wavelength nanomeasurement interferometer[J]. Journal of Zhejiang Sci-Tech University, 2011, 28(4): 525–528.
[7] 姜坤, 朱若谷. 用迈克尔逊干涉仪测微定位工作台的位移[J]. 中国计量学院学报, 2007, 17(4): 281–283.
Jiang Kun, Zhu Ruogu. Displacement of micropositioning table combined with michelson interferometer[J]. Journal of China Institute of Metrology, 2007, 17(4): 281–283.
[8] Fang Suping Fujio Hiroshiqe, Kubo Aizoh Toya Masahiro, Suznki Yoshikazu, Saitoh Yoshiaki, Suzuki Mitsuo. New optical system for reducing the interference fringe density in laser interferometric measurement of tooth flank form of a gear[J]. Machine Elements and Manufacturing, 2000, 43(2): 455–463.
[9] He Maogang, Guo Ying, Zhong Qiu. A new method of processing mach-zehnder interference fringe data in determination of diffusion cofficient[J]. Int. J. Thermophys, 2009, 30: 1823–1827. DOI:10.1007/s10765-009-0685-0
[10] Akihide Kimura, Wei Gao, Yoshikazu Arai, Zeng Lijiang. Design and construction of a two-degree-of-freedom linear encoder for nanometric measurement of stage position and straightness[J]. Precision Engineering, 2010, 3: 145–155.
[11] Jae Wan Kim, Chu Shik Kang, Jong Ahn Kim. A compact system for simultaneous measurement of linear and angular displacements of nano-stages[J]. Optical Express, 2007, 15(24): 15759–15766. DOI:10.1364/OE.15.015759
[12] Kimura A, Gao W, Kim W J, Hosono K, et al. A sub-nanometric three-axis surface encoder with short-period planar gratings for stage motion measurement. Precis Eng., 2012, 36(4): 576-585.