文章信息
- 张劭华, 何蕴龙, 孙伟
- ZHANG Shaohua, HE Yunlong, SUN Wei
- 守口堡胶凝砂砾石坝抗震性能
- Seismic behavior of Shoukoubu hardfill dam
- 武汉大学学报(工学版), 2016, 49(2): 193-200
- Engineering Journal of Wuhan University, 2016, 49(2): 193-200
- http://dx.doi.org/10.14188/j.1671-8844.2016-02-006
-
文章历史
- 收稿日期: 2015-08-15
胶凝砂砾石坝是近年来新兴的一种坝型[1, 2],由于这种坝型在结构、稳定、施工、造价、环境等方面突出的优势,使其受到坝工界广泛的关注[3].在国外已经成功修建了数座临时围堰和永久性大坝,例如Nagashima坝上游围堰、Tyubetsu坝上游围堰、Cindere[4]坝、Oyuk[5]坝等.在我国这种筑坝技术已在道塘水库上游围堰[6]、洪口水电站上游围堰[7]、沙沱水电站下游围堰等多座临时性工程得到成功应用,并取得了良好的实际效果.守口堡胶凝砂砾石坝工程是我国正在修建的第一座胶凝砂砾石坝永久性工程,它的成功修建,对于以后类似工程的研究与修建具有重要的理论意义和指导意义.
目前,针对胶凝砂砾石坝体抗震性能的研究较少.Toshio HIROSE[8]等日本学者采用拟静力法做了二维动力分析,并假定库水是不可压缩的,得出坝体在水平地震作用下主要产生剪切变形的结论,没有考虑坝体外部表面常态混凝土防渗层的作用.俄罗斯学者Liapichev Y P[9]分别选取刚性和软弱地基上的Hardfill混合坝,选取不同坝高和坝坡坡率,做了考虑地基与库水对坝体的影响的动力研究,这种计算坝型并非真正意义上的Hardfill,但对我们认识Hardfill坝的抗震性能有一定的指导作用.何蕴龙等人[10, 11]运用剪切楔法,将坝体假定为嵌固在基岩上的变截面线弹性梁,可以计算出坝体各水平截面的动力反应平均值,一定程度上反映了胶凝砂砾石坝的抗震性能.文献[12]曾做过胶凝砂砾石坝的流固耦合分析,但其分析局限在二维模型,并且没有考虑地基的辐射阻尼效应.同时对于没有设坝体横缝的守口堡坝这一类的胶凝砂砾石坝型,其研究的精确性有待验证.对于常规的坝型,如重力坝、拱坝、土石坝等的抗震性能研究相对较为成熟,在动力问题的研究方法与需要考虑的影响因素上有一定的借鉴意义.目前基于胶凝砂砾石坝的抗震性能的研究,存在研究方法较为简单、模拟方式较为粗糙、计算结果较难真实反映结构的抗震性能等缺点.
本文为了探讨胶凝砂砾石坝的抗震性能,及其相对于常规重力坝的特点,以守口堡工程为实例,分别建立了守口堡工程最后实际施工的胶凝砂砾石坝坝型与同等高度的常规混凝土重力坝坝型的坝体-库水-地基系统动力分析的三维有限元计算模型.为了科学地评价这种新坝型的抗震性能,基于自由场规范波的反演分析,得到深部基岩输入地震动,同时严格考虑地基辐射阻尼的影响,采用粘弹性边界实现地震动的输入.以流固耦合的方式考虑库水的作用,进行地震动力时程分析.并通过胶凝砂砾石坝与同等高度常规混凝土重力坝计算结果的对比,分析得出守口堡胶凝砂砾石坝的动力特性与动力响应情况.
1 计算原理与计算方法 1.1 流固耦合计算原理流固耦合系统的基本方程是指结构与流体组成的耦合系统,在结构与流体的交界面处,应保持速度和应力连续的边界条件.考虑库水的可压缩性,利用加权余量法的基本思想,用伽辽金法得到弹性结构-流体的流固耦合振动在一般情况下的有限元方程:
其中:MS、KS、FS为与结构有关的质量、刚度和荷载矩阵;MP、KP为与流体相关的“质量”、“刚度”矩阵;Q为流固交界面上的耦合矩阵,Q1、Q2为与流体流速有关的耦合矩阵,可以沿流固交界面用高斯积分法数值积分集成得到.
1.2 粘弹性边界理论刘晶波[13]基于平面SH波问题的分析,给出了粘弹性边界的一种有效外源输入方法,人工边界节点上施加等效荷载的计算公式为
式中:FB(t)为边界节点B处等效荷载;τ0为在原连续介质由位移ω0产生的应力;CB、KB分别为粘弹性人工边界法向、切向粘滞阻尼系数和弹簧刚度;ω0、0分别为入射波场位移和速度.
三维人工边界的弹簧-阻尼元件参数为
法向:
切向:
式中:ρ为介质密度;
采用基于一维剪切(压缩)波理论进行自由场地震波的反演分析,得到深部基岩输入地震动.假设自由场地震记录是在水平方向上无限延伸的水平成层地基地表取得的,它是深部基岩运动引起的通过具有粘滞阻尼的弹性体竖直向上传播的剪切或者压缩波所产生的.采用FFT技术,将地震加速度历程表述成有限个简谐运动之和.简谐运动在水平面上产生的剪应力为
在第m﹑m+1层的交接面上,位移和剪应力的连续条件为
式中:h为层厚;am=kmGm*/(km+1Gm+1*).由地表剪应力为零的条件可得E1=F1.根据地震记录的Fourier分析结果,可确定相应于频率ω的E1.如此便可求出全部待定常数EmFm.
将各频率对应的地震动输入层的各简谐运动进行反FFT变化即可得到深部基岩的地震加速度时程.
2 工程基本资料和计算模型 2.1 工程概况守口堡水库位于大同市阳高县境内海河流域黑水河上游段,在阳高县城西北方向约10 km,总库容为980万m3,工程等级为Ⅳ等.坝顶长354 m,坝顶高程1243.6m,最大坝高61.6 m,水库正常蓄水位1 240.0 m.坝址区河谷为“U”形谷,河谷宽约为220.0 m,地面高程1 204~1 210 m,地形较为平坦.河谷覆盖层为卵石混合土,厚度6.5~19.8 m,局部夹有细砂透镜体.下伏基岩为含辉石斜长角闪岩,局部为黑云二长片麻岩,粒状变晶结构,基岩面高程1 185.7~1 199.6 m.坝址区地质构造主要为一些小型断层及节理裂隙,无明显断距,碎裂岩、泥质充填.坝基强风化层厚度0.90~5.00 m,弱风化层厚度4.30~8.75 m.坝基覆盖层厚度较小,下伏基岩无软弱夹层和明显的断裂发育,不存在深层滑动和浅层滑动问题,具有胶凝砂砾石筑坝的条件.两岸山势险峻,右岸边坡较陡,坡度约为50°,左岸边坡相对较缓,坡度约为29°.
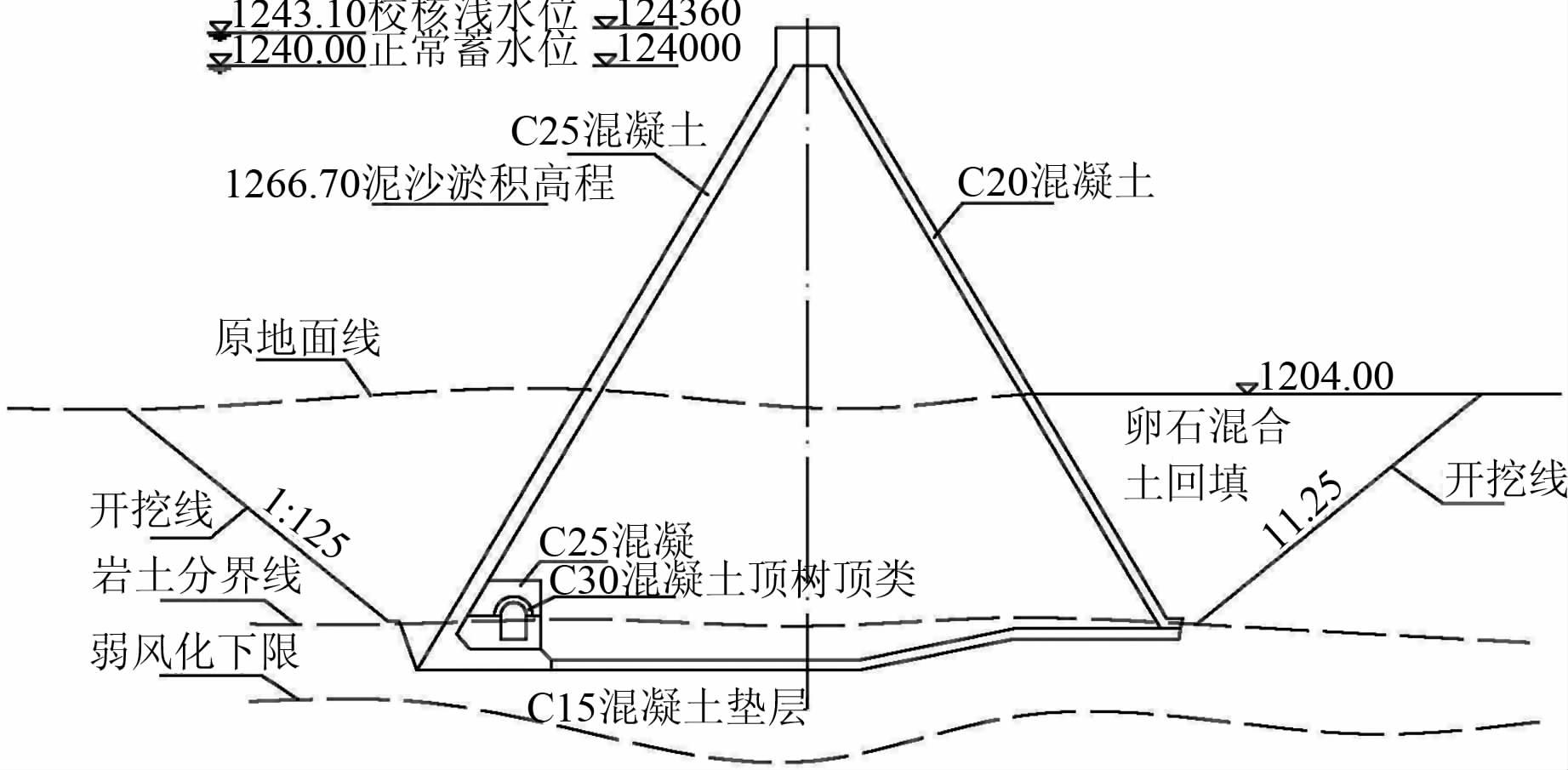
拦河大坝为胶凝砂砾石坝(断面图见图 1),胶凝材料水泥用量50 kg/m3,粉煤灰用量40 kg/m3.根据材料测试试件的试验结果[14],180 d龄期胶凝砂砾石材料强度为6 MPa左右,平均级配的立方体试件抗压强度为12.8MPa,弹性模量平均值为15.2 GPa,抗渗等级为W8.
|
| 图 1 守口堡胶凝砂砾石坝典型断面图 Figure 1 Typical section plan of Shoukoubu hardfill dam |
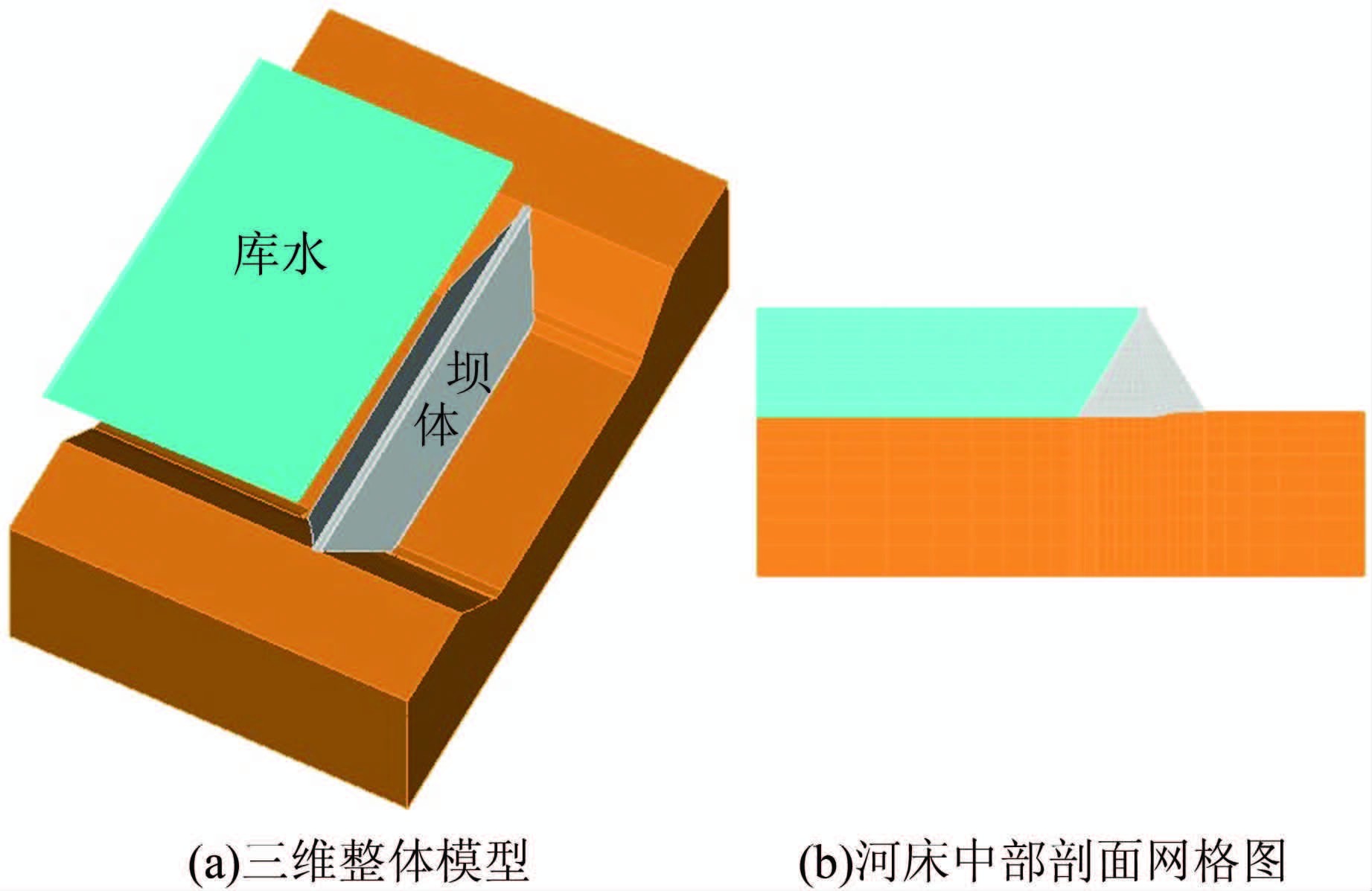
胶凝砂砾石坝流固耦合计算模型:坝高61.6m,坝基计算范围竖直向下及向下游方向取1.5倍坝高.为充分考虑水体的影响,库水计算范围向上游取3倍坝高[15].采用简化的均质地基模型进行计算.库水设置了无穷远边界条件,不考虑表面波动.严格考虑流固耦合作用,坝体与库水接触面以及地基与库水接触面为流固耦合界面.整个模型共有节点26 856个,单元24 216个.计算模型见图 2.
|
| 图 2 守口堡有限元计算模型 Figure 2 Finite element model of Shoukoubu hardfill dam |
根据守口堡胶凝砂砾石坝材料试验结果[14],同时综合考虑材料离散及工程现场施工条件等因素,计算中的胶凝砂砾石坝体材料弹性模量按15 GPa考虑,泊松比0.2,容重2 360 kN/m3.水体密度1 000 kg/m3.动态弹模在静态弹模的基础上增大30%.参数见表 1所示.
| 材料 | 弹性模量/GPa | 泊松比 | 容重/(kN·m-3) | 粘聚力/kPa | 摩擦系数 |
| 强风化岩体 | 6.0 | 0.21 | 23.0 | 300 | 0.55 |
| 弱风化岩体 | 12.0 | 0.21 | 23.0 | 500 | 0.70 |
| 微风化岩体 | 24.0 | 0.21 | 23.0 | 1200 | 1.2 |
| 新鲜岩体 | 60.0 | 0.21 | 23.0 | 2000 | 1.4 |
根据《水工建筑物抗震设计规范》以人工地震波进行输入.坝址区地震峰值加速度0.1g,对应设计地震基本烈度为7度.考虑地基的辐射阻尼效应,地震动采用粘弹性边界的方式输入,采用等效节点荷载的方式施加.各方向地震波时程如图 3所示.本文将人工地震波进行反演,得到基岩深部地震波作为模型输入的地震动.

|
| 图 3 地震波加速度时程曲线 Figure 3 Time histories of inputting seismic waves acceleration |
对胶凝砂砾石坝空库模型和满库流固耦合模型分别进行动力特性分析,提取前10阶振型进行比较(见表 2).由计算结果可知,守口堡大坝的满库自振频率较空库自振频率有所降低,自振周期较长.这是由于受库水的影响,使得体系的刚度没有变化而质量增加,从而使得坝体的自振频率减小.另外,随着阶数的增加,满库模型自振频率相对于空库模型下降的比率有波动增大的趋势.
| 振型序号 | 空库工况 | 满库工况 | 自振频率下降比率/% | ||
| 自振频率/Hz | 自振周期/s | 自振频率/Hz | 自振周期/s | ||
| 1 | 5.13 | 0.195 | 4.77 | 0.210 | 7.02 |
| 2 | 6.10 | 0.163 | 5.68 | 0.176 | 6.89 |
| 3 | 6.51 | 0.153 | 6.08 | 0.164 | 6.61 |
| 4 | 7.52 | 0.133 | 6.49 | 0.154 | 13.70 |
| 5 | 7.73 | 0.129 | 7.02 | 0.142 | 9.18 |
| 6 | 8.73 | 0.115 | 8.08 | 0.124 | 7.45 |
| 7 | 9.20 | 0.109 | 8.54 | 0.117 | 7.17 |
| 8 | 10.47 | 0.096 | 9.18 | 0.109 | 12.32 |
| 9 | 11.10 | 0.090 | 9.87 | 0.101 | 11.08 |
| 10 | 12.18 | 0.082 | 10.28 | 0.097 | 15.60 |
由空库模型和满库模型的各阶振型振动形态分析对比可知,两种模型的振型相差不大.除第3、7阶振型存在差异,振型方向明显不同,其他各阶振动形态基本相同,第1、2、5、6均以顺河向振动为主,第4、9阶均以横河向振动为主,第8、10阶均以竖直向振动为主.存在差异的主要原因为:由于满库流固耦合模型较大程度地反映了坝体与库水的耦合作用,库水的动力特性影响了坝体的振动幅值及主振型方向等,使得坝体产生振型差异.在整个振动过程中没有明显过大的振型参与系数的存在,反映了大坝的体型结构的质量、刚度的均匀性分布良好.
胶凝砂砾石坝与同等高度的重力坝流固耦合模型相比,系统的自振频率有所降低,第4、8、10阶振型存在较大的差异,振型方向明显不同,第1、2、3、5、6均以顺河向振动为主,第7阶均以竖直向振动为主,第9阶均以横河向振动为主.存在差异的主要原因为:混凝土材料相对于胶凝砂砾石料的材料性能差异以及结构体型的差异,使得体系的质量和刚度有了显著的变化,从而体系的振动方向及自振频率发生变化.此外,胶凝砂砾石坝上游倾斜坝面与重力坝上游铅直坝面的差异,改变了库水形状,胶凝砂砾石坝的库水形状为倾斜体状,一定程度上影响了体系的动力特性以及下文的动力响应.
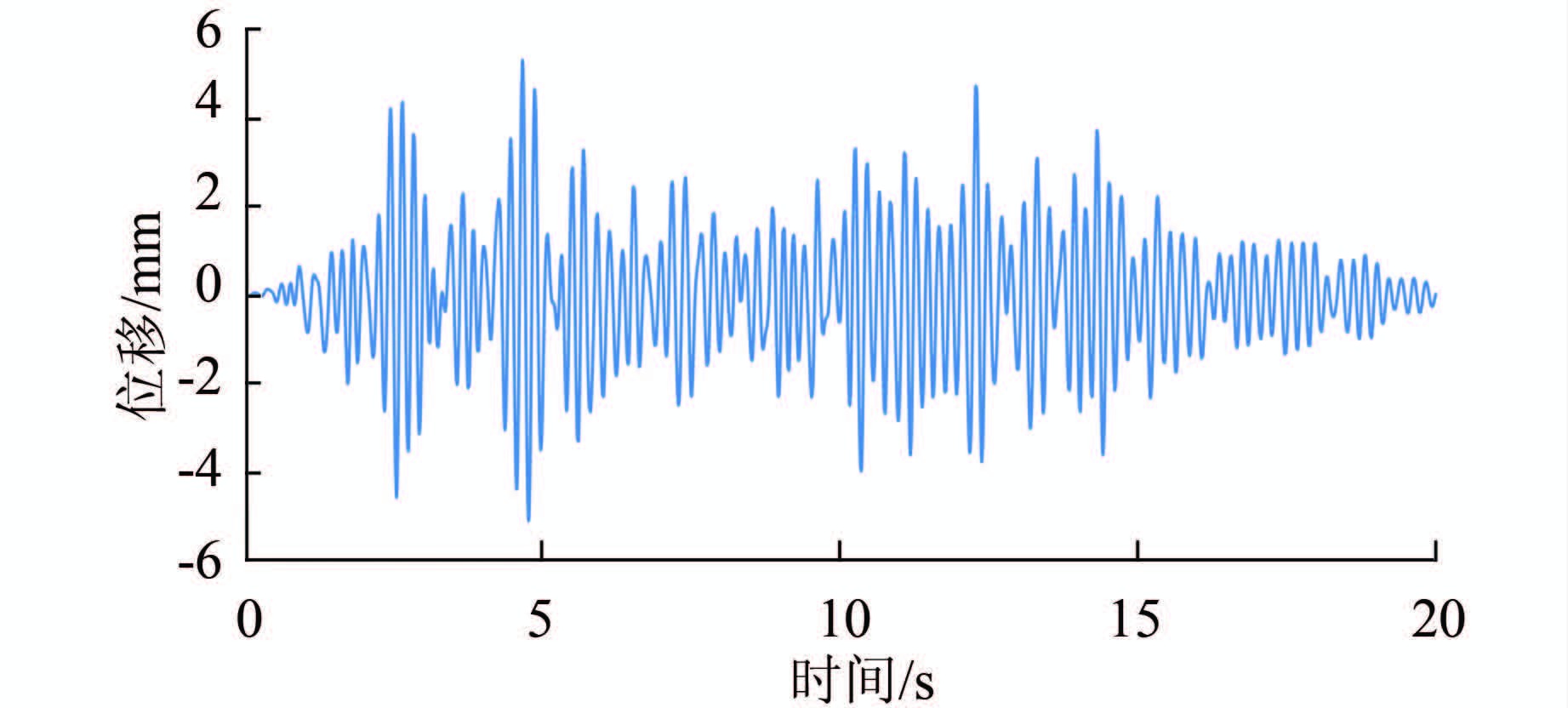
4 地震动力响应分析 4.1 位移响应分析满库工况下,由设计地震烈度引起的地震动位移总体呈现关于坝体中轴线对称分布的特征.顺河向动位移随着高程的增加而逐渐增大(见图 4),河床中部坝体动位移大于坝体两岸,最大值为5.20mm,出现在坝顶中部.横河向动位移分布规律基本类似,同一高程坝体水平截面上,上游侧动位移略大于下游侧,最大值2.11 mm,出现在坝顶处.竖直向动位移由坝体表面向坝体内部逐渐减小,最大值1.11 mm,出现在靠近坝体上游侧表面中部高程处.图 5为坝顶中央特征点的顺河向动位移时程曲线.由图可知顺河向动位移最大值出现时间为4.58 s.表 3为动位移响应比较.

|
| 图 4 河床中部坝体剖面顺河向动位移包络值分布图(单位:mm) Figure 4 Envelope diagram of horizontal dynamic displacement in central of the crest (unit: mm) |
|
| 图 5 坝顶中央顺河向动位移时程曲线 Figure 5 Time histories of dynamic displacement in central of the crest |
| 项目 | 横河向动位移 | 顺河向动位移 | 竖直向 动位移 | |
| 胶凝砂砾石坝空库工况 | 最大值/mm | 1.98 | 4.08 | 1.06 |
| 出现部位 | 坝顶上游侧中部 | 坝顶上游侧中部 | 靠近坝体上游侧表面中部高程处 | |
| 胶凝砂砾石坝满库工况 | 最大值/mm | 2.11 | 5.20 | 1.11 |
| 出现部位 | 坝顶上游侧中部 | 坝顶上游侧中部 | 靠近坝体上游侧表面中部高程处 | |
| 同等高度重力坝 | 最大值/mm | 5.10 | 12.81 | 4.27 |
| 出现部位 | 坝顶上游侧中部 | 坝顶中部 | 坝顶上游侧中部 | |
主要特点及分布规律:1)动位移分布随着高程的增加而逐渐增大;2)空库工况较满库工况的位移响应小,同一高程坝体水平截面上,满库工况上游侧动位移略大于下游侧;3)与同等高度同等地质条件下的重力坝相比,胶凝砂砾石坝的动位移明显较小.胶凝砂砾石坝的坝体下部的刚度较坝体上部刚度大,在动力作用下,坝体上部更易产生变形,所以动位移分布随高程增加而增大;动位移响应的剧烈程度主要受常规重力坝的三角形基本断面与胶凝砂砾石坝体的对称梯形断面的结构特性影响,基本断面为三角形的重力坝的悬臂梁结构型式使得坝体自下而上承受更大的弯曲变形,而对称梯形断面承受的弯曲变形较小,主要承受的是剪切变形;坝体剖面的增大使得坝体的动位移响应分布更加均匀;而又因为胶凝砂砾石坝的材料特点,在筑坝材料中掺入了胶凝材料,使得坝体具有较大的抗剪、抗冲、抗压能力.这样的变形特点,正好有利于发挥胶凝砂砾石坝的材料特性.胶凝砂砾石坝较小的动位移现象,也反映了胶凝砂砾石坝良好的抗震安全性能.
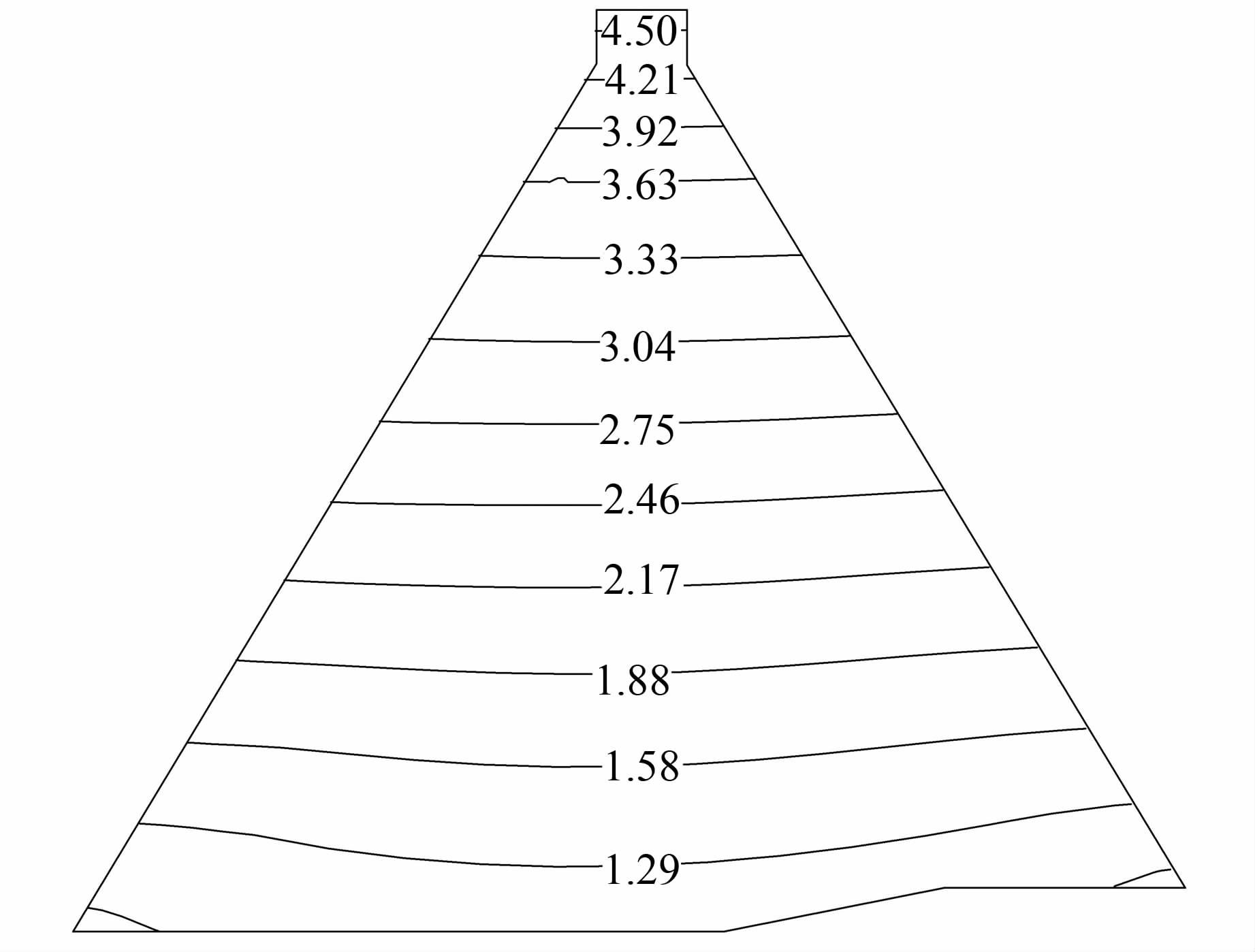
4.2 加速度响应分析满库工况下,河床中部坝体剖面顺河向加速度包络值分布如图 6所示.由图可知,大坝的顺河向加速度呈层分布,随着高程的增加而增大.河床中部坝体的加速度大于两岸坝体,在河床中部坝体顶部达到最大值4.61m/s2,放大系数为4.69.横河向加速度分布规律基本类似,同一高程坝体水平截面上,靠近坝体上游侧的地震加速度明显大于下游侧,在靠近坝顶上游侧中部达到最大值2.57 m/s2,放大系数为2.62.竖直向加速度呈现自上游面至下游面带状分布的规律,靠近上下游表面的加速度响应均较大,坝体内部中间偏下部位的加速度响应较小,在靠近坝体上游侧表面中部高程处达到最大值1.85 m/s2,放大系数为2.83.详见表 4所示.图 7为坝顶中央特征点的顺河向加速度时程曲线.由图可知顺河向加速度最大值出现时间为4.64 s.
|
| 图 6 河床中部坝体剖面顺河向加速度包络值分布图(单位:m/s2) Figure 6 Envelope diagram of horizontal dynamic acceleration in central of the crest (unit: m/s2) |

|
| 图 7 坝顶中央顺河向加速度时程曲线 Figure 7 Time histories of dynamic acceleration in central of the crest |
主要特点及分布规律:1)加速度随着高程的增加而增大,加速度总体呈现关于坝体中轴线对称分布的规律;2)空库工况的加速度响应较小,满库工况在靠近坝体上游侧的加速度响应稍剧烈;3)空库工况和满库工况下的竖直向加速度最大值都出现在坝体上游侧表面,而重力坝竖直向最大值出现在坝顶上游侧中部;4)与同等高度同等地质条件下的重力坝相比,胶凝砂砾石坝的加速度明显较小.由于和常规重力坝相比,除了坝体材料特性外,胶凝砂砾石坝的体型(体积和质量)更大,对称梯形的基本断面也使得坝底宽度(底面积)更大,坝体刚度增加,自振响应也有了一定程度的降低.同时相对于重力坝,由于胶凝砂砾石坝上游倾斜坝面的存在,坝库系统的动力相互作用有一定的增强,从某种程度上来说,也会对胶凝砂砾石坝的地震动力响应造成一定的影响.
| 项目 | 胶凝砂砾石坝空库工况 | 胶凝砂砾石坝满库工况 | 同等高度重力坝 | ||||||
| 最大值/(m·s-2) | 放大系数 | 出现部位 | 最大值/(m·s-2) | 放大系数 | 出现部位 | 最大值/(m·s-2) | 放大系数 | 出现部位 | |
| 横河向加速度 | 2.48 | 2.53 | 坝顶上游侧中部 | 2.57 | 2.62 | 坝顶上游侧中部 | 4.21 | 4.29 | 坝顶上游侧中部 |
| 顺河向加速度 | 4.27 | 4.35 | 坝顶上游侧中部 | 4.61 | 4.70 | 坝顶上游侧中部 | 9.05 | 9.23 | 坝顶上游侧中部 |
| 竖直向加速度 | 1.69 | 2.58 | 靠近坝体上游侧表面4/5高程处 | 1.85 | 2.83 | 靠近坝体上游侧表面中部高程处 | 3.81 | 5.83 | 坝顶上游侧中部 |
经过有限元计算,并按照最不利组合原则组合静态反应和动态反应得到综合反应.满库工况下,由图 8、9可知:应力在坝踵和坝趾处产生小范围的应力集中现象.胶凝砂砾石坝体的第一主应力只在坝顶位置和坝踵的很小范围内形成拉应力区,且拉应力数值小于0.4MPa.胶凝砂砾石坝顺河向应力最大值为0.13 MPa,出现在坝踵处.整体来说,胶凝砂砾石坝的地震动应力较小,大坝内部大部分区域处于受压状态.胶凝砂砾石坝体在靠近上下游表面中下部的地震动应力响应稍剧烈,但应力数值较小,且由于坝体外部表面常态混凝土层的存在,使坝体整体处于弹性状态,坝体应力远低于坝体材料的强度.

|
| 图 8 河床中部坝体剖面第一主应力包络值分布图(单位:MPa) Figure 8 Maximum envelope distribution of principal stress in central of the crest (unit: MPa) |

|
| 图 9 河床中部坝体剖面第三主应力包络值分布图(单位:MPa) Figure 9 Minimum envelope distribution of principal stress in central of the crest (unit: MPa) |
主要特点及分布规律:1)胶凝砂砾石坝体的动应力基本是呈现对称分布的特征;2)在靠近坝体表面和坝踵、坝趾位置处的数值较大,坝体内部应力较小,基本处于受压状态;3)空库工况较满库工况的应力响应小,应力分布规律基本类似;4)与同等高度同等地质条件下的重力坝相比,坝体整体动应力较小.这是由于胶凝砂砾石坝坝底宽度较大,应力沿底宽分布更均匀;坝体体型结构和材料特性等因素使得坝体刚度增加,坝体的地震响应程度也有所降低.由表 5可知,和重力坝相比,应力数值最多降低了84.13%.从结构动力学的角度,在梯形的对称基本断面的结构型式下,坝体受力条件较好,在胶凝砂砾石材料区域的坝体受力分布均匀,并且胶凝砂砾石材料的低弹模特性,降低了坝体应力响应水平,低弹模也有利于坝体抗裂.整体看来坝体在地震动力作用下,变形较小,应力响应较小.在强震作用下依然能够保持较低的应力水平,反映了这种坝型具有良好的抗震安全性能.在地震活动活跃区,修建这种坝型具有优势.
| MPa | |||
| 项目 | 胶凝砂砾石坝空库工况 | 胶凝砂砾石坝满库工况 | 同等高度重力坝 |
| 横河向应力 | 0.06 | 0.08 | 0.48 |
| 顺河向应力 | 0.11 | 0.13 | 0.75 |
| 竖直向应力 | 0.09 | 0.10 | 0.63 |
| 剪应力 | 0.12 | 0.16 | 0.30 |
| 第一主应力 | 0.25 | 0.39 | 1.21 |
| 第三主应力 | -1.98 | -2.80 | -3.96 |
本文主要分析了守口堡工程胶凝砂砾石坝的抗震性能,基于坝体-库水-地基系统的流固耦合三维有限元时程分析计算模型,考虑了地基的辐射阻尼效应.主要得出了以下几点结论:
1) 胶凝砂砾石坝系统的自振频率较低,满库工况相对于空库工况体系的自振频率也有所降低,库水特性在一定程度上影响了坝体的动力特性,这也从一定程度上体现了流固耦合的作用效果.
2) 胶凝砂砾石坝动位移与常规混凝土重力坝的分布规律基本类似,但胶凝砂砾石坝的动位移较常规混凝土重力坝小得多,胶凝砂砾石坝坝体的变形幅度较小,维持了坝体处于较高的稳定水平,反映了守口堡胶凝砂砾石坝体的结构型式和材料特性对坝体变形良好的作用效果.
3) 在地震动力作用下,胶凝砂砾石坝的地震加速度比常规重力坝小得多,胶凝砂砾石坝坝体刚度有所增加,同时上游侧倾斜坝面也可能影响了坝库系统的动力特性,地震加速度响应处于较低水平,反映了守口堡胶凝砂砾石坝的结构型式和材料特性对加速度响应的影响.
4) 在对称梯形断面结构型式下,坝体受力条件良好,应力分布也比较均匀.除坝趾坝踵少部分区域处于受拉状态,大部分坝体处于压应力状态.坝体在强震作用下,能够保持较低的应力水平,具有良好的抗震性能.
5) 胶凝砂砾石坝的地震动力响应在靠近坝体上下游表面及顶部较为明显.而守口堡胶凝砂砾石坝坝体表面常态混凝土层的存在使得坝体在强震状态下仍处于弹性状态,远低于坝体材料的强度,是非常有利的.但是我们从应力变形分布的规律也可以总结出,在靠近坝体表面位置的动应力数值随着高程的增加是在变化的,相对来说,坝体表面常态混凝土层在高程较低处应该稍厚一些以承受较大的动应力.而守口堡工程的坝体表面常态混凝土层自底而上等厚度设置,这部分表层混凝土刚度相对较大,在地震动力作用下可能容易产生裂缝.建议在今后的工程设计中对于胶凝砂砾石坝体表面混凝土层的设置采用不等厚的设置方案,深入融合抗震要求,同时综合抗渗要求和耐久性要求,具体的设置方案应根据具体的工程实际及抗震设计标准决定,需进一步论证,做到结构最优、经济合理.
| [1] | Raphael J M. The optimum gravity dam[C]// Proceeding Roller Compacted Concrete III, ASCE, San Diego, California, 1992: 5-19. |
| [2] | Londe P, Lino M. The faced symmetrical Hardfill dam: A new concept for RCC[C]//International Water Power & Dam Construction, 1992: 19-24. |
| [3] |
何蕴龙, 彭云枫, 熊堃. Hardfill坝筑坝材料工程特性分析[J].
水利与建筑工程学报, 2007, 5(4): 1–6.
He Yunlong, Peng Yunfeng, Xiong Kun. Analysis on material property of Hardfill dam[J]. Journal of Water Resources and Architectural Engineering, 2007, 5(4): 1–6. |
| [4] | Batmaz S.Cindere dam-107 m high roller compacted Hardfill dam(RCHD) in Turkey[C]// Proceeding 4th International Symposium on Roller Compacted Concrete Dams, 2003: 121-126. |
| [5] | Batmaz S, Koksal A, Ergeneman I, et al. Design of the Oyuk Hardfill Dam[J]. Hunan Hydro & Power, 2009(1): 92–95. |
| [6] |
杨朝晖, 赵其兴, 符祥平. CSG技术研究及其在道塘水库的应用[J].
水利水电技术, 2007, 38(8): 46–49.
Yang Zhaohui, Zhao Qixing, Fu Xiangping. Study on CSG dam construction technique and its application to Daotang reservoir project[J]. Water Resources and Hydropower Engineering, 2007, 38(8): 46–49. |
| [7] |
陈振华, 林胜柱, 王健亮. 洪口水电站碾压贫胶砂砾料筑坝技术研究[J].
水力发电, 2008, 34(1): 79–81.
Chen Zhenhua, Lin Shengzhu, Wang Jianliang. Research & application of construction technique for Hongkou dam using lean cement roll compacting aggregate[J]. Water Power, 2008, 34(1): 79–81. |
| [8] | Hirose T, Fujisawa T, Kawasaki H, et al. Design concept of trapezoid-shaped CSG dam[C]// Proceedings 4th International Symposium on Roller Compacted Concrete Dams, Madrid, 2003: 457-464. |
| [9] | Liapichev Y P. Seismic stability and stress-strain state of a new type of FSH-RCC dams[C]// Proceedings 4th International Symposium on Roller Compacted Concrete Dams, Madrid, 2003: 485-492. |
| [10] |
何蕴龙, 肖伟, 李平. Hardfill坝横向地震反应分析的剪切楔法[J].
武汉大学学报(工学版), 2008, 41(4): 38–42.
He Yunlong, Xiao Wei, Li Ping. Shear wedge method of lateral seismic response analysis of Hardfill dams[J]. Engineering Journal of Wuhan University, 2008, 41(4): 38–42. |
| [11] |
于跃, 张艳峰, 何蕴龙, 等. 基于剪切楔法的Hardfill坝自振特性和动力反应分析[J].
天津大学学报, 2009, 42(5): 327–334.
Yu Yue, Zhang Yanfeng, He Yunlong, et al. Analysis on free vibration and dynamic response of hardfill dams based on shear wedge method[J]. Journal of Tianjin University, 2009, 42(5): 327–334. |
| [12] |
裴镔. Hardfill坝地震动力响应的比较分析[J].
水电能源科学, 2010, 28(2): 85–88.
Pei Bin. Comparative analysis of seismic dynamic response of Hardfill dam[J]. Water Resources and Power, 2010, 28(2): 85–88. |
| [13] |
刘晶波, 吕彦东. 结构-地基动力相互作用问题分析的一种直接方法[J].
土木工程学报, 1998, 31(3): 55–64.
Liu Jingbo, Lu Yandong. A direct method for analysis of dynamic soil-structure interaction[J]. China Civil Engineering Journal, 1998, 31(3): 55–64. |
| [14] |
冯炜.胶凝砂砾石坝筑坝材料特性研究与工程应用[D].北京:中国水利水电科学研究院, 2013.
Feng Wei. Studies on cemented sand and gravel dam material and its application[D].Beijing: China Institute of Water Resources & Hydropower Research, 2013. http://cdmd.cnki.com.cn/Article/CDMD-82301-1013293880.htm |
| [15] |
黄耀英, 孙大伟, 田斌. 两种库水附加质量模型的重力坝动力响应研究[J].
人民长江, 2009, 40(7): 64–66.
Huang Yaoying, Sun Dawei, Tian Bin. The dynamic analysis of gravity dam under two added water mass models[J]. Yangtze River, 2009, 40(7): 64–66. |
 2016, Vol. 49
2016, Vol. 49




