文章信息
- 杨会娟, 付湘, 韩琦, 涂月明
- YANG Huijuan, FU Xiang, HAN Qi, TU Yueming
- 基于互信息熵的水库实时调度相关分析及预测
- Correlation analysis and forecast of realtime reservoir operation based on mutual information entropy
- 武汉大学学报(工学版), 2018, 51(5): 383-388
- Engineering Journal of Wuhan University, 2018, 51(5): 383-388
- http://dx.doi.org/10.14188/j.1671-8844.2018-05-002
-
文章历史
- 收稿日期: 2017-10-28
2. 武汉大学水资源安全保障湖北省协同创新中心,湖北 武汉 430072
2. Hubei Provincial Collaborative Innovation Center for Water Resources Security, Wuhan University, Wuhan 430072, China
水库调度系统是受多种因素影响的复杂非线性系统,针对水电站水库群系统的多目标、多变量与非线性的特点,越来越多的算法(动态规划、均匀动态规划、神经网络、遗传算法、差分进化算法等)被用于优化模拟水库的调度运行.在优化模拟过程中,研究者将所研究的水库系统概化为拥有一个或多个目标函数,且满足一组约束条件的数学方程,常常通过改善径流的预报精度或算法的结构来取得较好的模拟效果[1-5].但受算法复杂程度及模型概化的限制,加上水文、水力条件的随机性,导致水库优化调度结果也具有不确定性[6].
消除的不确定性即为获得的信息量[7],互信息熵是信息论中的一种信息度量,表示信息之间的关系、度量变量之间相关性的强弱.因其提供了一种通用的衡量两个变量间相关程度的方法,故而广泛应用于变量相关性的识别与评估.如:卢迪等[8]利用互信息熵法选择中长期径流预报模型的输入因子,有效地识别出多个预报因子与预报变量间的复合相关性;赵铜铁钢等[9]利用互信息熵判断待选预报因子与预报变量之间的相互关系,对三峡工程建成前宜昌水文站的日径流预报进行了研究;Hejazi等[10]根据熵与互信息熵理论,通过对历史流量数据分析,探讨了水文信息在水库管理者操作中所起的作用;路剑飞等[11]以广东省西江流域为例,用互信息熵进行径流和降水预报方案的优选.
互信息熵就是信息增益,表示某种属性数据的增加使得系统由不确定性变成确定性的能力增强.随着数据库管理系统广泛应用到水库调度中,水库调度部门积累的实测调度数据日益增多,数据库系统可以高效地实现数据的查询与统计等功能,但无法发现数据中存在的相关关系和规则,无法根据现有的数据预测未来的调度函数,导致出现数据丰富但信息贫乏的现象.如何在繁杂的实测数据中提取有价值的信息,减少不确定性,是摆在研究者面前的一个挑战.
本文针对水库实际运行中存在诸多不确定性的特点[10],根据收集到的水库调度实时数据,利用互信息熵的原理与方法,对水库调度决策数据与潜在相关因素数据进行相关分析,并准确剔除相关性高的潜在关联因素数据.最后,以筛选的强关联因素数据作为输入,建立各分期的水库调度预测模型,实现基于数据驱动的水库调度强关联因素识别及预测建模,用以指导今后的水库调度.
1 研究方法 1.1 互信息熵的计算随机变量X和Y之间互信息熵的定义有如下两种表达形式:
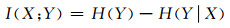 (1)
(1)
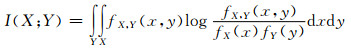 (2)
(2)
式中:H(Y)为随机变量Y的熵;H(Y|X)为已知自变量X下Y的熵(条件熵);I(X; Y)为X和Y的互信息,表示信息增益;fX, Y(x, y)为X和Y之间的联合密度函数;fX(x)和fY(y)分别为X、Y的边际密度函数.信息增益越大表示条件X对于系统的确定性贡献越大,在统计学意义上,互信息表达了两随机变量之间的相互依赖性.
由式(2)可知,互信息熵计算的关键在于估计联合概率密度,常见的方法有直方图法与核函数法.由于互信息熵估计的准确度受到联合概率密度估计的影响,因此,本文还采用k最邻近距离法计算互信息熵进行比较.
1.1.1 直方图法直方图法是非参数方法中最简单、最常用的一种,具有实现简单、计算效率高的特点,可以用来近似常见的分布.通过对坐标轴进行划分,统计落在各区间的样本的个数,即可求得变量的近似概率密度函数[12].直方图方法求得二维随机变量x、y的联合概率密度函数为
 (3)
(3)
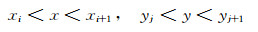
式中:n为样本容量;lx和ly为用来划分x轴和y轴的区间长度;xi和xi+1分别为x轴上第i个区间的始末坐标(i=1~I,共分为I个区间);yj和yj+1分别为y轴上第j个区间的始末坐标(j=1~J,共分为J个区间);ni, j为落在区间(xi, xi+1)、(yj, yj+1)内的样本点数目.
使用直方图法最重要的是确定划分坐标轴的区间长度l,不同的区间长度导致计算的互信息熵存在着差异.因此,l的取值要慎重,既不能取得过大使计算结果过于粗糙,也不能取得太小使结果失真.本文使用下式[13]计算区间的长度:
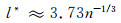 (4)
(4)
核函数方法的基本思想为:每个样本点的权重随其到目标点的距离平滑衰减.其计算方法与核函数的选择有关,常用的有均匀核、高斯核等.当选择高斯核作为核函数时,多维核密度估计[14]可表示为
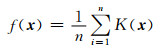 (5)
(5)
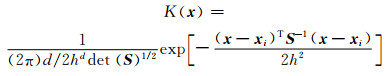 (6)
(6)
式中:K(x)为多维核函数,代表基于x和xi之间的距离而赋予xi的权重;x=[x1, x2, …, xd]T是d维随机向量;xi=[x1i, x2i, …, xdi],i=1~n,为样本向量;h为核带宽;S为关于xi的协方差矩阵,用来识别可能存在的线性关系.从式(5)可以看出,核密度估计为观测点在临近点中出现频率的局部权重平均值.
f(x)对带宽h的选择较为敏感,带宽过小会导致密度估计过于尖锐,过大则会导致过于平滑且不能保证估计的无偏性.这里选择使用简化的最优高斯带宽:
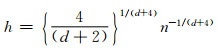 (7)
(7)
k最邻近距离法以落在xi为中心的体积为V的区域内k个样本的比例作为密度的近似值.计算互信息熵的方法如下[15](记L为Zi到其第k个临近点的距离):
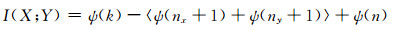 (8)
(8)
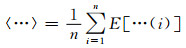 (9)
(9)
式中:ψ()为双伽马函数;n为样本容量;nx(i)为xi和xj之间的距离小于L的样本个数;ny(i)为yi和yj之间的距离小于L的样本个数.由于L为自由变量,nx(i)和ny(i)会随之波动,因此用其期望值代替.
1.2 非线性相关系数基于互信息熵的二元随机变量X、Y之间的相关系数可用下式[16]计算:
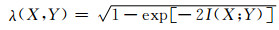 (10)
(10)
式中:λ(X, Y)为变量X和Y之间的相关系数.
1.3 相关性贡献的计算不同时期各水文变量对当前时段出库流量的相关性贡献由下式计算:
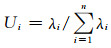 (11)
(11)
式中:Ui为第i个水文变量的相关性贡献;λi为第i个水文变量与当前时段出库流量之间的相关系数;n为水文变量的个数.
1.4 水库实时调度函数预测在获得多种关联因素的基础上,以较为简单的线性函数为基础,根据最小二乘原理,利用lingo软件预测调度函数,具体形式为
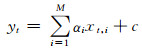 (12)
(12)
式中:xt, i为t时段的第i个自变量;αi为第i个自变量因子对应的拟合系数;c为残差项;yt为预测的t时段决策变量;M为自变量的总数.
2 实例研究将上述计算方法应用于三峡水库实时调度相关性分析与预测.三峡水库2003年6月进入围堰发电期,初步发挥发电、通航的作用;2006年9月进入初期运行期,水库按防洪、发电、航运等综合利用任务调蓄.因此,本文所使用数据为三峡水库正常运行期2007年5月1日-2015年10月31日实测的入库流量、出库流量、上游水位、下游水位数据.根据三峡水库的实际调度运行特点,将一年划分为集中消落期(5月上旬-6月上旬)、汛期(6月中旬-9月上旬)、蓄水期(9月中旬-10月下旬)、枯水期(11月上旬-4月下旬)4个时期,每个时期以日为时段,进行分析计算.
2.1 互信息的比较水库调度决策数据为当前时段出库流量(Rt),与决策变量潜在相关因子数据为当前时段入库流量(It)、前一时段入库流量(It-1)、前一时段出库流量(Rt-1)、水库可用水量AQt(为蓄水流量与当前时段入库水量之和).在水库集中消落期、汛期、蓄水期、枯水期,根据实测水库调度日数据,运用公式(1)~(9)分别计算因变量Rt与自变量It、It-1、Rt-1、AQt的互信息熵.由于受区间长度、核带宽及最邻近个数k的选择影响,3种方法计算的互信息熵存在差异,由图 1可知,直方图法、k最邻近距离法与核密度估计方法得到的Rt与AQt之间的互信息熵在4个时期均较小.对于其他3个因子,经计算可知,除了枯水期3种方法计算的互信息熵相对差值稍大外(50%以内),其余3个时期的相对差值均在20%以内,差别不大.此外,屈文建等[17]研究表明,与直方图方法、k最邻近距离方法相比,在估计精度和可操作性方面,核密度估计方法较为合理;牛君[18]也指出,与直方图方法相比,核密度估计方法精度高且连续,因此,下文均根据核密度估计方法的计算结果进行分析.
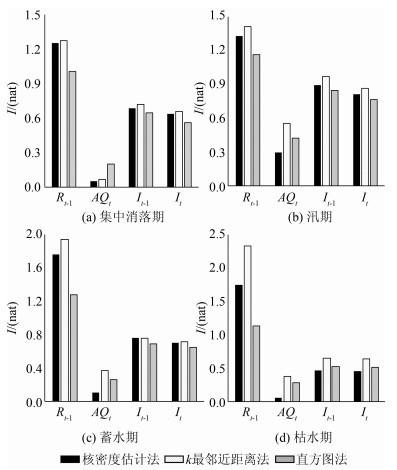
|
| 图 1 3种方法计算的互信息熵比较 Figure 1 Comparison of mutual information entropies |
由表 1可知,不论是在集中消落期、汛期、蓄水期还是枯水期,与当前时段出库流量之间互信息熵最大的均为前一时段的出库流量,而当前时段及前一时段的入库流量与当前时段出库流量之间的互信息熵相差不大,可用水量与当前时段出库流量之间的互信息熵则较小.这说明影响水库管理者做出泄流决策的水文信息有很大一部分来自于前一时段的出库流量,而并非一般优化模型中所考虑的当前时段的入库流量.
| 时期 | 互信息熵/(nat) | |||
| Rt-1 | AQt | It-1 | It | |
| 集中消落期 | 1.25 | 0.05 | 0.68 | 0.64 |
| 汛期 | 1.32 | 0.29 | 0.89 | 0.81 |
| 蓄水期 | 1.77 | 0.10 | 0.76 | 0.70 |
| 枯水期 | 1.74 | 0.05 | 0.47 | 0.45 |
根据式(10)计算各水文变量与出库流量之间的相关系数(包括线性相关和非线性相关).由表 2可知,在集中消落期、汛期、蓄水期及枯水期,当前时段的出库流量与当前时段及前一时段的入库流量、前一时段的出库流量相关性都比较大.总的来说,与当前时段出库流量相关性最强的为前一时段的出库流量,在4个时期的相关系数均达到了0.96以上;当前时段及前一时段的入库流量与当前时段的出库流量之间的相关性随时期不同而变化,除了在枯水期相关性稍弱之外,其余3个时期也存在较大的相关性(均在0.85以上);当前时段的可用水量与出库流量之间则表现出较弱的相关性.由于多个水文变量与当前时段的出库流量之间存在较强的相关性,在选择优化模型的变量时,若只考虑单一变量,则会因为输入信息不全面而导致优化模型难以在实际操作中充分发挥作用.
| 时期 | 相关系数 | |||
| Rt-1 | AQt | It-1 | It | |
| 集中消落期 | 0.96 | 0.32 | 0.86 | 0.85 |
| 汛期 | 0.96 | 0.67 | 0.91 | 0.90 |
| 蓄水期 | 0.99 | 0.42 | 0.88 | 0.87 |
| 枯水期 | 0.98 | 0.32 | 0.78 | 0.77 |
根据式(11)计算水文变量对当前时段出库流量的相关性贡献,经分析可知(表 3),前一时段入库流量与当前时段入库流量、前一时段出库流量之间存在较大的相关性(皮尔逊相关),而当前时段的入库流量与前一时段出库流量之间的相关性又稍弱,故在此只考虑前一时段出库流量与当前时段入库流量对当前时段出库流量的相关性贡献.
| R | 相关性 | |||
| 集中消落期 | 汛期 | 蓄水期 | 枯水期 | |
| It、It-1 | 0.91 | 0.92 | 0.93 | 0.98 |
| Rt-1、It | 0.72 | 0.78 | 0.80 | 0.77 |
| Rt-1、It-1 | 0.81 | 0.86 | 0.86 | 0.80 |
由计算可知,在集中消落期、汛期、蓄水期和枯水期,前一时段的出库流量对当前时段出库流量决策的相关性贡献均超过了50%;当前时段的入库流量对出库流量的相关性贡献在40%以上.这说明在使用历史调度数据时,需准确剔除相关性高的潜在关联因素数据,筛选出水库调度决策变量的强相关因素.
2.4 实时调度函数由上述分析可知,在各时期对当前时段出库流量影响最大的为前一时段的出库流量,但当前时段入库流量也存在一定的影响,不应被忽视,故选择前一时段出库流量、当前时段入库流量两个因子作为模拟变量,通过公式(12)对出库流量进行模拟预测.根据水库实际调度特点,式(12)中自变量为当前时段入库流量It与前一时段出库流量Rt-1两个因子,因变量yt替换为当前时段出库流量Rt.采用2007-2012年的数据进行拟合建模,2013-2015年的数据进行验证,以纳西效率系数作为指标来评价模拟效果的优劣,模拟和验证的结果见表 4及图 2.每个时期最终采用的拟合函数的形式为
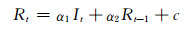 (13)
(13)
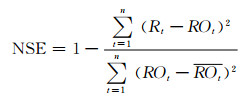 (14)
(14)
| 时期 | 拟合系数 | NSE | ||
| α1 | α2 | c | ||
| 集中消落期 | 0.35 | 0.71 | -156.82 | 0.88 |
| 汛期 | 0.25 | 0.71 | 831.48 | 0.91 |
| 蓄水期 | 0.16 | 0.84 | -643.99 | 0.96 |
| 枯水期 | 0.13 | 0.85 | 193.06 | 0.94 |
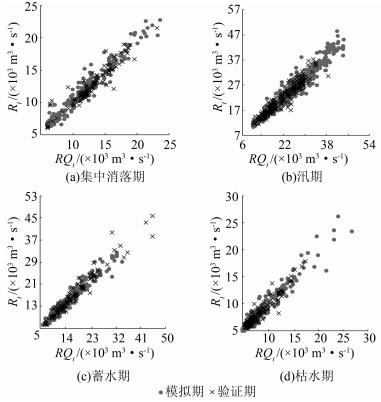
|
| 图 2 不同时期出库流量模拟(验证)趋势图 Figure 2 Simulation (validation) trends of reservoir release flows at different periods |
式中:NSE为验证期的纳西效率系数;ROt为实测的t时段出库流量,m3/s;
由表 4中的纳西效率系数可知,在集中消落期、汛期、蓄水期及枯水期,用2013-2015年的数据进行验证时,纳西效率系数均在0.88以上,说明在验证阶段模拟值与实测值较为接近,取得了较高的模拟精度.特别在蓄水期时,当出库流量较大时,验证阶段数据的变化趋势与模拟阶段相符(图 2(c)).
根据2013-2015年的入库流量数据及水库的调度规程,利用建立的调度函数模型进行分期预测,并计算相应的日出力.预测调度所得各时期日平均出力与实际日平均出力(2013-2015年)的对比如表 5所示.由表 5可知,在4个时期,由调度函数所得的日平均出力与实际日平均出力的相对差值均在±5%以内,这说明调度函数模型有较好的适用性.
| 时期 | 实际日均出力/(万kW) | 预测日均出力/(万kW) | 相对误差/% |
| 集中消落期 | 949 | 926 | -2.38 |
| 汛期 | 1 396 | 1 450 | 3.89 |
| 蓄水期 | 1 236 | 1 239 | 0.18 |
| 枯水期 | 627 | 612 | -2.39 |
本文运用互信息熵原理进行水库实时调度相关分析及预测,得出如下结论:
1) 通过收集实测水库调度日数据,运用直方图法、核密度估计法及k最邻近距离法3种方法计算水库调度决策数据与潜在相关因素数据的互信息熵.3种方法计算的互信息熵存在不同,但差异不大.
2) 利用互信息熵进行相关性贡献分析,并剔除相关性高的属性数据.识别出前一时段出库流量与当前时段入库流量两个自变量因子,作为水库调度决策变量的强相关因素,实现基于数据驱动的水库调度强关联因素筛选.
3) 以筛选出的自变量因子作为输入,在水库集中消落期、汛期、蓄水期和枯水期分别建立水库实时调度预测模型,取得了较高的精度并降低了建模的复杂度,解决了传统优化调度对实测数据库信息挖掘不足的问题.
| [1] |
陈璐, 卢韦伟, 周建中, 等. 水文预报不确定性对水库防洪调度的影响分析[J].
水利学报, 2016, 47(1): 77–84.
Chen Lu, Lu Weiwei, Zhou Jianzhong, et al. Effect of streamflow forecast uncertainty on reservoir operation[J]. Journal of Hydraulic Engineering, 2016, 47(1): 77–84. |
| [2] |
郑慧涛, 梅亚东, 胡挺, 等. 改进差分进化算法在梯级水库优化调度中的应用[J].
武汉大学学报(工学版), 2013, 46(1): 57–61.
Zheng Huitao, Mei Yadong, Hu Ting, et al. Improved differential evolution algorithm and its application to optimial operation of cascade reservoirs[J]. Engineering Journal of Wuhan University, 2013, 46(1): 57–61. |
| [3] |
何向阳, 周建中, 张勇传, 等. 基于改进NSGA-Ⅱ的梯级水电站多目标发电优化调度[J].
武汉大学学报(工学版), 2011, 44(6): 715–719.
He Xiangyang, Zhou Jianzhong, Zhang Yongchuan, et al. Multiobjective optimal dispatching of cascade hydropower stations using improved NSGA-Ⅱ[J]. Engineering Journal of Wuhan University, 2011, 44(6): 715–719. |
| [4] |
陈森林, 董建凡, 郭乐, 等. 基于改进基尼系数的水电站年最优发电量变化规律研究[J].
水利学报, 2014, 45(12): 1450–1457.
Chen Senlin, Dong Jianfan, Guo Le, et al. Improved Gini coefficient and annual optimal generation changing rules of hydropower station[J]. Journal of Hydraulic Engineering, 2014, 45(12): 1450–1457. |
| [5] |
刘攀, 郭生练, 雒征, 等. 求解水库优化调度问题的动态规划-遗传算法[J].
武汉大学学报(工学版), 2007, 40(5): 1–6.
Liu Pan, Guo Shenglian, Luo Zheng, et al. Optimization of reservoir operation by using dynamic programming-genetic algorithm[J]. Engineering Journal of Wuhan University, 2007, 40(5): 1–6. |
| [6] |
付湘, 刘庆红, 吴世东. 水库调度性能风险评价方法研究[J].
水利学报, 2012, 43(8): 987–990.
Fu Xiang, Liu Qinghong, Wu Shidong. Risk assessment approach for reservoir operation performance[J]. Journal of Hydraulic Engineering, 2012, 43(8): 987–990. |
| [7] |
周荫清.
信息理论基础[M]. 北京: 北京航空航天大学出版社, 2012.
Zhou Yinqing. Information Theory Basis[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2012. |
| [8] |
卢迪, 周惠成. 基于互信息量与BP神经网络的中长期径流预报方法研究[J].
水文, 2014, 34(8): 8–14.
Lu Di, Zhou Huicheng. Medium and long-term runoff forecasting based on mutual information and BP neural network[J]. Journal of China Hydrology, 2014, 34(8): 8–14. |
| [9] |
赵铜铁钢, 杨大文. 神经网络径流预报模型中基于互信息的预报因子选择方法[J].
水力发电学报, 2011, 30(1): 24–30.
Zhao Tongtiegang, Yang Dawen. Mutual information-based input variable selection method for runoff-forecasting neural network model[J]. Journal of Hydroelectric Engineering, 2011, 30(1): 24–30. |
| [10] | Hejazi M I, Cai X M, Ruddel B L. The role of hydrologic information in reservoir operation-Learning from historical releases[J]. Advances in Water Resources, 2008(31): 1636–1650. |
| [11] |
路剑飞, 陈子燊, 王扬圣. 基于MI-ANFIS的中长期水文预报方案优选研究[J].
水力发电学报, 2013, 32(2): 48–53.
Lu Jianfei, Chen Zishen, Wang Yangsheng. Optimization selection of mid and long-term hydrologic forecast schemes based on MI-ANFIS[J]. Journal of Hydroelectric Engineering, 2013, 32(2): 48–53. |
| [12] |
丁晶, 王文圣, 赵永龙. 以互信息为基础的广义相关系数[J].
四川大学学报(工程科学版), 2002(3): 1–5.
Ding Jing, Wang Wensheng, Zhao Yonglong. General correlation coefficient between variables based on mutual information[J]. Journal of Sichuan University (Engineering Science Edition), 2002(3): 1–5. |
| [13] |
龚伟. 基于信息熵和互信息的流域水文模型不确定性分析[D]. 北京: 清华大学, 2012.
Gong Wei. Watershed model university analysis based on information entropy and mutual information[D]. Beijing: Tsinghua University, 2012. |
| [14] | Moon Y, Rajagopalan B, Lall U. Estimation of mutual information using kernel density estimators[J]. Physical Review E, 1995, 52(3): 2318–2321. DOI:10.1103/PhysRevE.52.2318 |
| [15] | Kraskov A, Stogbauer H, Grassberger P. Estimating mutual information[J]. Physical Review E, 2004, 69(6): 6138–6153. |
| [16] | Khan S, Ganguly A R, Bandyopadhyay S, et al. Nonlinear statistics reveals stronger ties between ENSO and the tropical hydrological cycle[J]. Geophysical Research Letters, 2006, 33(24): 10. |
| [17] |
屈文建, 熊国经. 非参数密度估计法比较分析及应用[J].
沈阳农业大学学报, 2008, 39(4): 468–472.
Qu Wenjian, Xiong Guojing. Analysis and application research on nonparametric density estimation[J]. Journal of Shenyang Agricultural University, 2008, 39(4): 468–472. |
| [18] |
牛君. 基于非参数密度估计点样本分析建模的应用研究[D]. 济南: 山东大学, 2007.
Niu Jun. Application study based on point sample analysis and modeling using nonparametric density estimation[D]. Jinan: Shandong University, 2007. |
 2018, Vol. 51
2018, Vol. 51




