武汉大学学报 (工学版)   2017, Vol. 50 Issue (1): 1-17

文章信息

李典庆, 郑栋, 曹子君, 唐小松
LI Dianqing, ZHENG Dong, CAO Zijun, TANG Xiaosong
边坡可靠度分析的响应面方法比较研究
Comparison among response surface methods for slope reliability analysis
武汉大学学报 (工学版), 2017, 50(1): 1-17
Engineering Journal of Wuhan University, 2017, 50(1): 1-17
http://dx.doi.org/10.14188/j.1671-8844.2017-01-001

文章历史

收稿日期: 2016-10-31
 Abstract              PDF               Figures               Tables
引用本文 0
李典庆, 郑栋, 曹子君, 唐小松. 边坡可靠度分析的响应面方法比较研究[J]. 武汉大学学报(工学版), 2017, 50(1): 1-17.
LI Dianqing, ZHENG Dong, CAO Zijun, TANG Xiaosong. Comparison among response surface methods for slope reliability analysis[J]. Engineering Journal of Wuhan University, 2017, 50(1): 1-17.
边坡可靠度分析的响应面方法比较研究
李典庆1,2, 郑栋1,2, 曹子君1,2, 唐小松1,2     
1. 武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072;
 2. 武汉大学水工岩石力学教育部重点实验室，湖北 武汉 430072
收稿日期：2016-10-31
作者简介：李典庆 (1975-)，男，教授，主要从事岩土工程可靠度与风险分析方面的研究，E-mail：dianqing@whu.edu.cn.
基金项目：国家自然科学基金项目 (编号：51329901, 51579190, 51528901);湖北省自然科学基金创新群体项目 (编号：2014CFA001).
摘要：系统地总结了多种响应面法 (RSM) 在不同类型边坡可靠度问题中的应用情况，通过文献分析总结出4类典型土坡可靠度问题：问题Ⅰ, 单层土坡不考虑参数空间变异性；问题Ⅱ, 单层土坡考虑参数空间变异性；问题Ⅲ, 多层土坡不考虑参数空间变异性；问题Ⅳ, 多层土坡考虑参数空间变异性.重点研究了基于多项式的4种响应面法 (SQRSM、MQRSM、SSRSM和MSRSM) 在解决4类土坡可靠度问题 (问题Ⅰ~Ⅳ) 中的有效性.分别从计算精度和计算效率两个方面系统地比较了4种响应面法在黏性土坡和c-ϕ土坡可靠度问题中的适用性.结果表明：对于不考虑土性参数空间变异性的单层土坡可靠度问题 (问题Ⅰ)，推荐SQRSM；当单层土坡考虑土性参数空间变异性时 (问题Ⅱ)，推荐MSRSM；对于不考虑空间变异性的多层土坡可靠度问题 (问题Ⅲ)，推荐MQRSM；对于考虑参数空间变异性的多层土坡可靠度问题 (问题Ⅳ)，推荐采用MSRSM方法.
关键词：边坡稳定    可靠度    空间变异性    响应面法    失效概率    
Comparison among response surface methods for slope reliability analysis
LI Dianqing1,2, ZHENG Dong1,2, CAO Zijun1,2, TANG Xiaosong1,2     
1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;
 2. Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering of Ministry of Education, Wuhan University, Wuhan 430072, China
Abstract: The applications of various response surface methods (RSMs) in different slope reliability problems are systematically analyzed. On the base of literature review, four typical types of soil slope reliability problems (Problems Ⅰ-Ⅳ) are summarized. Problem I: single-layered soil slope ignoring spatial variability; Problem Ⅱ: single-layered soil slope considering spatial variability; Problem Ⅲ: multiple-layered soil slope ignoring spatial variability; Problem Ⅳ: multiple-layered soil slope considering spatial variability. Concentrating on dealing with the four typical types of problems, the validity of four polynomial-based RSMs (SQRSM, MQRSM, SSRSM and MSRSM) is studied. In terms of computational accuracy and efficiency, the applicability and feasibility of the four polynomial-based RSMs for cohesive and c-ϕ slopes are systematically compared. The results indicate that for the single-layered soil slope ignoring spatial variability (i.e. Problem Ⅰ), SQRSM is recommended. For the single-layered soil slope considering spatial variability (i.e. Problem Ⅱ), MSRSM is applicable. For the multiple-layered soil slope ignoring spatial variability (i.e. Problem Ⅲ), MQRSM is reasonable. For the multiple-layered soil slope considering spatial variability (i.e. Problem Ⅳ), MSRSM is suggested.
Key words: slope stability     reliability     spatial variability     response surface method     probability of failure    

在过去几十年里，土坡可靠度问题一直是岩土工程可靠度领域重点研究内容之一，国内外众多学者均对该问题进行了大量的研究[1-98]，提出了诸多的边坡可靠度计算方法，例如一次二阶矩法[3, 25-28]、一阶可靠度方法[5-6, 15, 29-32]、二阶可靠度方法[33]和蒙特卡洛模拟方法[6, 8, 21, 34-38]及其改进的蒙特卡洛模拟方法[11-13, 24, 39].除了上述方法外，响应面法 (RSM) 也常用于具有隐式功能函数的土坡可靠度问题[14, 16-23, 40-42].大量研究表明响应面法是一种高效的边坡可靠度计算方法[70].1985年Wong[40]首次将响应面法应用到土坡可靠度问题.随后，Xu和Low[41]采用基于多项式的响应面逼近边坡可靠度分析的功能函数，建立了边坡稳定数值分析模块与嵌有可靠度分析功能的EXCEL间的关系.随后，多位学者[43-47]提出了一种基于支持向量机 (SVM) 的响应面法，通过获取少量的真实功能函数值及输入参数值以逼近可靠度分析中的功能函数.Tan等[48]基于径向基函数神经网络 (RBFN) 的近似响应面作为真实功能函数，讨论了基于RBFN和SVM的两种响应面间的异同点.为减少功能函数的计算次数，Tan等[49]提出了两种样本产生方法和一种混合响应面法.与基于SVM的响应面类似，基于关联向量机 (RVM) 的FOSM被用于建立RVM模型[50]，以此逼近隐式功能函数，并得到具有足够准确性的偏导数.此外，向量投影[51]、随机响应面[67, 70]、人工神经网络 (ANN) 技术[7]、高斯过程回归 (GPR)[52, 54-55]、人工蜂群演算法 (ABC) 优化的支持向量回归 (SVR)[53]、高维模型表示 (HDMR)[56]和神经网络 (NN)[57-58]也都被用于建立边坡安全系数 (FS) 与土体参数之间的函数关系.不仅如此，基于二阶多项式的传统响应面[18, 59-61]因其简单且容易实现在土坡可靠度分析中也有很多应用.Luo等[62-63]、Zhang等[16, 18]、邓志平等[97]和苏永华等[64-65]采用基于Kriging的响应面模拟真实功能函数，证实了该方法在分析边坡可靠度问题的适用性.Yi等[66]的研究结果表明经粒子群算法优化后的Kriging模型具有较好的曲线拟合功能.近年来，在采用响应面法的边坡可靠度分析中，响应面法的一个重要进展是多重响应面法的提出并将其成功应用于解决边坡系统可靠度问题.Zhang等[17]于2011年首次提出了用于边坡可靠度分析的多重响应面法.Ji和Low[14]针对边坡的最有可能失效模式，建立了一组多层响应面，得到了边坡在多失效模式下的系统可靠度水平.Zhang等[19]拓展了Hassan和Wolff[25]于1999年提出的一种搜寻关键性滑动面的方法，基于该滑动面利用展开的二阶多项式计算了多层土坡系统可靠度，为边坡系统可靠度分析提供了一种有效的分析工具.

上述研究为响应面法用于边坡可靠度分析作了大量有益的研究工作，然而这些研究均没有考虑土性参数的空间变异性.为此，Ji[91]首次在考虑土体参数空间变异性的情况下利用带有交叉项的二阶展开多项式分析了土坡可靠度问题.Jiang等[20, 68]提出了一种非侵入式随机有限元法，利用单重随机响应面[20, 68, 69]得到了考虑不排水抗剪强度空间变异性时的边坡可靠度.此外，基于二阶多项式的多重响应面[23, 42]和多重随机响应面[21]也被证实能够有效地解决考虑土性参数空间变异性的多层土坡可靠度问题.

综上所述可以看出，响应面法在边坡可靠度问题中得到了长足的发展并得到了广泛的应用.本质上说，响应面是利用一种高效的代理模型去逼近真实模型 (如极限平衡法和有限元法)，在此基础上利用已建立的显式功能函数进行边坡可靠度分析.表 1总结了国内外响应面法在边坡可靠度分析中的研究成果.根据土体参数的不确定性模型和土坡的分层特征，可以将土坡可靠度问题分为4类 (见表 2)：1) 单层土坡不考虑参数空间变异性 (Ⅰ类问题)；2) 单层土坡考虑参数空间变异性 (Ⅱ类问题)；3) 多层土坡不考虑参数空间变异性 (Ⅲ类问题)；4) 多层土坡考虑参数空间变异性 (Ⅳ类问题).

表 1 响应面法在土坡可靠度分析中的应用 Table 1 Summary of applications of RSMs in soil slope reliability analyses
编号 作者 年份 响应面类型 单重
响应面		 多重
响应面		 空间变异性 边坡类型 确定性 (稳定性) 分析
No Yes 单层 多层
1 Wong[40] 1985 二阶多项式 √ √ √ FEM
2 苏永华等[59] 2005 不带交叉项的二阶多项式 √ √ √ FEM
3 Xu和Low[41] 2006 不带交叉项的二阶多项式 √ √ √ LEM (Spencer)、FEM
4 Zhao[43] 2008 基于SVM的响应面 √ √ √ √ LEM (Simplied Bishop，
Spencer)
5 陈昌富等[61] 2008 不带交叉项的二阶多项式 √ √ √ √ LEM (Morgenstern-Price)
6 Cho[7] 2009 基于ANN的响应面 √ √ √ FDM
7 苏永华等[60] 2009 不带交叉项的二阶多项式 √ √ √ LEM (Spencer)
8 Chowdhury和
Rao[56]		 2010 基于HDMR的响应面 √ √ √ LEM (Simplied Bishop，Janbu，Morgenstern-Price，Spencer，GLE)
9 王宇等[51] 2011 基于向量投影的响应面 √ √ √ FEM
10 Chen等[84] 2011 基于SVM的响应面 √ √ √ LEM (Morgenstern-Price)
11 Tan等[48] 2011 基于RBFN和SVM的响应面 √ √ √ FEM
12 Samui等[50] 2011 基于RVM的响应面 √ √ √ LEM (Simplified Bishop)
13 Samui等[46] 2013 基于LSSVM的响应面 √ √ √ LEM (Simplified Bishop)
14 Luo等[62] 2012 基于Kriging的响应面 √ √ √ √ FDM
15 Luo等[63] 2012 基于Kriging的响应面 √ √ √ √ FEM
16 Ji等[14] 2012 不带交叉项的二阶多项式 √ √ √ LEM (Spencer)
17 Ji和Low[91] 2012 不带交叉项的二阶多项式 √ √ √ LEM (Ordinary，Spencer)
18 Zhang等[16] 2011 基于Kriging的响应面 √ √ √ FDM
19 Zhang等[17] 2011 不带交叉项的二阶多项式 √ √ √ √ LEM (Morgenstern-Price)
20 苏国韶等[54-55] 2011 基于GPR的响应面 √ √ √ √ LEM (Simplified Bishop，Spencer)
21 Zhang等[18] 2013 传统不带交叉项的响应面，不带交叉项的二阶多项式，基于Kriging的响应面 √ √ √ LEM (Simplified Bishop)
22 Zhang等[19] 2013 不带交叉项的二阶多项式 √ √ √ LEM (Simplified Bishop)
23 Li等[45] 2013 基于改进的SVM响应面 √ √ √ LEM (Simplified Bishop，Spencer)
24 Tan等[49] 2013 二阶多项式 LEM (Morgenstern-Price)
25 左育龙等[58] 2013 基于BP神经网络的响应面 √ √ √ LEM (Simplified Bishop)
26 何婷婷等[47] 2013 基于SVM的响应面 √ √ √ LEM (Spencer)
27 蒋水华等[67] 2013 Hermite随机多项式 √ √ √ 有限元滑面应力法
28 苏永华等[64-65] 2013 基于Kriging的响应面 √ √ √ √ LEM (Janbu，Simplified Bishop，Spencer)
29 Piliounis和
Lagaros[57]		 2014 基于NN的响应面 √ √ √ LEM (Simplified Bishop)
30 Jiang等[20] 2014 Hermite随机多项式 √ √ √ LEM (Morgenstern-Price)
31 蒋水华等[68] 2014 Hermite随机多项式 √ √ √ LEM (Simplified Bishop)
32 肖特等[69] 2014 Hermite随机多项式 √ √ √ FEM
33 Jiang等[21] 2015 Hermite随机多项式 √ √ √ LEM (Simplified Bishop)
34 Li等[23] 2015 不带交叉项的二阶多项式 √ √ √ √ LEM (Simplified Bishop)
35 Li和Chu[42] 2015 不带交叉项的二阶多项式 √ √ √ LEM (Ordinary)
36 Yi等[66] 2015 基于PSO Kriging的响应面，传统不带交叉项的响应面 √ √ √ FDM
37 Kang等[52] 2015 基于GPR的响应面 √ √ √ LEM (Simplified Bishop)
38 Kang和Li[53] 2015 基于ABC-SVR的响应面 √ √ √ LEM (Simplified Bishop)
注：SVM为支持向量机；ANN为人工神经网络；HDMR为高维模型表示；RBFN为径向基函数神经网络；RVM为关联向量机；LSSVM为最小二乘支持向量机；NN为神经网络；PSO为粒子群算法；GPR为高斯过程回归；ABC-SV为人工蜂群算法优化的支持向量回归；LEM为极限平衡法；FEM为有限单元法；FDM为有限差分法.
表选项
表 2 4类土坡可靠度问题及相应的响应面法 Table 2 Four types of soil slope reliability problems and corresponding adopted RSMs
问题类型 响应面法 不确定性模型 响应面类型 后续概率分析方法
Ⅰ 二阶多项式 (Wong40]) 随机变量 单重响应面、
多重响应面		 MCS，FOSM，FORM
基于SVM的响应面 (Zhao[43])
基于RVM的响应面 (Samui等[50])
基于向量投影的响应面 (王宇等[51])
不带交叉项的二阶多项式 (Zhang等[17]，陈昌富等[61])
Hermite随机多项式 (蒋水华等[67])
基于Kriging的响应面 (Luo等[62-63]，苏永华等[65])
基于LSSVM的响应面 (Samui等[46])
基于NN的响应面 (Piliounis等[57])
Ⅱ Hermite随机多项式 (Jiang等[20-21]，蒋水华等[68]) 随机场 单重响应面、
多重响应面		 MCS，FORM
不带交叉项的二阶多项式 (Ji等[91]，Li等[23])
Ⅲ 不带交叉项的二阶多项式 (Xu和Low[41]，Zhang等[17-19]，Ji和Low[14]，Tan等[43]，陈昌富等[61]，苏永华等[59-60]) 随机变量 单重响应面、
多重响应面		 MCS，FOSM，FORM，
四阶矩法
基于SVM的响应面 (Zhao[43]，Chen等[84]，Tan等[48]，何婷婷等[47])
基于ANN的响应面 (Cho[7])
基于BP神经网络的响应面 (左育龙等[58])
高维模型表现 (Chowdhury和Rao[56])
基于RBFN的响应面 (Tan等[48])
基于Kriging的响应面 (Zhang等[16, 18]，Luo等[62-63]，苏永华等[64-65])
传统不带交叉项的响应面 (Zhang等[18])
基于改进的SVM响应面 (Li等[45])
基于PSO Kriging的响应面、传统不带交叉项的响应面 (Yi等[66])
基于GPR的响应面 (Kang等[52]，苏国韶等[54-55])
基于ABC-SVR的响应面 (Kang和Li[53])
Ⅳ 不带交叉项的二阶多项式 (Li等[23]，Li和Chu[42]，肖特等[69]) 随机场 多重响应面 MCS
注：MCS为蒙特卡洛模拟；FORM为一次可靠度法；FOSM为一次二阶矩法.
表选项

本文主要目的在于系统总结响应面法在4类土坡问题 (问题Ⅰ~Ⅳ) 中的应用情况，在此基础上研究4种响应面法在边坡可靠度问题中的适用性和有效性.以不排水土坡和c-ϕ土坡为例，从计算准确性和计算效率两方面对4类响应面方法进行了系统的比较.首先对研究的4类土坡可靠度问题 (问题Ⅰ~Ⅳ) 进行了简要介绍.接着介绍了单重和多重响应面方法基本内容.随后以4个典型土坡 (2个粘性土坡和2个c-ϕ土坡) 为例，研究了4种响应面法的适用性和有效性.最后，为每一类典型土坡问题推荐了最合适的响应面方法.

1 4类边坡可靠度分析问题

土作为一种天然材料，在形成过程中其性质受多个因素影响，包括周围土体属性、风化和侵蚀过程、沉积条件等[71-77].为了有效地表征土性参数的不确定性，各种不确定性模型常用于表征土体材料不确定性[3, 28, 36, 78-80].土体参数不确定性模型主要包括随机变量和随机场模型[2, 34, 16-19, 81].如表 2所示，采用响应面法计算土坡可靠度问题可以分为4类，下文将依次介绍.

1.1 问题Ⅰ：单层土坡不考虑空间变异性

Ⅰ类问题研究对象是均质土坡，属于土坡可靠度分析中较为简单的情况.1985年Wong[40]在不考虑参数空间变异性条件下，采用基于二阶多项式的响应面分析了单层土坡可靠度问题.随后，众多学者[17, 43, 46, 50-51, 61-63, 65, 67, 82]采用基于各种不同算法的响应面研究了Ⅰ类问题，包括SVM、RVM、不带交叉项的二阶多项式、Kriging和神经网络等.对于一个均质土坡，由于临界确定性滑动面和其他大量潜在滑动面的安全系数是高度相关的，所以该确定性滑动面是边坡的最主要失效模式，其失效概率近似等于边坡的系统失效概率[17].

1.2 问题Ⅱ：单层土坡考虑空间变异性

土性参数固有的空间变异性是岩土工程最重要的不确定性之一，大量研究表明空间变异性对边坡稳定可靠度有明显的影响[6, 8, 13-14, 20-24, 36, 38, 78-79, 81, 83, 91].当考虑参数空间变异性时，边坡存在多种潜在失效模式，这显著增加了边坡失效概率计算难度[13].因此，在考虑参数空间变异性条件下进行边坡可靠度分析更为复杂.Jiang等[20-21]采用基于Hermite混沌多项式展开的响应面分析了考虑参数空间变异性下的土坡可靠度问题 (Ⅱ类问题).类似地，Li等[23]利用基于不带交叉项的二阶多项式的响应面分析了Ⅱ类问题.

1.3 问题Ⅲ：多层土坡不考虑空间变异性

与上述两类问题不同的是，Ⅲ类问题重点研究不考虑参数空间变异性时的多层土坡可靠度问题.如表 2所示这类问题的研究较多.与单层均质土坡不同的是，多种失效模式常出现在多层土坡中[9, 14, 17, 19, 32, 52-53, 85].如果仅使用临界确定性滑动面评估多层土坡可靠度则不能充分考虑多种失效模式对边坡系统可靠度的影响[1, 2, 17, 86]，这会进一步导致整个边坡的系统失效概率水平被低估.因此，在分析多层土坡可靠度时，应充分考虑所有代表性失效模式的影响，从而得到更为合理的边坡系统可靠度.

1.4 问题Ⅳ：多层土坡考虑空间变异性

Ⅳ类问题是考虑空间变异性的多层土坡可靠度，对于考虑空间变异性的多层土坡，代表性滑动面及其空间分布很大程度上取决于土性空间变异性和边坡的分层特性.由此产生的多种复杂的失效模式使得Ⅳ类问题分析成为一个极具挑战性的问题.Li和Chu[42]研究发现不考虑竖向参数空间变异性时代表性滑动面数目等于边坡层数，且土性空间变异性对代表性滑动面的数目有明显的影响.同时，Li等[23]提出了一种基于不带交叉项的二阶多项式的多重响应面法，采用拓展的Cholesky分解技术离散相关非高斯随机场，较好地解决了考虑空间变异性的多层土坡可靠度问题 (问题Ⅳ).

2 响应面法

表 2总结了上述4类边坡可靠度问题及其求解的响应面方法.可以看出，只有不带交叉项的二阶多项式被用于解决所有4类问题[14-15, 17-19, 23, 34, 41-43, 59-61, 69].此外，尽管文献中Hermite随机多项式只被用于分析Ⅰ和Ⅱ类问题[20-21, 67-68]，理论上讲它也可用于分析所有4类问题.因此，下文重点研究两类基于多项式的响应面法：不带交叉项的二阶多项式和Hermite随机多项式[17-21, 23, 41, 61, 67-68, 91]在4类问题 (问题Ⅰ、Ⅱ、Ⅲ和Ⅳ) 中的适用性和有效性.

2.1 单重响应面法 (SQRSM & SSRSM)

对于土坡的一个潜在滑动面，其安全系数 (FS) 和输入参数间的关系可以用一个二阶多项式表示[17, 19, 41, 87]：

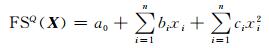    (1)

式中：FSQ(X) 为该滑动面的安全系数；X=(x1, …, xi, …, xn) 为输入的一组随机变量，n是随机变量或随机场离散后的网格数目；a=(a0, a1, b1, …, bn, c1, …, cn)T为多项式的待定系数.为确定多项式的待定系数，需确定该滑动面在 (2n+1) 个点：{μx1, μx2, …, μxn}, {μx1±kσx1, μx2, …, μxn}, {μx1, μx2±kσx2, …, μxn}, …, {μx1, μx2, …, μxn±kσxn}处的安全系数.本文中k取为2，采用基于最小二乘法的回归方法得到待定系数a[23].如式 (1) 所示不带交叉项的单个二阶显式表达式为单重二阶响应面，用建立的该响应面近似代替边坡某一潜在滑动面原始功能函数并进行边坡稳定性评估的方法，即为单重二阶多项式响应面法 (Single Quadratic Response Surface Method, SQRSM).

对于随机响应面，采用Hermite随机多项式建立潜在滑动面安全系数与输入变量之间的关系[88-90]：

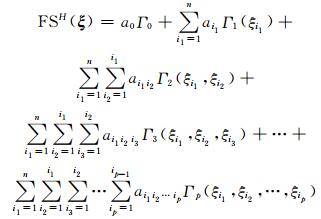    (2)

式中：FSH(ξ) 为滑动面的安全系数；n为随机变量的个数；a=(a0, ai1, …, ai1 i2… in) 为待定系数；ξ=(ξi1, ξi2, …, ξin) 为表征具有不确定性的输入参数相应的独立标准正态随机向量；Γp(·) 为阶数为p的Hermite多项式，本文中取p=2.如式 (2) 所示的基于Hermite随机多项式展开得到的单个显式表达式为单重随机响应面，利用该式近似代替边坡某一潜在滑动面原始功能函数并进行边坡可靠度分析的方法，即为单重随机响应面法 (Single Stochastic Response Surface Method, SSRSM).

本文中单重响应面法包括单重二阶响应面法 (SQRSM) 和单重随机响应面法 (SSRSM).其中，对于单重二阶响应面法 (SQRSM)，替代功能函数的代理模型如式 (1) 所示，其建立的是所有潜在滑动面中最小安全系数与原始空间输入变量X间的显式函数关系.如式 (2) 所示的单重随机响应面 (SSRSM) 也可作为一个代理模型，提供了一种显式近似的功能函数用以得到边坡稳定性分析的安全系数[89-90].需要注意的是，单重随机响应面 (SSRSM) 建立的是所有潜在滑动面最小安全系数与独立标准正态向量ξ之间的关系.

2.2 多重响应面法 (MQRSM & MSRSM)

与单重响应面法不同的是，多重响应面常被用于解决有多失效模式的边坡可靠度问题.多重响应面法包括多重二阶多项式响应面法 (MQRSM) 和多重随机响应面法 (MSRSM).

基于2.1节介绍的单重二阶多项式响应面的原理，可对边坡多个潜在失效模式分别构建每一失效模式下对应的潜在滑动面的近似二阶显式多项式，由此构建的多个二阶显式表达式 (功能函数) 即为多重二阶多项式响应面，基于该过程构建能代替边坡系统多个潜在失效模式的原始功能函数并基于此进行边坡系统可靠度分析的方法即为多重二阶多项式响应面法 (MQRSM).具体地，MQRSM利用多个二阶多项式去逼近所有潜在滑动面的安全系数和原始空间中输入变量间的功能函数关系，其中每一个响应面对应每一个潜在滑动面的原始功能函数.当得到多重二阶多项式响应面后，采用拓展的Cholesky分解技术[23]产生NMC次随机场XNG, F.若不考虑土性参数空间变异性，通过Nataf变换[96, 99-100]得到NMC组随机变量XNG, V.将NMC次实现的随机场或随机变量XNG代入到多重二阶多项式响应面函数中，得到NMC个安全系数FSmin.其中，FSmin=minFSjQ(XNG), j=1, 2, …, Ns，Ns为所有潜在滑动面的个数.接着，统计NMC个FSmin中小于1的个数计为NF，则边坡系统失效概率为Pf=NF/NMC.

与MQRSM不同的是，MSRSM建立的是所有潜在滑动面的安全系数与独立标准正态输入变量ξ之间的函数关系，相同之处在于两者都是利用构建的近似多重显式表达式代替边坡整个系统中多个潜在失效模式的原始功能，并进行边坡系统可靠度分析以评估整个边坡系统的稳定性.为此，需采用Karhunen-Loève分解技术[92-95]产生Np次独立或具有互相关性的随机场.本文采用二阶指数型 (SQX) 自相关函数[10, 23, 72, 81]作为模拟参数空间变异性的自相关函数.基于Np次随机场实现，采用极限平衡法 (如简化bishop法等) 进行Np次边坡稳定性分析，得到每一个潜在滑动面的安全系数.于是，由安全系数FS和输入随机向量ξ即能得到式 (2) 中的待定系数.重复以上过程Ns次，得到所有Ns个滑动面与输入向量ξ间的近似函数关系，即多重随机响应面.若不考虑土性参数空间变异性，进行稳定性分析时的土体输入变量由Nataf变换产生.最后，基于得到的多重随机响应面，进行蒙特卡洛模拟 (MCS) 产生NMC组输入向量ξ.将每一组向量ξk, k=1, 2, …, NMC，代入到多重随机响应面中，得到NMC个安全系数FSmin.其中，FSmin=minFSjH(ξk), j=1, 2, …, Ns.确定NMC个FSmin中小于1的数目NF，则边坡系统失效概率Pf为NF/NMC.

3 基于响应面法的边坡可靠度分析

上文总结了4类边坡可靠度问题 (问题Ⅰ、Ⅱ、Ⅲ和Ⅳ) 及其求解的4种响应面方法 (SQRSM、SSRSM、MQRSM和MSRSM)，本部分重点介绍如何评价4种响应面法在4类问题 (问题Ⅰ~Ⅳ) 中的准确性和计算效率.对于每一个土坡，其失效概率的均值Pf和变异系数COV[Pf]由20次独立可靠度分析获取的失效概率分别计算得到，均值Pf是判断失效概率准确性的一个重要指标.

本文采用另一个重要指标Unit COV (记为Δ)[101-102]用于评价每一种响应面法的计算效率，其计算公式为

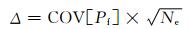
式中：Ne为每一次独立可靠度分析中需要的边坡原始功能函数 (如极限平衡分析) 等效计算次数.等效计算次数表示为Ne=Npe +t′/t，Npe为构建单重或多重响应面需要的边坡原始功能函数计算次数 (即稳定性分析次数)，t为一次原始功能函数计算需要的时间，t′为基于已经建立的响应面进行后续MCS需要的时间.在4种方法 (SQRSM、SSRSM、MQRSM和MSRSM) 中，较小的Unit COV对应的响应面法被认为具有较高的计算效率.

在边坡可靠度分析中，极限状态方程 (LSF) 通常记为g(X)=FS (X)-1=0.FS (X) 为确定性分析 (如极限平衡法) 得到的安全系数，本文4个算例均采用简化Bishop法进行边坡稳定性分析.

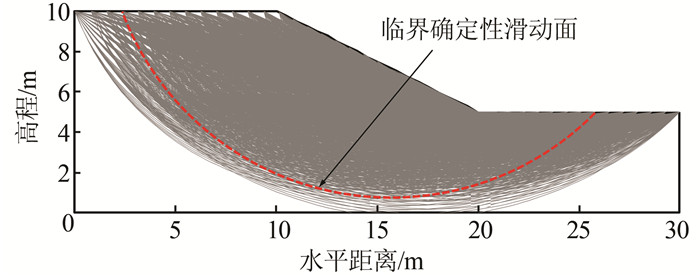
4 响应面法在黏性土坡中的应用 4.1 问题Ⅰ：单层黏性土坡 (算例1，不考虑空间变异性)

首先考虑如图 1所示不排水边坡 (算例1)，该模型来自于Cho[8]和Jiang等[21].坡高5 m，坡角26.6°，土体容重20 kN/m3.不排水抗剪强度参数cu呈对数分布，均值和标准差分别是23 kPa和0.3.基于土体参数均值，采用简化Bishop法进行边坡稳定性分析，得到边坡最小安全系数FSmin为1.356，与Cho[8]和Jiang等[21]结果一致.图 1给出了采用SLOPE/W[103]中“剪入和剪出”功能得到覆盖整个区域的4 851条潜在滑动面.

图 1 算例1边坡计算模型 Figure 1 The geometry of the slope (Example#1)
图选项

表 3总结了针对问题Ⅰ算例1在不考虑空间变异性时的计算结果.可以看出，4种响应面法SQRSM、MQRSM、SSRSM和MSRSM得到的失效概率均值Pf分别为0.173、0.173、0.172和0.172，与本文采用MCS的结果0.173和Cho[8]采用FORM的结果0.186保持一致，这说明4种响应面法针对问题Ⅰ均具有较好的精度.由于4种响应面法中SQRSM具有最小的Unit COV，这说明SQRSM计算效率最高.因此，对算例1这样不考虑参数空间变异性的单层不排水土坡 (问题Ⅰ)，推荐采用SQRSM进行可靠度分析.

表 3 单层黏性土坡问题Ⅰ的计算结果 (算例1，不考虑土性参数空间变异性) Table 3 Results for type Ⅰ problem: a single-layered cohesive slope (Example#1, No ISV)
响应面法 每一次运行需要等效的功
能函数 (稳定性) 计算次数		 Pf COV[Pf] Unit COV
SQRSM 3.02 0.173 0.002 0.003
MQRSM 4.47 0.173 0.003 0.006
SSRSM 3.01 0.172 0.022 0.038
MSRSM 3.57 0.172 0.022 0.042
MCS 100.00 0.173 0.030 0.260
表选项
4.2 问题Ⅱ：单层黏性土坡 (算例1，考虑空间变异性)

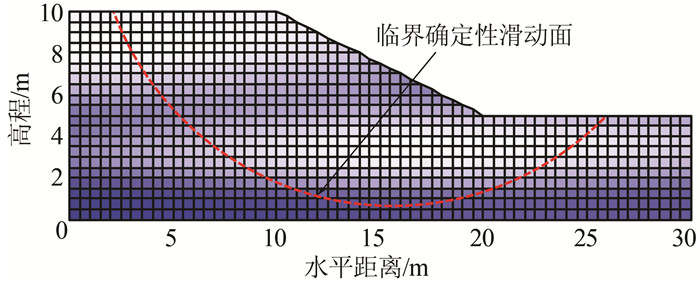
同样采用图 1所示的计算模型，与算例1中问题Ⅰ不同的是，问题Ⅱ考虑不排水抗剪强度cu的空间变异性.本节重点研究4种响应面法在算例1考虑空间变异性时 (问题Ⅱ) 的适用性和有效性.采用对数正态随机场表征不排水抗剪强度的空间变异性，其水平和竖直自相关距离θln, h、θln, v分别是20和2.0 m.图 2所示为一次典型随机场实现，不排水土坡被分成边长为0.5 m的910个小单元.

图 2 算例1边坡的一次典型随机场实现 Figure 2 A typical realization of random field (Example#1)
图选项

表 4呈现的是算例1中问题Ⅱ的计算结果.可以看出，响应面作为分析具有隐式功能函数的边坡可靠度问题的一种代理模型，方法MQRSM、SSRSM和MSRSM得到的失效概率均值Pf分别为0.082、0.081和0.079，计算结果与表 5中Cho[8]得到的0.076、Jiang等[21]得到的0.083以及直接MCS得到的0.078(表 4) 较为吻合.但采用SQRSM得到的0.276会明显高估算例1中问题Ⅱ的失效概率.说明对于本算例这样一个单层土坡考虑不排水抗剪强度cu的空间变异性时，SQRSM不能很好地逼近原始功能函数，导致了失效概率估计有偏差.采用MQRSM和MSRSM均得到较小的Unit COV (分别是0.446和0.327)，且明显小于采用MCS时的2.860.与MQRSM和MSRSM相比，SSRSM得到的Unit COV为0.694，这说明其计算效率低于MQRSM和MSRSM.综合考虑以上结果，MQRSM和MSRSM均被推荐用于解决单层黏性土坡中的问题Ⅱ.

表 4 单层黏性土坡问题Ⅱ的计算结果 (算例1，考虑土性参数空间变异性) Table 4 Results for type Ⅱ problem: a single-layered cohesive slope (Example#1, ISV)
响应面法 每一次运行需要等效的功
能函数 (稳定性) 计算次数		 Pf COV[Pf] Unit COV
SQRSM 1 821.30 0.276 0.008 0.337
MQRSM 1 823.75 0.082 0.010 0.446
SSRSM 1 000.04 0.081 0.022 0.694
MSRSM 1 001.47 0.079 0.010 0.327
MCS 1 000.00 0.078 0.090 2.860
表选项
表 5 单层黏性土坡问题Ⅱ的参考结果 (算例1，考虑土性参数空间变异性) Table 5 Results for type Ⅱ problem obtained from the references (Example#1, ISV)
方法 Pf 来源
MCS (100 000个样本) 0.076 Cho[8]
MSRSM 0.079 Jiang等[21]
MCS (1 000个样本) 0.083 Jiang等[21]
表选项
4.3 问题Ⅲ：多层黏性土坡 (算例2，不考虑空间变异性)

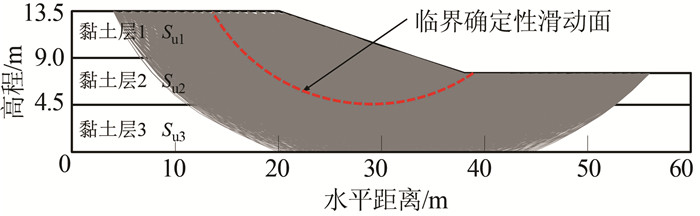
算例1研究的是单层土坡可靠度问题，但是多种潜在失效模式常发生于多层边坡中.因此，本算例 (算例2) 采用一个3层黏性土坡研究响应面法用于解决问题Ⅲ的有效性.算例2的计算模型来自Feng和Fredlund[104]、Zhang等[19]、Li和Chu[42]以及Kang等[52].计算模型如图 3，土体参数见表 6. 3个土层的不排水抗剪强度Su1、Su2和Su3被看作相互独立的随机变量.基于所有参数的均值，采用简化Bishop法得到边坡最小安全系数FSmin为1.282，与Kang等[52]的结果完全相同.图 3给出了利用SLOPE/W中“剪入和剪出”功能[103]得到能覆盖边坡整个区域的14 896条潜在滑动面.

图 3 算例2边坡计算模型 Figure 3 The geometry of the slope (Example#2)
图选项
表 6 算例2中土性参数的统计值 Table 6 Statistical properties of soil parameters in Example#2
边坡土层 参数变量 土体容重γ /(kN·m-3) 不排水抗剪强度Su
均值/kPa 变异系数 分布类型
黏土层1 Su1 18 18 0.3 对数正态
黏土层2 Su2 18 20 0.2 对数正态
黏土层3 Su3 18 25 0.3 对数正态
表选项

表 7得到的是算例2中问题Ⅲ的计算结果.为便于计较，表 8总结了其他文献中针对该同一问题的相关结果.4种响应面法SQRSM、MQRSM、SSRSM和MSRSM得到的失效概率均值分别为0.216、0.184、0.219和0.240.相比于Zhang等[19]和Kang等[52]得到的0.185左右 (见表 8) 的失效概率和直接MCS得到的0.197(表 7)，4种响应面法的结果均略高估了边坡失效概率.对于4种响应面法的计算效率，从表 7可以看出，SQRSM和MQRSM相比于SSRSM和MSRSM具有较小的Unit COV.因此，SQRSM和MQRSM均被推荐用于解决算例2黏性土坡中问题Ⅲ.

表 7 多层黏性土坡问题Ⅲ的计算结果 (算例2，不考虑土性参数空间变异性) Table 7 Results for type Ⅲ problem: a three-layered cohesive slope (Example#2, No ISV)
响应面法 每一次运行需要等效的功
能函数 (稳定性) 计算次数		 Pf COV[Pf] Unit COV
SQRSM 7.05 0.216 0.002 0.005
MQRSM 15.61 0.184 0.002 0.009
SSRSM 10.04 0.219 0.534 1.694
MSRSM 15.37 0.240 0.522 2.047
MCS 100.00 0.197 0.095 0.952
表选项
表 8 多层黏性土坡问题Ⅲ的参考结果 (算例2，不考虑土性参数空间变异性) Table 8 Results for type Ⅲ problem obtained from the references (Example#2, No ISV)
方法 Pf 来源
MCS (10 000个样本) 0.187 Zhang等[19]
拓展的Hassan and Wolff方法 (10 000个样本) 0.184 Zhang等[19]
MCS using GPR-based RSM (10 000个样本) 0.186 Kang等[52]
MCS using GPR-based RSM (20 000个样本) 0.185 Kang等[52]
MCS using GPR-based RSM (100 000个样本) 0.186 Kang等[52]
表选项
4.4 问题Ⅳ：多层黏性土坡 (算例2，考虑空间变异性)

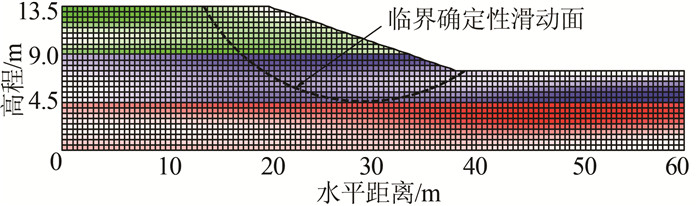
基于算例2的几何模型，本问题 (问题Ⅳ) 中采用对数随机场表征3个土层不排水抗剪强度Su1、Su2和Su3的空间变异性.模拟随机场时每一土层中采用的水平和竖直自相关距离θln, h、θln, v分别是20和2.0 m，且3个随机场相互独立.图 4所示为一次随机场的典型实现，从上到下3个土坡分别分为495、939和1 080个小单元.

图 4 算例2边坡的一次典型随机场实现 Figure 4 A typical realization of random field (Example#2)
图选项

表 9总结了算例2中问题Ⅳ的可靠度计算结果.4种响应面法SQRSM、MQRSM、SSRSM和MSRSM得到的失效概率均值分别为0.027、0.057、0.088和0.031.把采用MCS得到的失效概率0.057(表 9) 作为准确值，4种响应面法与MCS的结果均较为接近，说明了4种方法均具有较高的准确性.值得注意的是SQRSM和MSRSM会略低估边坡失效概率、SSRSM会略高估边坡失效概率，这种差异可能源自两个方面：首先，土坡有3个土层且考虑土性参数空间变异性增加了问题Ⅳ的复杂性；其次，SQRSM、MSRSM和SSRSM不能完全逼近土坡潜在滑动面的原始功能函数.考虑到MSRSM在4种响应面方法中具有最小的Unit COV (0.69)，因此，本算例中MSRSM是问题Ⅳ的推荐方法.

表 9 多层黏性土坡问题Ⅳ的计算结果 (算例2，考虑土性参数空间变异性) Table 9 Results for type Ⅳ problem: a three-layered cohesive slope (Example #2, ISV)
响应面法 每一次运行需要等效的功
能函数 (稳定性) 计算次数		 Pf COV[Pf] Unit COV
SQRSM 5 029.43 0.027 0.03 2.34
MQRSM 5 033.10 0.057 0.02 1.43
SSRSM 800.08 0.088 0.08 2.19
MSRSM 801.50 0.031 0.02 0.69
MCS 1 000.00 0.057 0.08 2.54
表选项
4.5 黏性土坡可靠度问题的推荐方法

对于算例1和2中的2个黏性土坡可靠度问题，表 10总结了4种响应面法 (SQRSM、MQRSM、SSRSM和MSRSM) 在解决4类问题 (问题Ⅰ~Ⅳ) 中的有效性.表 10中，从计算准确性和效率两个角度，为每一类问题推荐了一种或多种合适的响应面方法.表 10中对于每类问题标有“√”的方法说明其计算准确性满足要求.如上文提到的，Unit COV是评价计算效率的重要指标.表 10中对于每一类问题，按照4种方法计算效率的情况从高到低依次标记为数字1到4.综合考虑计算准确性和计算效率后，为每一类问题推荐了相应的方法 (表 10).对于不考虑土性参数空间变异性的单层黏性土坡可靠度问题，推荐的方法是SQRSM；对于考虑土性参数空间变异性的单层黏性土坡可靠度问题，MQRSM和MSRSM均为合适的方法.此外，SQRSM和MQRSM均被推荐用于解决不考虑土性参数空间变异性的多层黏性土坡可靠度问题；对于考虑土性参数空间变异性的多层黏性土坡，MSRSM是推荐的方法.

表 10 黏性土坡中4类可靠度问题推荐的响应面方法 Table 10 Recommendations of selecting appropriate RSMs for four types of reliability problems of a cohesive slope
问题类型 判断标准 SQRSM MQRSM SSRSM MSRSM 推荐的方法
单层土坡不考虑参数
空间变异性 (Ⅰ)		 准确性 √ √ √ √ SQRSM
效率 1 2 3 4
单层土坡考虑参数
空间变异性 (Ⅱ)		 准确性 √ √ √ MQRSM、MSRSM
效率 2 3 4 1
多层土坡不考虑参数
空间变异性 (Ⅲ)		 准确性 √ √ √ √ SQRSM、MQRSM
效率 1 2 3 4
多层土坡考虑参数
空间变异性 (Ⅳ)		 准确性 √ √ √ √ MSRSM
效率 4 2 3 1
表选项
5 响应面法在c-ϕ土坡中的应用 5.1 问题Ⅰ：单层c-ϕ土坡 (算例3，不考虑空间变异性)

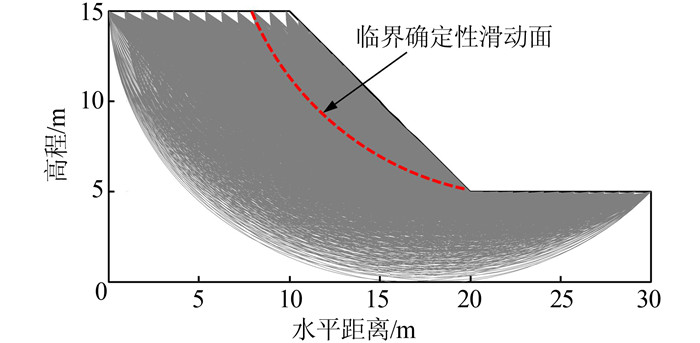
算例1和2考虑的均是土坡在不排水工况下 (ϕ=0) 的可靠度问题，因此采用简化Bishop法和瑞典条分法进行稳定性分析得到的安全系数是一样的，且潜在滑动面的原始功能函数G是线性函数[1].为进一步研究响应面法在c-ϕ土坡可靠度问题中的适用性，算例3采用如图 5所示的c-ϕ土坡，坡高10 m，坡角45°.该计算模型源自Cho[8]和Jiang等[21].土性参数统计值见表 11.基于土体参数均值，采用简化Bishop法得到边坡最小安全系数FSmin为1.206，与Jiang等[21]的1.206相等且与Cho[8]的1.204很接近，说明了计算结果的准确性.图 5给出了利用SLOPE/W中“剪入和剪出”功能[103]得到能覆盖边坡整个区域的5 491条潜在滑动面.

图 5 算例3边坡计算模型 Figure 5 The geometry of the slope (Example#3)
图选项
表 11 算例3中土性参数的统计值 Table 11 Statistical properties of soil parameters in Example#3
Parameter 均值 变异系数 分布类型 相关系数
粘聚力c 10 kPa 0.3 对数正态 r=-0.7
内摩擦角ϕ 30° 0.2 对数正态
容重γ 20 kN/m3 - - -
注：符号“―”表示相应的数据不存在.
表选项

表 12总结了算例3问题Ⅰ中一个不考虑参数空间变异性的单层c-ϕ土坡的可靠度分析结果.3种响应面法SQRSM、MQRSM和SSRSM得到的失效概率均值分别为0.043、0.042和0.040，与采用MCS方法得到的失效概率0.039很接近，说明这3种方法的计算准确性.但采用MSRSM得到的失效概率0.079明显高于MCS得到的0.039(表 12)，说明对于边坡可靠度分析的功能函数具有一定非线性的单层c-ϕ土坡来说，MSRSM不能很好地逼近原始功能函数，计算精度较低.注意到SQRSM在4种响应面方法中具有最小的Unit COV，意味着SQRSM在4种方法中计算效率最高.因此，对于c-ϕ土坡中的问题Ⅰ(单层土坡不考虑土性参数空间变异性)，推荐采用SQRSM.

表 12 单层c-ϕ土坡问题Ⅰ的计算结果 (算例3，不考虑土性参数空间变异性) Table 12 Results for type Ⅰ problem: a single-layered c-ϕ slope (Example#3, No ISV)
响应面法 每一次运行需要等效的功
能函数 (稳定性) 计算次数		 Pf COV[Pf] Unit COV
SQRSM 5.04 0.043 0.005 0.011
MQRSM 8.25 0.042 0.005 0.014
SSRSM 6.01 0.040 0.752 1.843
MSRSM 7.91 0.079 1.824 5.129
MCS 250.00 0.039 0.131 2.067
表选项
5.2 问题Ⅱ：单层c-ϕ土坡 (算例3，考虑空间变异性)

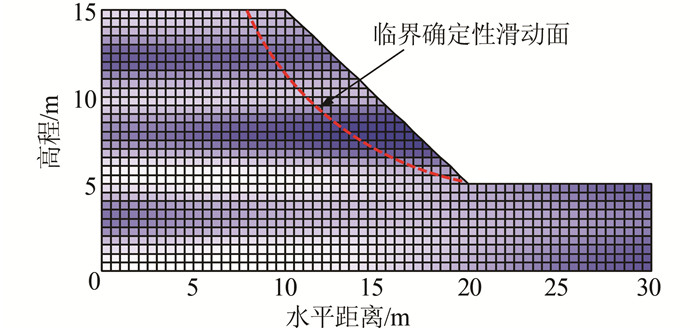
与算例3问题Ⅰ(没有考虑土性参数的空间变异性) 不同的是，问题Ⅱ中采用相关二维对数随机场表征黏聚力c和内摩擦角ϕ的空间变异性，模拟随机场时采用的水平和竖直自相关距离θln, h、θln, v分别是20和2.0 m.图 6所示的一次随机场典型实现，土层被离散为具有1 210个边长为0.5 m的单元.

图 6 算例3边坡的一次典型随机场实现 Figure 6 A typical realization of random field (Example#3)
图选项

表 13总结了算例3中问题Ⅱ的计算结果.为了方便比较，表 14给出了其他文献的计算结果.与本文采用MCS得到的0.004 1、0.003 9(Cho[8])、(0.003 9~0.004 9)(Jiang等[21]) 相比，SSRSM (0.005 2) 和MSRSM (0.005 1) 均具有较高的计算精度.但SQRSM和MQRSM均高估了边坡的失效概率，这说明对于同时考虑粘聚力c和内摩擦角ϕ空间变异性的单层土坡可靠度问题，采用SQRSM和MQRSM不能很好地逼近边坡的原始功能函数，从计算准确性的角度看只有SSRSM和MSRSM满足要求.尽管SSRSM和MSRSM的Unit COV (分别为2.56和3.57) 与MQRSM的3.71不相上下且高于SQRSM的0.96，但考虑到计算精度的要求，SSRSM和MSRSM被同时推荐为c-ϕ土坡中问题Ⅱ的最合适的方法.

表 13 单层c-ϕ土坡问题Ⅱ的计算结果 (算例3，考虑土性参数空间变异性) Table 13 Results for type Ⅱ problem: a single-layered c-ϕ slope (Example#3, ISV)
响应面法 每一次运行需要等效的功
能函数 (稳定性) 计算次数		 Pf COV[Pf] Unit COV
SQRSM 4 541.61 0.082 8 0.01 0.96
MQRSM 4 547.58 0.011 2 0.06 3.71
SSRSM 1 000.23 0.005 2 0.08 2.56
MSRSM 1 020.06 0.005 1 0.11 3.57
MCS 2 500.00 0.004 1 0.22 10.99
表选项
表 14 单层c-ϕ土坡问题Ⅱ的参考结果 (算例3，考虑土性参数空间变异性) Table 14 Results for type Ⅱ problem obtained from the references (Example#3, ISV)
方法 Pf 文献
MCS (50 000个样本) 0.003 9 Cho[8]
MSRSM 0.004 9 Jiang等[21]
MCS (10 000个样本) 0.004 4 Jiang等[21]
MCS (50 000个样本) 0.003 9 Jiang等[21]
表选项
5.3 问题Ⅲ：多层c-ϕ土坡 (算例4，不考虑空间变异性)

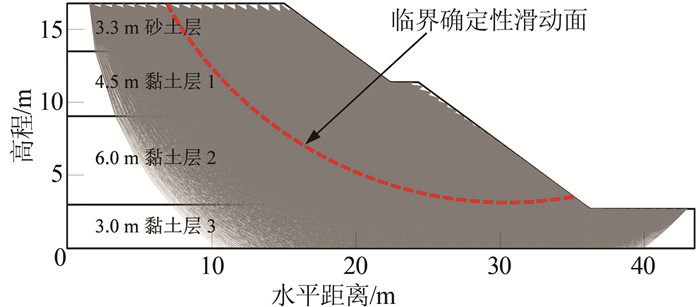
算例4(Congress Street Cut) 采用如图 7所示的几何计算模型，多位学者如Oka和Wu[86]、Chowdhury和Xu[1-2]、Ching等[11]、Chowdhury和Rao[56]以及Ji和Low[14]等对此问题进行了研究.边坡由最上部的砂土层和下部的3黏土层构成.表 15总结了土层剪切强度参数 (如粘聚力c和内摩擦角ϕ) 的统计值及土体容重 (γ)，该数据主要来自Oka和Wu[86]、Chowdhury和Xu[1-2]、Chowdhury和Rao[56].采用简化Bishop法得到了边坡在土体参数取均值时的最小安全系数FSmin为1.392.利用SLOPE/W中“剪入和剪出”功能[103]得到能覆盖边坡整个区域的25 947条潜在滑动面如图 7所示.

图 7 算例4边坡计算模型 Figure 7 The geometry of the slope (Example#4)
图选项
表 15 算例4中土性参数的统计值 Table 15 Statistical properties of soil parameters in Example#4
边坡土层 土体容重γ
/(kN·m-3)		 粘聚力c 内摩擦角ϕ
均值/kPa 变异系数 分布类型 均值/(°) 变异系数 分布类型
砂土层 21.0 0 - - 30 - - -
黏土层1 19.5 55 0.37 对数正态 5 0.2 对数正态
黏土层2 19.5 43 0.19 对数正态 7 0.21 对数正态
黏土层3 20.0 56 0.20 对数正态 15 0.24 对数正态
表选项

表 16总结了算例4中问题Ⅲ的计算结果，与直接MCS的结果0.010相比，4种响应面法中MQRSM得到的结果最为准确，其他3种方法SQRSM、SSRSM和MSRSM得到的边坡失效概率 (分别为0.057、0.086和0.106) 均偏离MCS的结果 (0.010).考虑到MQRSM的Unit COV为0.04，远小于4.20(SSRSM) 和5.57(MSRSM)，因此，MQRSM被推荐为c-ϕ土坡中问题Ⅲ的最合适的方法.

表 16 多层c-ϕ土坡问题Ⅲ的计算结果 (算例4，不考虑土性参数空间变异性) Table 16 Results for type Ⅲ problem: a three-layered c-ϕ slope (Example#4, No ISV)
响应面法 每一次运行需要等效的功
能函数 (稳定性) 计算次数		 Pf COV[Pf] Unit COV
SQRSM 13.04 0.057 0.005 0.02
MQRSM 23.19 0.010 0.009 0.04
SSRSM 28.03 0.086 0.793 4.20
MSRSM 37.82 0.106 0.743 4.57
MCS 20 000* 0.010 0.071 9.98
注：*表示蒙特卡洛模拟次数为20 000.
表选项
5.4 问题Ⅳ：多层c-ϕ土坡 (算例4，考虑空间变异性)

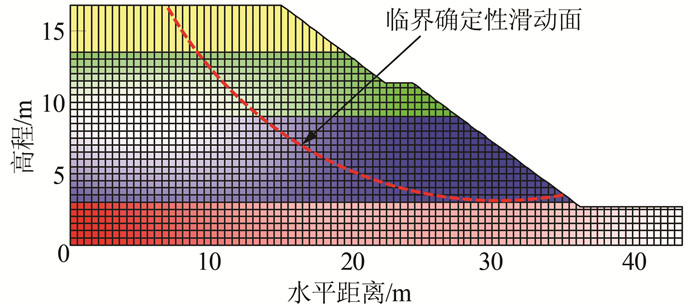
该部分重点研究考虑土性参数空间变异性时多层c-ϕ土坡可靠度问题，即c-ϕ土坡中的问题Ⅳ.基于算例4(Congress Street Cut) 问题Ⅲ的几何模型，采用对数随机场表征黏土黏聚力c和内摩擦角ϕ的空间变异性，水平和竖直自相关距离θln, h、θln, v分别是20和6.0 m.图 8为一次随机场的典型实现，边坡黏土层从上往下依次被分为434、773和552个边长为0.5 m的网格.

图 8 算例4边坡的一次典型随机场实现 Figure 8 A typical realization of random field (Example#4)
图选项

表 17是c-ϕ土坡中问题Ⅳ的计算结果.可以看出，采用SQRSM和SSRSM得到的边坡失效概率 (分别为0.054 3和0.007 2) 均高于MCS得到的失效概率0.002 7；由MQRSM和MSRSM得到的失效概率 (分别为0.002 1和0.001 5) 与MCS的结果较吻合，说明MQRSM和MSRSM解决c-ϕ土坡问题Ⅳ的准确性.此外，MQRSM和MSRSM的Unit COV (分别为9.31和2.15) 均远低于SSRSM的68.42，说明了MQRSM和MSRSM在解决问题Ⅳ时计算效率较高.综合考虑计算精度和计算效率，推荐MQRSM和MSRSM为c-ϕ土坡中问题Ⅳ最合适的方法.

表 17 多层c-ϕ土坡问题Ⅳ的计算结果 (算例4，考虑土性参数空间变异性) Table 17 Results for type Ⅳ problem: a three-layered c-ϕ slope (Example#4, ISV)
响应面法 每一次运行需要等效的功
能函数 (稳定性) 计算次数		 Pf COV[Pf] Unit COV
SQRSM 6 918.84 0.054 3 0.02 1.93
MQRSM 7 064.21 0.002 1 0.11 9.31
SSRSM 1 000.07 0.007 2 2.16 68.42
MSRSM 1 013.77 0.001 5 0.07 2.15
MCS 70 000* 0.002 7 0.07 19.40
注：*表示蒙特卡洛模拟次数为70 000.
表选项
5.5 c-ϕ土坡可靠度问题的推荐方法

与4.5节黏性土坡类似，该节针对c-ϕ土坡为每一类问题 (问题Ⅰ~Ⅳ) 推荐一种或多种响应面方法，结果如表 18、19所示.可以看出，SQRSM被推荐用于解决不考虑土性参数空间变异性的单层c-ϕ土坡可靠度问题 (问题Ⅰ)，当考虑空间变异性时 (问题Ⅱ)，SSRSM和MSRSM均是合适的.对于不考虑空间变异性时多层c-ϕ土坡 (问题Ⅲ)，MQRSM是最合适的分析方法；当考虑土性参数空间变异性时 (问题Ⅳ)，MSRSM是被推荐的方法.

表 18 c-ϕ土坡中4类问题推荐的响应面方法 Table 18 Recommendations of selecting appropriate RSMs for four types of reliability problems of a c-ϕ slope
问题类型 判断标准 SQRSM MQRSM SSRSM MSRSM 推荐的方法
单层土坡不考虑参数
空间变异性 (Ⅰ)		 准确性 √ √ √ SQRSM
效率 1 2 3 4
单层土坡考虑参数
空间变异性 (Ⅱ)		 准确性 √ √ SSRSM、MSRSM
效率 1 4 2 3
多层土坡不考虑参数
空间变异性 (Ⅲ)		 准确性 √ MQRSM
效率 1 2 3 4
多层土坡考虑参数
空间变异性 (Ⅳ)		 准确性 √ √MSRSM
效率 1 3 4 2
表选项
表 19 土坡可靠度问题推荐的响应面方法 Table 19 Selected RSMs for soil slope reliability problems
问题类型 推荐的方法
单层土坡不考虑参数空间变异性 (Ⅰ) SQRSM
单层土坡考虑参数空间变异性 (Ⅱ) MSRSM
多层土坡不考虑参数空间变异性 (Ⅲ) MQRSM
多层土坡考虑参数空间变异性 (Ⅳ) MSRSM
表选项
6 总结和结论

本文系统地总结了多种响应面法在不同类型边坡可靠度问题中的应用情况，通过文献分析总结出4类典型土坡可靠度问题：问题Ⅰ，单层土坡不考虑土性参数空间变异性；问题Ⅱ, 单层土坡考虑土性参数空间变异性；问题Ⅲ，多层土坡不考虑土性参数空间变异性；问题Ⅳ，多层土坡考虑土性参数空间变异性.在此基础上重点研究了基于多项式的4种响应面法 (SQRSM、MQRSM、SSRSM和MSRSM) 在解决4类土坡可靠度问题 (问题Ⅰ~Ⅳ) 中的有效性.针对每一类问题分别从计算精度和计算效率两个方面系统地比较了4种响应面法 (SQRSM、MQRSM、SSRSM和MSRSM) 在黏性土坡和c-ϕ土坡可靠度问题中的适用性.基于计算结果为每一类可靠度问题推荐了相应的方法.

对于不考虑土性参数空间变异性的单层土坡可靠度问题 (问题Ⅰ)，关键临界确定性滑动面主导了边坡的潜在失效模式，土坡失效模式较单一，简单的SQRSM就能保证足够的精度.当单层土坡考虑土性参数空间变异性时 (问题Ⅱ)，与均质边坡相比其潜在失效模式数目有明显的增加，边坡失效模式变得较为复杂，此时MSRSM可较好地解决这类问题.此外，边坡的分层特征也会明显地影响边坡的潜在失效模式，并导致多种失效模式 (问题Ⅲ)，对于这类问题MQRSM是有效的方法.当边坡同时存在分层特征和空间变异性时，相应的可靠度问题 (问题Ⅳ) 较为复杂，此时推荐采用MSRSM方法.

参考文献
[1] Chowdhury R N, Xu D W. Slope system reliability with general slip surfaces[J]. Soils and Foundations, 1994, 34(3): 99–105. DOI:10.3208/sandf1972.34.3_99
[2] Chowdhury R N, Xu D W. Geotechnical system reliability of slopes[J]. Reliability Engineering and System Safety, 1995, 47(3): 141–151. DOI:10.1016/0951-8320(94)00063-T
[3] Christian J T, Ladd C C, Baecher G B. Reliability applied to slope stability analysis[J]. Journal of Geotechnical Engineering, 1994, 120(12): 2180–2207. DOI:10.1061/(ASCE)0733-9410(1994)120:12(2180)
[4] Baecher G B, Christian J T. Reliability and Statistics in Geotechnical Engineering[M]. New York: John Wiley & Sons, 2003.
[5] Low B K, Tang W H. Reliability analysis using object-oriented constrained optimization[J]. Structural Safety, 2004, 26(1): 69–89. DOI:10.1016/S0167-4730(03)00023-7
[6] Cho S E. Effects of spatial variability of soil properties on slope stability[J]. Engineering Geology, 2007, 92(3): 97–109.
[7] Cho S E. Probabilistic stability analyses of slopes using the ANN-based response surface[J]. Computers and Geotechnics, 2009, 36(5): 787–797. DOI:10.1016/j.compgeo.2009.01.003
[8] Cho S E. Probabilistic assessment of slope stability that considers the spatial variability of soil properties[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(7): 975–984. DOI:10.1061/(ASCE)GT.1943-5606.0000309
[9] Cho S E. First-order reliability analysis of slope considering multiple failure modes[J]. Engineering Geology, 2013, 154: 98–105. DOI:10.1016/j.enggeo.2012.12.014
[10] Fenton G A, Griffiths D V. Risk Assessment in Geotechnical Engineering[M]. New York: John Wiley and Sons, 2008.
[11] Ching J Y, Phoon K K, Hu Y G. Efficient evaluation of reliability for slopes with circular slip surfaces using importance sampling[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(6): 768–777. DOI:10.1061/(ASCE)GT.1943-5606.0000035
[12] Wang Y, Cao Z J, Au S K. Efficient Monte Carlo simulation of parameter sensitivity in probabilistic slope stability analysis[J]. Computers and Geotechnics, 2010, 37(7): 1015–1022.
[13] Wang Y, Cao Z J, Au S K. Practical reliability analysis of slope stability by advanced Monte Carlo simulations in a spreadsheet[J]. Canadian Geotechnical Journal, 2011, 48(1): 162–172. DOI:10.1139/T10-044
[14] Ji J, Low B K. Stratified response surfaces for system probabilistic evaluation of slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(11): 1398–1406. DOI:10.1061/(ASCE)GT.1943-5606.0000711
[15] Ji J. A simplified approach for modeling spatial variability of undrained shear strength in out-plane failure mode of earth embankment[J]. Engineering Geology, 2014, 183: 315–323. DOI:10.1016/j.enggeo.2014.09.004
[16] Zhang J, Zhang L M, Tang W H. Kriging numerical models for geotechnical reliability analysis[J]. Soils and Foundations, 2011, 51(6): 1169–1177. DOI:10.3208/sandf.51.1169
[17] Zhang J, Zhang L M, Tang W H. New methods for system reliability analysis of soil slopes[J]. Canadian Geotechnical Journal, 2011, 48(7): 1138–1148. DOI:10.1139/t11-009
[18] Zhang J, Huang H W, Phoon K K. Application of the Kriging-based response surface method to the system reliability of soil slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 139(4): 651–655.
[19] Zhang J, Huang H W, Juang C H, et al. Extension of Hassan and Wolff method for system reliability analysis of soil slopes[J]. Engineering Geology, 2013, 160: 81–88. DOI:10.1016/j.enggeo.2013.03.029
[20] Jiang S H, Li D Q, Zhang L M, et al. Slope reliability analysis considering spatially variable shear strength parameters using a non-intrusive stochastic finite element method[J]. Engineering Geology, 2014, 168: 120–128. DOI:10.1016/j.enggeo.2013.11.006
[21] Jiang S H, Li D Q, Cao Z J, et al. Efficient system reliability analysis of slope stability in spatially variable soils using Monte Carlo simulation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, 141(2): 04014096. DOI:10.1061/(ASCE)GT.1943-5606.0001227
[22] 李典庆, 蒋水华, 周创兵, 等. 考虑参数空间变异性的边坡可靠度分析非侵入式随机有限元法[J]. 岩土工程学报, 2013, 35(8): 1413–1422.
Li Dianqing, Jiang Shuihua, Zhou Chuangbing, et al. Reliability analysis of slopes considering spatial variability of soil parameters using non-intrusive stochastic finite element method[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1413–1422.
[23] Li D Q, Jiang S H, Cao Z J, et al. A multiple response-surface method for slope reliability analysis considering spatial variability of soil properties[J]. Engineering Geology, 2015, 187: 60–72. DOI:10.1016/j.enggeo.2014.12.003
[24] Li D Q, Xiao T, Cao Z J, et al. Enhancement of random finite element method in reliability analysis and risk assessment of soil slopes using Subset Simulation[J]. Landslides, 2016, 13(2): 293–303. DOI:10.1007/s10346-015-0569-2
[25] Hassan A M, Wolff T F. Search algorithm for minimum reliability index of earth slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(4): 301–308. DOI:10.1061/(ASCE)1090-0241(1999)125:4(301)
[26] Duncan J M. Factors of safety and reliability in geotechnical engineering[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(4): 307–316. DOI:10.1061/(ASCE)1090-0241(2000)126:4(307)
[27] Xue J F, Gavin K. Simultaneous determination of critical slip surface and reliability index for slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(7): 878–886. DOI:10.1061/(ASCE)1090-0241(2007)133:7(878)
[28] Suchomel R, Maši D. Comparison of different probabilistic methods for predicting stability of a slope in spatially variable c-φ soil[J]. Computers and Geotechnics, 2010, 37(1): 132–140.
[29] Low B K, Tang W H. Probabilistic slope analysis using Janbu's generalized procedure of slices[J]. Computers and Geotechnics, 1997, 21(2): 121–142. DOI:10.1016/S0266-352X(97)00019-0
[30] Low B K. Reliability analysis of rock slopes involving correlated nonnormals[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 922–935. DOI:10.1016/j.ijrmms.2007.02.008
[31] Hong H P, Roh G. Reliability evaluation of earth slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(12): 1700–1705. DOI:10.1061/(ASCE)1090-0241(2008)134:12(1700)
[32] Zeng P, Jimenez R. An approximation to the reliability of series geotechnical systems using a linearization approach[J]. Computers and Geotechnics, 2014, 62: 304–309. DOI:10.1016/j.compgeo.2014.08.007
[33] Low B K. FORM, SORM, and spatial modeling in geotechnical engineering[J]. Structural Safety, 2014, 49: 56–64. DOI:10.1016/j.strusafe.2013.08.008
[34] El-ramly H, Morgenstern N R, Cruden D M. Probabilistic slope stability analysis for practice[J]. Canadian Geotechnical Journal, 2002, 39(3): 665–683. DOI:10.1139/t02-034
[35] El-ramly H, Morgenstern N R, Cruden D M. Probabilistic assessment of stability of a cut slope in residual soil[J]. Geotechnique, 2005, 55(1): 77–84. DOI:10.1680/geot.2005.55.1.77
[36] Griffiths D V, Fenton G A. Probabilistic slope stability analysis by finite elements[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(5): 507–518. DOI:10.1061/(ASCE)1090-0241(2004)130:5(507)
[37] Hsu S C, Nelson P P. Material spatial variability and slope stability for weak rock masses[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(2): 183–193. DOI:10.1061/(ASCE)1090-0241(2006)132:2(183)
[38] Huang J S, Griffiths D V, Fenton G A. System reliability of slopes by RFEM[J]. Soils and Foundations, 2010, 50(3): 343–353. DOI:10.3208/sandf.50.343
[39] 张曼, 唐小松, 李典庆. 含相关非正态变量边坡可靠度分析的子集模拟方法[J]. 武汉大学学报 (工学版), 2012, 45(1): 41–45.
Zhang Man, Tang Xiaosong, Li Dianqing. Reliability analysis of slope stability involving correlated non-normal variable using subset simulation method[J]. Engineering Journal of Wuhan University, 2012, 45(1): 41–45.
[40] Wong F S. Slope reliability and response surface method[J]. Journal of Geotechnical Engineering, 1985, 111(1): 32–53. DOI:10.1061/(ASCE)0733-9410(1985)111:1(32)
[41] Xu B, Low B K. Probabilistic stability analyses of embankments based on finite-element method[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(11): 1444–1454. DOI:10.1061/(ASCE)1090-0241(2006)132:11(1444)
[42] Li L, Chu X S. Multiple response surfaces for slope reliability analysis[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(2): 175–192. DOI:10.1002/nag.v39.2
[43] Zhao H B. Slope reliability analysis using a support vector machine[J]. Computers and Geotechnics, 2008, 35(3): 459–467. DOI:10.1016/j.compgeo.2007.08.002
[44] Chen C F, Xiao Z Y, Zhang G B. Time-variant reliability analysis of three-dimensional slopes based on support vector machine method[J]. Journal of Central South University of Technology, 2011, 18: 2108–2114. DOI:10.1007/s11771-011-0950-9
[45] Li S J, Zhao H B, Ru Z L. Slope reliability analysis by updated support vector machine and Monte Carlo simulation[J]. Natural Hazards, 2013, 65(1): 707–722. DOI:10.1007/s11069-012-0396-x
[46] Samui P, Lansivaara T, Bhatt M R. Least square support vector machine applied to slope reliability analysis[J]. Geotechnical and Geological Engineering, 2013, 31(4): 1329–1334. DOI:10.1007/s10706-013-9654-2
[47] 何婷婷, 尚岳全, 吕庆, 等. 边坡可靠度分析的支持向量机法[J]. 岩土力学, 2013, 34(11): 3269–3276.
He Tingting, Shang Yuequan, Lü Qing, et al. Slope reliability analysis using support vector machine[J]. Rock and Soil Mechanics, 2013, 34(11): 3269–3276.
[48] Tan X H, Bi W H, Hou X L, et al. Reliability analysis using radial basis function networks and support vector machines[J]. Computers and Geotechnics, 2011, 38(2): 178–186. DOI:10.1016/j.compgeo.2010.11.002
[49] Tan X H, Shen M F, Hou X L, et al. Response surface method of reliability analysis and its application in slope stability analysis[J]. Geotechnical and Geological Engineering, 2013, 31(4): 1011–1025. DOI:10.1007/s10706-013-9628-4
[50] Samui P, Lansivaara T, Kim D. Utilization relevance vector machine for slope reliability analysis[J]. Applied Soft Computing, 2011, 11(5): 4036–4040. DOI:10.1016/j.asoc.2011.03.009
[51] 王宇, 王春磊, 汪灿, 等. 边坡可靠性评价的向量投影响应面研究及应用[J]. 岩土工程学报, 2011, 33(9): 1434–1439.
Wang Yu, Wang Chunlei, Wang Can, et al. Reliability evaluation of slopes based on vector projection response surface and its application[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(9): 1434–1439.
[52] Kang F, Han S X, Salgado R, et al. System probabilistic stability analysis of soil slopes using Gaussian process regression with Latin hypercube sampling[J]. Computers and Geotechnics, 2015, 63: 13–25. DOI:10.1016/j.compgeo.2014.08.010
[53] Kang F, Li J J. Artificial bee colony algorithm optimized support vector regression for system reliability analysis of slopes[J]. Journal of Computing in Civil Engineering, 2016, 30(3): 04015040. DOI:10.1061/(ASCE)CP.1943-5487.0000514
[54] 苏国韶, 肖义龙. 边坡可靠度分析的高斯过程方法[J]. 岩土工程学报, 2011, 33(6): 916–920.
Su Guoshao, Xiao Yilong. Gaussian process method for slope reliability analysis[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(6): 916–920.
[55] 苏国韶, 赵伟, 彭立锋, 等. 边坡失效概率估计的高斯过程动态响应面法[J]. 岩土力学, 2014, 35(12): 3592–3601.
Su Guoshao, Zhao Wei, Peng Lifeng, et al. Gaussian process-based dynamic response surface method for estimating slope failure probability[J]. Rock and Soil Mechanics, 2014, 35(12): 3592–3601.
[56] Chowdhury R, Rao B N. Probabilistic stability assessment of slopes using high dimensional model representation[J]. Computers and Geotechnics, 2010, 37(7): 876–884.
[57] Piliounis G, Lagaros N D. Reliability analysis of geostructures based on metaheuristic optimization[J]. Applied Soft Computing, 2014, 22: 544–565. DOI:10.1016/j.asoc.2014.04.026
[58] 左育龙, 朱合华, 李晓军. 岩土工程可靠度分析的神经网络四阶矩法[J]. 岩土力学, 2013, 34(2): 513–518.
Zuo Yulong, Zhu Hehua, Li Xiaojun. An ANN-based four order moments method for geotechnical engineering reliability analysis[J]. Rock and Soil Mechanics, 2013, 34(2): 513–518.
[59] 苏永华, 赵明华, 邹志鹏, 等. 基于能量原理的边坡稳定概率计算[J]. 岩石力学与工程学报, 2005, 24(19): 3470–3475.
Su Yonghua, Zhao Minhua, Zou Zhipeng, et al. Probability calculation of slope stability based on energy principle[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(19): 3470–3475.
[60] 苏永华, 孙晓明, 颜永国. 基于极限平衡的边坡稳定概率显式功能函数逐步修正求解[J]. 工程力学, 2009, 26(3): 15–20.
Su Yonghua, Sun Xiaoming, Yan Yongguo. Stepwise revises solution of slope stability probability by approximative explicit functional function based on limit equilibrium method[J]. Engineering Mechanics, 2009, 26(3): 15–20.
[61] 陈昌富, 朱剑锋, 龚晓南. 基于响应面法和Morgenstern-Price法土坡可靠度计算方法[J]. 工程力学, 2008, 25(10): 166–172.
Chen Changfu, Zhu Jianfeng, Gong Xiaonan. Calculation method of earth slope reliability based on response surface method and Morgenstern-Price procedure[J]. Engineering Mechanics, 2008, 25(10): 166–172.
[62] Luo X F, Li X, Zhou J, et al. A Kriging-based hybrid optimization algorithm for slope reliability analysis[J]. Structural Safety, 2012, 34(1): 401–406. DOI:10.1016/j.strusafe.2011.09.004
[63] Luo X F, Cheng T, Li X, et al. Slope safety factor search strategy for multiple sample points for reliability analysis[J]. Engineering Geology, 2012, 129: 27–37.
[64] 苏永华, 杨红波. 基于代理模型的边坡稳定可靠度算法[J]. 应用力学学报, 2012, 29(6): 705–711.
Su Yonghua, Yang Hongbo. Reliability algorithm of slope stability based on Kriging metamodel[J]. Chinese Journal of Applied Mechanics, 2012, 29(6): 705–711.
[65] 苏永华, 罗正东, 张盼凤, 等. 基于Kriging的边坡稳定可靠度主动搜索法[J]. 岩土工程学报, 2013, 35(10): 1863–1869.
Su Yonghua, Luo Zhengdong, Zhang Panfeng, et al. Active searching algorithm for slope stability reliability based on Kriging model[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1863–1869.
[66] Yi P, Wei K T, Kong X J, et al. Cumulative PSO-Kriging model for slope reliability analysis[J]. Probabilistic Engineering Mechanics, 2015, 39: 39–45. DOI:10.1016/j.probengmech.2014.12.001
[67] 蒋水华, 冯晓波, 李典庆, 等. 边坡可靠度分析的非侵入式随机有限元法[J]. 岩土力学, 2013, 34(8): 2347–2354.
Jiang Shuihua, Feng Xiaobo, Li Dianqing, et al. Reliability analysis of slope using non-intrusive stochastic finite element method[J]. Rock and Soil Mechanics, 2013, 34(8): 2347–2354.
[68] 蒋水华, 李典庆, 曹子君, 等. 考虑参数空间变异性的边坡系统可靠度分析[J]. 应用基础与工程科学学报, 2014, 22(5): 841–855.
Jiang Shuihua, Li Dianqing, Cao Zijun, et al. Slope system reliability analysis considering spatial variability[J]. Journal of Basic Science and Engineering, 2014, 22(5): 841–855.
[69] 肖特, 李典庆, 周创兵, 等. 基于有限元强度折减法的多层边坡非侵入式可靠度分析[J]. 应用基础与工程科学学报, 2014, 22(4): 718–732.
Xiao Te, Li Dianqing, Zhou Chuangbing, et al. Non-intrusive reliability analysis of muti-layered slopes based on strength reduction method[J]. Journal of Basic Science and Engineering, 2014, 22(4): 718–732.
[70] 蒋水华, 李典庆, 方国光. 结构可靠度分析的响应面法和随机响应面法的比较[J]. 武汉大学学报 (工学版), 2012, 45(1): 46–53.
Jiang Shuihua, Li Dianqing, Phoon Kokkwang. A comparative study of response surface method and stochastic response surface method for structural reliability analysis[J]. Engineering Journal of Wuhan University, 2012, 45(1): 46–53.
[71] Cao Z J, Wang Y. Bayesian approach for probabilistic site characterization using cone penetration tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(2): 267–276. DOI:10.1061/(ASCE)GT.1943-5606.0000765
[72] Cao Z J, Wang Y. Bayesian model comparison and selection of spatial correlation functions for soil parameters[J]. Structural Safety, 2014, 49: 10–17. DOI:10.1016/j.strusafe.2013.06.003
[73] Ching J Y, Phoon K K. Transformations and correlations among some clay parameters-the global database[J]. Canadian Geotechnical Journal, 2014, 51(6): 663–685. DOI:10.1139/cgj-2013-0262
[74] Le T M H. Reliability of heterogeneous slopes with cross-correlated shear strength parameters[J]. Georisk, 2014, 8(4): 250–257.
[75] Li D Q, Qi X H, Phoon K K, et al. Effect of spatially variable shear strength parameters with linearly increasing mean trend on reliability of infinite slopes[J]. Structural Safety, 2014, 49: 45–55. DOI:10.1016/j.strusafe.2013.08.005
[76] Lloret-cabot M, Fenton G A, Hicks M A. On the estimation of scale of fluctuation in geostatistics[J]. Georisk, 2014, 8(2): 129–140.
[77] Jamshidi Chenari R, Alaie R. Effects of anisotropy in correlation structure on the stability of an undrained clay slope[J]. Georisk, 2015, 9(2): 109–123.
[78] Srivastava A, Babu G S. Effect of soil variability on the bearing capacity of clay and in slope stability problems[J]. Engineering Geology, 2009, 108(1): 142–152.
[79] Srivastava A, Babu G S, Haldar S. Influence of spatial variability of permeability property on steady state seepage flow and slope stability analysis[J]. Engineering Geology, 2010, 110(3): 93–101.
[80] Cao Z J, Wang Y. Bayesian model comparison and characterization of undrained shear strength[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(6): 04014018. DOI:10.1061/(ASCE)GT.1943-5606.0001108
[81] Phoon K K, Kulhawy F H. Characterization of geotechnical variability[J]. Canadian Geotechnical Journal, 1999, 36(4): 612–624. DOI:10.1139/t99-038
[82] Piliounis G, Lagaros N D. Reliability analysis of geostructures based on metaheuristic optimization[J]. Applied Soft Computing, 2014, 22: 544–565. DOI:10.1016/j.asoc.2014.04.026
[83] Hicks M A, Spencer W A. Influence of heterogeneity on the reliability and failure of a long 3D slope[J]. Computers and Geotechnics, 2010, 37(7): 948–955.
[84] Chen C F, Xiao Z Y, Zhang G B. Time-variant reliability analysis of three-dimensional slopes based on support vector machine method[J]. Journal of Central South University of Technology, 2011, 18: 2108–2114. DOI:10.1007/s11771-011-0950-9
[85] Low B K, Zhang J, Tang W H. Efficient system reliability analysis illustrated for a retaining wall and a soil slope[J]. Computers and Geotechnics, 2011, 38(2): 196–204. DOI:10.1016/j.compgeo.2010.11.005
[86] Oka Y, Wu T H. System reliability of slope stability[J]. Journal of Geotechnical Engineering, 1990, 116(8): 1185–1189. DOI:10.1061/(ASCE)0733-9410(1990)116:8(1185)
[87] Bucher C G, Bourgund U. A fast and efficient response surface approach for structural reliability problems[J]. Structural Safety, 1990, 7(1): 57–66. DOI:10.1016/0167-4730(90)90012-E
[88] Huang S P, Liang B, Phoon K K. Geotechnical probabilistic analysis by collocation-based stochastic response surface method: An Excel add-in implementation[J]. Georisk, 2009, 3(2): 75–86.
[89] Li D Q, Chen Y F, Lu W B, et al. Stochastic response surface method for reliability analysis of rock slopes involving correlated non-normal variables[J]. Computers and Geotechnics, 2011, 38(1): 58–68. DOI:10.1016/j.compgeo.2010.10.006
[90] 李典庆, 周创兵, 陈益峰, 等. 边坡可靠度分析的随机响应面法及程序实现[J]. 岩石力学与工程学报, 2010, 29(8): 1513–1523.
Li Dianqing, Zhou Chuangbing, Chen Yifeng, et al. Reliability analysis of slope using stochastic response surface method and code implementation[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1513–1523.
[91] Ji J, Liao H J, Low B K. Modeling 2-D spatial variation in slope reliability analysis using interpolated autocorrelations[J]. Computers and Geotechnics, 2012, 40: 135–146. DOI:10.1016/j.compgeo.2011.11.002
[92] Ghiocel D M, Ghanem R G. Stochastic finite-element analysis of seismic soil-structure interaction[J]. Journal of Engineering Mechanics, 2002, 128(1): 66–77. DOI:10.1061/(ASCE)0733-9399(2002)128:1(66)
[93] Phoon K K, Huang S P, Quek S T. Implementation of Karhunen-Loeve expansion for simulation using a wavelet-Galerkin scheme[J]. Probabilistic Engineering Mechanics, 2002, 17(3): 293–303. DOI:10.1016/S0266-8920(02)00013-9
[94] Ghanem R G, Spanos P D. Stochastic Finite Elements: A Spectral Approach[M]. New York: Dover Publications, 2003.
[95] Vorřechovský M. Simulation of simply cross correlated random fields by series expansion methods[J]. Structural Safety, 2008, 30(4): 337–363. DOI:10.1016/j.strusafe.2007.05.002
[96] Lebrun R, Dutfoy A. A generalization of the Nataf transformation to distributions with elliptical copula[J]. Probabilistic Engineering Mechanics, 2009, 24(2): 172–178. DOI:10.1016/j.probengmech.2008.05.001
[97] 邓志平, 蒋水华, 曹子君, 等. 考虑参数空间变异性边坡可靠度分析的Kriging方法[J]. 武汉大学学报 (工学版), 2014, 47(6): 743–749.
Deng Zhiping, Jiang Shuihua, Cao Zijun, et al. Reliability analysis of slope stability considering spatially varying soil properties using Kriging method[J]. Engineering Journal of Wuhan University, 2014, 47(6): 743–749.
[98] 熊敏, 蒋水华, 李典庆. 中国与欧洲规范关于坝坡抗滑稳定分析方法的比较[J]. 武汉大学学报 (工学版), 2013, 46(5): 593–598.
Xiong Min, Jiang Shuihua, Li Dianqing. A comparative investigation on slope stability analysis of embankment dams between Chinese and European geotechnical design codes[J]. Engineering Journal of Wuhan University, 2013, 46(5): 593–598.
[99] Tang X S, Li D Q, Zhou C B, et al. Impact of Copulas for modeling bivariate distributions on system reliability[J]. Structural Safety, 2013, 44: 80–90. DOI:10.1016/j.strusafe.2013.06.004
[100] Tang X S, Li D Q, Zhou C B, et al. Copula-based approaches for evaluating slope reliability under incomplete probability information[J]. Structural Safety, 2015, 52: 90–99. DOI:10.1016/j.strusafe.2014.09.007
[101] Au S K, Ching J Y, Beck J L. Application of subset simulation methods to reliability benchmark problems[J]. Structural Safety, 2007, 29(3): 183–193. DOI:10.1016/j.strusafe.2006.07.008
[102] Schuëller G I, Pradlwarter H J. Benchmark study on reliability estimation in higher dimensions of structural systems-an overview[J]. Structural Safety, 2007, 29(3): 167–182. DOI:10.1016/j.strusafe.2006.07.010
[103] Stability Modeling With SLOPE/W: An Engineering Methodology[S]. GEO-SLOPE International Ltd., 2012.
[104] Feng T Q, Fredlund M. SVSLOPE: Verification Manual[M]. SoilVision Systems Ltd., 2012.