文章信息
- 金磊, 曾亚武, 叶建华
- JIN Lei, ZENG Yawu, YE Jianhua
- 土石混合体细观力学参数对宏观力学特性影响研究
- Study of effect of mesomechanical parameters on macromechanical characteristics of soilrock mixture
- 武汉大学学报(工学版), 2018, 51(5): 409-417
- Engineering Journal of Wuhan University, 2018, 51(5): 409-417
- http://dx.doi.org/10.14188/j.1671-8844.2018-05-006
-
文章历史
- 收稿日期: 2016-10-19
2. 浙江省丽水市50省道莲都段指挥部,浙江 丽水 323000
2. Headquaters of Liandu Section of 50 Provincial Road, Lishui 323000, China
土石混合体(soil and rock mixture, SRM)是由具有一定尺寸的强度较高的块石、强度相对较低的填充土体等组成的非均质、不连续的复杂地质体[1].土石混合体的力学行为与其各组成成分的物理力学属性和内部的细观结构特征等关系密切,与均质的岩土体有着较大的差别.这种复杂的岩土体在自然界中分布非常广泛,地质成因各异,如我国三峡库区和西南山区广泛存在的滑坡堆积体等.开展土石混合体力学特性与变形破坏机理的研究,对土石混合体滑坡等地质灾害的防治和涉及到土石混合体的工程建设的设计与施工均具有重要的理论意义和实用价值.
近年来,随着我国大规模水利水电、公路、铁路等工程建设的快速发展,土石混合体作为一种有别于一般土体和岩石的特殊地质材料,已逐渐成为岩土工程领域研究的热点问题之一,许多专家学者对其物理力学特性进行了较为系统的研究,取得了一系列研究成果.有关土石混合体的研究主要包括原位地质调查[2, 3]、大型原位试验[4-6]、室内试验[7-9]和数值模拟[1-3, 10-16]等.土石混合体是由较大的块石和细粒土体所组成的非均质非连续的颗粒材料,采用试验研究以及传统的连续介质的力学分析方法均难以揭示其复杂的变形破坏机理,而颗粒离散元因其能较好地模拟颗粒体系的非线性、大变形和颗粒间复杂的相互作用等,比较适合从细观水平上来探究土石混合体的力学特性和变形破坏机理.徐文杰等[12, 13]基于三维颗粒离散元法,进行了不同含石量、不同岩性的土石混合体大型直剪试验的数值模拟研究,但其模型中将块石简化球体与实际情况有一定差异.丁秀丽等[14, 15]对由数字图像处理得到的土石混合体实测模型进行了双轴试验和直剪试验的二维颗粒流数值模拟,对土石混合体与均质土体的力学特性和变形破坏特征进行了对比分析.Graziani等[2]采用二维颗粒流对土石混合体的双轴试验和直剪试验进行了数值模拟,分析了含石量、块石形状和块石粗糙度等因素对土石混合体内摩擦角和黏聚力的影响规律,但模型中块石形状为三角形和矩形等规则的二维多边形与自然界中块石的三维不规则形态仍然具有一定差异.金磊等[16]提出了一种不规则块石三维离散元模型随机生成技术,并建立了符合宏观统计规律的土石混合体三维离散元模型,对土石混合体大三轴试验进行了数值模拟,深入分析了土石混合体的变形破坏机理.
从已有研究成果可以看到,虽然针对土石混合体的颗粒离散元模拟已有不少研究成果,但均未就土石混合体细观力学参数对其宏观力学响应的影响进行系统的探究,而这恰恰是采用颗粒离散元研究岩土材料力学特性首先要解决的关键问题.为此,本文在文献[16]提出的土石混合体三维离散元随机模型的基础上,对土石混合体大三轴试验进行了三维颗粒流数值模拟,获得了不同石-土颗粒法向刚度的比值、不同石-土颗粒法切向刚度比的比值、不同石-土颗粒摩擦系数的比值和不同石-土颗粒间黏结强度等情形下土石混合体的应力应变特征,并从微裂纹演化、摩擦功和块石颗粒平均旋转量等方面深入分析了不同颗粒细观力学参数对宏观力学特性影响的细观机理.
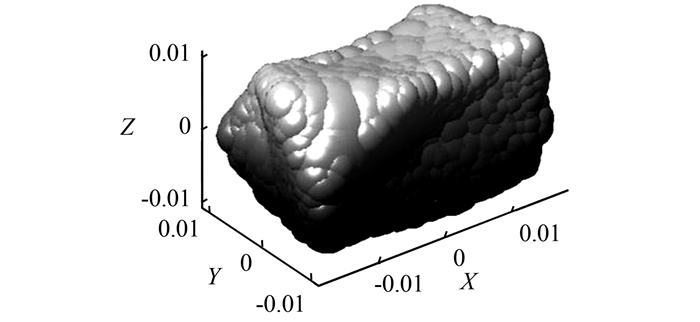
1 土石混合体大三轴数值试验 1.1 土石混合体数值模型要准确模拟土石混合体的力学性质和运动特性,必须首先实现不规则块石的模拟.文献[16]提出了一种基于球度和凹凸度的不规则块石体数值模型随机生成技术,具体的方法是以球度和凹凸度作为不规则块石体的几何特征控制参数,首先生成符合统计规律的随机不规则块石体几何模型,然后采用球体可重叠算法转换为离散元模型并进行球体数量和密度优化,即可获得与天然土石混合体中块石形态特征相似的不规则块石三维离散元模型,如图 1所示,模型参数与文献[16]相同.
|
| 图 1 典型不规则块石三维离散元模型 Figure 1 Typical DEM model of IRS rock block |
本文研究所建立的大三轴数值试样是直径为200 mm、高度为500 mm的圆柱形试样.根据Medley等[17]研究,土石阈值可定义为
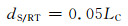 (1)
(1)
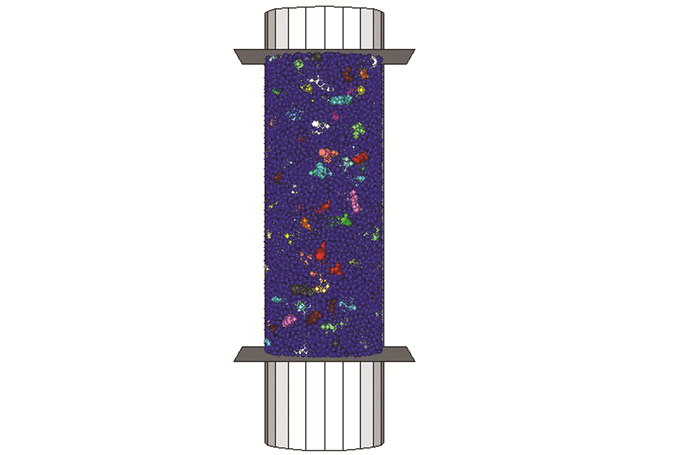
式中:dS/RT为土/石阈值;LC为土石混合体的工程特征尺度,对于三轴试验试样,可取为试样直径,因此本文的土/石阈值可定为10 mm.考虑到当前计算机的计算能力,为了提高计算效率,本文对土石混合体颗粒级配进行了一定程度的简化处理,土体颗粒简化为球体,粒径取值范围为8~10 mm,块石粒径简化为在20~40 mm范围内服从正态分布,这里所说的粒径并不是块石的实际粒径,而是指与该粒径的球体体积相同的当量粒径.采用文献[16]中所述的土石混合体三维离散元模型建模方法建立含石量为50%(块石体积与土石总体积的比值)的土石混合体三维颗粒流模型,如图 2所示,土颗粒为蓝色,块石由不同颜色的clumps表示.
|
| 图 2 土石混合体大三轴数值试样 Figure 2 Numerical specimen of SRM |
三维颗粒流PFC3D提供了3种基本的接触本构模型,他们分别是接触刚度模型、滑移模型和黏结模型[18].其中黏结模型分为接触黏结和平行黏结,接触黏结适用于胶结物质含量很少的松散土体,平行黏结适用于致密的强胶结的岩石类材料.根据土石混合体的结构组成特征,本文选取线性接触刚度模型、滑移模型和接触黏结模型来进行模拟.土石混合体中块石的强度和刚度较细粒土体基质要大得多,在低围压下基本不会发生颗粒破碎,因此采用clump来模拟不规则块石是比较合适的.
土石混合体数值模型需要确定的细观力学参数包括块石颗粒的法向刚度、法向刚度与切向刚度的比值、细观摩擦系数, 土体颗粒的法向刚度、法向刚度与切向刚度的比值、细观摩擦系数、法向黏结强度、法向黏结强度与切向黏结强度的比值以及土-石颗粒间黏结强度.已有颗粒材料宏细观力学参数相关关系的研究成果表明:颗粒的法向刚度主要影响体系的弹性模量,法向刚度越大弹性模量越大;颗粒的法切向刚度比主要影响体系的泊松比,法切向刚度比越大泊松比越大;细观摩擦系数和法向黏结强度主要影响体系的峰值强度和残余强度,强度随摩擦系数和黏结强度的增大而增加;法切向黏结强度的比值主要影响体系的破坏形式,随着法切向黏结强度比值的增大,试样的破坏逐渐由以张拉破坏为主转向以剪切破坏为主[19-21].
参考已有的黏性土、岩石和土石混合体的颗粒流模拟的相关文献[12-15, 19-22],本文选取了一组具有代表性的细观力学参数作为土石混合体模型的基本参数,其中土颗粒之间黏结的法向强度为200 kPa,土颗粒与块石颗粒之间黏结的法向强度与土颗粒间法向强度相同,法、切向黏结强度的比值均为1,块石与块石颗粒间无黏结,土颗粒与块石颗粒间接触的摩擦系数设为两者中的较小值.上下边界墙的法向刚度为1×109 N/m,侧墙的法向刚度为1×105 N/m,切向刚度和摩擦系数均为0,其他参数见表 1.在模拟的过程中,土体颗粒的细观力学参数保持不变,分别研究石-土颗粒法向刚度的比值、石-土颗粒法切向刚度比的比值、石-土颗粒细观摩擦系数的比值和石-土颗粒间黏结强度与土颗粒间黏结强度的比值变化对土石混合体宏观力学特性的影响.
| 颗粒 | 密度/(kg·m-3) | 法向刚度/(N·m-1) | 法切向刚度比 | 摩擦系数 |
| 土 | 2 300 | 1×106 | 10 | 0.3 |
| 块石 | 2 680 | 1×108 | 2 | 0.6 |
进行数值试验时,首先要利用伺服控制程序加围压并保持围压恒定,模型的上下边界墙作为加载板,加载速度为0.05 m/s,需要说明的是准静态数值模拟中的速度和现实中的速度是不同的[18].采用应变控制加载方式,当轴向应变达到15%时停止加载并终止试验.本文研究围压选为0.2、0.4和0.8 MPa,为了保证试验过程中时间步足够小,将允许的最大时步设为1×10-7 s/step.在加载过程中对轴向偏应力、轴向应变、体应变、摩擦能、动能、应变能、微裂纹总数、剪切裂纹数、张拉裂纹数、土颗粒间裂纹数、土与块石颗粒间裂纹数等量进行了采样和记录,以便后续进行分析.
2 试验结果及分析下面将分别对不同石-土颗粒法向刚度的比值、不同石-土颗粒法切向刚度比的比值、不同石-土颗粒摩擦系数的比值和不同石-土颗粒间黏结强度与土-土颗粒间黏结强度的比值等情形下土石混合体的宏观力学响应与相应的细观机理进行详细的分析.
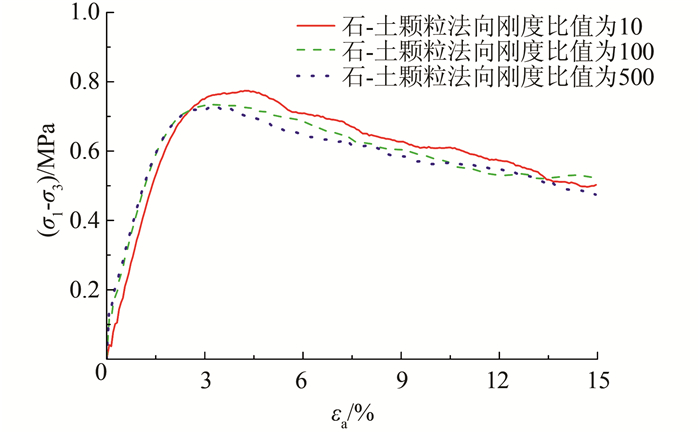
2.1 石-土颗粒法向刚度的比值在第1.2节中给出的土石混合体细观力学基本参数的基础上,考察石-土颗粒法向刚度的比值分别为10、100和500三种情形.限于篇幅,本文仅给出围压为0.4MPa时的试验结果(下同),图 3、4分别为不同石-土颗粒法向刚度比值的土石混合体大三轴试样的偏应力-轴向应变关系曲线和体应变-轴向应变关系曲线.
|
| 图 3 不同石-土颗粒法向刚度比值的偏应力-轴向应变关系曲线 Figure 3 Deviatoric stress-axial strain relationship curves of SRM with different ratios of rock to soil particle normal stiffness |
|
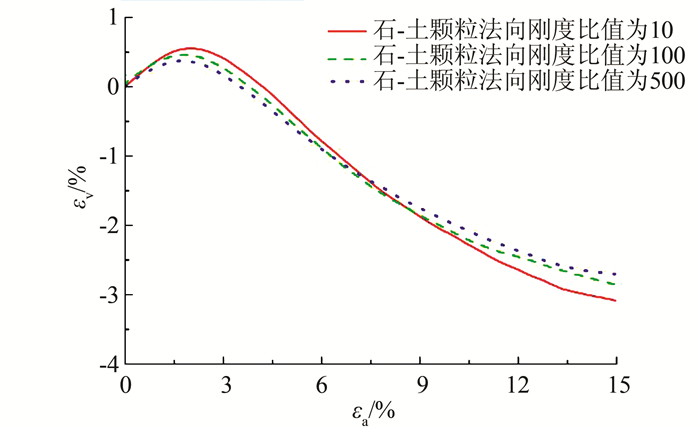
| 图 4 不同石-土颗粒法向刚度比值的 Figure 4 Volumetric-axial strain relationship curves of SRM with different ratios of rock to soil particle normal stiffness |
从图 3和4可以看到,不同石-土颗粒法向刚度比值的土石混合体试样均表现出显著的应变软化和剪胀特性.应力应变曲线大体上包括弹性阶段、屈服阶段、硬化至峰值阶段、峰后软化阶段和残余阶段,对应的体变曲线初始为剪缩、在屈服点时进入剪胀、剪胀快速发展阶段和剪胀逐步稳定阶段.随着石-土颗粒法向刚度比值的增大,初始模量增大,破坏应变和峰值强度均减小,残余强度基本相同,剪缩和剪胀性均减弱.
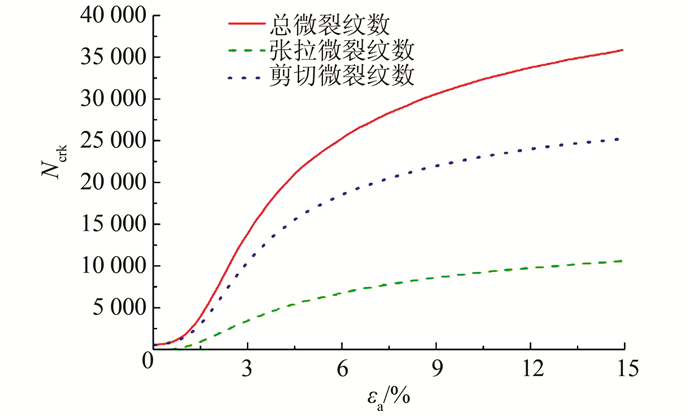
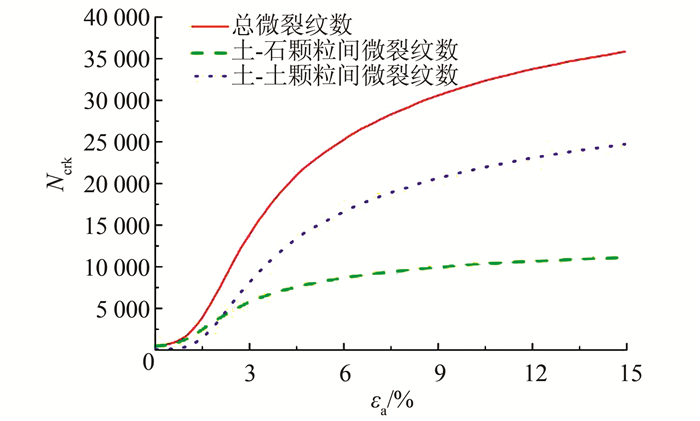
要解释上述不同石-土颗粒法向刚度比值对土石混合体强度和变形特性影响的机理,首先要揭示土石混合体的变形破坏机理,这里以基本参数的试样为例来进行阐述.图 5给出了加载结束时试样的黏结网络图、中间纵截面上的位移矢量图和块石颗粒间接触力分布图,图 5(c)中黑色短线即为接触力,其粗细代表接触力大小.图 6、7分别为加载过程中不同类型的微裂纹和不同位置的微裂纹数随轴向应变的演化规律.从图 5可以看到,加载结束时试样中已存在明显的从左上、左下向右中发育的剪切带,剪切带内黏结大部分已破坏,剪切带两侧颗粒位移方向明显不同,块石颗粒已相互接触,并传递轴向荷载.从图 6、7可以看到,微裂纹随轴向应变的发展规律基本相同:应变较小时,微裂纹较少且增加缓慢,初始屈服后试样中微裂纹开始迅速扩展,残余阶段微裂纹数渐趋稳定.由图 6可知试样中微裂纹主要是剪切裂纹,这与图 5中观察到的剪切破坏是对应的.由图 7可知,初始屈服(轴向应变为2%左右)前微裂纹主要在土-石界面处产生,随后则主要在土体中扩展.土石混合体试样中由于土体和块石刚度差异较大,两者所分担的荷载差异亦较大,这样在土-石界面处容易产生应力集中,土体和块石的变形也不协调,所以试样中的微裂纹最初在土-石界面处生成,又由于块石相对于土体强度较大,微裂纹随后绕过块石在土体中扩展,最后联通形成了剪切带,发生剪切破坏.

|
| 图 5 加载结束时试样的黏结网络、中间纵截面上的位移场和块石间接触力 Figure 5 Contact bond network, displacement of middle vertical cross-section and contact forces among rock blocks at the loading end |
|
| 图 6 不同类型微裂纹数与轴向应变关系曲线 Figure 6 Relationship between microcrack number of different types and axial strain |
|
| 图 7 不同位置微裂纹数与轴向应变关系曲线 Figure 7 Relationships between microcrack number and axial strain at different locations |
图 8给出了不同石-土颗粒法向刚度比值的土石混合体试样中微裂纹随轴向应变的发展速率,微裂纹发展速率定义为
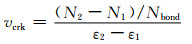 (2)
(2)
|
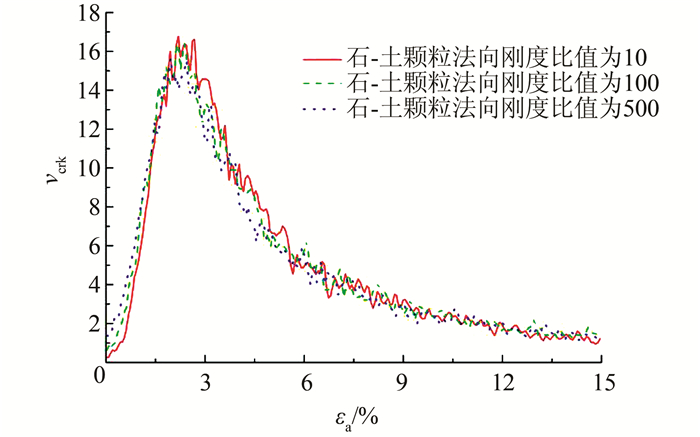
| 图 8 不同石-土颗粒法向刚度比值的微裂纹发展速率-轴向应变关系曲线 Figure 8 Relationships between microcrack propagation speed and axial strain of SRM with different ratios of rock to soil particle normal stiffness |
式中:vcrk为微裂纹发展速率;Nbond为试样初始状态下黏结的总数;N1和N2分别为轴向应变为ε1和ε2时所对应的微裂纹数目.
从图 8可知,随着石-土颗粒法向刚度比值的增大,土石界面处应力集中和变形不协调程度加大,微裂纹发生的时间越早,早期扩展的速率也较大,所以破坏应变和峰值强度越小.在轴向应变较小的弹性阶段,微裂纹很少且随机分布,土石整体压缩,而随着石-土颗粒法向刚度比值的增大,块石刚度增大,这样试样的初始整体刚度亦较大.在应变软化后的残余阶段,各试样中接触黏结大部分已破坏,微裂纹发展渐趋稳定,各试样应力应变关系基本相同.
2.2 石-土颗粒法切向刚度比的比值在第1.2节中给出的土石混合体细观力学基本参数的基础上,考察石-土颗粒法切向刚度比的比值分别为0.2、0.6和1.0三种情形.图 9为不同石-土颗粒法切向刚度比比值的土石混合体大三轴试样偏应力-轴向应变关系曲线.从图 9可以看到,石-土颗粒法切向刚度比的比值从0.2增加到1.0,土石混合体试样的宏观力学响应基本相同,说明石-土颗粒法切向刚度比的比值对土石混合体的宏观力学行为影响不显著.

|
| 图 9 不同石-土颗粒法切向刚度比比值的偏应力-轴向应变关系曲线 Figure 9 Deviatoric stress-axial strain relationship curves of SRM with different ratios of rock to soil particle stiffness |
在第1.2节中给出的土石混合体细观力学基本参数的基础上,考察石-土颗粒摩擦系数的比值分别为1、2和3三种情形.图 10为不同石-土颗粒摩擦系数比值的土石混合体大三轴试样的偏应力-轴向应变关系曲线.
|
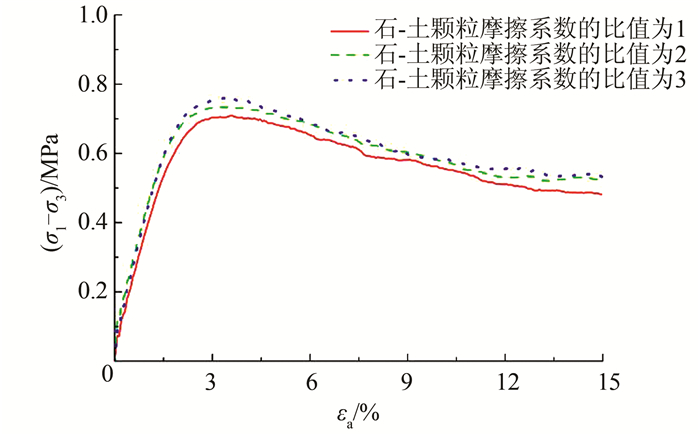
| 图 10 不同石-土颗粒摩擦系数比值的偏应力-轴向应变关系曲线 Figure 10 Deviatoric stress-axial strain relationship curves of SRM with different ratios of rock to soil particle friction coefficient |
从图 10可以看到,不同石-土颗粒摩擦系数比值的土石混合体试样均表现出应变软化特征,峰后曲线均有明显波动,这是由于黏结破坏后试样中块石颗粒不断调整位置所致.随着石-土颗粒摩擦系数比值的增大,初始模量稍有增加,破坏应变几乎不变,峰值强度和残余强度均有所提高.
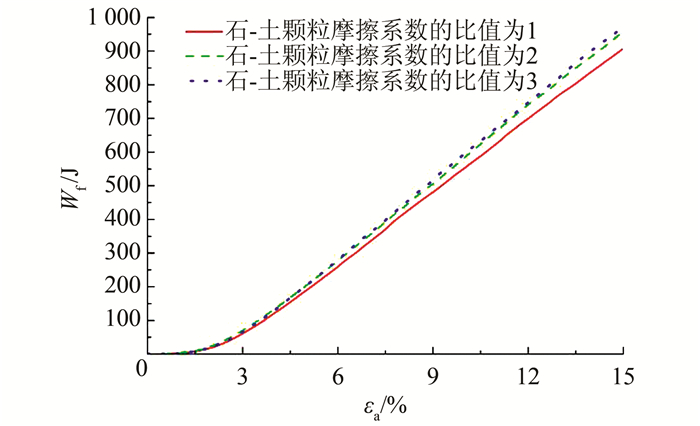
图 11、12分别给出了不同石-土颗粒摩擦系数比值的土石混合体试样在试验过程中摩擦功和试样中各块石颗粒转动分量绝对值的平均值随轴向应变的变化过程,这里的转动分量是块石颗粒相对于块石(clump)的质心绕3个坐标轴的转动量.从图 11、12可以看到,土石混合体试样在初始屈服前摩擦功基本为0,块石颗粒旋转量增加较缓慢,这是因为轴向应变较小时黏结基本未被破坏,颗粒间摩擦滑移等相互作用还未发生.随着轴向应变的增加,试样中黏结开始破裂,块石颗粒间相互作用增强,接触咬合(如图 5)与摩擦滑移交替出现,颗粒位置不断调整,试样摩擦功开始快速增长,块石颗粒平均旋转量亦不断增加.
|
| 图 11 不同石-土颗粒摩擦系数比值的摩擦功-轴向应变关系曲线 Figure 11 Relationships between frictional work and axial strain of SRM with different ratios of rock to soil particle friction coefficient |
|
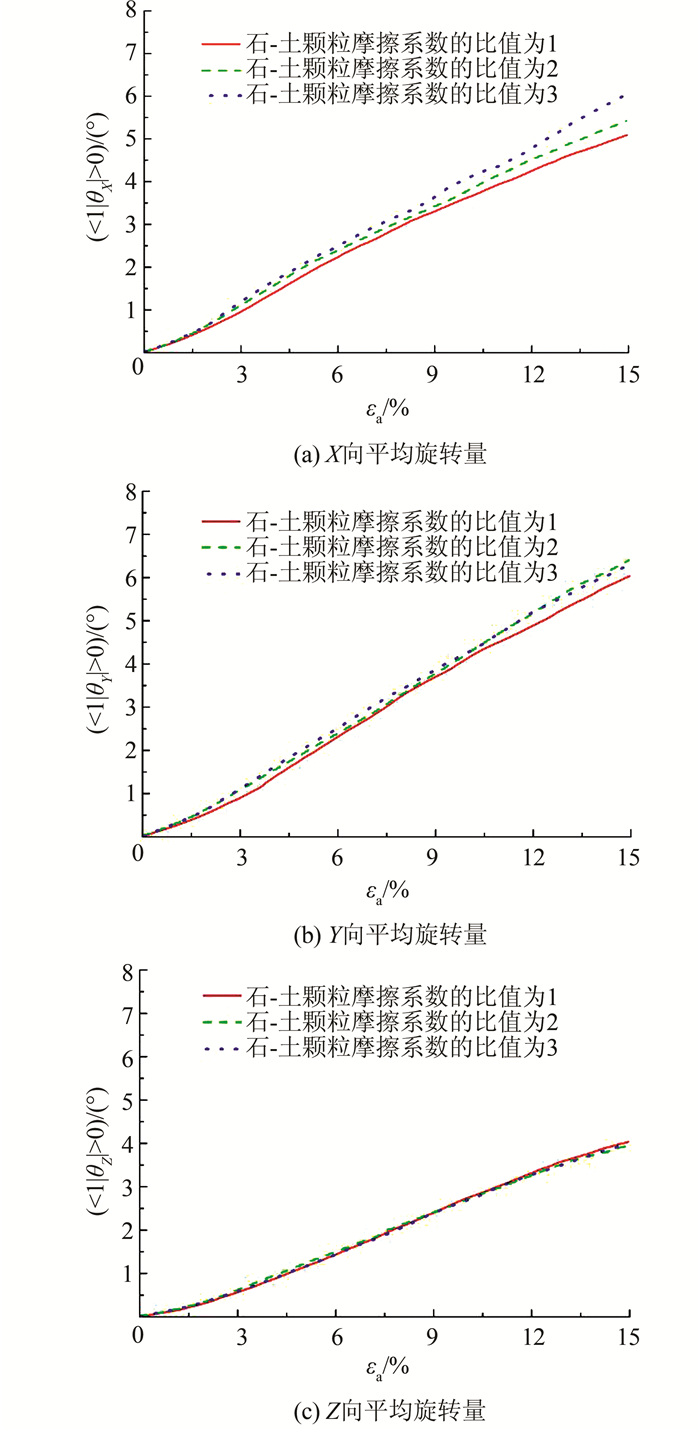
| 图 12 不同石-土颗粒摩擦系数比值的块石平均旋转量-轴向应变关系曲线 Figure 12 Relationships between mean rotation of rock blocks and axial strain of SRM with different ratios of rock to soil particle friction coefficient |
从图 11、12还可以发现,随着试样中石-土颗粒摩擦系数比值增大,摩擦功、块石X向平均旋转量和Y向平均旋转量也随之增大,且其增大的幅度随着轴向应变的增加而不断加大,而块石Z向平均旋转量基本相同.这说明,试样中石-土颗粒摩擦系数比值越大,也就是块石颗粒摩擦系数越大,块石颗粒间相互作用越强,所以试样的峰值强度和残余强度均有所提高.
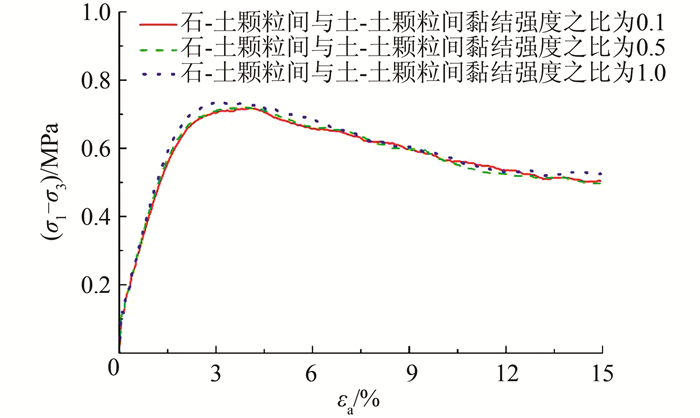
2.4 石-土颗粒间黏结强度变化在第1.2节中给出的土石混合体细观力学基本参数的基础上,考察石-土颗粒间黏结法向强度与土-土颗粒间黏结法向强度的比值分别为0.1、0.5和1.0三种情形,法切向黏结强度的比值仍为1.图 13为不同石-土颗粒间黏结强度的土石混合体大三轴试样的偏应力-轴向应变关系曲线.图 14为不同石-土颗粒间黏结强度的土石混合体大三轴试样的微裂纹发展速率-轴向应变关系曲线.
|
| 图 13 不同石-土颗粒间黏结强度的偏应力-轴向应变关系曲线 Figure 13 Deviatoric stress-axial strain relationship curves of SRM with different bond strengths between rock and soil particles |
|
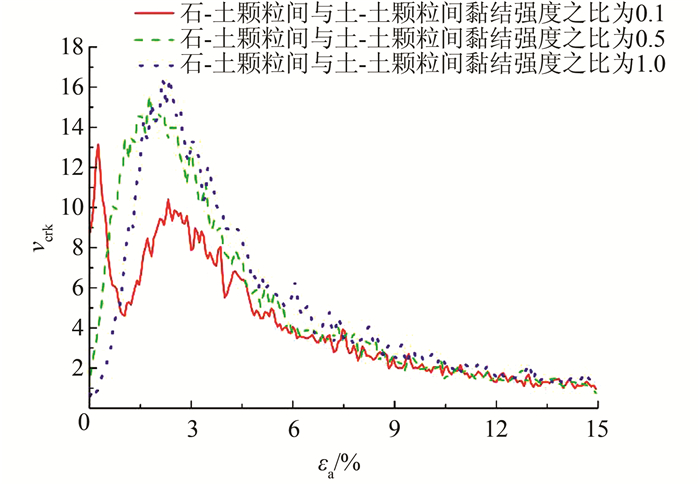
| 图 14 不同石-土颗粒间黏结强度的微裂纹发展速率-轴向应变关系曲线 Figure 14 Relationship between microcrack propagation speed and axial strain of SRM with different bond strengths between rock and soil particles |
从图 13可以看到,不同石-土颗粒间黏结强度与土-土颗粒间黏结强度比值的土石混合体大三轴试样的偏应力-轴向应变关系曲线基本相同,比值为1.0的试样较比值为0.1和0.5的试样峰值强度稍有提高.从图 14可知,石-土颗粒间黏结强度与土-土颗粒间黏结强度比值越大,试样在峰值应力前的微裂纹扩展速率越慢,峰值后则正好相反,残余阶段基本相同.石-土颗粒间黏结强度与土-土颗粒间黏结强度的比值为0.1的试样的微裂纹发展规律比较特殊,其存在两个波峰,其中第一个波峰在加载后不久即出现,历时非常短暂,这可能是由于土-石界面黏结强度很低,在加载的初始扰动下少数黏结即迅速破裂所致,随后发展规律与其他黏结强度的试样相同.
3 结论基于符合宏观统计规律的土石混合体三维离散元模型,针对不同石-土颗粒法向刚度的比值、不同石-土颗粒法切向刚度比的比值、不同石-土颗粒摩擦系数的比值和不同石-土颗粒间黏结强度与土-土颗粒间黏结强度的比值等情形下的土石混合体进行了大三轴试验三维颗粒流数值模拟,在揭示土石混合体变形破坏机理的基础上深入地分析了这些细观参数对土石混合体宏观力学特性影响的细观机理,在理论上获得了一些有意义的结论:
1) 土石混合体由于土体和块石刚度差异较大,两者所分担的荷载差异亦较大,在土-石界面处容易产生应力集中,土体和块石的变形也不协调,所以试样中的微裂纹最初在土-石界面处产生,又因为块石相对于土体强度较大,微裂纹随后绕过块石在土体中扩展,最后联通形成了剪切带,宏观上主要表现为剪切破坏.
2) 土石混合体在三轴压缩条件下表现出显著的应变软化和剪胀特性.
3) 随着石-土颗粒法向刚度的比值的增大,试样初始模量增大,破坏应变和峰值强度均减小,残余强度基本相同,剪胀性减弱.
4) 石-土颗粒法切向刚度比的比值对土石混合体的宏观力学行为影响不显著.
5) 石-土颗粒摩擦系数的比值越大,块石颗粒间相互作用越强,试样的摩擦功、块石颗粒平均旋转量、峰值强度和残余强度越大.
6) 石-土颗粒间黏结强度与土-土颗粒间黏结强度的比值对土石混合体的宏观力学行为影响不显著.
本文的研究成果可以为土石混合体颗粒离散元模拟中细观力学参数的合理确定提供一定的指导,同时也进一步完善了土石混合体力学理论体系.当然,本文在研究时,并未考虑含石量和土体基质细观力学参数不同所带来的潜在影响,相关结论还需进一步验证.
| [1] |
徐文杰, 胡瑞林, 岳中琦, 等. 土石混合体细观结构及力学特性数值模拟研究[J].
岩石力学与工程学报, 2007, 26(2): 300–311.
Xu Wenjie, Hu Ruilin, Yue Zhongqi, et al. Mesostructural character and numerical simulation of mechanical properties of soil-rock mixtures[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(2): 300–311. |
| [2] |
油新华. 土石混合体的随机结构模型及其应用研究[D]. 北京: 北方交通大学, 2001.
You Xinhua. Stochastic structural model of the earth-rock aggregate and its application[D]. Beijing: Northern Jiaotong University, 2001. |
| [3] | Graziani A, Rossini C, Rotonda T. Characterization and DEM modeling of shear zones at a large dam foundation[J]. International Journal of Geomechanics, 2012, 12(6): 648–664. DOI:10.1061/(ASCE)GM.1943-5622.0000220 |
| [4] |
李晓, 廖秋林, 赫建明, 等. 土石混合体力学特性的原位试验研究[J].
岩石力学与工程学报, 2007, 26(12): 2377–2384.
Li Xiao, Liao Qiulin, He Jianming, et al. Study on in-situ tests of mechanical characteristics on soil-rock aggregate[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(12): 2377–2384. DOI:10.3321/j.issn:1000-6915.2007.12.001 |
| [5] |
徐文杰, 胡瑞林, 曾如意. 水下土石混合体的原位大型水平推剪试验研究[J].
岩土工程学报, 2006, 28(7): 814–818.
Xu Wenjie, Hu Ruilin, Zeng Ruyi. Research on horizontal push-shear in-situ test of subwater soil-rock mixture[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(7): 814–818. |
| [6] | Coli N, Berry P, Boldini D. In situ non-conventional shear tests for the mechanical characterisation of a bimrock[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(1): 95–102. DOI:10.1016/j.ijrmms.2010.09.012 |
| [7] |
董云. 土石混合料强度特性的试验研究[J].
岩土力学, 2007, 28(6): 1269–1274.
Dong Yun. Experimental study on intensity character of rock-soil aggregate mixture[J]. Rock and Soil Mechanics, 2007, 28(6): 1269–1274. |
| [8] |
廖秋林, 李晓, 李守定. 土石混合体重塑样制备及其压密特性与力学特性分析[J].
工程地质学报, 2010, 18(3): 385–391.
Liao Qiulin, Li Xiao, Li Shouding. Sample remodeling, compactness characteristic and mechanical behaviors of rock-soil mixtures[J]. Journal of Engineering Geology, 2010, 18(3): 385–391. |
| [9] | Afifipour M, Moarefvand P. Mechanical behavior ofbimrocks having high rock block proportion[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 65(1): 40–48. |
| [10] |
徐文杰, 胡瑞林, 岳中崎. 土-石混合体随机细观结构生成系统的研发及其细观结构力学数值试验研究[J].
岩石力学与工程学报, 2009, 28(8): 1652–1665.
Xu Wenjie, Hu Ruilin, Yue Zhongqi. Development of random mesostructure generating system of soil-rock mixture and study of its mesostructural mechanics based on numerical test[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1652–1665. |
| [11] |
丁秀丽, 张宏明, 黄书岭, 等. 基于细观数值试验的非饱和土石混合体力学特性研究[J].
岩石力学与工程学报, 2012, 31(8): 1553–1566.
Ding Xiuli, Zhang Hongming, Huang Shuling, et al. Research on mechanical characteristics of unsaturated soil-rock mixture based on numerical experiments of mesostructure[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(8): 1553–1566. |
| [12] |
徐文杰, 张海洋, 许强, 等. 土石混合体直剪离散元数值试验研究[J].
计算力学学报, 2014, 31(2): 228–233.
Xu Wenjie, Zhang Haiyang, Xu Qiang, et al. Numerical simulations of direct shear test with soil-rock mixture using discrete element method[J]. Chinese Journal of Computational Mechanics, 2014, 31(2): 228–233. DOI:10.7511/jslx201402015 |
| [13] |
贾学明, 柴贺军, 郑颖人. 土石混合料大型直剪试验的颗粒离散元细观力学模拟研究[J].
岩土力学, 2010, 31(9): 2695–2703.
Jia Xueming, Chai Hejun, Zheng Yingren. Mesomechanics research of large direct shear test on soil and rock aggregate mixture with particle flow code simulation[J]. Rock and Soil Mechanics, 2010, 31(9): 2695–2703. |
| [14] |
丁秀丽, 李耀旭, 王新. 基于数字图像的土石混合体力学性质的颗粒流模拟[J].
岩石力学与工程学报, 2010, 29(3): 477–484.
Ding Xiuli, Li Yaoxu, Wang Xin. Particle flow modeling mechanical properties of soil and rock mixtures based on digital image[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 477–484. |
| [15] |
周剑, 张路青, 戴福初, 等. 基于黏结颗粒模型某滑坡土石混合体直剪试验数值模拟[J].
岩石力学与工程学报, 2013, 32(增1): 2650–2659.
Zhou Jian, Zhang Luqing, Dai Fuchu, et al. Numerical simulation of direct shear tests for rock and soil mixture in a landslide based on bonded-particle model[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(Sup.1): 2650–2659. |
| [16] |
金磊, 曾亚武, 李欢, 等. 基于不规则颗粒离散元的土石混合体大三轴数值模拟[J].
岩土工程学报, 2015, 37(5): 829–838.
Jin Lei, Zeng Yawu, Li Huan, et al. Numerical simulation of large-scale triaxial tests on soil-rock mixture based on DEM of irregularly shaped particles[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(5): 829–838. DOI:10.11779/CJGE201505008 |
| [17] | Medley E W. The engineering characterization of melanges and similar block-in-matrix rocks (bimrocks)[D]. Dept. of Civil Engineering, Univ. of California, Berkeley, CA, 1994. |
| [18] | Itasca Consulting Group Inc. Universal Distinct Element Code Version 3.1[M]. Minneapolis: Itasca Consulting Group, 2006. |
| [19] |
徐小敏, 凌道盛, 陈云敏, 等. 基于线性接触模型的颗粒材料细-宏观弹性常数相关关系研究[J].
岩土工程学报, 2010, 32(7): 991–998.
Xu Xiaomin, Ling Daosheng, Chen Yunmin, et al. Correlation of microscopic and macroscopic elastic constants of granular materials based on linear contact model[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(7): 991–998. |
| [20] |
周博, 汪华斌, 赵文锋, 等. 黏性材料细观与宏观力学参数相关性研究[J].
岩土力学, 2012, 33(10): 3171–3178.
Zhou Bo, Wang Huabin, Zhao Wenfeng, et al. Analysis of relationship between particle mesoscopic and macroscopic mechanical parameters of cohesive materials[J]. Rock and Soil Mechanics, 2012, 33(10): 3171–3178. |
| [21] |
赵国彦, 戴兵, 马驰. 平行黏结模型中细观参数对宏观特性影响研究[J].
岩石力学与工程学报, 2012, 31(7): 1491–1498.
Zhao Guoyan, Dai Bing, Ma Chi. Study of effects of microparameters on macroproperties for parallel bonded model[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(7): 1491–1498. |
| [22] |
周键, 王家全, 曾远, 等. 土坡稳定分析的颗粒流模拟[J].
岩土力学, 2009, 30(1): 86–90.
Zhou Jian, Wang Jiaquan, Zeng Yuan, et al. Simulation of slope stability analysis by particle flow code[J]. Rock and Soil Mechanics, 2009, 30(1): 86–90. |
 2018, Vol. 51
2018, Vol. 51




