文章信息
- 魏纲, 李志渊
- WEI Gang, LI Zhiyuan
- 矩形顶管施工引起的土体超孔隙水压力分布研究
- Research on distribution of initial excess pore water pressure due to rectangular pipe jacking
- 武汉大学学报(工学版), 2016, 49(6): 886-892
- Engineering Journal of Wuhan University, 2016, 49(6): 886-892
- http://dx.doi.org/10.14188/j.1671-8844.2016-06-015
-
文章历史
- 收稿日期: 2015-06-17
近年来,由于城市地面交通拥堵情况愈发严重,矩形顶管在地下人行通道、地铁站出入口、城市地下道路等城市建设工程中运用越来越多.矩形顶管虽然有效使用面积比圆形顶管大[1],但施工对土体的扰动也会更大.矩形顶管施工后带来的土体扰动会引起土体中超孔隙水压力的产生,其消散导致的工后沉降会对周边环境产生较大影响.
在盾构隧道中,施工引起的初始孔隙水压力的研究主要采用理论分析[2-9]、数值模拟[10-11]、现场实测[12]等方法进行,且多为关于盾构隧道的研究.其中理论分析方面:魏纲[2]基于应力释放理论研究隧道轴线上方土体工后沉降,推导得出盾构隧道中衬砌相邻的拱顶处土体初始超孔隙水压力,以及地面长期沉降的理论计算值;张冬梅等[3]通过应力路径法,计算隧道上方1 m范围的土体超孔隙水压力并对其分布进行研究,进而研究固结沉降;肖立等[4]在Mohr-Coulomb屈服准则的基础上,推导得出掘进时产生的土体超孔隙水压力的计算公式,同时考虑φ变化的情况下超孔隙水压力值大小与塑性区范围的变化;申林方等[5]基于Terzaghi-Rendulic二维固结理论,建立隧道周围土体超孔隙水压力分布的控制方程,并推导出其消散的解析解;王志良等[6]采用应力路径法,基于修正剑桥模型推导得到盾构施工产生的土体超孔隙水压力峰值;Skempton[7]、Henkel[8]推导出了初始超孔隙水压力的计算公式,需要许多待定参数;魏新江等[9]通过计算盾构施工引起周边土体中任一点的超孔隙水压力峰值,运用应力释放理论推导得出隧道周边土体的超孔隙水压力值,通过应力传递理论得到其分布,并通过算例分析其变化规律.综上所述,现有土体初始超孔隙水压力研究主要为盾构施工引起的,关于矩形顶管施工引起的土体超孔隙水压力分布的研究目前还是空白,因此有必要进行研究.
本文首次基于应力释放理论研究矩形顶管施工引起的土体初始超孔隙水压力,具体步骤为:1)计算出隧道周围土体中超孔隙水压力;2)确定土体初始超孔隙水压力的分布范围;3)运用应力传递理论推导出土体中任意一点的初始超孔隙水压力计算公式;4)做算例分析来研究土体超孔隙水压力的分布规律.
1 土体初始超孔隙水压力计算 1.1 本文研究思路本文研究对象为矩形顶管施工引起的土体初始超孔隙水压力.矩形顶管隧道施工对土体的扰动机理与盾构相似,因此研究中可以借鉴盾构的方法.
现有盾构隧道中用于计算施工引起的土体超孔隙水压力的方法,经研究后发现不能直接引用到矩形顶管隧道中.因此本文作了以下创新:
1) 盾构隧道的初始超孔隙水压力计算点在水平轴线处,笔者认为由于矩形顶管隧道相比于圆形隧道更不易发生水平方向的收敛,因此基于隧道几何形状更适合参考挡土墙理论,将初始超孔隙水压力计算点假设在隧道角点A2处(见图 1),图中A1、A2分别为盾构隧道和矩形顶管隧道的初始超孔隙水压力计算点.
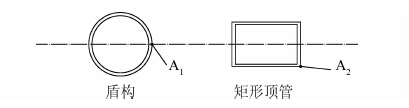
|
| 图 1 盾构隧道与矩形顶管隧道初始超孔隙水压力计 Figure 1 Initial excess pore water pressure calculation points of shield tunnel and rectangular pipe jacking tunnel |
2) 在隧道周围土体超孔隙水压力的应力传递研究中,由于圆形盾构隧道顶部与土体接触部分很小,因此通常令盾构隧道顶部向上传递应力的土体宽度为L,其大小可以通过对实测值反分析得到.如蒋洪胜[13]实例中:U0=53 kPa,L=1 m,(H0+L)/(H0+2R)=0.7;易宏伟[14]实例中:U0=100 kPa,L=2 m,(H0+L)/(H0+2R)=0.7.故魏纲[15]提出令(H0+L)/(H0+2R)=0.7,所以:
式中:U0为隧道周边土体初始超孔隙水压力值;H0为盾构隧道覆土埋深;L为隧道顶部向上传递应力的土体宽度;R为盾构隧道外半径.
而在矩形顶管隧道中,笔者认为可以通过应力传递土体的位置和几何关系,计算出一个等效的半径R,再代入式(1)计算.
3) 由于圆形盾构隧道的几何性质,隧道水平截面形状上不存在转角,因此隧道周围土体中孔隙水压力分布呈连续状.关于矩形顶管隧道,因为隧道存在转角,周围土体中隧道侧面孔隙水压力与底部孔隙水压力中间存在4个过渡区域.由于现有文献中没有关于这方面的研究,本文参考土力学[16]中普朗德尔地基整体剪切破坏模式中中心区域与被动区域的连接,假设由一组对数螺旋线组成,以此来计算并分析其中孔隙水压力大小及分布规律.
在计算前作以下假设:1)借鉴计算盾构施工引起的土体初始超孔隙水压力中运用的方法;2)文中出现的初始超孔隙水压力为土体中最大超孔隙水压力;3)假设矩形顶管隧道一侧为一挡土墙;4)土体中应力释放[2]导致土体中初始超孔隙水压力的产生,且隧道周围应力释放率大小相等.
其中假设三是因为矩形顶管相比圆形顶管横向收敛较小,在力学模型上接近挡土墙;假设四是由于目前对隧道周围应力释放率大小的研究非常缺乏,为计算简便,根据应力释放理论做出的.
1.2 矩形顶管隧道周围土体初始超孔隙水压力计算 1.2.1 隧道围压的计算方法矩形顶管隧道的围压受力模式见图 2[17],图中γ为土体重度,由于有多层土体,采用加权平均得出;H为覆土埋深;h为隧道外部高;l为隧道外部宽;K0为土体静止压力系数;θ为计算点与隧道水平夹角,取值为-π/2;P1为上覆土压力;P2为侧面土压力;P3为隧道自身重量.
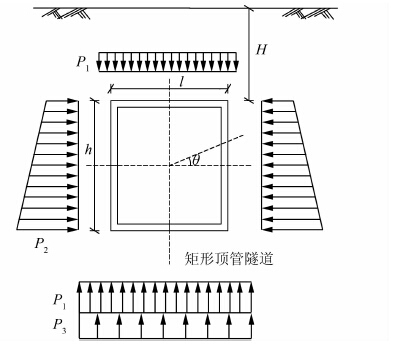
|
| 图 2 矩形顶管隧道受力图 Figure 2 Diagram of rectangular pipe jacking tunnel forced |
上部应力:
侧向应力:
下部应力:
根据文献[10],隧道角点处初始超孔隙水压力计算公式为
式中:U′0为隧道角点处土体的初始超孔隙水压力;Δσz为平面应变条件下第二主应力的变化量;Δσr与Δσθ分为径向和切向应力的变化量;Ps为隧道对土体的支护应力;Henkel孔隙水压力系数ε、λ中,ε=(3A-1)/2,且在饱和土取值为:A=0.5,λ=1;K0为土体静止压力系数;σ′0为土体初始有效应力;u0为静止孔隙水压力;G=E/(2(1+μ)),G为土体Lame弹性系数,E、μ分别为土体的弹性模量和泊松比;ηCF=12(R/tc)2;D0=Ectc/(1-μc2),μc和tc分别为隧道管道的泊松比和厚度.
1.2.3 土体应力释放率计算土体应力释放率α可以通过土体初始超孔隙水压力值除以相应点的法向水土压力得到,本文通过式(5)与式(4)计算得到隧道角点处土体的α值.
1.2.4 隧道周围土体初始超孔隙水压力计算矩形顶管隧道周围土体超孔隙水压力可以通过隧道围压乘以前文所得的应力释放率α得到.因为隧道存在转角,周围土体中隧道侧面孔隙水压力与顶部及底部孔隙水压力中间存在4个过渡区.
由前文所述,过渡区域假定由一组对数螺旋线ρ=r0exp(a0θ′)组成,其中r0、a0为对数螺旋线参数,可以通过曲线两端已知的围压大小联立计算得到;ρ和θ′为对数螺旋线函数的变量,分别代表超孔隙水压力大小和该位置处与水平方向的夹角.由此可计算得到过渡区域中土体围压,进而得到土体初始超孔隙水压力.
1.3 分布范围内任一点土体超孔隙水压力计算 1.3.1 土体扰动范围确定在矩形顶管施工过程中,许多施工工法与盾构隧道施工非常相似[18],因此在引起地层扰动的机理上也有许多相近之处,扰动区域中土体发生的变形也相近,因此可以借鉴盾构施工隧道的研究方法.
魏纲等[19]分析研究表明:盾构掘进会使隧道周围土体产生剪切扰动和开挖卸载,并形成剪切扰动区.通过极限平衡原理可知,土体中的剪切扰动区应与塑性区的边界相切,且边界线的水平仰角β等于45°+φ/2,与主动土压力角相同.魏新江等[9]研究表明:盾构施工在粘性土中引起的土体初始超孔隙水压力的分布范围为一曲线,在文献[19]的研究基础上提出了分布范围的具体计算方法.
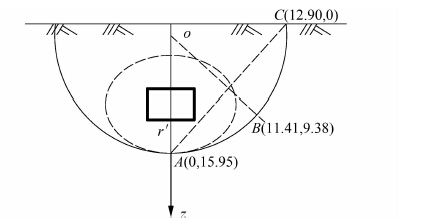
取隧道右半横截面为例,矩形顶管施工扰动范围如图 3所示,本文参考文献[9]的计算方法,可确定A、B、C点的具体位置.
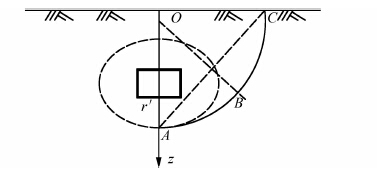
|
| 图 3 矩形顶管施工扰动范围 Figure 3 Disturbance zone of rectangular pipe jacking |
根据现有研究及实测资料[9],推导得出剪切扰动区半径 r′(扰动区边缘到隧道轴心距离)约为${{r}^{'}}=\sqrt{{{(3D)}^{2}}+{{H}^{2}}}\sin [{{45}^{{}^\circ }}+\varphi /2-\arctan (H/3D)]$,D为矩形顶管的尺寸高和宽的平均数[20].A、B、C及圆心O的坐标为:A(0,H+h/2+r′),B(e,H+h/2),O(x,y),C(r′/sin(45°+φ/2)+hcot(45°+φ/2),0).其中e、x、y的表达式为
式中:a、b为使公式简便而设的参数,a=h+r′,$b=\frac{{{r}^{'}}}{\sin ({{45}^{{}^\circ }}+\varphi /2)}+h\cot ({{45}^{{}^\circ }}+\varphi /2)$.
1.3.2 土体任一点初始超孔隙水压力计算方法以隧道横截面为例,本文中应力传递模型见图 4.假定:1)土体扩散面(边界)与水平面夹角为β=45°+φ/2,且应力从下往上传递并扩散;2)在计算中沿顶进方向的长度均取1 m,由于该方向距离较长,因此简化为平面应变问题;3)沿隧道管道边缘任一点垂直方向,土体内各点的超孔隙水压力峰值发生变化;4)土体水平向压力随着垂直距离变化而变化,并在距隧道一定范围内均匀分布,其值为U(z);5)侧面土体压力分布均匀;6)周边土体各点的超孔隙水压力峰值不受其余处影响,仅由该处相对的与隧道管道相邻处超孔隙水压力峰值U0传递.
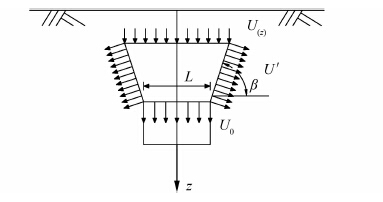
|
| 图 4 隧道周围土体超孔隙水压力向四周传递的示意图 Figure 4 Diagram of stress transfer of excess water pore pressure in soil around tunnel |
令隧道顶部向上传递应力的土体宽度为L,在矩形顶管中L等于隧道外宽度l.初始超孔隙水压力值为U0,U0=αPθ=90°,其中Pθ=90°为隧道顶部围压值.由竖向受力平衡,推导得出侧面土压力U′为
同理可得,离地面z深度处土体的竖向超孔隙水压力U(z)为
扰动边界往上距离f处土体的竖向超孔隙水压力U(f)为
式中:d为隧道到扰动边界的距离.
1.3.2.3 隧道侧向土体以隧道水平轴线上的侧向土体为例,隧道侧向距离k处土体的竖向超孔隙水压力U(k)为
式中:j为隧道到扰动边界的距离.
1.4 实例验证温锁林[21]对上海轨道交通2号线东延伸段金科路站4号出入口联络通道施工现场,进行了土体沉降和孔隙水压力的实测,得出了一些关于施工对周边环境影响的规律性结论.该隧道覆土深度为5.1~4.6m,外形尺寸为6.9 m×4.2 m.距离顶管外边线1 m处孔内设置2个孔压计,深度分别为4 m和7.1 m,测点编号为KY2、KY3,实测超孔隙水压力值分别为53.23、91.37 kPa.运用本文方法计算得出这两点的超孔隙水压力值分别为53.31、76.02 kPa,与实测值较为接近.
2 算例分析引用上海市轨道交通6号线浦电路车站3号出入口施工为例,进行算例分析.顶管隧道长42 m,共28个管节,每个管节长1.5m,内部尺寸为高3.36 m、长5.24 m,厚度tc=0.5 m,埋深H=7.2 m,隧道弹性模量Ec=34.5 GPa,泊松比取0.2,隧道所用钢筋混凝土重度取25 kN/m3,地下水位0.56 m.土体各参数取值如下:粘聚力c=11.84 kPa,内摩擦角φ=19.37°,重度γ=17.31 kN/m3,孔隙比e=1.21,含水率ω=42.34%,土体静止压力系数K0=0.53,弹性模量E=14.5 MPa,泊松比μ=0.35.
2.1 标准工况算例分析通过式(5)~(9)可计算得到隧道角点处的土体初始超孔隙水压力为33.01kPa,由式(2)~(4)计算得到该处隧道围压为106.05 kPa,相除得到应力释放率α为31.12%.隧道顶部围压为124.63 kPa,因此超孔隙水压力为38.79 kPa.
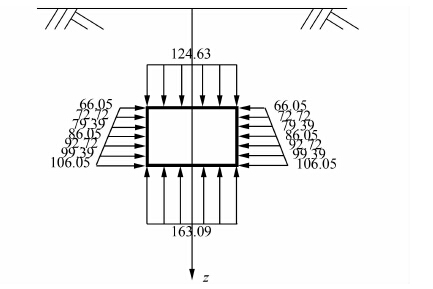
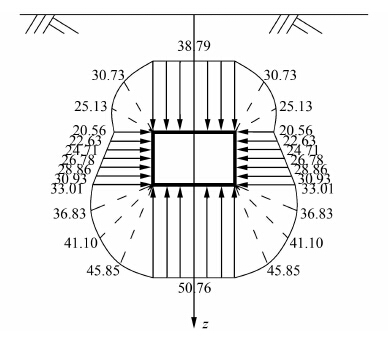
图 5和图 6分别为隧道法向围压受力图和土体初始超孔隙水压力分布图.由图 5可得隧道底部围压最大,侧向土压力呈线性变大.由图 6得出隧道周围土体初始孔隙水压力分布呈上小下大形状.
|
| 图 5 隧道周边土体法向围压(单位:kPa) Figure 5 Confining pressure of soil around the tunnel(unit: kPa) |
|
| 图 6 邻近隧道的土体初始超孔隙水压力大小 (单位:kPa) Figure 6 Value of initial excess pore water pressure of soil close to tunnel (unit: kPa) |
采用1.3.1节的方法,计算得到矩形顶管隧道施工引起的土体扰动范围,结果见图 7.
|
| 图 7 隧道施工引起的土体初始超孔隙水压力范围 (单位:m) Figure 7 Distribution of initial excess pore water pressure of soil around the rectangular pipe jacking tunnel(unit:m) |
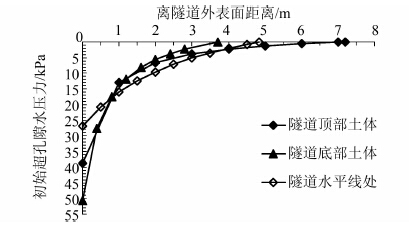
分别取隧道顶部、底部及水平轴线处,计算土体中不同位置处的初始超孔隙水压力,结果见图 8.如图所示,隧道周围不同位置处的土体初始超孔隙水压力形状变化相似,都为凹曲线变化,且都随着离隧道中心距离的增加而衰减.衰减的程度存在差别,对于隧道顶部土体,由于到地表距离相比其他部分较长,其衰减较慢;对于隧道底部的土体,由于到临界点的距离很小,则其衰减最快;对于隧道水平轴线上的土体,衰减速度介于前面两者之间.
|
| 图 8 不同位置处的土体初始超孔隙水压力(单位:kPa) Figure 8 Initial excess pore water pressure of soil at different location (unit: kPa) |
现根据前文算例,分别计算H=6 m和H=10 m时隧道周边超孔隙水压力分布,其他条件不变.当H取6 m时,隧道角点处围压为95.05kPa,初始超孔隙水压力大小为29.30 kPa,应力释放率为30.82%.当H取10 m时,隧道角点处围压为131.74 kPa,初始超孔隙水压力大小为41.67 kPa,应力释放率为31.62%.最终隧道周边土体的初始超孔隙水压力计算结果见图 9和图 10.
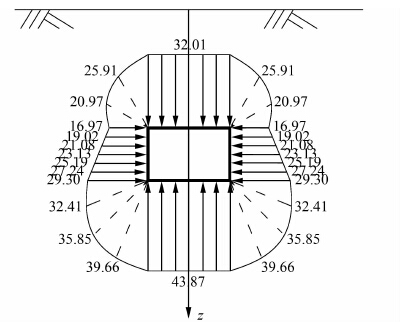
|
| 图 9 H=6 m时隧道周边土体的初始超孔隙水压力 (单位:kPa) Figure 9 Value of initial excess pore water pressure of soil close to tunnel for H=6 m (unit: kPa) |
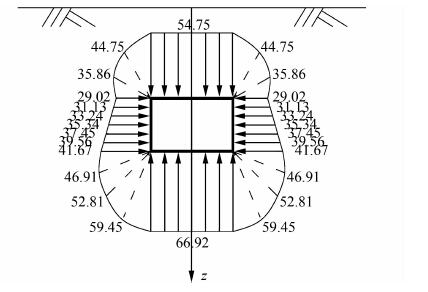
|
| 图 10 H=10 m时隧道周边土体初始超孔隙水压力 (单位:kPa) Figure 10 Value of initial excess pore water pressure of soil close to tunnel for H=10 m (unit: kPa) |
由图 9和图 10分析得出,随着埋深增加,隧道周围的初始超孔隙水压力也同时增加,呈上小下大形状,且孔隙水压力分布形状相似.
3 结语1) 本文基于应力释放理论,借鉴盾构隧道的研究方法,对矩形顶管施工引起的土体初始超孔隙水压力进行研究,提出其峰值及分布范围的计算方法,且发现二者随着隧道埋深变化而改变.
2) 算例分析结果表明:隧道周围不同位置处的土体初始超孔隙水压力形状变化相似,都为凹曲线变化,且都随着离隧道中心距离的增加而衰减.
由于矩形顶管施工引起的土体超孔隙水压力分布的研究尚处于初步阶段,需收集更多实测数据来验证本文方法的可靠性.对于土体扰动范围和超孔隙水压力的分布,也需要作进一步研究,例如考虑地下水位、不同性质土层等因素对其的影响.
| [1] |
彭立敏, 王哲, 叶艺超, 等. 矩形顶管技术发展与现状研究[J].
隧道建设, 2015, 35(1): 1–8.
Peng Limin, Wang Zhe, Ye Yichao, et al. Technological development and research status of rectangular pipe jacking method[J]. Tunnel Construction, 2015, 35(1): 1–8. |
| [2] |
魏纲. 盾构施工引起地面长期沉降的理论计算研究[J].
岩石力学与工程学报, 2008, 27(Sup.1): 2960–2966.
Wei Gang. Research on theoretical calculation of long-term ground settlement caused by shield tunneling[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(Sup.1): 2960–2966. |
| [3] |
张冬梅, 黄宏伟, 王箭明. 软土隧道地表长期沉降的黏弹性流变与固结耦合分析[J].
岩石力学与工程学报, 2003, 22(Sup.1): 2359–2362.
Zhang Dongmei, Huang Hongwei, Wang Jianming. Analysis of long-term settlements over tunnels using visco-elastic constitutive model coupled with consolidation theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(Sup.1): 2359–2362. |
| [4] |
肖立, 张庆贺, 朱继文, 等. 盾构施工引起的超孔隙水压力解析解[J].
同济大学学报(自然科学版), 2011, 39(2): 194–198.
Xiao Li, Zhang Qinghe, Zhu Jiwen, et al. Analytical solution of excess pore water pressure caused by shield tunneling[J]. Journal of Tongji University (Natural Science), 2011, 39(2): 194–198. |
| [5] |
申林方, 王志良, 魏纲, 等. 盾构施工引起土体超孔隙水压力消散问题的研究[J].
铁道学报, 2015, 37(6): 112–118.
Shen Linfang, Wang Zhiliang, Wei Gang, et al. Research on dissipation of excess pore water pressure caused by shield tunnelling[J]. Journal of the China Railway Society, 2015, 37(6): 112–118. |
| [6] |
王志良, 申林方, 魏纲. 盾构隧道施工引起周围土体超孔隙水压力的分析[J].
现代隧道技术, 2014, 51(4): 67–72.
Wang Zhiliang, Shen Linfang, Wei Gang. Analysis of excessive pore water pressure of soil induced by shield tunnelling[J]. Modern Tunnelling Technology, 2014, 51(4): 67–72. |
| [7] | Skempton A W. The pore pressure coefficients A and B[J]. Géotechnique, 1954, 4(4): 143–147. DOI:10.1680/geot.1954.4.4.143 |
| [8] | Henkel D J. The shearstrength of saturated remoulded clays[C]// Proceedings, Research Conference on Shear Strength of Cohesive Soils. Boulder, Colorado, 1960: 533-560. |
| [9] |
魏新江, 陈伟军, 魏纲. 盾构施工引起土体超孔隙水压力峰值的计算及影响因素分析[J].
岩土工程学报, 2012, 34(2): 280–285.
Wei Xinjiang, Chen Weijun, Wei Gang. Calculation and factors for distribution of initial distribution of peak value of excess pore water pressure due to shield construction[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(2): 280–285. |
| [10] |
敖日汗, 张义同. 盾构施工引起的固结沉降分析[J].
岩土力学, 2011, 32(7): 2157–2161.
Ao Rihan, Zhang Yitong. Analysis of consolidation settlements caused by shield tunneling[J]. Rock and Soil Mechanics, 2011, 32(7): 2157–2161. |
| [11] |
许金华, 何川, 夏炜洋. 水下盾构隧道渗流场应力场耦合效应研究[J].
岩土力学, 2009, 30(11): 3519–3522.
Xu Jinhua, He Chuan, Xia Weiyang. Research on coupling seepage field and stress field analyses of underwater shield tunnel[J]. Rock and Soil Mechanics, 2009, 30(11): 3519–3522. |
| [12] |
袁大军, 尹凡, 王华伟, 等. 超大直径泥水盾构掘进对土体的扰动研究[J].
岩石力学与工程学报, 2009, 28(10): 2074–2080.
Yuan Dajun, Yin Fan, Wang Huawei, et al. Study of soil disturbance caused by super-large diameter slurry shield tunnelling[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(10): 2074–2080. |
| [13] |
蒋洪胜, 侯学渊. 盾构掘进对隧道周围土层扰动的理论与实测分析[J].
岩石力学与工程学报, 2003, 22(9): 1514–1520.
Jiang Hongsheng, Hou Xueyuan. Theoretical study and analysis of site observation on the influence of shield excavation on soft clays around tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(9): 1514–1520. |
| [14] |
易宏伟, 孙钧. 盾构施工对软粘土的扰动机理分析[J].
同济大学学报, 2000, 28(3): 277–281.
Yi Hongwei, Sun Jun. Mechanism analysis of disturbance caused by shield tunnelling on soft clays[J]. Journal of Tongji University, 2000, 28(3): 277–281. |
| [15] |
魏纲, 周洋, 魏新江. 盾构隧道施工引起的工后地面沉降研究[J].
岩石力学与工程学报, 2013, 32(Sup.1): 2891–2896.
Wei Gang, Zhou Yang, Wei Xinjiang. Research on post-construction surface settlement caused by shield tunneling[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(Sup.1): 2891–2896. |
| [16] |
张克恭, 刘松玉.
土力学[M]. 北京: 中国建筑工业出版社, 2010.
Zhang Kegong, Liu Songyu. Soil Mechanics[M]. Beijing: China Architecture & Building Press, 2010. |
| [17] |
熊翦. 矩形顶管关键受力分析[D]. 北京: 中国地质大学, 2013.
Xiong Jian. Analysis of critical mechanics of rectangular pipe jacking[D]. Beijing: China University of Geosciences, 2013. http://cn.bing.com/academic/profile?id=616abdaa1043f46bb6d74c11e79430ab&encoded=0&v=paper_preview&mkt=zh-cn |
| [18] |
房营光, 莫海鸿, 张传英. 顶管施工扰动区土体变形的理论与实测分析[J].
岩石力学与工程学报, 2003, 22(4): 601–605.
Fang Yingguang, Mo Haihong, Zhang Chuanying. Theoretic and testing analysis of soil deformation in the area of disturbance caused by pipe-jacking[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(4): 601–605. |
| [19] |
魏纲, 魏新江, 龚慈, 等. 软土中盾构法隧道引起的土体移动计算研究[J].
岩土力学, 2006, 27(6): 995–999.
Wei Gang, Wei Xinjiang, Gong Ci, et al. Study on calculation for shield tunneling-induced ground movements in clays[J]. Rock and Soil Mechanics, 2006, 27(6): 995–999. |
| [20] |
周顺华, 廖全燕, 刘建国, 等. 矩形顶管隧道顶进过程的地层损失[J].
岩石力学与工程学报, 2001, 20(3): 342–345.
Zhou Shunhua, Liao Quanyan, Liu Jianguo, et al. Stratum loss during pipe jacking of rectangle tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(3): 342–345. |
| [21] |
温锁林. 大断面矩形顶管施工对环境影响研究[J].
中国市政工程, 2011(5): 37–39.
Wen Suolin. A study of environmental influence caused by large section rectangular pipe jacking construction[J]. China Municipal Engineering, 2011(5): 37–39. |
 2016, Vol. 49
2016, Vol. 49



