武汉大学学报(工学版)   2016, Vol. 49 Issue (5): 779-786

文章信息

张丽波, 郭将, 刘晓
ZHANG Libo, GUO Jiang, LIU Xiao
响应面法与蒙特卡洛法边坡可靠性评价方法对比研究
Comparative study of methodologies between response surface methods and Monte Carlo methods in slope reliability analysis
武汉大学学报(工学版), 2016, 49(5): 779-786
Engineering Journal of Wuhan University, 2016, 49(5): 779-786
http://dx.doi.org/10.14188/j.1671-8844.2016-05-023

文章历史

收稿日期: 2016-04-15
 Abstract              PDF               Figures               Tables
引用本文 0
张丽波, 郭将, 刘晓. 响应面法与蒙特卡洛法边坡可靠性评价方法对比研究[J]. 武汉大学学报(工学版), 2016, 49(5): 779-786.
ZHANG Libo, GUO Jiang, LIU Xiao. Comparative study of methodologies between response surface methods and Monte Carlo methods in slope reliability analysis[J]. Engineering Journal of Wuhan University, 2016, 49(5): 779-786.
响应面法与蒙特卡洛法边坡可靠性评价方法对比研究
张丽波, 郭将, 刘晓     
中国地质大学(武汉) 教育部长江三峡库区地质灾害研究中心，湖北 武汉 430074
收稿日期: 2016-04-15
作者简介: 张丽波(1991-)，男，硕士研究生，主要从事岩土体工程性质与稳定性研究，E-mail:824229615@qq.com.
通讯作者: 刘晓(1977-)，男，工学博士，副研究员，主要从事工程地质模拟、滑坡演化机制和控制理论方面的研究，E-mail:liuxiao@china.com
摘要: 考虑影响边坡稳定性的主要因素强度参数c、φ的不确定性，以蒙特卡洛法计算结果作为可靠性分析的基准解，在极限平衡法理论框架下开展不同可靠性评价方法之间的对比研究.采用c、φ为基本随机变量建立二次多项式响应面，以重构功能函数，并结合一次可靠度法和蒙特卡洛法进行边坡可靠性分析.通过对均质边坡的圆弧滑动破坏、非均质边坡的非圆弧滑动破坏、三峡库区谭家坪滑坡破坏这3个案例的可靠性分析结果对比得出：1)二次多项式响应面法原理简单，对于隐式功能函数，有较好的计算精度和求解效率，适用于可靠性分析的近似计算，特别是在参数服从正态分布的情况下，能够达到很高的精度；2)求解响应面时应优先采用Spencer法、Morgenstern-Price法，对圆弧滑动面边坡，也可以选用简化Bishop法.
关键词： 极限平衡法     响应面法     可靠性分析     一次可靠度法     蒙特卡洛法    
Comparative study of methodologies between response surface methods and Monte Carlo methods in slope reliability analysis
ZHANG Libo, GUO Jiang, LIU Xiao     
Three Gorges Research Center for Geo-hazard of Ministry of Education, China University of Geosciences, Wuhan 430074, China
Abstract: Considering the uncertainties of strength parameters cohesion c and interal friction angle φ, which have a significant impact on slope stability, a comparative study of different reliability evaluation methods was conducted under the theoretical framework of the limit equilibrium method. Taking Monte Carlo solution as a benchmark reference, a quadratic response surface function was established to reconstruct performance function with c and φ as the basic random variables. The response surface was implemented by two routes, namely first-order reliability method and Monte Carlo method. Three cases, which are circular slide in homogeneous slope, non-circular slide in inhomogeneous slope, and Tanjiaping landslide in Three Gorges Reservoir Area, were taken in the comparative study. The results are summarized into two aspects: 1) The quadratic polynomial response surface method is characterized by easy to implement, high efficiency and high accuracy. So, it is suitable to approximate calculation of reliability analysis, especially for the case with normal distribution of parameters, which will result in considerable accuracy. 2) The Spencer method and Morgenstern-Price method are preferred embodiments when solving the response surface. Besides, for a circular slide case, the simplified Bishop method is also acceptable.
Key words: limit equilibrium method     response surface method     reliability analysis     first-order reliability method     Monte Carlo method    

边坡稳定性问题是岩土工程领域的基本问题之一.随着学科的不断深化发展和工程实践由粗放型向精细化的转变，对边坡稳定性评估提出了更高的要求.由于边坡自然赋存条件与计算参数信息的不确定性[1]，单纯的确定性评价方法已经越来越难以满足解决实际问题的需要.以稳定性系数为评价指标的常规边坡稳定性分析方法[2, 3]基于确定性分析，没有考虑对边坡稳定有重要影响的因素的不确定性，因此得到的结果往往与实际情况存在明显偏差.而可靠性分析理论[4]则是基于概率统计理论，将边坡稳定性影响因素(如岩土特性参数、结构荷载、渗透系数等)作为随机变量来看待，每一组随机变量对应于一次确定性分析，通过大量的确定性分析得出统计规律，即实现对边坡的可靠性评价.从这个意义上来说，可靠性分析评价指标[5]体系本身涵盖了确定性理论框架下的稳定性系数，其来源于确定性理论，又高于确定性理论.

自Crawford[6]等首次将可靠性理论应用于土坡的稳定性分析以来，岩土工程界开始经历了确定性到不确定性的飞跃.进入21世纪，边坡可靠性分析已经成为岩土工程可靠性的一个重要研究领域，其评价方法的研究得到了快速发展，涌现出多种可靠性分析方法[7-15]，其中常用的方法有一次可靠度法(first-order reliability method,FORM)、随机有限元法(stochastic finite element method,SFEM)、响应面法(response surface method,RSM)和蒙特卡洛模拟法(Monte Carlo method,MC)等，各种分析方法有其各自的优缺点和适用范围，其中蒙特卡洛法计算结果精度较高，一般将其作为检验其他分析方法精度的标准，其缺点是计算量较大.因此，在满足精度要求的情况下，提出求解效率更高的方法成为一种研究趋势.杨海菲[16]等对各种可靠性分析方法的适用条件、灵活、精确程度进行了阐述.一般而言，这些研究常常致力于提出新的方法，对各种方法评价结果之间的差异性研究较少.鉴于此，本文致力于对极限平衡法理论框架下的可靠性分析方法进行横向对比和量化分析，并就此对边坡可靠性分析模型的选择提出建议.

1 蒙特卡洛模拟法

为达成各种方法之间的对比分析，需采用一种方法作为基准.本文以学术界广泛认可的蒙特卡洛方法作为评判精度的标准.蒙特卡洛法[10, 17]基本原理：已知随机变量X服从某种概率分布，通过随机数发生器产生服从变量X概率分布的M组随机数Xi=(xi1，xi2，…，xin)(其中：i=1，2，…，M；n为基本随机变量的个数)，将M组随机数代入状态函数g(X)，计算g(X)的值，统计g(X)≤0的个数，g(X)≤0说明此组随机数处于失效域内，求解流程图见图 1.假设M组随机数中存在m组数据使得g(X)≤0，那么当随机样本数量M足够大时，失效概率Pf为

${{P}_{f}}=P\left( g\left( {{X}_{i}} \right)\le 0 \right)=m/M$    (1)

可靠度指标：

$\beta ={{\Phi }^{-1}}\left( 1-{{P}_{f}} \right)$    (2)
图 1 蒙特卡洛法求解流程图 Figure 1 Progchart of Monte Carlo method
图选项
2 响应面法及其两种实现形式 2.1 建立响应面函数

响应面法[7, 18](RSM)是以近似的显式功能函数来代替真实的功能函数.当得到这一近似功能函数后，还需结合一定的可靠性分析方法(如一次可靠度法、蒙特卡洛模拟法等)进行可靠度计算，具体求解流程图见图 2.

设边坡有n个随机变量，响应Z是n个随机变量x1，x2，…，xn的函数，在保证计算精度的前提下，通常采用不含交叉项的二次多项式来模拟响应面，建立响应面函数：

$\bar{Z}=\bar{g}\left( X \right)={{a}_{0}}+\sum\limits_{i=1}^{n}{{{a}_{i}}{{x}_{i}}}+\sum\limits_{i=1}^{n}{{{a}_{ii}}{{x}_{i}}^{2}}$    (3)

式中，共有2n+1待定系数，待定系数通过下式确定的2n个轴向点+中心点的中心复合设计取样来确定，α 的取值取决于设计要求和影响因素的数量.

$\left. \begin{align} & {{x}_{i}}={{\mu }_{{{x}_{i}}}}\pm \alpha {{\sigma }_{{{x}_{i}}}} \\ & \alpha ={{2}^{n/4}} \\ \end{align} \right\}$    (4)
2.2 构造功能函数

采用二次响应面建立稳定性系数与参数ci,φi,…,γi之间的显式函数关系，将参数视为随机变量X=(x1,x2,…,xn)T，则功能函数的显示表达式为

$\begin{align} & Z=g\left( X \right)={{F}_{s}}-1\approx \bar{Z}=\bar{g}\left( X \right) \\ & ={{a}_{0}}+\sum\limits_{i=1}^{n}{{{a}_{i}}{{x}_{i}}}+\sum\limits_{i=1}^{n}{{{a}_{ii}}}{{x}_{i}}^{2} \\ \end{align}$    (5)

其中：Z<0表示边坡失效；Z>0表示边坡稳定；Z=0表示边坡处于极限平衡状态.

建立显示功能函数表达式以后，在极限平衡法理论框架下，采用中心复合设计取样求解待定系数.目前常用的极限平衡法包括瑞典条分[19]、简化Bishop[20]、简化Janbu[21]、Spencer[22]和Morgenstern-Price (M-P)[23]等，这些条分法都是以极限平衡理论为基础，通过假定条块之间的作用力满足某种函数关系以求得稳定性系数，各种条分法的假定和适用条件见表 1，通过不同的条分法可以建立不同的功能函数，分析不同的极限平衡稳定性计算模型对可靠度指标的影响.

图 2 RSM法求解流程图 Figure 2 Flowchart of RSM method
图选项
表 1 不同极限平衡法的假定和适用条件 Table 1 Different assumptions and applicable conditions of limit equilibrium method
极限平衡法静力平衡条件(是否平衡)假定条件滑面形状
力矩静力条间正应力E条间剪应力Y
瑞典条分是否否否Y=0，E=0圆弧
简化Bishop是否是否Y=0，E≥0圆弧
简化Janbu否是是否Y=0，E≥0任意
Spencer是是是是Y/E=tanθ任意
M-P是是是是Y/E=λf(x)任意
*注：① θ为常数；② λ 为待定常数，f(x)为剪力分布函数.
表选项
2.3 响应面实现方法一(RSM-FORM)

一次可靠度法包含中心点法和验算点法，验算点法克服了中心点法不考虑基本随机变量的实际分布的问题，对于独立正态分布随机变量直接采用一次二阶矩法，进行可靠性分析.对于非正态分布和存在相关性的随机变量应该先进行变量的当量正态化(JC法)和变量的正交变换，将非正态分布的随机变量转化为独立正态分布的随机变量，然后再进行可靠性计算.边坡可靠性分析通常将对其稳定性有重要影响的结构荷载、岩土参数、地下水等不确定因素作为基本随机变量来考虑，记为xi(i=1,2,…,n).响应面实现方法一(见图 2)通过响应面代理建立包括基本变量在内的显式功能函数，即式(5).并将功能函数Z=g(x)在 x*=(x1,x2,…,xn)T处按泰勒级数展开并保留其1次项：

$Z=g({{x}^{*}})+{{\sum\limits_{i=1}^{n}{\left( \frac{\partial g}{\partial {{X}_{i}}} \right)}}_{x*}}\left( {{X}_{i}}-{{x}^{*}} \right)$    (6)

可靠度指标：

$\beta =\frac{{{\mu }_{z}}}{{{\sigma }_{z}}}$    (7)

变量的灵敏度系数：

${{\alpha }_{{{X}_{i}}}}=-\frac{{{\left( \frac{\partial g}{\partial {{X}_{i}}} \right)}_{x*}}\cdot {{\sigma }_{{{X}_{i}}}}}{\sqrt{\sum\limits_{i=1}^{n}{{{\left[ {{\left( \frac{\partial g}{\partial {{X}_{i}}} \right)}_{x*}} \right]}^{2}}\cdot {{\sigma }_{{{X}_{i}}}}^{2}}}}$    (8)

验算点：

${{x}_{i}}^{*}={{\mu }_{{{X}_{i}}}}+\beta {{\alpha }_{{{X}_{i}}}}{{\sigma }_{{{X}_{i}}}}i=1,2,\cdots ,n$    (9)

失效概率：

${{P}_{f}}=1-\Phi \left( \beta \right)$    (10)
2.4 响应面实现方法二(RSM-MC)

响应面实现方法二(见图 2)通过响应面代理建立包括基本变量在内的显式功能函数作为可靠性分析的近似功能函数，然后用第1节详述的蒙特卡洛法进行求解，并比较计算结果，同时借此检验一次可靠度法的计算精度.

3 实例分析

本文采用均质边坡、非均质边坡和实际滑坡3个实例进行边坡可靠性分析方法之间的对比，旨在考查不同案例情况下，不同可靠性评价方法之间的差异.

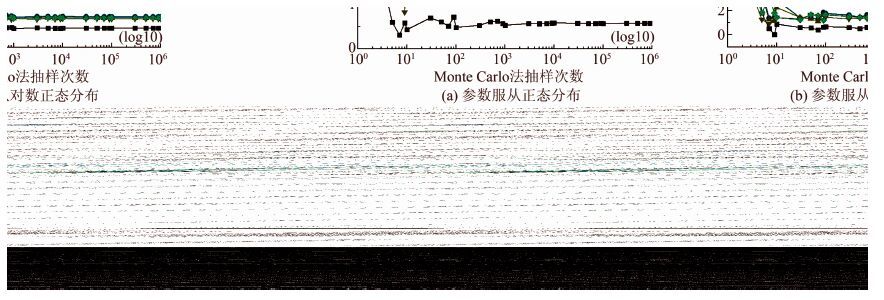
3.1 某均质边坡

已知简单均质黏性土边坡[24]，为简化计算，暂不考虑土性参数相关性，忽略土的重度变异性对可靠性的影响，土体的破坏符合Mohr-Coulomb破坏准则，不考虑地下水的作用和地震作用，其几何形态参数为高H=9.6 m，坡角θ=56.5°，土的容重γ=18 kN/m3，最危险滑裂面、滑弧圆心及土坡模型见图 3.土的抗剪强度参数黏聚力c的平均值μc=20 kPa，标准差σc=4 kPa；内摩擦角φ的平均值μφ=23°，标准差σφ=4.6°，将黏聚力c和内摩擦角φ作为随机变量来处理，并假定c、φ统计上相互独立，参数分别服从正态分布、对数正态分布.图 4所示为不同的极限平衡法下参数服从不同概率分布的Monte Carlo模拟样本数量与可靠度指标之间的关系，横坐标采用对数坐标显示，针对不同的参数分布、不同的方法所得可靠度指标整体变化趋势相同，且在样本数量达到1万次以后，可靠度指标的变化逐渐趋于稳定.为获取较好的效果，在此取Monte Carlo模拟样本数量为10万次的计算结果作为可靠性分析的基准解.可靠性计算结果见表 2、3，不同计算方法下的可靠度指标见图 5.

图 3 均质边坡几何模型(单位：m) Figure 3 Geometric model of homogeneous slope (unit:m)
图选项
图 4 不同参数分布均质边坡Monte Carlo模拟抽样曲线 Figure 4 Monte Carlo simulation sampling curve of homogeneous slope with different parameter distributions
图选项
表 2 均质边坡参数正态分布可靠度指标计算结果 Table 2 Reliability index calculation results of homogeneous slope with normal distribution parameters
极限平衡法MC法RSM-MC法RSM-FORM法
ⅠⅡⅢⅣⅤⅥⅦ
ββ对Ⅰ列取误差/%迭代次数β对Ⅰ列取误差/%对Ⅱ列取误差/%
瑞典条分0.5820.587-0.8640.5721.722.56
简化Bishop1.5691.611-2.6861.582-0.831.80
简化Janbu1.4671.474-0.4861.4481.301.76
Spencer1.3961.408-0.8651.3880.571.42
M-P1.4451.486-2.8451.474-2.010.81
表选项
表 3 均质边坡参数对数正态分布可靠度指标计算结果 Table 3 Reliability index calculation results of homogeneous slope with lognormal distribution parameters
极限平衡法MC法RSM-MC法RSM-FORM法
ⅠⅡⅢⅣⅤⅥⅦ
ββ对Ⅰ列取误差/%迭代次数β对Ⅰ列取误差/%对Ⅱ列取误差/%
瑞典条分0.5670.5414.5950.46917.2813.31
简化Bishop1.5131.831-21.0291.774-17.253.11
简化Janbu1.4111.588-12.5481.514-7.304.66
Spencer1.3421.506-12.2281.431-6.634.98
M-P1.4131.621-14.7281.559-10.333.82
表选项
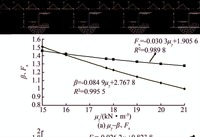
图 5 均质边坡不同计算方法下可靠度指标 Figure 5 The reliability index of homogeneous slope under the different calculation methods
图选项
3.2 非均质边坡

选用文献[2]中的澳大利亚计算机应用协会(ACADS)考核题EX1C进行非均质边坡可靠性分析，物理力学参数见表 4，最危险滑动面采用文献[25]公布的坐标，土坡剖面如图 6所示.共3个土层，将土层一的黏聚力c作为确定性变量，内摩擦角φ作为随机变量，土层二、三的黏聚力c、φ全部作为随机变量，则共有5个随机变量，暂不考虑随机变量之间的相关性，且都服从正态分布，可靠性分析结果见表 5.

表 4 EX1C物理力学参数 Table 4 Physical and mechanical parameters of EX1C
土层编号容重γ/(kN·m-3)黏聚力c/kPa内摩擦角φ/(°)
均值标准差均值标准差
一19.50038.05.71
二19.55.30.723.02.86
三19.57.20.220.02.86
表选项
图 6 非均质边坡EX1C剖面图 Figure 6 Cross section of inhomogeneous slope EX1C
图选项
表 5 非均质边坡EX1C可靠度指标计算结果 Table 5 Reliability index calculation results of inhomogeneous slope EX1C
极限平衡法MC法RSM-MC法RSM-FORM法
ⅠⅡⅢⅣⅤⅥⅦ
ββ对Ⅰ列取误差/%迭代次数β对Ⅰ列取误差/%对Ⅱ列取误差/%
简化Janbu2.2052.235-1.3652.234-1.320.04
Spencer3.0973.257-5.1743.238-4.550.58
M-P3.0683.224-5.0853.209-4.600.47
表选项
3.3 三峡库区谭家坪滑坡

谭家坪滑坡[26]位于三峡库区巴东县城迁建新址规划区，由谭家坪古滑坡和白岩沟、白水沟两个次级滑坡组成，两个次级滑坡作为老滑坡分解的产物，位于老滑坡的东西两侧，其中白水沟次生滑坡分布于谭家坪古滑坡的西侧，该次生滑坡后缘高程260 m，前缘剪出口高程175 m，滑体南北长225 m，东西宽180 m，面积约40 500 m2，滑体平均厚度11.5 m.谭家坪滑坡物理力学参数见表 6，计算剖面图见图 7.取强度参数c、φ作为边坡可靠性分析的基本随机变量，滑带土：μc=28 kPa，σc=8.4 kPa,μφ=15°，σφ=2.4°;滑体：μc=18 kPa,σc=5.4 kPa,μφ=25°，σφ=4.0°.假定c、φ统计上相互独立，且服从正态分布，分别采用响应面法和蒙特卡洛模拟法(取N=10万次)，可靠度指标计算结果见表 7.

图 7 谭家坪滑坡工程地质主剖面图 Figure 7 Main profile of Tanjiaping landslide engineering geology
图选项
表 6 滑坡体的物理力学参数 Table 6 Physical and mechanical parameters of the landslide
岩性重度γ/(kN·m-3)黏聚力c/kPa内摩擦角φ/(°)
均值标准差均值标准差
滑带土21.3288.4152.4
滑体24.6185.4254.0
表选项
表 7 谭家坪滑坡可靠度指标计算结果 Table 7 Reliability index calculation results of Tanjiaping landslide
极限平衡法MC法RSM-MC法RSM-FORM法
ⅠⅡⅢⅣⅤⅥⅦ
ββ对Ⅰ列取误差/%迭代次数β对Ⅰ列取误差/%对Ⅱ列取误差/%
简化Janbu0.2660.2544.5140.2621.50-3.15
Spencer0.4810.492-2.2930.482-0.212.03
M-P0.4470.4352.6840.4411.34-1.38
表选项
3.4 结果分析

通过以上3个实例，包括均质边坡的圆弧滑动破坏、非均质边坡的非圆弧滑动破坏、谭家坪滑坡破坏可靠性分析结果可知：

1) 岩土参数c、φ相同条件下，不同极限平衡法下可靠度指标计算结果的对比分析.据表 2、3和图 5的均质边坡圆弧滑动破坏可靠性分析可知，不同极限平衡法可靠度指标计算结果差异较大，其中瑞典条分法可靠度指标计算结果偏小，简化Bishop法可靠度指标计算结果偏大；据表 5、7非均质边坡的非圆弧滑动破坏和谭家坪滑坡破坏可靠性分析可知，简化Janbu法下可靠度指标计算结果偏小，故适用于任意滑动面的Spencer法和M-P法计算模型下可靠度指标计算结果可作为可靠性分析的最优解.这是由不同极限平衡法的假定条件和适用条件所决定的，Spencer法和M-P法作为满足所有平衡条件的精确条分法，其稳定性系数经多次迭代求得，可作为可靠性分析的准确响应，建立的功能函数精度较高，故而可靠性分析结果更加准确.

2) 相同极限平衡法条件下，岩土参数c、φ不同概率分布以及不同可靠性评价方法之间的对比分析.据表 2、3、5、7，以MC法作为评定基准，由RSM-MC法和MC法结果对比所得误差列(上述各表格第Ⅲ列) 可知，引入二次响应面函数作为可靠性分析的功能函数，在参数服从正态分布的条件下，可以满足精度要求，计算结果相对误差不超过5%；在参数服从对数正态分布的情况下，计算结果误差较大，瑞典条分法相对误差最小为4.59%，简化Bishop法误差最大达到-21.02%.此时，若对结果精度要求较高，应该通过响应面迭代或者选用高次响应面来拟合功能函数.由RSM-FORM法和RSM-MC法结果对比所得误差列(上述各表格第Ⅶ列)可知，在响应面(即功能函数)一定的情况下，一次可靠度法构建的近似求解方法所带来的误差较小.总体上由RSM-FORM法和MC法结果对比所得误差列(上述各表格第Ⅵ列)和各表格第Ⅳ列可知，RSM-FORM法只需要进行较少次数迭代即可取得较好的结果，求解效率较高，特别是在参数服从正态分布条件下，误差较小，接近基准解.

3) 综合分析，在一定条件下响应面法精度满足要求，且计算效率较高，原理简单，适用于功能函数无法用显式表达的近似可靠性分析.据表 2、3、5、7误差列分析可知，在可靠性分析中，不同极限平衡法稳定性计算模型所带来的影响要远大于可靠性分析具体实现方法的影响.故若对可靠性分析结果要求较高，首先要选用适当的极限平衡稳定性计算模型；其次可以选用高次响应面或进行响应面迭代拟合精度较高的功能函数.

4 结论与建议

1) 响应面法(RSM法)具有较高精度，它的一次可靠度法实现形式RSM-FORM法能大大提高计算效率，特别是在参数服从正态分布情况下，能取得更好的分析结果.在参数服从对数正态分布的情况下，计算结果误差明显增大.二次多项式响应面对于隐式功能函数有较好的计算精度和求解效率.

2) 在响应面法中，不同的极限平衡稳定性计算模型所得可靠度指标计算结果偏差较大.一般情况下，应优先选用适用于任意滑动面的Spencer法和M-P法；其次，对圆弧滑动面边坡也可以选用简化Bishop法.

参考文献
[1] Tang X S, Li D Q, Zhou C B, et al. Copula-based approaches for evaluating slope reliability under incomplete probability information[J]. Structural Safety, 2015, 52: 90–99. DOI:10.1016/j.strusafe.2014.09.007
[2] 陈祖煜. 土质边坡稳定分析——原理、方法、程序[M]. 北京: 中国水利水电出版社, 2003.
Chen Zuyu. Stability Analysis of Soil Slope-principle, Method and Procedure[M]. Beijing: China Water Power Press, 2003.
[3] 刘立平, 姜德义, 郑硕才, 等. 边坡稳定性分析方法的最新进展[J]. 重庆大学学报(自然科学版), 2000, 23(3): 115–118.
Liu Liping, Jiang Deyi, Zheng Shuocai, et al. The recent progress of the slope stability analysis methods[J]. Journal of Chongqing University(Natural Science Edition), 2000, 23(3): 115–118.
[4] 张璐璐, 张洁, 徐耀, 等. 岩土工程可靠度理论[M]. 上海: 同济大学出版社, 2011.
Zhang Lulu, Zhang Jie, Xu Yao, et al. Geotechnical Engineering Reliability Theory[M]. Shanghai: Tongji University Press, 2011.
[5] 刘晓, 唐辉明, 熊承仁. 边坡动力可靠性分析方法的模式——问题与发展趋势[J]. 岩土力学, 2013, 34(5): 1217–1234.
Liu Xiao, Tang Huiming, Xiong Chengren. Patterns, problems, and development trends of analysis methods for slope dynamic reliability[J]. Rock and Soil Mechanics, 2013, 34(5): 1217–1234.
[6] Crawford C B, Eden W J. Stability on natural slope in sensitive clay[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1967, 93(SM4): 419–436.
[7] Li D Q, Jiang S H, Cao Z J, et al. A multiple response-surface method for slope reliability analysis considering spatial variability of soil properties[J]. Engineering Geology, 2015, 187(1): 60–72.
[8] Zhao H B. Slope reliability analysis using a support vector machine[J]. Computers & Geotechnics, 2008, 35(3): 459–467.
[9] Wang Y W, Cao Z C, Au S K K. Practical reliability analysis of slope stability by advanced Monte Carlo simulations in a spreadsheet[J]. Canadian Geotechnical Journal, 2011, 48(1): 162–172. DOI:10.1139/T10-044
[10] 李侃, 巨能攀. 基于蒙特卡洛方法的边坡可靠性评价[J]. 中国地质灾害与防治学报, 2014, 25(1): 23–27.
Li Kan, Ju Nengpan. Integrated application of Monte Carlo simulation for landslide reliability analysis[J]. The Chinese Journal of Geological Hazard and Control, 2014, 25(1): 23–27.
[11] 邓志平, 蒋水华, 曹子君, 等. 考虑参数空间变异性边坡可靠度分析的Kriging方法[J]. 武汉大学学报(工学版), 2014, 47(6): 743–749.
Deng Zhiping, Jiang Shuihua, Cao Zijun, et al. Reliability analysis of slope stability considering spatially varying soil properties using Kriging method[J]. Engineering Journal of Wuhan University, 2014, 47(6): 743–749.
[12] 蒋水华, 祁小辉, 曹子君, 等. 基于随机响应面法的边坡系统可靠度分析[J]. 岩土力学, 2015, 36(3): 809–818.
Jiang Shuihua, Qi Xiaohui, Cao Zijun, et al. System reliability analysis of slope with stochatic response surface method[J]. Rock and Soil Mechanics, 2015, 36(3): 809–818.
[13] 李亮, 褚雪松, 郑榕明. Rosenblueth法在边坡可靠度分析中的应用[J]. 水利水电科技进展, 2012, 32(3): 53–55.
Li Liang, Chu Xuesong, Zheng Rongming. Application of Rosenblueth method in reliability analysis of soil slopes[J]. Advances in Science and Technology of Water Resources, 2012, 32(3): 53–55.
[14] Malkawi A I H, Hassan W F, Abdulla F A. Uncertainty and reliability analysis applied to slope stability[J]. Sturctural Safty, 2000, 22(2): 161–187. DOI:10.1016/S0167-4730(00)00006-0
[15] 彭振斌, 李俊, 彭文祥. 基于Bishop条分法的边坡可靠度应用研究[J]. 中南大学学报(自然科学版), 2010, 41(2): 668–672.
Peng Zhenbin, Li Jun, Peng Wenxiang. Application analysis of slope reliability based on Bishop analytical method[J]. Journal of Central South University(Science and Technology), 2010, 41(2): 668–672.
[16] 杨海菲, 杨仕教, 曾晟. 岩土工程可靠度计算方法研究[J]. 水利与建筑工程学报, 2008, 6(2): 28–31.
Yang Haifei, Yang Shijiao, Zeng Sheng. Study on calculating method for reliability of geotechnical engineering[J]. Journal of Water Resources and Architectural Engineering, 2008, 6(2): 28–31.
[17] Li D Q, Zhang F P, Cao Z J, et al. Efficient reliability updating of slope stability by reweighting failure samples generated by Monte Carlo simulation[J]. Computers & Geotechnics, 2015, 69: 588–600.
[18] 谭晓慧, 王建国, 刘新荣. 改进的响应面法及其在可靠度分析中的应用[J]. 岩石力学与工程学报, 2005, 24(S2): 5874–5879.
Tan Xiaohui, Wang Jianguo, Liu Xinrong. Improved response surface method and its application to reliability analysis[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2005, 24(S2): 5874–5879.
[19] 殷宗泽. 土工原理[M]. 北京: 水利水电出版社, 2007.
Yin Zongze. Geotechnical Principle[M]. Beijing: China Water Power Press, 2007.
[20] Bishop A W. The use of the slip circle in the stability analysis of slopes[J]. Géotechnique, 1955, 5(1): 7–17. DOI:10.1680/geot.1955.5.1.7
[21] Janbu N. Slope stability computations, soil mechanics and foundation engineering report[R]. The Technical University of Norway, Trondheim,1968.
[22] Spencer E. A method of analysis of the stability of embankments assuming parallel inter-slice forces[J]. Géotechnique, 1967, 17(1): 11–26. DOI:10.1680/geot.1967.17.1.11
[23] Morgenstern N R, Price V E. The analysis of the stability of general slip surfaces[J]. Géotechnique, 1965, 15(1): 79–93. DOI:10.1680/geot.1965.15.1.79
[24] 刘宇飞. 基于Matlab的土质边坡稳定可靠度计算及应用研究[D].长沙: 中南大学, 2008.
Liu Yufei. Reliability calculation and application research of soil slope based on Matlab[D]. Changsha: Central South University, 2008.
[25] Tang H M, Liu X, Xiong C R, et al. Proof of nondeterministic polynomial-time complete problem for soil slope-stability evaluation[J]. International Journal of Geomechanics, 2015: C4015004.
[26] 戴光忠, 刘昌雄. 三峡库区巴东县谭家坪滑坡地质模型分析[J]. 资源环境与工程, 2012, 26(1): 54–57.
Dai Guangzhong, Liu Changxiong. Geological model analysis of Tanjiaping landslide in the Three Gorges Reservoir area[J]. Resources Environment & Engineering, 2012, 26(1): 54–57.