文章信息
- 郝淑英, 孙永宾, 张昆鹏, 申俊杰
- HAO Shuying, SUN Yongbin, ZHANG Kunpeng, SHEN Junjie
- 对接焊缝数值模拟方法研究
- Study of numerical simulation for butt weld
- 武汉大学学报(工学版), 2016, 49(1): 110-114
- Engineering Journal of Wuhan University, 2016, 49(1): 110-114
- http://dx.doi.org/10.14188/j.1671-8844.2016-01-019
-
文章历史
- 收稿日期: 2015-06-27
焊接热源是实现焊接过程的基本条件.焊接温度场和应力场的模拟精度直接取决于焊接热源模型的精度.莫春立[1]对热源模型的选取与各热源模型的适用条件做了比较全面的分析.王庆能[2]等研究得出热源模型形状参数对焊接残余应力及变形的影响不容忽视.
目前广泛应用的焊接过程的模拟方法主要有两类:考虑材料添加和不考虑材料添加.孟庆国[3]从多道焊的热循环曲线的角度指出考虑材料添加优于不考虑材料添加,没研究两种分析方法对熔池形态、温度场和应力场分布的影响.
目前焊接工艺中存在着匀速焊接和变速焊接.匀速焊接在起弧阶段往往存在未焊透的缺陷,且未焊透造成的焊接破坏又占有很大的比例.变速焊接是想通过调整焊接速度避免未焊透,但起弧阶段焊接速度的确定通常是凭感觉和经验,很难完全避免未焊透缺陷.目前的焊接数值模拟多是研究匀速条件下焊缝的温度场和残余应力分布[4],对于变速焊接的数值模拟还未见报道.
本文建立了单道对接焊有限元分析模型,对双椭球热源参数的选取方法进行了完善,分析了考虑和不考虑材料添加过程两种数值模拟方法对单道焊熔池形态、三维温度场、应力场的影响.对匀速焊接的焊接缺陷进行了仿真,通过调节起弧阶段的焊接速度,最终避免了匀速焊接起弧阶段的未焊透缺陷,该方法可用于指导变速焊接工艺中焊接速度的制定.
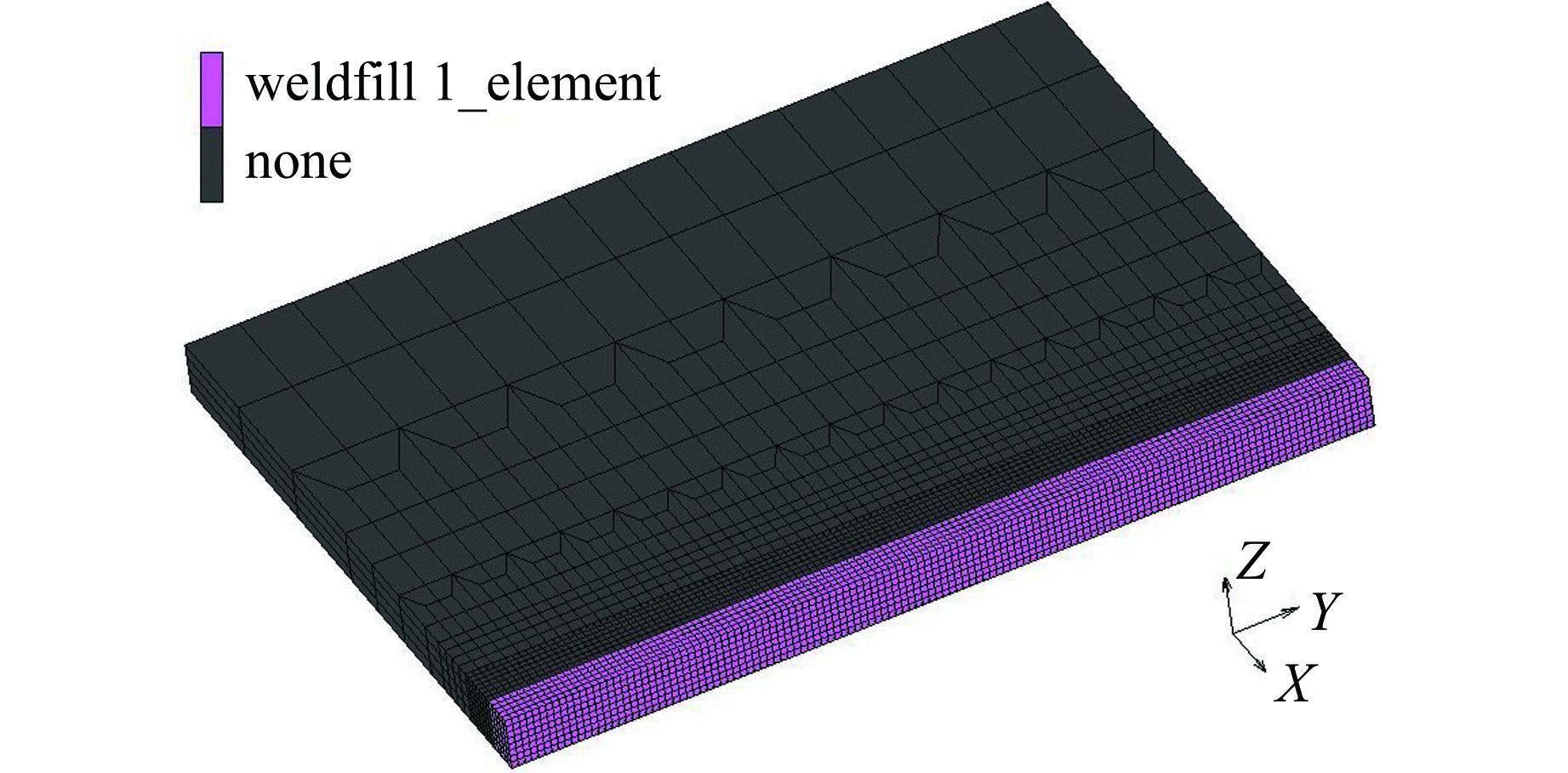
1 对接焊缝有限元分析模型本文建立了SUS310全奥氏体不锈钢对接焊缝的有限元模型,如图 1所示,模型尺寸[5]为160 mm×120 mm×10 mm,由于对称性取其一半进行建模,为保证计算精度且减少计算时间采用了过渡网格的方式.
|
| 图 1 对接焊缝有限元模型 Figure 1 Finite element model of butt weld |
在焊接过程中焊接材料要经历从室温到金属熔点的温度变化,其物理性能也随温度而变化,本文采用的材料的热物理性能参数见表 1[5, 6].由于熔池内流体的流动也增加了材料的热传导速度,文中采用增大导热系数的方法[7]间接考虑熔池内流体流动对整个温度场的影响.研究表明:考虑相变潜热的温度场比不考虑相变潜热的温度场与试验结果吻合更好[5],本文采用潜热释放率与金属凝固分数成正比的方法考虑相变潜热:
式中:ΔH为单位体积的熔化潜热;fs为固相分数,固相分数随温度的变化率可通过液淬法得到[6].
| 温度T/℃ | 热导率λ/(W·m-1·℃-1) | 比热c/(J·m-3·℃-1) | 熔化潜热qi/(J·m-3·℃-1) | 辐射换热β/( J·m-2·s-1) |
| 0~1 250 | 15.013+1.363×10-2T | |||
| 1 250~1 340 1 340~1 375 | 56.8+1.98×10-2T | 4.109×106+1.138×103T | 2.58×106 1.326×107 | 10+0.118 32 T |
| 1 375~1 400 | 6.496×107 | |||
| >1 400 | 84.52 | 5.702 6×106 | 175.52 |
焊件与周围介质的换热主要是通过辐射换热和对流换热,高温时以辐射换热为主,低温时以对流换热为主,在模型的对称面施加绝热边界条件.根据牛顿定律,对于某一与流动的气体或液体接触的固体表面微元,其对流换热密度:
式中:H为对流换热系数;Ts为固体表面温度;T∞为环境温度.
空气自然对流的对流换热系数大致量级为5~25,结合文献中的方法,定义H=9 W/(m2·K).
根据斯蒂芬-波尔兹曼定律,受热单元的单位表面、单位时间辐射的热量,即其辐射换热密度:
式中:σ为热辐射系数;ε为黑度(为软件内部设定);Ts为固体表面温度;T∞为环境温度.
2 热源模型 2.1 焊接热源模型选取在经典的雷卡林公式中,点热源和线热源主要用于温度场的解析法,其计算结果误差较大.高斯热源是在二维计算时取得的面热源,但其未考虑电弧在熔深方向的加热作用,只适用于在电弧挺度较小、对熔池冲击力较小的情况,一般多应用于薄板焊接的热源模拟.双椭球热源模型是在半球型热源模型和椭球形热源模型的基础上发展起来的,它解决了实际热源中前半部分温度梯度大和后半部分温度梯度小的问题,并且考虑了电弧挺度对熔池的影响,适用于熔深和电弧挺度较大的情况,一般多用于厚板焊接的热源模拟.本文采取的焊接工艺熔深和电弧挺度都比较大,因此选用双椭球热源模型.
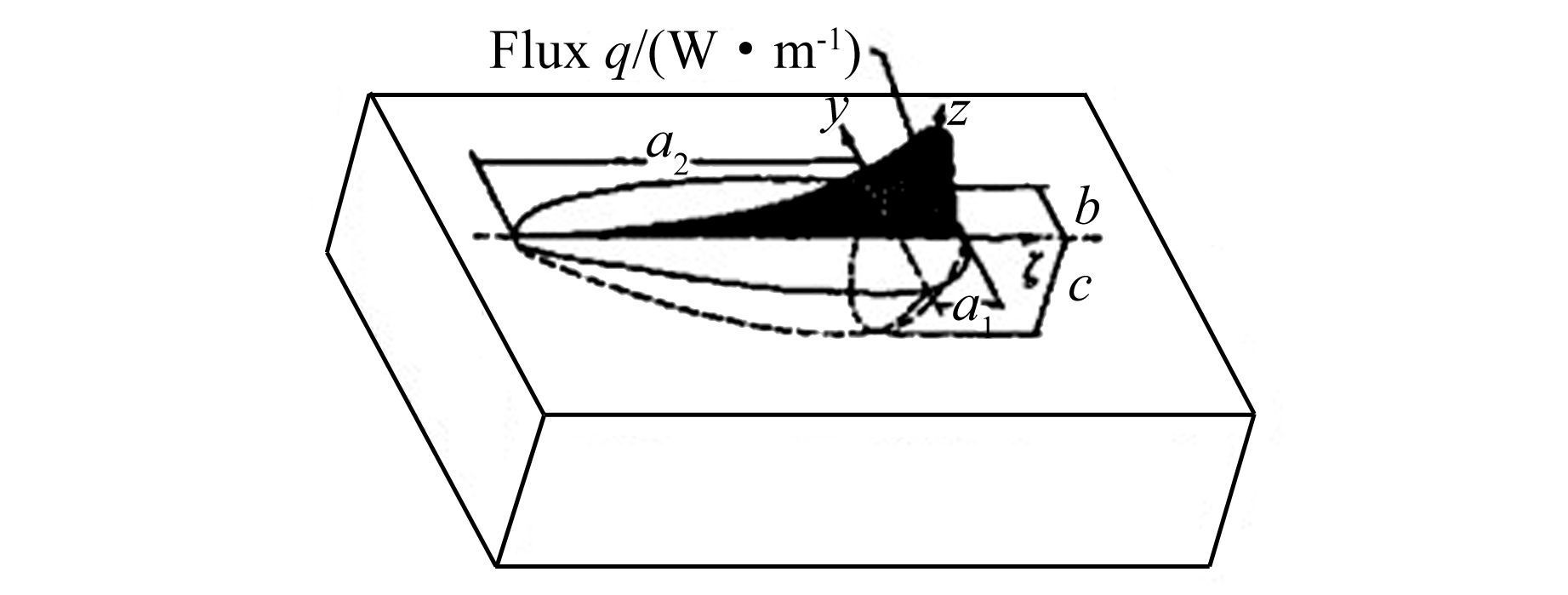
2.2 双椭球热源模型参数选取双椭球热源模型[8]由Goldak研究提出,见图 2所示.前、后两半部分均为1/4椭球.图中:a1、a2分别表示前、后1/4椭球的长半轴;b表示双椭球的短半轴;c表示双椭球在z轴方向的长度;ff、fr分别为总输入功率在熔池前、后两部分的分配指数,ff+fr=2,通常ff取0.6,fr取1.4.前半部分椭球内热源分布为
|
| 图 2 双椭球热源模型 Figure 2 Double ellipsoid heat source configuration |
后半部分椭球内热源分布为
由式(4) 、(5) 可知,a1和 a2决定了熔池在长度方向的尺寸以及温度梯度,b和c分别决定了熔池在宽度和深度方向的尺寸,因此a1、a2、b和c是影响双椭球热源模型模拟精度主要参数.
关于双椭球热源模型参数的选取方法,以前的研究者没有给出比较完善的方法,这在一定程度上影响了模拟温度场的准确性.焊接热源的作用效果是产生熔池,对于一种特定的焊接工艺,通过调节热源模型参数可以调节熔池的形态以及温度分布,因此稳态熔池的形态以及温度场分布可以作为某一种焊接工艺下模拟热源精度的标尺.
结合以前研究者的计算经验,本文提出了双椭球热源模型参数的选取方法:首先要测得这种焊接工艺在试验时的熔池形态以及温度分布,熔池形态主要包括稳态熔池的宽度、深度以及长度,温度分布包括稳态熔池的最高温度和沿熔池某一方向上的温度分布;其次是双椭球热源模型参数的选取,很多文献和教程中建议热源模型参数b和c选取熔池尺寸的80%,这虽然没有理论依据,但是有一定的计算经验在里面,文献[1]中建议a1取焊缝宽度的一半,a2取焊缝宽度的2倍,但是未给出b和c的选取方法.本文结合以上分析以及自己的仿真经验,认为b、c直接作用于熔池的宽度和深度,而a1、a2 决定了熔池双椭球的形状,基于此,初步选取b和c分别为试验测得熔池宽度、深度的80%,a1=0.5×b,a2=2×b;然后从稳态熔池的形态以及温度分布两方面比较模拟结果与试验结果.
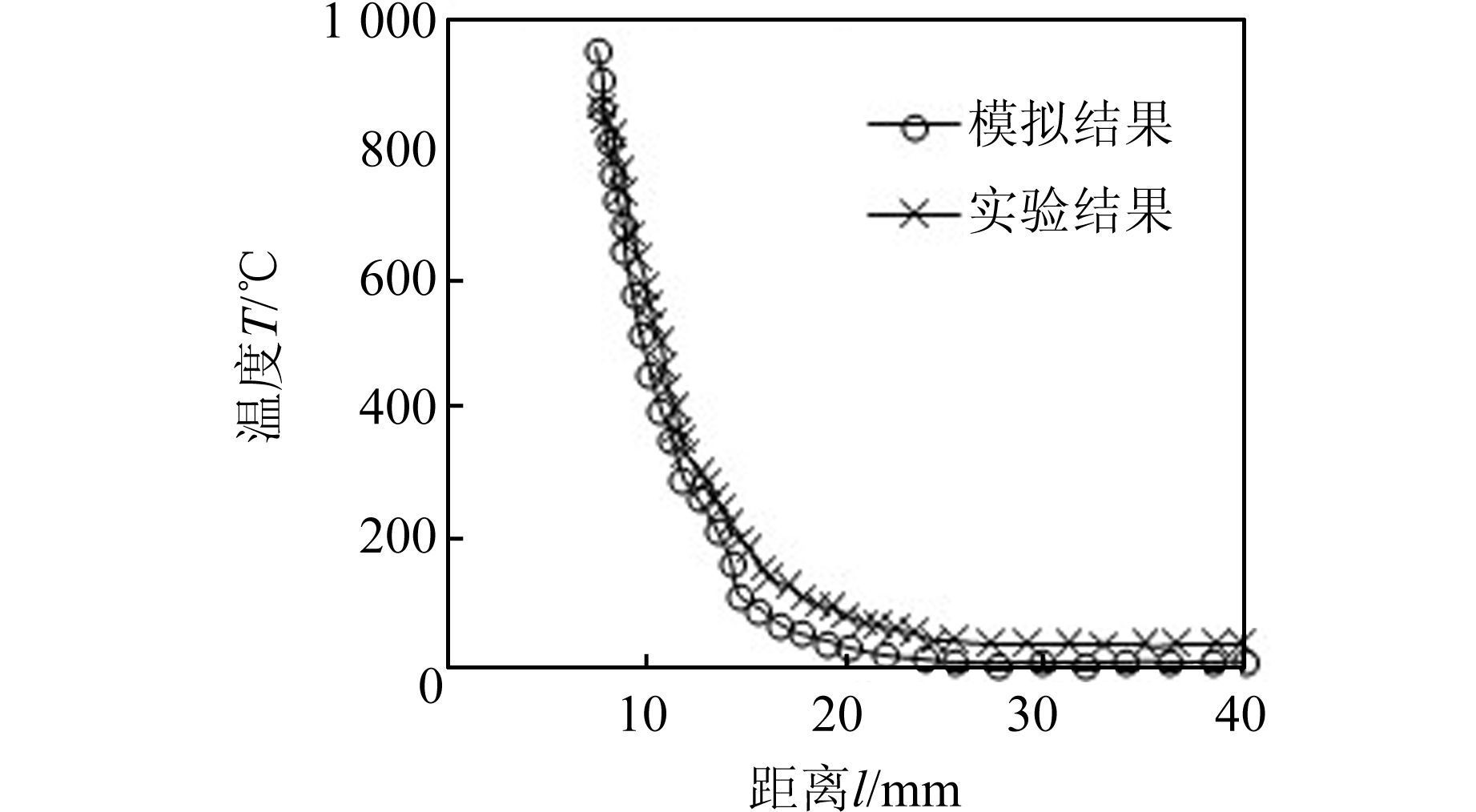
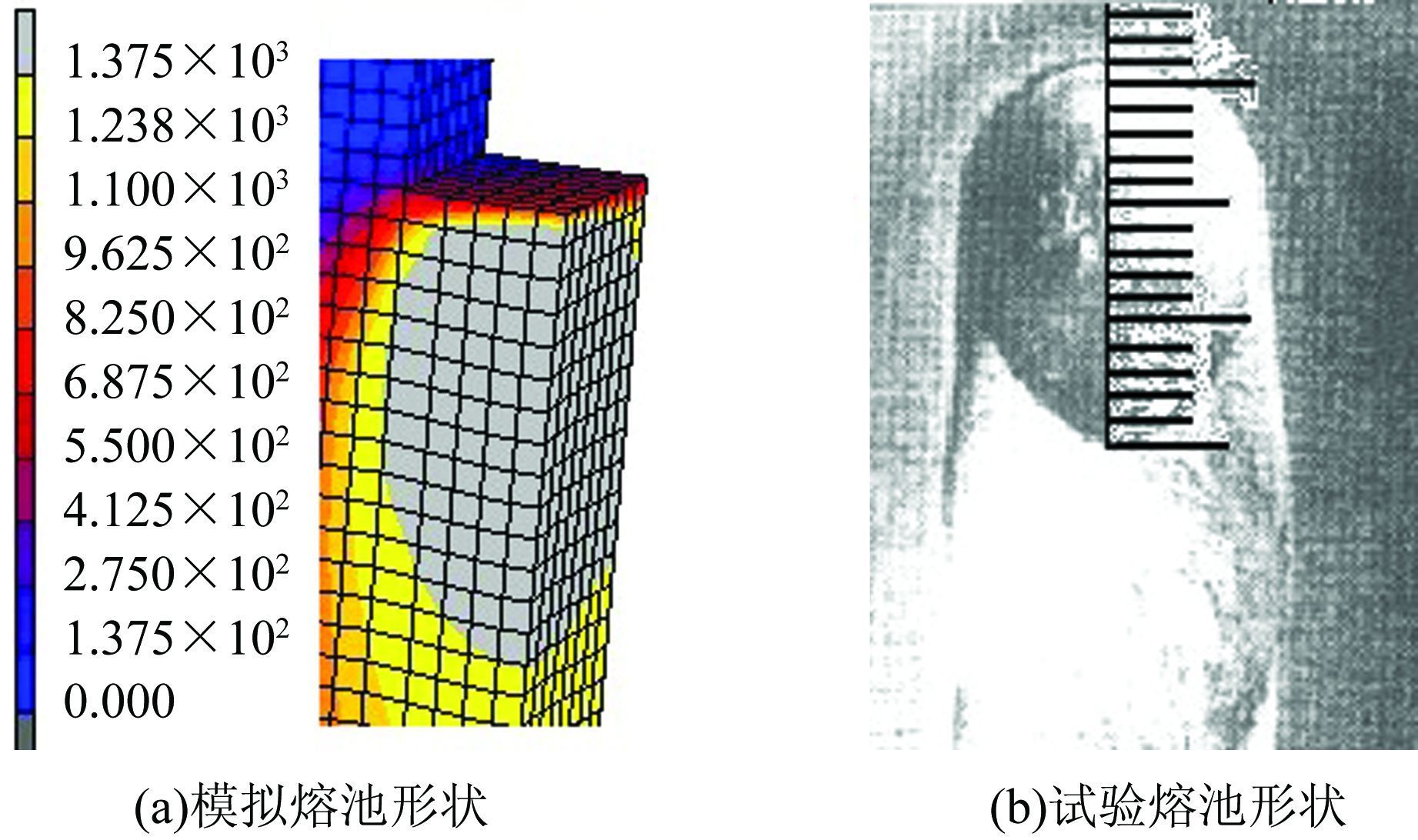
2.3 算例本文采用文献[5]中的焊接工艺参数:电流I=200 A,电压U=13.5V,焊接速度v=2 mm/s.应用上述焊接热源模型参数的选取方法,可知熔池宽度为13 mm,长度为16 mm,深度为10 mm,按照上述方法选取热源模型参数为b=5 mm,c=8 mm,a1=2 mm,a2=8 mm,进行焊接过程数值模拟,并将模拟结果与试验结果进行对比,得出二者在熔池形态和温度分布上均十分接近.图 3为焊接时间50 s时,在垂直于焊缝方向工件上表面温度分布曲线,可以看出数值模拟和试验结果的温度分布非常相近.图 4所示为数值模拟与试验所得稳态熔池形态,数值模拟稳态熔池宽度为13.2 mm,稍大于试验熔池宽度13 mm,熔池深度刚好达到试验深度10 mm,模拟熔池长度为16.2 mm,稍大于试验熔池长度16 mm,熔池基本形状也与实际熔池形状相似,均为双椭球形.由此可知本文提出的热源参数选取方法可以准确地模拟当前工艺下的焊接热源.
|
| 图 3 垂直于焊缝方向工件上表面温度分布 Figure 3 Comparison between the simulated temperature and measured one |
|
| 图 4 熔池形状 Figure 4 The shape of weld pool |
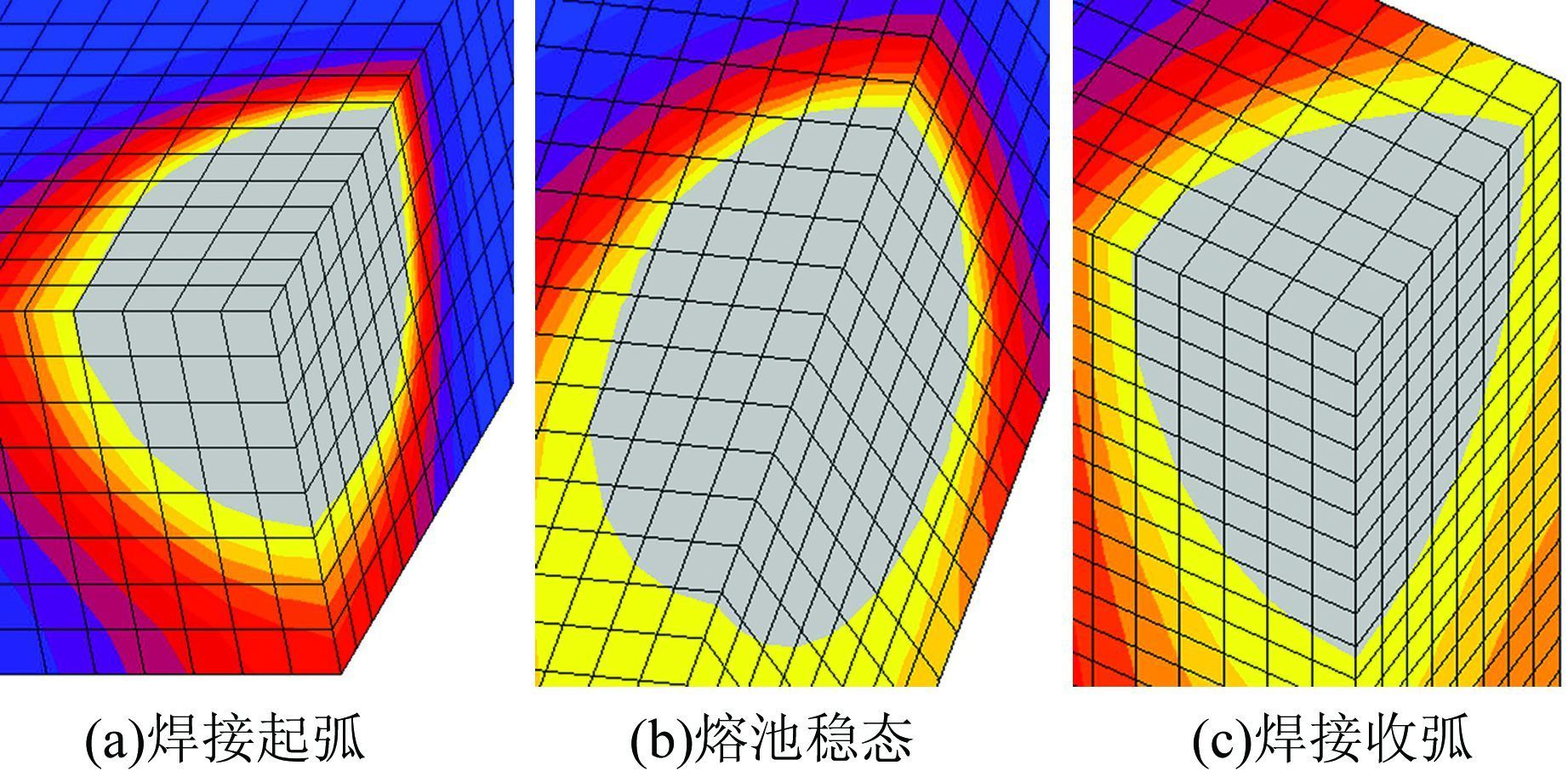
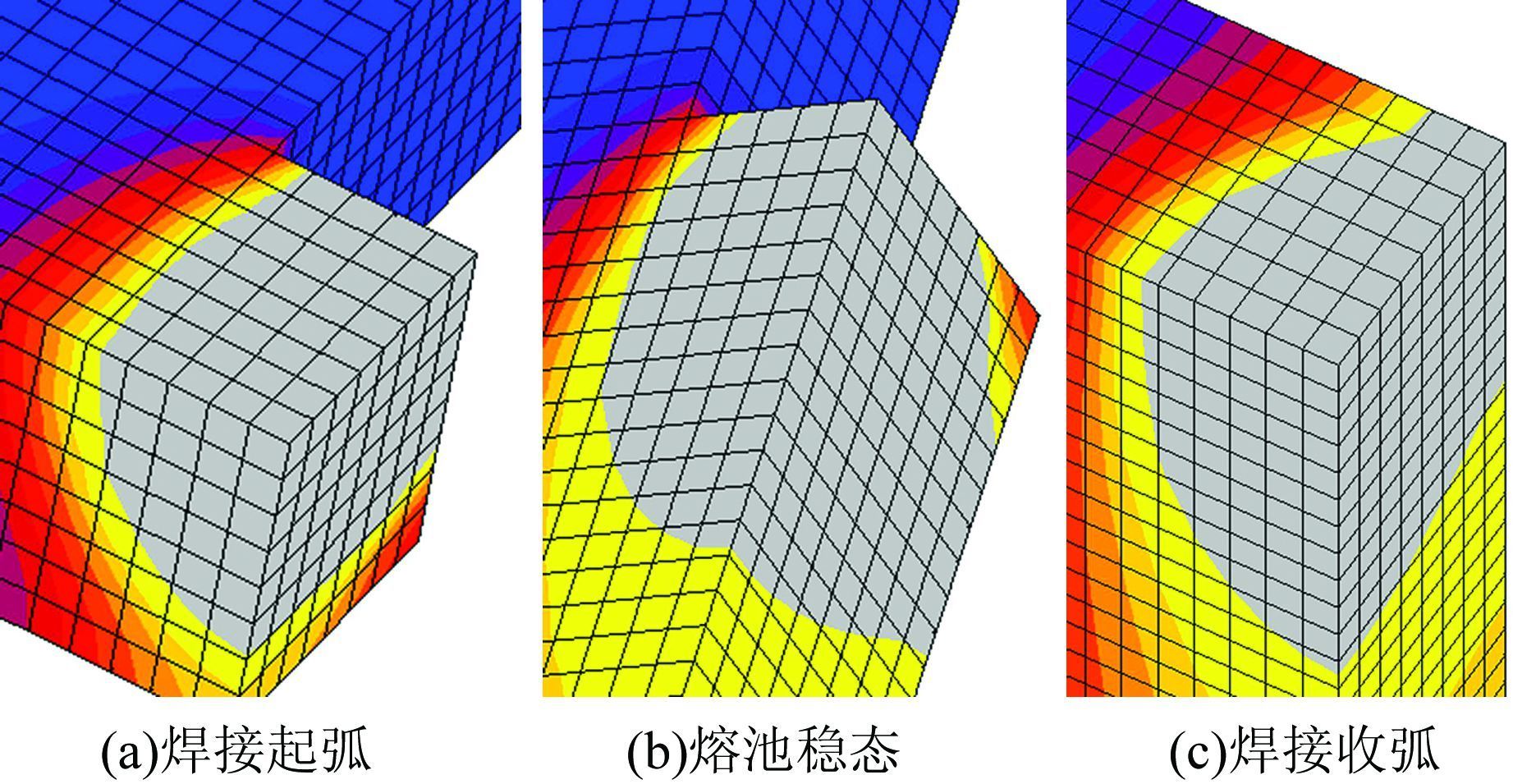
在相同的焊接工艺下,取相同的热源模型及参数进行数值仿真,图 5和图 6分别为不考虑材料添加过程和考虑材料添加过程时焊接起弧、熔池稳态、焊接收弧阶段的熔池形态,图中灰色部分表示温度在材料熔点1 375 ℃以上的区域,表 2给出了焊接起弧、熔池稳态和焊接收弧3个阶段的熔池尺寸.
|
| 图 5 不考虑材料添加过程 Figure 5 Without considering the material adding procedure |
|
| 图 6 考虑材料添加过程 Figure 6 Considering the material adding procedure |
| 方案 | 方向 | 熔池 | 焊缝 | ||
| 起弧 | 稳态 | 收弧 | |||
| 不考虑材料添加 | 宽度 | 10.4 | 10.4 | 13 | 13 |
| 深度 | 6.25 | 6.5 | 8.25 | 10 | |
| 考虑材料添加 | 宽度 | 11.7 | 13 | 13.5 | 13 |
| 深度 | 7.5 | 10 | 10 | 10 | |
结合图 5、6和表 2可以看出:在焊接起弧、熔池稳态、焊接收弧3个状态下不考虑材料添加的熔池尺寸均未达到焊缝的宽度和深度,考虑材料添加的熔池尺寸在熔池稳态和收弧阶段均满足了焊接要求,起弧阶段由于热累计不足熔池尺寸未达焊缝尺寸.说明考虑材料添加的模拟方法在熔池形态和温度场上与实际焊接过程更接近,导致这一现象的原因是不考虑材料添加的模拟方法在熔池前方存在材料,熔池前方热量通过热传导的方式传递给金属;考虑材料添加的模拟方法在熔池前方不存在材料,熔池前方热量通过热辐射的方式散发入空气.通过比较两种热量散发方式可得不考虑材料添加要远比考虑材料添加的熔池前方流失更多的热能,直接导致采用不考虑材料添加模拟的焊缝不能焊透.而这必然导致残余应力场计算的偏差.由图 7(a)的曲线4可知,在焊缝下表面的中心线上不考虑材料添加的纵向应力均为拉应力,与焊接残余应力的分布规律不吻合;考虑材料添加的纵向应力在焊缝的两端均出现了压应力区,如曲线8所示,应力场分布规律与实际相一致;在焊缝上、下表面的中心线上,考虑材料添加均比不考虑材料添加最大应力值大.由图 7(b)和7(c)可以看出,在焊缝上表面垂直焊缝方向,考虑材料添加比不考虑材料添加的最大应力值约大50 MPa,即不考虑材料添加的模拟方法偏于不安全.
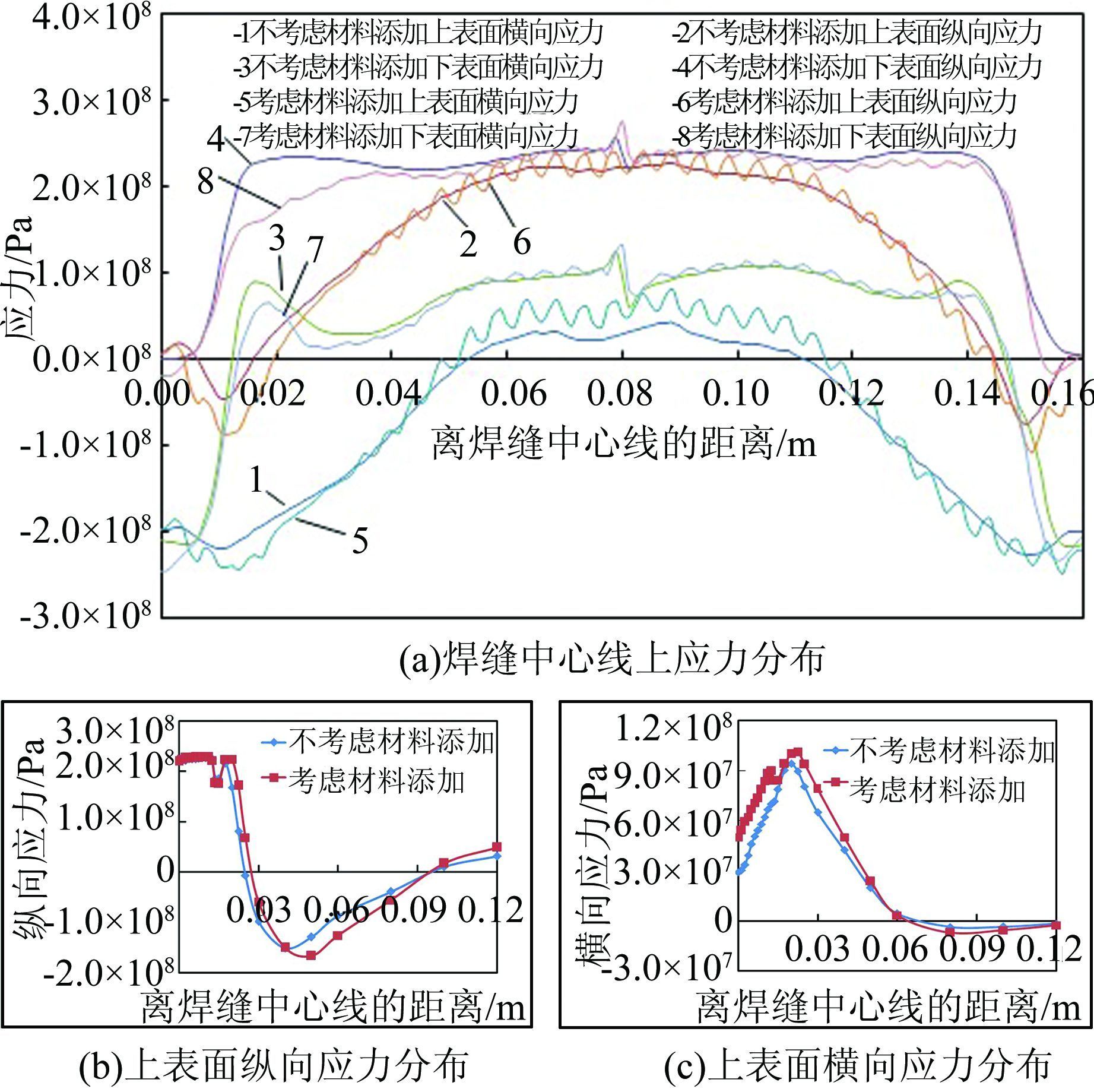
|
| 图 7 残余应力分布比较 Figure 7 Comparison of residual stress distributions |
通过以上分析可得,采用考虑材料添加模拟出的温度场、应力场均比不考虑材料添加的方法要准确,因此考虑材料添加的方法要优于不考虑材料添加的方法.
4 变速焊接焊接时由焊接能源输入给单位长度焊缝上的热量,称为焊接线能量.焊接线能量为
式中:I为焊接电流;U为焊接电压;v为焊接速度;q为焊接线能量.
当焊接电流和焊接电压一定时,焊接速度越小,焊接线能量越大,即在单位长度焊缝上输入的热量越多,热量的累计会造成熔池的增大.
焊接过程分为起弧、熔池稳态和收弧3个阶段.熔池稳态时,宽度方向尺寸正好达到焊缝宽度要求,深度方向正好焊透,因此在熔池未达稳态的起弧阶段,焊缝是未焊透的.实际焊接工艺制定的多为匀速焊接,匀速焊接存在的一个问题就是起弧阶段热累计不足,导致有相当一段长度的焊缝存在未焊透缺陷.图 8(a)所示为焊接速度为2 mm/s的匀速焊接的数值模拟结果,结合图 8(a)和表 3可得熔池在起弧阶段熔池宽度最大为11.7mm,熔池深度最深为7.5 mm,均未达到焊缝宽度13 mm和焊缝深度10 mm,即均未焊透,该工艺下起弧阶段有5 mm长的焊缝未焊透.
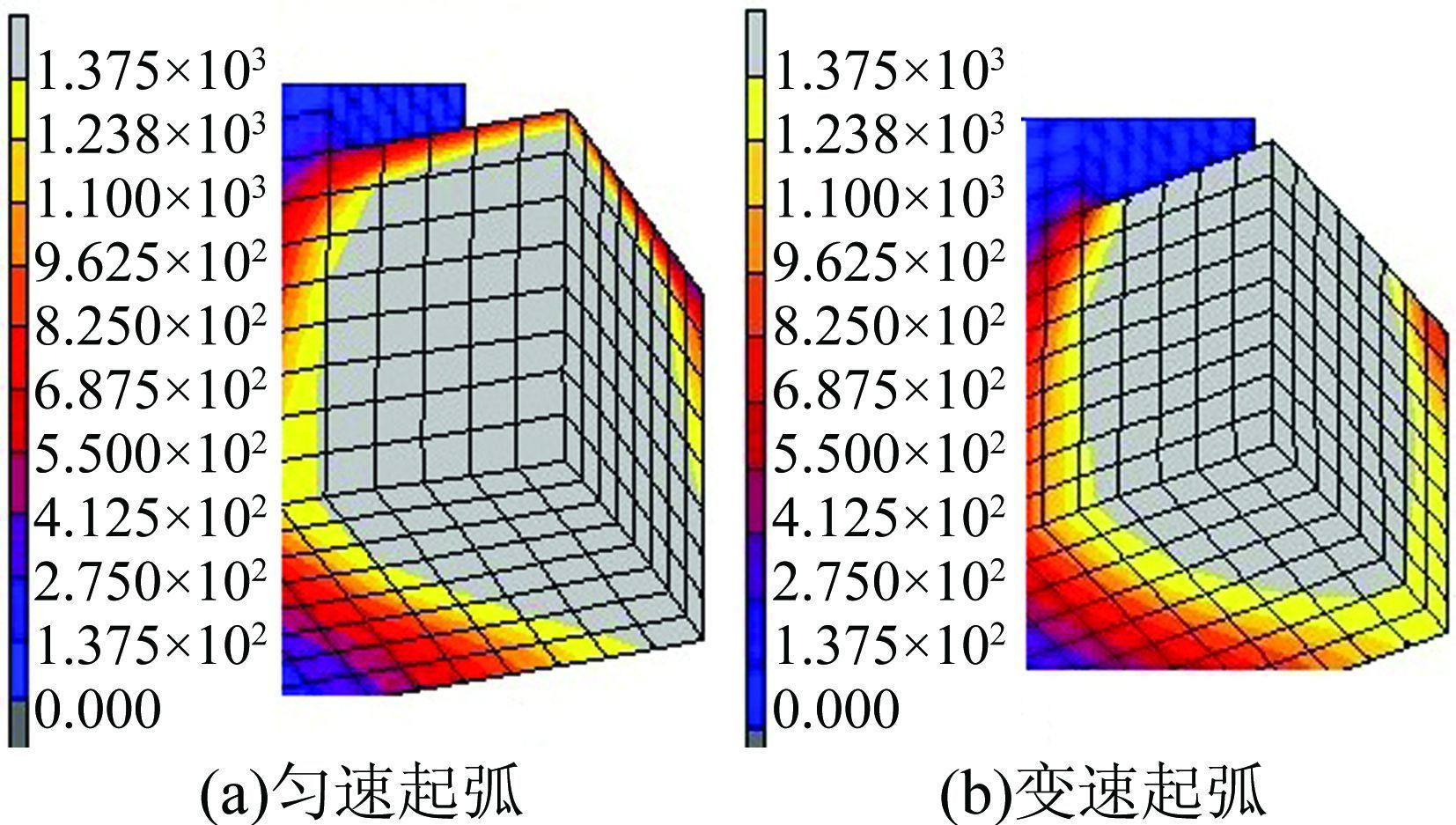
|
| 图 8 起弧熔池形状比较 Figure 8 Comparison between arc weld pool shapes |
| mm | ||||
| 方案 | 方向 | 熔池 | 焊缝 | |
| 焊接起弧 | 熔池稳态 | |||
| 匀速焊接 | 宽度 | 11.7 | 13 | 13 |
| 深度 | 7.5 | 10 | 10 | |
| 变速焊接 | 宽度 | 13 | 13 | 13 |
| 深度 | 10 | 10 | 10 | |
针对上述问题,本文采用仿真实验模拟变速焊接过程,通过降低起弧阶段的焊接速度,提高起弧阶段的热输入量,从而增大熔池尺寸,使焊缝在起弧阶段完全熔透,为焊接工艺的制定提供依据.针对本文的计算模型,经多次模拟实验得到了使焊缝在整个焊接过程中均达到完全焊透的焊接速度,即在0~2 s的焊接速度为1 mm/s,之后的焊接速度一直是2 mm/s.结合图 8(b)和表 3可得变速焊接起弧阶段由于我们降低了焊接速度,增大了线能量,使熔池宽度达到了13 mm,深度达到了10 mm,二者均达到了焊缝焊透尺寸,从而有效避免了未焊透焊接缺陷,为实际焊接工艺的制定提供了指导.
5 结语1) 完善了双椭球热源模型热源参数的确定方法,为应用双椭球热源模型模拟焊接过程选取热源参数提供了指导.
2) 焊接过程的数值仿真计算时只有考虑材料添加过程才能获得与实际相吻合的熔池形态和温度场,不考虑材料添加的模拟方法偏于不安全.
3) 可通过仿真实验确定起弧阶段的焊接速度,避免未焊透的焊透缺陷,为实际工艺制定提供指导.
| [1] |
莫春立, 钱百年, 国旭明, 等. 焊接热源计算模式的研究进展[J].
焊接学报, 2001, 22(3): 93–96.
Mo Chunli, Qian Bainian, Guo Xuming., et al. Progress in research of welding heat source model[J]. Welding Journal, 2001, 22(3): 93–96. |
| [2] |
王庆能, 童彦刚, 邓德安. 热源形状参数对薄板焊接残余应力和变形的影响[J].
焊接学报, 2012, 33(12): 97–101.
Wang Qingneng, Tong Yangang, Deng Dean. Heat source shape parameter effects on welding residual stress and deformation of thin plate[J]. Welding Journal, 2012, 33(12): 97–101. |
| [3] |
孟庆国, 方洪渊, 徐文立, 等. 考虑金属逐步填充的多道焊温度场数值模拟[J].
焊接学报, 2004, 25(5): 53–59.
Meng Qingguo, Fang Hongyuan, Xu Wenli, et al. Metal filled numerical simulation on multi-pass welding temperature field[J]. Welding Journal, 2004, 25(5): 53–59. |
| [4] | Sattari-Far I, Farahani M R. Effect of the weld groove shape and pass number on residual stresses in butt-welded pipes[J]. International Journal of Pressure Vessels and Piping, 2009, 86(11): 723–731. DOI:10.1016/j.ijpvp.2009.07.007 |
| [5] |
董志波, 魏艳红, 刘仁培, 等. 不锈钢焊接温度场的三维数值模拟[J].
焊接学报, 2004, 25(2): 9–14.
Dong Zhibo, Wei Yanhong, Liu Renpei, et al. Three-dimensional numerical simulation of the welding temperature field of stainless steel[J]. Welding Journal, 2004, 25(2): 9–14. |
| [6] |
吴爱萍, 任家烈, 鹿安理. 焊缝凝固时的应力应变过程分析[J].
航空材料学报, 1993, 13(3): 36–40.
Wu Aiping, Ren Jialie, Lu Anli. Analysis of the stress and strain of weld solidification process[J]. Journal of Aeronautical Materials, 1993, 13(3): 36–40. |
| [7] |
魏艳红. 焊接凝固裂纹温度场的数值模拟[J].
焊接学报, 1999, 20(3): 199–204.
Wei Yanhong. Numerical simulation of temperature fields for welding solidification crack[J]. Welding Journal, 1999, 20(3): 199–204. |
| [8] |
张文钺.
焊接传热学[M]. 北京: 机械工业出版社, 1987.
Zhang Wenyue. Welding of Heat Transfer[M]. Beijing: Mechanical Industry Publishing House, 1987. |
 2016, Vol. 49
2016, Vol. 49




