武汉大学学报(工学版)   2016, Vol. 49 Issue (6): 899-904

文章信息

陈飞扬, 张洁, 彪仿俊
CHEN Feiyang, ZHANG Jie, BIAO Fangjun
服役期内土体液化失效概率分析
Soil liquefaction probability analysis during a given exposure time
武汉大学学报(工学版), 2016, 49(6): 899-904
Engineering Journal of Wuhan University, 2016, 49(6): 899-904
http://dx.doi.org/10.14188/j.1671-8844.2016-06-017

文章历史

收稿日期: 2016-05-24
 Abstract              PDF               Figures               Tables
引用本文 0
陈飞扬, 张洁, 彪仿俊. 服役期内土体液化失效概率分析[J]. 武汉大学学报(工学版), 2016, 49(6): 899-904.
CHEN Feiyang, ZHANG Jie, BIAO Fangjun. Soil liquefaction probability analysis during a given exposure time[J]. Engineering Journal of Wuhan University, 2016, 49(6): 899-904.
服役期内土体液化失效概率分析
陈飞扬1, 张洁1, 彪仿俊2     
1. 同济大学地下建筑与工程系，上海 200092;
 2. 上海堃熠工程减震科技有限公司，上海 201114
收稿日期: 2016-05-24
作者简介: 陈飞扬（1993），男，硕士研究生，研究方向为地下工程风险与可靠度，E-mail:tjucecfy@163.com.
通讯作者: 张洁(1980-)，男，副教授，主要从事岩土及地下工程风险评估及管理方面的研究。E-mail:cezhangjie@gmail.com
基金项目: 上海市青年科技启明星计划资助项目(15QA1403800).
摘要: 利用2015年美国建筑抗震规范中的衰减模型，结合美国地质勘查局提供的地震灾害地图，利用全概率定理，提出了土体服役期内液化概率的计算方法.算例分析表明，地震参数对土体液化概率具有显著的影响.提出的方法可以合理地考虑服役期内各种可能出现的地震对土体液化评价的影响.关键词：地震；液化；概率分析；静力触探试验；安全系数
关键词： 地震     液化     概率分析     静力触探试验     安全系数    
Soil liquefaction probability analysis during a given exposure time
CHEN Feiyang1, ZHANG Jie1, BIAO Fangjun2     
1. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China;
 2. Shanghai Kunyi Engineering Vibration Reduction Co. Ltd., Shanghai 201114, China
Abstract: This paper presents a method to predict the liquefaction probability in a given exposure time using the attenuation models in the 2015 Nation Earthquake Hazards Reduction Program Provision as well as the hazard curves derived from the U.S. Geological Survey seismic hazard maps. The results show that the ground motion parameters have great impact on the liquefaction potential evaluation. The method suggested can readily take the uncertainties in the earthquake into consideration during the soil liquefaction potential evaluation process. Key words: earthquake; liquefaction; probabilistic analysis; cone penetration test; factor of safety
Key words: earthquake     liquefaction     probabilistic analysis     cone penetration test     factor of safety    

在地震时可大规模地发生砂土液化并造成严重危害.在中国1966年的邢台地震、1975年的海城地震和1976年的唐山地震以及2008年汶川地震中，砂土液化对人民生产生活安全造成了巨大的危害[1].国外也有类似的例子，在美国1964年的阿拉斯加地震、日本1964年的新泻地震中，砂土液化也使许多建筑物下沉、歪斜和毁坏，有的地下结构甚至浮升到地面[2].

土体液化分析中涉及大量的不确定性因素.为考虑这些不确定性因素的影响，基于概率的液化分析方法受到了广泛关注.近年来，随着地震工程中基于性能的设计理念的兴起，如何评价土体在服役期内的液化概率成为岩土抗震问题中的重要课题.Kramer最早研究了服役期内土体的液化概率[3]，并由此计算了土体液化灾害发生的回归周期.Juang等学者提出了服役期内土体液化概率计算的简化分析方法[4-8].采用与Juang类似的理念，刘芳等计算了服役期内土体因液化产生侧向变形的概率[9].这些研究对推动基于性能的岩土抗震设计起到了重要的作用.如何考虑地震的不确定性是计算土体服役期内液化概率的关键.上述研究均采用2009版美国抗震设计规范[10](以下简称“2009规范”)确定服役期内地震动参数的不确定性.最近，美国已颁布并采用2015版抗震设计规范[11](以下简称“2015规范”).目前，如何基于新规范对土体液化进行分析尚未见报道.

本文的目的是研究基于2015规范计算土体服役期内液化概率的方法.目前，随着我国地震动测试资料的积累，我国也计划在未来参考美国制定我国的地震动衰减模型[12].因此，相关研究对我国的地震液化抗震设计也具有重要意义.

1 液化分析中的不确定性因素

砂土液化是指饱水的疏松粉、细砂土在振动作用下由于孔隙水压力上升、有效应力减小所导致的砂土从固态变化到液态的现象.土体液化评价的方法有剪应力法、剪应变法、能量法、综合判断法等[6].在国际上，由加州大学伯克利分校Seed教授开创的剪应力简化分析理论获得了广泛应用[2].该理论通过将历史震害调查获得的土体液化案例与标准贯入试验中的锤击数进行相关性分析，获得土体的抗液化能力模型，由此计算土体的抗液化安全系数.目前已发展出基于静力触探[13]和剪切波速的液化评价方法[14].这些方法中，土体液化模型的输入参数可分为土性参数和地震动参数两大类.在土体液化分析中，土性参数和地震动参数都存在不确定性.此外，由于液化现象的复杂性，采用简化模型对液化进行分析时，还不可避免地存在模型误差.

一般而言，土性参数的不确定性可由勘察数据获得，而模型误差可由比较模型预测与土体实际是否发生液化而获得.土性参数不确定性和模型误差对土体液化概率的影响可分开考虑，也可合并考虑.目前，考虑土体不确定性和模型误差影响的液化分析已取得了较多成果.

在土体液化分析中，地震动参数包括地面最大加速度amax以及矩震级Mw.地震动参数的不确定性可由场地周围断裂带活动特征及地震动衰减关系获得.该方法的使用需要较多的工程地震分析及预测专长.为方便工程应用，美国地质勘查局(USGS)和美国抗震设计规范给出了地震峰值加速度(PGA)超越概率曲线、不同灾害等级下地震震级概率分布曲线以及土体地震动衰减模型.因此，如能根据美国地质勘查局(USGS)数据及美国2015规范获得amax和Mw的联合概率密度函数，土体在服役期内液化概率的分析则可大大简化.

2 地震动强度指标概率分析 2.1 PGA和amax概率分布

美国地质勘查局(USGS)以年平均超越概率的形式提供了给定地点的地震峰值加速度的分布数据.然而，由于液化计算中需要考虑地表处的地震峰值加速度amax，因此，需要把基岩处的峰值加速度PGA转化为地表处的amax，此时，需要考虑计算地震作用放大系数F，并通过该系数，完成地震加速度从基岩到地表的转化，即

${{a}_{\max }}=F\cdot PGA$    (1)

在2009规范中，对于地震作用放大系数的计算采用的是基于强震数据库的回归分析方法，其所得到的强度指标放大系数与其本身大小直接关联，并考虑地质条件的影响：

$\ln (F)=a+b\ln (PGA)+\varepsilon $    (2)

其中：F为地震作用放大系数；a、b为基于回归分析所得到的回归系数；ε为均值为零、标准差为σ的误差项，其取值与场地地质条件有关[15].对应不同场地类别，回归系数的取值均不同，如表 1所示.

表 1 2009规范地震作用放大系数计算公式回归系数取值 Table 1 Regression coefficients for amplification factor in the 2009 national earthquake hazards reduction program (NEHRP) provision
场地分类abσ
Hlm-0.59-0.390.47
Qa-0.15-0.130.52
Hc-0.11-0.100.52
Hm-0.50-0.330.51
NEHRP B0.090.050.48
NEHRP C-0.06-0.050.55
NEHRP D0.08-0.070.57
NEHRP E-0.60-0.500.46
Geot. B0.070.070.55
Geot.C0.11-0.040.60
Geot.D-0.02-0.080.56
Geot.E-0.82-0.630.40
表选项

在2015规范中，认为液化和土体强度损失主要受峰值加速度、震级和地质条件影响，并引入参数场地剪切波速VS30来区分不同场地地质条件的影响，对于不同的场地地质条件，通过不同的VS30取值，以反映不同地质条件在计算地震作用放大系数时的区别.Seyhan和 Stewart[16-19]的相关文献中也对此进行了详细描述.

2015规范给出的进行土体液化稳定分析时地震作用放大系数的计算公式为

$\ln ({{F}_{S,B}})=\ln ({{F}_{lin}})+\ln ({{F}_{nl}})+{{\varepsilon }_{n}}$    (3)

其中：FS,B表示地震作用放大系数，服从对数正态分布；Flin表示放大系数中的线性部分，Fnl表示放大系数中的非线性部分；εn为一均值为零、标准差为σn的误差项.分别定义如下：

${{F}_{lin}}=\left\{ \begin{align} & c\ln (\frac{{{V}_{S30}}}{{{V}_{ref}}}){{V}_{S30}}\le {{V}_{c}} \\ & c\ln (\frac{{{V}_{c}}}{{{V}_{ref}}}){{V}_{S30}}>{{V}_{c}} \\ \end{align} \right.$    (4)
$\ln ({{F}_{nl}})={{f}_{1}}+{{f}_{2}}\ln (\frac{PG{{A}_{r}}+{{f}_{3}}}{{{f}_{3}}})$    (5)
${{f}_{2}}={{f}_{4}}[\exp \{{{f}_{5}}(\min ({{V}_{S30}},760)-360)\}-\exp \{{{f}_{5}}(760-360)\}]\ $    (6)

其中：c为计算模型参数；VS30表示地表 30 m以下评价剪切波速；Vref表示场地基准剪切波速，一般取值为760 m/s；f1、f2、f3、f4、f5为回归分析参数，根据文献[16-19]，各个系数的取值分别为：c=-0.6000，Vc=1 500 m/s，Vref=760 m/s，f1=0，f3=0.1，f4=-0.150 0，f5=-0.007 01；PGAr为地震峰值加速度PGA的中位数，可通过拟合PGA概率密度函数获得.

由上面介绍可以看出，地震作用放大系数F的概率分布取决于PGA的数值，按2009规范或2015规范可计算条件概率f(F|PGA).另一方面，PGA的概率密度函数f(PGA)可通过PGA的超越概率曲线获得[4].在获得f(PGA)和f(F|PGA)后，amax的概率密度函数可按下式获得：

$f({{a}_{\max }})=f(F\cdot PGA)=f(F|PGA)f(PGA)$    (7)
2.2 amax和Mw联合概率分布

上一节中给出了如何基于2009规范和2015规范获得地震动参数条件概率分布f(amax|PGA)的方法.下面将介绍amax、Mw联合概率密度函数的构建方法.根据条件概率公式，p(Mw,PGA>h)可按下式计算：

$p({{M}_{w}},PGA>h)=p({{M}_{w}}\text{ }\!\!|\!\!\text{ }PGA>h)p(PGA>h)$    (8)

p(PGA>h)、p(Mw|PGA>h)分别可由USGS地质灾害科学中心所公布的灾害曲线(Hazard curves application)[20]和地震分析工具(Seismic hazard analysis tools)[21]获得. 根据上式，给定PGA条件下Mw的概率密度函数可按下式计算：

$f\left( {{M}_{w}},PGA \right)=\frac{\partial p({{M}_{w}},PGA>h)}{\partial h}$    (9)
$f\left( {{M}_{w}}\text{ }\!\!|\!\!\text{ }PGA \right)=\frac{f({{M}_{w}},PGA)}{f\left( PGA \right)}$    (10)

在PGA已知的情况下，amax、Mw统计独立.因此，给定PGA条件下，amax、Mw的联合概率密度函数可按下式计算：

$f\left( {{a}_{\max }},{{M}_{w}}\text{ }\!\!|\!\!\text{ }PGA \right)=f\left( {{a}_{\max }}\text{ }\!\!|\!\!\text{ }PGA \right)f\left( {{M}_{w}}\text{ }\!\!|\!\!\text{ }PGA \right)$    (11)

其中:f(amax|PGA)为给定PGA条件下amax的概率分布.该分布由抗震规范给出，其计算方法已在上一节中做了详细介绍.

根据全概率定理，amax、Mw的联合概率密度函数为

$f\left( {{a}_{\max }},{{M}_{w}} \right)\text{=}\int{f\left( {{a}_{\max }},{{M}_{w}}\text{ }\!\!|\!\!\text{ }PGA \right)f\left( PGA \right)\text{d}PGA}$    (12)

由于USGS地震分析工具所获得的p(Mw|PGA>h)是以离散变量的形式给出，为方便应用，式(12)也可写成如下离散变量的形式：

$p\left( {{a}_{\max }},{{M}_{w}} \right)\text{=}\sum\limits_{i=1}^{n}{p\left( {{a}_{\max }},{{M}_{w}}\text{ }\!\!|\!\!\text{ }PGA=h \right)p\left( PGA={{h}_{i}} \right)}$    (13)

其中:n为PGA转化为离散变量后可能的取值数；p(PGA= hi)为PGA等于hi的可能性.

3 设计周期内土体液化失效概率计算模型

如果记L=1为发生液化，令p(L=1|amax，Mw)代表给定amax、Mw条件下土体的液化概率.上一节详细介绍了设计周期内地震动参数amax、Mw联合概率分布函数p(amax，Mw)的计算方法.根据全概率定理，考虑所有地震可能性条件下场地的液化概率为

${{P}_{L}}=\sum\limits_{({{a}_{\max }},{{M}_{w}})}{p(L=1|{{a}_{\max }},{{M}_{w}})\cdot p({{a}_{\max }},{{M}_{w}})\ \ \ }$    (14)

作为方法的介绍，本文采用Ku等[22]提出的方法计算给定地震动参数下土体的液化概率p(L=1|amax,Mw).在该模型中，采用Robertson和Wride[23, 24]方法计算土体的安全系数.给定地震动参数条件下土体的液化概率按下式计算：

$p(L=1|{{a}_{\max }},{{M}_{w}})=1-\Phi [\frac{0.102+\ln ({{F}_{S}})}{0.276}]$    (15)

其中：FS为土体抗液化安全系数，其计算方法可通过查询相关文献资料(Ku等2012[20])获得，本文中不再赘述.

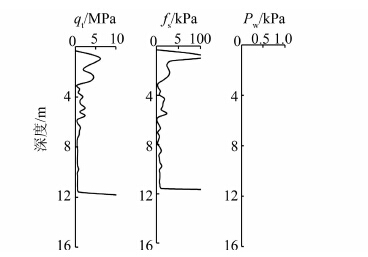
4 算例分析 4.1 工程背景

选取计算地点为美国加利福尼亚州洛玛-普里埃塔(Loma Prieta)，其经度为-121.83°，纬度为37.10°.在该场地，地下水位位于地面以下2.3m处.查阅USGS所提供的地震灾害地图(hazard maps)[25]可知，该场地属于地震高发地带.图 1给出了该场地某处的静力触探资料，qt、fs、Pw分别为椎体压入阻力、摩阻力和孔隙水压力[20]，在该算例中孔隙水压力均为0.下面将按本文提出的方法计算该静力触探位置土体在50年服役周期内的液化概率.

图 1 选取地点静力触探资料图 Figure 1 Profiles of CPT parameters at given site
图选项

地震的发生一般服从泊松分布.根据泊松分布的性质，对于年平均超越概率为λ的事件，其在设计周期为T内发生的概率为

${{P}_{LT}}=1-{{e}^{-\lambda T}}$    (16)

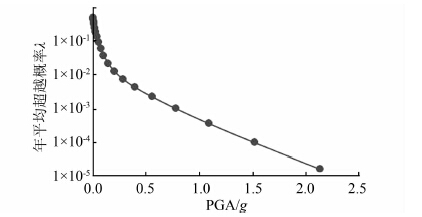
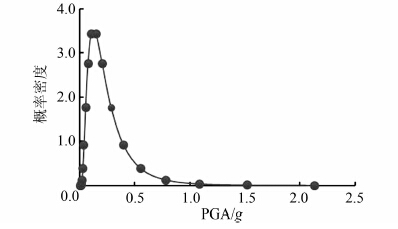
在本例中，假定设计周期取T=50 a.将图 2中的危险性曲线代入式(16)，可获得T=50 a内的累积概率密度函数.根据获得的累积概率分布函数，可得PGA的概率密度函数如图 3所示.

图 2 地震峰值加速度(PGA)危险性曲线 Figure 2 Hazard curves for typical site
图选项
图 3 PGA概率密度曲线 Figure 3 Probability density function of PGA
图选项
4.2 PGA的概率分布和Mw的条件概率分布

根据该点的经度、纬度坐标，通过查询本文2.2节所提到的灾害曲线，可获得当地PGA年平均超越概率λ，即可获得当地地震峰值加速度的危险性曲线，如图 2所示.

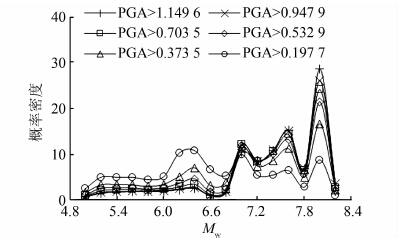
根据PGA在50 a内的不同超越概率可将地震灾害分为6个等级[25]，如表 2所示；对应每个灾害等级条件下Mw的概率分布如图 4所示.

表 2 灾害等级分类 Table 2 Six used hazard levels
灾害等级123456
50 a内超越概率/%125102050
PGA/g1.149 60.947 90.703 50.532 90.373 50.197 7
回归周期/a4 9752 47597547522472
表选项
图 4 不同灾害等级下地震震级概率分布曲线 Figure 4 Conditional distribution of Mw at six hazard levels
图选项
4.3 amax和Mw联合概率分布计算

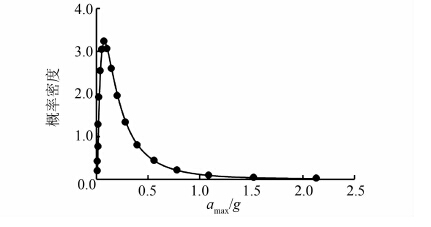
由美国地质勘查局剪切波速地图(VS30 maps)[25, 26]可获得计算地点处剪切波速为：VS30=760 m/s，则由式(3)~(6)可得地震作用放大系数为：F=1，其标准差σln(F)=0.7.则根据amax=F·PGA可以获得amax服从对数正态分布，均值为-1.591，标准差为1.001，其概率密度曲线如图 5所示.

图 5 地表最大加速度概率密度曲线 Figure 5 Probability density function of amax
图选项

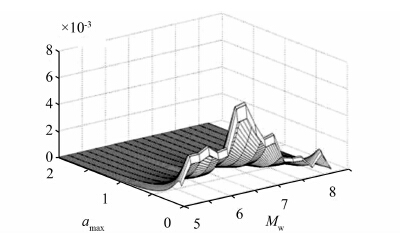
根据公式(7)~(13)可以获得amax和Mw联合概率分布，如图 6所示，由图 6可以看出，在50 a内amax和Mw具有很大的不确定性.其最有可能的组合约为Mw=6.4,amax=0.08g.

图 6 amax和Mw联合概率分布 Figure 6 Joint probability distribution of amax and Mw
图选项
4.4 土层液化概率分析

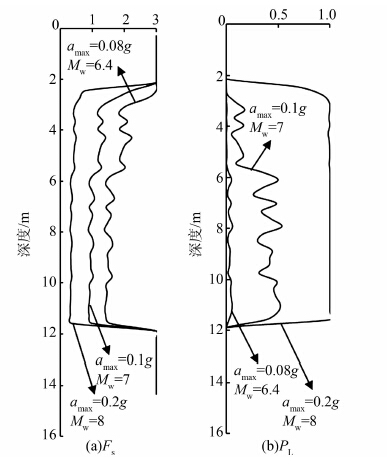
地震动参数对土体液化的发生具有重要的影响.例如，图 7中分别给出了选取amax=0.08g和Mw=6.4时，amax=0.1g和Mw=7时，amax=0.2g和Mw=8时3种情况下土体抗液化安全系数和液化概率沿深度的分布.当地震动强度较小时(amax=0.08g，Mw=6.4)，土体的液化概率很小且接近于0，显示该处土体不会发生液化.当发生强烈的地震动时(amax=0.2g，Mw=8)，地表以下3~12 m内的土体几乎都会发生液化.当地震动强度介于两者之间时(amax=0.1g和Mw=7)，6~12 m之间的土体约有50%的概率会发生液化.由于场地液化的评价结果极其依赖地震动参数的输入，必须对地震动参数出现的各种可能予以充分考虑.

图 7 选取不同amax和Mw的组合时土体安全系数Fs 及液化概率PL随深度变化示意图 Figure 7 Computed factor of safety and liquefaction probability choosing different amax and Mw
图选项

基于本文提出的方法获得了amax和Mw的联合概率分布，如图 6所示.该图给出了设计周期内地震动参数出现的各种可能性.利用公式(13)可以考虑各种可能发生的地震对土体液化的影响.在应用公式(13)的过程中，对于给定的amax和Mw组合，p(L=1|amax,Mw)沿深度方向都不一样.本文中取沿深度方向液化概率的最大值作为该地震动参数组合下的液化概率.基于上述计算，该处土体在50 a内发生液化的概率为PL=0.5270

通过利用公式(16)反算，可以得到该场地每年发生液化的概率约为0.015，即该地点液化发生重现周期约为67 a.

5 结论

如何评价服役期内土体的液化概率是基于性能的岩土工程设计的重要内容.本文介绍了基于2015版美国抗震设计规范的地震动放大系数概率分布的确定方法，推导了震级(Mw)和地表峰值加速度(amax)的联合概率计算公式，在此基础上，采用全概率定理计算了土体服役期内液化概率.算例表明，地震参数对土体液化概率具有显著的影响，提出的方法可以合理地考虑服役期内各种可能出现的地震对土体液化评价的影响.

参考文献
[1] 陈国兴, 金丹丹, 常向东, 等. 最近二十年地震中场地液化现象的回顾与土体液化可能的评价准则[J]. 岩土力学, 2013, 34(10): 2737–2755.
Chen Guoxing, Jin Dandan, Chang Xiangdong, et al. Review of soil liquefaction characteristics during earthquakes of recent twenty years and soil liquefaction susceptibility criteria[J]. Rock and Soil Mechanics, 2013, 34(10): 2737–2755.
[2] Seed H B, Idriss I M. A simplified procedure for evaluating soil liquefaction potential[J]. Journal of Soil Mechanics & Foundations Div, 1971, 97: 1249–1273.
[3] Kramer S L, Mayfield R T. Return period of soil liquefaction[J]. Journal of Geotechnical & Geoenviro-nmental Engineering, 2007, 133(7): 802–813.
[4] Juang C H, Li D K, Fang S Y, et al. Simplified procedure for developing joint distribution of amax and Mw for probabilistic liquefaction hazard analysis[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2008, 134(8): 1050–1058.
[5] Juang C H, Ou C Y, Lu C C, et al. Probabilistic framework for assessing liquefaction hazard at a given site in a specified exposure time using standard penetration testing[J]. Canadian Geotechnical Journal, 2010, 47(6): 674–687. DOI:10.1139/T09-127
[6] Juang C H, Lu C C, Hwang J H. Assessing probability of surface manifestation of liquefaction at a given site in a given exposure time using CPTU[J]. Engineering Geology, 2009, 104(3): 223–231.
[7] Juang C H, Jiang T, Andrus R D. Assessing probability-based methods for liquefaction potential evaluation[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2002, 128(7): 580–589.
[8] Juang C H, Jiang T, Andrus R D. Assessing probability based methods for liquefaction potential evaluation[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2002, 128(7): 580–589.
[9] 刘芳, 李震, 蒋明镜, 等. 考虑地震随机特征的液化侧向变形超越概率[J]. 岩土力学, 2015(12): 3548–3555.
Liu F, Li Z, Jiang M J, et al. Exceedance probability of liquefaction-induced lateral displacement considering seismic randomness[J]. Rock and Soil Mechanics, 2015(12): 3548–3555.
[10] National Institute of Building Sciences. NEHRP recommended seismic provisions[R]. Developed for the Federal Emergency Management Agency, Washington, DC, 2009. http://nehrp.gov/pdf/fema450provisions.pdf
[11] National Institute of Building Sciences. NEHRP Recommended Seismic Provisions, Part1 (Provision), Part2 (Commentary) and Part3 (Resource Papers)[R]. Developed for the Federal Emergency Management Agency, Washington, DC, 2015.
[12] 潘华, 高孟潭, 李金臣. 新版美国地震区划图源及其参数模型的分析与评述[J]. 震灾防御技术, 2009, 4(2): 131–140.
Pan Hua, Gao Mengtan, Li Jinchen. Comments on the models of seismic source and parameters used in the new edition of United States national seismic hazard maps[J]. Technology for Earthquake Disaster Prevent-ion, 2009, 4(2): 131–140.
[13] Juang C H, Fang S Y, Khor E H. First-order reliability method for probabilistic liquefaction triggering analysis using CPT[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2006, 132(3): 337–350.
[14] Youd T L, Idriss I M. Liquefaction resistance of soils: summary report from the 1996 NCEER and 1998 NCEER∕NSF workshops on evaluation of liquefaction resistance of soils[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2001, 127(4): 817–833.
[15] Stewart J P, Liu A H, Choi Y. Amplification factors for spectral acceleration in tectonically active regions[J]. Bulletin of the Seismological Society of America, 2003, 93(1): 332–352. DOI:10.1785/0120020049
[16] Seyhan E, Stewart J P. Site response in NEHRP provisions and NGA models[J]. American Society of Civil Engineers, 2012, 1(1): 359–379.
[17] Boore D M, Stewart J P, Seyhan E, et al. NGA-West2 equations for predicting PGA, PGV, and 5% damped PSA for shallow crustal earthquakes[J]. Earthquake Spectra, 2014, 30(3): 1057–1085. DOI:10.1193/070113EQS184M
[18] Seyhan E, Stewart J P. Semi-empirical nonlinear site amplification from NGA-west2 data and simulations[J]. Earthquake Spectra, 2014, 30(3): 1241–1256. DOI:10.1193/063013EQS181M
[19] Kamai R, Abrahamson N A, Silva W J. Nonlinear horizontal site amplification for constraining the NGA-west2 GMPEs[J]. Earthquake Spectra, 2014, 30(3): 1223–1240. DOI:10.1193/070113EQS187M
[20] Building Seismic Safety Council of the United States Geological Survey (USGS). National seismic hazard maps website[EB/OL]. http://geohazards.usgs.gov/hazardtoo l/application.php
[21] United States Geological Survey (USGS). National Seismic Hazard Maps website for deaggregation[EB/OL]. http: //geohazards.usgs.gov/deaggint /2008/
[22] Ku Chih Sheng, Hsein J, Chang Chi Wen, et al. Probabilistic version of the Robertson and Wride method for liquefaction evaluation: development and application[J]. Canadian Geotechnical Journal, 2011, 49(1): 27–44.
[23] Robertson P K. Performance based earthquake design using the CPT[C]// International Conference on Performance-Based Design in Earthquake, 2009.
[24] Robertson P K, Wride C E. Evaluating cyclic liquefaction potential using the cone penetration test[J]. Canadian Geotechnical Journal, 1998, 35(3): 442–459. DOI:10.1139/t98-017
[25] United States Geological Survey (USGS). Custom Hazard Maps[EB/OL]. http://geohazards.usgs.gov/hazards/ apps/cmaps/
[26] United States Geological Survey (USGS). Global VS30 Map Server[EB/OL]. http://earthquake.usgs.gov/hazards/apps/vs30/