文章信息
- 刘宾顺, 陈曦, 王冬勇, 苗姜龙, 程勇刚
- LIU Binshun, CHEN Xi, WANG Dongyong, MIAO Jianglong, CHENG Yonggang
- 基于局部随机场有限元理论的古丈县二龙庵滑坡分析
- Erlongan slope failure analysis based on stochastic finite element method and local random field
- 武汉大学学报(工学版), 2016, 49(5): 726-732
- Engineering Journal of Wuhan University, 2016, 49(5): 726-732
- http://dx.doi.org/10.14188/j.1671-8844.2016-05-014
-
文章历史
- 收稿日期: 2016-02-25
2. 武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072
2. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China
滑坡是一种典型的地质灾害,它不仅给人类生命财产带来威胁,而且对环境、资源、工程设施等带来严重破坏.如何降低滑坡导致的经济损失和人员伤亡是滑坡灾害研究的目的.目前确定性分析方法仍旧是滑坡问题的主要分析方法.然而,从可靠度的角度来看,一个安全系数为1.5、标准差为0.5的边坡会具有比安全系数为1.2、标准差为0.1的边坡更高的失效概率,因此采用单一的安全系数来反映边坡的安全性具有明显的局限性.目前,利用可靠度分析方法进行滑坡分析正在成为一个重要发展趋势,通过考虑多种不确定性因素甚至它们之间的相互作用,实现对滑坡问题更加全面的分析.
我国学者在可靠度研究方面做了大量工作,高大钊[1]、祝玉学[2]、陈祖煜[3]等对可靠度基本理论进行了详细的研究;刘宁[4]研究了随机有限元方法在土坡可靠度分析中的应用;康海贵等[5]对边坡稳定性分析两大评定体系(安全系数法与可靠指标法)的联系与差异作了对比分析;李典庆等[6]提出了考虑土体参数空间变异性的边坡可靠度分析的非侵入式随机有限元法;于玉贞等[7]和陈曦等[8]采用强度折减技术对边坡的稳定性进行了研究.一些学者基于随机场理论对边坡的稳定性进行了概率分析,例如,Vanmarcke[9, 10]提出土体剖面的自相关特性的随机场模型,提出用波动范围(scale of fluctuation)来描述土体参数的空间变异性,并给出具体计算方法.在此基础上,Vanmarcke[11]、Ghanem[12]等学者进行了大量的工作,对随机场模型和理论进行了完善.陈曦等[13]基于水热场和应力场的非耦合分析方法,将随机有限元理论应用于冻土路基边坡的稳定性分析.
本文首先基于Griffiths[14]编写的随机有限元程序对简单均质边坡进行了随机分析,强调考虑土体空间变异性的重要性.自开发随机有限元程序,基于陈曦开发有限元的冻土工程分析软件(FSoil v1.0)查看有限元网格的划分情况,并利用Monte-Carlo模拟的随机有限元法对古丈县二龙庵滑坡稳定系数和失效概率进行了系统的研究,详细分析了各土层对失效概率的影响,以此说明局部随机场展开适合实际的工程应用.
1 随机有限元基本原理在随机有限元法中,除了需要考虑材料参数的空间变异性,获得随机有限元方程列式以及求解随机算子和随机矩阵的求逆外,还需要对随机场进行离散.
随机场的局部平均细分法是将随机细分法与局部平均结合起来,它使用低次的、有效的插值函数,更适合随机有限元计算模型.基本流程见表 1,具体算法如下:
1) 通过局部平均理论,得到一个单元的局部平均值Z10,Z10服从均值为0的正态分布.
2) 如表 1所示为局部细分法递归图,将Z10所代表的区域平均分成两部分,产生两个服从正态分布的变量Z11、Z21,它们的均值和方差必须满足3个条件:
| Z10 | ||||||||
| Z11 | Z21 | |||||||
| Z12 | Z22 | Z32 | Z42 | |||||
| Z13 | Z23 | Z33 | Z43 | Z53 | Z63 | Z73 | Z83 | |
a)Z11、Z21的方差与局部平均理论计算得到的方差一致;
b)Z11、Z21相关;
c)Z11、Z21的平均值等于母单元的平均值,即0.5×(Z11+Z21)=Z10.
3) 将Z11、Z21所代表的区域平均分成两部分,产生4个服从正态分布的变量Z12、Z22、Z32、Z42,其均值和方差须满足3个条件:
a)Z12、Z22、Z32、Z42的方差与局部平均理论计算得到的方差一致;
b)Z12、Z22、Z32、Z42相关;
c)Z12、Z22、Z32、Z42的平均值要等于母单元的平均值,即0.5×(Z12+Z22)= Z11和0.5×(Z32+Z42)= Z21.
依次类推,直至获得所需的细分精度.
局部细分平均表达式为
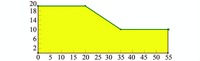
计算模型如图 1所示,边坡坡比为1:1.5,采用摩尔库伦准则,模型参数为γ=20 kN/m3、c=10 kPa、φ=20°.
|
| 图 1 计算模型 Figure 1 Calculation model |
采用Morgenstern-Price (M-P)极限平衡法结合圆弧滑裂面搜索算法进行边坡稳定性分析,并采用蒙特卡罗(Monte-Carlo)法进行可靠度分析.Phoon和Kulhawy[15-16]、Duncan[17]以及李小勇等[18]曾对一些常用土参数的变异性进行了调研,认为重度变异系数维持在0~10%范围内,变异性较小,因此本文计算中忽略重度变异性的影响,只考虑强度参数c、φ的变异性.对于土体参数统计特性,可参考松尾稔[19]、宁宝宽[20]以及刘春等[21]的研究.
如图 2~5所示,失效概率和变异水平以失效概率Pf =50%为界限值,当Pf >50%时随着变异水平的增大失效概率不断减小,当Pf<50%时随着变异水平的增大失效概率不断增大.对于失效概率和安全系数以安全系数Fs=1为界限值,当安全系数Fs<1时相同安全系数情况下,随着变异水平增加失效概率不断减小,当安全系数Fs>1时随着变异水平的增大失效概率不断增大.

|
| 图 2 c、φ正态分布不同变异水平条件下边坡的失效概率 Figure 2 Failure probability of slope with c,φ in normal distribution and different variability levels |

|
| 图 3 c、φ对数正态分布不同变异水平条件下边坡的失效概率 Figure 3 Failure probability of slope with c,φ in lognormal distribution and different variability levels |

|
| 图 4 c、φ正态分布不同变异水平条件下边坡的失效概率和安全系数 Figure 4 Failure probability and FOS of slope with c,φ in normal distribution and different variability levels |

|
| 图 5 c、φ对数正态分布不同变异水平条件下边坡的失效概率和安全系数 Figure 5 Failure probability and FOS of slope with c,φ in lognormal distribution and different variability levels |
选取正态分布和对数正态分布下黏聚力均值μc=5、μc=11以及变异系数ccov=0.1、0.5、1.0的概率密度函数作解释,如图 6~7所示.由计算可知均值μc=7时,安全系数Fs=1.001.当均值μc=5时,利用概率密度函数进行随机取值,变异系数较小时抽取到>7的概率较小,导致失效概率较大.随着变异系数的不断增大,取值>7的概率不断增大,从而导致失效概率不断减小;同理,当均值μc=11时利用概率密度函数进行随机取值,变异系数较小时抽取到<7的概率较小,导致失效概率较小.随着变异系数的不断增大,取值<7的概率不断增大,也就导致失效概率不断增大.

|
| 图 6 正态分布的概率密度函数 Figure 6 Probability density function of normal distribution |

|
| 图 7 对数正态分布的概率密度函数 Figure 7 Probability density function of lognormal distribution |
基于Griffiths和Fenton编写的蒙特卡罗模拟的随机有限元程序,研究正态分布下变换水平δx和竖向δy的波动范围和方差σ2对滑坡的影响,如表 2所示.不考虑空间变异性见图 8,计算结果如图 9、10所示.
| σ2 | δx | δy |
| 1 | 1 | |
| 3 | 5 | 2 |
| 15 | 10 | |
| 1 | 20 | 2 |
| 4 | 20 | 2 |

|
| 图 8 不考虑空间变异性 Figure 8 Without considering the spatial variability |

|
| 图 9 不同的波动范围 Figure 9 Different fluctuation ranges |
|
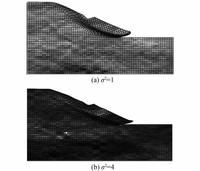
| 图 10 不同的方差 Figure 10 Different variances |
如图 9、10所示,对边坡进行随机有限元分析:均方差为定值时,当水平和竖向相关距离取值比较小时,土性参数的空间分布比较零散且单元间基本无连续性,当水平向相关距离比较大时,边坡的土性参数的空间分布在水平向呈现出连续性,并且边坡滑裂面呈现出很大的差异性;当水平和竖向相关距离取为定值时,随着均方差的不断变大,通过图 10所示参数空间分布对比可以明显看出单元颜色变化比较大,表明土性参数在空间的分布差异性比较大,由此导致边坡产生的滑裂面变化比较大.
3 工程案例介绍 3.1 工程概况湖南古丈县二龙庵滑坡地质灾害地处古丈县古阳镇三道河二龙庵一侧山坡.2014年8月,由于连续暴雨作用引发了山体变形开裂,滑坡体滑坡后缘与中部发现多条裂缝,开裂宽度最大已达20 cm左右,且随时有整体下滑的可能.场区地势较高,位于山体的腰部,地下水以基岩裂隙水和暂时性的松散堆积层孔隙水为主,勘查时钻孔均为干孔,未见地下水.
3.2 岩土层物理力学参数采取室内试验和原位测试等多种测试方法,获得了如表 3所示的土性参数值.
| 岩土名称 | 天然 | 饱和 | ||||
| γ/(kN·m-3) | φ/(°) | c/kPa | γ/(kN·m-3) | φ/(°) | c/kPa | |
| 第1层粉质黏土 | 19 | 19 | 24 | 20 | 15 | 20 |
| 第2层碎石土 | 21 | 32 | 6 | 22 | 27 | 5.4 |
| 第3层滑带土 | 19 | 19 | 16 | 20 | 17 | 14 |
| 第4层中风化砂岩 | 24 | 47 | 200 | 25 | - | - |
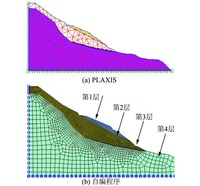
本文采用PLAXIS软件和自开发有限元软件开展了边坡稳定性分析,计算模型和网格如图 11所示.
|
| 图 11 有限元模型及网格划分 Figure 11 Finite element model and its mesh |
本节主要研究土性参数空间变异性对滑坡的影响,采用基于蒙特卡罗的随机有限元可靠度分析,具体模拟方案如下:
第一:对滑坡土层进行敏感性分析可知,第1层粉质黏土和第4层基岩对滑坡影响很小,因此将其选为定值,只对第2层碎石土和第3层的滑带土进行随机有限元分析.
第二:依次对第2层和第3层土进行随机有限元分析,参数服从正态分布,相关距离取定值δx=δy=5 m,变异系数分别选取ccov=0.3、ccov=0.5和ccov=0.8三种情况,综合考虑计算时间和结果的可靠性,将蒙特卡罗模拟次数选取为200次.
图 12为针对第2层土的黏聚力c和内摩擦角φ进行200次蒙特卡罗模拟所获得的安全系数的概率分布.由图 12(a)可见,只考虑黏聚力c的变异系数变化(即ccov=0.3、0.5、0.8)时,安全系数分别集中在1.07~1.08、1.06~1.09和1.06~1.09范围内,其范围变化很小,可见第二层土的黏聚力c对滑坡影响很小;由图 12(b)可见,当只考虑内摩擦角φ的变异系数变化时,随着变异系数的不断增大,第2层土的安全系数变化范围逐渐扩大,并且安全系数Fs<1的概率也在逐渐增大.

|
| 图 12 概率分布函数图(针对第2层土) Figure 12 Probability distribution function diagram |
图 13为分别变换第3层土的黏聚力c和内摩擦角φ的变异系数,进行200次蒙特卡罗模拟后获得的安全系数概率分布图.图 13(a)只考虑黏聚力c的变异系数变化,ccov=0.3时安全系数变化范围集中在1.06~1.09,ccov=0.5时安全系数变化范围扩大且集中在1.05~1.10,ccov=0.8时安全系数变化范围进一步扩大,但概率值均匀分布在区间1.04~1.11;图 13(b)只考虑内摩擦角φ的变异系数变化,随着变异系数的不断增大,安全系数Fs<1的概率逐渐增大即边坡失效概率不断增大.数据对比可知,第3层的内摩擦角φ比黏聚力c对滑坡影响更大,且随着变异系数不断增大,随机变量落在任一区间上的概率值不断减小.

|
| 图 13 概率分布函数图(针对第3层土) Figure 13 Probability distribution function diagram |
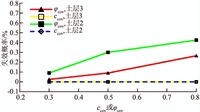
图 11给出自编程序的土层划分,从图 14可得滑坡分层随机场展开计算结果:对于土层2和土层3中黏聚力,随着方差不断增大,失效概率为0;对于土层2和土层3中内摩擦角,随着方差不断增大,失效概率不断增大,土层2中失效概率比土层3变化范围更大,并且通过200次蒙特卡洛模拟获得了安全系数变化范围.对于土层2,安全系数变化范围为0.485~1.243,对于土层3,安全系数变化范围为0.748~1.157.综上可知,相比土层3,土层2对滑坡影响更大;相比黏聚力,内摩擦角对滑坡影响更大.
|
| 图 14 滑坡分层随机场展开计算结果 Figure 14 Calculation results of landslide based on random expansion of single soil layer |
在随机有限元理论研究方面,目前已进行了大量的工作,但随机有限元理论在实际工程中的应用还十分有限.本文针对工程案例自开发了随机有限元程序,结合有限元强度折减法进行了滑坡的随机分析,获得了如下结论:
1) 随机变量模型下的边坡稳定性分析,对于失效概率和变异水平以失效概率Pf =50%为界限值时,当Pf >50%时随着变异水平的增大失效概率不断减小,当Pf <50%时随着变异水平的增大失效概率不断增大;对于失效概率和安全系数以安全系数Fs=1为界限值时,当安全系数Fs<1时相同安全系数情况下,随着变异水平增加失效概率不断减小,当安全系数Fs>1时随着变异水平的增大失效概率不断增大.在计算中将土层看作均质材料具有明显的局限,不能很好地反映工程实际.
2) 自开发程序进行局部随机场展开,能够考虑各个土层的空间变异性以及各土层空间变异性的变化对滑坡的影响.针对湖南古丈县二龙庵滑坡进行了随机分析,结果表明:局部随机场展开可以用于分析各土层参数对滑坡的影响,在c不同变异水平下滑坡失效概率为0; 随着φ变异水平增大,滑坡失效概率逐渐增大,与第3层土相比,第2层土对滑坡影响比较大;而相比黏聚力,内摩擦角对滑坡影响更大;因此有必要对该层土的参数(尤其是内摩擦角)进行更加精准的测量,以便获得更加可靠的分析结果.
| [1] |
高大钊.
土力学可靠性原理[M]. 北京: 中国建筑工业出版社, 1989.
Gao Dazhao. The Reliability Principle of Soil Mechanics[M]. Beijing: China Architecture & Building Press, 1989. |
| [2] |
祝玉学.
边坡可靠性分析[M]. 北京: 冶金工业出版社, 1993.
Zhu Yuxue. Slope Reliability Analysis[M]. Beijing: Metallurgical Industry Press, 1993. |
| [3] |
陈祖煜.
土质边坡稳定分析[M]. 北京: 中国水利水电出版社, 2003.
Chen Zuyu. Stability Analysis of Soil Slope[M]. Beijing: China Water & Power Press, 2003. |
| [4] |
刘宁.
可靠度随机有限元法及其工程应用[M]. 北京: 中国水利水电出版社, 2001.
Liu Ning. Reliability Stochastic Finite Element Method and Its Engineering Application[M]. Beijing: China Water & Power Press, 2001. |
| [5] |
康海贵, 李炜. 边坡稳定安全系数及其土性参数及失效概率关系研究[J].
大连理工大学学报, 2008, 48(6): 856–862.
Kang Haigui, Li Wei. Research on slope safety factor and its relationship with shear strength parameters and failure probability[J]. Journal of Dalian University of Technology, 2008, 48(6): 856–862. |
| [6] |
李典庆, 蒋水华, 周创兵, 等. 考虑参数空间变异性的边坡可靠度分析非侵入式随机有限元法[J].
岩土工程学报, 2013, 35(8): 1413–1422.
Li Dianqing, Jiang Shuihua, Zhou Chuangbing, et al. Reliability analysis of slopes considering spatial variability of soil parameters using non-intrusive stochastic finite element method[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1413–1422. |
| [7] |
于玉贞, 林鸿州, 李荣建, 等. 非稳定渗流条件下非饱和土边坡稳定分析[J].
岩土力学, 2008, 29(11): 2892–2898.
Yu Yuzhen, Lin Hongzhou, Li Rongjian, et al. Stability analysis of unsaturated soil slope under transient seepage flow state[J]. Rock and Soil Mechanics, 2008, 29(11): 2892–2898. |
| [8] | Chen X, Wu Y, Yu Y, et al. A two-grid search scheme for large-scale 3-D finite element analyses of slope stability[J]. Computers and Geotechnics, 2014, 62: 203–215. DOI:10.1016/j.compgeo.2014.07.010 |
| [9] | Vanmarcke E H. Probabilistic modeling of soil profiles[J]. ASCE:Journal of Geotechnical Engineering Division, 1977a, 103(GT11): 1227–1246. |
| [10] | Vanmarcke E H. Reliability of earth slopes[J]. ASCE:Journal of Geotechnical Engineering Division, 1977b, 103(GT11): 1247–1265. |
| [11] | Vanmarcke E H. Random Fields:Analysis and Synthesis[M]. Cambridge,Mass: MIT Press, 1983. |
| [12] | Ghanem, Roger G, Pol D S. Stochastic finite elements: A spectral approach[Z]. Courier Corporation, 2003. |
| [13] | Chen X, Liu J K, Xie N, et al. Probabilistic analysis of embankment slope stability in frozen ground regions based on random finite element method[J]. Sciences in Cold and Arid Regions, 2015, 7(4): 0354–0364. |
| [14] | Griffiths D V, Fenton G A. Probabilistic slope stability analysis by finite elements[J]. Joumal of Geotechnical and Geoenvironmental Engineering, 2004, 130(5): 507–518. DOI:10.1061/(ASCE)1090-0241(2004)130:5(507) |
| [15] | Phoon K K, Kulhawy F H. Characterization of geotechnical variability[J]. Canadian Geotechnical Journal, 1999, 36(4): 612–624. DOI:10.1139/t99-038 |
| [16] | Phoon K K, Kulhawy F H. Evaluation of geotechnical property variability[J]. Canadian Geotechnical Journal, 1999, 36(4): 625–639. DOI:10.1139/t99-039 |
| [17] | Duncan J M. Factors of safety and reliability in geotechnical engineering[J]. Journal of Geotechnical and Geoenviromental Engineering, 2000, 126(04): 307–316. DOI:10.1061/(ASCE)1090-0241(2000)126:4(307) |
| [18] |
李小勇.
土工参数空间概率特征[M]. 北京: 原子能出版社, 2006.
Li Xiaoyong. The Spatial Probabilistic Characteristics of Geotechnical Parameters[M]. Beijing: Atomic Energy Press, 2006. |
| [19] |
松尾稔.
地基工程学[M]. 北京: 人民交通出版社, 1990.
Song Weiren. Foundation Engineering[M]. Beijing: China Communications Press, 1990. |
| [20] |
宁宝宽, 陈四利, 杨军. 区域性黏土物理力学指标的相关性分析[J].
土工基础, 2005, 19(1): 51–53.
Ning Baokuan, Chen Sili, Yang Jun. Interrelation of physical and mechanical indexes on regional clay[J]. Soil Engineerng and Foundation, 2005, 19(1): 51–53. |
| [21] |
刘春, 白世伟, 赵洪波. 黏性土土性指标的统计规律研究[J].
岩土力学, 2003, 10(24): 180–184.
Liu Chun, Bai Shiwei, Zhao Hongbo. Statistical regularity research of physical and mechanical indexes of clay[J]. Rock and Soil Mechanics, 2003, 10(24): 180–184. |
 2016, Vol. 49
2016, Vol. 49




