武汉大学学报(工学版)   2016, Vol. 49 Issue (3): 423-428

文章信息

黄俊杰, 阮羚, 熊宇, 陈孝明, 李晨, 王威, 张天浩
HUANG Junjie, RUAN Ling, XIONG Yu, CHEN Xiaoming, LI Chen, WANG Wei, ZHANG Tianhao
一种动态参数优化的绝缘子等值盐密预测模型
A forecast model of ESDD for insulator based on dynamic parameters optimization
武汉大学学报(工学版), 2016, 49(3): 423-428
Engineering Journal of Wuhan University, 2016, 49(3): 423-428
http://dx.doi.org/10.14188/j.1671-8844.2016-03-018

文章历史

收稿日期: 2015-11-26
 Abstract              PDF               Figures               Tables
引用本文 0
黄俊杰, 阮羚, 熊宇, 陈孝明, 李晨, 王威, 张天浩. 一种动态参数优化的绝缘子等值盐密预测模型[J]. 武汉大学学报(工学版), 2016, 49(3): 423-428.
HUANG Junjie, RUAN Ling, XIONG Yu, CHEN Xiaoming, LI Chen, WANG Wei, ZHANG Tianhao. A forecast model of ESDD for insulator based on dynamic parameters optimization[J]. Engineering Journal of Wuhan University, 2016, 49(3): 423-428.
一种动态参数优化的绝缘子等值盐密预测模型
黄俊杰1, 阮羚1, 熊宇1, 陈孝明1, 李晨2, 王威2, 张天浩2     
1. 国网湖北省电力公司电力科学研究院，湖北 武汉430077;
 2. 武汉大学测绘遥感信息工程国家重点实验室，湖北 武汉430079
收稿日期: 2015-11-26
作者简介: 黄俊杰(1976-)，男，博士，工程师，从事状态监测系统、输电线路防灾技术的研究，E-mail:hbdky2@sina.cn..
摘要: 绝缘子污秽是电力输电线路污闪事故发生的主要原因，评估和预测污秽积累情况对指导清污工作和预防污闪事故具有重要的意义.针对绝缘子经典等值盐密预测模型参数固定和误差较大的问题，提出一种基于四阶Runge-Kutta和模拟退火算法的动态参数优化预测模型.首先，采用切线方程对经典预测模型进行参数动态化处理，得到以一阶欧拉方程表示的离散化的经典预测模型，然后，引入四阶Runge-Kutta算法对上述欧拉方程进行高阶求导迭代以抑制欧拉模型的离散误差，最后，借助模拟退火算法对模型参数进行最优估计，从而实现高精度的等值盐密预测模型.实验结果表明，改进模型的预测值与实测值的相关系数高于0.97，绝对误差在一般情况下较经典模型降低50%，预测值均方根误差较经典模型减小30%以上.这说明改进模型不仅很好地反映绝缘子等值盐密的动态变化规律，而且能够对等值盐密进行更精准、更稳定的预测.
关键词： 污秽绝缘子     累积规律     等值盐密预测     四阶Runge-Kutta算法     模拟退火    
A forecast model of ESDD for insulator based on dynamic parameters optimization
HUANG Junjie1, RUAN Ling1, XIONG Yu1, CHEN Xiaoming1, LI Chen2, WANG Wei2, ZHANG Tianhao2     
1. Hubei Electric Power Test & Research Institute, Wuhan 430077, China;
 2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
Abstract: Contaminated insulator is the main reason for transmission line flashover accident, so it attaches much significance to evaluate and predict filthy accumulation to guide the clean-up work and prevention of pollution flashover accident. Aiming at the problem that insulators’ classical equivalent salt deposit density (ESDD) prediction model has fixed parameters and large error, this paper puts forward a dynamic parameters optimization prediction model based on four-order Runge-Kutta algorithm and simulated annealing algorithm. This model firstly uses tangential equation to make a dynamic processing for the parameters of the classical prediction model, which gets expressed as a first order Euler equation discretization of classical prediction model. And then the four-order Runge-Kutta algorithm is introduced to make high order derivative iteration for the Euler equation in order to inhibit the discretization error of the Euler model. Finally, the model’s parameters are estimated optimally with the help of simulated annealing algorithm to achieve high precision of the equivalent salt deposit density forecasting model. The experimental results reveal that the fitting coefficient of the improved model’s predicted values and measured values is larger than 0.97; and the absolute error of the model is lower than that of classical model about 50% in the general case. The root mean square error of the predictive value decrease more than 30% than that of classical model. The new model not only well reflects the dynamic change regulation of insulator equivalent salt deposit density, but also makes more accurate and stable prediction for equivalent salt deposit density.
Key words: contaminated insulator     cumulative rule     forecast of equivalent salt deposit density     four-order Runge-Kutta algorithm     simulated annealing    

绝缘子是一种能够在架空输电线路中起到重要作用的绝缘控件，我国电力系统中的输电线路和变电站等都装有大量的绝缘子[1].由于我国大气环境中污染物较多，绝缘子表面会随着时间的累积附着较多的污秽物.在不利气象条件下(如雾、露、毛毛雨、溶雪等)，逐渐湿润的污秽物在电磁场作用下发生强烈放电即污闪现象[2, 3].随着我国工业的发展，大气污染物逐年增多，加剧了绝缘子表面污秽物的堆积，使得污闪的风险日益增大.电网污闪事故涉及范围广，停电时间长，直接危及电网的运行安全.污闪事故数在电网事故排行中位居第二，仅仅低于雷害事故的数量，而污闪事故造成的损失却是雷害事故的10倍[4].自20世纪80 年代以来的电网事故调查表明，导致我国电网大面积停电的首要原因是污闪事故，占全部电网大面积停电原因的60%以上[5].因此，减少、预防污闪事故的发生对于电网安全可靠运行具有十分重要的意义.

为了预防污闪事故的发生，运行中采取的主要措施有：增加爬电比距、采用新型防污型绝缘子或使用防污涂料、对绝缘子进行定期清洗[6-8]等.以上方法均需要耗费大量人力或经济成本.因此，研究绝缘子污秽累积规律、建立动态预测模型并根据预测结果进行定点清扫对预防污闪事故具有重要意义.

针对绝缘子污秽的累积情况，国内外已有了大量的研究成果，其中，大部分研究采用统计分析方法，讨论了不同的绝缘子类型、气象条件、大气污染等因素与等值盐密(ESDD: equivalent salt deposit density)之间的定性关系[9-16].此外，钱之银等[17]、王少华等[18]采用了绝缘子等值盐密动态累积规律经典模型对等值盐密随时间变化情况进行仿真建模.本文在上述工作的基础上，通过模型参数动态化和引入参数优化算法的方式从物理原理角度改进了绝缘子等值盐密动态累积模型，并利用人工积污试验数据[17]和武汉地区3个站点ESDD在线监测数据对模型进行了验证.

1 动态参数优化等值盐密日均预测模型 1.1 模型原型的选择

近年来，对于绝缘子积污特性的动态规律已有相关研究，但大多数研究基于线性回归、经验分析或神经网络开展，并没有固定的规律模型.钱之银等[17]研究了累积时间和积污量的模型，王少华等[18]改进了钱之银等提出的等值盐密累积规律公式，在利用自然积污数据验证模型的可用性和可靠性后，提出经验公式如下所示：

$\text{ESDD}=\text{ }A\left( 1-K\exp \text{ }\left( -t/\tau \right) \right)$    (1)

其中:A为饱和等值盐密,mg/cm2，与绝缘子的结构型号和运行环境有关；K为常数；t为积污时间；τ为表征积污速率的常数.

该模型假定积污速率为积污时间的函数，能准确地预测外界环境不发生变化的情况下，绝缘子污秽的累积量，但忽略了污染程度变化对积污速率的影响.由于这一假设，该模型无法动态地修改参数，从而造成自然条件下预测误差较大.针对这一问题，本文提出一种基于四阶Runge-Kutta和模拟退火算法的动态参数优化绝缘子污秽预测模型.该模型使用不断自调整的积污速率来表征不包含降雨的外界环境因素在正常范围内变化的过程.首先，采用切线方程对经典预测模型进行参数动态化处理，得到以一阶欧拉方程表示的离散化的经典预测模型，然后，引入四阶Runge-Kutta对上述欧拉方程进行高阶求导迭代以抑制欧拉模型的离散误差，最后，借助模拟退火算法对模型参数进行全局最优估计，从而实现高精度的等值盐密预测模型.具体流程如图 1所示.

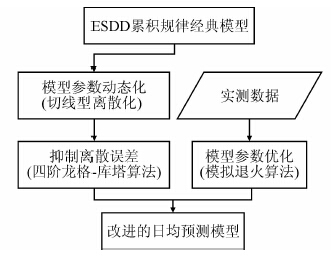
图 1 等值盐密预测模型改进流程图 Figure 1 Flowchart for improving forecast model of ESDD
图选项
1.2 模型参数的动态化

虽然经典模型揭示了绝缘子等值盐密动态累积规律，但是在零时刻，预测结果可能为负值，这与累积规律并不相符合；而且当降水等气象要素和大气污染程度发生变化时，积污速率将不再是与时间无关的常数，绝缘子ESDD时间序列也将不再随时间呈负指数变化趋势，而是和气象要素以及大气污染程度有着较为复杂的关系[16, 19].

因此，为了实现模型的参数动态化，本文考虑通过切线型离散化的方式对经典模型进行处理，即将任意时刻ESDD的增长速率表示为该时刻ESDD的函数，由于t=0时，累积盐密为0，故K=1.记ESDD累积量为时间的函数

$\frac{\text{dS}}{dt}=\frac{A}{\tau }\exp (-\frac{t}{\tau })$    (2)

将S(t)代入式(2)得:

${{S}^{'}}(t)=\left( A-S \right)/\tau $    (3)

对式(1)进行切线型离散化处理，可得：

${{S}_{k}}=A\ \left( 1-\exp \left( -{k}/{\tau }\; \right) \right)$    (4)

采用k时刻的一阶近似:

${{S}_{k+1}}-{{S}_{k}}=A\left( \exp \left( -\frac{k}{\tau } \right)-\exp \left( -\frac{k+1}{\tau } \right) \right)\approx A\times \exp \left( -\frac{k}{\tau } \right)\times \frac{1}{\tau }$    (5)

因此，k+1时刻ESDD可以表示为

${{\text{S}}_{k+1}}\ ={{\text{S}}_{k}}+\frac{A}{\tau }\cdot \exp \left( -\frac{k}{\tau } \right)$    (6)

由式(6)可知，通过对连续模型的切线型离散化处理，得到相邻时间段的ESDD差值为参数A、k和τ的函数.即若已知本月的参数A、k和τ值，则可根据式(6)对下一时刻的ESDD进行预测.

当k=0时，S0=0，则Sk可以写为如下形式：

${{S}_{k}}=A-A{{(1-\frac{1}{\tau })}^{k}}$    (7)

当τ>1时，Sk收敛到A.而从王少华等[18]的研究中可知，τ>1与拟合结果一致.

1.3 抑制离散误差

式(6)通过上一时刻的ESDD对下一时刻的ESDD进行预测，但在对连续型经典模型进行离散化的过程中，不可避免地会引入离散误差.因此，本文引入经典四阶龙格-库塔算法来抑制此误差.

龙格-库塔(Runge-Kutta)算法是由一阶欧拉法改进得来，精度较高，能够对离散误差进行较好地抑制；尤其是四阶的龙格-库塔算法，其精确度达到步长五次方的同时也平衡了高阶导数所带来的误差抖动问题，因此在工程上得到广泛的应用.若令初值问题表现如下式：

$\begin{align} & y'=f(t,y) \\ & y({{t}_{0}})={{y}_{0}} \\ \end{align}$    (8)

经典四阶龙格-库塔算法的思路是下一时刻的预测值yn+1由当前时刻的值yn加上时间间隔δt和一个估算的斜率的乘积共同决定.该斜率是多阶斜率的加权平均，如下所示：

${{y}_{n+1}}={{y}_{n}}+\frac{h}{6}\left( {{k}_{1}}+2{{k}_{2}}+2{{k}_{3}}+{{k}_{4}} \right)$    (9)

式中：k1是开始时刻的斜率；k2是时间段中点的斜率，通过欧拉法用斜率k1 来决定y在点tn+h/2的值；k3也是中点的斜率，但采用斜率k2决定y值；k4是时间段终点的斜率，其y值用k3决定.

对于形如式(6)的预测模型，本文在采用步长Δh均为1d的情况下，使用四阶龙格-库塔算法可以有效地抑制预测误差，获得较为精确的预测结果.

1.4 基于模拟退火的模型参数估计

尽管四阶龙格-库塔能较好地解决离散化所带来的误差，但是却给模型参数的拟合带来了极大的困难，为了能使新的预测更为准确，本文采用了可获得全局最优解的模拟退火算法，对绝缘子等值盐密预测模型的参数进行估计.

模拟退火算法最早由Metropolis在1953年提出,1983年由Kirkpatrick等成功引入组合优化领域,目前己在工程中得到了广泛的应用[20-22].模拟退火算法源于对热力学中退火过程的模拟，在给定初始温度下，通过缓慢下降温度参数，使算法能够在一定时间内给出一个近似最优解.它是一种通用概率算法，用来在一个大的搜寻空间内找寻命题的全局最优解.绝缘子等值盐密累积过程与热力学中退火过程有着相似的物理基础，因此，本文选择模拟退火算法对污秽累积模型的参数进行估计，以获取参数的全局最优解.

对于ESDD预测模型来说，本文需要根据已测得的数据拟合出饱和等值盐密A(mg/cm2)、常数K和积污速率的常数τ(日-1)3个参数，对于非线性高阶模型来说，采用模拟退火算法能在一定的迭代步数内迅速拟合出这3个参数的最优估计值.

2 实验及结果分析

本文分别利用人工积污数据和实际条件下得到的在线监测数据来检查预测模型的准确性和鲁棒性.其中在线监测数据由湖北省电力科学研究院提供，在线监测设备为康普公司ODU-11型装置.该设备根据光传感原理，在未带电条件下，对湖北省内在线监测点上的备用绝缘子串进行测量.据官方验证，该ODU-11型设备对ESDD的测量误差在10%以内，基本满足实验需求.由于上述两类数据的测量方法、自然条件以及研究区域均具有代表性差异，因此，适用于评估改进模型和经典模型的预测能力.在两类实验中，均将实验数据分为两部分：一部分数据用于模型建立，另一部分数据用于模型验证.

2.1 人工积污实验数据验证

人工积污实验数据验证中的实验数据来自钱之银等[17]文中的人工积污实验数据.该积污实验设计制造了人工积污循环装置，模拟了自然状况下的污染、风、雨、雾等因素对绝缘子积污量的影响.实验选择了两类绝缘子，分别为普通型和钟罩型，获取8个周期的人工积污循环试验数据，测定了每个周期结束后普通型和钟罩型绝缘子串的盐密测量值.数据如表 1所示.

表 1 人工积污实验等值盐密实测值 Table 1 Experimental data of ESDD in artificial contaminated cumulation research mg/cm2
周期普通型绝缘子钟罩型绝缘子
周期10.153 90.199 7
周期20.264 30.351 8
周期30.333 10.458 1
周期40.381 00.524 7
周期50.406 00.576 8
周期60.428 90.612 2
周期70.443 50.641 4
周期80.449 70.658 1
表选项

在人工积污实验数据验证中，前5个周期的数据用于模型参数拟合，后3个周期的数据用于预测.图 2为钱之银等[17]人工积污循环试验数据使用基于式(6)的改进模型的拟合结果和预测结果.

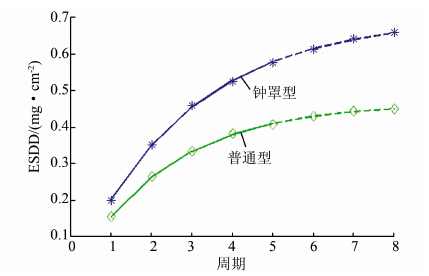
图 2 人工积污循环试验ESDD的拟合和预测结果 Figure 2 Results of fitting and forecast in ESDD data of artificial contaminated cumulation
图选项

图 2中的实线是拟合模型，虚线是预测模型.从图中可以看出对于两种类型的绝缘子，改进模型均能很好地反演和预测其等值盐密的累积规律.本文也拟合出经典模型的参数并求出预测值，并将两组预测值分别与实测值拟合求出了拟合相关系数R和拟合的均方根误差RMSE，如表 2所示.

表 2 人工积污饱和盐密预测R值以及预测RMSE值T Table 2 The correlation coefficient and root mean square errors in forecast of artificial ESDD experiment
预测模型预测值与实测值的相关系数R预测值与实测值的均方根误差
原模型(钟罩型)0.998 30.015 6
改进模型(钟罩型)0.998 90.002 8
原模型(普通型)0.994 90.010 2
改进模型(普通型)0.993 60.002 1
表选项

表 2显示新旧模型在建立时均有着很高的拟合精度，但是进行预测时改进模型预测值的RMSE仅为原模型预测值的约1/5，这表明改进模型的预测能力要显著地优于经典方法.这一现象说明，尽管固定参数模型能够较好地表征绝缘子ESDD的累积规律，然而，由于没有考虑外部因素对累积速率的影响，导致预测误差明显高于改进模型.

2.2 武汉地区在线监测数据验证

武汉地区在线监测数据验证选取3个在线监测站点：阳滩线053号、热轧线018号、热和线003号.数据采集时间为2013年1月4-21日，该时段为持续无降水期.监测数据如图 3所示.

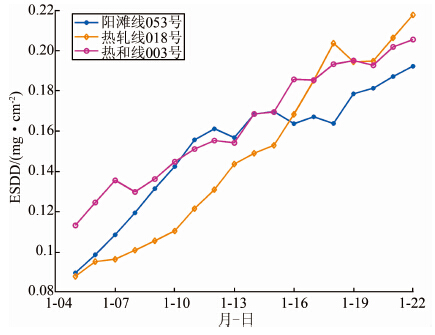
图 3 武汉自然积污绝缘子在线监测数据 Figure 3 Online ESDD measurement of natural contamination of insulators in Wuhan
图选项

在武汉地区在线监测数据验证中，前15 d的数据用于模型参数的估计，后3 d的数据用于预测值的检验.图 4分别利用了阳滩线053号、热轧线018号和热和线003号3处在线监测数据，运用改进模型对其绝缘子等值盐密分别进行拟合和预测.

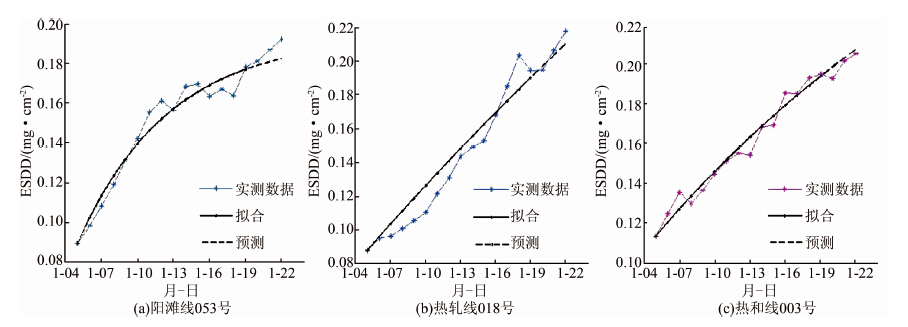
图 4 ESDD在线监测数据的拟合和预测 Figure 4 Fitting and forecast for ESDD data of online measurement
图选项

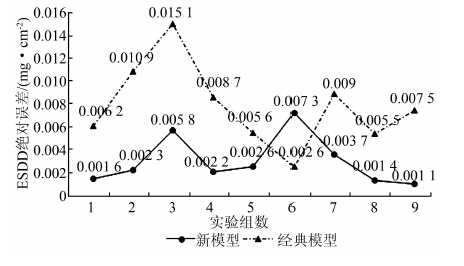
从图 4可知：在自然条件下的等值盐密在线监测数据比人工实测等值盐密数据具有更大的随机性，改进模型对前15 d数据的拟合效果较好，拟合相关系数均高于0.97.本文为了验证3组数据后3 d预测的准确性，采用绝对误差(absolute error)和均方根误差RMSE来评价改进模型的预测准确度.通过对比经典模型，绝对误差的对比结果如图 5所示，RMSE的对比结果如图 6所示.

图 5 两种模型等值盐密预测值与实测值的绝对误差对比 Figure 5 Comparison of sbsolute errors between forecast and true values of ESDD from two models
图选项
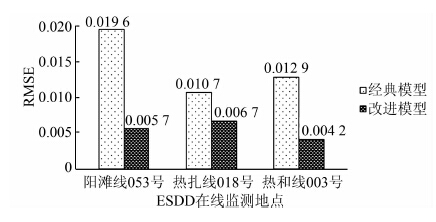
图 6 两种模型等值盐密预测值与实测值的均方根误差对比 Figure 6 Comparison of root mean square errors in forecast and true values of ESDD between two models
图选项

从图 5预测数据与实测数据的绝对误差对比中可以发现：经典模型的平均绝对误差约为0.007 9 mg/cm2，而改进模型的平均绝对误差约为0.003 1 mg/cm2，仅为前者的39.2%.而改进模型在热轧线第3次(第6组数据)的预测结果较差，本文分析是由于ESDD在预测前的骤降及预测中的骤升误导了参数变化趋势，而这种变化趋势可能是由无法排除的ESDD测量误差导致，这恰恰使得不考虑变化趋势的经典模型预测较准确，但这种ESDD累积规律属于特殊情况；改进模型9个预测值中有8次预测结果都比经典模型更接近实测值，说明改进模型的预测结果在一般情况下较经典模型更准确.

从图 6预测数据的评价因子均方根误差可直观地看出改进模型预测值的RMSE较原模型预测值的RMSE小(改进后模型预测结果的RMSE分别为经典模型预测结果RMSE的29.1%、62.6%、35.5%)，这再次证明改进模型相比经典模型不仅能较好地拟合绝缘子等值盐密动态累积规律，而且在预测中能降低预测误差，预测结果更加稳定.

3 结论

针对经典绝缘子等值盐密累积规律模型的优点和不足，首先通过切线型离散化的方式使模型参数动态化，然后采用四阶龙格-库塔算法对离散后的模型进行高阶迭代来抑制离散误差，同时结合实测数据利用模拟退火算法进行参数最优估计，从而得到离散的累积规律预测模型.通过来源不同、测量条件不同的ESDD实测数据验证试验，总结如下：

1) 改进模型对实测数据的拟合相关系数均高于0.97，说明该模型具有与绝缘子等值盐密动态累积规律高度一致的特性.

2) 改进模型的预测结果的绝对误差较经典模型减小了50%，说明改进模型能够对等值盐密进行更精准的预测.

3) 改进模型预测结果均方根误差RMSE较经典模型减小30%以上，表明改进模型对等值盐密的预测具备更好的稳定性.

参考文献
[1] 彭功茂, 关志成, 张福增, 等. 复合绝缘子的直流人工污秽试验方法[J]. 高电压技术, 2011(3): 570–576.
Peng G M, Guan Z C, Zhang F Z, et al. Test method of DC artificial contaminated composite insulators[J]. High Voltage Engineering, 2011(3): 570–576.
[2] 张志劲, 蒋兴良, 孙才新. 污秽绝缘子闪络特性研究现状及展望[J]. 电网技术, 2006, 30(2): 35–40.
Zhang Z J, Jiang X L, Sun C X. Present situation and prospect of research on flashover characteristics of polluted insulators[J]. Power System Technology, 2006, 30(2): 35–40.
[3] 刘兆林. 华东电网电瓷外绝缘污秽等级的划分[J]. 高电压技术, 1994, 20(3): 55–59.
Liu Z L. Ranking the contamination degree of the porcelain air-insulation in the East China Power System[J]. High Voltage Engineering, 1994, 20(3): 55–59.
[4] 王宏江. 基于SMS的低功耗高压绝缘子污秽检测装置的研究 [D]. 西安:西安理工大学, 2005.
Wang H J. Research on high voltage insulator contaminant detection equipment of low power consumption based on SMS [D]. Xi’an :Xi’an University of Technology, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10700-2005050686.htm
[5] 王华云, 万军彪, 陈智, 等. 江西省输电线路现场污秽度测量与防污闪研究[J]. 江西电力, 2009(1): 1–3.
Wang H Y, Wan J B, Chen Z, et al. Mesurement and research on transmission contaminant in Jiangxi Province[J]. Jiangxi Power System, 2009(1): 1–3.
[6] 汪涛, 欧其和, 吴江虹, 等. 用盐密指导高压输电线路清扫的试验研究[J]. 电网技术, 2004, 28(4): 22–26.
Wang T, Ou Q H, Wu J H, et al. Test and research on cleaning of high voltage transmission line based on salt density[J]. Power System Technology, 2004, 28(4): 22–26.
[7] 李德超, 张玉环, 李景禄, 等. 架空线路外绝缘污闪及其防护[J]. 绝缘材料, 2009, 42(1): 50–54.
Li D C, Zhang Y H, Li J L, et al. The pollution flashover of external overhead line insulation and anti-contamination measures[J]. Insulating Materials, 2009, 42(1): 50–54.
[8] 王自力, 张云刚. 浅析绝缘子污闪原因及预防措施[J]. 云南电力技术, 2010, 38(1): 44–45.
Wang Z L, Zhang Y G. Analysis of reason and measures of insulators’flashover[J]. Yunnan Electric Power Technology, 2010, 38(1): 44–45.
[9] Lin X, Chen Z, Liu X, et al. Natural insulator contamination test results on various shed shapes in heavy industrial contamination areas[J]. IEEE Transactions on Electrical Insulation, 1992, 27(3): 593–600. DOI:10.1109/14.142724
[10] Takasu K, Shindo T, Arai N. Natural contamination test of insulators with DC voltage energization at inland areas[J]. IEEE Transactions on Power Delivery, 1988, 3(4): 1847–1853. DOI:10.1109/61.193992
[11] Zixia C, Xidong L, Yongyong W, et al. Investigation on composite insulators in contaminated areas [C]//Proceedings of the Electrical Insulation and Dielectric Phenomena, 2002 Annual Report Conference on, 2002, IEEE.
[12] Baker A, Farzaneh M, Gorur R, et al. Insulator selection for AC overhead lines with respect to contamination[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1633–1641. DOI:10.1109/TPWRD.2009.2024666
[13] 成波, 刘新平. 华东500 kV绝缘子自然污秽试验研究[J]. 华东电力, 1996(4): 5–8.
Cheng B, Liu X P. Research on Huadong 500 kV insulator natural contaminant experinment[J]. EastChina Electric Power, 1996(4): 5–8.
[14] 胡霁, 董彦武, 陈怡, 等. 大气环境参数与电网污秽等级划分间经验算式的修正[J]. 高电压技术, 2012(3): 632–638.
Hu J, Dong Y W, Chen Y, et al. Revise of empirical formula of atmosphere environment parameter and dividing grid pollution level[J]. High Voltage Engineering, 2012(3): 632–638.
[15] Chrzan K, Abdi S, Mekhaldi A. Impact of environmental conditions in West Europe, Poland and Algeria on outdoor insulators performance and selection [C]//Proceedings of the International Symposium on High Voltage Engineering, Ljubljana, Slovenia, 2007.
[16] 詹清华, 阮江军, 钟连宏. 珠三角地区架空线路绝缘子的自然积污特性[J]. 高电压技术, 2010(11): 2662–2667.
Zhan Q H, Ruan J J, Zhang L H. Natural contamination of Pearl River delta region overhead transmission line insulators[J]. High Voltage Engineering, 2010(11): 2662–2667.
[17] 钱之银, 肖嵘. 华东电网500 kV线路绝缘子人工和自然积污比较[J]. 高电压技术, 2010(3): 705–710.
Qian Z Y, Xiao R. Comparison between artificial pollution and nature pollution of 500 kV transmission line insulators in East China Grid[J]. High Voltage Engineering, 2010(3): 705–710.
[18] 王少华, 方玉群, 胡旭光, 等. 自然积污绝缘子等值盐密的累积规律[J]. 绝缘材料, 2011(4): 52–54.
Wang S H, Fang Y Q, Hu X G, et al. Accumulation rule of ESDD of insulators covered with natural pollution[J]. Insulating Materials, 2011(4): 52–54.
[19] 李恒真, 刘刚, 李立涅. 广州地区线路盘式防污型玻璃绝缘子的自然积污规律[J]. 中国电机工程学报, 2011, 31(25): 118–124.
Li H Z, Liu G, Li L N. Natural contamination deposit law of line disc anti-contamination glass insulator in Guangzhou area[J]. Proceedings of the CSEE, 2011, 31(25): 118–124.
[20] Kirkpatrick S, Gelatt C D, Vecchi M P. Optimization by simmulated annealing[J]. Science, 1983, 220(4598): 671–680. DOI:10.1126/science.220.4598.671
[21] B Lte A, Thonemann U W. Optimizing simulated annealing schedules with genetic programming[J]. European Journal of Operational Research, 1996, 92(2): 402–416. DOI:10.1016/0377-2217(94)00350-5
[22] 庞峰. 模拟退火算法的原理及算法在优化问题上的应用 [D] . 长春: 吉林大学, 2006.
Pang F. The principle of SA algorithm and algorithm’s application on optimization problem [D]. Changchun:University of Jilin, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10183-2007017704.htm