武汉大学学报(工学版)   2016, Vol. 49 Issue (6): 955-960

文章信息

陈正, 张小轩, 李慧敏, 张世荣
CHEN Zheng, ZHANG Xiaoxuan, LI Huimin, ZHANG Shirong
基于PSO的最小二乘支持向量机稀疏化算法
Optimal sparseness approach for least square support vector machine based on PSO
武汉大学学报(工学版), 2016, 49(6): 955-960
Engineering Journal of Wuhan University, 2016, 49(6): 955-960
http://dx.doi.org/10.14188/j.1671-8844.2016-06-026

文章历史

收稿日期: 2016-04-15
 Abstract              PDF               Figures               Tables
引用本文 0
陈正, 张小轩, 李慧敏, 张世荣. 基于PSO的最小二乘支持向量机稀疏化算法[J]. 武汉大学学报(工学版), 2016, 49(6): 955-960.
CHEN Zheng, ZHANG Xiaoxuan, LI Huimin, ZHANG Shirong. Optimal sparseness approach for least square support vector machine based on PSO[J]. Engineering Journal of Wuhan University, 2016, 49(6): 955-960.
基于PSO的最小二乘支持向量机稀疏化算法
陈正, 张小轩, 李慧敏, 张世荣     
武汉大学动力与机械学院，湖北 武汉 430072
收稿日期: 2016-04-15
作者简介: 陈正(1971-)，男，博士，从事复杂工业系统能效优化方面研究，E-mail: zchen@whu.edu.cn.
基金项目: 国家自然科学基金资助项目(编号：51475337)；湖北省自然科学基金资助项目(编号：2011CDB277).
摘要: 针对最小二乘支持向量机(LSSVM)失去稀疏特性及经典迭代剪切稀疏化算法容易陷入性能指标函数局部收敛的问题，提出一种基于粒子群优化(PSO)的LSSVM稀疏化算法.将LSSVM稀疏化过程描述为一个最优化问题，以校验样本和预测输出之间的均方根误差RMSE为优化目标，以模型训练样本剪切率ε(%)为优化变量.并针对此非线性优化问题提出基于PSO的求解方法.以大型电厂飞灰含碳量LSSVM模型为例，对此算法进行了实例研究.结果表明，该方法能有效解决经典算法的局部收敛问题获得最优剪切率，具有更好的预测和泛化能力.
关键词： 最小二乘支持向量机     最优稀疏化     粒子群优化算法     局部收敛    
Optimal sparseness approach for least square support vector machine based on PSO
CHEN Zheng, ZHANG Xiaoxuan, LI Huimin, ZHANG Shirong     
School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072,China
Abstract: In term of the lack of sparseness of the least square support vector machine (LSSVM), some classic pruning methods are successively proposed. However, the local convergence characteristic of the performance index may hinder the classical methods to get an optimal pruning rate of the training data set. This paper proposes a particle swarm optimization (PSO) based optimal sparseness approach for LSSVM models. The new approach firstly formulates the sparseness of LSSVM as a general optimization problem, where root-mean-square error (RMSE) between predicted values and real values is taken as an objective function for minimization; and then the pruning rate is employed as optimization variable, PSO is further proposed to solve this nonlinear optimization problem. A LSSVM model of carbon content in fly ash is taken as a case study. The operation data of a large-scale coal-fired power plant is collected for comparative investigation. The results show that the newly proposed approach has the ability to conquer the local convergence problem; and consequently an optimal pruning rate of the training data set is obtained. Compared with the classic methods, the new approach is better both in prediction performance and generalization performance.
Key words: least square support vector machine (LSSVM)     optimal sparseness     particle swarm optimization (PSO)     local convergence    

支持向量机(SVM)是Vapnik等人提出的一种机器学习方法[1]，在国内外学术界受到广泛重视，尤其在模式识别和函数估计方面获得广泛应用[2-4].SVM建模过程需要求解一个受不等式约束的二次型规划问题，计算过程较复杂.为了减少支持向量机的计算复杂度，Suykens提出了最小二乘支持向量机(LSSVM)，把支持向量机的学习问题转化为解线性方程组问题，具有更快的运算速度[5].其负面作用是使得LSSVM的支持向量值与误差成正比，即α=γe(γ为LSSVM模型目标函数的惩罚系数).这样一来，所有的样本均成为支持向量，导致LSSVM失去稀疏特性，模型变得“臃肿”，影响预测计算速度.因此，对模型进行稀疏化处理是LSSVM工程应用中的关键环节.

Suykens提出了一种经典的LSSVM稀疏算法[6]，该方法对样本的|αi|进行排序，并删除具有较小|ai|的样本来实现模型稀疏化.文献[7]则通过删除最小引入误差的样本来获得稀疏性.文献[8-10]将这种传统的方法运用到了实际工程和后续研究中.在文献[11]中提出了加权稀疏化方法，基本思想是为误差加上一个权重，再对该误差对应的|αi|进行排序，继而剪切样本.文献[12]利用分类矩阵K的相关成分d对α进行计算，并利用迭代方法将重要的α所对应样本保留.以上稀疏化过程实质上是一个迭代过程，若性能指标为非单调函数，当性能指标开始劣化时，迭代过程就立即停止，并将当前结果当作模型稀疏化的最终结果，致使模型的性能指标陷入局部收敛，无法获得性能的全局最优值.文献[13]表明经典稀疏化算法在LSSVM短期负荷预测中应用较好，但稀疏化过程的局部收敛问题导致长期预测结果不令人满意；文献[14, 15]使用矩阵递归建立了新的稀疏化方法，简化了LSSVM模型建模过程，但其稀疏化原理依然借鉴传统算法，易陷入局部收敛.

本文将LSSVM稀疏过程建立为一个最优化问题，并利用粒子群优化算法(Particle Swarm Optimization-PSO)实现全局寻优，能突破经典算法易于局部收敛的局限，具有更好的性能,并以火电厂飞灰含碳量LSSVM模型为例，对本文提出的方法进行验证.

1 LSSVM及其稀疏性

根据SVM理论，非线性函数φ(·)将输入空间Rn映射到一个特征空间Z，并采用如下形式函数对未知函数进行预估[1]：

${y_{\rm{t}}}({\bf{x}}) = {{\bf{\omega }}^T}\varphi ({\bf{x}}) + b$    (1)

式中：x为输入向量；向量ω和偏置b为待求参数；yt为预测输出.LSSVM是SVM的一种拓展，它将SVM优化问题的不等式约束改进为等式约束，并用误差平方代替松弛变量，由式(1)得LSSVM回归优化问题为

$\left\{ {\begin{array}{*{20}{l}} {\min J({\bf{\omega }},{\bf{e}}) = \frac{1}{2}{{\bf{\omega }}^T}{\bf{\omega }} + \gamma \frac{1}{2}\sum\limits_i^N {e_k^2} }\\ {s.t.}\\ {{y_k} = {{\bf{\omega }}^T}\varphi ({{\bf{x}}_k}) + b + {e_k}} \end{array}} \right.$    (2)

式中:e=[e1 e2…eN],为预测输出与真实输出间的误差变量;γ为惩罚系数.为求解该优化问题，定义拉格朗日函数：

$\begin{array}{l} L({\bf{\omega }},b,{\bf{e}},{\bf{\alpha }}) = J({\bf{\omega }},{\bf{e}}) - \\ \sum\limits_{k = 1}^N {{\alpha _k}} \left\{ {{{\bf{\omega }}^T}\varphi ({{\bf{x}}_k}) + b + {e_k} - {y_k}} \right\} \end{array}$    (3)

式中：α=[α1 α2…αn]，为拉格朗日乘子.根据KKT条件，分别求出L(ω,b,e,α)对ω、b、e、α的偏导，得式(2)的最优条件如下：

$\left\{ \begin{array}{l} \frac{{dL}}{{d{\bf{\omega }}}} = 0 \to {\bf{\omega }} = \sum\limits_{k = 1}^N {{\alpha _k}\varphi ({{\bf{x}}_k})} \\ \frac{{dL}}{{db}} \to \sum\limits_{k = 1}^N {{\alpha _k} = 0} \\ \frac{{dL}}{{d{e_k}}} = 0 \to {\alpha _k} = \gamma {e_k}\\ \frac{{dL}}{{d{\alpha _k}}} = 0 \to {{\bf{\omega }}^T}\varphi ({{\bf{x}}_k}) + b + {e_k} - {y_k} = 0 \end{array} \right.$    (4)

消去式(4)中的ω和ek，得如下线性系统：

$\left[ {\begin{array}{*{20}{c}} 0&{{E^T}}\\ E&{\Omega + {\gamma ^{ - 1}}I} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} b\\ {\bf{\alpha }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ {\bf{y}} \end{array}} \right]$    (5)

式中:y=[y1 y2…yN]T;E=[1…1]1×NT；I为相应维数的单位矩阵;

$\begin{array}{l} \Omega :{\Omega _{kd}} = \varphi {({x_k})^T}\varphi ({x_k}) = K({{\bf{x}}_k},{{\bf{x}}_d})\\ k,d = 1,...N \end{array}$    (6)

式中:k(xk,xd)为核函数，实现原输入空间Rn非线性问题到高维再生核特征空间Z的线性问题的转换.令U=(Ω+γ-1I)-1，根据式(5)可得：

$b = \frac{{{E^T}U{\bf{y}}}}{{{E^T}UE}}$    (7)
${\bf{\alpha }} = U\left( {{\bf{y}} - \frac{{E{E^T}U{\bf{y}}}}{{{E^T}UE}}} \right)$    (8)

从而，LSSVM的预测模型可以表示为

${y_{\rm{t}}}({\bf{x}}) = \sum\limits_{k = 1}^N {{\alpha _k}K({\bf{x}},{{\bf{x}}_k}) + b} $    (9)

式中：αk为对应用样本的支持值.由式(4)可知αk=γek，一般有ek≠0,故αk=0，即所有训练样本成为支持向量，LSSVM失去了稀疏性.且式(9)表明，|αi|值越大，对预测的贡献越大[16]，反之则越小.当训练数据量较大时，模型维数高，在线预测计算量会急剧增大，故必须对LSSVM模型进行稀疏化处理.

2 基于PSO的LSSVM稀疏化方法 2.1 经典LSSVM稀疏化方法

为了解决LSSVM丢失稀疏性的问题，Suykens提出了一种简单的稀疏化算法，以迭代的形式每次删除具有较小|αi|的训练样本(例如，5%)，重新训练LSSVM模型，并用校验样本计算模型的整体性能指标以判断是否停止迭代.

定义模型训练样本为{xk,yk}k=1N，校验样本为{x′k,y′k}k=1Z,xk∈Rn,yk∈R.取校验样本输出与LSSVM预测输出的均方根误差RMSE为性能指标：

$RMSE=\sqrt{\frac{1}{Z}\sum\limits_{i=1}^{Z}{{}}{{(y_{ti}^{'}-y_{i}^{'})}^{2}}}$    (10)

式中:y′ti为LSSVM模型预测输出；y′i为校验样本的输出采样值.经典剪切算法的步骤如下：

1) 初始化核函数K(xi,xj)及惩罚系数γ；

2) 以训练样本集{(xk,yk)}k=1N训练LSSVM模型获得{αk}k=1N和b，并根据校验样本集计算初始性能指标RMSE；

3) 将当前LSSVM模型对应的支持值的绝对值|αk|排序，剪切5%具有最小|αk|的训练样本，形成新的训练样本集并再次训练LSSVM模型，计算新的性能指标RMSE′；

4) 将RMSE′与前一次剪切获得的性能指标RMSE对比：

$\left\{ \begin{array}{l} RMSE′≤RMSE，转步骤(3)\\ RMSE′>RMSE，结束 \end{array} \right.$

显然，这种经典稀疏化算法在性能RMSE劣化时(RMSE′>RMSE)停止迭代，若性能指标为非单调函数，会使目标函数陷入局部收敛，无法获得最佳剪切率.

2.2 LSSVM的最优稀疏化

为解决经典稀疏化算法存在的弊端，将LSSVM稀疏化问题转化为一个最优化问题.本优化问题将训练样本的剪切率ε作为优化变量，并将校验样本输出与模型预测输出的均方根误差作为优化目标.寻优过程为：根据训练样本所对应的|α|将训练样本重新排列，切除ε%的具有较小|α|那部分样本，再利用剩下的样本重新训练LSSVM模型，计算其性能指标，寻找使性能指标最优的剪切率.

LSSVM最优稀疏化问题可以写为

$\begin{align} & \min RMSE(\varepsilon )=\sqrt{\frac{1}{Z}\sum\limits_{i=1}^{Z}{{{(\sum\limits_{k=1}^{{{N}^{\varepsilon }}}{\alpha _{k}^{\varepsilon }}K({{x}_{i}},{{x}_{k}})+{{b}^{\varepsilon }}-y_{i}^{'})}^{2}}}} \\ & \begin{matrix} subject & to \\ \end{matrix} \\ & {{\mathbf{\alpha }}^{\varepsilon }}={{U}_{\varepsilon }}\left( {{\mathbf{y}}^{\varepsilon }}-\frac{{{E}_{\varepsilon }}{{E}_{\varepsilon }}^{\text{T}}{{U}_{\varepsilon }}{{\mathbf{y}}^{\varepsilon }}}{{{E}_{\varepsilon }}^{\text{T}}{{U}_{\varepsilon }}{{E}_{\varepsilon }}} \right) \\ & {{b}^{\varepsilon }}=\frac{{{E}_{\varepsilon }}^{\text{T}}{{U}_{\varepsilon }}{{\mathbf{y}}^{\varepsilon }}}{{{E}_{\varepsilon }}^{\text{T}}{{U}_{\varepsilon }}{{E}_{\varepsilon }}} \\ & {{N}^{\varepsilon }}=(1-\varepsilon )N \\ \end{align}$    (11)

式中：yk=1ε为将原始训练样本xk,ykN剪切ε(%)样本后形成的新训练样本集的输出；Uε和Eε为与yε对应的矩阵U和E；y′i为预测样本集的实际输出；N为初始训练样本总数.该问题的最优解ε*为使性能指标RMSE取最小值的最优样本剪切率.

2.3 基于PSO的LSSVM稀疏化

最优化问题(11)为复杂非线性问题，采用常规优化方法难以求解，本文拟采用PSO进行智能寻优.PSO算法是一种基于种群的随机优化技术，由Eberhart和Kennedy于1995年提出[17].设D维空间中m个粒子组成一个群体，每个粒子都有其位置xi=(xi1,xi2,…,xiD)(i=1,2，…，m)和飞行速度vi=(vi1,vi2,…,viD)，根据各粒子的适应度值，找到每个粒子的个体最优位置Pbest=(pi1,pi2,…,piD)，即个体极值，和所有粒子当前的全局最佳位置Gbest=(g1,g2,…,gD)，即全局极值.每个粒子根据下式更新粒子的速度和位置：

$\begin{array}{l} v_{id}^{k + 1} = wv_{id}^k + {c_1}{r_1}(p_{id}^k - x_{id}^k) + \\ {\kern 1pt} {c_2}{r_2}(g_d^k - x_{id}^k) \end{array}$    (12)
$x_{id}^{k + 1} = x_{id}^k + v_{id}^{k + 1}$    (13)

式中:d=1,2，…，D;k为迭代次数；c1和c2为加速度常数；w为惯性权重系数；r1和r2是(0,1)之间的随机数;vidk+1和xidk+1分别为第k+1次迭代粒子i速度向量和位置向量的第d维分量;pidk和gdk分别为第k次迭代粒子i最优位置和所有粒子最优位置的第d维分量.

PSO突破了搜索过程中函数单调性的限制，能实现全局寻优，针对式(11)的优化问题，设定各粒子位置为εi，其适应度值为RMSE(εi).算法步骤如下：

1) 确定训练样本{(xk,yk)}k=1N和校验样本；核函数K(xi,xj)及惩罚因子γ;

2) 训练获得初始LSSVM模型及支持向量值{αk}k=1N;

3) 设定PSO寻优最大迭代数Max和粒子总数m；对RMSE(ε)进行PSO寻优，搜索出最佳的ε值；

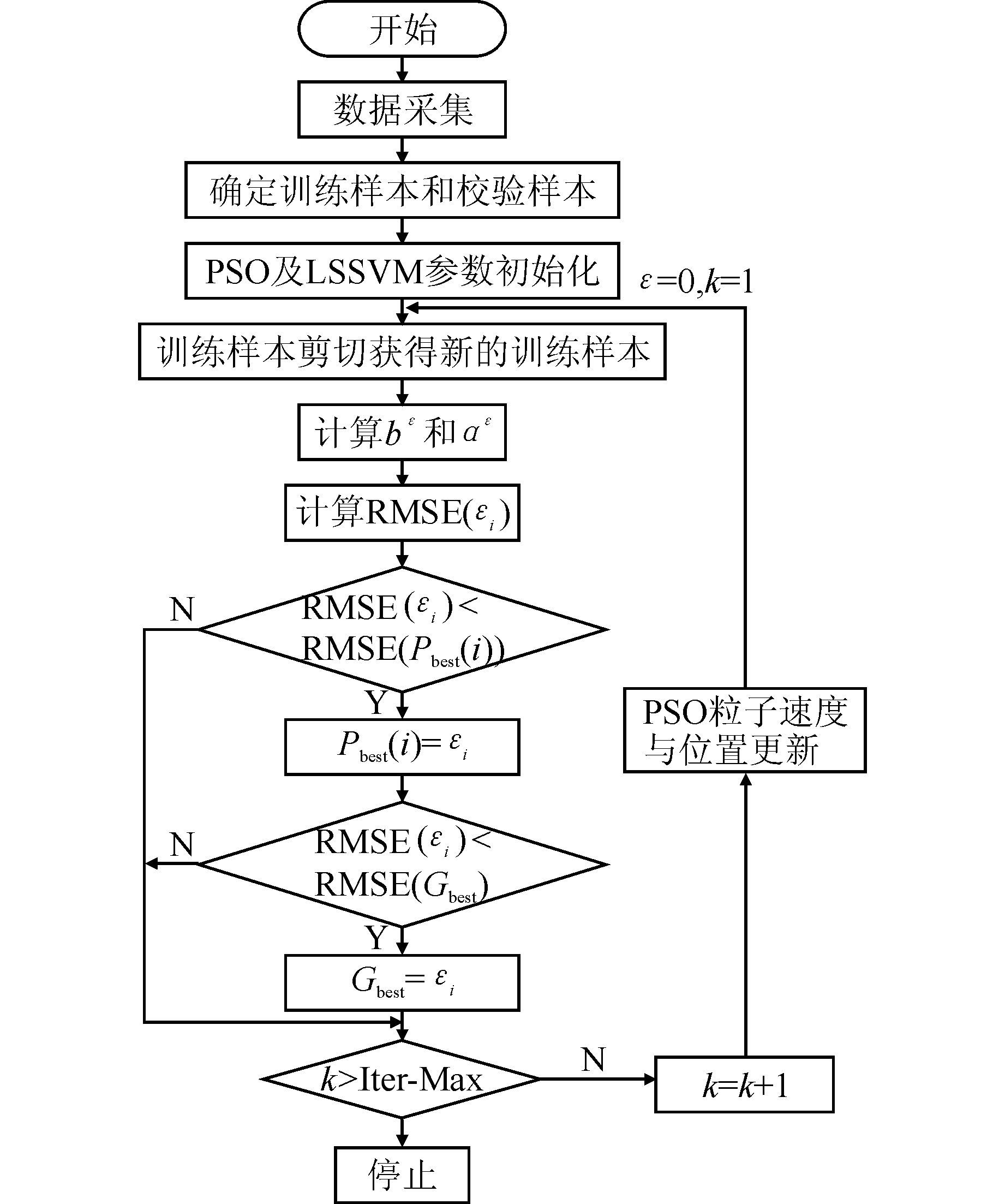
4) 输出寻优结果ε、稀疏化后的训练样本{(xiε,yjε)}i=1Nε以及LSSVM回归模型.算法框架如图 1所示.

图 1 基于PSO的稀疏化算法框架 Figure 1 Flow chart of optimal sparseness approach based on PSO
图选项
3 仿真与结果 3.1 锅炉飞灰含碳量的LSSVM模型

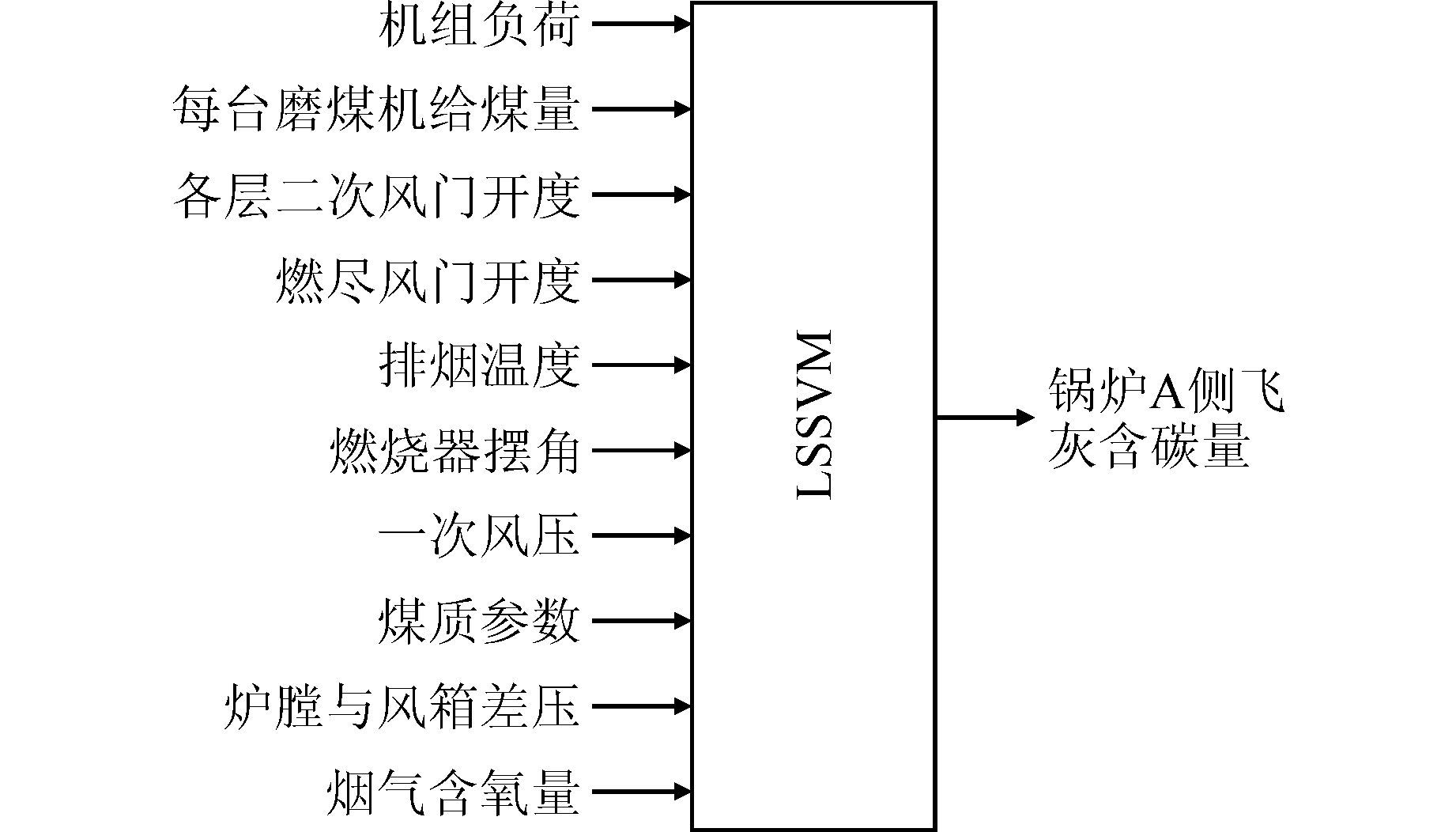
飞灰含碳量是影响锅炉效率的关键因素之一，也是锅炉燃烧优化调整的重点目标，但由于燃烧过程的复杂性，无法建立其机理模型，故本文基于LSSVM建立飞灰含碳量的学习模型.本文的研究对象为广东某电厂600 MW机组，锅炉采用四角切圆燃烧器组织形式.其飞灰含碳量LSSVM模型的输入量x：机组负荷、每台磨对应的给煤量、各层二次风门开度、燃尽风开度、排烟温度、燃烧器摆角、煤质参数(包括发热量、挥发分、灰分和水分等)、炉膛与风箱差压、烟气含氧量、一次风压；输出量y：锅炉A侧飞灰含碳量.模型结构如图 2所示，为了建模研究，从该厂SIS系统收集了从2013年6月30日00点至8月30日00点的相关运行数据，采样周期为5 min，共计17 659组数据.

图 2 飞灰含碳量LSSVM模型 Figure 2 Model structure of LSSVM model of carbon content in fly ash
图选项
3.2 仿真结果分析

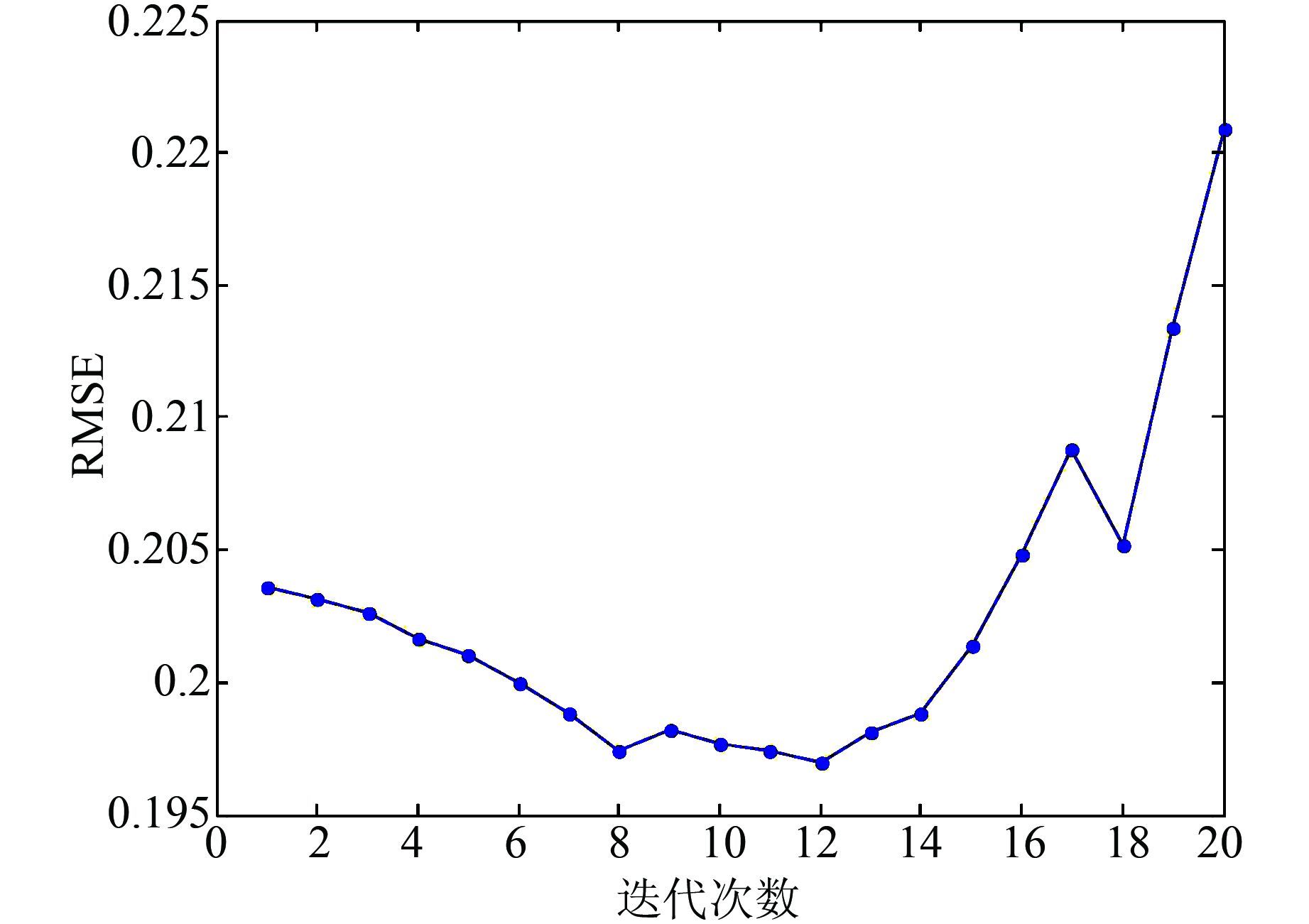
为了研究性能函数的特征，随机从采样数据中取1 200组数据当训练样本，另外200组数据作校验样本.首先，按照Suykens经典稀疏化方法将剪切率固定为5%，进行了20次迭代，性能如图 3所示.

图 3 性能指标与迭代次数关系 Figure 3 Relationship between RMSE and iterations
图选项

从图 3中可以看出，当迭代8次时性能函数出现第一个局部最优点，在第12次达到全局最优.若按照经典算法的结束准则，此稀疏化迭代过程将停止于第8次迭代，输出第一个局部最优解.可见，针对图 3所示非单调性能指标，经典稀疏化算法无法获得最优剪切率.

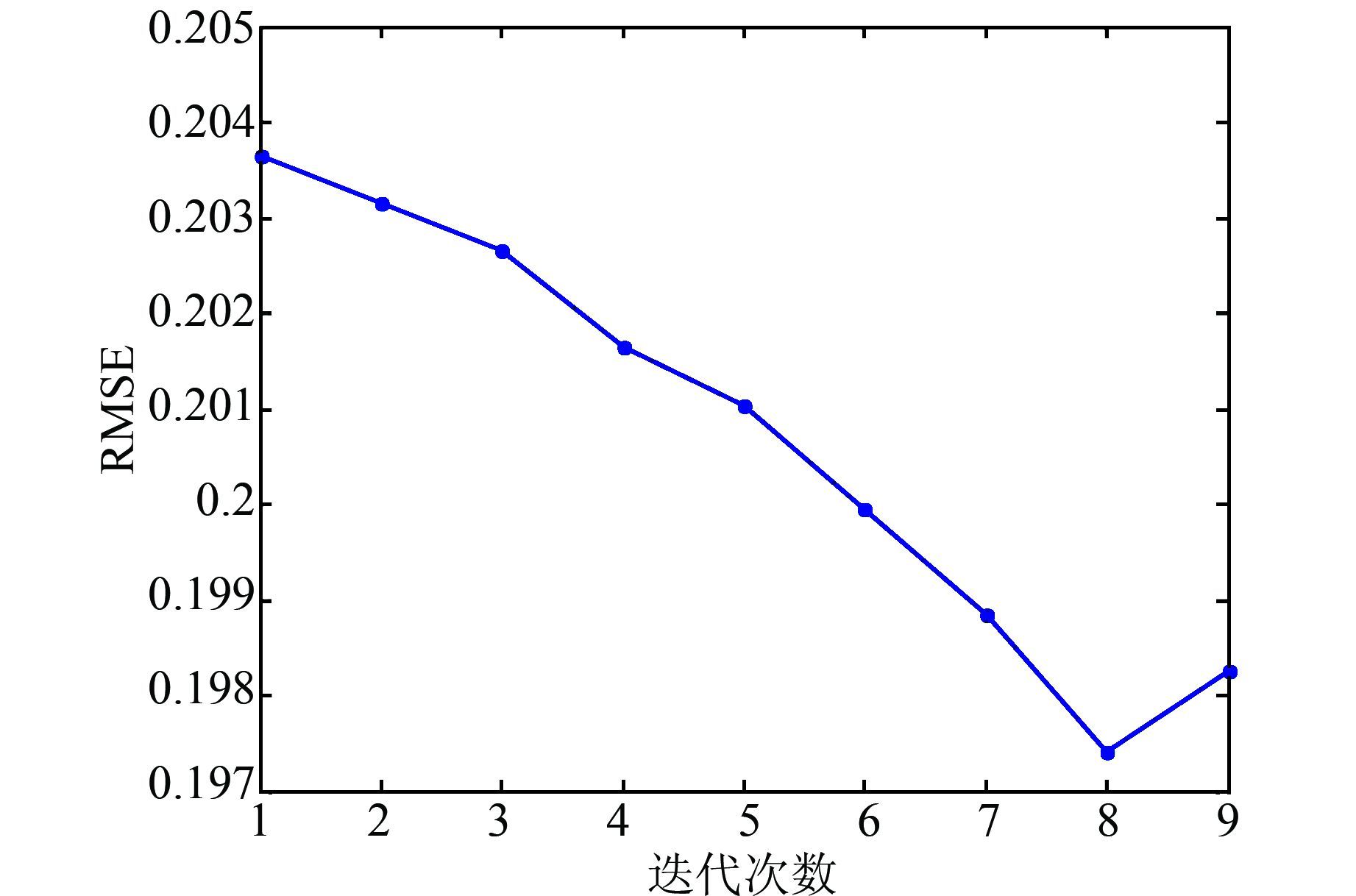
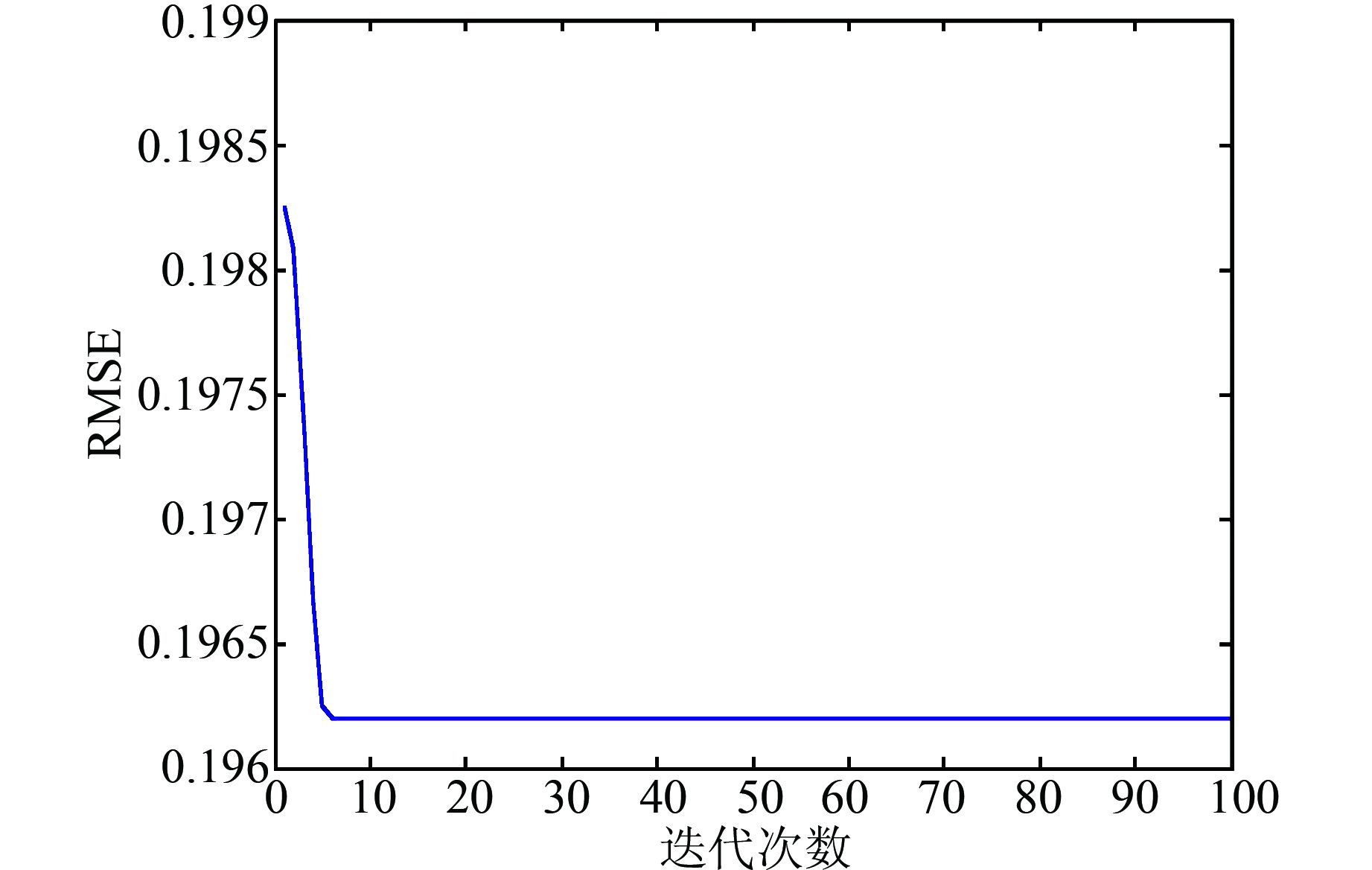
为了对该种算法进行对比研究，我们对相同的训练样本集合校验样本集分别采用两种算法进行稀疏化.利用以上样本，设定LSSVM的参数为γ=9.500，RBF核函数系数σ2=1.2679.经典算法和基于PSO的稀疏化算法的性能指标的变化分别如图 4和图 5所示.经典稀疏化算法，迭代9次后算法停止，第8次为最终结果，得到性能指标RMSE=0.197 4，裁剪率ε=33.58%；基于PSO的稀疏化算法能得到性能指标RMSE=0.196 2，裁剪率ε=36.35%.相比而言，最优稀疏化方法利用PSO的全局寻优能力获取最小RMSE，且剪切率更大.

图 4 经典稀疏化方法 Figure 4 Classic pruning method
图选项
图 5 基于PSO的稀疏化方法 Figure 5 Optimal sparseness approach based on PSO
图选项

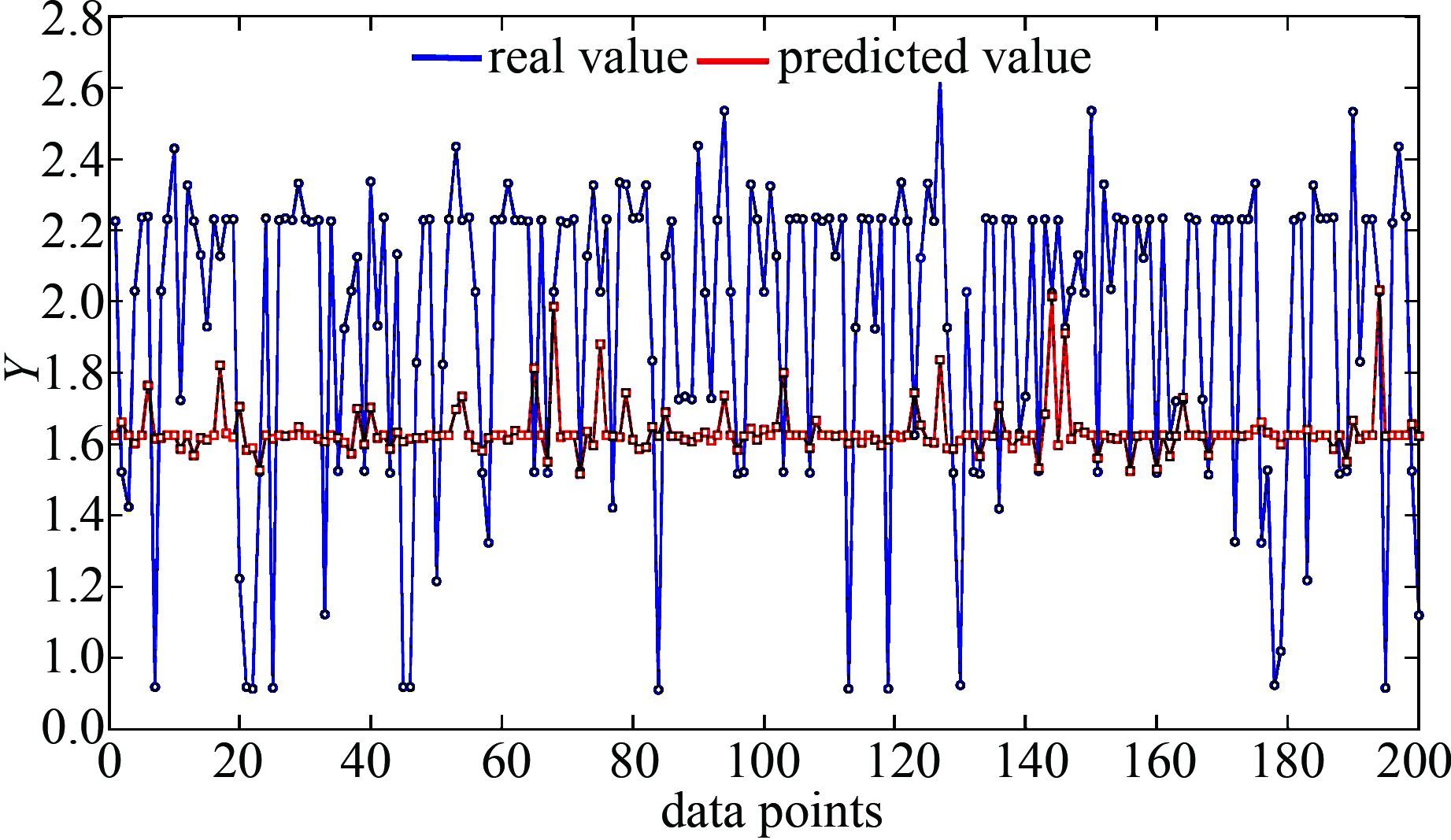
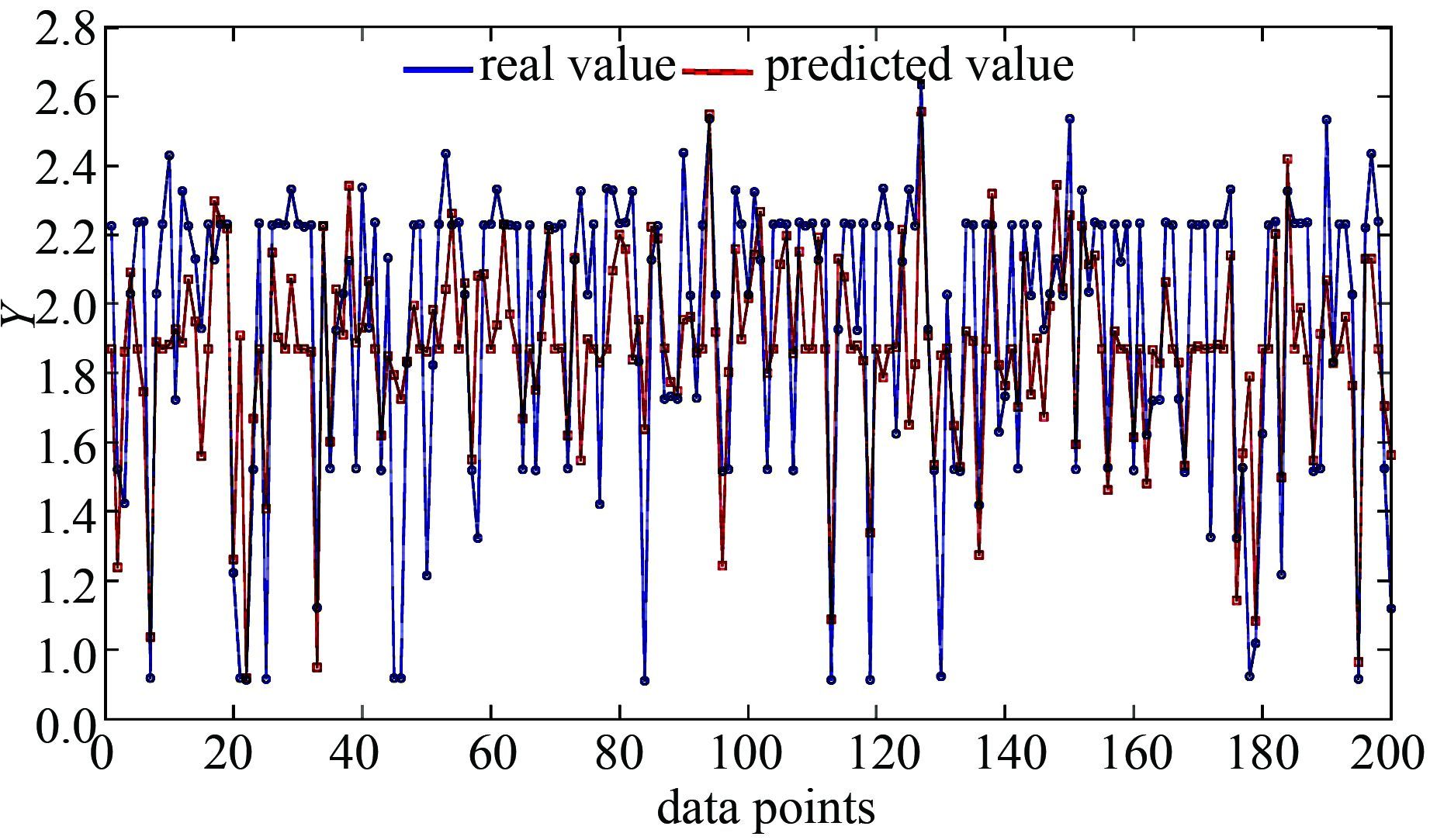
最后，从样本数据中随机取200组用于模型的泛化能力测试.采用经典方法稀疏化的模型预测结果如图 6所示，而采用优化方法的模型预测结果如图 7所示.可见新的稀疏化方法同时确保了较好的泛化能力.具体而言，图 6中采样值和预测值的RMSE=0.5221，而图 7中RMSE=0.316 8.为进一步验证此方法的鲁棒性，按照前续方法随机取训练样本和校验样本，重复以上过程，各指标参数如表 1所示.

图 6 经典稀疏化算法模型泛化性能 Figure 6 Generalization ability of classic pruning method
图选项
图 7 基于PSO改进的LSSVM模型泛化性能 Figure 7 Generalization ability optimal LSSVM model based on PSO
图选项
表 1 经典方法和PSO方法参数对比 Table 1 Comparison of performance parameters between classical and PSO based approaches
实验序号 剪切算法 校验样本RMSE ε/% 泛化样本RMSE
1 经典 0.197 4 33.58 0.522 1
PSO 0.196 2 36.35 0.316 8
2 经典 0.198 8 33.58 0.553 0
PSO 0.198 3 35.55 0.312 2
3 经典 0.210 5 30.09 0.555 6
PSO 0.202 2 35.12 0.420 0
表选项

表 1表明，基于PSO的方法在各种算例中都优于经典稀疏化方法.

4 结论

LSSVM是SVM的一种扩展，通过简化运算提升了在线性能.然而，LSSVM丢失了稀疏性，导致模型高维数问题.稀疏化是LSSVM模型的关键环节，本文在经典剪切算法基础上提出一种基于PSO的LSSVM稀疏化算法，将LSSVM的稀疏化演变为最优化问题，并提出了基于PSO的解法，以大型电厂飞灰含碳量LSSVM模型进行了验证，结果表明，基于PSO的最优稀疏化方法能获取最佳剪切率，得到的LSSVM模型预测性能和泛化性能更优，有效地解决了经典算法易陷入性能函数局部收敛的问题.

参考文献
[1] Vapnik V N. The Nature of Statistical Learning Theory[M]. New York: Springer-Verlag, 1995.
[2] Cherkassky V, Mulier F. Learning from Data—Concepts, Theory and Methods[M]. New York: John Wiley Sons, 1998.
[3] Joachims T, Text categorization with support vector machines: Learning with many relevant features[C]// Proceedings of the European Conference on Machine Learning, 1998: 137-142.
[4] Guyon I, Weston J, Barnhill S. Gene selection for cancer classification using support vector machines[J]. Machine Learning, 2002, 46(1): 389–422.
[5] Suykens J A K, Vandewale J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293–300. DOI:10.1023/A:1018628609742
[6] J A K, Suykens J. De Brabanter L Luckas, et al. Weighted least squares support vector machines: robustness and sparse approximation[J]. Neuro-computing, 2002 , 48 ( 4) : 85-105.
[7] De Kruif B J, DeVries T J A. Pruning error minimiza tion in least squares support vector machines[J]. IEEE Transactions on Neural Networks, 2003, 14(3): 696–702. DOI:10.1109/TNN.2003.810597
[8] 赵永平, 孙建国. 关于稀疏最小二乘支持向量回归机的改进剪枝算法[J]. 系统工程理论与实践, 2009, 29(6): 166–171.
Zhao Yongping, Sun Jianguo. Improved pruning algorithms for sparse least squares support vector regression machine[J]. Systems Engineering—Theory & Practice, 2009, 29(6): 166–171.
[9] 李丽娟. 最小二乘支持向量机建模及预测控制算法研究[D]. 杭州:浙江大学, 2008.
Li Lijuan. The study of modeling algorithm based on LS-SVM and predictive control algorithm[D]. Hangzhou:Zhejiang University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10335-2009057417.htm
[10] 王定成, 姜斌. 在线稀疏最小二乘支持向量机回归的研究[J]. 控制与决策, 2007, 22(2): 132–139.
Wang Dingcheng, Jian Bin. Online sparse least square support vector machines regression[J]. Control and Decision, 2007, 22(2): 132–139.
[11] 司刚全, 曹晖, 张彦斌, 等. 一种基于密度加权的最小二乘支持向量机稀疏化算法[J]. 西安交通大学学报, 2009, 43(10): 11–17.
Si Gangquan, Cao Hui, Zhang Yanbin, et al. Density weighted pruning method for sparse least squares support vector machines[J]. Journal of Xi’an Jiaotong University, 2009, 43(10): 11–17.
[12] 陶少辉, 陈德钊, 胡望明. 基于CCA对LSSVM分类器的稀疏化[J]. 浙江大学学报(工学版), 2007, 41(7): 1093–1096.
Tao Shaohui, Chen Dezhao, Hu Wangming. CCAsparse least squares support vector machine classifiers[J]. Journal of Zhejiang University(Engineering Science), 2007, 41(7): 1093–1096.
[13] 刘耀年, 沈轶群, 姜成元, 等. 基于LSSVM 与SMO 稀疏化算法的短期负荷预测[J]. 继电器, 2008, 16(3): 63–66.
Liu Yaonian, Shen Yiqun, Jian Chengyuan, et al. A short-term load forecasting approach based on imposing sparseness upon LSSVM integrated SMO algorithms[J]. RELAY, 2008, 16(3): 63–66.
[14] 甘良志, 孙宗海, 孙优贤. 稀疏最小二乘支持向量机[J]. 浙江大学学报(工学版), 2007, 41(2): 245–248.
Gan Liangzhi, Sun Zonghai, Sun Youxian. Sparse least squares support vector machine[J]. Journal of Zhejiang University(Engineering Science), 2007, 41(2): 245–248.
[15] 周欣然, 滕召胜, 易钊. 构造稀疏最小二乘支持向量机的快速剪枝算法[J]. 电机与控制学报, 2009, 13(4): 626–630.
Zhou Xinran, Teng Zhaosheng, Yi Zhao. Fast pruning algorithm for designing sparse least squares support vector machine[J]. Eelectric Machines and Control, 2009, 13(4): 626–630.
[16] Suykens J A K, Lukas L ,Vandewalle J. Sparse least squares support vector machine classifier[C]// European Symposium On Artificial Neural Networks, Bruges, Belgium, 2000-04 : 37-42.
[17] James Kennedy, Russell Eberhart. Particle swarm optimization[C]// IEEE Machine and Human Science, 1995:39-43.