文章信息
- 刘文黎, 吴贤国, 覃亚伟, 沈梅芳, 腾佳颖
- LIU Wenli, WU Xianguo, QIN Yawei, SHEN Meifang, TENG Jiaying
- 基于支持向量机代理模型的地铁施工诱发临近建筑扰动的参数全局敏感性分析
- A global sensitivity analysis of building movements induced by tunnel excavating based on PSO-LSSVM meta-model
- 武汉大学学报(工学版), 2016, 49(6): 871-878
- Engineering Journal of Wuhan University, 2016, 49(6): 871-878
- http://dx.doi.org/10.14188/j.1671-8844.2016-06-013
-
文章历史
- 收稿日期: 2016-05-23
2. 吉林建筑大学经济与管理学院,吉林 长春 130118
2. School of Economic and Management, Jilin Jianzhu University, Changchun 130021, China
地铁隧道施工会引起周围的环境扰动,进而影响周围的临近构筑物(建筑、公路、桥梁等)的安全,而地铁隧道施工的本体以及周围临近构筑物的安全是一个地铁工程项目安全风险管理工作的重点[1].为了保证地铁施工的安全,隧道施工中需要对一些参数(如盾构推进压力、地表土体加固范围等)进行精确的调整和控制,为了保证这些控制措施的有效性,减少保护措施的经济代价,需要大量的有关隧道施工对周围环境扰动影响的经验知识.由于地铁隧道施工环境的复杂性和特殊性,目前有关隧道施工对周围环境扰动影响的经验知识相当有限,存在因知识不足而出现的认知不确定性,对隧道施工的安全风险管理非常不利.
隧道、土体和建筑之间存在复杂的相互影响过程,很难严格而精准地描述这三者之间的相互作用关系[2].一些文章研究将经验分析法和数值仿真结合起来,预测地铁施工诱发周围建筑物沉降值[3].Miro S和 Mollon G等[4, 5]分析了隧道开挖对周围土体沉降影响的各参数敏感度.吴贤国等[6]提出了地铁施工邻近建筑物安全风险等级划分方法和标准.目前在国内外研究中,隧道施工对周围建筑影响的参数敏感性分析的文献很少,导致在对工程安全评价时存在因知识不全而产生的认知不确定性.
为研究地铁施工对周围建筑的影响,本文以武汉地铁二号线越江段为研究背景,分析了地铁施工对周围的几栋建筑物的影响规律,采用随机有限元法构建了隧道及周围建筑的精准数值仿真模型,得到了180组精确的有限元模拟数据;采用支持向量机(support vector machine)构建了基于原始随机有限元的代理模型,得到有10 000组数据的数据集;利用傅里叶幅度灵敏度检验扩展法(extended Fourier amplitude sensitivity test)对10 000组数据进行全局敏感性分析,得到了各个参数的全局敏感度大小.
1 方法 1.1 随机有限元传统有限元法主要关注确定性问题的求解,但是岩土工程中存在多重不确定性因素[7],如土质参数的不确定性、荷载不确定性以及计算模型不确定性等.为了描述这些不确定性问题,提出了随机有限元法,综合考虑材料性能的分散性、载荷的随机性以及其他不确定性特征,更适合于不确定性和随机性模型的求解.
随机有限元法(SFEM)是计算随机力学的一个重要分支,将随机分析理论与有限元方法相结合,在传统的有限元方法基础上发展出一种随机的数值分析方法,既可以处理结构参数随机问题,也可以处理系统输入随机问题.随机有限元法的目的可归结为3点[8]: 求解在随机因素影响下结构的随机响应、计算结构的可靠度和获得结构安全性对设计参数的敏感性(灵敏度).本文将采用随机有限元法对隧道施工诱发周围建筑安全风险的各参数的敏感度进行分析.
1.2 支持向量机支持向量机算法主要用于解决模式识别问题和函数拟合问题[9],基本思想是通过用内积函数定义的非线性变换将输入空间变换到一个高维空间,在这个高维空间中寻找输入变量和输出变量之间的一种非线性关系.本文主要运用SVM进行数据的函数拟合.
本文基于支持向量机的基本分析流程,根据选取的RBF(radial basis function)核函数,采用PSO算法对SVM中的相关参数(C,g)进行优化选取,得到改进SVM预测模型的建模流程具体步骤,如图 1所示.
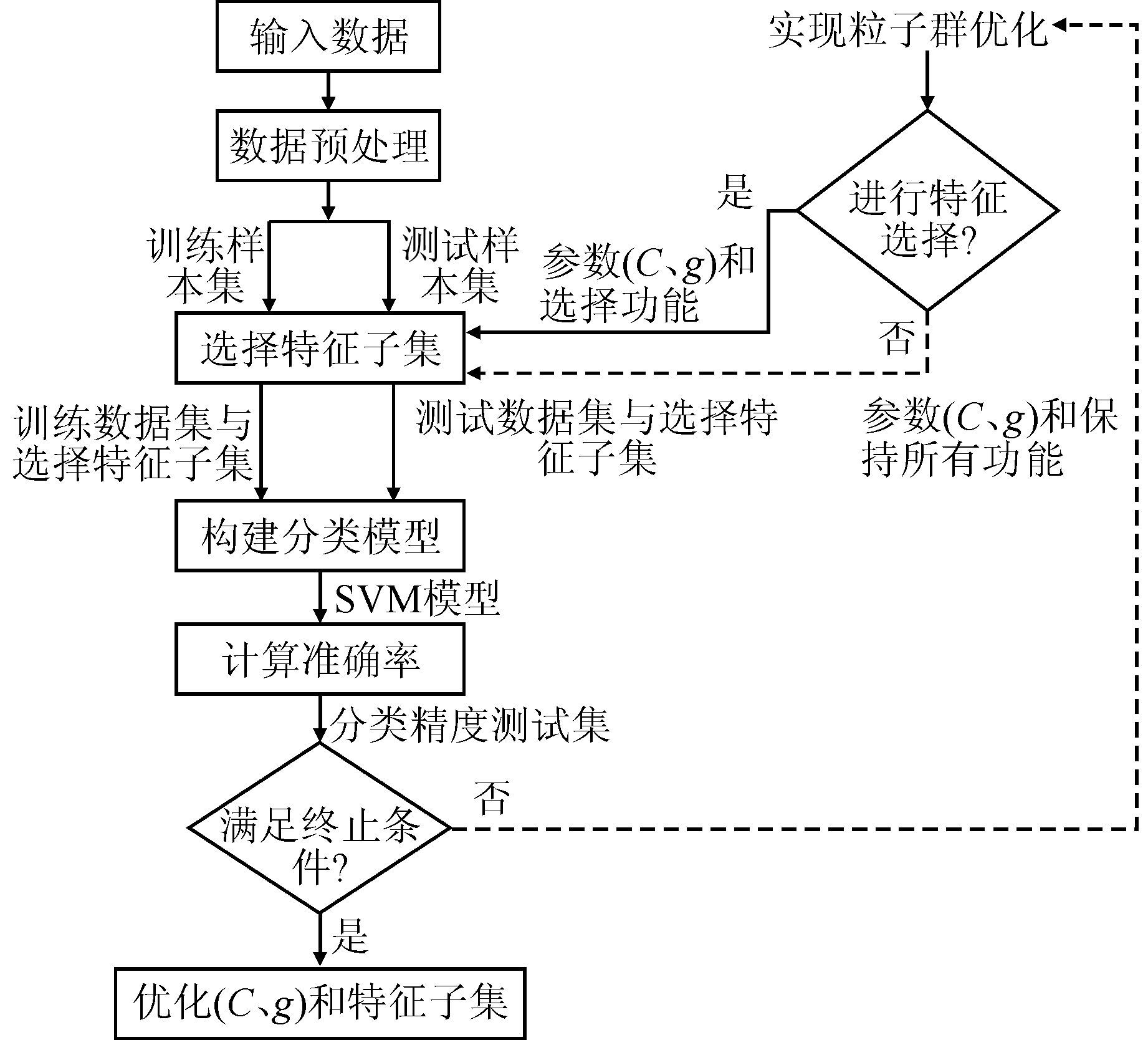
|
| 图 1 SVM预测模型的建模流程 Figure 1 The architecture of feature selection approach for SVM |
Saltelli等结合Sobol’法和FAST的优点,提出了傅里叶幅度灵敏度检验扩展法(extended Fourier amplitude sensitivity test)[10].该方法是基于方差的定量全局敏感性分析方法,即通过输入参数变化而产生的模型结果的方差来反映研究参数的重要性(或敏感度)和对模型结果变化的贡献程度.一阶灵敏度只反映了某一参数的不确定性对模型输出方差的直接贡献.参数总灵敏度反映了模型输出方差中,为某一参数的不确定性直接贡献加上该参数与其他参数交互作用所产生的间接贡献的总和.根据EFAST方法的一阶敏感度和总敏感度计算公式如下:
其中: Si为参数的一阶敏感度值;Vi为某个参数的方差;V为系统的总方差;STi为参数的总敏感度值;Ns为参数模拟次数:
M为常数,通常取为4或6;ωmax是ωi中的最大值,ωi是非线性相关系数.
武汉轨道交通二号线越江段隧道工程是继中国首条长江公路隧道——武汉长江隧道后修建的中国第一条穿越长江的地铁隧道工程,位于武汉长江一、二桥之间.隧道江北起点为江汉路站,江南终点为积玉桥站,在武汉关轮渡码头附近越江,东岸在武昌新生路、江南明珠园附近转向南,沿和平大道到达积玉桥站,全长约3 100 m.
该越江隧道汉口段根据盾构掘进方向自DK12+400(汉口江滩)~DK11+739(江汉路站接收井),约660 m.隧道沿线建筑物主要包括好乐迪KTV(1号)、四明银行与好乐迪KTV之间民房(2号)、四明银行(3号)、宝利金国际广场(4号)、中国银行武汉关支行(5号)和金色江滩KTV(6号)等6栋建筑,建筑物平面位置如图 2所示.
2.1 建筑的特征属性由于每栋建筑的几何尺寸、结构形式等属性不尽相同,故而每栋建筑受到盾构施工的影响并不相同.为了区分不同建筑之间的差异性,本文将从4个
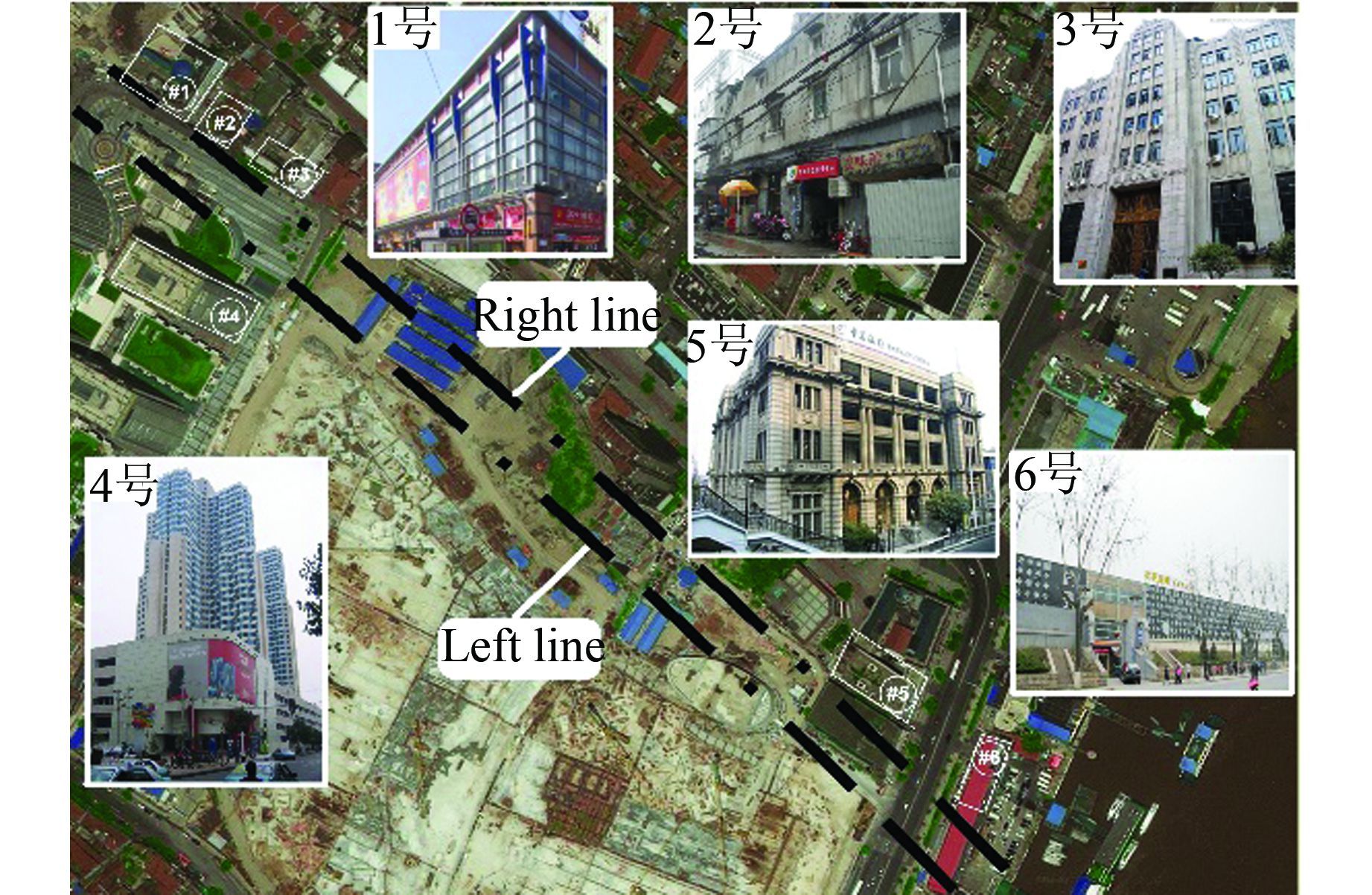
|
| 图 2 地铁附近的6栋建筑平面位置图 Figure 2 The 6 buildings adjacent the tunnel |
方面定义建筑的特征属性: 1) 建筑的层高;2) 建筑距盾构掘进路线的水平距离;3) 建筑的结构形式;4) 地铁盾构机的埋深.建筑物的这4个特征属性值如表 1所示.
| 建筑编号 | 距盾构水平距离/m | 盾构埋深/m | 建筑层高 | 建筑形式 |
| 1号 | 下穿 | 17 | 6层 | 框架(Type-1) |
| 2号 | 2 | 18 | 3层 | 砌体(Type-3) |
| 3号 | 7 | 19 | 7层 | 框架(Type-1) |
| 4号 | 15 | 17 | 34层 | 剪力墙(Type-3) |
| 5号 | 10 | 31 | 4层 | 框架(Type-1) |
| 6号 | 5 | 32 | 3层 | 砌体(Type-3) |
在地铁施工中有许多复杂的环境因素都对隧道和建筑之间的相互作用关系有较明显的影响,因此,需要在模型中使用大量的输入变量用以精确描述隧道和建筑的相互作用机理.根据相关的专家经验以及参考一些文献[4, 5, 11],本文选择了11个参数作为独立的随机变量输入到模型中,其均值、参数变异率和分布形式见表 2,而其他的输入参数则被假定为定值.
| 缩写 | 名称 | 单位 | 分布形式 | 均值 | 变异系数/% |
| E1 | 第1层土的弹性模量 | MPa | 正态分布 | 5 | 10 |
| E2 | 第2层土的弹性模量 | MPa | 正态分布 | 15 | 10 |
| μ1 | 第1层土的泊松比 | — | 正态分布 | 0.35 | 5 |
| μ2 | 第2层土的泊松比 | — | 正态分布 | 0.3 | 5 |
| DT | 隧道埋深 | m | 正态分布 | 15 | 5 |
| EBP | 建筑对地面的等效压力 | MPa | 正态分布 | 10 | 20 |
| FP | 推进压力 | MPa | 正态分布 | 3.10 | 20 |
| GP | 注浆压力 | MPa | 正态分布 | 1.55 | 20 |
| HD | 建筑和隧道的水平距离 | m | 正态分布 | 0, 5, 10 | 10 |
| BL | 建筑长 | m | 正态分布 | 20 | 5 |
| BW | 建筑宽 | m | 正态分布 | 10 | 5 |
通常情况下隧道上方的地表沉降直接反映了隧道对周围环境的影响,因此,地表沉降经常作为评判隧道施工安全状态的重要指标.同时,考虑到需要对隧道临近建筑的安全进行评价,参考相关专家经验,本文选取建筑附近最大沉降(Smax)、建筑最大倾斜(Imax)、建筑最大水平位移(Hmax)作为输出参数,用以对建筑安全状态进行评定.
3 隧道诱发建筑扰动模型建立 3.1 确定性有限元分析本文利用ABAQUS来模拟隧道开挖对周围环境的影响,土体采用Drucker-Prager本构模型,混凝土和钢筋采用弹性本构.其弹性模量、泊松比、黏聚力和摩擦角等系数见表 3.
| 材料 | 密度/(kN·m-3) | 泊松比 | 弹性模量/MPa | 摩擦角/(°) | 黏聚力/kPa |
| 管片混凝土 | 25.5 | 0.2 | 36 200 | - | - |
| 管片钢筋 | 38.5 | 0.2 | 203 000 | - | - |
| 建筑混凝土 | 24 | 0.2 | 220 000 | - | - |
| 土层1 | 17.6 | 0.3 | 5 | 28 | 11 |
| 土层2 | 18.3 | 0.35 | 15 | 31 | 8 |
| 土层3 | 19.2 | 0.4 | 112 | 35 | 5 |
本文建立的3D有限元模型包括确定性有限元分析和随机有限元分析两个过程,模型尺寸为50 m×40 m×60 m,总共得到47 940个单元,模型如图 3所示.其中,盾构机长度为9 m,内径为6.2 m,厚度为0.4 m,衬砌管片的内径为6 m,管片厚度为0.3 m,注浆区域的内径为6.6 m、注浆加固土厚度为0.2 m,边界条件为固定XZ底面单元,限制YZ侧面的X方向位移,限制XY侧面的Z方向位移.
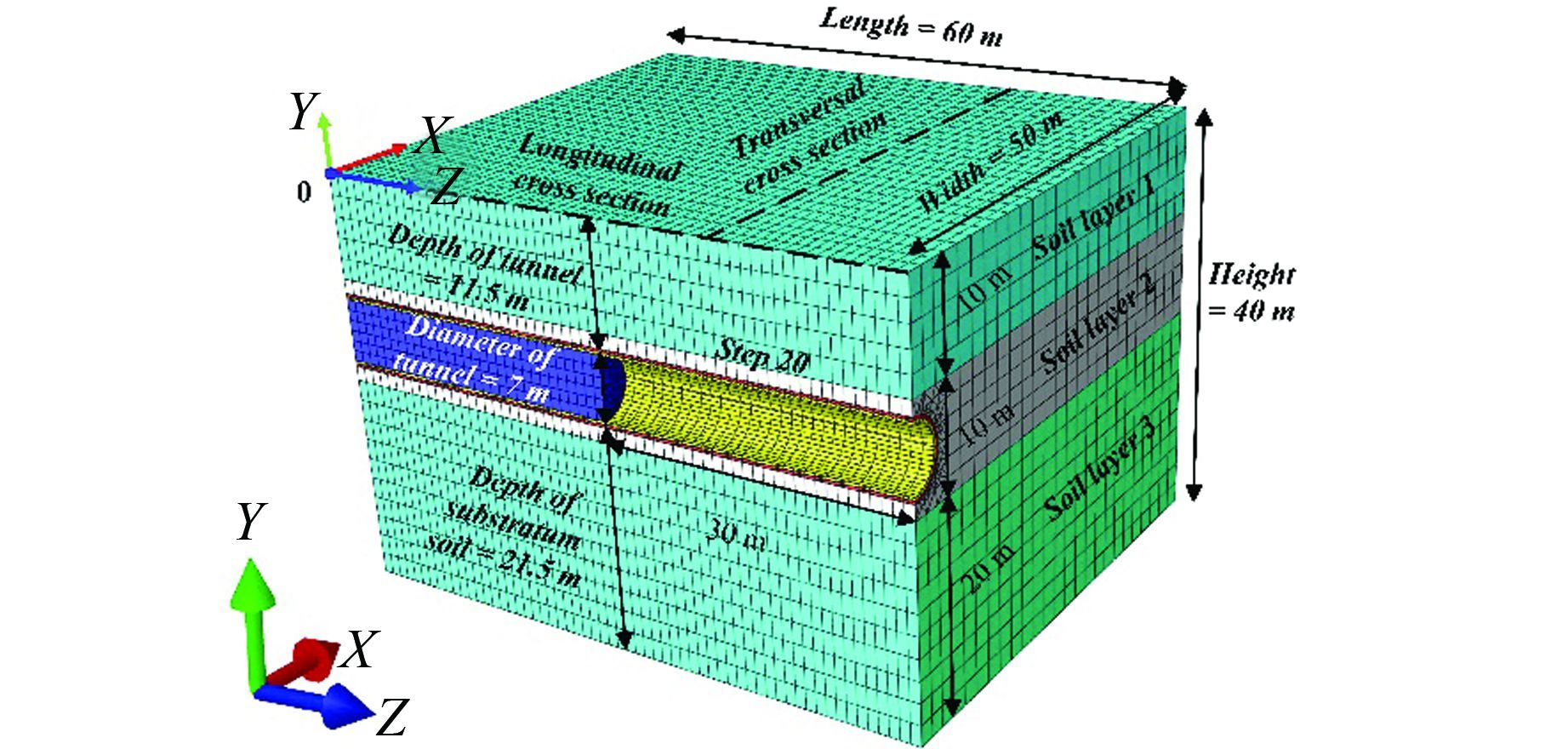
|
| 图 3 隧道有限元模型 Figure 3 FE model for tunnel excavating simulation |
为评估有限元模型中隧道对建筑物扰动的大小,本文分别分析了不同建筑(第3节中的1~6号建筑物)的扰动情况.本文讨论的地表位移是隧道施工诱发的地表位移,即有限元模拟结束时的总地表位移减去建筑自重导致的位移.图 4展示了1号建筑物下隧道掘进模型的模拟结果.
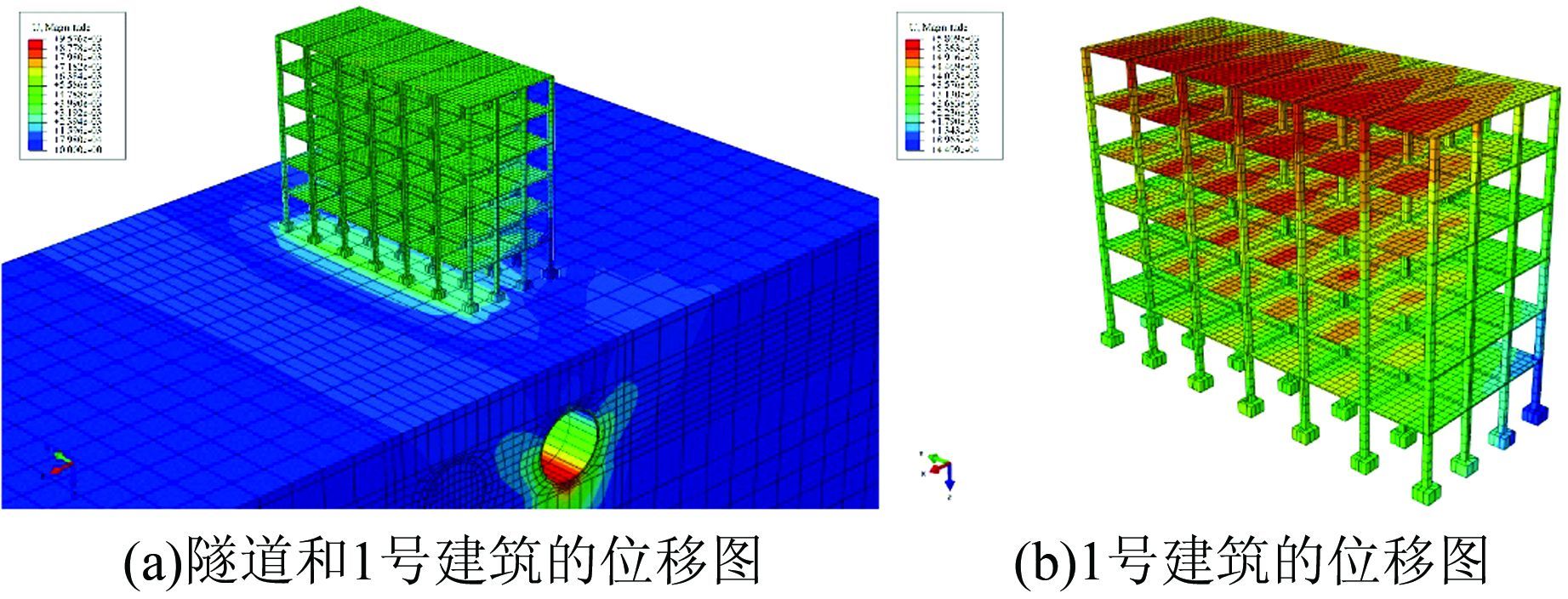
|
| 图 4 有限元模型中的位移图 Figure 4 Displacement of FE model |
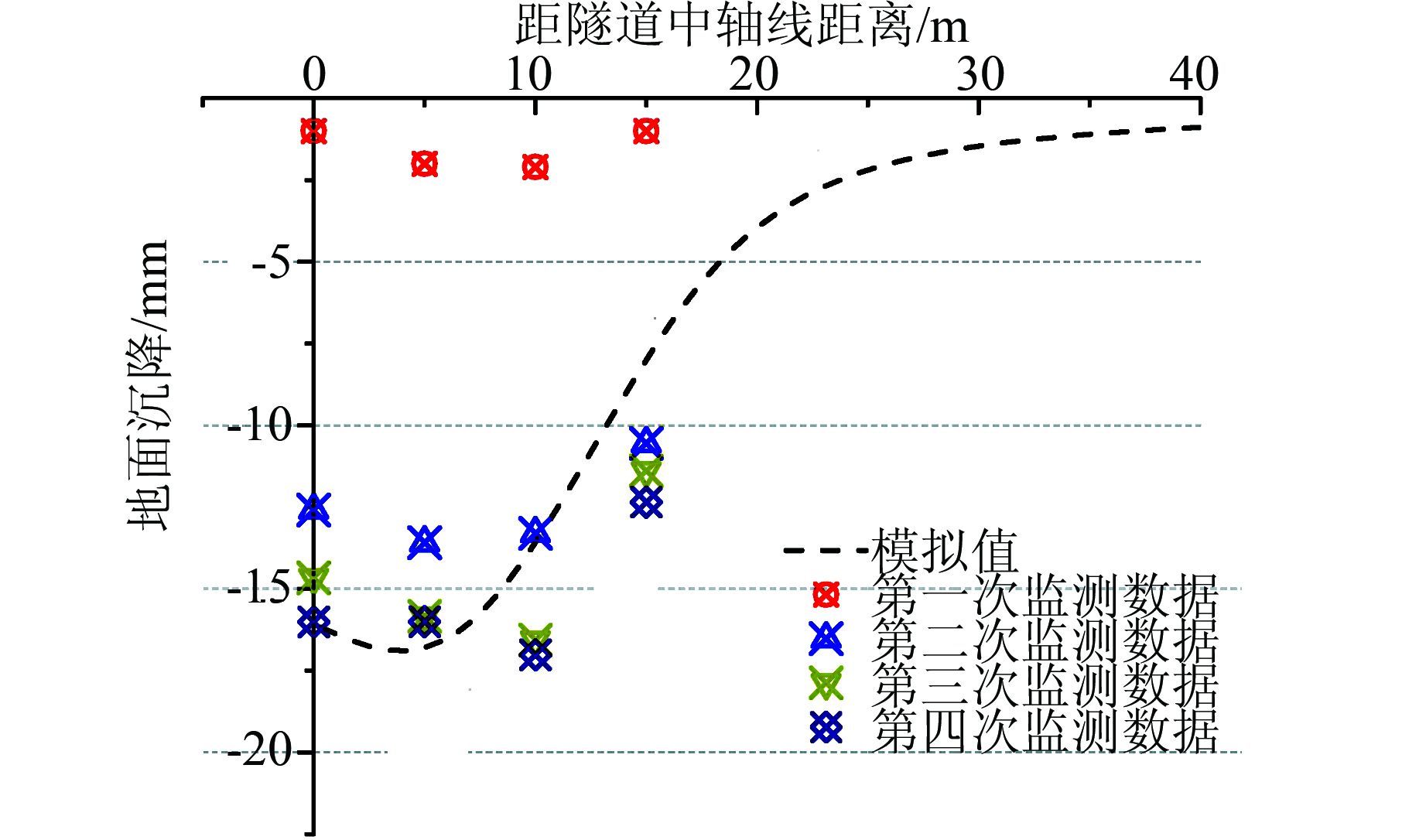
为验证上述有限元模型并调查隧道掘进过程中建筑的运动模式,将地面沉降的模拟结果与3号建筑物的监测数据进行比较.四次监测数据分别为盾构开始到达监测点时、盾构机完全通过监测点、盾构通过一周之后、盾构通过两周之后,分别于同一监测点得到监测数据.分析监测结果发现,第一次数据比较小,第二次数据比较大,而后沉降值继续有微小的增加,最终趋于稳定.从图 5中可以发现,有限元仿真的数据与实际监测数据大致吻合,这验证了有限元模型的准确性.
|
| 图 5 模拟结果与实测结果对比 Figure 5 Comparison between simulating values and monitoring data |
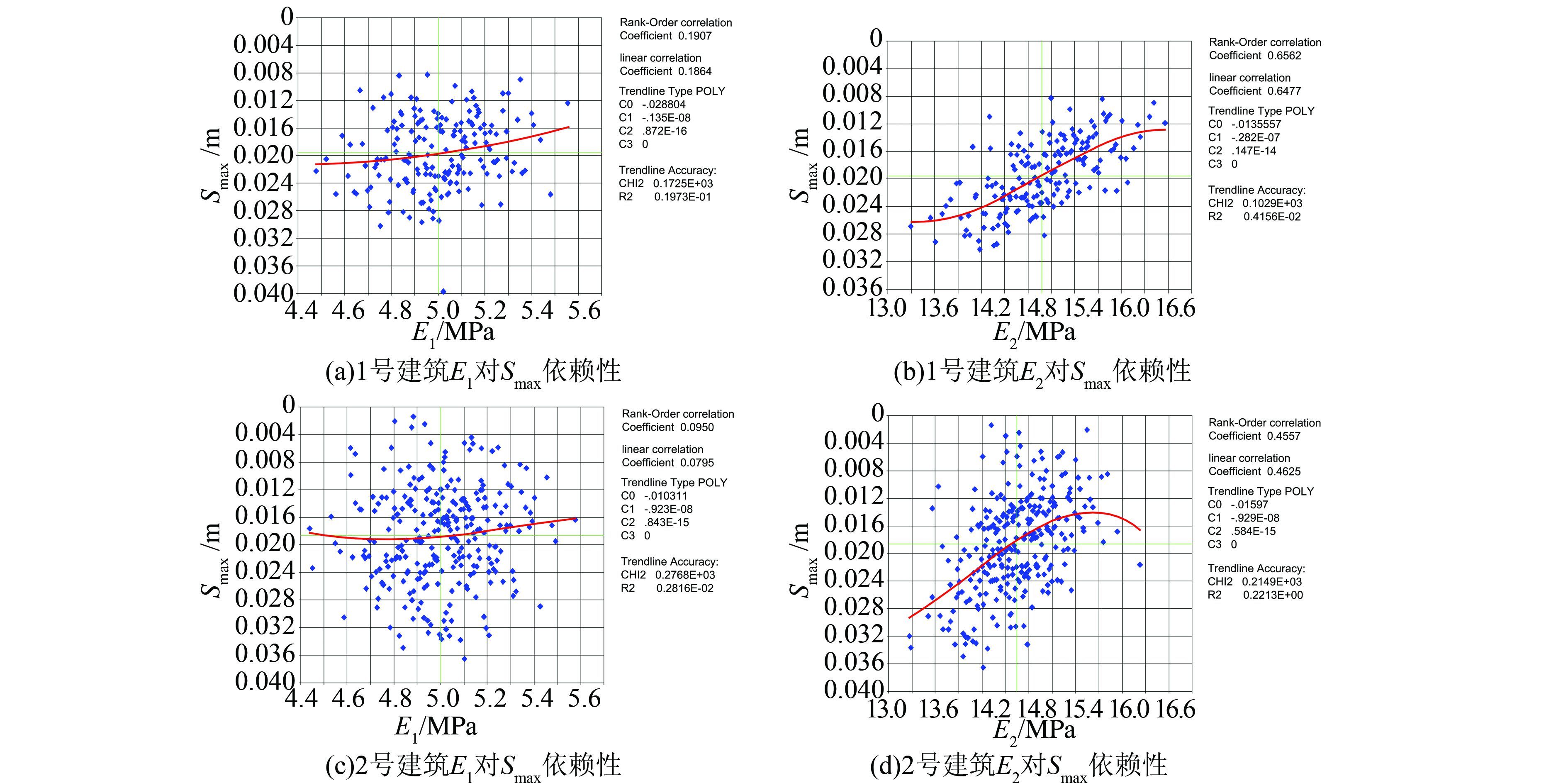
本文为研究输入变量和输出参数之间的相互关系,以1号和3号建筑物的E1、E2对Smax的散点图为例进行说明.线性相关系数是利用数据计算积差相关系数,而Spearman相关系数是用数据的秩次计算积差相关系数.为了对比分析参数之间的相关性,本文对比采用了Spearman秩相关性系数和线性相关性系数来描述参数间的关联性,如图 6.1号建筑E1、E2对Smax的秩相关性分别为0.191、0.656,3号建筑E1、E2对Smax的秩相关性分别为0.095、0.456;1号建筑E1、E2对Smax的线性相关系数为0.186、0.648,3号建筑E1、E2对Smax的线性相关系数为0.081、0.463.两个参数的相关系数越接近1,两个参数越独立.在1号建筑物和3号建筑物中,E2对Smax的影响作用比E1对Smax的更大.图 6中的数据点是利用随机有限元计算的180个离散的数据点,故而数据点的形式比较稀疏和离散.本文对比采用一次至五次曲线拟合的曲线形式,发现一次、二次曲线的线型比较简单,不能完全反映参数之间的相关性随参数值变化而变化的关系,而四次五次曲线相比于三次曲线的变化不大,故本文采用三次曲线来简单描述参数之间的关联性.图 6中采用三次方曲线作为趋势线拟合散点图,以描述参数之间的相关性.从趋势线可以看出,在1号建筑物和3号建筑物中,E2对Smax的影响作用比E1对Smax更大.
|
| 图 6 随机有限元模型中1号和3号建筑物的E1、E2 对Smax的散点图 Figure 6 Scatter plots of E1, E2 to Smax on No.1 and No.3 buildings by stochastic FE method |
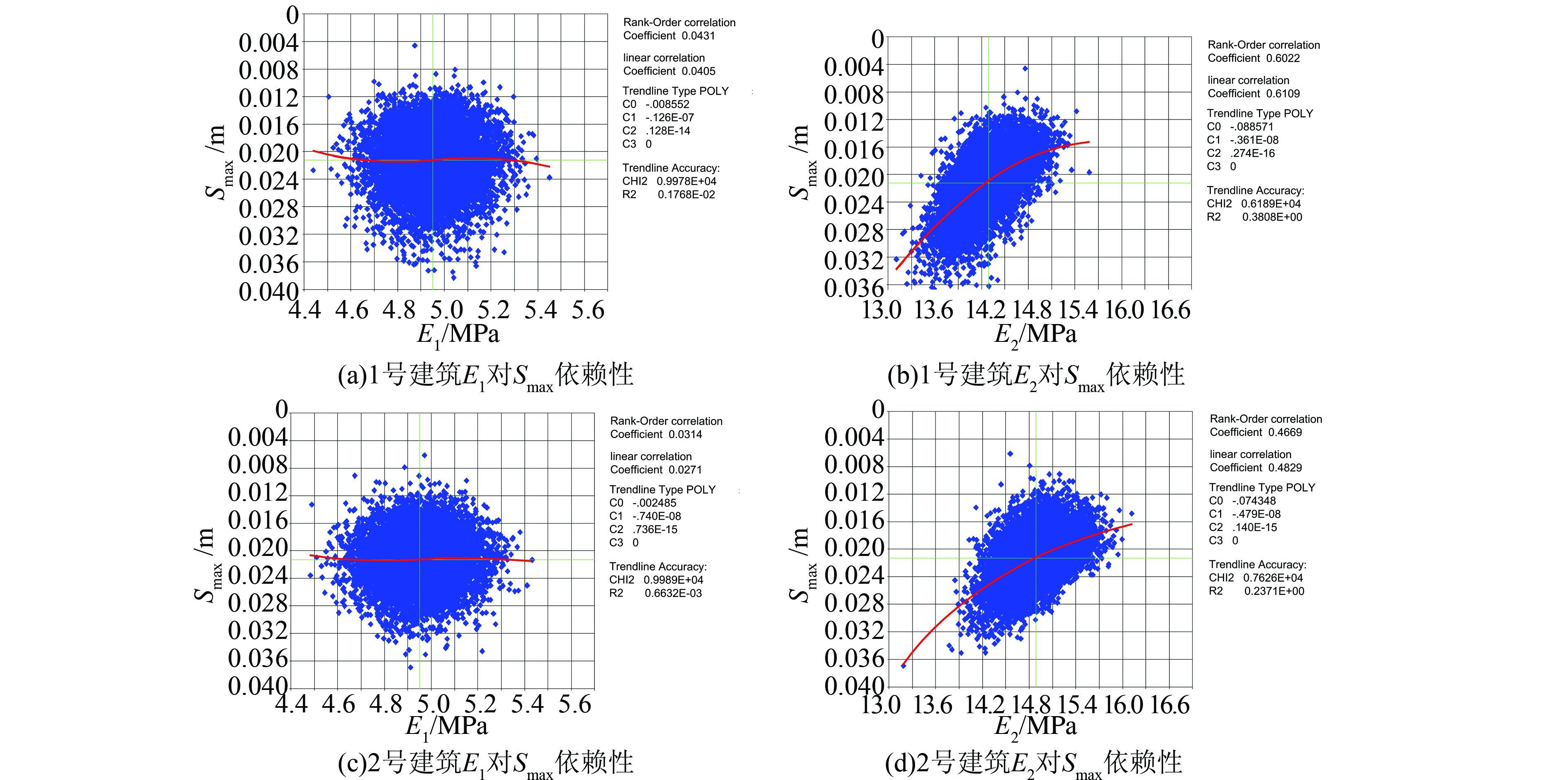
代理模型构建之后,可以生成1 000组数据集,为研究输入变量和输出变量之间的相关性,以1号和3号建筑物的E1、E2对Smax的散点图为例进行说明,如图 7.1号建筑物E1、E2对Smax的秩相关性为0.043、0.602,3号建筑物为0.031、0.467.1 号建筑物E1、E2对Smax的线性相关性为0.041、0.611,3号建筑物为0.027、0.483.在1号建筑物和3号建筑物中,E2对Smax的影响作用比E1对Smax的更大.图 7中采用三次方曲线作为趋势线拟合散点图,以描述参数之间的相关性.从趋势线可以看出,在1号建筑物和3号建筑物中,E2对Smax的影响作用比E1对Smax更大.同时,从散点图的分布规律来看,两个参数之间越独立,散点图越分散,反之亦然.比较图 6和7,并比较基于原始有限元模型模拟的180组数据和基于代理模型生成的1 000组数据,发现参数的秩相关性和线性相关性非常相似,这验证了代理模型的准确性.
|
| 图 7 代理模型中1号和3号建筑物的E1、E2 对Smax的散点图 Figure 7 Scatter plots of E1, E2 to Smax on No.1 and No.3 buildings by stochastic FE method by meta-model |
基于SVM构建代理模型的计算结果,两个参数之间全局敏感度(GSI)值可以用来评估参数之间的相关性.
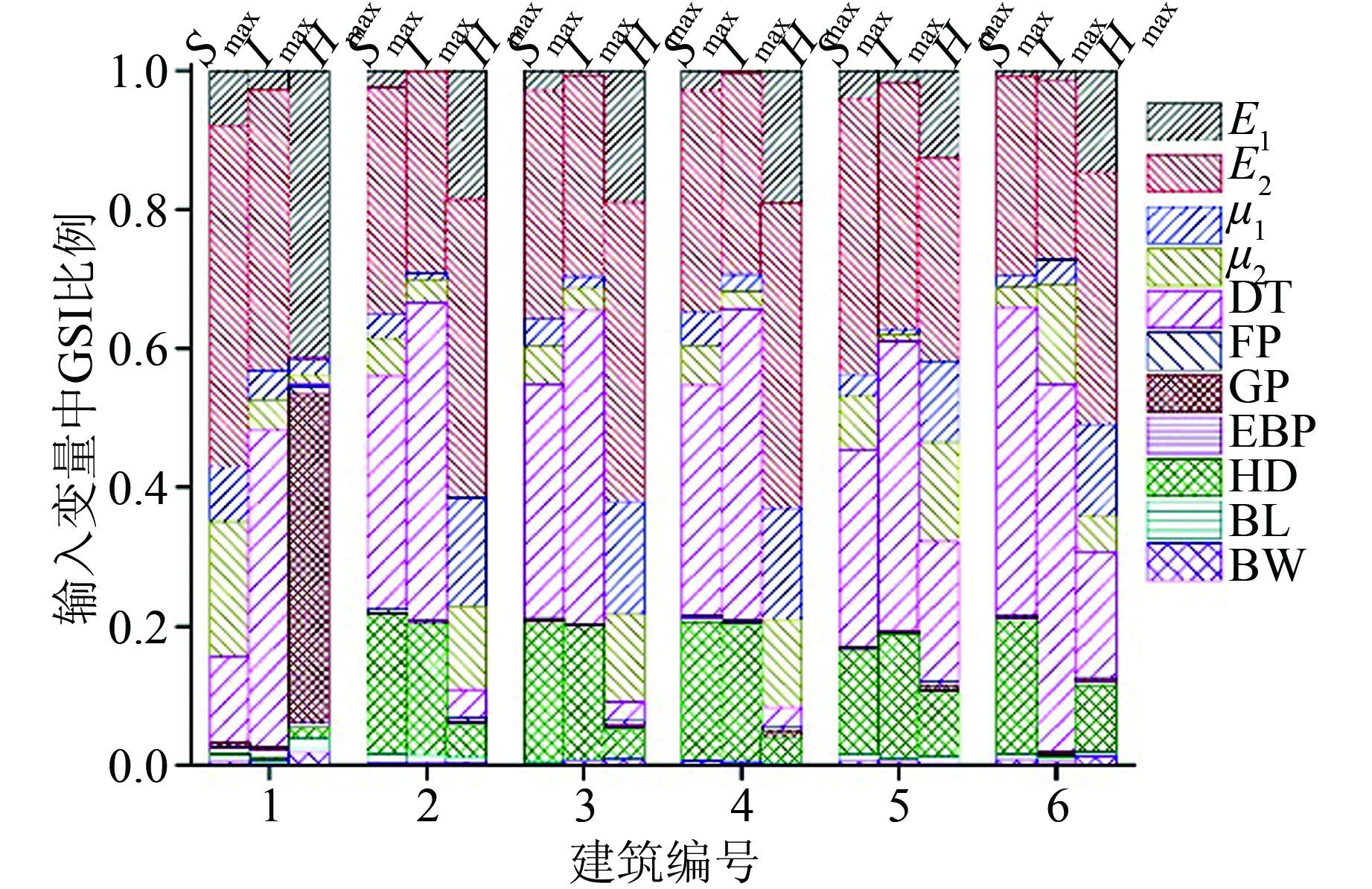
为了辨别每个输入变量中全局敏感度(GSI)的占比,本文将所有输入变量中总的GSI值设定为1,而每个输入变量中GSI计算值如图 8所示.6栋建筑物的11个输入变量相对3个输出参数的计算结果如图 8所示.
|
| 图 8 各建筑的各个参数的全局敏感度比例值 Figure 8 The GSI proportions of input variables in 6 buildings |
由于盾构施工过程中周围建筑环境的复杂性,不同建筑输入变量的敏感性差异较大.图 8表明: 1号建筑输入变量的敏感性与其他建筑的差异性最大,其可能原因是地铁盾构施工在1号建筑物正下方,对其扰动显著,因此,1号建筑物的各项输入变量的敏感性系数也比较显著.
在地铁盾构施工过程中,安全管理和分析人员要辨识和管控隧道周围可能发生的多种风险.全局敏感性分析结果可以辨识不同参数在本工程及其他类似工程中的安全性.如图 8所示,对Smax最敏感的输入变量是E2、DT和HD,对Hmax最敏感的输入变量也是E2、DT和HD,对Imax最敏感的输入变量是E1 、E2和μ1.由GSA分析结果可知,有较高全局敏感性的输入变量需要在地铁掘进施工中重点管控,这将有利于降低地铁施工对建筑物的扰动和破坏,降低安全风险.另外,不同建筑物的自身特性各不相同,部分输入变量的GSI在某些情况下取值低,在另一些情况下又比较高,这些输入变量值得关注.
4.2 不同特征属性和GSI的关联性分析从上一节的分析中可知,当盾构周围建筑的结构形式以及与盾构之间的几何位置等特征属性发生变化时,各个输入变量对输出变量影响的敏感性也会发生变化.本文从4个特征属性的角度分析这些因素对敏感性的影响规律: 1) 不同的建筑与盾构之间的水平距离;2) 不同的隧道埋深;3) 不同的建筑层高;4) 不同的建筑结构形式.
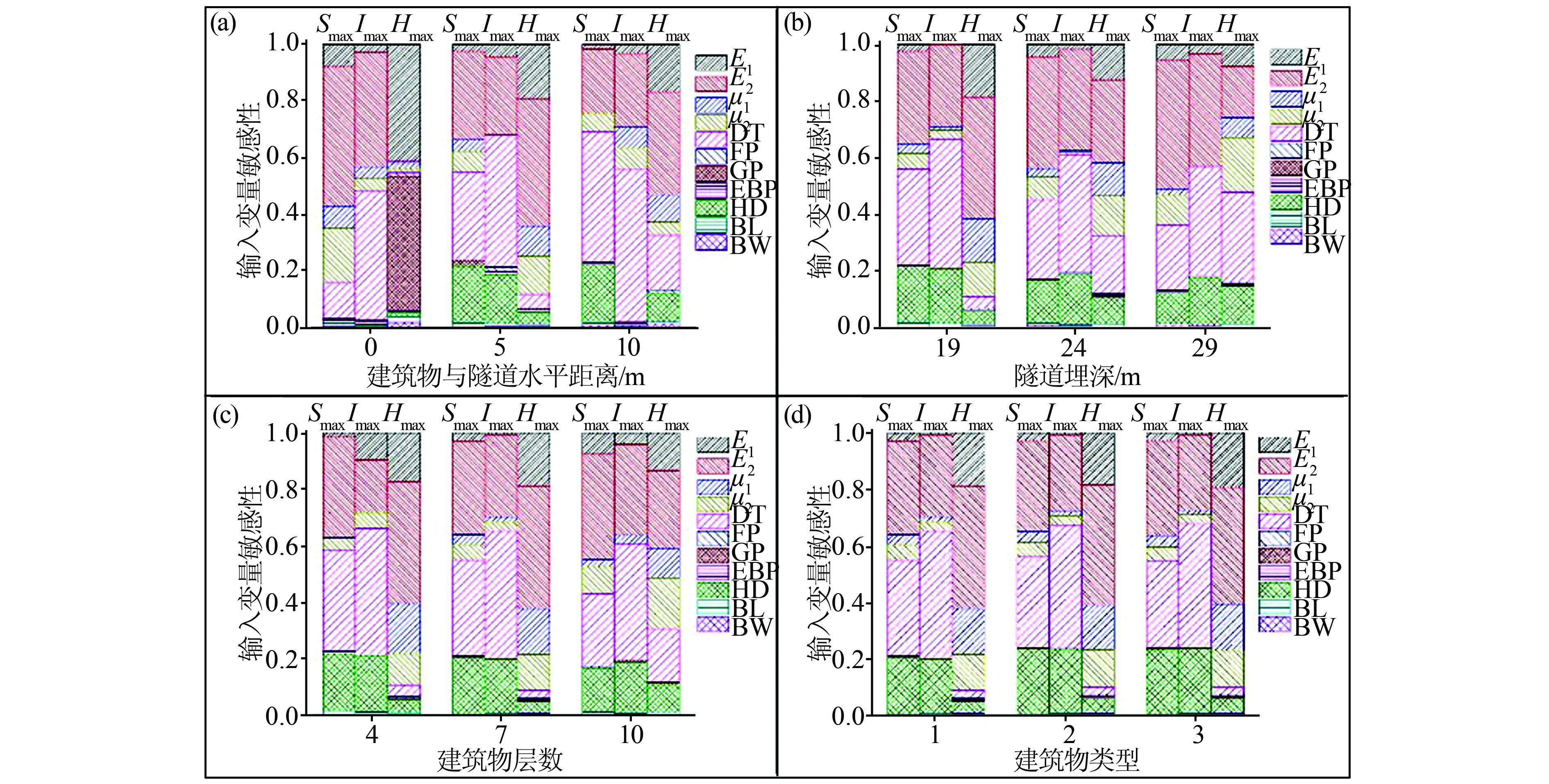
4.2.1 建筑物与盾构隧道水平距离建筑物与盾构隧道水平距离的不同影响建筑物的位移情况.将所有输入变量的总GSI设定为1,每个输入变量的GSI计算结果如图 9(a)所示,以1号建筑物为例展示当建筑物和隧道的水平距离分别为0、5 m和10 m时输入变量的敏感性.由图 9(a)可知,输入变量的敏感性在不同的HD取值下存在显著差异.
|
| 图 9 不同输入变量下各个参数的全局敏感度比例值 Figure 9 The GSI proportions of input variables with different factors |
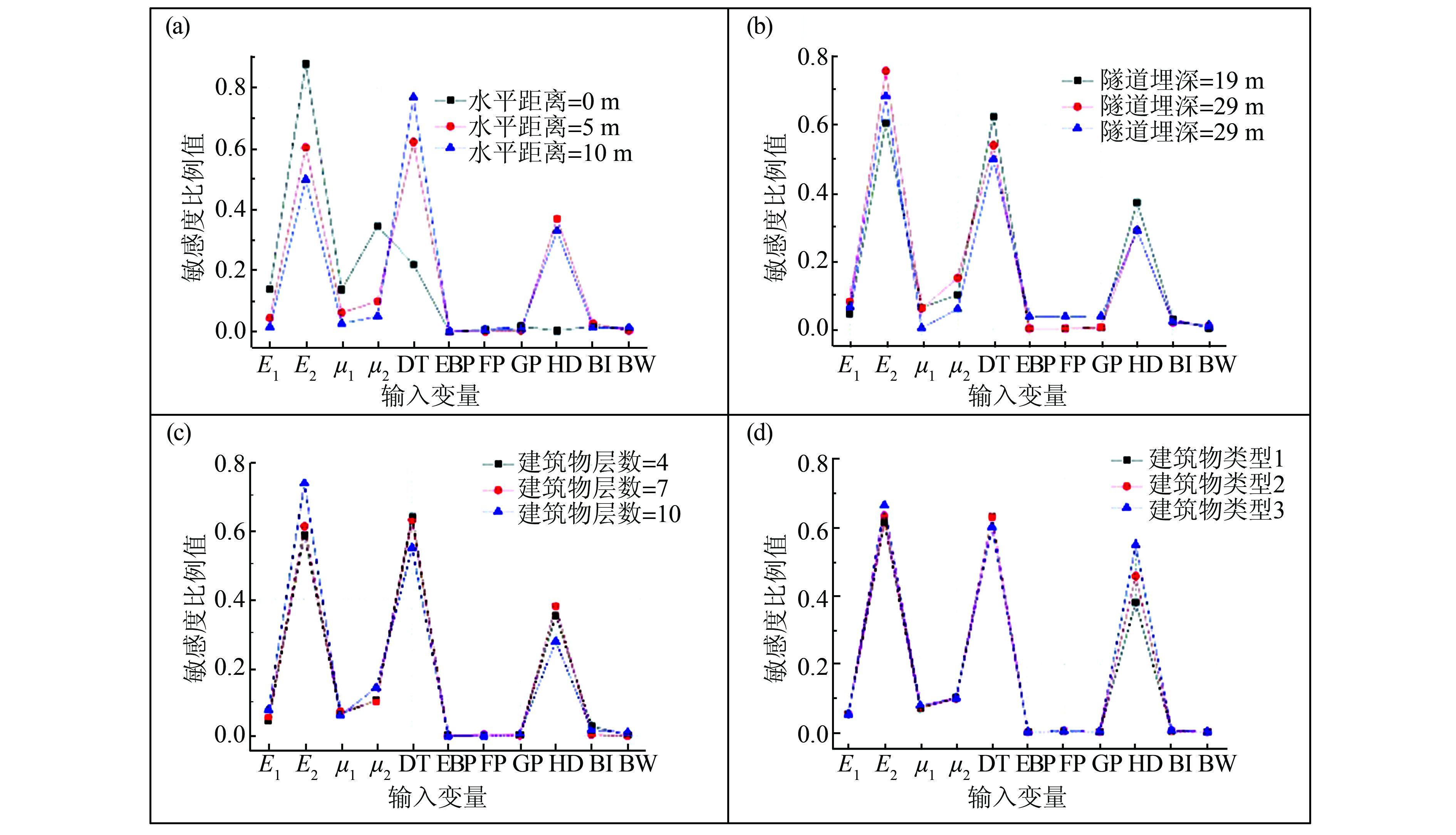
以输入参数Smax为例,图 10(a)展示了输入变量的敏感性情况,其中,有3个输入变量DT、 E2、μ2对HD 最敏感.当HD分别为0、5 m和10 m时,输入变量DT的敏感度分别为0.221、0.621、0.767;输入变量μ2的敏感度分别为0.346、0.101、0.051;输入变量E2的敏感度分别为0.876、0.603、0.498;输入变量HD的敏感度分别为0.003、0.370、0.331.当DT增大时,输入变量DT的敏感性增加,输入变量E2 和μ2的敏感性降低,输入变量HD的敏感性系先增加后小幅度下降.
|
| 图 10 以Smax输出参数时各个参数的全局敏感度比例值 Figure 10 The variation of input variables sensitivities with different factors when taking Smax as output parameter |
如图 9(b),以3号建筑物为例说明当隧道埋深分别为19、24、29 m时,输入变量的敏感性系数变化情况,当盾构隧道埋深变化时,输入变量的敏感性变化比较大.
如图 10(b)所示,输入变量E2、μ2、DT、HD的敏感性最显著,当DT分别取值19、24、29 m时,输入变量E2的敏感度分别为0.603、0.755、0.681;输入变量μ2的敏感度分别为0.101、0.149、0.058;输入变量DT的敏感度分别为0.621、0.538、0.496;输入变量HD的敏感度分别为0.370、 0.289、 0.288.当DT增大时,输入变量DT和HD的敏感性增加,输入变量E2和μ2的敏感性先降低然后小幅度上升.
4.2.3 建筑物层数如图 9(c),以3号建筑物为例说明当建筑物层数分别取4、7和10时输入变量的敏感性变化情况.当建筑物层数不同时,输入变量的敏感性也不同.当建筑物层数变化时,输入变量的敏感性变化很微弱,即输入变量对建筑物层数的敏感性较弱.
如图 10(c)所示,输入变量E2、μ2、DT、HD的敏感性最显著,当建筑物层数分别取4、7和10时,输入变量E2的敏感度分别为0.587、0.614、 0.740;输入变量μ2的敏感度分别为0.104、0.101、0.142;输入变量DT的敏感度分别为0.641、0.631、0.551;输入变量HD的敏感度分别为0.352、0.38、 0.277.当建筑物层数增加时,输入变量E2和DT的敏感性下降,输入变量μ2的敏感性先小幅度上升然后下降,输入变量HD的敏感性先上升然后小幅下降.
4.2.4 建筑物类型如图 9(d),以3号建筑物为例说明当建筑物类型分别为Type-1、Type-2和Type-3时输入变量的敏感性变化情况.当建筑物类型不同时,输入变量的敏感性也不同.当建筑物类型变化时,输入变量的敏感性变化很弱,即输入变量对建筑物类型的敏感性非常微弱.
如图 10(d)所示,输入变量HD的敏感性最显著,当建筑物类型分别为Type-1、Type-2和Type-3时,输入变量HD的敏感系数分别为0.380、0.457和 0.549.当建筑物层类型变化时,输入变量HD的敏感性增加,而其他输入变量的敏感性没有显著变化.
5 决策建议由于周围复杂环境和各种不确定性因素的影响,目前有关隧道施工对周围环境扰动影响的经验知识相当有限,存在因知识不足而出现的认知不确定性,对隧道施工的安全风险管理非常不利.因此,本文通过对隧道施工诱发建筑物扰动的各因素进行全局敏感性分析,得到了对建筑物安全影响较大的那些因素,并在此基础上加强对敏感度较高因素的管理和控制,可以为隧道施工的风险管理提供有效的决策支持.另外,敏感度较高因素即是影响建筑安全的强致险因素,在隧道施工中需要增加对这些因素信息的收集工作,这样有助于减少对隧道施工诱发临近建筑安全风险的认知不确定性.
6 结论在武汉地铁二号线过江段中使用了泥水盾构掘进机进行地铁隧道施工,盾构掘进过程中会对临近环境造成一定的扰动影响.由于隧道施工周围环境的随机性和不确定性,通过传统经验知识对隧道诱发临近建筑物的扰动进行预测和评价容易出现较大的偏差.为减少这种由于知识缺乏而出现的认知不确定性,本文采用了基于PSO-LSSVM的代理模型和EFSAT的全局敏感性分析算法,对隧道施工诱发建筑物扰动的各因素进行全局敏感性分析,得到了对建筑物安全影响较大的那些因素.
有较高全局敏感度的因素(即: 第1、2层土的弹性模量,第1层土的泊松比,隧道埋深和建筑距隧道的水平距离)需要在地铁掘进施工中重点管控,这将有利于降低地铁施工对建筑物的干扰和破坏,降低安全风险.
| [1] |
吴贤国, 姚春桥, 余群舟, 等. 某地铁深基坑施工中广电大楼的沉降控制[J].
土木工程学报, 2011(S1): 177–181.
Wu Xianguo, Yao Chunqiao, Yu Qunzhou, et al. Settlement control of the broadcasting building during deep excavation in metro construction[J]. China Civil Engineering Journal, 2011(S1): 177–181. |
| [2] | Zhang L, Wu X, Chen Q, et al. Towards a safety management approach for adjacent buildings in tunneling environments: Case study in China[J]. Building and Environment, 2014, 75: 222–235. DOI:10.1016/j.buildenv.2014.02.005 |
| [3] | Comodromos E M, Papadopoulou M C, Konstantinidis G K. Numerical assessment of subsidence and adjacent building movements induced by TBM-EPB tunneling[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140: 0401406111. |
| [4] | Miro S, Koenig M, Hartmann D, et al. A probabilistic analysis of subsoil parameters uncertainty impacts on tunnel-induced ground movements with a back-analysis study[J]. Computers and Geotechnics, 2015, 68: 38–53. DOI:10.1016/j.compgeo.2015.03.012 |
| [5] | Mollon G, Dias D, Soubra A. Probabilistic analyses of tunneling-induced ground movements[J]. Acta Geotechnica, 2013, 8(2): 181–199. DOI:10.1007/s11440-012-0182-7 |
| [6] |
吴贤国, 陈晓阳, 丁烈云, 等. 地铁隧道施工邻近建筑物安全风险等级评价[J].
施工技术, 2011(07): 78–80.
Wu Xianguo, Chen Xiaoyang, Ding lieyun, et al. Safety risk rank evaluation of adjacent buildings during metro tunneling construction[J]. Construction Technology, 2011(07): 78–80. |
| [7] |
李典庆, 蒋水华, 周创兵, 等. 基于非侵入式随机有限元法的地下洞室可靠度分析[J].
岩土工程学报, 2012(01): 123–129.
Li Dianqing, Jiang Shuihua, Zhou Chuangbing, et al. Reliability analysis of slopes considering spatial variability of soil parameters using non-intrusive stochastic finite element method[J]. Chinese Journal of Geotechnical Engineering, 2012(01): 123–129. |
| [8] |
王鸷. 地下洞室随机有限元分析和可靠度计算[D]. 西安:西北工业大学, 2006.
Wang Zhi. The stochastic finite element method and structural reliability of underground cavity [D]. Xi’an: Northwestern Polytechnical University, 2006. |
| [9] | Garcia Nieto P J, Garcia-Gonzalo E, Alonso Fernandez J R, et al. Hybrid PSO-SVM-based method for long-term forecasting of turbidity in the Nalon river basin: A case study in Northern Spain[J]. Ecological Engineering, 2014, 73: 192–200. DOI:10.1016/j.ecoleng.2014.09.042 |
| [10] |
余衍然. 轨道车辆平稳性的随机参数全局灵敏度分析[D]. 苏州:苏州大学, 2014.
Yu Yanran, The Global Sensitivity Analysis on ride quality of railway vehicle with stochastic parameters [D].Suzhou: Soochow University, 2014. |
| [11] | Mirhabibi A, Soroush A. Effects of building three-dimensional modeling type on twin tunneling-induced ground settlement[J]. Tunnelling and Underground Space Technology, 2013, 38: 224–234. DOI:10.1016/j.tust.2013.07.003 |
 2016, Vol. 49
2016, Vol. 49




