文章信息
- 王云鹤, 刘姜涛, 邓其军, 刘永东, 肖志怀
- WANG Yunhe, LIU Jiangtao, DENG Qijun, LIU Yongdong, XIAO Zhihuai
- 基于可调电感的无线能量传输系统优化设计
- Optimal design of wireless energy transmission system based on adjustable inductance
- 武汉大学学报(工学版), 2018, 51(1): 85-90
- Engineering Journal of Wuhan University, 2018, 51(1): 85-90
- http://dx.doi.org/10.14188/j.1671-8844.2018-01-013
-
文章历史
- 收稿日期: 2016-12-02
2. 湖北第二师范学校物理与机电工程学院,湖北 武汉 430205;
3. 中国电力企业联合会标准化中心,北京 100761
2. School of Physics and Mechanical and Electrical Engineering, Hubei University of Education, Wuhan 430205, China;
3. China Electric Power Enterprise Association Standardization Center, Beijing 100761, China
无线能量传输技术在电动汽车无线充电、植入式医疗器械无线供电、无线智能家居供电等领域有较好的应用前景[1-8],由于系统的电感、电容等参数的漂移直接影响系统的谐振频率,从而会影响系统的传输效率和传输功率[9-11].本文将可调电感装置引入到电能的发射端和接收端,对无线电能传输系统进行优化设计,实现系统谐振频率的失调补偿,提高系统的传输效率及稳定性.
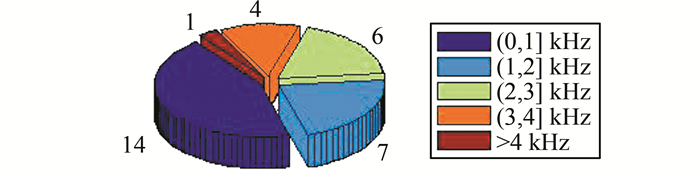
1 系统谐振频率失调分析为了分析无线电能传输系统谐振频率漂移的程度,现随机选取同一型号的16套传输线圈和电容,统计其组成的32个谐振电路的谐振频率漂移情况,如图 1所示.
|
| 图 1 32个谐振频率漂移统计图 Figure 1 Distribution of rosonant frequency deviation |
从图 1可以看出,32组参数都存在偏差,并且漂移量大于1 kHz的超过了一半.这一统计说明,在实际无线电能传输系统中,即使谐振电路采用相同型号的传输线圈和电容,谐振频率也不能完全匹配[12].因此,即使在发射端与接收端传输距离不变、接收端负载固定的情况下,传输线圈存在少许参数漂移,都可能导致系统传输效率的降低.
2 优化调谐本文采用双线圈磁耦合谐振无线电能传输系统.为了提高系统电能传输的性能,本文研究了系统参数与系统最佳工作状态的关系.
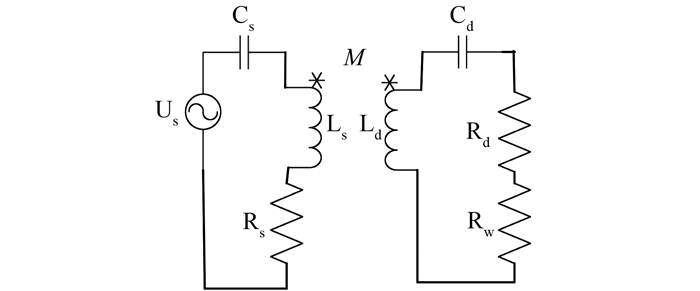
2.1 调谐目标系统等效电路图如图 2所示,图 2中,Rs、Ls、Cs分别表示发射端的等效电阻、电感和电容;Rd、Ld、Cd分别表示接收端的等效电阻、电感和电容;Us表示发射端电压;为了便于研究,将负载Rw视为纯电阻;互感M是传输线圈Ls和Ld的耦合.
|
| 图 2 系统等效电路 Figure 2 Equivalent circuit diagram of system |
取系统的工作频率为ω,Zs为发射端阻抗,Zd为接收端阻抗,如下式所示:
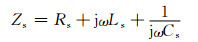 (1)
(1)
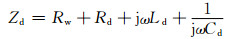 (2)
(2)
假设Zr为接收端映射到发射端的阻抗:
 (3)
(3)
根据基尔霍夫电压定律,可以得到发射端电流Is和接收端电流Id,分别表示为
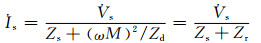 (4)
(4)
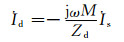 (5)
(5)
发射端功率Ps和接收端功率Po分别为
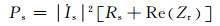 (6)
(6)
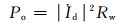 (7)
(7)
由式(3)、(4)可得
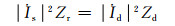 (8)
(8)
根据式(8),接收端的有效功率可以等效为映射阻抗Zr的有效功率.因此,传输效率可由下式表示:
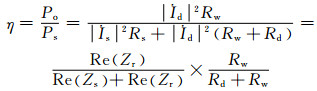 (9)
(9)
其中,Zr的实部可由下式表示:
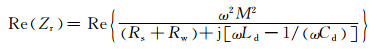 (10)
(10)
根据式(9)、(10)可得:
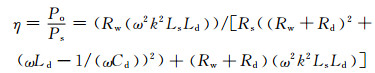 (11)
(11)
Re(Zr)对ω求导,系统效率η达到最大, 可得:
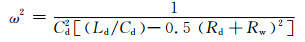 (12)
(12)
如果Ld/Cd远大于0.5 (Rd+Rw)2, 那么,ω为系统接收端的谐振频率.
根据式(4)~(7)、(10), 可得:
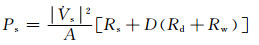 (13)
(13)
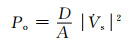 (14)
(14)
式中:
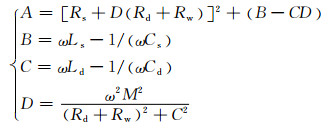
系统耦合系数k为
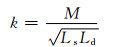 (15)
(15)
M随着两线圈的距离改变而变化[13].利用椭圆积分结合式(15)可以计算互感系数M.
当两线圈中心轴距离为55 mm时,耦合系数k=0.019.令Cs=Cd=2 500 pF, Rs=Rd=490 mΩ, ω=2πf, f=192 kHz, 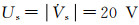
|
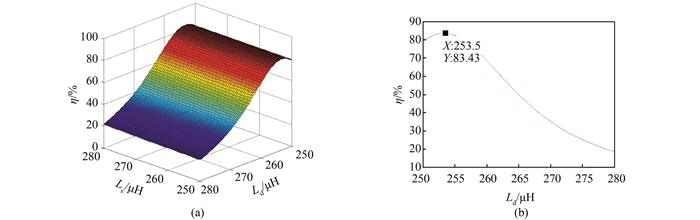
| 图 3 系统传输效率η与Ls、Ld的关系曲线 Figure 3 Relation curves of system transmission efficiency η with Ls and Ld |
为了在较高的传输效率下得到更高的传输功率,通过仿真实验,研究系统的传输效率η、传输功率Ps、接收功率Po与Ls、Ld的关系.
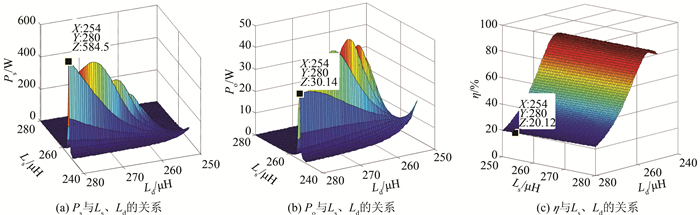
情况1:如图 4所示,当发射功率Ps达到最大值584.5 W时, 接收功率Po=30.14 W, 传输效率η=25.12%.发射功率最高,接收功率和传输效率均不高,说明系统中发射端和接收端没有达到最佳的匹配状态.
|
| 图 4 η、Ps、Po与Ls、Ld的关系 Figure 4 Relation curves of η, Ps and Po with Ls and Ld when Ps obtains maximum |
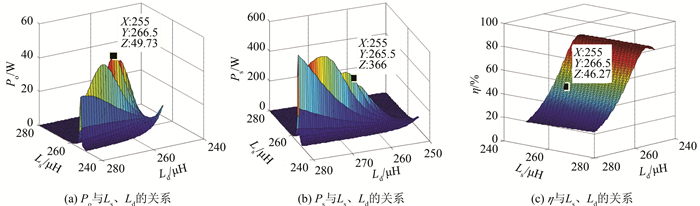
情况2:如图 5所示,当接收功率Po达最大值49.73 W时, 发射功率Ps=366 W, 传输效率η=46.27%.
|
| 图 5 η、Ps、Po与Ls、Ld的关系 Figure 5 Relation curves of η, Ps and Po with Ls and Ld when Po obtains maximum |
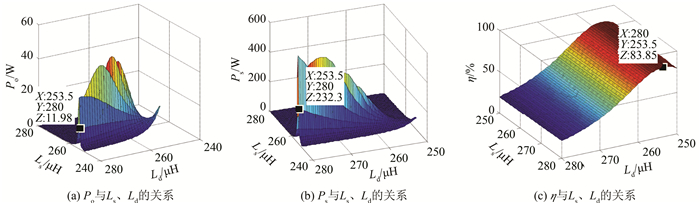
情况3:如图 6所示,当传输效率η=83.85%时,接收功率Po达到11.98 W时, 发射功率Ps=232.3 W.
|
| 图 6 η、Ps、Po与Ls、Ld的关系曲线 Figure 6 Relation curves of η, Ps and Po with Ls and Ld under optimal state of system |
通过以上3种情况的对比,在最大传输功率下,输出功率不能达到最大.当发射端和接收端达到最佳匹配状态时,来自接收端的反射阻抗达到最大,发射端电流减少,因此,发射功率降低.接收端的功率增加,传输效率增加.这是本文要找的最佳状态.
3 系统优化通过前面的研究可知,如果可以调节系统中发射端和接收端的电感大小,那么,就可以对系统进行优化,从而在较高的传输效率下提高系统的接收功率.本文在无线电能传输系统中加入电感调谐电路,实现对系统的优化.
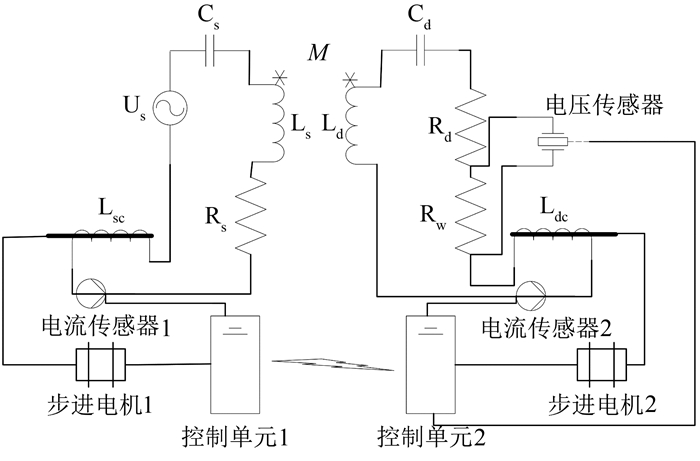
3.1 电感调谐电路为了在较高传输效率下提高系统的接收功率,本文提出基于一种新颖的电感调谐电路的系统优化设计,该电感调谐电路采用小型步进电机来调整电感Lsc和Ldc.电感调谐电路主要包括可调电感设备、电流传感器1、电流传感器2、电压传感器、控制单元1和控制单元2,系统结构图如图 7所示.可调电感Lsc和Ldc分别安装在系统的发射端和接收端.步进电机1调节可调电感Lsc,步进电机2调节可调电感Ldc,可调电感可调范围为3~33 μH.电流传感器1获取发射端电流,电流传感器2获取接收端电流,电压传感器获取接收端电压.依据所采集的数据,控制步进电机1调整可调电感Lsc, 控制步进电机2调整可调电感Ldc.各部分的连接如图 7所示.
|
| 图 7 调谐电路示意图 Figure 7 Tuning circuit diagram |
本文提出基于可调电感的谐振耦合无线电能传输系统参数匹配优化算法,该算法依据发射端和接收端所测参数确定两端匹配的谐振参数,这些所测参数主要包括电流传感器1测量的发射端电流Is、电流传感器2测量的接收端电流Ip和电压传感器测量的接收端电压Uo,Us是发射端的输入电压.在第i时刻, Po_i=Ip_i×Uo_i, Ps_i=Is_i×Us, η_i=Ps_i/Po_i.根据情况3调谐特征, 本文将在较高传输效率下搜寻最大接收功率Po,具体算法设计如下:
1) 当发射端断开时,比较Ps_i和Ps_i+1.如果Ps_i<Ps_i+1, 那么让步进电机1向正方向运行一步,否则,按照反方向运行一步,直到Ps_i达到最大.
2) 当发射端连接时,比较Po_i和Po_i+1, η_i和η_i+1.当Po_i<Po_i+1和η_i<η_i+1时, 让步进电机2向正方向运行一步,否则,按照反方向运行一步,直到Po_i和η_i达到最大.
4 实验验证为了验证本文提出的调谐方法之可行性,本文设计了一个实验平台,其实物图如图 8所示.实验平台主要包括谐振线圈和调谐电路.两线圈中心轴间距为55 cm.调谐电路主要包括可调电感装置、电流传感器1、电流传感器2、电压传感器、控制单元1和控制单元2,框图如图 7所示.可调电感装置主要由可调电感Lsc和Ldc、步进电机1和步进电机2组成.可调电感Lsc和Ldc分别安装在系统的发射端和接收端,可调电感Lsc与步进电机1连接,可调电感Ldc与步进电机2连接.可调电感Lsc和Ldc可以在3~33 μH连续变化.

|
| 图 8 无线电能传输系统的实验平台 Figure 8 Experiment platform of wireless power transfer system |
当系统运行频率f=192 kHz时, 发射端电压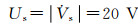
1) 断开接收端,并使Lsc在3~33 μH范围内变化, 发射功率Ps变化曲线如图 9(a)所示.
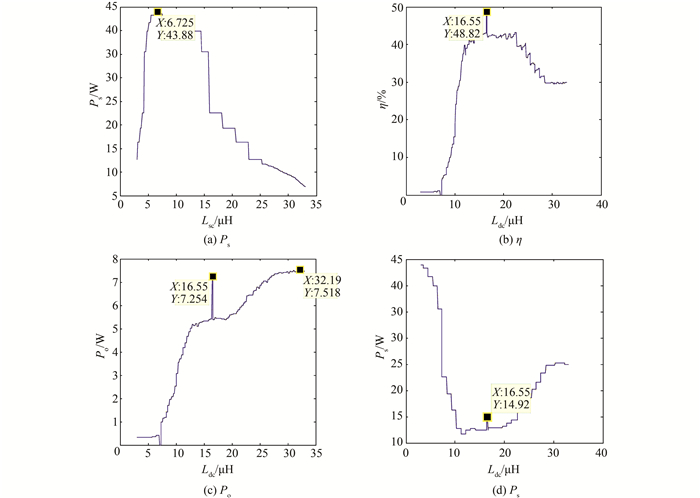
|
| 图 9 Po、Ps、η与Lsc、Ldc的关系曲线 Figure 9 Relation curves of Po, Ps, η with Lsc and Ldc |
当Lsc=6.725 μH时, 发射功率Ps达到最大值43.88 W.保持Lsc的取值不变,进行第2步实验.
2) 连接接收端,并在3~33 μH范围内改变Ldc, 可以得到接收端功率Po、发射端功率Ps、传输效率η分别与可调电感Ldc的关系曲线,如图 9(b)、(c)和(d)所示.
传输效率η的变化曲线如图 9(b)所示,当Ldc=16.55 μH时,η达到最大值48.62%.接收功率Po的变化曲线如图 9(c)所示, 当Ldc=16.55 μH时,Po=7.254 W.射功率Ps的变化曲线如图 9(d)所示, 当Ldc=16.55 μH时,Ps=14.92 W.
当接收端反射电阻达到最大时,表明系统两端的谐振参数最佳匹配.因此,发射功率降低,接收功率趋近最大值,传输效率较高,属于最优状态.实验结果与理论分析一致,说明本文提出的方案可行.
5 结论本文针对磁耦合谐振无线电能传输系统的参数漂移影响能量传输性能问题,将可调电感Lsc和Ldc分别安装在发射端和接收端,利用小型步进电机控制可调电感Lsc和Ldc,通过这一新技术对系统进行优化设计.本文分析了调谐目标和特征,设计了调谐电路和优化算法,并依据所测数据确定发射端和接收端的匹配参数.为了验证调谐方法的可行性,搭建了实验平台,做了相关的实验验证.后续将研究如何将本文的优化设计方案应用于电动汽车无线充电系统中.
| [1] |
杨庆新, 章鹏程, 祝丽花, 等. 无线电能传输技术的关键基础与技术瓶颈问题[J].
电工技术学报, 2015, 30(5): 1–8.
Yang Qingxin, Zhang Pengcheng, Zhu Lihua, et al. Key fundamental problems and technical bottlenecks of the wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 1–8. |
| [2] |
张献, 苑朝阳, 章鹏程, 等. 基于电磁谐振耦合的无线电能传输系统传输能力估算与验证[J].
电工技术学报, 2015, 30(19): 47–54.
Zhang Xian, Yuan Zhaoyang, Zhang Pengcheng, et al. Transmitting capacity estimation and verification for wireless power transmission system via electromagnetic resonant coupling[J]. Transactions of China Electrotechnical Society, 2015, 30(19): 47–54. DOI:10.3969/j.issn.1000-6753.2015.19.008 |
| [3] | Pinuela M, Yates D, Lucyszyn S, Mitcheson P. Maximizing DC-to-load efficiency for inductive power transfer[J]. IEEE Trans. Power Electron., 2013, 28: 2437–2447. |
| [4] |
罗斌, 生茂棠, 吴仕闯, 等. 磁谐振耦合式单中继线圈无线功率接力传输系统的建模与分析[J].
中国电机工程学报, 2013, 21: 170–177.
Luo Bin, Sheng Maotang, Wu Shichuang, et al. Modeling and analysis of magnetic resonance coupling wireless relay power transfer system with single intermediate coil resonator[J]. Proceedings of the CSEE, 2013, 21: 170–177. |
| [5] |
翟渊, 孙跃, 戴欣, 等. 磁共振模式无线电能传输系统建模与分析[J].
中国电机工程学报, 2012, 32(12): 155–160.
Zhai Yuan, Sun Yue, Dai Xin, et al. Modeling and analysis of magnetic resonance wireless power transmission systems[J]. Proceedings of the CSEE, 2012, 32(12): 155–160. |
| [6] | Zhang W, Wong S C, Tse C K, Chen Q. Design for efficiency optimization and voltage controllability of series-series compensated inductive power transfer systems[J]. IEEE Trans. Power Electron., 2014, 29(1): 191–200. DOI:10.1109/TPEL.2013.2249112 |
| [7] | Beh T C, Kato M, Imura T, Hori Y. Wireless power transfer system via magnetic resonant coupling at fixed resonance frequency-power transfer system based on impedance matching[C]// Proc. the 25th World Battery, Hybrid and Fuel Cell Electric Vehicle Symposium & Exhibition, 2010:5-9. |
| [8] | Czarkowski D, Bojarski M, Leon de F. Resonant Inverter Topology and Control Method[P]. U.S. Provisional Patent, 2014. |
| [9] | Jonah O, Georgakopoulos S V. Wireless power transfer inconcrete via strongly coupled magnetic resonance[J]. IEEE Transactionson Antennas and Propagation, 2013, 61: 1378–1384. DOI:10.1109/TAP.2012.2227924 |
| [10] | Deng Q, Liu J, Czarkowski D, et al. Design of a wireless charging system with aphase-controlled inverter under varying parameters[J]. IEEE Trans. Power Electron., 2016, 9(3): 2461–2470. |
| [11] | Deng Q, Liu J, Czarkowski D, et al. Frequency-dependent resistance of Litz-wire square solenoid coils and quality factor optimization for wireless power transfer[J]. IEEE Trans. Ind. Electron., 2016, 63(5): 2825–2837. DOI:10.1109/TIE.2016.2518126 |
| [12] |
孙跃, 夏晨阳, 戴欣, 等. CPT系统效率分析与参数优化[J].
西南交通大学学报, 2010, 45(6): 836–842.
Sun Yue, Xia Chenyang, Dai Xin, et al. Efficiency analysis and parameter optimization of CPT system[J]. Journal of Southwest Jiaotong University, 2010, 45(6): 836–842. |
| [13] |
程志远, 朱春波, 魏国, 等. 串-并补偿结构大功率感应充电系统谐振变换器[J].
电工技术学报, 2014, 29(9): 44–48.
Cheng Zhiyuan, Zhu Chunbo, Wei Guo, et al. Resonant converter for high power ICPT system with series-parallel compensation[J]. Transactions of China Electrotechnical Society, 2014, 29(9): 44–48. |
 2018, Vol. 51
2018, Vol. 51




