文章信息
- 陈俊, 陈仕修, 高深, 季曾超
- CHEN Jun, CHEN Shixiu, GAO Shen, JI Zengchao
- 电子束用聚焦静电透镜的优化设计
- Optimal design of electrostatic focusing lens for electron beam
- 武汉大学学报(工学版), 2018, 51(5): 465-470
- Engineering Journal of Wuhan University, 2018, 51(5): 465-470
- http://dx.doi.org/10.14188/j.1671-8844.2018-05-015
-
文章历史
- 收稿日期: 2017-06-27
2. 湖北工业大学电气与电子工程学院, 湖北 武汉 430068
2. School of Electrical & Electronic Engineering, Hubei University of Technology, Wuhan 430068, China
在高功率微波技术的发展过程中,先后涌现出许多不同类型的高功率微波源,其中一类很重要的微波源是通过电子束与波的相互作用把电子束的能量转化为高频电磁场能量来产生高功率微波.课题组前期分析了真空二极管辐射微波的物理过程,提出电子束与等离子体相互作用是辐射产生的主要原因,通过实验得到不同电子束流大小和束半径下的辐射时频图[1].一般电子枪通过导流系数、压缩比和射程等主要参量来衡量电子束的品质,电磁聚焦系统设计对电子枪性能影响至关重要.为了获得较大的电子束电流,真空电弧等离子阴极作为电子束源已得到广泛应用.Oks采用200~300 kV电压从一种典型结构的空心阳极电弧等离子中提取大电流电子束[2].磁场聚焦[3-5]分为脉冲磁场聚焦和永磁聚焦两种,脉冲磁场一般是由线圈绕制,磁场由脉冲电流激励,可根据等离子体密度调整激励电流,改变磁场强度,其缺点是制作工艺和脉冲电流激励方式决定了脉冲磁场的持续时间,不利于长脉冲的产生.永磁聚焦采用永磁材料通过合理设计能够产生均匀的磁场,无需外部激励,对于产生长脉冲束具有较好的应用潜力,主要缺点在于磁路形成后,能够聚焦的电子束流无法调整.文献[3]采用先磁后电的方式,在电压为33 kV、脉冲磁场强度为500~1 500 Gs(0.05~0.15 T)时,产生脉宽500 μs、幅值70 A的电子束,束斑直径10 cm.文献[4]中采用先电后磁方式,脉冲磁场强度0.1~1 T,电压10~20 kV,提取束流达70 A,束斑直径0.8 cm,脉宽100 μs.文献[5]采用永磁体通过合理设计磁轭产生均匀的磁场,其提取磁场强度为6~10 mT, 电压20 kV,束流100 A, 直径1~6 cm, 脉宽100 μs,其主要优点是无需外部激励,装置体积较小.
本文介绍一种从真空直流电弧等离子体中提取电子[6, 7]的装置,借助计算机仿真软件,采用无磁场引导静电聚焦的方式,提取具有一定能量且半径满足实验要求的长脉宽电子束,将束电子的部分能量转化为微波场的能量,从而产生高功率微波.
1 静电聚焦基本理论静电透镜的电场实际上是一种特殊类型的轴对称场,在忽略空间电荷效应情况下,对称轴的电位分布函数φ(z)完全决定了轴对称场的整个空间电位U(r, z)分布[8]:
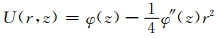
其中:z轴方向与场的对称轴一致;r为径向.
电子所受的径向力为
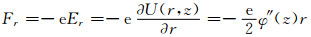
对称轴电位分布函数的二阶导数φ″(z)对分析透镜的汇聚或发散起主要作用,当φ″(z)>0时其作用是使电子汇聚.
由电磁学原理[9]知,电子束内外场强分布如图 1所示,r0为电子束边界.在均匀电荷密度下,利用高斯定理可求得束边缘及束外的场强分别为
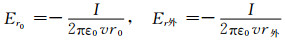
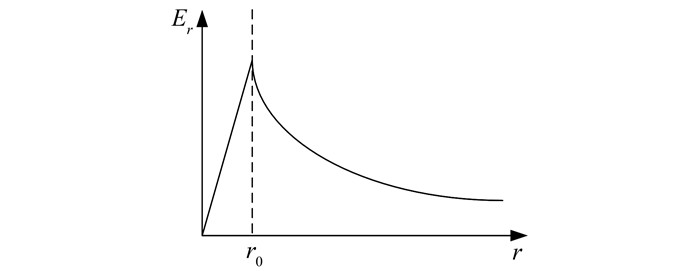
|
| 图 1 轴对称电子束内外电场分布 Figure 1 Distribution of electric field of axisymmetric electron beam |
有了边缘的电场就可以求出边缘电子轨迹方程[8]:
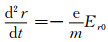
在无场空间、傍轴条件下有
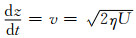
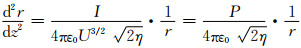 (1)
(1)
式中:P为导流系数; η为电子荷质比.
考虑到空间电荷效应,渡越通道内电位分布分两个区间来讨论.轴对称电子束的轴线位置r=0与电子束边界r=r0之间的电位差ΔU内由下式决定:
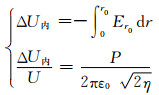 (2)
(2)
轴对称电子束边界r=r0与电子束的渡越通道管壁r=ra之间的电位差ΔU外由下式决定:
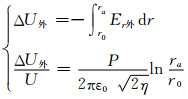 (3)
(3)
以该处的平均电位U为基准点,总的电位差为
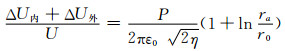 (4)
(4)
由式(4)可知,电压的变化与导流系数、电子束尺寸和漂移管的内径有关.当电子束与漂移管壁之间的空隙很小时,电位下垂并不大,而且比电子束内部的电位下垂小很多;但是如果电子束与漂移管之间的间隙比电子束直径大,则主要的电位下垂是在电子束外面空间.电荷分布不均匀时对空间电位的影响很大,在设计和计算器件尺寸时还应考虑空间电荷的影响.目前电子束引出系统数值模拟的方法应用广泛[13-15],通过对物理模型进行分析,经过数学处理得到轨迹方程的解,存在计算量大和可能不收敛等问题.
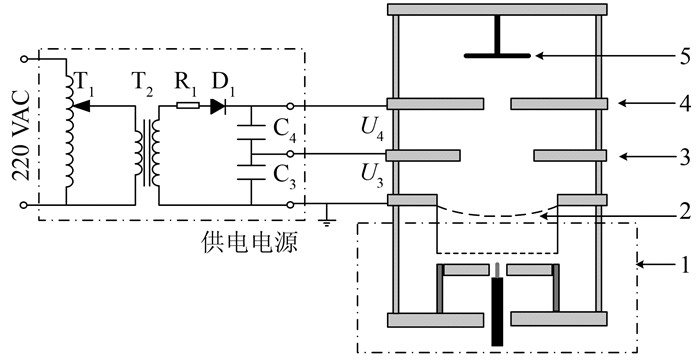
2 实验装置及其线路图实验装置结构如图 2所示,图中1为电子源[6],2为电子发射面,3为聚焦极,4为提取极,5为收集极.采用接入单相220 V交流电,经调压器T1和升压变压器T2(用于产生高压),并经高压硅堆D1半波整流.R1为充电回路限流电阻,高压脉冲电容C3和C4储能,给3、4两电极供电,其电压分别为U3和U4,且U3=U4.
|
| 图 2 实验装置示意图及其接线图 Figure 2 Schematic diagram of experimental device and test circuit |
静电聚焦的效果与静电透镜的场强有很大的关系[16-18],而场强主要取决于静电透镜电极的尺寸、结构以及外施电压,当透镜极上空间的平均场强大于下空间的平均场强时,透镜极附近等位线向下凹;两侧场强相等时,与透镜极等电位的等位线为一直线.两侧场强比值越大,透镜极处等位线凹得越明显,汇聚电场力对电子束的作用区域越大.考虑到电子束与等离子体相互作用区域及器件大小,聚焦效果的量化指标为:射程小于150 mm,电子束的直径不能大于10 mm.实验中通过观察接收极(荧光板)上亮斑的亮度和直径来观测聚焦效果,接收极直径为100 mm.
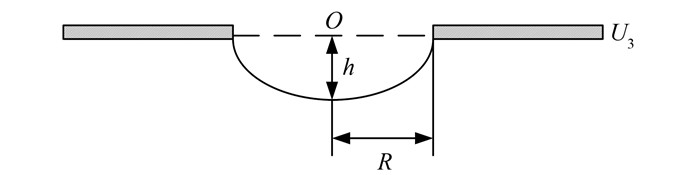
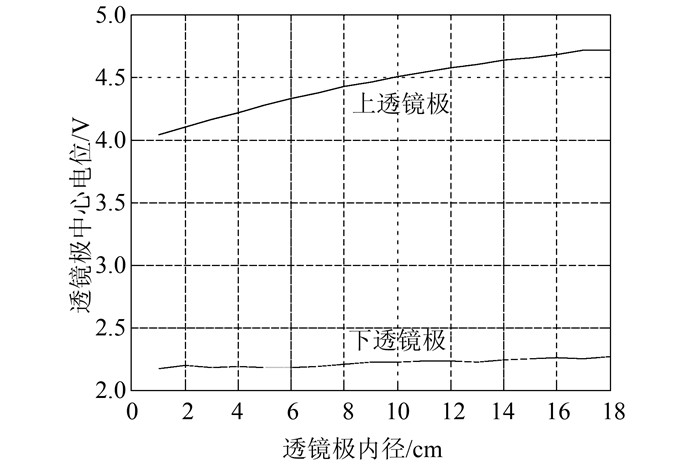
不妨设透镜极电位为U,电位为U的等位线最低点距离透镜中心点的高度为h(图 3),则电场优化计算的目标函数为:调整透镜极的孔径使h达到极大值,即
|
| 图 3 加压后等位线图 Figure 3 Distribution of equipotential line after applying voltage |
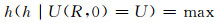 (5)
(5)
但在实际操作中使用此目标函数并不方便,要寻找对称轴上电位等于U的点的位置需要进行插值计算,既不精确又增加工作量.
在不考虑空间电荷时,电场中的每一点的电位分布满足拉普拉斯方程,所以透镜区域的电位是空间坐标的解析函数.由此可以推断,当与透镜极电位相等的等位线的最低点距离透镜极中心越远时,透镜中心位置的电位越高,反之亦然.目标函数[18]可以更改为:透镜极内径为某一数值时,透镜极中心的电位最高.通过电磁仿真软件ANSYS[19, 20]很方便读取透镜极中心的电位值,只要将模型的网格划分足够细,就可达到所要求的精度.
以电极3为例,坐标系选用圆柱坐标系,其坐标原点取透镜极3的中心位置,在读取坐标原点的过程中应保持透镜极4、3的电位恒定.
具体的优化目标函数为

图 4为不同内径下透镜中心点电位,在保持下透镜极孔径不变的情况下,上透镜极中心点的电位随透镜极内径的减小而减小,即其作用区域随透镜内径的减小而减小.只考虑此因素时,应该尽可能将透镜极3的内径做大.
|
| 图 4 不同内径透镜极中心电位 Figure 4 Central potential of the lens at different inner diameters |
实验中采用的透镜类型为内径较大的膜孔透镜,其焦距计算参照下式[17]:
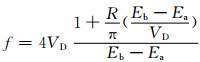 (7)
(7)
其中:f为透镜焦距; VD为膜片电位; Ea、Eb分别为膜片两侧的场强.由式(7)可知,其他条件不变时,内径越大,焦距越长,其汇聚能力变弱.还有一点需要考虑,即电子束到达透镜极3所在平面的扩散半径,应该确保电子束通过透镜极3的内孔.综合考虑上述因素,确定透镜极3的内径为100 mm.
设透镜电极之间的距离为l(如l 34为电极3、4之间的距离)以及各透镜极的内孔径Φ(如透镜极3的内孔径为Φ3),主要尺寸有:l23=72 mm,l34=32 mm;Φ2=120 mm,Φ3=100 mm,Φ4=80 mm.运用Magic粒子模拟软件[21]进行仿真,仿真结果如图 5所示,图 5(a)~(d)分别为1.908、2.494、4.399和8.210 ns时的电子束运动轨迹,电子从阴极发射出来有一定角度的扩散,经过静电透镜的聚焦作用,电子逐步朝轴线汇聚,稳定的束斑直径为8.93 mm.

|
| 图 5 Magic仿真结果 Figure 5 Results of Magic simulation |
电子轰击荧光板时会发出蓝白色的亮斑,从荧光板上亮斑的亮度和直径,可以粗略估计电子密度的大小和聚束的效果.在保证电子源不变的前提下,通过不断调节加速电极的电压得到图 6结果.为改善聚焦效果,发射面改为球面结构[10],如图 2所示.

|
| 图 6 不同电压下的聚焦效果 Figure 6 Focusing effect at different voltages |
由图 6可得如下结论:
1) 在没有透镜电压或透镜电压较低时,电子束几乎没有聚焦效果.电压30 kV时可以看出,接收极上荧光粉发光的范围较大,密度分布较均匀,亮度较弱.
2) 当透镜极电压加到40 kV左右时,接收极中心首次出现亮斑,亮度较强,边界稍模糊,可以看出电子束得到了聚焦;电压继续升高,亮斑逐渐变亮,面积越来越小,证明电子束逐渐汇聚,接收极接受到的电子密度越来越高.在电压加到60 kV时达到最好聚焦效果,此时亮斑比较明亮,直径约为10 mm.
3) 电压继续升高,电子束在接收极位置逐步扩散,70 kV时几乎观察不到亮斑.
对透镜极3的孔径进行优化设计,实验中不同的聚焦效果如图 7所示,10 cm孔径聚焦效果最好,10 cm也正是本次设计优化计算得到的结果.同时,注意到实验得到的束斑比仿真结果略大,主要的原因是空间电荷效应的影响,其次,器件安装的精度也会影响实验的结果.

|
| 图 7 不同孔径下的聚焦效果 Figure 7 Focusing effect at different apertures |
1) 采用ANSYS有限元分析软件与Magic粒子模拟软件相结合的方法对实验装置进行设计,优化了器件参数,避免了复杂的数值模拟运算.
2) 透镜极位置及电位固定的情况下,寻找透镜作用区域最大的方法,即将寻找与透镜极等电位的等位线的最低点转化为寻找使透镜极中心电位达到最大值的对应透镜极内径.
3) 实验中随着外加电压逐步增加,收集极上的光斑向中心汇聚,亮度增强,电压过高时焦距变短光斑发散,60 kV时达到理想的聚焦效果.
| [1] |
季曾超, 陈仕修, 高深, 等. 真空二极管辐射微波的机理分析[J].
物理学报, 2016, 65(14): 145202.
Ji Zengchao, Chen Shixiu, Gao Shen, et al. Analysis of mechanism of radiating microwave from vacuum diode[J]. Acta Physica Sinica, 2016, 65(14): 145202. DOI:10.7498/aps.65.145202 |
| [2] | Oks E M. Generation of electron beams from vacuum arc plasmas[C]//Discharges and Electrical Insulation in Vacuum, 2000. Proceedings. ISDEIV. XIXth International Symposium on. IEEE, 2000, 2: 605-608. https://ieeexplore.ieee.org/document/879062/ |
| [3] | Bugaev A S, Gushenets V I, Khuzeev Y A, et al. High-density plasma low energy electron gun based on vacuum arc in a strong magnetic field[C]//Discharges and Electrical Insulation in Vacuum, 2000. Proceedings. ISDEIV. XIXth International Symposium on. IEEE, 2000, 2: 629-632. https://ieeexplore.ieee.org/document/879068/ |
| [4] | Oks E M, Brown I G. Electron beam extraction from a broad-beam vacuum-arc metal plasma source[J]. IEEE Transactions on Plasma Science, 1998, 26(5): 1562–1565. DOI:10.1109/27.736062 |
| [5] | Goncharov A A, Dobrovolskiy A M, Dunets S M, et al. Electrostatic plasma lens for focusing negatively charged particle beams[J]. Review of Scientific Instruments, 2012, 83(2): 2B–723B. |
| [6] | Jiang Haiyan, Gai Fei, Chen Shixiu, et al. Experimental study of electron gun with hollow-anode vacuum-arc-plasma cathode[J]. IEEE Transactions on Electron Devices, 2004, 61(6): 1895–1899. |
| [7] |
陈俊, 陈仕修, 盖斐, 等. 空心阳极等离子体阴极提取电子束的实验分析[J].
高电压技术, 2015, 41(2): 560–564.
Chen Jun, Chen Shixiu, Gai Fei, et al. Experimental analysis of electron beam extracting from a device with hollow-anode vacuum-arc-plasma cathode[J]. High Voltage Engineering, 2015, 41(2): 560–564. |
| [8] |
张以忱.
电子枪与离子束技术[M]. 北京: 冶金工业出版社, 2014.
Zhang Yichen. Electron Gun and Ion Beam Technology[M]. Beijing: Metallurgical Industry Press, 2014. |
| [9] |
赵凯华, 陈熙谋.
电磁学[M]. 北京: 高等教育出版社, 2003.
Zhao Kaihua, Chen Ximou. Electromagnetics[M]. Beijing: Higher Education Press, 2003. |
| [10] |
张顺华.
离子源和大功率中性束源[M]. 北京: 原子能出版社, 1987.
Zhang Shunhua. Ion Source and High Power Neutral Beam Source[M]. Beijing: Atomic Energy Press, 1987. |
| [11] | Molokovsky S I, Sushkov A D. Intense Electron and Ion Beams[M]. Springer, 2005. |
| [12] | Miller R B. Intense Charged Partical Beams[M]. Springer, 1982. |
| [13] |
仲雪飞, 屠彦, 朱豪. 静电透镜的优化设计[J].
电子器件, 1998, 21(4): 118–122.
Zhong Xuefei, Tu Yan, Zhu Hao. Optimization of the electrostatic lens[J]. Journal of Electron Device, 1998, 21(4): 118–122. |
| [14] |
高广君, 和存立. 静电聚焦的微机模拟[J].
齐齐哈尔师范学院学报(自然科学版), 1991, 11(4): 5–9.
Gao Guangjun, He Cunli. The simulation of electrostatic focusing by computer[J]. Journal of Qiqihar Normal College (Nature Sciences), 1991, 11(4): 5–9. |
| [15] |
孙伯尧, 汪健如.
电子离子光学计算机辅助设计[M]. 北京: 清华大学出版社, 1991.
Sun Boyao, Wang Jianru. Electronic Ion Optical Computer Aided Design[M]. Beijing: Tsinghua University Press, 1991. |
| [16] |
应根裕.
电子光学[M]. 北京: 清华大学出版社, 1984.
Ying Genyu. Electronic Optics[M]. Beijing: Tsinghua UniversityPress, 1984. |
| [17] |
杜秉初, 汪健如.
电子光学[M]. 北京: 清华大学出版社, 2002.
Du Bingchu, Wang Jianru. Electronic Optics[M]. Beijing: Tsinghua University Press, 2002. |
| [18] |
陈仕修. 静电透镜式电场优化计算的目标函数的提法[J].
高电压技术, 1998, 24(4): 9–12.
Chen Shixiu. Indication on criterion function for optimizing computation on ESLF[J]. High Voltage Engineering, 1998, 24(4): 9–12. |
| [19] |
阎照文.
ANSYS 10.0工程电磁分析技术与实例详解[M]. 北京: 中国水利水电出版社, 2006.
Yan Zhaowen. Engineering Electromagnetic Analysis Techniques and Examples at ANSYS 10[M]. Beijing: China Water & Power Press, 2006. |
| [20] |
倪光正, 杨仕友, 钱秀英, 等.
工程电磁场数值计算[M]. 北京: 机械工业出版社, 2004.
Ni Guangzheng, Yang Shiyou, Qian Xiuying, et al. Engineering Electromagnetic Field Numerical Calculation[M]. Beijing: Machinery Industry Press, 2004. |
| [21] | Goplen B, Ludeking L, Smithe D, et al. User-configurable MAGIC for electromagnetic PIC calculation[J]. Computer Physics Communications, 1995, 87(1-2): 54–86. DOI:10.1016/0010-4655(95)00010-D |
 2018, Vol. 51
2018, Vol. 51



