武汉大学学报(工学版)   2016, Vol. 49 Issue (4): 603-609

文章信息

马晓博, 柯德平, 孙元章
MA Xiaobo, KE Deping, SUN Yuanzhang
含分布式电源的配电网保护方案对比及应用分析
Comparison and application analysis of protection scheme of distribution network with DG
武汉大学学报(工学版), 2016, 49(4): 603-609
Engineering Journal of Wuhan University, 2016, 49(4): 603-609
http://dx.doi.org/10.14188/j.1671-8844.2016-04-020

文章历史

收稿日期: 2015-07-01
 Abstract              PDF               Figures               Tables
引用本文 0
马晓博, 柯德平, 孙元章. 含分布式电源的配电网保护方案对比及应用分析[J]. 武汉大学学报(工学版), 2016, 49(4): 603-609.
MA Xiaobo, KE Deping, SUN Yuanzhang. Comparison and application analysis of protection scheme of distribution network with DG[J]. Engineering Journal of Wuhan University, 2016, 49(4): 603-609.
含分布式电源的配电网保护方案对比及应用分析
马晓博1,2, 柯德平1, 孙元章1     
1. 武汉大学电气工程学院，湖北 武汉 430072;
 2. 天津市电力公司，天津 300202
收稿日期: 2015-07-01
作者简介: 马晓博(1990-)，女，硕士研究生，主要从事电力系统继电保护研究，E-mail：Xiaob-Ma@whu.edu.cn..
通讯作者: 孙元章(1954-)，男，教授，博士生导师，主要从事电力系统运行及控制研究，E-mail:yzsun@whu.edu.cn.
基金项目: 国家重点基础研究计划(973计划)资助项目(编号：2012CB215101).
摘要: 含分布式电源(Distributed Generation，DG)的配电网线路发生故障时，DG的注入电流可能会影响流过保护装置的短路电流，使传统3段式电流保护发生拒动或者误动.针对此问题，提出3种含DG配电网的保护方案.详细对比了3种保护方案的适用范围及其优缺点，并应用到实际配电系统算例中进行仿真分析，结果验证了所提保护方案的有效性和合理性.在设计保护方案时，需要从配电网结构、DG接入情况、故障类型等多个方面进行评估，选择适应具体条件的最优保护方案，确保配电系统的安全可靠运行.
关键词： 分布式电源     配电网     阶段式电流保护     准入容量     保护方案    
Comparison and application analysis of protection scheme of distribution network with DG
MA Xiaobo1,2, KE Deping1, SUN Yuanzhang1     
1. School of Electrical Engineering, Wuhan University, Wuhan 430072, China;
 2. Tianjin Electric Power Company, Tianjin 300202, China
Abstract: When short fault occurs at different positions of distribution system connected with distributed generation(DG),it may have some effect on the traditional stagewise current protection and lead to the maloperation of protection. Three new protection schemes for distribution system with DG are proposed to solve this problem. The merits, demerits and application of every scheme are compared and applied to the practical distribution system. The effectivenesses and rationalities of the schemes proposed are shown by the simulation and comparison. The optimal scheme which meets the specific situation by evaluating the configuration of distribution system, DG condition and fault type is selected to ensure the safety and stability of operation.
Key words: distributed generation (DG)     distribution network     stagewise current protections     permitted capacities     protection scheme    

以太阳能发电、风力发电、小型燃气轮机、燃料电池等为代表的分布式电源(Distributed Generation，DG)已得到了越来越多的应用.DG一般分布在负荷附近，可以为电网带来节省投资、降低网损、提高供电可靠性等一系列经济效益；同时，DG接入配电系统后，改变了原有配电网的单电源、放射状结构以及系统的潮流方向，使之变为多端电源供电系统，严重影响配电网的潮流，增加配电网的短路电流，使电压调节变得困难.

已有大量文献研究DG接入对配电网的线路潮流[1]、静态电压[2]、谐波[3]、网损[4]和短路电流分布[5]的影响，其中，评估分布式电源接入对配电网中电流保护的影响已引起了相关电力工作者和研究人员的广泛关注，针对此问题制定出合理的调整措施和解决方案，可以为将来更多带有分布式电源的配电网的稳定运行打好基础.目前含DG的配电网保护方案主要有：1)限制DG的接入位置和接入容量，如文献[6]提出了考虑相间短路故障对保护影响的DG准入容量的计算模型，但是只针对2个DG接入的情况，不具有普适性.2)限制故障点短路电流，文献[7-9]都是在串联电抗器的基础上研究如何减小故障电流.3)采用通信网络实现配电网保护间的信息交换，但是需要依靠发达可靠的通信网络[10].4)开发继电保护整定计算系统，但大部分都没有考虑DG实际运行中随机性出力的问题[11].5)改变配电网原有保护方案.由于DG的多样性和运行方式的灵活性，固定的保护方案很难全面适应配电网的不同场景，又由于不同的保护方案出发点不同，适用范围、实现方法以及优缺点也不相同，因此在具体设计保护方案时，需要从配电网结构、DG接入情况、故障类型等多个方面进行评估，选取最优的保护方案，国内外目前尚无此方面的报道.

通过归类短路故障相对于DG的位置，详细分析了DG接入配电网导致传统3段式电流保护误动、拒动或无法识别故障的情况，针对此问题，提出了3种含DG配电网的保护方案：1)在原有线路保护配置不变的基础上，限制DG的接入容量.2)在DG接入情况(类型、容量、接入位置)确定的前提下，对传统电流保护原则重新整定.3)将配电网系统分区改进，DG上游区域配置方向纵联保护，同时仍保留定时限过电流保护.详细对比了3种保护方案的适用范围及其优缺点，并应用到实际配网算例中进行仿真计算，结果表明，有针对性的分析不同配电网场景，选择适合其条件的最优保护方案，可以规避甚至消除DG对配电网电流保护的影响.

1 DG接入的配电网系统 1.1 DG接入对配电网电流保护的影响

分布式电源接入配电网以后，现有保护的选择性、灵敏性以及可靠性都会受到影响，下面通过归类短路故障相对于DG的位置来分析DG接入配网对3段式电流保护的影响.

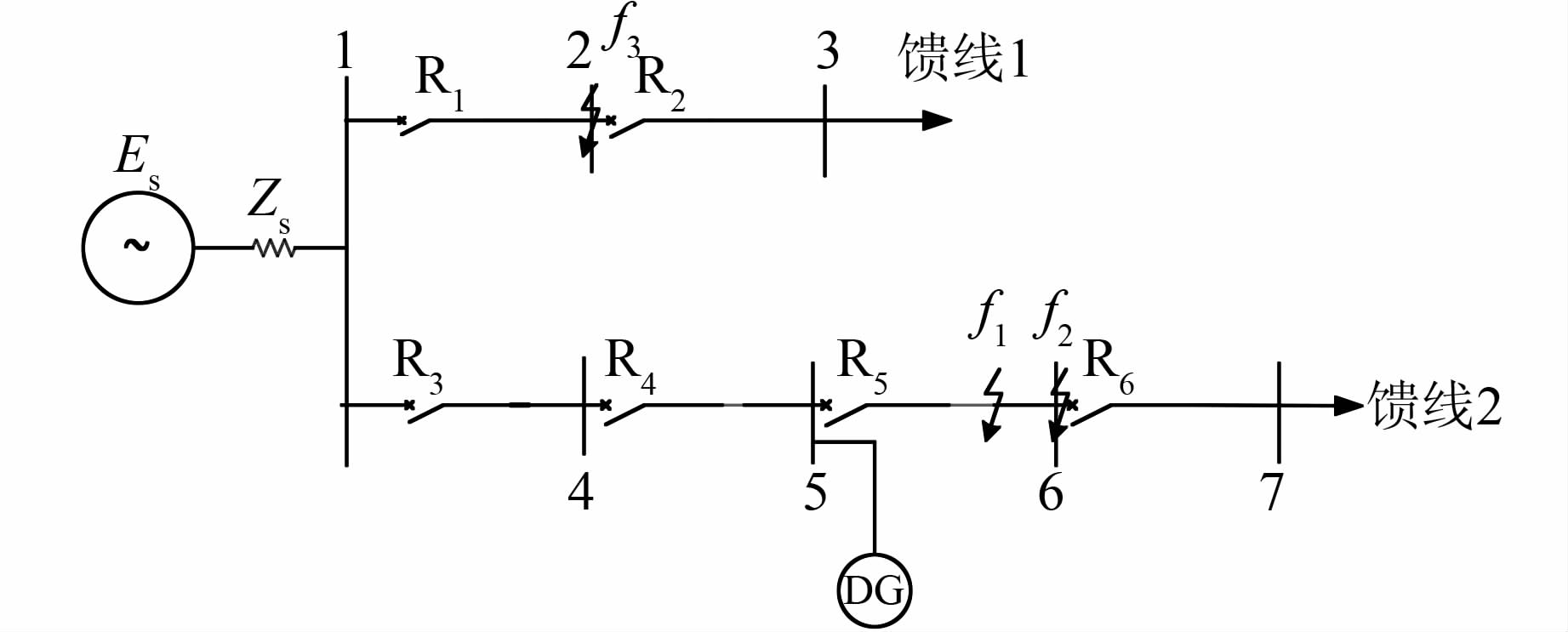
图 1是某典型10 kV配电网示意图，由两线馈线组成，母线3和母线7位于馈线末端，直接与负荷相连，断路器编号R1，R2，…，R6分别表示保护1，保护2,…,保护6.DG通过变压器接入配电网，从继电保护的角度分析，由于只需要考虑线路故障期间DG提供的短路电流，DG可以用一个电源串联电抗的模型表示，不同类型的DG提供的短路电流不同，但这并不影响分析结论.以对电力系统危害最为严重的三相短路故障为例进行分析.

图 1 DG接入的配电网系统 Figure 1 Distribution system with DG
图选项
1.1.1 故障发生在DG上游

DG的上游线路发生短路故障时，DG提供的反向注入电流可能会影响流过上游保护的短路电流，导致其误动作.比如：在线路1-4上发生短路故障，有可能导致R4(Ⅰ段或Ⅱ段保护)误动作.因为R4的Ⅱ段保护整定值比Ⅰ段要小，同时，DG上一段相邻线路1-4的所有故障点中，1-4末端发生短路故障流过保护R4的电流最大.因此，只要保证R4的Ⅱ段保护正确动作，使流过保护R4的最大短路电流小于其Ⅱ段保护整定值，DG上游的其他保护均不会误动作.

值得注意的是，DG上游发生短路故障时，即使保护可靠动作切除故障，DG仍将向故障点提供电流，导致自动重合闸失败，瞬时性故障有可能会发展成为永久性故障.因此，需要在DG处安装孤岛检测装置，在此情况下将DG主动从电网解列，停止向故障点提供持续的短路电流.

1.1.2 故障发生在DG下游

DG下游线路发生短路故障(如f1处)，保护R5能准确动作切除故障，但是DG注入的短路电流对流过保护R4的电流产生汲流作用，使其电流减小.因为R4的Ⅰ段保护只作为本线路的主保护，不受电流值减小的影响，故其保护范围不变；由于DG接在母线上，Ⅱ段保护范围虽然减小，但是仍能保护到本线路的全长；而Ⅲ段保护作为本线路的后备保护，保护范围减小，有可能发生拒动，因此，要保证R4的Ⅲ段至少要保护到下一段相邻线路的全长，即要求线路6-7首端f2发生短路时，流过保护R4的短路电流要大于R4的Ⅲ段保护整定值.

当线路6-7上发生短路故障，本应由R6的瞬时电流保护动作切除故障，但DG接入系统后，DG和系统电源一起向短路点提供故障电流，可能导致R5的Ⅰ段保护误动作，即Ⅰ段保护范围延伸到下一段线路，从而与R6的Ⅰ段保护失去选择性(文章只讨论保护范围延伸到下一段相邻线路的情况).线路6-7所有可能的故障点中，首端f2处短路时流过R5的短路电流最大，因此要保证流过保护R5的最大短路电流不引起其Ⅰ段保护误动作，此分析方法也适用于DG下游其他保护的Ⅰ段.

虽然DG接入后使流过保护R5的故障电流增大，从而使其Ⅱ段保护范围扩大，但是R5的Ⅱ段保护整定值始终大于R6的Ⅰ段保护整定值，即R5的Ⅱ段保护范围不会超过R6的Ⅰ段保护范围，R5的Ⅱ段保护不会误动作.

1.1.3 故障发生在DG相邻线路

当DG相邻线路2-3上发生短路故障时，本应由保护R2动作切除故障，DG接入系统后向保护R1提供反向注入电流，可能导致R1的Ⅰ段保护误动作，即Ⅰ段保护范围延伸到下一段相邻线路，从而失去选择性.由1.2小节分析可知：线路2-3所有可能的故障点中，首端f3处短路时流过R1的短路电流最大，因此要保证此最大电流不引起其Ⅰ段保护误动作.R1的Ⅱ段保护的分析方法与1.2小节R5的Ⅱ段保护一致，即R1的Ⅱ段保护范围不会超过R2的Ⅰ段保护范围而误动作.由于1.1小节中已经对流过R4的短路电流进行约束(保证R4的Ⅱ段保护不误动作)，当DG相邻线路上发生故障时，DG上游保护R3和R4均可靠动作.

多个DG同时接入配网系统的情况与单个DG相似，仍将系统分为3个区域(DG上游、下游以及相邻线路)进行分析.

1.2 含DG配电网的馈线保护方案 1.2.1 方案1

详细分析了DG接入配电网对传统3段式电流保护的影响，从配电网原有线路保护可靠动作的角度出发，建立了计算分布式电源准入容量的数学模型，并采用小生境遗传算法求解模型.规划人员可以方便地运用该方案确定配电网系统中分布式电源的准入容量.

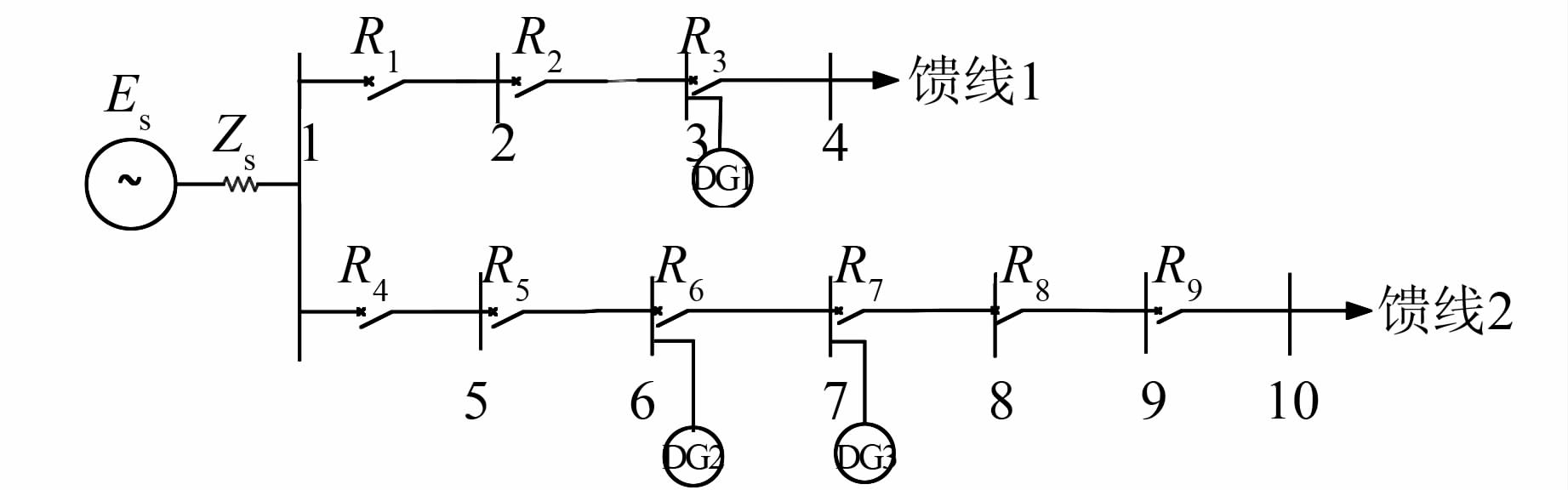
在图 2所示配电系统的母线3、6、7处接入3个DG，建立DG最优接入容量的规划模型，目标函数取max(SDG1+SDG2+SDG3)，以配网原有3段式电流保护正确动作为约束条件.

图 2 多个DG接入的配电网系统 Figure 2 Distribution system with multiple DG
图选项
$\begin{gathered} \max ({S_{{\text{DG}}1}} + {S_{{\text{DG}}2}} + {S_{{\text{DG}}3}}) \hfill \\ {\text{s}}{\text{.t}}\left\{ {\begin{array}{*{20}{c}} {{I_1} < I_{{{\text{R}}_{\text{1}}}}^{\text{I}},{I_2} < I_{{{\text{R}}_2}}^{Ⅱ}(线路2 - 3首端短路)} \\ {{I_2} < I_{{{\text{R}}_2}}^{\text{I}}(线路3 - 4首端短路)} \\ {{I_2} > I_{{{\text{R}}_2}}^{Ⅲ}(线路3 - 4末端短路)} \\ {{I_5} < I_{{{\text{R}}_5}}^{Ⅱ},{I_4} < I_{{{\text{R}}_4}}^{\text{I}}(线路1 - 5末端短路)} \\ {{I_6} < I_{{{\text{R}}_6}}^{11},{I_5} < I_{{{\text{R}}_5}}^{\text{I}}(线路5 - 6末端短路)} \\ {{I_6} < I_{{{\text{R}}_6}}^{\text{I}},{I_5} > I_{{{\text{R}}_5}}^{Ⅲ}(线路7 - 8首端短路)} \\ {{I_7} < I_{{{\text{R}}_7}}^{\text{I}},{I_6} > I_{{{\text{R}}_6}}^{Ⅲ}(线路8 - 9首端短路)} \\ {{I_8} < I_{{{\text{R}}_8}}^{\text{I}}(线路9 - 10首端短路)} \end{array}} \right. \hfill \\ \end{gathered} $    (1)

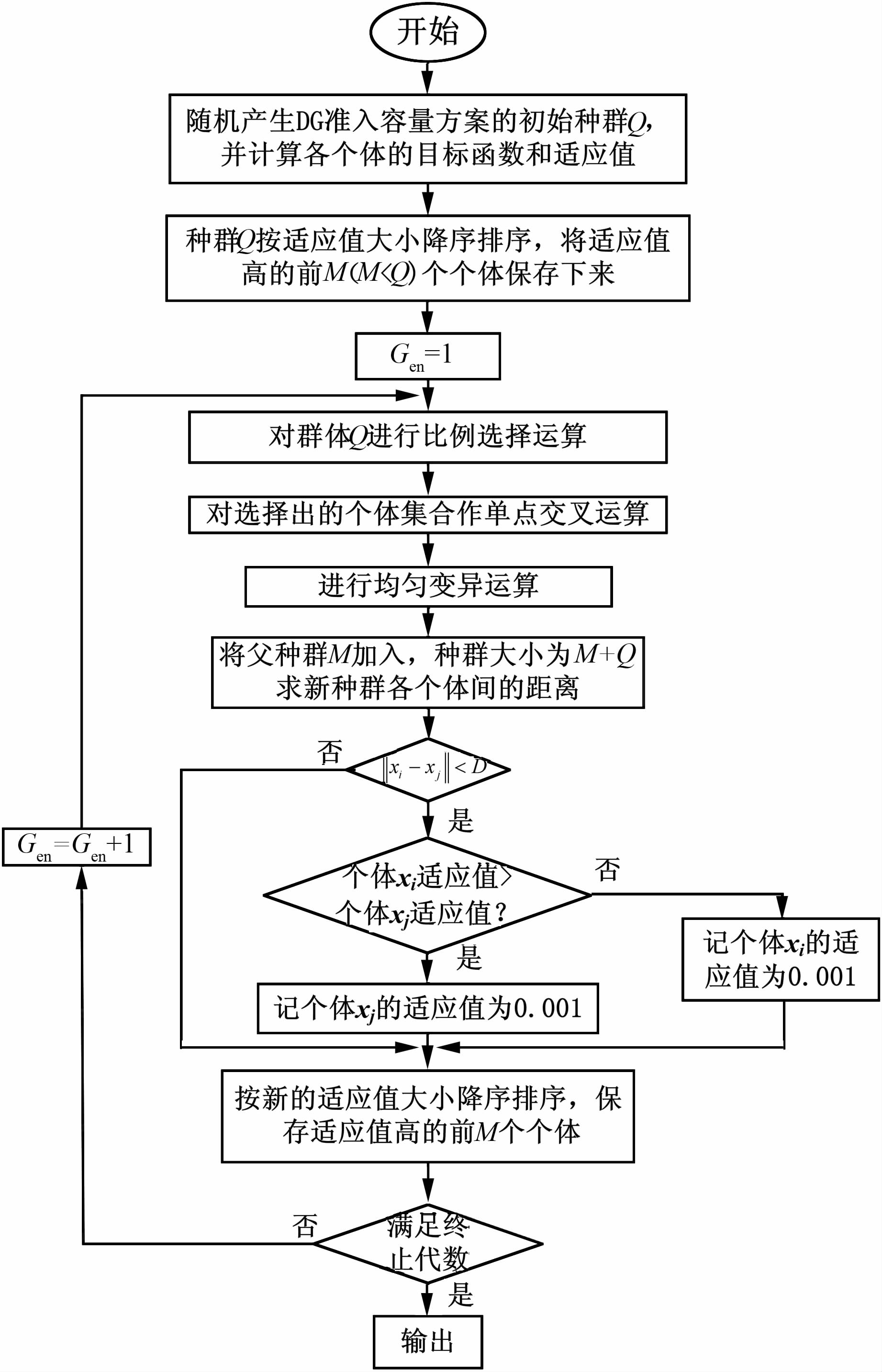
上述模型为混合整数非线性规划模型，很难运用确定性规划理论对其求解；人工智能算法具有获取全局最优解的能力，故采用小生境遗传算法来求解所建立的准入容量计算模型，具体步骤如下[12].

1) 随机产生DG准入容量方案的初始种群Q，并计算各个体的目标函数和适应值.

2) 将种群Q按适应值大小进行降序排序，将适应值高的前M个个体保存下来.

3) 对群体Q进行比例选择运算.

4) 对选择出的个体集合作单点交叉运算.

5) 进行均匀变异运算.

6) 求出新种群各个体的目标函数和适应值，将步骤(2)中保存的父种群M加入，种群大小为M+Q.

7) 计算各个体间距离：

$\left\| {{x_i} - {x_j}} \right\| = \sqrt {\sum\limits_{k = 1}^Q {({x_{ik}} - {x_{jk}})} } $
$i=1,2,\ldots ,Q+M-1;j=i+1,\ldots ,Q+M$

当‖xi－xj‖<D时，若个体xi的适应值大于个体xj的适应值，则记xj的适应值为0.001，反之则记xj的适应值为0.001，这样在距离D内只存在一个优良个体，既维护了种群的多样性，又使个体能够在整个约束空间分散开.

8) 根据M+Q个个体的新适应值进行降序排序，保存适应值高的前M个个体.

9) 若不满足终止代数，则跳转到步骤(3)，重新计算；若满足终止次数，则输出计算结果，算法结束.

具体流程如图 3所示.

图 3 小生境遗传算法流程图 Figure 3 Flowchart of niche genetic algorithm
图选项

此方案在原有保护配置保持不变的基础上，通过限制多个DG的准入容量来保证保护的准确可靠动作，操作简单，工程上易实现.但是DG的接入容量受到很大制约，这违背了在配电网中接入DG的初衷，没有达到充分利用可再生能源、减少输电投资的目的.

1.2.2 方案2

在分布式电源接入情况(类型、容量、位置)确定的前提下，需要对馈线保护原则重新整定以保证线路各保护可靠动作.假设DG以某一确定容量接入图 1所示系统的母线5处，考虑DG的随机性出力变化，电流保护整定值相应调整.

1) DG上游保护的整定计算

对于DG上游的保护R4，当R4下游发生短路故障时，R4只流过系统提供的短路电流，DG的接入对其产生汲流作用，由1.2小节分析可知，R4的Ⅰ段和Ⅱ段保护均不会误动作，因此仍按照原系统最大运行方式下线路末端三相短路时，流过保护的短路电流进行整定，即

$I_{{{\text{R}}_{\text{4}}}(原)}^{\text{I}}\text{=}K_{\text{rel}}^{\text{I}}I_{f\text{B}\max }^{(3)}$    (2)
$I_{{{\text{R}}_{4}}(原)}^{\text{II}}=K_{\text{rel}}^{\text{II}}I_{{{\text{R}}_{5}}(原)}^{\text{I}}$    (3)

由于R4的Ⅲ段电流保护作为本线路的后备保护，保护范围减小，有可能发生拒动，因此，要保证R4的Ⅲ段保护至少要保护到下一段相邻线路的全长，要求Ⅲ段保护的动作电流小于线路6-7首端f2发生故障时的短路电流，即

$I_{\text{R}_4}^{\text{III}}={{I}_{4}}(线路6\text{-}7首段短路)$    (4)

最后，取$I_{{{R}_{4}}}^{\text{III}}和I_{{{R}_{4}}}^{\text{III}}(原)$之间的最小值作为R4的Ⅲ段保护整定值.

当R4的上游及其相邻线路发生短路故障，有可能导致其误动，因此，需要对R4(Ⅰ段和Ⅱ段)重新整定.DG接入系统以后，保护R4的上游线路1-4发生故障时，相当于DG单电源向R4及其上游供电，短路点距离R4越近，此时流过的短路电流越大，R4越有可能误动作，因此，R4的Ⅰ段保护应按躲过线路1-4末端发生三相短路故障的短路电流来整定，即

$I_{{{\text{R}}_{\text{4}}}}^{\text{I}}{\text{ = }}{I_4}{\kern 1pt} {\kern 1pt} {\kern 1pt} (线路1 - 4末端)$    (5)

然后，取$I_{{{R}_{4}}}^{\text{I}}和I_{{{R}_{4}}}^{\text{I}}(原)$之间的最大值作为R4的Ⅰ段保护整定值.

同理

$I_{{{\text{R}}_{\text{4}}}}^{\text{Ⅱ}}{\text{ = }}{I_4}{\kern 1pt} {\kern 1pt} {\kern 1pt} (线路1 - 4末端)$    (6)

取$I_{{{R}_{4}}}^{\text{II}}和I_{{{R}_{4}}}^{\text{II}}(原)$之间的最大值作为R4的Ⅱ段保护整定值.

对于DG上游保护R3，分析原理同R4类似：当DG下游发生短路故障时，保护R3(Ⅰ段、Ⅱ段和Ⅲ段)不会误动作，保护仍按照原配电网结构整定.当R3的上游线路发生短路故障时，R3的Ⅰ段和Ⅱ段保护应按躲过线路1-2首端发生三相短路故障的短路电流来整定，然后与原整定值相比取较大者.

2) DG下游保护的整定计算

DG接入配电网，对于DG下游的保护而言，相当于系统电源和DG组成的双电源系统向其供电，当DG下游发生短路故障时，保护R5和R6可能发生误动(Ⅰ段和Ⅱ段)，因此要对保护重新整定：

$I_{{{\text{R}}_{\text{5}}}}^{\text{I}}{\text{ = }}K_{{\text{rel}}}^{\text{I}}I_{fB\max 5}^{(3)}$    (7)
$I_{{{\text{R}}_{\text{6}}}}^{\text{I}}{\text{ = }}K_{{\text{rel}}}^{\text{I}}I_{fB\max 6}^{(3)}$    (8)

其中，IfBmax5(3)、IfBmax6(3)分别为双电源系统最大运行方式下R5和R6所在线路末端发生三相短路故障时，流过保护的最大短路电流.

对于R5的Ⅱ段保护，整定公式：

$I_{{{\text{R}}_{\text{5}}}}^{\text{I}}{\text{ = }}K_{{\text{rel}}}^{Ⅱ}I_{{\text{R6}}}^{\text{I}}$    (9)

其中，IR6Ⅰ为DG接入配网后，双电源系统下相邻线路保护R6的Ⅰ段动作电流.

保护R6安装在馈线末端母线，只设置了瞬时电流速断保护(Ⅰ段)和定时限过电流保护(Ⅲ段)2段式电流保护.

3) DG相邻线路上保护的整定计算

由1.3节分析可知，DG接入配电网，其相邻线路发生短路故障时，相当于系统电源和DG组成的双电源系统向保护R1和R2提供反向短路电流，可能导致其误动作，需要重新对保护(Ⅰ段和Ⅱ段)进行整定.原理同DG下游保护的整定相似.

此方案在DG接入情况(接入容量、位置、类型、数量)确定的前提下，对传统3段式电流保护重新整定，考虑DG随机性出力的特点，实现了保护整定值随DG输出功率变化自动调整，但是保护的灵敏度、可靠性可能受到影响.

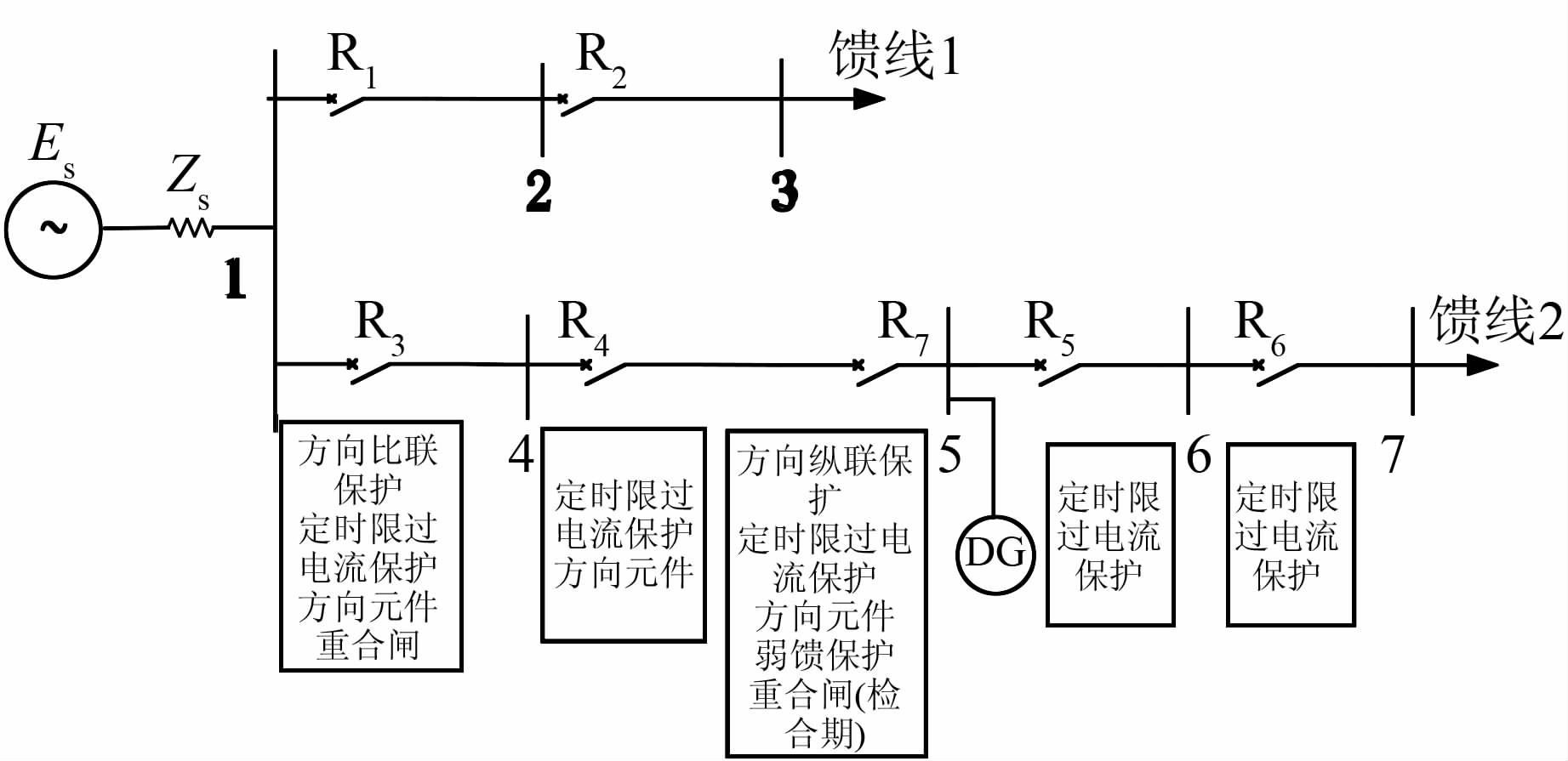
1.2.3 方案3

提出了一种新的保护方案，能够在不改变配电系统原有断路器配置的前提下快速准确地将故障线路从两端切除：将配网系统分区进行改进，DG上游区域配置方向纵联保护，整条馈线则保留定时限过电流保护.

如图 4所示配电网，在馈线2的母线5处接入分布式电源后，DG上游区域相当于双电源供电系统，若发生短路故障，原继电保护只在系统侧装设断路器，这样即使保护可以可靠动作，DG仍会向故障点持续注入短路电流，若故障为瞬时性故障，将导致重合闸失败.因此，需要保护在故障线路两端同时切除故障.在保护R3和R7处配置方向纵联保护，可以瞬时动作切除DG上游区域的任何故障点，同时，在保护R3和R4处配置带有方向元件的定时限过电流保护.特别地，当DG接入容量较小或者已经运出运行时，保护R7的灵敏度可能不足以动作，这时还应在R7处配置弱馈保护[13]，无论DG接入容量如何变化，R3和R7处的方向纵联保护都可以准确保护DG上游的整个区域.同时，在保护R3和R7处配置重合闸装置，当保护R3切除故障后，R3处的自动重合闸启动恢复系统供电，由于此时保护R7处的断路器已经断开，R3的重合闸装置不需要检同期；而R7的重合闸功能在R3动作后才可以启动，此时DG已经接入配电网，R7的重合闸装置需要检同期功能.将DG上游区域看成一个整体，任一点发生短路故障时，R3和R7的重合闸装置可以恢复系统供电，若故障为永久性故障，则由R3和R4处的定时限过电流保护选择性切除.

图 4 配电网线路保护配置图 Figure 4 Protection configuration of dstribution system
图选项

对于DG下游区域，相当于单端供电系统，保留原馈线上的定时限过电流保护，同时根据实际情况，采用前加速或者后加速的电流保护方案，可以有选择性地切除故障线路.对于没有接DG的相邻馈线，按照传统的重合闸前加速或后加速方式的电流保护进行配置.

按照上述方案重新配置以后，当DG上游发生短路故障时，R3和R7纵联保护的方向元件判断故障为正方向，认为发生了区内故障，可以瞬时动作，断路器断开故障两侧线路.随后，R3处的断路器动作合闸，若为瞬时性故障，R7的断路器接着重合，线路恢复供电；若故障为永久性故障，此时需要R3和R4的定时限过电流保护选择性切除故障.当DG下游发生短路故障，若馈线配置后加速电流保护，R5和R6的定时限过电流保护可以有选择地切出故障线路，与此同时重合闸动作，若重合于永久性故障，保护装置立即无延时、无选择性地再次断开断路器.当DG相邻线路发生故障时，由于DG上游线路的过电流保护均配置了方向元件，保护R3和R4不会因流过反方向短路电流而误动作.

该方案在原有保护配置基础上引入方向纵联保护，改善了配电网保护性能，不限制DG的准入容量，同时不需要DG退出运行.但是对原有保护的改动较大，成本较高.表 1列出了3种保护方案的适用范围以及优缺点.

表 1 3种保护方案的适应范围及优缺点 Table 1 Application ranges advantages and disadvantages of three protection schemes
解决方案适用范围优点缺点
方案1线路原有保护配置保持不变保护可以快速可靠动作.操作简单，工程上易实现DG接入容量受到很大制约，故障时DG对系统稳定性支持不足
方案2DG接入情况(容量、位置、类型)确定考虑DG出力随机性变化，保护可以准确快速动作保护灵敏度、可靠性可能受到影响
方案3在原有保护功能的基础上进行改进改善了配网保护性能，不限制DG的接入容量，不需要将DG退出运行对原有保护改动较大，成本较高
表选项
2 应用实例 2.1 方案1

用于仿真计算的配电网系统如图 2所示，架空线路型号及参数选取为R=0.27 Ω/km，X=0.347 Ω/km (LGJ-120/25)；电缆线路型号及参数选取为R=0.259 Ω/km，X=0.093 Ω/km(YJLV22-150).馈线1含有3段线路，1-2为架空线路(4 km)，线路上装自动重合闸装置.2-3(6 km)、3-4(6 km)为电缆线路.馈线2含有6段线路，1-5(2 km)和5-6(2 km)为架空线路，1-4线路上装有自动重合闸装置，6-7(7 km)、7-8(7 km)、8-9(14 km)、9-10(14 km)为电缆线路.馈线、母线及保护编号参见图 2.每条母线处各接有额定容量为6 MVA、额定功率因数为0.85的负荷.选取配电网系统的基准容量为100 MVA，基准电压为10.5 kV，电源内电抗在最大运行方式下为Xsmax=0.091 Ω，最小运行方式下为Xsmin=0.126 Ω.将DG1、DG2、DG3分别接在母线3、6、7上，其暂态电抗为0.5 pu，以DG容量为基准值.

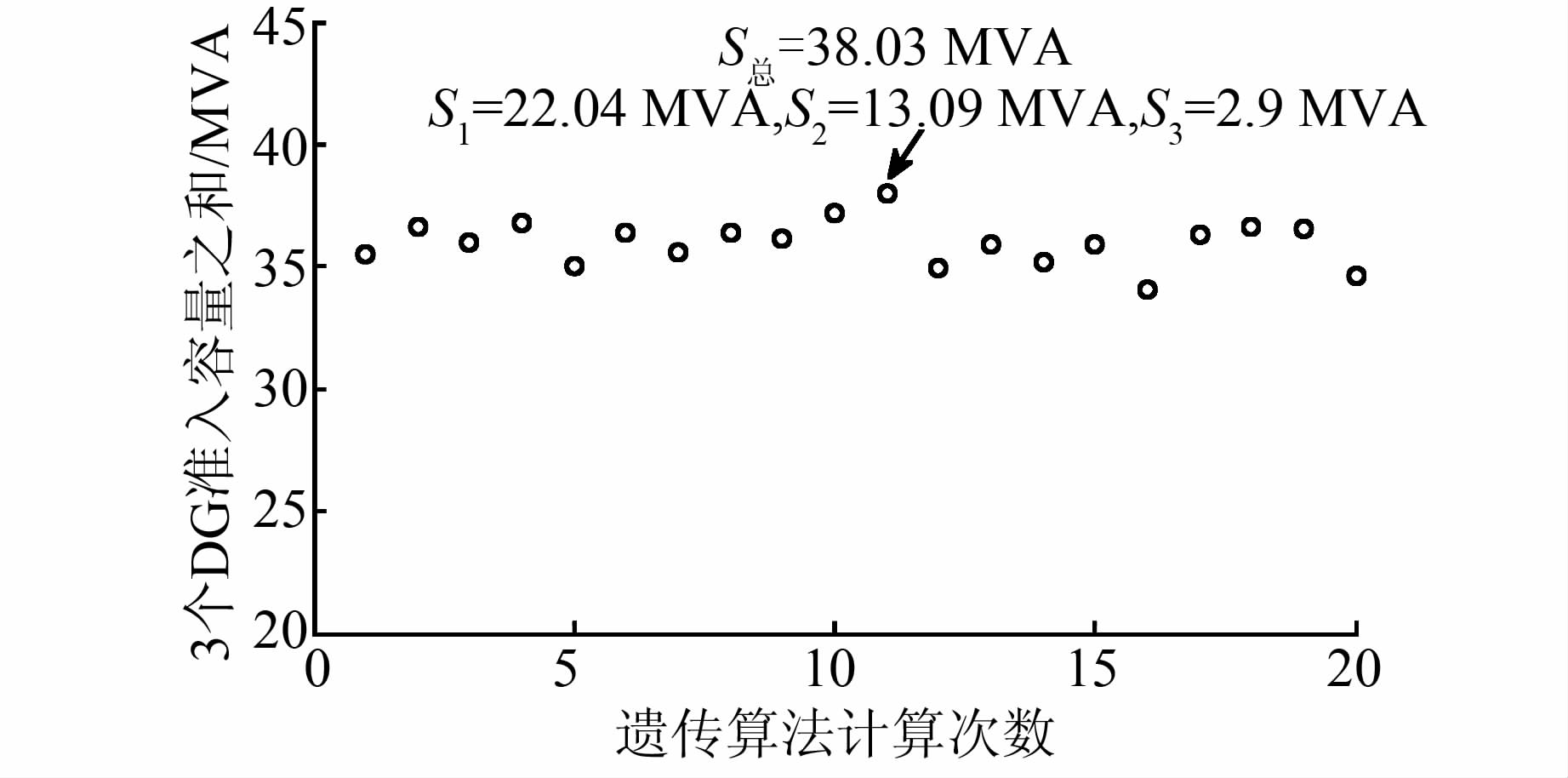
根据式(1)多个DG接入配电网的准入容量计算模型，运用小生境遗传算法(操作参数设置：种群规模为50，迭代次数为100，交叉率为0.8，变异率为0.2)，可以求得3个DG的最大准入容量.由于小生境遗传算法存在一定的随机性，在20次仿真结果中，选取使目标函数max(SDG1+SDG2+SDG3)最大的DG接入容量作为其准入容量.由图 5可知，DG接入容量之和最大值S总=38.03 MVA对应的3个DG的准入容量分别为S1=22.04 MVA、S2=13.09 MVA、S3=2.9 MVA.仿真结果表明，在保证配电网继电保护可靠动作的同时，牺牲了DG接入容量.

图 5 3个DG的准入容量曲线图 Figure 5 Curve of penetration capacity with 3 DGs
图选项
2.2 方案2

利用电力系统计算分析软件BPA对含DG配电网的电流保护原则重新整定计算，DG以50 MVA接入图 1所示配网系统的母线5处.线路型号参数选取以及负荷情况与方案1相同，线路1-2(4 km)、1-4(2 km)和4-5(2 km)为架空线路，2-3(6 km)、5-6(7 km)和6-7(14 km)为电缆线路.根据传统3段式电流保护的整定原则，可以求出配电网(无DG接入)线路保护(Ⅰ段、Ⅱ段和Ⅲ段)的整定值，如表 2所示.

表 2 配电网(无DG接入)线路保护整定值 Table 2 Setting values of current protection without DG connectingkA
保护保护整定值过电流保护整定值
Ⅰ段Ⅱ段
R14.082.700.47
R22.250.47
R37.734.860.47
R44.052.480.47
R52.071.210.47
R61.010.47
表选项

根据1.2节的分析推导，对DG上游、下游以及相邻线路上保护的动作值分别重新整定，当DG出力在10~50 MVA范围内变化，仿真计算线路各保护的动作电流如表 3所示.算例结果表明，电流保护整定值相应变化以适应DG接入容量和故障电流水平.

表 3 配电网(DG接入)线路保护整定值 Table 3 Setting values of current protection with DG
DG接入容量/MVAⅠ/Ⅱ/Ⅲ段保护整定值/kA
R1R2R3R4R5R6
504.08/2.70/0.0472.25/0.0477.73/4.86/0.0474.05/2.48/0.0472.07/1.21/0.0471.01/0.047
404.08/2.70/0.0472.25/0.0477.73/4.86/0.0474.05/2.85/0.0472.92/1.40/0.0471.16/0.047
304.08/2.70/0.0472.25/0.0477.73/4.86/0.0474.05/2.48/0.0472.77/1.37/0.0471.14/0.047
204.08/2.70/0.0472.25/0.0477.73/4.86/0.0474.05/2.48/0.0472.58/1.31/0.0471.09/0.047
104.08/2.70/0.0472.25/0.0477.73/4.86/0.0474.05/2.48/0.0472.33/1.25/0.0471.04/0.047
表选项
2.3 方案3

配网系统在无DG接入的情况下，定时限过电流保护的整定值如表 2所示.为保证各保护之间的时限配合，保护R6整定为瞬时动作，各保护的动作时限从电网末端到电源逐级增大一个时限阶段，Δt取0.5 s，在母线5处接入某额定容量的DG，需要在DG上游线路配置方向纵联保护.系统最大运行方式下，各段线路末端发生三相短路时流过保护的电流如表 4所示.仿真结果表明，该方案可以快速准确地将故障线路从两端切除，不需将DG退出运行，维持其对周围负荷的持续供电，同时也不需要限制DG的接入容量.

表 4 线路保护改进后流过馈线2保护的短路电流 Table 4 Short circuit current for protections of feeder 2 after improving the traditional protection configuration
DG/MVA保护短路电流/kA
1-4末端4-5末端5-6末端6-7末端
0R36.363.301.670.80
R43.321.680.81
R51.700.82
R60.83
50R36.363.300.990.38
R43.321.000.38
R52.530.97
R60.98
表选项
3 结语

详细分析了DG接入配电网对传统3段式电流保护的影响，为消除此影响提出了3种含DG配电网的保护方案，并分析了各自的适用范围及优缺点.由于DG的多样性和运行方式的灵活性，固定的保护方案很难全面适应配电网的不同运行场景，又由于不同的保护方案出发点不同，适用范围、实现方法以及优缺点也不相同，因此在具体设计保护方案时，需要从配电网结构、DG接入情况、故障类型等多个方面进行评估，选取最优的保护方案，在满足保护四性的基础上，实现方案的经济高效和可扩展性.

参考文献
[1] 胡骅, 吴汕, 夏翔, 等. 考虑电压调整约束的多个分布式电源准入功率计算[J]. 中国电机工程学报, 2006, 26(19): 13–17.
Hu Ye, Wu Can, Xia Xiang, et al. Computing the maximum penetration level of multiple distributed generators in distribution network taking into account voltage regulation constraints[J]. Proceedings of the CSEE, 2006, 26(19): 13–17.
[2] 黄伟, 熊军, 徐祥海, 等. 考虑配电网电压调节的分布式电源准入功率极限计算[J]. 电力系统自动化, 2007, 31(14): 43–46.
Huang Wei, Xiong Jun, Xu Xianghai, et al. Penetration level calculation considering tap changer oscillations[J]. Automation of Electric Power Systems, 2007, 31(14): 43–46.
[3] 江南, 龚建荣, 甘德强. 考虑谐波影响的分布式电源准入功率计算[J]. 电力系统自动化, 2007, 31(3): 19–23.
Jiang Nan, Gong Jianrong, Gan Deqiang. Computing the maximum penetrating level of distributed generators in distribution network by taking into account of harmonic constraints[J]. Automation of Electric Power System, 2007, 31(3): 19–23.
[4] 范雪峰, 夏懿, 贾春蓉, 等. 融合网损约束的分布式电源容量优化布置分析[J]. 电力系统及其自动化学报, 2013, 25(5): 121–126.
Fan Xuefeng, Xia Yi, Jia Chunrong, et al. Analysis of optimal placement of distributed generation capacity with limited power grid lose[J]. Proceedings of the CSU-EPSA, 2013, 25(5): 121–126.
[5] 冯希科, 邰能灵, 宋凯, 等. DG容量对配电网电流保护的影响及对策研究[J]. 电力系统保护与控制, 2010, 38(22): 156–165.
Feng Xike, Tai Nengling, Song Kai, et al. Research on the impact of DG capacity on the distribution network current protection and countermeasure[J]. Power System Protection and Control, 2010, 38(22): 156–165.
[6] 雷金勇, 黄伟, 夏翔, 等. 考虑相间短路影响的分布式电源准入容量计算[J]. 电力系统自动化, 2008, 32(3): 82–86.
Lei jinyong, Huang wei, Xia xiang, et al. Penetration level calculation with considerations of phase-to-phase short circuit fault[J]. Automation of Electric Power System, 2008, 32(3): 82–86.
[7] 吴罡, 陆于平, 花丽丹, 等. 分布式发电采用故障限流器对继电保护性能的影响[J]. 江苏电机工程, 2007, 26(2): 1–4.
Wu Gang, Lu Yuping, Hua Lidan, et al. Impact of fault limiter to the permance of relay protection in distributed generation[J]. Jiangsu Electrical Engineering, 2007, 26(2): 1–4.
[8] kAuhaniemi K,Kumpulainen L.Impact of distributed generation on the protection of distribution networks developments in power system protection[C]// Eighth IEEE International Conference on Volum I,2004:315-318.
[9] 吴峰, 郑建勇, 梅军, 等. 基于可控串补的故障限流器[J]. 中国电机工程学报, 2012, 36(2): 53–57.
Wu Feng, Zheng Jianyong, Mei Jun, et al. Theoretical study and simulation of TCSC based fault current limiter[J]. Proceedings of the CSEE, 2012, 36(2): 53–57.
[10] 张艳霞, 代凤仙. 含分布式电源配电网的馈线保护新方案[J]. 电力系统自动化, 2009, 33(12): 71–74.
Zhang Yanxia, Dai Fengxian. New schemes of feeder protection for distribution networks including distributed generation[J]. Automation of Electric Power System, 2009, 33(12): 71–74.
[11] 陈朝晖, 周红阳, 石东源, 等. 大型互联电网继电保护整定计算数据一体化管理系统[J]. 电力系统自动化, 2012, 36(3): 106–110.
Chen Chaohui, Zhou Hongyang, Shi Dongyuan, et al. Data integrated management system for relay protection setting calculation of interonnected power system[J]. Automation of Electric Power System, 2012, 36(3): 106–110.
[12] 曹景亮.分布式电源对配电网继电保护的影响研究[D].武汉:华中科技大学,2008.
Cao Jingliang.Study of the impact of DG on the protection of distribution network[D].Wuhan:Huazhong University of Science and Technology,2008.
[13] 孙景钌, 李永丽, 李盛伟, 等. 含分布式电源配电网保护方案[J]. 电力系统自动化, 2009, 33(1): 81–84.
Sun Jingliao, Li Yongli, Li Shengwei, et al. A protection scheme for distribution system with distributed generations[J]. Automation of Electric Power Systems, 2009, 33(1): 81–84.