文章信息
- 宫凤强, 侯尚骞, 李夕兵
- GONG Fengqiang, HOU Shangqian, LI Xibing
- 岩土参数截尾分布的正态信息扩散推断方法
- Truncated distribution deduction method for geotechnical parameters based on normal information diffusion method
- 武汉大学学报(工学版), 2016, 49(5): 661-667
- Engineering Journal of Wuhan University, 2016, 49(5): 661-667
- http://dx.doi.org/10.14188/j.1671-8844.2016-05-004
-
文章历史
- 收稿日期: 2016-04-01
2. 中南大学高等研究中心,湖南 长沙 410083
2. Center for Advanced Study, Central South University, Changsha 410083, China
在岩土工程可靠度分析中,很多物理力学参数被认为服从正态分布、对数正态分布、威布尔分布、贝塔分布、极值分布等一些经典分布.除了贝塔分布以外,在这些经典分布中,随机变量的取值范围通常从-∞到+∞或从0到+∞.但是在实际工程中,所有岩土体的物理力学参数(比如密度、容重、弹模、强度、黏聚力、内摩擦角、裂隙间距等等)均为实测值,具体数值一般不能小于0,同时也不可能为无穷大值.而且许多岩土参数仅在有限范围内是有定义的,超出了这个范围就失去了物理意义[1].因此各参数的分布区间实际上为有限区间,利用上述经典分布的定义区间来匹配岩土参数的实际区间显然并不合适.为此,很多研究人员根据岩体工程随机参数分布区间有限的事实,进行了截尾处理,例如李典庆对黏聚力及内摩擦角进行截尾处理后计算了边坡安全度[2],张钰等采用两端截尾分布对与断裂韧性相关的设计进行了概率法分析[3],毕忠伟等对截尾分布在岩体中的应用进行了研究[4],秦净净在重力坝的分析过程中,研究了截尾后可靠度指标的变化[5],李松辉以结构可靠度理论为基础,引入了车辆荷载效应的截尾分布模型[6].但是进行截尾后会带来一个明显不足,即在截尾区间内累积概率值一般达不到1,为此,传统的做法是将原有的概率密度函数除以正规化常数,进行线性变化处理,该方法只是从数值上将概率累积值变为1,正规化常数的科学意义并不明确.研究截尾分布问题的关键点有两个:1)截尾点如何选取的问题.对该问题目前还没有统一的标准,一般凭经验而定.对岩土这种天然材料而言,各种物理力学参数的不确定性相对较大,获取的现场样本一般又为小样本,因此带来的变异性也较大,确定其合理的截尾区间必须考虑岩土参数变异性大的特点.2)寻找更优的概率密度函数推断方法.如果在截尾的区间内所寻找到的概率密度函数能够通过检验,并且更加逼近实际数据的分布,同时累积概率值能够达到或者非常接近1,则达到了理想效果.针对该问题,利用经典的概率分布拟合法无法解决.另外,利用经典分布拟合实测岩土参数数据时还存在一个无法克服的问题,即大多数情况下由于岩土介质的不确定性导致实测数据的分布具有一定的波动性,但是现有经典分布均为单峰型分布,进而无法反映样本数据分布的随机波动.鉴于上述存在的问题,必须探寻经典概率分布拟合法之外的岩土参数概率分布推断方法.
基于正态信息扩散(Normal Information Diffusion,简称NID)原理的参数概型推断方法本质上属于一种核密度估计法,它可以最大限度地保留原始数据中所包含的原始信息.该方法在2006年被宫凤强等引用到岩土工程领域[7],并显示出了很好的逼近效果[8-10].然而如前所述,以往的截尾区间在确定时通常根据经验,并没有统一的标准,而且也没有做过系统的研究.实际上,对于截尾区间的选择,实测数据的分布范围是最基本的依据(不论对经典拟合法还是正态信息扩散法,一个共同的假设和前提是实测数据应真实有效,关于无效数据的剔除不在本文研究范围之内),但是在样本容量较小的情况下,所获得的样本信息完备性不足,因此推断得到的岩体参数的概率密度函数分布区间不能仅限于[xmin,xmax]区间内,而是应该包含该区间,并根据数据的变异性进行合理的扩展.本文以正态信息扩散原理为基础,结合5组岩土参数的实际样本,研究了5种截尾分布情况,并与传统的经典分布拟合法从截尾区间、拟合优度检验值、累积概率值和概率分布曲线4个方面进行了综合比较,提出了确定合理截尾分布区间的建议方法.
1 正态信息扩散原理在信息分配法的基础上创立并发展起来的信息扩散原理,是通过一定方式将原始信息直接过渡到模糊关系,从而避开关于隶属函数的计算,以最大限度地保留原始数据中所包含的原始信息.大量的专家学者不断尝试将信息扩散原理运用到保险、自然灾害风险评价、工业生产、测绘、人工智能、计算机仿真、诊断和决策、环境评价等方面并且取得了显著的成果.基于信息扩散原理,经推导得到概率密度函数fx的正态信息扩散估计[11]为
式中:n为样本容量;xi为样本观测值;h为标准正态扩散时的窗宽,h=σΔn.
概率分布函数为
设xi的最大值为xmax、最小值为xmin,根据正态信息扩散原理的择近原则,可求解h=γ(xmax-xmin)/(n-1),γ的取值见文献[12].
2 正态信息扩散分布的截尾区间取值对样本数据进行截尾时,需要明确3点:① 确定随机参数的概率密度函数分布区间时必须考虑该参数的实际情况,比如岩体力学参数一般为正值,因此,区间下限必须≥0,同时区间上限也不可能无限大,必须依据实测数据综合取舍;② 目前可靠度计算中对金属材料参数往往取[μ±2σ]的有限区间[13],但岩土材料属于天然的地质材料,其随机性和不确定性更加明显,因此把金属材料的区间标准用于岩土材料可能导致岩土参数的区间偏窄,应该在[μ±3σ]左右调整,同时也不能取得太宽;③ 确定分布区间范围的标准是尽量满足在该区间上的概率累积值逼近1.本文考虑5种区间取值情况:
1) (xmin,xmax),记为m.即以实际数据的最小值和最大值作为分布区间两个端点.
2) [μ-3σ,μ+3σ],记为3σ.在假设随机变量服从正态分布的情况下,按照3σ原则,可以确定在此区间内概率累积值可以达到0.997 ,并以此区间作为样本分布的有效区间.该方法未考虑实际数据普遍存在偏度这一事实,默认为对称分布.
3) [μ-(3-c)σ,μ+(3+c)σ],参考偏度进行双侧调整,记为c33.区间以[μ-3σ,μ+3σ]为基础,按照偏度进行双侧调整.上下界x′min 及x′max的估计值为x′min=μ-(3-c)σ,x′max=μ+(3+c)σ,即取值区间为 [μ-(3-c)σ,μ+(3+c)σ], 区间长度等于6σ,其中偏度c=μ/σ3.
4) 以[μ-3σ,μ+3σ]为基础,参考偏度c进行单侧调整,记为c3.c<0时,分布左偏,减小下限,左端取μ-(3-c)σ,右端不变;c>0时,分布右偏,增大上限,右端取μ+(3+c)σ,左端不变.
5) [μ-4σ,μ+4σ],记为4σ.
限于篇幅,文中选取相关文献中已发表的5组代表性的岩土参数数据作为实际样本[14,15].这5组数据利用经典拟合法时分别服从正态分布、对数正态分布、贝塔分布、威布尔分布和极值I型分布.利用正态信息扩散法得到5组数据对应的概率密度函数后,从区间长度、拟合优度检验值、概率累积值和概率分布曲线(图 1~5分别为利用经典分布和正态信息扩散分布得到的概率密度函数曲线和概率分布函数曲线)4个方面进行综合比较,分析确定合适的截尾区间取值范围.
| 岩土参数 | 样本容量 | 样本数据 | 经典分布类型 | 文献来源 |
| 内摩擦角正切值tanφ | 24 | 0.070,0.080,0.087,0.105,0.114,0.114,0.114,0.114,0.114,0.123,0.123,0.123,0.123,0.123,0.123,0.123,0.123,0.123,0.132,0.141,0.158,0.203,0.203,0.222 | 正态分布 | [14] |
| 液限WL/% | 26 | 36.9,37.2,37.9,42.1,44.7,45.2,47.2,47.3,48.5,48.5,48.5,48.5,48.6,48.7,51.0,52.0,52.6,53.5,53.8,55.3,56.0,56.0,57.5,58.9,66.5,69.5 | 对数正态分布 | [14] |
| 黏聚力c/kPa | 21 | 7.2,8.8,9.1,9.2,9.2,10.8,12.3,12.3,12.8,15.4,15.4,16.0,16.4,16.9,16.9,16.9,17.6,19.1,20.0,21.6,23.1 | 贝塔分布 | [14] |
| 350号混凝土断裂韧度KIc/(MN·m-3/2) | 35 | 0.566,0.628,0.640,0.652,0.665,0.665,0.726,0.738,0.738,0.756,0.763,0.763,0.775,0.788,0.788,0.800,0.812,0.824,0.837,0.837,0.837,0.849,0.849,0.849,0.861,0.874,0.886,0.898,0.911,0.923,0.935,0.96,0.972,1.058,1.108 | 威布尔分布 | [15] |
| 标准风压W/kPa | 25 | 798,1012,1114,1189,1267,1381,1381,1431,1482,1604,1804,1980,1980,1980,1980,2020,2042,2142,2183,2225,2396,3144,3529,3744,4367 | 极值I型分布 | [1] |
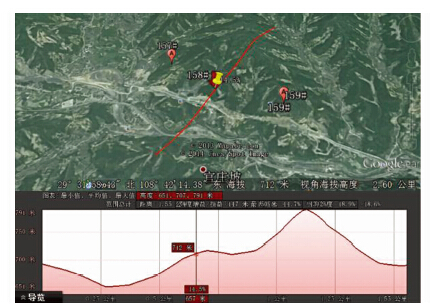
表 2中给出了上述5组数据的偏度(都属于正偏分布或右偏分布),并根据5种截尾方法分别给出了对应的截尾区间.表 2显示,对大多数参数,在m、3σ、c33和c3等4种情况下都可以直接截尾,但是当区间长度进一步扩展到4σ型时,则左端截尾点经常会出现负值,因此只能截断为0;对于风压这种极值型数据,则比较特殊,取3σ型时左端已经出现需要截断为0的情况.由此可见,对小样本数据,进行区间截尾时不能在两端扩展很大,尤其是左端,即使扩展到μ-4σ时,会出现较多的负值情况,这也意味着截尾区间并不是取得越宽越好.图 1~5给出了5种截尾区间的直观展示图(图中红色实线代表正态信息扩散分布曲线,蓝色虚线代表经典分布曲线),由下到上图示分别代表m、3σ、c33、c3和4σ截尾区间.从图中可以看出,5种截尾区间存在较大差异,尤其对于黏聚力,利用经典分布拟合直至其服从贝塔分布,但是贝塔分布的具体表现形式和截尾区间的取法直接相关,在图 3中可以看出当截尾区间取m型时,贝塔分布的形式属于奇异分布,并不适合,可见截尾区间不是越小越好.下面进一步结合检验值、概率累积值和概率函数曲线的比较,确定相对最优的截尾区间.
| 土工参数 | 偏度 | m | 3σ | c33 | c3 | 4σ |
| 内摩擦角正切值tanφ | 1.191 0 | [0.07,0.22] | [0.02,0.24] | [0.06,0.28] | [0.02,0.28] | [0,0.27] |
| 液限WL | 0.386 5 | [36.9,69.5] | [26.9,74.05] | [29.94,77.09] | [26.9,77.09] | [19.04,81.91] |
| 黏聚力c | 0.049 6 | [7.2,23.1] | [1.08,28.16] | [1.31,28.38] | [1.08,28.38] | [0,32.67] |
| 350号混凝土断裂韧度KIc | 0.192 4 | [0.57,1.11] | [0.46,1.17] | [0.48,1.19] | [0.46,1.19] | [0.34,1.29] |
| 标准风压W | 1.139 1 | [798,4 367] | [0,4 641] | [372,5 641] | [0,5 641] | [0,5 519] |
| 注:数值下划线表示左端截尾出现负值,进而截断为0的情况. | ||||||
|
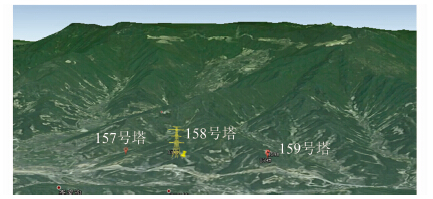
| 图 1 内摩擦角正切值概率密度、分布曲线图 Figure 1 The PDF and CDF curve of tanφ |
|
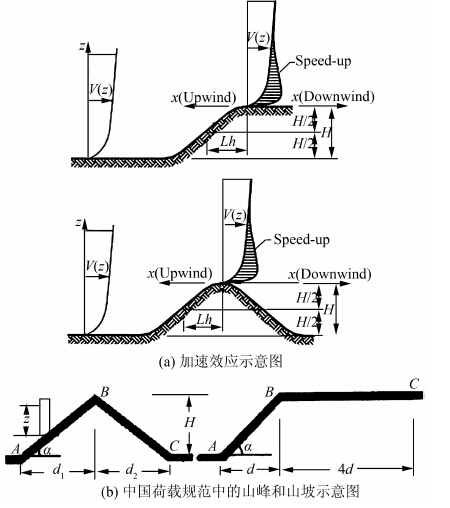
| 图 2 液限概率密度、分布曲线图 Figure 2 The PDF and CDF curve of liquid limit |
|
| 图 3 黏聚力概率密度、分布曲线图 Figure 3 The PDF and CDF curve of cohension |
|
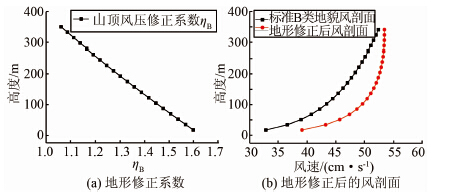
| 图 4 断裂韧度概率密度、分布曲线图 Figure 4 The PDF and CDF curve of fracture toughness |

|
| 图 5 标准风压概率密度、分布曲线图 Figure 5 The PDF and CDF curve of standard wind pressure |
岩土参数绝大多数情况下为小样本,一般采用K-S检验法对所得概率分布进行拟合良好性检验.表 3为5种参数在上述5种区间下的K-S检验结果,可以看出,对前4种参数,经典分布拟合法和正态信息扩散法都可以通过检验.对标准风压,则在m和c33两种类型区间不能通过检验,即截尾区间取这两种类型不太合适.需要特别指出的是,对于通过检验的情况,所有正态信息扩散分布的检验值都小于经典分布的检验值,这说明正态信息扩散分布更加逼近实际数据的分布.
| 土工参数 | m | 3σ | c33 | c3 | 4σ | α=0.05临界值 | |||||
| 经典分布 | NID分布 | 经典分布 | NID分布 | 经典分布 | NID分布 | 经典分布 | NID分布 | 经典分布 | NID分布 | ||
| 内摩擦角正切值tanφ | 0.199 7 | 0.076 0 | 0.147 0 | 0.104 3 | 0.180 8 | 0.093 8 | 0.147 0 | 0.104 3 | 0.145 8 | 0.104 3 | 0.274 8 |
| 液限WL | 0.081 9 | 0.068 5 | 0.082 1 | 0.047 4 | 0.081 6 | 0.047 4 | 0.082 1 | 0.047 4 | 0.082 2 | 0.047 4 | 0.264 0 |
| 黏聚力c | 0.233 4 | 0.086 5 | 0.112 0 | 0.064 4 | 0.101 3 | 0.064 4 | 0.109 1 | 0.064 4 | 0.218 1 | 0.064 4 | 0.289 2 |
| 350号混凝土断裂韧度KIc | 0.103 0 | 0.039 9 | 0.068 7 | 0.025 6 | 0.072 8 | 0.025 6 | 0.068 7 | 0.025 6 | 0.060 0 | 0.025 6 | 0.230 0 |
| 标准风压W | 0.347 5 | 0.062 3 | 0.256 3 | 0.031 2 | 0.291 4 | 0.032 2 | 0.256 3 | 0.031 2 | 0.256 3 | 0.031 2 | 0.270 0 |
| 注:下划线为未通过检验的情况. | |||||||||||
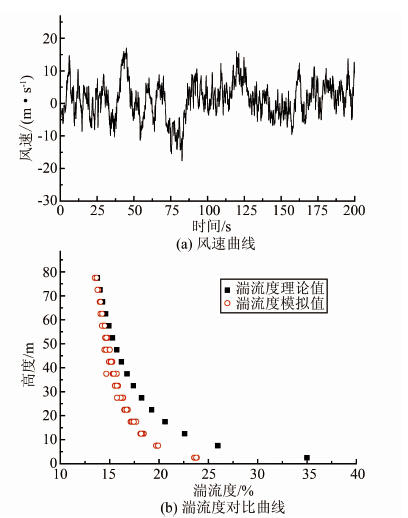
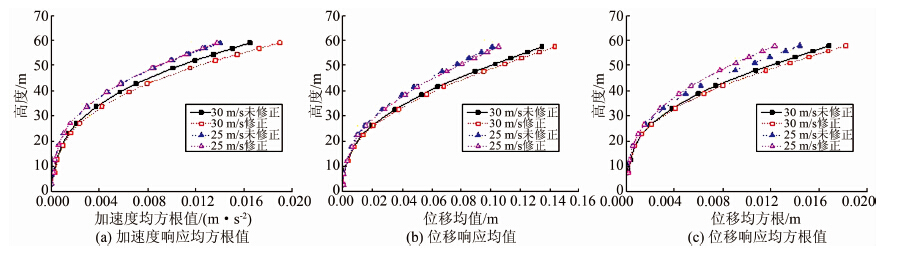
图 6给出了利用两种方法推断内摩擦角正切值tanφ和黏聚力c所得分布的检验值对比(图中横坐标数字1~5分别代表m、3σ、c33、c3、4σ等5种截尾区间),可以非常直观地看出经典分布的检验值比正态信息扩散分布的检验值大很多,对其他3种参数也存在类似情形.为了进一步显示这种差距,用检验值除以临界值,得到不同情况下检验值与临界值的比,并绘制箱图(见图 7).对于经典分布,检验值与临界值的比值起伏很大,甚至出现了无法通过检验的情况,平均为0.5~0.6,5种区间取法的检验值总体水平为0.2~1.3(>1意味着未通过检验).而正态信息扩散分布相对来讲更加稳定,平均水平在0.2附近,总体水平皆处于0.4以下,普遍优于经典分布.对于正态信息扩散分布,截尾区间的改变对检验结果影响相对较小,并可以保证拟合效果处在一个较好的水平.
|
| 图 6 tanφ和c的检验值对比图 Figure 6 Test value contrast diagram of tanφ and c |
|
| 图 7 检验值与临界值比值箱图 Figure 7 The ratio of test value and critical value box figure |
表 4给出了不同截尾区间下各岩土参数分布的累积概率值.在m型区间内,可以看出累积概率值普遍较低,最低的只有0.821 50,在这种情况下进行后期正规化处理,即使累积概率值达到了1,也失去了科学意义.理想情况应该是尽可能不进行正规化处理,而使得累积概率值接近1.表 4显示,整体上累积概率值会随着取值区间的扩大而增大,而正态信息扩散分布随着区间的扩大收敛至1的速度比经典分布更快.在10-5量级的水平上,正态信息扩散分布的累积概率值在取3σ型区间时有1组样本达到1,取c33型区间时有3组样本达到1,而当区间取为c3型时,正态信息扩散分布的累积概率值全部达到1.对于经典分布,截尾区间取3σ型、c33型、c3型和4σ型时,分别只有1组样本的累积概率值达到1.尤其针对标准风压参数,即使区间取4σ型时,利用极值I型分布所得到的累积概率值只有0.914 55,误差量级在10-2水平上,而正态信息扩散分布早已达到1.可见,从截尾的科学意义上讲,正态信息扩散分布比传统的经典分布好很多,在10-5量级的水平上取c3型区间时,即可达到累积概率值等于1的要求.如果误差要求在更小的量级水平上,可以考虑截尾区间左端点取到0,截尾区间右端点可取到4σ.
| 土工参数 | m | 3σ | c33 | c3 | 4σ | |||||
| 经典分布 | NID 分布 | 经典分布 | NID 分布 | 经典分布 | NID 分布 | 经典分布 | NID 分布 | 经典分布 | NID 分布 | |
| 内摩擦角正切值tanφ | 0.941 01 | 0.949 10 | 0.997 30 | 0.997 72 | 0.964 76 | 0.989 43 | 0.998 64 | 1.000 00 | 0.999 77 | 1.000 00 |
| 液限WL | 0.956 91 | 0.931 33 | 0.994 33 | 0.999 73 | 0.996 86 | 0.999 99 | 0.997 35 | 1.000 00 | 0.999 27 | 1.000 00 |
| 黏聚力c | 0.991 14 | 0.938 23 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 | 1.000 00 |
| 350号混凝土断裂韧度KIc | 0.953 49 | 0.970 93 | 0.990 15 | 0.999 93 | 0.986 14 | 1.000 00 | 0.990 24 | 1.000 00 | 0.998 90 | 1.000 00 |
| 标准风压W | 0.821 50 | 0.948 89 | 0.914 28 | 0.996 12 | 0.879 47 | 0.999 06 | 0.914 55 | 1.000 00 | 0.914 55 | 1.000 00 |
图 1~5给出了2种方法所得到的概率密度函数和概率分布函数曲线以及直方图的比较.可以看出,5种参数中只有混凝土断裂韧度值的分布不存在波动,其余4种参数的分布存在多个峰值情况,利用经典分布来表示实际分布时无法克服这一困难.但是对于正态信息扩散分布则显示出了极大的优越性,尤其在内摩擦角正切值和标准风压这两项参数的概率分布函数图中,可以看出所得函数曲线更加接近阶梯状的实际数据累积概率折线,克服了经典分布无法体现岩土参数随机波动的不足.
3 结论1) 针对岩土物理力学参数具有非负值的特点,提出了一种基于正态信息扩散原理的概率分布函数截尾处理方法.即以3σ统计原理为基础,同时考虑偏度进行调整的截尾区间确定标准.该方法不像传统的截尾处理方法那样对概率密度及分布函数产生影响,而是通过选择合理的截尾区间,不改变所得概率分布函数的形式,从而省略了截尾经典分布的正规化处理,完全保留了初始概率分布函数.
2) 利用5种具有代表性的物理力学参数,分别得到其对应的正态信息扩散分布,并采用了5种截尾区间,分别从区间取值情况、检验值、累积概率值和概率函数曲线等4个方面进行比较.研究结果表明,正态信息扩散分布的检验值均低于经典分布的检验值,说明更加逼近实际数据的分布;考察累积概率值发现,对于正态信息扩散分布,当区间取c3型时,在误差为10-5量级的水平上,概率累积值已经全部达到1;但是对于经典分布,即使截尾区间取为4σ型,概率累积值也很难达到1;最后通过概率函数曲线的比较可知,正态信息扩散分布可以反映实际数据分布的随机波动性,但对于单峰型的经典分布却无法做到.
3) 正态信息扩散分布属于正态分布的线性组合形式,求解过程和表达形式非常简单,是一种比较理想的推断岩土参数概率分布的方法.
| [1] |
高大钊.
土力学可靠性原理[M]. 北京: 中国建筑工业出版社, 1989.
Gao Dazhao. Reliability Principle of Soil Mechanics[M]. Beijing: China Architecture & Building Industry Press, 1989. |
| [2] |
李典庆, 周创兵. 考虑多失效模式相关的岩质边坡体系可靠度分析[J].
岩石力学与工程学报, 2009, 28(3): 541–551.
Li Dianqing, Zhou Chuangbing. System reliability analysis of rock slope considering multiple correlated failure modes[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(3): 541–551. |
| [3] |
张钰, 王丹, 张风和, 等. 断裂韧性的两端截尾分布概率法设计[J].
机械设计与制造, 1999(6): 1–2.
Zhang Yu, Wang Dan, Zhang Fenghe, et al. Probability methods of fracture toughness on the basis of cutting off-tail distribution[J]. Machinery Design & Manufacture, 1999(6): 1–2. |
| [4] |
丁德馨, 毕忠伟, 綦春明. 两端截尾概率分布下围岩可靠度研究[J].
中国安全科学学报, 2008, 18(4): 111–115.
Ding Dexing, Bi Zhongwei, Qi Chunming. Research on the reliability calculation of wall-rock under two-end truncated probability distribution[J]. China Safety Science Journal, 2008, 18(4): 111–115. |
| [5] |
秦净净, 王刚, 管莉莉. 基于几何优化算法的重力坝坝基抗滑稳定可靠度分析[J].
水力发电, 2015, 41(4): 39–42.
Qin Jingjing, Wang Gang, Guan Lili. Reliability analysis of foundation stability against sliding of gravity dam based on geometric optimization algorithm[J]. Water Power, 2015, 41(4): 39–42. |
| [6] |
李松辉. 基于车辆荷载效应截尾分布的桥梁限载分析方法[J].
工程力学, 2014, 31(2): 117–124.
Li Songhui. Analytical approach for determining truck weight limits with truncated distributions of live load effects on highway bridges[J]. Engineering Mechanics, 2014, 31(2): 117–124. |
| [7] |
宫凤强, 李夕兵, 邓建. 小样本岩土参数概率分布的正态信息扩散法推断[J].
岩石力学与工程学报, 2006, 25(12): 2559–2564.
Gong Fengqiang, Li Xibing, Deng Jian. Probability distribution of small samples of geotechnical parameters using normal information spread method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(12): 2559–2564. |
| [8] |
宫凤强, 侯尚骞, 岩小明. 基于正态信息扩散原理的Mohr-Coulomb强度准则参数概率模型推断方法[J].
岩石力学与工程学报, 2013, 32(11): 2225–2234.
Gong Fengqiang, Hou Shangqian, Yan Xiaoming. Probability model deduction method of Mohr-Coulomb criteria parameters based on normal information diffusion principle[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(11): 2225–2234. |
| [9] |
黄达, 曾彬, 王庆乐. 粗粒土孔隙比及级配参数与渗透系数概率的相关性研究[J].
水利学报, 2015, 46(8): 900–907.
Huang Da, Zeng Bing, Wang Qingle. Study on probabilistic relation between permeability coefficient and void ratio and grain composition of coarse grained soils using Copula theory[J]. Journal of Hydraulic Engineering, 2015, 46(8): 900–907. |
| [10] |
魏凯, 管志川, 马金山, 等. 一钻井地质参数的不确定性表征及分析方法[J].
中国石油大学学报(自然科学版), 2015, 39(5): 89–93.
Wei Kai, Ma Zhichuan, Ma Jinshan, et al. Assessment method for uncertainty of geological parameters in well drilling[J]. Journal of China University of Petroleum, 2015, 39(5): 89–93. |
| [11] |
黄崇福.
自然灾害风险评价理论与实践[M]. 北京: 科学出版社, 2005.
Huang Chongfu. Risk Assessment of Natural Disaster Theory & Practice[M]. Beijing: Science Press, 2005. |
| [12] |
王新洲. 基于信息扩散原理的估计理论?方法及其抗差性[J].
武汉测绘科技大学学报, 1999, 24(3): 240–244.
Wang Xinzhou. The theory, method and robustness of the parameter estimation based on the principle of information spread[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1999, 24(3): 240–244. |
| [13] |
张风和, 何雪红, 孙志礼, 等. 一种新的截尾分布模型[J].
东北大学学报, 1998, 19(4): 405–407.
Zhang Fenghe, He Xuehong, Sun Zhili, et al. A new theory of tail-cutting of distribution at two ends[J]. Journal of Northeastern University, 1998, 19(4): 405–407. |
| [14] |
孟庆山, 雷学文. 土工参数的统计方法及其工程应用[J].
武汉冶金科技大学学报:自然科学版, 1999, 22(4): 414–417.
Meng Qingshan, Lei Xuewen. Statistical methods and application to engineering of geotechnical parameters[J]. Journal of Wuhan Yejin University of Science & Technical (Natural Science Edition), 1999, 22(4): 414–417. |
| [15] |
于骁中.
岩石和混凝土断裂力学[M]. 长沙: 中南工业大学出版社, 1991.
Yu Xiaozhong. Fracture Mechanics of Rock and Concrete[M]. Changsha: Central South University of Technology Press, 1991. |
 2016, Vol. 49
2016, Vol. 49



