文章信息
- 徐涛, 李明贞, 刘毅刚, 周文俊, 徐研, 周承科
- XU Tao, LI Mingzhen, LIU Yigang, ZHOU Wenjun, XU Yan, ZHOU Chengke
- 基于韦布尔分布的无失效数据参数估计的高压电缆寿命评估
- High-voltage cable life assessment based on zero-failure data parameter estimation of Weibull distribution
- 武汉大学学报(工学版), 2017, 50(2): 233-238
- Engineering Journal of Wuhan University, 2017, 50(2): 233-238
- http://dx.doi.org/10.14188/j.1671-8844.2017-02-012
-
文章历史
- 收稿日期: 2016-03-09
2. 武汉大学电气工程学院,湖北 武汉 430072;
3. 英国格拉斯哥苏格兰大学,格拉斯哥 G4 0BA
2. School of Electrical Engineering, Wuhan University, Wuhan 430072, China;
3. Glasgow Caledonian University, Glasgow, G4 0BA, UK
电力电缆输电具有视觉美观、节省土地资源等优点,充分满足了资源节约、环境友好的要求[1],已被广泛应用于城市配电网中,大容量中心变电站进入市区,其进线几乎全部采用高压电缆[2].我国投入使用的电力电缆已有多年历史,很多电缆已经达到甚至超过预期使用寿命,这些早期制造的电缆由于制造工艺、敷设条件限制,加之在运行过程中受到电场、温度、水分等因素的共同影响而发生绝缘老化导致绝缘性能下降,不仅给电缆的安全运行带来了极大的隐患[3],还会造成不良的社会和经济影响.
高压电缆的故障一般分为3个阶段,即早期故障,在0~5 a内发生,故障原因多是安装和质量问题;中期故障,在5~25 a内发生,多是偶发性故障,故障原因为外力破坏;晚期故障,一般发生在25 a以后,电缆由于在各种力、热、机械以及环境等应力的长期作用下,绝缘出现老化,发生老化故障[4].早中期故障多为人为事故或其他不可预知的外力事故,通过提高运行维护管理水平,提升电缆制作工艺可以有效抑制这类事故的发生.因电缆的老化不可避免,故需要对运行电缆的老化状态进行准确评估,以指导运行维护更换老化的电缆,保障系统运行稳定.
在高压电缆老化的寿命评估领域,主要有2种路径来评估电缆的老化状态:1) 通过试验的方法研究其理化特性从而确定老化的状态量;2) 通过数据建模分析的方法评估电缆的老化状态.杜伯学等采用温差法对10 kV交联聚乙烯电缆水树老化进行了评估[5].刘刚等对电缆样品进行等温松弛实验对110 kV高压电缆老化状况进行了评估[6].王志强等采用实验室加速热老化并结合Arrhenius方程,对丁基绝缘新电缆的使用寿命进行预测[7].这些方法都是通过试验获取数据,而试验获得的数据与现场运行的数据存在一些差异,未必能够反映电缆真实的老化情况.Liu等认为电缆寿命可以用其电介质强度低于某一阈值的时刻定义[8],在Weibull分布的基础上确定了10~60 a寿命电缆分布情况.本文采用真实的现场运维数据,在Weibull分布的基础上,通过数据建模分析的方法来评估电缆寿命.本文估计出,大约12 500 d时有累计50%可能性的电缆会老化失效,该时间是30~40 a之间,与文献[8]得到的30、40 a寿命的电缆老化曲线相似.
1 Weibull分布及其参数估计在国内,绝大部分运行中的电缆还没有进入老化期;加之电力公司为方便扩充容量,电缆载流量留有很大裕度,通常实际运行中绝大部分高压电缆没有满负荷运行,实际电流量只有额定电流量的40%~60%,因此,由老化引起的故障相对较少.与实验室获得的数据不同,现场的运行维护数据不如实验室获得的数据完整,很难出现统计学意义的完全样本,而只能得到1组不完全样本.
考虑到寿命数据的统计分析大体上有2个方面的问题:1) 建立寿命分布模型并检验其确实性;2) 参数估计.本文选择Weibull分布作为寿命分布模型,其首要优点是能够在极少量样本的情况下提供准确的故障分析和故障预测[9].
1.1 Weibull分布Weibull分布最早由Waloddi Weibull教授于1937年提出[10],广泛用于研究机械、化工、电气、电子、材料的失效,甚至人体疫病等领域.Weibull分布有很多种形式,其中应用最多的是2参数和3参数Weibull分布,2参数Weibull分布的概率密度函数为[11]
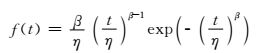 (1)
(1)
式中:t为故障前运行时间;β为形状参数;η为尺度参数.当β>1时,表明故障率在上升;当β < 1时,表明故障率在下降;当β=1时,表明故障率不变.此时,Weibull分布退化为指数分布.
2参数Weibull分布的分布函数为
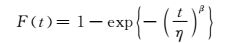 (2)
(2)
记为T~Wei(β, η)[12].确定1个2参数Weibull分布的决定性因素就是β和η的数值,下面介绍1种比较有典型性的传统参数估计方法——极大似然函数法,来估计这2个参数.
1.2 基于截尾样本的极大似然估计不完全样本有2种基本类型:1) 定时截尾寿命试验,假设将随机抽取的n个产品在时间t=0时同时投入试验,试验进行到事先规定的截尾时间t0停止.如试验截止时共有r个产品失效,它们的失效时间分别为0≤t1≤t2≤…≤tr≤t0,此时r是一个随机变量,所得的样本t1, t2, …, tr称为定时截尾样本.2) 定数截尾寿命试验,假设将随机抽取的r个产品在时间t=0时同时投入试验,试验进行到有r个产品失效时停止.r个失效产品的失效时间分别为0≤t1≤t2≤…≤tr,tr是随机变量,所得的样本t1, t2, …, tr称为定数截尾样本[13, 14].
极大似然函数法(MLE):假设产品的寿命分布函数为F(t),密度函数为f(t),现有n个产品进行定时截尾寿命试验,截尾时间为t0,假设在观察时间内有r个产品失效,观察到的失效时间为t1≤t2≤…≤tr<t0,那么它的极大似然函数为
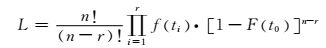 (3)
(3)
将Weibull分布的密度函数和分布函数代入式(3),并对其取对数可得
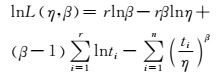 (4)
(4)
式(4) 就是Weibull分布的极大似然函数表达式的对数形式.分别对式(4) 求极大似然函数关于β和η 2参数的偏微分方程,可得
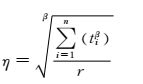 (6)
(6)
通过式(5) 可以估计出形状参数β值.将式(5) 的估计值代入式(6) 可以估计出尺度参数η值.
2 无失效数据的参数估计作为一种传统的参数估计方法,极大似然函数法估计在样本量较大情况下的估计结果较准确.但是当样本量较小时,传统的参数估计方法很难有效估计出需要的参数.而随着科学技术的进步、制作工艺水平的提升,交联聚乙烯电缆的产品质量越来越好.根据中国南部某城市的高压电缆1999-2011年的运行维护数据,从投运开始到1999-2011年的时间段为止,没有一起电缆本体的故障是由于老化引起的.传统的统计学方法在这样的情况下并不适用,本文使用了一种无失效数据的参数估计方法——修正的极大似然函数法(MMLE),来估计Weibull分布的形状参数和尺度参数.
2.1 无失效数据对某产品进行k次定时截尾试验,截尾时间为ti,t1≤t2≤…≤tk,相应的试验样品数为ni,i=1, 2, …, k.若试验的结果是所有样品无一失效,则称(ti, ni)为无失效数据,也称为零失效数据(zero-failure data)[15, 16].
本文原始数据来自某市供电公司的高压电缆运行维护数据,而这些运行中的电缆绝大多数尚未进入老化期,截止到2011年12月31日,没有1起事故是由本体老化失效引起的,因此获得的数据属于无失效数据,传统的参数估计方法不再适用,本文使用一种修正的极大似然函数法估计无失效数据参数.
2.2 修正的极大似然函数法从式(6) 中不难看出,在传统的极大似然函数法估计参数时,当数据量较大,产品失效数量适当的时候,估计值是比较准确的.但是在产品失效数量为0这种极端情况下,尺度参数η的估计值将是无穷大,这表明Weibull密度函数曲线会平缓到近似于1条直线,这意味着寿命的极大似然估计值平均分布在[0, +∞]的区间内,这种情况显然与实际不符.类似地,当样本数量很大,而产品失效数量很小时,尺度参数η的估计值将很大,平均寿命的极大似然估计值也会非常大,这种情况往往与实际相去甚远.
从物理意义的角度解释,出现上述情况的原因是截尾时间t0的选择不合适.就电缆而言,假设电缆的设计寿命是30 a,而电缆的运行时间只有20 a,这样截尾时间t0≤20 a就偏短,在这样的截尾时间内由老化引起的产品失效数量为0的可能性较高.而在实际情况中把截尾时间选择到大于30 a的“合适值”是不现实的.
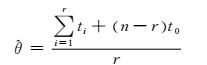 (7)
(7)
当r较大时,平均寿命θ的估计值与真值的偏差不大;而当r很小甚至为0的时候,平均寿命θ的估计值与真值的偏差很大.从数值的角度解释,很大的偏差来源于式(7) 的分子项与分母项在数值上不匹配.因此,将平均寿命θ的估计值修正为
 (8)
(8)
比较式(8) 与式(7) 不难看出,式(8) 只是在式(7) 的分母项上加了一个修正项S,为了使式(8) 的修正方法更有推广意义,这里将S的意义解释为在时间区间[tr, t0]内的模拟累计失效数;而r+S的意义是在截尾时间t0内的模拟累计失效数.显然,时间区间[tr, t0]内S≤1,一旦出现故障数量为0的情况,修正项S将有效地修正平均寿命θ的估计值,使其不至于大至无穷大,只要合适选择S值,θ的估计精度将不受影响.
这种修正方法不仅当r=0的时候适用,同样当r相对于样本总量很小的时候也适用.甚至是另一种极端情况:在式(7) 或式(8) 的分子项上的总试验时间相差不大,一旦截尾时间t0选择得稍大(tr≤t0)或者稍小(tr-1≤t0<tr),分母项可能相差1;在这种极端情况下式(8) 依然成立.
由式(8) 反推到极大似然函数,这种修正方法的实质是把式(3) 修正为
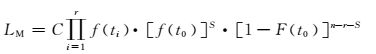 (9)
(9)
其中,C为一个常数.C的数值并没用明确的物理意义,也不影响最终的参数估计,故本文不再深究.
2.3 Weibull分布下的无失效数据的参数估计在2参数的Weibull分布情况下,需要估计的参数就只有形状参数β和尺度参数η.特别地,当r=0时将式(1)、(2) 代入式(9),由于在k次试验中没有发生老化失效,而每次试验时间ti不同,故修正项Si也可能不同,因此有
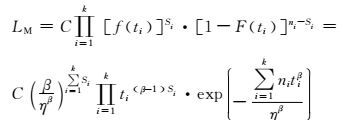 (10)
(10)
联立方程组:
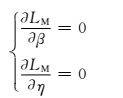 (11)
(11)
将式(10) 代入式(11) 推导出:
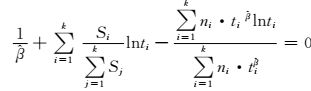 (12)
(12)
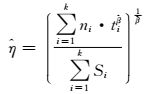 (13)
(13)
可以证明式(12) 的解存在且唯一[15],有数值解但没有解析解.下面的问题就转化为Si的确定.
对于有n个样本k次试验的Weibull分布而言,设T~Wei(β, η),则期望值
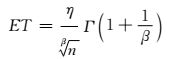 (14)
(14)
因此,Si的值不妨认为是
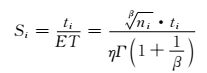 (15)
(15)
由于出现r=0的原因是试验时间ti的选择偏短,而寿命的期望值是ET(ti≤ET),当r=0时,Si的意义就是在试验时间ti内,出现失效元件数量的模拟值(≤1).
于是,当认为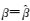
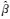
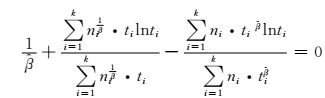 (16)
(16)
这样,就可以直接用式(16) 和式(13) 估计Weibull分布的参数,对于式(13) 分母项的处理,可以认为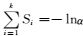
本文数据来源于某市供电公司截止到2011年12月31日的高压电缆运行维护数据,如表 1所示.
| 序号 | 投运日期 | 截止日期 | 试验时间/d |
| 1 | 2011/12/22 | 2011/12/31 | 9 |
| 2 | 2011/12/9 | 2011/12/31 | 22 |
| 3 | 2011/11/30 | 2011/12/31 | 31 |
| … | … | … | … |
| 261 | 1985/9/21 | 2011/12/31 | 9 597 |
| 262 | 1985/9/21 | 2011/12/31 | 9 597 |
用各条高压电缆线路的投运日期到2011年12月31日的时间跨度作为试验时间ti.经过剔除部分无效数据和并非本体老化原因的故障数据后,还剩下262组电缆正常运行的数据.由于每条电缆的投运时间不同,本文将其看作262次独立试验,即k=262,每次试验只有1组数据,即ni=1, (i=1, 2, …, k),各次试验均为定时截尾试验.
将这些数据代入到式(16) 和式(13),采用99.99%的置信度进行估计,那么α=0.000 1.用MATLAB编程求解得,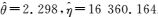
|
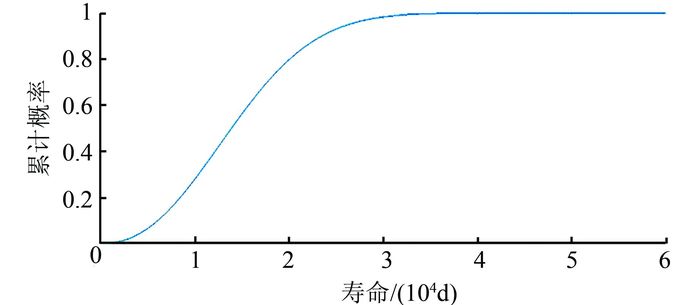
| 图 1 韦布尔分布的分布函数 Figure 1 Distribution function of Weibull |
|
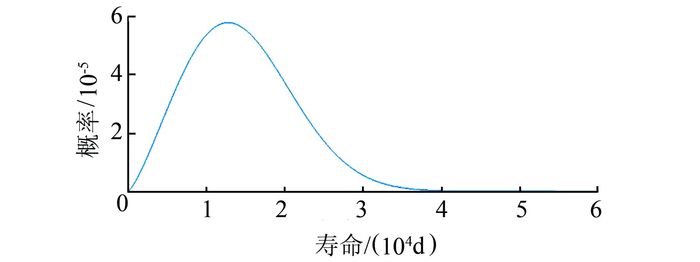
| 图 2 韦布尔分布的密度函数 Figure 2 The density function of Weibull |
图 1、2给出了Weibull分布的分布函数和密度函数,其中横坐标为寿命时间,密度函数中的纵坐标是概率值,分布函数中的纵坐标是累计概率.图 1、2展示了试样电缆的整体寿命分布情况.从中不难看出,当大约5 000 d(14 a)的时候,累计函数的上升速度开始加快,这表明大约在5 000 d(14 a)的时候开始有老化失效的电缆但概率不大;在大约12 500 d(34 a)的时候,有累计50%可能性的电缆会老化失效,可以认为这个时候电缆进入老化期;在大约40 000 a(110 a)的时候,有累计100%可能性的电缆会因老化失效,从概率的角度认为该市的电缆寿命没有可能会超过40 000 d(110 a).图 1显示大约12 500 d的时候,有累计50%可能性的电缆会老化失效相当于是30~40 a,与康涅狄格大学一项研究得到的30、40 a寿命的电缆老化曲线相似.
4 结论1) 基于Weibull分布模型,使用了一种无失效数据的参数估计方法,估计出了Weibull分布的2个参数.结果表明,即使是在完全没有有效统计数据的情况下,利用无失效的数据同样可以估计出Weibull分布的参数.
2) 比较MLE和MMLE这2种参数估计方法,说明了2种方法的适用范围和MMLE在无失效数据参数估计中的优势.
3) 由于产品失效数据的缺失,无法验证结果的拟合程度,无法进行分布的拟合检验,但这种方法与国外的研究比较,估计出来的结果相似.
| [1] |
周远翔, 赵健康, 刘睿, 等. 高压/超高压电力电缆关键技术分析及展望[J].
高电压技术, 2014, 40(9): 2593–2612.
Zhou Yuanxiang, Zhao Jiankang, Liu Rui, et al. Key technical analysis and prospect of high voltage and extra-high voltage power cable[J]. High Voltage Engineering, 2014, 40(9): 2593–2612. |
| [2] |
周韫捷, 张丽. 以均衡眼光看XLPE电缆与充油电缆的使用[J].
上海电力, 2001, 4(4): 10–14.
Zhou Yunjie, Zhang Li. A balanced perspective of XLPE cable and oil-filled cable[J]. Shanghai Electric Power, 2001, 4(4): 10–14. |
| [3] | Tang Zeyang, Zhou Chengke, Jiang Wei, et al. Analysis of significant factors on cable failure using the cox proportional hazard model[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 951–957. DOI:10.1109/TPWRD.2013.2287025 |
| [4] |
唐泽洋, 姜伟, 姚帅, 等. 电力电缆故障数据的统计模型分析[J].
武汉大学学报(工学版), 2012, 45(5): 677–672.
Tang Zeyang, Jiang Wei, Yao Shuai, et al. Statistical model analysis of cable failure data[J]. Engneering Journal of Wuhan University, 2012, 45(5): 677–672. |
| [5] |
杜伯学, 马宗乐, 高宇, 等. 采用温差法的10 kV交联聚乙烯电缆水树老化评估[J].
高电压技术, 2011, 37(1): 143–149.
Du Boxue, Ma Zongle, Gao Yu, et al. Insulation evaluation of water-tree aged 10 kV XLPE cables using thermal step method[J]. High Voltage Engineering, 2011, 37(1): 143–149. |
| [6] |
刘刚, 张高言, 周凡. 基于等温松弛法的110 kV高压电缆老化状况评估[J].
高电压技术, 2014, 40(2): 497–504.
Liu Gang, Zhang Gaoyan, Zhou Fan. Aging state assessment of 110 kV high-voltage cable by iddsothermal relaxation method[J]. High Voltage Engineering, 2014, 40(2): 497–504. |
| [7] |
王志强, 周长亮, 李文文, 等. 船用丁基橡胶绝缘电缆剩余寿命评估[J].
中国电机工程学报, 2012, 32(34): 189–195.
Wang Zhiqiang, Zhou Changliang, Li Wenwen, et al. Residual life assessment of butyl rubber insulated cables in shipboard[J]. Proceedings of the CSEE, 2012, 32(34): 189–195. |
| [8] | Liu R, Boggs S. Cable life and the cost of risk[J]. Electrical Insulation Magazine, IEEE, 2009, 25(2): 13–19. DOI:10.1109/MEI.2009.4802594 |
| [9] |
邬吉波. 线性模型参数估计的若干性质研究[D]. 重庆: 重庆大学, 2013.
Wu Jibo. Research on the properties of parameter estimation in linear regression model[D]. Chongqing: Chongqing University, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10611-1013044681.htm |
| [10] | Robert B Abernethy. The New Weibull Handbook[M]. North Palm Beach: Robert B. Abernethy, 2001. |
| [11] | Lai C D, Min Xie, Murthy D N P. A modified Weibull distribution[J]. IEEE Transactions on Reliability, 2003, 52(1): 33–37. DOI:10.1109/TR.2002.805788 |
| [12] |
雷刚. Weibull分布寿命数据的参数估计[D]. 武汉: 华中科技大学, 2006.
Lei Gang. Parameter estimation of lifetime data in Weibull distribution[D]. Wuhan: Huazhong University of Science & Technology, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10487-2008021702.htm |
| [13] |
盛骤, 谢式千, 潘承毅.
概率论与数理统计[M]. 北京: 高等教育出版社, 2008.
Sheng Zhou, Xie Shiqian, Pan Chengyi. Probability and Mathematical Statistics[M]. Beijing: Higher Education Press, 2008. |
| [14] | Wu E Y, Vollertsen R-P. On the Weibull shape factor of intrinsic breakdown of dielectric films and its accurate experimental determination. Part Ⅰ: theory, methodology, experimental techniques[J]. IEEE Transactions on Election Devices, 2002, 49(12): 2131–2140. DOI:10.1109/TED.2002.805612 |
| [15] |
王玲玲, 王炳兴. 无失效数据的统计分析——修正似然函数方法[J].
数理统计与应用概率, 1996, 11(1): 64–70.
Wang Lingling, Wang Bingxing. Statistical analysis for no-failure data—modified likelihood function method[J]. Mathematical Statistics and Applied Probability, 1996, 11(1): 64–70. |
| [16] |
张镱议. 基于运行状态和寿命评估的电力变压器全寿命周期检修决策研究[D]. 重庆: 重庆大学, 2014.
Zhang Yiyi. Study on life cycle cost based maintanence decision making for power transformers considering condition assessment and insulation life assessment[D]. Chongqing: Chongqing University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10611-1014042835.htm |
| [17] |
刘鸿铭. 无失效数据下复杂系统可靠度的Bayes估计[D]. 哈尔滨: 哈尔滨理工大学, 2014.
Liu Hongming. Bayesian estimation of reliability for a complex system under zero-failure data[D]. Harbin: Harbin University of Science and Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10214-1014193427.htm |
| [18] |
林姝男. 无失效数据及单一失效数据的客观贝叶斯分析[D]. 上海: 华东师范大学, 2014.
Lin Shunan. Objective Bayesian analysis of zero-failure data and one-failure data[D]. Shanghai: East China Normal University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10269-1014322522.htm |
| [19] |
杜林, 袁蕾, 熊浩, 等. 应用蒙特卡罗模拟法的电力变压器热特性绝缘寿命评估[J].
高电压技术, 2010, 36(4): 856–861.
Du Lin, Yuan Lei, Xiong Hao, et al. Insulation life assessment of power transformer thermal characteristics using Monte Carlo simulation[J]. High Voltage Engineering, 2010, 36(4): 856–861. |
 2017, Vol. 50
2017, Vol. 50




