文章信息
- 张珂斐, 郭江, 肖志怀
- ZHANG Kefei, GUO Jiang, XIAO Zhihuai
- 模糊综合评价和改进证据理论相融合的变压器状态评价方法研究
- Research on state evaluation method of transformer based on fusion of fuzzy comprehensive evaluation and improved D-S evidence theory
- 武汉大学学报(工学版), 2016, 49(2): 279-284
- Engineering Journal of Wuhan University, 2016, 49(2): 279-284
- http://dx.doi.org/10.14188/j.1671-8844.2016-02-021
-
文章历史
- 收稿日期: 2015-06-23
随着国家经济发展和国民生活水平的提高,对电力系统的供电可靠性和安全性的要求也随之提高,电力系统逐渐向超高压、大容量方向发展,为了应对日渐增长的用电需求和用电品质,迫切需要开展电力设备的状态检修工作,减少由于计划检修而造成的资源浪费,提高供电的可靠性和安全性.因此,采用先进的状态监测手段及准确可靠的评价体系来确定设备状态,进而依据设备状态开展变压器状态检修将是未来的必然趋势[1, 2].
目前,国内各高校和研究机构已开展了一系列有关变压器状态评价的研究.文献[3]中提出了利用灰色聚类法对变压器的运行状态进行评价的方法;文献[4]中采用信息融合的方法对变压器的运行状态进行了评价尝试;除此以外,还有文献通过故障树法[5]、支持向量机[6]、可拓分析法[7]、云理论[1]等方法对变压器进行评价.这些方法的应用极大地推动了变压器状态评价研究的发展,也在状态评价的实际工作中起到了重要的指导作用.
电力变压器作为一个复杂设备,其运行状态受众多因素的影响,仅靠单一指标无法确定变压器的运行状态,并且部分因素又存在不确定性和模糊性,大大降低了状态评价方法的有效性和准确性.
而模糊集是处理数据边界模糊的有力工具,D-S证据理论则是处理不确定信息的有效手段,但证据理论在进行高冲突证据的合成时,得到的融合结果往往有悖于常理.鉴于以上分析并结合变压器运行实际情况及专家经验,本文提出了模糊综合评价和改进D-S证据理论相融合的变压器状态评价方法,有效地消除了多源信息间的不确定因素,为变压器的安全稳定运行及检修试验工作的制定提供了科学依据.
1 变压器状态评价指标研究 1.1 变压器评价指标变压器作为输变电系统的核心设备,它的运行状态直接关系到整个电力系统的安全稳定,构建合理有效的变压器状态评价方法有助于评估变压器运行状态,及时发现潜在缺陷,为变压器的状态检修提供必要的技术支撑.变压器的状态信息数据包含众多试验和监测数据,并且各信息数据间关系错综复杂.本文通过对变压器上述各项评价因素的研究分析,并结合专家经验,参照评价指标选取的原则,选取电气试验、绝缘油试验和油中溶解气体分析的部分状态量作为评价指标,如表 1所示[8, 9].
| 参数类型 | 参数名称 |
| 电气试验X1 | 极化指数(X11) 介质损耗tanδ/%(X12) 绝缘电阻/MΩ(X13) 直流不平衡系数/%(X14) |
| 绝缘油试验X2 | 油的介质损耗/%(X21) 油中微水质量分数/(mg·L-1)(X22) 击穿电压/kV(X23) 糠醛/(mg·L-1)(X24) |
| 油中溶解气体分析X3 | CH4(X31) C2H4(X32) C2H6(X33) C2H2(X34) H2(X35) |
在构建模糊综合评价模型时,评价指标的权重系数直接影响综合评判结果的准确性,是模型构建成功与否的关键因素之一.本文选择采用应用较为广泛的层次分析法来确定评价指标的权重系数,各评价指标的权重系数可按以下步骤确定:
1) 根据专家给定的重要程度信息构建层次分析法的判断矩阵.
综合考虑专家和电网管理人员给定的重要程度信息后,将同一层次中的各个指标进行两两比较,得到判断矩阵,各指标之间的重要标度如表 2所示,其中油中溶解气体试验的判断矩阵D3如下所示:
| 尺度 | 重要程序 |
| 1 | 两元素i、j相比,i因素与j因素相同重要 |
| 3 | 两元素i、j相比,i因素比j因素略重要 |
| 5 | 两元素i、j相比,i因素比j因素较重要 |
| 7 | 两元素i、j相比,i因素比j因素非常重要 |
| 9 | 两元素i、j相比,i因素比j因素绝对重要 |
| 2,4,6,8 | 以上前后两级之间的标度值 |
2) 计算判断矩阵的最大特征根λmax,求出对应的特征向量.
求出判断矩阵的最大特征根λmax,得到最大特征根对应的特征向量,以此根求出它的特征向量R=(λ1,λ2,…,λk),进行归一化处理后即可得到各指标的权重集.对判断矩阵D3求解权重集B3=(0.185,0.252 7,0.124 5,0.313 2,0.124 5).
3) 得到权重集后,需按CR=CI/RI对判断矩阵进行一致性检验.
矩阵D3的C
| 参数类型 | 参数名称 | 权重 |
| X1 | X11 X12 X13 X14 | 0.2637 0.243 2 0.2004 0.292 7 |
| X2 | X21 X22 X23 X24 | 0.2061 0.219 8 0.2314 0.342 7 |
| X3 | X31 X32 X33 X34 X35 | 0.185 0.2527 0.124 5 0.3132 0.124 5 |
电力变压器作为一个复杂设备,其运行状态受众多因素的影响,并且部分因素又存在不确定性和模糊性,为了应对变压器的特殊性,特别提出了模糊综合评价和改进证据理论相融合的变压器状态评价方法.
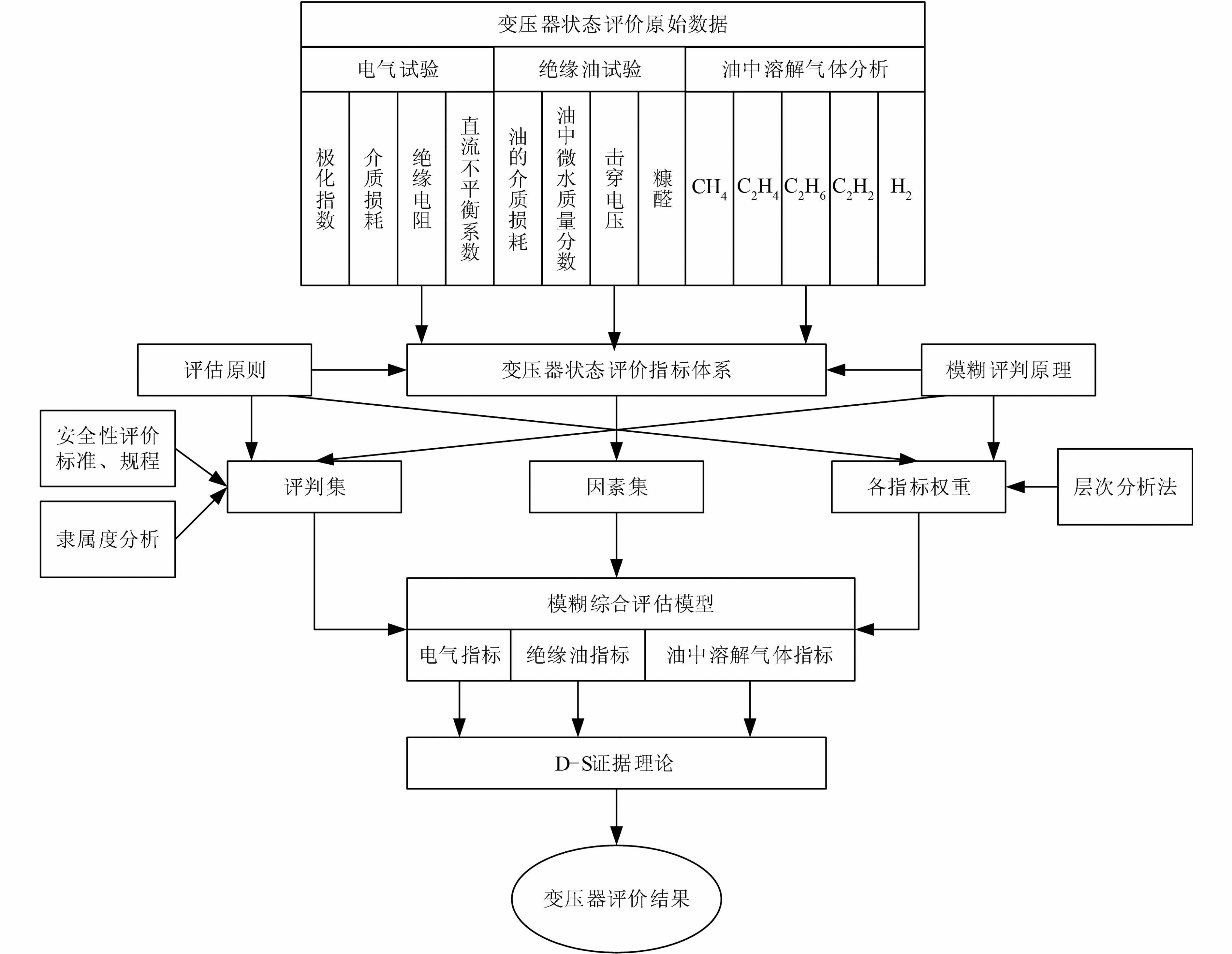
通过引入模糊综合评价,很好地解决了电力变压器因素众多且各因素存在模糊性的问题,但单一模糊综合评价的结果又往往存在片面性,评价准确度难以保证.因此,通过将模糊综合评价和改进D-S证据理论进行结合,利用D-S证据理论处理不确定性信息的优势,融合多类状态评价结果,并且通过基本概率赋值的修正,防止高冲突证据融合时相悖现象的出现,提高评价结果的准确性.相融合的变压器状态评价方法示意图如图 1所示.
|
| 图 1 相融合的变压器状态评价方法示意图 Figure 1 Architecture of fusion state evaluation method |
模糊综合评价是研究数据不确定性和量化变压器运行状态的典型方法,具体评价步骤如下所示:
1) 确定模型的因素集
与变压器运行状态相关的影响因素包括:电气指标、绝缘油指标和油中溶解气体指标,因素集可用U表示,记为
单因素又可以分解为子系统评价因素,相应因素集Ui可表示为
式中:Ui为因素集,Uij为第i个因素集中的第j个分项因素指标.
2) 确定模型的评价集
根据变压器的实际运行管理经验并为了便于电网管理者准确判断变压器的运行状态,合理安排试验和检修计划,特别将变压器的运行状态分为如下4类,分别是正常、注意、异常、严重.因此,评判集根据上文分析可记为
式中:V1~V4分别对应变压器的4类运行状态.
3) 确定模型的隶属度函数
在变压器状态评价方法中,因素指标可以根据参数性能趋势分为两类,分别是越小越优型指标,如介质损耗;越大越优型指标,如极化指数.
任一评价指标uij的各评价等级都具有一个指标标准值Sijk,可作为各个评价等级的划分界限,而各等级标准值是离散分布的,为了实现因素指标隶属度函数的连续性分布,本文模型的隶属度函数采用正余弦函数曲线分布形态.则指标因素隶属于正常状态(k=1)时的相关隶属函数可表示为
因素隶属于注意、异常状态(k=2,3)时的相关隶属函数可表示为
因素隶属于严重状态(k=4)时的相关隶属函数可表示为
式(1)~(3)适用于评价指标为越小越优型的指标,而针对评价值越大越优型的指标可将式中“<”和“>”互换即可.
根据目前国内外研究机构对于变压器状态评价的研究成果,并结合现行的变压器状态评价相关规程与导则,各评价指标的状态指标标准值如表 4所示.
| 评价指标 | V1 | V2 | V3 | V4 |
| X11 | 2.0 | 1.5 | 1.2 | 1.0 |
| X12 | 0 | 0.8 | 0.9 | 1.0 |
| X13 | 0 | 100 | 5 000 | 10 000 |
| X14 | 0 | 2.0 | 2.5 | 3.0 |
| X21 | 0 | 1 | 2 | 4 |
| X22 | 0 | 25 | 30 | 35 |
| X23 | 35 | 40 | 55 | 70 |
| X24 | 0 | 1 | 2 | 4 |
| X31 | 0 | 120 | 260 | 400 |
| X32 | 0 | 50 | 75 | 100 |
| X33 | 0 | 65 | 80 | 100 |
| X34 | 0 | 1 | 5 | 9 |
| X35 | 0 | 150 | 400 | 700 |
D-S证据理论是一种不确定性推理方法,它能够融合多个证据源所提供的依据,依靠证据的积累,不断缩小假设集.它具有较强的决策处理能力,在数据融合与目标识别领域有着比较广泛的应用[11].
D-S证据理论的证据组合规则的一般形式为
其中:$K=\sum\nolimits_{X\cap Y=\varnothing }{{{m}_{1}}}(X){{m}_{2}}(Y)$,m1(X)和m2(Y)分别为X的基本可信度函数1和Y的基本可信度函数2.
而在实际研究和应用中发现,不同传感器提供的各个证据可能存在冲突,但D-S证据理论在进行高冲突证据的合成时,得到的融合结果往往有悖于常理,为了避免此类现象的出现,提出了一种改进证据理论[12, 13].
在辨识框架内以每个证据的基本概率赋值为坐标建立Rn维空间,则每个证据都成为该空间内的一组证据向量pi=(mi(A1),mi(A2),…,mi(An))T.所有证据可以组成一个含有N个证据向量的集合P,其中任意两个向量pi和pj的夹角余弦为
式中:${{p}_{i}}^{\text{T}}{{p}_{j}}=\sum\limits_{k=1}^{n}{{{m}_{i}}({{A}_{k}}){{m}_{j}}({{A}_{k}})}(ij=1,2,\cdots ,N)$;φcij为向量pi和pj的夹角;Simij为证据m
则证据mi与其他证据的平均相似度为
而冲突证据判别因子为
式中:$\alpha =\underset{1\le i\le N}{\mathop{\min }}\,\text{Si}{{\text{m}}_{i}}$,$\beta =\underset{1\le i\le N}{\mathop{\max }}\,\text{Si}{{\text{m}}_{i}}$.
当Δi=0时,表明证据mi与其他证据不存在冲突;当Δi=1时,表明证据mi与其他证据高度冲突;因此Δi越接近于1,冲突性越大,越接近于0,冲突性越小.根据Δi即可以对证据间的冲突性进行判断,若Δi>τ,判定mi为冲突证据,其中τ为判别阈值.
对于大部分传感器证据信息是可靠且值得信任的,而证据冲突导致的错误诊断是个别异常证据造成的,因此只需要对大量传感器数据进行冲突检验,找出冲突证据并对其进行局部修正,即可减少异常信息对诊断系统的影响,从而提高诊断精度,过度的修正反而会降低诊断精度.
根据式(6)可以得出证据mi的可信度为
在确定了证据mi的相似度后,对判别出的冲突证据进行修正,得到冲突证据的修正后的基本概率赋值${{{m}'}_{i}}({{A}_{k}})$为
通过式(9)对冲突证据的判定与修正,可以得出改进证据理论的基本概率赋值的一般表达式为
为了验证本文提出评价模型的准确性,特针对某型号220 kV变压器进行状态评价,该变压器的相关评价数据如表 5~7所示.
| 油的介 质损耗/% | 油中微水质量分 数/(mg·L-1) | 击穿 电压/kV | 糠醛/ (mg·L-1) |
| 2.97 | 19.5 | 40.8 | 0.16 |
根据指标隶属度函数计算公式(1)~(3)分别计算各评价指标的隶属度分布,结果如表 8所示.
| 评价指标 | 1 | 2 | 3 | 4 |
| X11 | 0.077836 | 0.922164 | 0 | 0 |
| X12 | 0.095492 | 0.904508 | 0 | 0 |
| X13 | 1 | 0 | 0 | 0 |
| X14 | 0.484295 | 0.515705 | 0 | 0 |
| X21 | 0 | 0 | 0.476468 | 0.523553 |
| X22 | 0.114743 | 0.885257 | 0 | 0 |
| X23 | 0 | 0.992998 | 0.007002 | 0 |
| X24 | 0.938153 | 0.061847 | 0 | 0 |
| X31 | 0.992998 | 0.007002 | 0 | 0 |
| X32 | 0.997781 | 0.002219 | 0 | 0 |
| X33 | 0.998687 | 0.001313 | 0 | 0 |
| X34 | 0.793893 | 0.206107 | 0 | 0 |
| X35 | 0.121502 | 0.878498 | 0 | 0 |
根据1.2节由层次分析法计算得到的指标权重系数与表 8中内容相乘即可获得各类指标的变压器状态评价结果,并以此作为证据理论中各证据的基本概率赋值,如表 9所示.
| 证据 | m(Θ) | m(A) | |||
| 1 | 2 | 3 | 4 | ||
| 1 | 0 | 0.385 9 | 0.614 1 | 0 | 0 |
| 2 | 0 | 0.346 7 | 0.445 6 | 0.099 8 | 0.107 9 |
| 3 | 0 | 0.824 0 | 0.175 9 | 0 | 0 |
将各证据的基本概率赋值代入公式(6)、(7)、(8)即可获得各证据与其他证据的相似度Simi、冲突证据检测因子Δi和可信度Crdi,如表 10所示.
| 参数名称 | 证据1 | 证据2 | 证据3 |
| Simi | 0.83 | 0.851 8 | 0.718 9 |
| Δi | 0.164 | 0 | 1 |
| Crdi | 0.345 7 | 0.354 8 | 0.299 5 |
从表 10中可以看出,证据3与其他两个证据存在明显冲突,因此根据公式(9)对证据修正后的基本概率赋值为如表 11所示.
| 证据 | m(Θ) | m(A) | |||
| 1 | 2 | 3 | 4 | ||
| 1 | 0 | 0.385 9 | 0.614 1 | 0 | 0 |
| 2 | 0 | 0.346 7 | 0.445 6 | 0.099 8 | 0.107 9 |
| 3 | 0.700 5 | 0.246 7 | 0.052 7 | 0 | 0 |
针对修正后的基本概率赋值和未修正的基本概率赋值分别使用D-S证据理论进行融合,得到结果如表 12所示.从表 12中可以看出,未修正的参数融合后的结果显示变压器运行状态为“正常”,而经过修正后的参数融合后的结果显示变压器运行状态为“注意”.针对变压器实际运行数据进行进一步分析可发现,油中溶解气体中H2含量较高,而且电气试验和绝缘油试验的数据也显示出该变压器绝缘油可能存在一定的劣化或受潮现象,应在日常的运行管理中加强监视,因此根据实际情况,本变压器实际状态应为“注意”状态,改进证据理论融合后的结果更符合实际情况.
| 结果 | m(Θ) | m(A) | |||
| 1 | 2 | 3 | 4 | ||
| 未修改 | 0 | 0.6961 | 0.3039 | 0 | 0 |
| 修正后 | 0 | 0.3808 | 0.6192 | 0 | 0 |
通过实例分析,表明本文提出的模糊状态评价和改进证据理论相融合的状态评价模型能够较好地融合高冲突证据,削弱相悖证据对于融合准确性的影响,使状态评价结果具有更高的可信度.
4 结论本文提出了一种模糊综合评价和改进证据理论相融合的变压器状态评价方法,并用电力系统实际运行数据进行检验,得出以下结论:
1) 在变压器状态评价方法中引入模糊综合评价可以有效地解决变压器存在的不确定性和模糊性问题,克服其他评价方法在评价时参数边界过于绝对的问题.
2) 在变压器状态评价方法中引入改进D-S证据理论,对多类状态评价指标进行融合,提高了状态评价方法的准确性和可信度,避免了在高冲突证据融合时相悖现象的产生.
3) 实例表明,模糊综合评价和改进证据理论相融合的状态评价方法得到的结果能够与变压器实际运行情况相吻合.该评价方法能定量地从各层次和整体反映变压器的运行状况,模型原理清晰,相关指标参数易于获取,评价结果为了解变压器运行状况和对设备性能的进一步改进提供了科学依据.
| [1] |
张镱议, 廖瑞金, 杨丽君, 等. 基于云理论的电力变压器绝缘状态评估方法[J].
电工技术学报, 2012, 27(05): 13–20.
Zhang Yiyi, Liao Ruijin, Yang Lijun, et al. An assessment method for insulation condition of power transformer based upon cloud model[J]. Transactions of China Electrotechnical Society, 2012, 27(05): 13–20. |
| [2] |
姚建刚, 肖辉耀, 章建, 等. 电力设备运行安全状态评估系统的方案设计[J].
电力系统及其自动化学报, 2009, 21(01): 52–58.
Yao Jiangang, Xiao Huiyao, Zhang Jian, et al. Design of electric equipment operation security condition assessment system[J]. Proceedings of the CSU-EPSA, 2009, 21(01): 52–58. |
| [3] |
袁志坚, 孙才新, 袁张渝, 等. 变压器健康状态评估的灰色聚类决策方法[J].
重庆大学学报(自然科学版), 2005, 28(03): 22–25.
Yuan Zhijian, Sun Caixin, Yuan Zhangyu, et al. Method of grey clustering decision-making to state assessment of power transformer[J]. Journal of Chongqing University (Natural Science Edition), 2005, 28(03): 22–25. |
| [4] |
谢红玲, 律方成. 基于信息融合的变压器状态评估方法研究[J].
华北电力大学学报, 2006, 33(02): 8–11.
Xie Hongling, Lu Fangcheng. Transformer condition evaluation based on information fusion[J]. Journal of North China Electric Power University, 2006, 33(02): 8–11. |
| [5] |
姚峰, 张忠会, 张毅明, 等. 基于故障树法和层次分析法的电力变压器状态综合评估[J].
电气应用, 2013(11): 66–69.
Yao Feng, Zhang Zhonghui, Zhang Yiming, et al. Power transformer condition assessment based on fault tree analysis and analytic hierarchy process[J]. Electrotechnical Application, 2013(11): 66–69. |
| [6] |
张哲, 赵文清, 朱永利, 等. 基于支持向量回归的电力变压器状态评估[J].
电力自动化设备, 2010, 30(04): 81–84.
Zhang Zhe, Zhao Wenqing, Zhu Yongli, et al. Power transformer condition evaluation based on support vector regression[J]. Electric Power Automation Equipment, 2010, 30(04): 81–84. |
| [7] |
廖瑞金, 张镱议, 黄飞龙, 等. 基于可拓分析法的电力变压器本体绝缘状态评估[J].
高电压技术, 2012, 38(03): 521–526.
Liao Ruijin, Zhang Yiyi, Huang Feilong, et al. Power transformer condition assessment strategy using matter element analysis[J]. High Voltage Engineering, 2012, 38(03): 521–526. |
| [8] |
熊浩, 孙才新, 张昀, 等. 电力变压器运行状态的灰色层次评估模型[J].
电力系统自动化, 2007, 31(07): 55–60.
Xiong Hao, Sun Caixin, Zhang Yun, et al. A hierarchical grey evaluation model for operation condition of power transformers[J]. Automation of Electric Power Systems, 2007, 31(07): 55–60. |
| [9] |
俞乾, 李卫国. 模糊集对分析模型在大型电力变压器状态评价中的应用[J].
中南大学学报(自然科学版), 2013, 44(02): 598–603.
Yu Qian, Li Weiguo. Application of fuzzy set pair analysis model to power transformer condition assessment[J]. Journal of Central South University (Science and Technology), 2013, 44(02): 598–603. |
| [10] |
董玉亮, 顾煜炯, 马履翱. 基于证据推理的汽轮机组状态评价方法[J].
中国电机工程学报, 2007, 27(29): 74–79.
Dong Yuliang, Gu Yujiong, Ma Lüao. Condition evaluation on steam turbine units based on evidential reasoning[J]. Proceedings of the CSEE, 2007, 27(29): 74–79. |
| [11] |
刘从法, 罗日成, 雷春燕, 等. 基于AHP灰色定权聚类的电力变压器状态评估[J].
电力自动化设备, 2013, 33(06): 104–107,133.
Liu Congfa, Luo Richeng, Lei Chunyan, et al. Power transformer condition assessment based on AHP grey fixed-weight clustering[J]. Electric Power Automation Equipment, 2013, 33(06): 104–107,133. |
| [12] |
刘希亮, 陈桂明, 李方溪, 等. 基于改进证据理论的齿轮泵故障诊断方法研究[J].
机械科学与技术, 2014, 33(02): 183–188.
Liu Xiliang, Chen Guiming, Li Fangxi, et al. Research on fault diagnosis of gear pump based on improved evidence theory[J]. Modern Manufacturing Engineering, 2014, 33(02): 183–188. |
| [13] |
刘希亮, 陈桂明, 李方溪, 等. 基于改进证据理论的故障诊断方法研究及应用[J].
振动与冲击, 2013, 32(18): 54–58.
Liu Xiliang, Chen Guiming, Li Fangxi, et al. A fault diagnosis method based on improving evidence theory and its application[J]. Journal of Vibration and Shock, 2013, 32(18): 54–58. |
 2016, Vol. 49
2016, Vol. 49




