文章信息
- 李亚馨, 陈红坤, 杨睿茜, 陶玉波
- LI Yaxin, CHEN Hongkun, YANG Ruixi, TAO Yubo
- 双馈风电机组动态等值模型仿真研究
- Dynamic equivalence model simulation of DFIG-based wind turbine
- 武汉大学学报(工学版), 2017, 50(3): 401-408
- Engineering Journal of Wuhan University, 2017, 50(3): 401-408
- http://dx.doi.org/10.14188/j.1671-8844.2017-03-013
-
文章历史
- 收稿日期: 2016-02-22
2. 国网湖南省电力公司检修公司,湖南 长沙 410004
2. Maintenance Company of State Grid Hunan Electric Power Corporation, Changsha 410004, China
为了深刻揭示风电场与电力系统的相互作用机理,为新型能源结构下的电力系统安全稳定运行奠定理论基础,有必要对大型风电场进行仿真建模.目前对大型风电场建模主要有两种思路:第一种是建立详细风机模型,将各模型输出结果叠加作为风电场输出;第二种是用单台或较少风机表征整个风电场,求解这几台代表风机的模型结果并叠加作为整体输出结果.第一种思路求得的结果能最精确地表述整个风电场对电力系统的影响,然而其求解难度大、对计算机性能要求高、对参数变化的适应性不强、模型修改工作量大;第二种思路虽在描述整体系统上存在一定误差,但模型简单,物理意义明确,模型便于修正,简化物理问题的同时能得出准确的结论,在研究风电场对电力系统的影响方面具有重要意义.
近几年来,有不少文献针对风电场的等值问题进行了研究,其关注点主要包括:分群指标、参数聚合方法、风电场至并网点的集电网络等效.文献[1-4]的关注点主要在分群指标上,包括:风速、有功、风机状态组成的向量[1],故障切除时的转速[2],风速、风向、风电机组编号的三维相关系数矩阵[3],由风速、铭牌参数、功率曲线得到的13个状态变量[4].文献[5-7]关注点主要在参数聚合方法上,参数聚合方法大多采用容量加权法,或在此基础上用单纯形、遗传优化算法对参数优化[5, 6].集电网络等效上,一种思路是基于等效前后端电压相等,将串联支路并联化,另一种是基于功率损耗相等,用单阻抗等值集电网络[7].等值模型的评价标准基本都是比较等值前后模型的输出有功曲线、无功曲线的吻合程度,国内外也没有形成统一的标准.也有文献以动态电压作为评价指标[8].
有文献从其他角度解决风电场的等值问题.文献[9]最早从频域角度对鼠笼式风电机组进行等值,通过实测数据经高斯牛顿优化方法获取等值机组传递函数中各系数,并反推求取等值后的电气参数.由于双馈感应发电机转子侧含变流器结构,此方法不适用于双馈机组.近年来,有学者开始尝试将参数辨识思想应用到风电场等值上[10-13].文献[10]验证了短路故障扰动数据能有效辨识出风电机组的电气参数,阵风扰动数据能有效辨识出风电机组的机械参数.文献[11]用粒子群优化算法对定速风电机组的机械参数进行了辨识.文献[12]提出了基于粒子群优化方法的双馈式风电机的电气参数辨识,并对算法的不足进行了改进.文献[13]运用粒子群优化算法调整等值后机组的电压/无功参考值,用单机等值整个风电场,有效解决了输入风速差异大的双馈发电机风电场等值问题.
本文以最少数量的等值机组尽可能准确地描述多台双馈式机组的输出特性,即先采用容量加权方法将多台双馈机组等值成单台,运用粒子群算法优化电气参数、优化无功参考值、优化有功控制器参数、优化有功和直流母线电压控制器参数,再依次对比优化后的等值模型与原详细模型的有功出力曲线,验证了当风电场并网点发生三相短路故障时,采用容量加权等值成单机后,通过优化有功和直流母线电压控制器参数得到的等值模型与原详细模型的动态特性最相近.
1 双馈风机的数学模型双馈风机在同步旋转坐标轴下的状态方程同时考虑了机械动态、定子和转子动态.同步旋转坐标系下的电机电压方程为
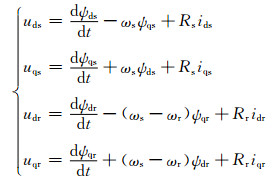 (1)
(1)
式中:uds、uqs、udr、uqr、ids、iqs、idr、iqr分别为d轴、q轴定、转子绕组电压与电流;ψds、ψqs、ψdr、ψqr分别为d轴、q轴定、转子绕组磁链;Rs、Rr分别为定、转子绕组电阻;ωs为坐标系旋转角速度,此时等于同步转速ω0;ωr为转子旋转角速度.
相应的磁链方程为
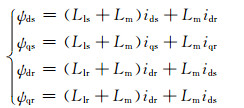 (2)
(2)
式中:Lls、Llr分别为定、转子每相漏感;Lm为互感.
简化后的DFIG三阶模型将发电机等效为暂态阻抗Z′=Rs+jX′,暂态电压源E′=E′d+jE′q.忽略定子磁通暂态过程就可以得到简化后的三阶动态模型:
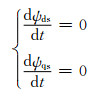 (3)
(3)
则定转子电压方程和转子运动方程一起构成的DFIG三阶动态模型为
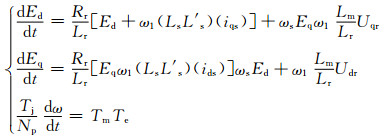 (4)
(4)
式中:L′s为定子暂态电感;Ed、Eq为DFIG等值内电势d、q轴分量;ωs=ω1ωr.
2 容量加权方法参数聚合容量加权思想认为等值机组的某参数等于单机中该参数乘以权重,但实际上,各台风机的总体特性完全等于单台风机特性的叠加必须是建立在特定假设条件下,如转速一致.从风力机向电网侧看,需要等值的参数主要包括:转动惯量(也有模型对应的是惯性时间常数),阻尼系数,定子电阻,定子漏感,转子电阻,转子漏感,定转子互感,各个PI控制器的比例、积分常数,连接转子侧、网侧变流器的直流母线电容,网侧变流器与并网点间的阻抗参数,风机出口处箱式变压器参数.对于各台风机转速不同的情况,还需对输入风速进行等值,通常等值风速为各机组风速乘以相应机组的容量加权系数.各参数等值公式如下:
等值转动惯量:
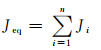 (5)
(5)
式中:下角标eq表示等值机组的参数;下角标i(i=1, 2, …,n)表示被等值机组的参数;n为风电场内需等值的机组台数.
等值惯性时间常数:
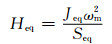 (6)
(6)
式中:ωm是风机机械转速的标准值,即发电机转子处于同步转速时对应的机械转速;Seq为等效的风机容量,为待等值机组容量的代数和.对于转动惯量相同、容量相同的风电机组,等值机组惯性时间常数等于每台机组的惯性时间常数.阻尼系数在风力机参数中多以标幺值形式出现,等值阻尼系数为各机组阻尼系数乘以相应的容量加权系数.
等值发电机阻抗参数、网侧变流器与并网点间的阻抗参数为
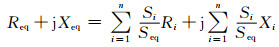 (7)
(7)
式中:Ri、Xi、Si分别为第i台机组的电阻、电抗、风机容量.
转子侧变流器和网侧变流器中各个PI控制器参数的等值遵循标幺值相等的原则,比例、积分常数与等值机组和待等值机组容量的倍数成正比:
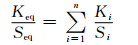 (8)
(8)
式中:Ki为各PI控制器的比例、积分常数的有名值.
等值两侧变流器之间的直流母线电容为
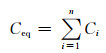 (9)
(9)
风机出口处至并网点的箱式变压器阻抗参数的等效类比于发电机阻抗参数的等效,等值后箱变的容量等于各风电机组的箱变容量之和.
3 粒子群参数辨识等值方法在风电场发生三相对称短路故障时,定转子电流中均包含直流暂态分量、交流分量以及稳态分量[14].定转子的交流分量分别与工频、转子角频率相关,稳态分量与电压跌落深度有关.通过仿真发现,当设置风电场并网点发生三相短路故障时,故障过程中动态误差并不大,因为仿真设置的故障多为金属性接地故障,电压接近0,暂态电流对有功曲线影响不大.而在故障恢复过程中,容量加权方法得到的单机等值模型与详细模型的动态误差很大.故障恢复过程类似于风电机组的瞬间并网过程,与故障切除时风机并网点电压的相角、风电机组的转速等因素有关.由于并网过程的暂态功率难以定量刻画,目前文献大多关注双馈风电机组的并网控制策略.在故障恢复过程中详细模型和等值模型的动态误差较难定量地表示,因此,可以通过优化某些影响双馈机组动态特性的参数,来使等值模型与详细模型输出特性相近.
采用辨识手段来获取物理元件参数准确值的方法,已经广泛应用于同步发电机和电力负荷[15].参数辨识方法在双馈风电机组动态等值问题上同样具有一定优势,它只需知道每台风机出厂时的电气、机械参数,作为一个优选的初值,再通过优化算法迭代寻优,便能实现对整个风电场的动态特性等值.合适的初值选择和合适的算法都有利于快速找到最优解,提高仿真效率.但参数辨识的难点在于需要获取扰动数据,难以在正常情况下获得.本文的参数辨识方法暂时仅在仿真环境中进行.
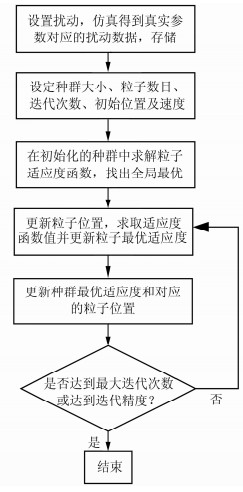
粒子群优化算法具有全局性能好.收敛速度快等特点,广泛应用于电力系统及其他工程领域.粒子群算法每次迭代中,粒子跟踪两个极值:一个是粒子本身迄今为止找到的最优解,另一个是整个种群迄今为止找到的最优解.基本粒子群算法在双馈风机的参数辨识中的流程图如图 1所示.
|
| 图 1 基本粒子群算法优化双馈风机参数流程图 Figure 1 Flowchart of PSO algorithm |
参数辨识的适应度函数为
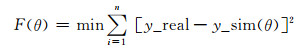
寻找最优的θ,使适应度函数值最小.
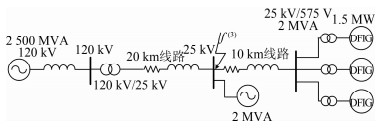
4 粒子群辨识算法动态等值优化仿真 4.1 容量加权等值模型对基于MATLAB/Simulink平台中的双馈风力发电机模型进行仿真.3台1.5 MW的双馈风机接入120 kV系统,如图 2所示.
|
| 图 2 双馈风机接入120 kV系统示意图 Figure 2 DFIG integrated with a 120 kV power system |
以仿真开始时刻为计时起点,在t=1.2 s时,25 kV母线上发生三相短路故障,故障持续时间0.05 s后切除.每台风机及风机出口处箱式变压器的参数完全一致,每台风机输入风速均为9 m/s.假定不考虑故障过程中转子crowbar回路动作,不考虑线路保护动作.先将3台风机容量加权等值成单机,参数聚合方法见第2节,变压器参数聚合则容量叠加,阻抗参数以标幺值一致为原则,等值机组的机械、电气参数和控制器参数分别见表 1、2.
| 机械、电气参数 | 单台机 | 等值机 |
| 额定功率/MVA | 1.5/0.9 | 5 |
| 定子端电压/kV | 0.575 | 0.575 |
| 额定频率/Hz | 60 | 60 |
| 惯性时间常数/s | 5.04 | 5.04 |
| 机械阻尼系数 | 0.01 | 0.01 |
| 网侧电阻/p.u. | 0.001 5 | 0.001 5 |
| 网侧电感/p.u. | 0.15 | 0.15 |
| 定子电阻/p.u. | 0.007 06 | 0.007 06 |
| 绕线转子电阻/p.u. | 0.005 | 0.005 |
| 励磁电感/p.u. | 2.9 | 2.9 |
| 定子漏感/p.u. | 0.171 | 0.171 |
| 转子漏感/p.u. | 0.156 | 0.156 |
| 直流电容/μF | 1 000 | 3 000 |
| 直流母线电压/kV | 1.2 | 1.2 |
| 比例常数 | 积分常数 | ||||
| 单台机 | 等值机 | 单台机 | 等值机 | ||
| 转子侧内环 | 0.05 | 0.15 | 1.5 | 4.5 | |
| 转子侧有功外环 | 0.166 67 | 0.5 | 16.667 | 50 | |
| 转子侧无功外环 | 0.008 33 | 0.025 | 0.833 3 | 2.5 | |
| 网侧内环 | 0.166 67 | 0.5 | 16.667 | 50 | |
| 网侧直流电压外环 | 0.000 333 | 0.001 | 0.008 33 | 0.025 | |
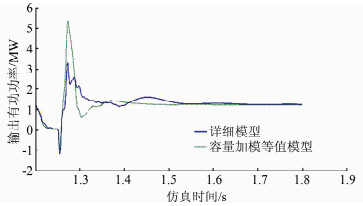
截取故障发生之后0.6 s内的数据,容量加权等值模型与详细模型的有功、无功动态曲线分别如图 3、4所示.
|
| 图 3 容量加权模型与详细模型的有功动态曲线 Figure 3 Dynamic active power curves of capacity weighted model and detailed model |
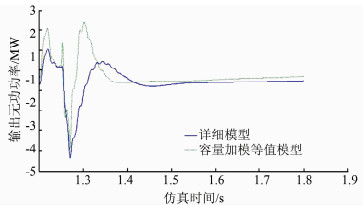
|
| 图 4 容量加权模型与详细模型的无功动态曲线 Figure 4 Dynamic reactive power curves of capacity weighted model and detailed model |
在故障恢复过程至重新达到稳态时,容量加权等值模型与详细模型的动态特性具有较大误差.运用粒子群优化算法分别对等值机组的电气参量、无功参考值、有功控制器参数、直流母线电压控制器参数进行优化,设定粒子数目为5,自变量个数分别设为5、1、1、2、2,最大迭代次数为100,学习因子1和2均设为2,采用恒定的惯性权重0.2.
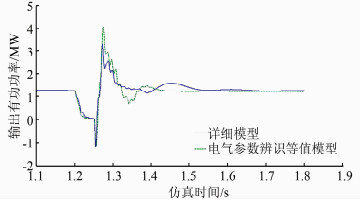
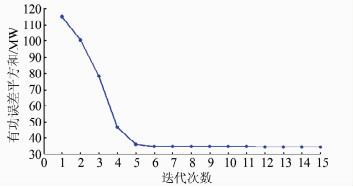
4.2 粒子群优化模型对比 4.2.1 优化电气参数电网侧故障能激起风电场电气部分的快动态模式[10],电气参数对故障恢复的动态过程也有一定影响,在容量加权聚合参数的基础上,运用基本粒子群算法优化等值机组的电气参数能减小故障恢复过程中的动态误差.经过20次迭代后,优化等值模型与详细模型的有功曲线对比如图 5所示,各次迭代误差如图 6所示.详细模型、单机等值模型、电气参数优化后单机等值模型的有功曲线对比如图 7所示.
|
| 图 5 电气参数优化等值模型与详细模型有功曲线对比 Figure 5 Active power curves of equivalent model with optimized electrical parameters and detailed model |
|
| 图 6 等值模型电气参数优化的各次迭代误差 Figure 6 Iterative errors of optimized electrical parameters of equivalent model |
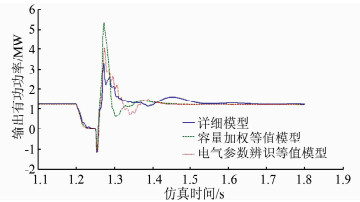
|
| 图 7 详细模型、单机等值模型、电气参数优化等值模型有功曲线对比 Figure 7 Active power curves of detailed model, single equivalent model and equivalent model with optimized electrical parameters |
由图 6、7可以看出,优化电气参数后的单机等值模型更接近详细模型,但在描述详细模型暂态过程的特性方面仍然存在一定误差.由图 6可以看出,电气参数优化等值模型的迭代误差在15次迭代后基本保持不变,表明详细模型的暂态特性不仅由电气参数表征,还有其他影响因素.
4.2.2 优化无功参考值双馈风机的无功特性影响动态过程中的等值精度.通过给双馈风机的无功参考量叠加一个补偿量ΔQ,运用粒子群算法寻找最优的ΔQ,满足动态过程中平均相对误差最小.值得注意的是,优化ΔQ可能造成静态误差增大.经过优化无功参考值后等值模型与详细模型的有功曲线及各次迭代误差如图 8、9所示.对无功参考值增加一个补偿量,虽然能减小单机等值模型的动态误差,但在迭代15次后误差仍为一个较大数值.
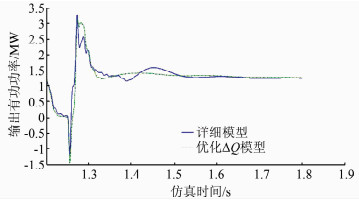
|
| 图 8 优化无功参考值等值模型与详细模型有功曲线对比 Figure 8 Active power curves of equivalent model with optimized reactive power reference value and detailed model |
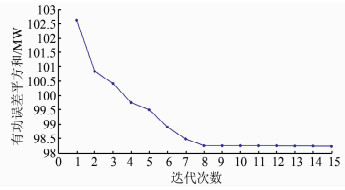
|
| 图 9 等值模型无功参考值优化的各次迭代误差 Figure 9 Iterative errors of optimized reactive power reference value of equivalent model |
在双馈机组的变流器中,转子侧若采用定子磁链定向的控制策略,则与有功输出特性相关的电气量主要是Irq,通过优化有功控制器参数,使等值机组的Irq_ref与详细模型的Irq_ref具有一致性,从而有效减小动态误差.采用粒子群算法优化有功控制器的参数,经15次迭代后,最优解已趋于平稳.优化后的有功控制器参数kp为0.051 2,ki为6.011.优化有功控制器参数后等值模型与详细模型的有功曲线对比、各次迭代误差分别如图 10、11所示.
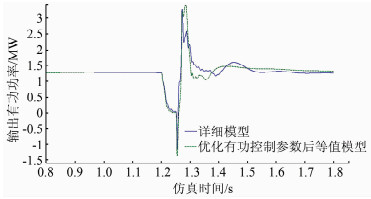
|
| 图 10 优化有功控制器参数等值模型与详细模型的有功曲线对比 Figure 10 Active power curves of equivalent model with optimized active power reference value and detailed model |
|
| 图 11 等值模型优化有功控制器参数的各次迭代误差 Figure 11 Iterative errors of optimized active power reference value of equivalent model |
优化有功控制器参数后,详细模型与等值模型的Irqref和Irq如图 12所示.
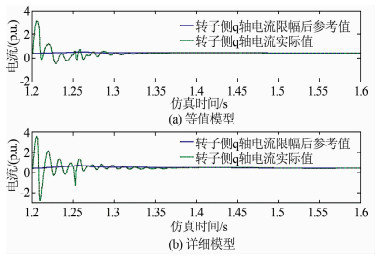
|
| 图 12 优化有功控制器参数后等值模型与详细模型的Irqref与Irq Figure 12 Irqrefand Irqcurves of equivalent model with optimized active power reference value and detailed model |
双馈风机的网侧变流器中与有功相关的参量主要是直流母线电压Udc,在优化有功控制器参数后,优化Udc控制器参数可进一步减小动态误差.
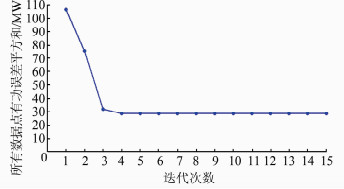
经过17次迭代后,直流电压控制器参数优化值kp为0.000 561 8,ki为0.001 67.优化直流电压控制器参数后等值模型与详细模型的有功曲线对比及各次迭代误差如图 13、14所示.
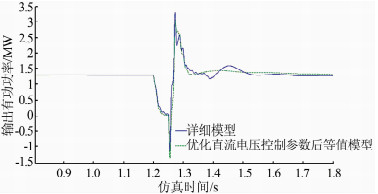
|
| 图 13 优化直流电压控制器参数后等值模型与详细模型的有功曲线对比 Figure 13 Active power curves of equivalent model with optimized DC voltage controller parameters and detailed model |
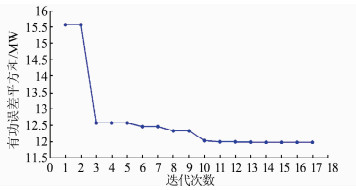
|
| 图 14 等值模型优化直流电压控制器参数的各次迭代误差 Figure 14 Iterative errors of optimized DC voltage controller parameters of equivalent model |
各优化模型参数最终优化结果如表 3所示,表中电气参数和无功参数单位均为p.u.,控制器参数为无量纲.
| 模型1 | Rs | Rr | Lls | Llr | Lm |
| 0.002 70 | 0.012 6 | 0.262 | 0.291 | 2.061 | |
| 模型2 | ΔQ | ||||
| 0.243 | |||||
| 模型3 | kp | ki | |||
| 0.051 2 | 6.011 | ||||
| 模型4 | P_kp | P_ki | Udc_kp | Udc_ki | |
| 0.051 2 | 6.011 | 0.000 561 8 | 0.001 67 | ||
| 注:模型1为优化电气参量等值模型;模型2为优化无功参考值等值模型;模型3为优化有功控制器参数等值模型;模型4为优化有功和直流电压控制器参数等值模型. | |||||
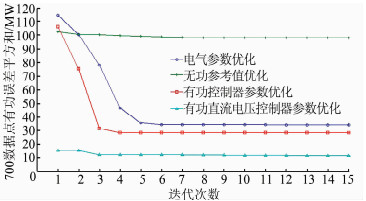
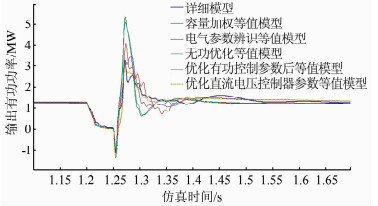
各优化模型的15次迭代误差及t=1.1~1.7 s内的有功动态曲线如图 15、16所示,由图可以看出,对有功、直流母线电压控制器参数优化后的模型与详细模型之间的动态误差最小,无功参考值优化和直流母线电压控制器参数优化效果,相比电气参数优化和有功控制器参数优化不太明显.
|
| 图 15 各优化模型前15次迭代误差 Figure 15 The first 15 iteration errors of each optimized model |
|
| 图 16 t=1.1~1.7 s内各优化模型有功输出曲线 Figure 16 Active power curves of each optimized model in t=1.1~1.7 s |
分别将详细模型及各优化模型的有功曲线、转子侧变流器电流Ird、Irq参考值及实际值、直流母线电压Udc参考值及实际值、网侧变流器电流Id、Iq参考值及实际值曲线进行对比,可以得出,转子侧变流器电流Ird和网侧变流器电流Iq对有功动态特性的影响很小.相对而言,转子侧变流器参数对有功动态特性的影响比网侧变流器参数更大.
为了建立风电场不论静态还是动态时的精度较高的等值模型,可以先在静态时通过优化输入风速得到等值机组输入风速,再基于容量加权方法建立单机等值模型,最后通过优化有功控制器参数和直流电压控制器参数获得动态过程中的较高精度,得到整体静、动态性能与详细模型最接近的等值模型.
5 结论本文采用“先聚合后优化”的思想,先将风电场多台机组用容量加权方法聚合成一台机组,由于在短路故障情况下,容量加权模型与详细模型之间存在较大的动态误差,动态误差较大时段集中在故障切除至恢复稳态过程,应用基本粒子群算法分别对电气参数、无功参考值、有功控制器参数、有功直流电压控制器参数进行优化,对比各种等值模型与详细模型在三相短路故障时的动态等值误差,研究结果表明:
1) 对有功直流电压控制器参数优化后,等值模型与详细模型之间动态误差最小,能较精确地描述风电场详细模型的动态过程;
2) 相对网侧变流器参数而言,转子侧变流器参数对有功动态特性影响更大;
3) 变流器中与无功相关的参数对有功动态特性影响较小.
本文的仿真输入条件为建立在风速恒定情况下,且未考虑短路故障时转子crowbar投入,未考虑短路故障时保护装置动作,后续研究工作应深入考虑这些因素对风电场动态等值的影响.
| [1] |
王鑫. 风电场动态等值模型研究[D]. 北京: 华北电力大学, 2008.
Wang Xin.Research on dynamic equivalent model of wind farm[D].Beijing:North China Electric Power University, 2008. |
| [2] |
米增强, 苏勋文, 杨奇逊, 等. 风电场动态等值模型的多机表征方法[J].
电工技术学报, 2010, 25(5): 162–169.
Mi Zengqiang, Su Xunwen, Yang Qixun, et al. Multi-machine representation method for dynamic equivalent model of wind farms[J]. Electrical Technology, 2010, 25(5): 162–169. |
| [3] |
曹娜, 于群. 风速波动情况下并网风电场内风电机组分组方法[J].
电力系统自动化, 2012, 36(2): 42–46.
Cao Na, Yu Qun. A grouping method for wind turbines in a grid connected wind farm during wind speed fluctuation[J]. Automation of Electric Power Systems, 2012, 36(2): 42–46. |
| [4] |
陈树勇, 王聪, 申洪, 等. 基于聚类算法的风电场动态等值[J].
中国电机工程学报, 2012, 32(4): 11–19.
Chen Shuyong, Wang Cong, Shen Hong, et al. Dynamic equivalence for wind farms based on clustering algorithm[J]. Proceedings of the CSEE, 2012, 32(4): 11–19. |
| [5] |
刘力卿, 余洋, 王哲, 等. 变速恒频双馈风电机组的动态等值方法[J].
电力系统及其自动化学报, 2012, 24(2): 63–71.
Liu Liqin, Yu Yang, Wang Zhe, et al. Dynamic equivalence method of variable speed wind turbine with doubly-fed induction generators[J]. Proceedings of the CSU-PSA, 2012, 24(2): 63–71. |
| [6] |
张保会, 李光辉, 王进, 等. 风电接入对继电保护的影响(二)——双馈式风电场电磁暂态等值建模研究[J].
电力自动化设备, 2013, 33(2): 1–7.
Zhang Baohui, Li Guanghui, Wang Jin, et al. Impact of wind farm integration on relay protection(2): DFIG-based wind farm electro-magnetic transient equivalent model[J]. Electric Power Automation Equipment, 2013, 33(2): 1–7. |
| [7] |
金宇清, 黄桦, 鞠平, 等. 用于风电场聚合建模的内部集电网络变换方法[J].
电力系统保护与控制, 2012, 40(16): 34–41.
Jin Yuqing, Huang Hua, Ju Ping, et al. Collector network transformation methods for wind farm aggregated modeling[J]. Power System Protection and Control, 2012, 40(16): 34–41. DOI:10.3969/j.issn.1674-3415.2012.16.006 |
| [8] |
周明, 葛江北, 李庚银. 基于云模型的DFIG型风电场动态电压等值方法[J].
中国电机工程学报, 2015, 35(5): 1097–1105.
Zhou Ming, Ge Jiangbei, Li Gengyin. Cloud model based DFIG wind farm dynamic voltage equivalence method[J]. Proceedings of the CSEE, 2015, 35(5): 1097–1105. |
| [9] |
孙建锋, 焦连伟, 吴俊玲. 风电场发电机动态等值问题的研究[J].
电网技术, 2004, 28(7): 58–61.
Sun Jianfeng, Jiao Lianwei, Wu Junling. Research on multi-machine dynamic aggregation in wind farm[J]. Power System Technology, 2004, 28(7): 58–61. |
| [10] |
潘学萍, 鞠平, 徐倩, 等. 双馈风力发电机参数分步辨识及观测量的选择[J].
中国电机工程学报, 2013, 33(13): 116–126.
Pan Xueping, Ju Ping, Xu Qian, et al. A two-step method for estimating DFIG parameters in a wind turbine and the measurement selection[J]. Proceedings of the CSEE, 2013, 33(13): 116–126. |
| [11] |
潘学萍, 高远, 金宇清, 等. 风电机组驱动系统参数辨识[J].
电网技术, 2013, 37(7): 1990–1994.
Pan Xueping, Gao Yuan, Jin Yuqing, et al. Parameter identification of drive system for fixed-speed wind power generation units[J]. Power System Technology, 2013, 37(7): 1990–1994. |
| [12] |
刘永康, 潘学萍, 鞠平. 基于改进粒子群算法的双馈感应发电机参数辨识[J].
河海大学学报(自然科学版), 2014, 42(3): 273–277.
Liu Yongkang, Pan Xueping, Ju Ping. Identification of DFIG parameters based on improved PSO algorithm[J]. Journal of Hohai University (Natural Sciences), 2014, 42(3): 273–277. |
| [13] |
金宇清, 鞠平, 潘学萍. 基于双馈感应发电机风电场等效建模中控制器聚合方法分析[J].
电力系统自动化, 2014, 38(3): 19–24.
Jin Yuqing, Ju Ping, Pan Xueping. Analysis on controller aggregation method for equivalent modeling of DFIG-based wind farm[J]. Automation of Electric Power Systems, 2014, 38(3): 19–24. DOI:10.7500/AEPS201211101 |
| [14] |
李辉, 赵猛, 叶仁杰, 等. 电网故障下双馈风电机组暂态电流评估及分析[J].
电机与控制学报, 2010, 14(8): 45–51.
Li Hui, Zhao Meng, Ye Renjie, et al. Evaluation and analysis of transient current of a DFIG wind generation system under grid fault[J]. Electric Machines and Control, 2010, 14(8): 45–51. |
| [15] |
鞠平.
电力系统建模理论与方法[M]. 北京: 科学出版社, 2010.
Ju Ping. Theory and Method of Power System Modeling[M]. Beijing: Science Press, 2010. |
 2017, Vol. 50
2017, Vol. 50



