武汉大学学报(工学版)   2016, Vol. 49 Issue (4): 577-584

文章信息

安晨帆, 杜志叶, 甘艳, 李慧慧, 周涛涛
AN Chenfan, Du Zhiye, GAN Yan, LI Huihui, ZHOU Taotao
双回并行超高压输电线路无线电干扰计算方法
Radio interference calculation method for double parallel EHV transmission lines
武汉大学学报(工学版), 2016, 49(4): 577-584
Engineering Journal of Wuhan University, 2016, 49(4): 577-584
http://dx.doi.org/10.14188/j.1671-8844.2016-04-016

文章历史

收稿日期: 2015-05-13
 Abstract              PDF               Figures               Tables
引用本文 0
安晨帆, 杜志叶, 甘艳, 李慧慧, 周涛涛. 双回并行超高压输电线路无线电干扰计算方法[J]. 武汉大学学报(工学版), 2016, 49(4): 577-584.
AN Chenfan, Du Zhiye, GAN Yan, LI Huihui, ZHOU Taotao. Radio interference calculation method for double parallel EHV transmission lines[J]. Engineering Journal of Wuhan University, 2016, 49(4): 577-584.
双回并行超高压输电线路无线电干扰计算方法
安晨帆, 杜志叶1, 甘艳1, 李慧慧2, 周涛涛1     
1. 武汉大学电气工程学院，湖北 武汉 430072;
 2. 华中电网有限公司，湖北 武汉 430077
收稿日期: 2015-05-13
作者简介: 安晨帆(1991-)，女，硕士研究生，研究方向为电磁场数值仿真计算，E-mail：896676843@qq.com..
通讯作者: 杜志叶(1974-)，男，博士，副教授，硕士生导师，从事电磁场计算、电网故障与安全、电磁兼容等研究，E-mail:duzhiye@126.com.
摘要: 针对超高压输电线路无线电干扰计算问题，分析了国内外各研究机构推荐的经验公式法和激发函数法的计算条件和参数差异，讨论了导线表面电场强度取值的方法.基于逐次镜像法计算导线表面电场强度，提高了各子导线表面电场强度的计算精度，并应用到各个推荐公式.对2条并行的500 kV超高压输电线路进行计算，并与基于马克特-门德尔方法计算的表面电场进行对比，比较各种计算方法同实测结果之间的差异，讨论各种参数的适用条件，验证了该方法更适用于并行双回超高压线路的无线电干扰计算.基于本文确定的激发函数，研究了不同相序、对地高度、分裂间距、子导线直径对线路无线电干扰变化的影响，提出了减小线路下方无线电干扰的措施，为架空输电线路的建设提供参考.
关键词： 超高压     输电线路     激发函数法     无线电干扰    
Radio interference calculation method for double parallel EHV transmission lines
AN Chenfan, Du Zhiye1, GAN Yan1, LI Huihui2, ZHOU Taotao1     
1. School of Electrical Engineering, Wuhan University, Wuhan 430072, China;
 2. Central China Grid Company Limited, Wuhan 430077, China
Abstract: Aiming at the evaluation problem of radio interference(RI) for the extra high voltage(EHV) transmission lines, the paper analyzes the calculation condition and parameters by both empirical formula and the excitation function method which are recommended by domestic and abroad research institutes. Methods for calculating maximum electric field intensity of surface of sub-conductor are discussed in detail. The surface electric field intensity of sub-conductors is calculated and compared based on the successive image method and markt-Mengele method respectively. Thereafter the calculated values are applied to the recommended formulas. A double parallel 500 kV EHV transmission line is taken for example, the differences between the various calculation methods and the measured results are compared and discussed. The applicable conditions of various parameters are recommended. The method proposed in this article is validated to be more suitable for the RI calculation of EHV transmission line. Based on the determined excitation function, the factors which affect the RI, such as phase sequence, line height, bundle spacing and sub-conductor diameter of bundle conductor are studied in depth; and the measures for decreasing RI under the transmission lines are put forward, so as to provide reference for transmission lines construction in engineering practice.
Key words: extra-high voltage (EHV)     transmission lines     excitation function method     radio interference(RI)    

架空输电线路无线电干扰是线路导线和连接金具发生电晕时产生的副作用.电晕放电产生高频电流、电压脉冲，频带宽在3 kHz~30 MHz之间，覆盖了无线电频带的大部分，可对正常无线电通信信号产生干扰.随着超、特高压输电线路的发展，一些超高压输电线路通常需要跨越城镇居民区，线路走廊附近的无线电干扰已成为线路设计和运营中的限制条件，引起附近居民和环境保护部门的关注.

对于高压输电线路无线电干扰计算和评估方法的研究，从20世纪60年代以来，国际上很多研究机构和组织均基于各自的成果，提出了相应的计算方法和推荐公式，总结起来可分为2大类：经验公式法和激发函数法.其中最为著名的是国际无线电干扰特别委员会(CISPR18-3)推荐的公式.文献[1]列出了美国、德国、日本、意大利、加拿大等机构的经验公式并给出了详细的应用条件及参数选取说明.文献[2]中详细介绍了 EPRI、 EDF、 IREQ、 BPA、 CIGRE等研究机构根据线路或者导线的电晕笼试验提出的激发函数.由于各个研究机构的推荐方法基于各自的试验线路和测量结果提出的，推荐公式中适用条件、线路参数要求都有较大的区别.其中对计算结果影响较为显著的一个参数是导线表面电场强度，常用的有导线平均电场强度、导线最大电场强度以及各子导线最大电场强度的平均值(对于分裂导线).国内的研究机构通常直接引用这些标准，或者参照这些实验数据进行相应的拓展.如我国的电力行业标准[3]中的计算方法就直接引用CISPR18-3的推荐公式[4].国内很多文献中也常引用上述文献中的推荐公式或者主要结论，但是在公式适用条件、计算参数选取方面表述较为简略[5-8]，常常引起读者的误解.特别是对导线表面电场强度的引用，大多文献采用了“导线最大表面电场强度”，忽视了不同机构推荐公式之间的差异，计算结果偏差较大.

文章分析了各个研究结构推荐的经验公式法和激发函数法的计算条件和参数差异，基于逐次镜像法计算导线表面电场强度，提高了各子导线表面电场强度的计算精度，并应用到各个推荐公式.对华中地区2条并行的500 kV超高压输电线路进行计算，并与基于马克特-门德尔方法计算的导线表面电场进行了对比，对比各种计算方法同实测结果之间的差异，讨论了各种参数的选取条件，验证了本文方法更适用于超高压线路的无线电干扰计算.文章还考虑了不同相序、导线对地高度、分裂间距、子导线直径等因素的影响.

1 无线电干扰计算方法 1.1 经验公式法

根据GB15707-1995的规定[9]，输电线路的无线电干扰主要以线路边相外20 m处、频率为0.5 MHz 时的无线电干扰场强80%/80%值为考核标准.80%/80%原则，即在80%的时间中，无线电干扰场强不超过限值且具有 80%的置信度.其中，500 kV交流架空送电线路无线电干扰限值为55 dB.国际无线电干扰特别委员会(CISPR18-3,1986)推荐的无线电干扰计算方法适用于单回、分裂数不大于4的三相架空线路.回路中一相输电线产生的频率为0.5 MHz的无线电干扰计算公式[3]为

${{E}_{i}}=3.5{{g}_{\text{maxi}}}+12r-33\lg ({{D}_{i}}/20)-30 $    (1)

式中：Ei为距离第i相导线直接距离Di处，地面上2 m处的无线电干扰场强，dB；gmaxi为第i相导线表面最大电场强度(有效值)，kV/cm；r为单根导线半径，对于分裂导线，取子导线半径，cm；Di为第i相导线到测量点的直接距离，m.

采用式(1)可以计算每一相导线产生的无线电干扰.三相线路则需考虑：如果Ea、Eb指三相中两相较大的场强值，当Ea>Eb+3 dB时，三相线路的无线电干扰场强E=Ea；否则场强计算公式为

$E=\frac{{{E}_{a}}+{{E}_{b}}}{2}+1.5$    (2)

对于多回线路，将m回线路的同名相导线产生的场强进行几何叠加：

${{E}_{i}}=20\lg {{[\sum\limits_{m=1}^{N}{{{({{10}^{\frac{{{E}_{mi}}}{20}}})}^{2}}}]}^{\frac{1}{2}}}$    (3)

式中：Ei为多回路第i相导线在测量点处产生的干扰场强，dB；Emi为第m回第i相导线在测量点处产生的干扰场强，dB.

该公式是在实验线路通过长期的实验观测数据拟合得到，试验电压范围为200~750 kV，导线表面最大电场强度为12~20 kV/cm.式(1)计算得的为好天气下(50%)的无线电干扰水平，换算到80%/80%标准下的无线电干扰水平，还需增加6~10 dB[3, 9].

由上式可以看出，无线电干扰计算结果同线路参数如子导线半径、线路高度、相间距以及工作电压等有关.其他组织和机构推荐的公式也大多采用形如上式的形式，但具体的系数和修正参数取值上有一些区别.其中容易混淆的一个参数就是导线表面电场强度，不同组织的定义有着各自的特点.比如意大利(ENEL)的推荐公式[1]为

$\begin{align} & E=47+3.8({{g}_{av}}-15)+40\lg \frac{d}{5}+10\lg n+ \\ & 30\lg \frac{20}{D}+20\lg \frac{1+{{0.5}^{2}}}{1+{{f}^{2}}}+\Delta {{N}_{FW}} \\ \end{align}$    (4)

式中：f为干扰频率，MHz；对于坏天气，ΔNFW=14~18 dB；gav为导线表面平均电场强度(有效值)，kV/cm；对于分裂导线：

${{g}_{av}}=\frac{{{g}_{max}}}{1+\beta d/2S}$    (5)

式中：β为电场不均匀系数；S为分裂间距.注意到式(4)选取的是gav作为计算参数，而其他研究组织均采用gmax，这是计算中应该注意的.

1.2 激发函数法

激发函数法基于高压试验线段或电晕笼测量而得的大雨条件下的无线电干扰产生激发函数Γ，通过一定的模量变换，得出各相导线的脉冲电流，再获得这些电流产生的场，即无线电干扰[10].

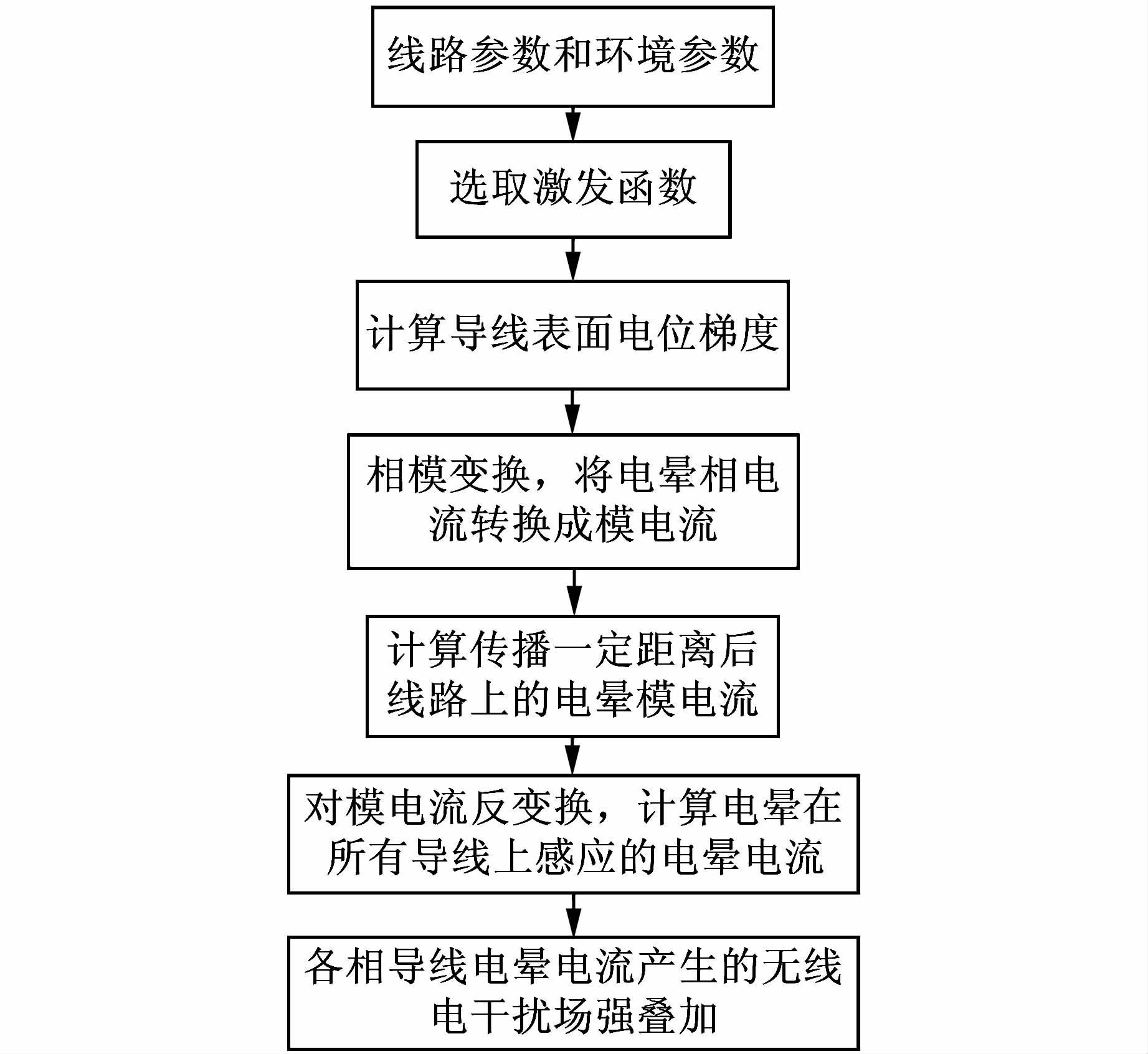
利用激发函数法计算无线电干扰的计算流程如图 1所示.

图 1 激发函数法计算无线电干扰流程图 Figure 1 Flowchart of radio interference calculation with excitation function method
图选项

该方法的关键就是确定激发函数，由于线路发生电晕、产生无线电干扰的过程十分复杂，并有随机性，极易受到天气、海拔、测量仪器等因素的影响，且后期数据处理方法也各不相同，因此各研究机构得到的激发函数存在区别.

CISPR[4]推荐了利用激发函数法计算多分裂导线的无线电干扰的公式，提出大雨时无线电干扰的激发函数为

${{\Gamma }_{\text{CISPR}}}=70-585/{{g}_{\text{mav}}}+35\lg d-10\lg n$    (6)

式中：gmav为各个子导线表面电场强度最大值的平均值(有效值)，kV/cm； d为线路子导线的直径，cm；n为相导线的分裂根数.

该式适用于子导线分裂间距S与直径d之比为10~15时的线路，当S/d较小时，实际的激发函数值要比计算得到的值高，特别是分裂数大于10时更为明显.

当子导线直径较大时(大于40 cm)或者分裂数大于10时，CISPR提出线路的无线电干扰的激发函数为

${{\Gamma }_{\text{CISPR}}}=-121+120\lg {{g}_{\text{max}}}+40\lg d$    (7)

式中：gmax为各子导线表面最大电场强度(有效值)，kV/cm.

该公式适用条件为大雨，但导线表面电场强度的取值同式(4)不同.美国EPRI提出的大雨状况下的无线电干扰的激发函数[2]为

${{\Gamma }_{\text{EPRI}}}= 81.1 - 580/{{g}_{\text{max}}} + 38\lg (d/3.8)$    (8)

式中导线表面电场强度的选取同式(5)完全相同.它是在8~12 mm自然降雨相当的人工降雨情况下通过电晕笼试验得到的.其他研究机构推荐的公式形式上相差不大，但具体的参数值有所不同，应用时要注意适用范围的差异.

我国电力行业标准DL/T 691-1999标准推荐的激发函数参考CISPR18-3/1996的推荐标准公式，适用于计算多分裂导线的交流架空输电线路无线电干扰数值.

2 导线表面电场计算方法

输电线路导线表面电场强度的计算方法有基于求取导线等效半径的马克特-门德尔法、有限元法、模拟电荷法、矩量法和逐次镜像法等[11].马克特-门德尔法从工程角度推荐应用[12]，但无法获得子导线表面电场强度.有限元法开域边界需取多次验证截断误差以满足要求，且计算精度受剖分方式的影响很大，建模略显麻烦[13-17]；逐次镜像法单独处理每根子导线，考虑了子导线间的影响，是一种较为精确的计算方法，可以求得无线电干扰各类推荐公式所需的导线表面场强的任意值[18].文献[11]对比了马克特-门德尔法、模拟电荷法、矩量法以及逐次镜像法对于10种不同排列类型输电线路的导线表面电场强度的计算精度，发现马克特-门德尔法在计算分裂数小于4的导线表面电场强度时能够满足工程精度，而逐次镜像法在所有形式线路中都有较高的计算精度和最高的一致性.

2.1 逐次镜像法

逐次镜像法是以维持各导线表面成等位面为边界条件，在各个导线内逐次放置镜像电荷.多导线系统中每根导线上的分布电荷可被一系列的点电荷等效表示.由于每一次镜像过程都使系统中每根导线的表面向等电位面趋近一步，当所研究的问题在某次镜像后已得到满足精度要求的结果时，逐次镜像过程即可结束.

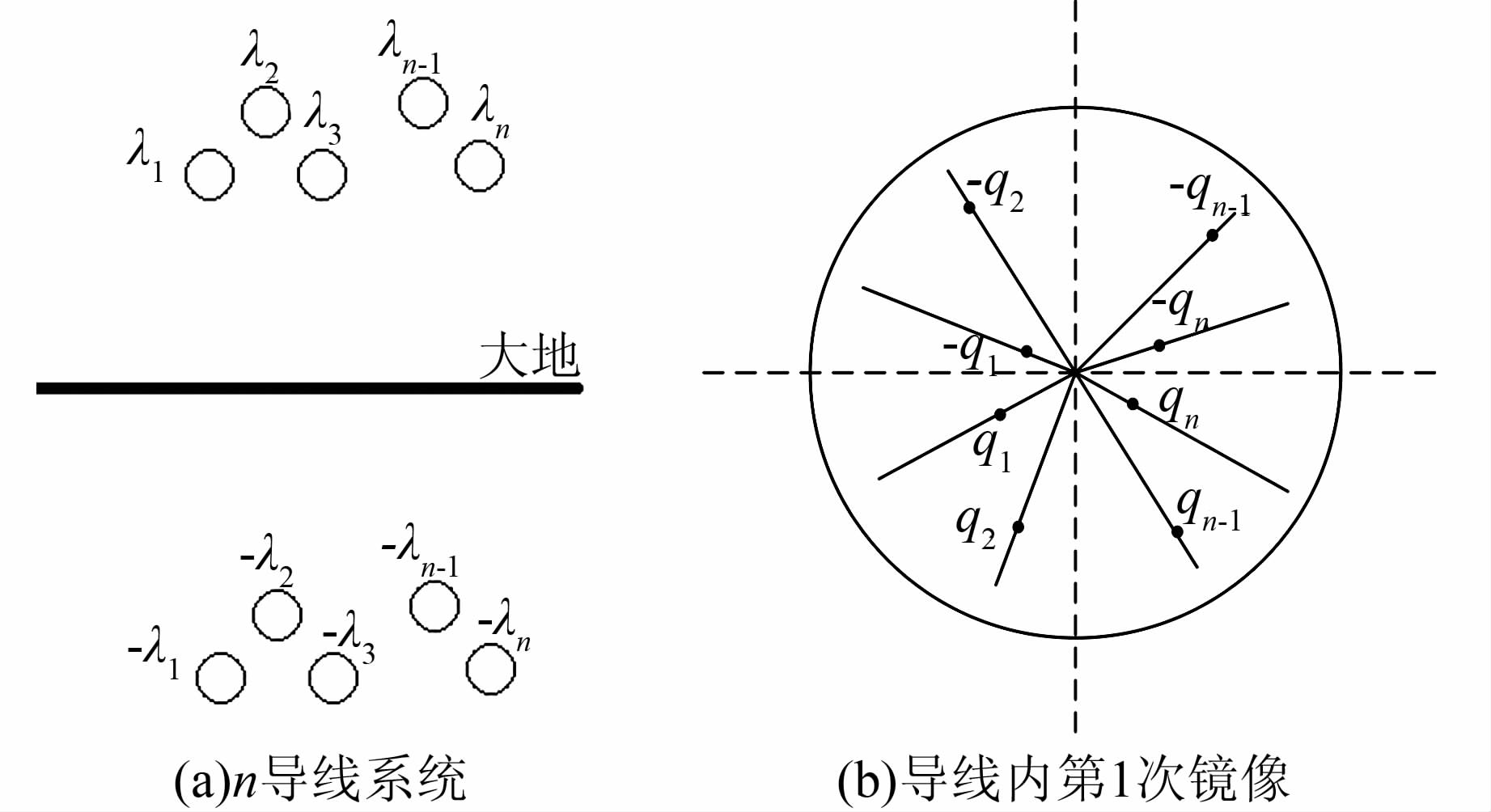
如图 2(a)所示的导线系统，各导线对地电位和表面电荷分别假定为V1，V2，…，Vn和λ1，λ2，…，λn，大地的影响用镜像导线来等效，其电位和电荷分别为-V1，-V2，…，-Vn和-λ1，-λ2，…，-λn，因此，地面之上的导线被一个2n根导线的等效电荷系统取代.

图 2 n导线系统及镜像示意图 Figure 2 n wire system and images diagram
图选项

每根导线上的电荷，都可以用所有其他导线上的电荷来表示，在放置这些电荷时，要求使被考虑的导线表面成为一个等电位面.例如第i根导线，经第1次镜像后的所有镜像电荷分布如图 2(b)所示.导线上的镜像电荷总个数为2n-1，而这些电荷的代数和仍为λi.依此类推，当第1次镜像过程结束时，每根导线上都有 2n-1个镜像电荷.

第2次镜像时，由于每根导线上的电荷都被2n-1个等效电荷所表示，所以当镜像过程结束时，每根导线上的电荷都被2×(2n-1)个镜像电荷所取代.这样的镜像过程无限制地进行下去，直到求得精确解.实际应用中，相导线的分裂半径与导线半径之比大于10，仅需镜像1次就能使计算误差小于2%[12].

2.2 导线表面电场强度参数选取

根据前述公式中导线表面电场强度的表述，对于分裂导线，对各个公式中引用的导线表面电场强度值进行定义，包括：导线表面最大电场强度gmax、各个子导线表面电场强度最大值的平均值gmav以及导线表面电场强度平均值gav：

${{g}_{\text{max}}}=\max ({{g}_{n-\text{max}}}) $    (9)
${{g}_{\text{mav}}}=\frac{1}{n}\sum\limits_{n}{{{g}_{n-\text{max}}}}\text{ }$    (10)
${{g}_{\text{av}}}=\frac{1}{n}\sum\limits_{n}{(\frac{1}{2\pi }\int_{0}^{2\pi }{{{g}_{n}}(\theta )d}}\theta )\text{}$    (11)

式中：gn-max为第n个子导线表面电场最大值；gn(θ)为第n个子导线表面θ点的电场强度；对于马克特-门德尔法，计算得到的是gav，则最大电场强度gmax可近似给出：

${{g}_{\text{max}}}={{\text{g}}_{\text{av}}}\text{(1}+\text{(}n\text{-1)}r/R\text{)}$    (12)

式中：R为导线分裂半径.

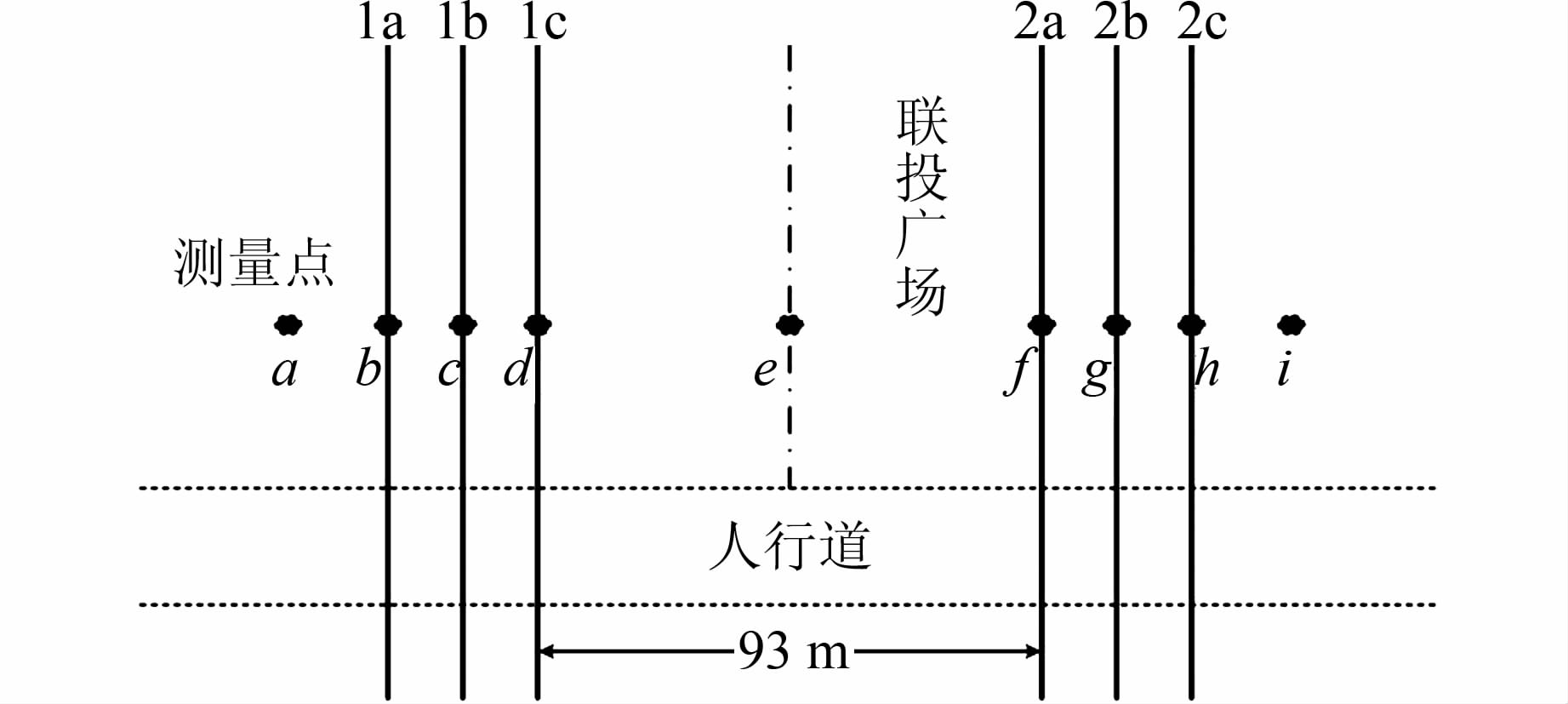
3 计算结果与分析 3.1 线路分布及参数

以实际运行的2条并行走向的500 kV线路为例，线路排列如图 3所示，两回线路均为单回水平排列，横跨1条公路、人行道以及居民活动广场.测量点布置在广场区域，现场布置测点a~i共9个测点如图 3所示，测量距地面2 m处无线电干扰.其中e点是两回线路的中心线上一点，取为测量原点；点b、c、d及f、g、h分别是左、右边回路相导线正下方测量点；点a和i在距左、右回路边相导线20 m处.相导线呈水平排列方式，导线分裂数为4、正方形布置，分裂间距为450 mm，子导线采用LGJ-500/45钢芯铝绞线，直径为30 mm；地线选用GJ-100镀锌钢绞线，直径为13.0 mm.

图 3 输电线路及测量点布置示意图 Figure 3 Diagram of transmission lines and measurement points layout
图选项
3.2 仿真计算结果

对图 3所示线路分别采用马克特-门德尔法和逐次镜像法计算其导线表面电场强度，计算结果见表 1.

表 1 导线表面场强计算结果 Table 1 Calculation results of conductor surface field strengths
计算方法/(kV·cm-1)
马克特-门德尔法逐次镜像法
gavgmavgmaxgavgmavgmax
左回路1a12.4614.2212.4614.2014.46
1b12.9914.8212.9914.8114.82
1c12.4914.2512.4914.2414.49
右回路2a12.2413.9412.2413.9614.21
2b12.7214.5212.7214.5114.52
2c12.2113.9412.2213.9314.18
表选项

从表 1可以看出，马克特-门德尔方法计算的值同逐次镜像法gav基本相等，而gmax较低，实质上相当于平均意义上的最大电场强度，同gmav接近.总体来讲，2种方法计算结果均能达到工程要求的精度.

分别采用国际机构推荐的不同的经验公式计算线路下方各个测量点的无线电干扰强度，包括德国的FG、加拿大的Ontario Hydro、意大利的ENEL以及CISPR，这些推荐公式均适合计算500 kV 4分裂线路，计算时注意各自的修正系数之间的区别.将计算结果与实际测量结果对比，测量点a和i的数值如表 2所示.

表 2 经验公式结果与实测值对比 Table 2 Comparison between empirical formula results and measured values
dB
经验公式马克特-门德尔法逐次镜像法
aiai
FG41.8840.2541.8340.20
Ontario Hydro25.1223.0325.0522.96
ENEL52.6950.9852.6450.93
CISPR34.6632.9734.6232.92
实测值48.547.848.547.8
注：无线电干扰值均是好天气下无线电干扰值，下同.
表选项

根据表 2中数据分析可知，意大利ENEL推荐的经验公式计算结果比其他经验公式更接近实测值.利用逐次镜像法计算意大利经验公式比马克特-门德尔法的计算结果更接近实测数据.

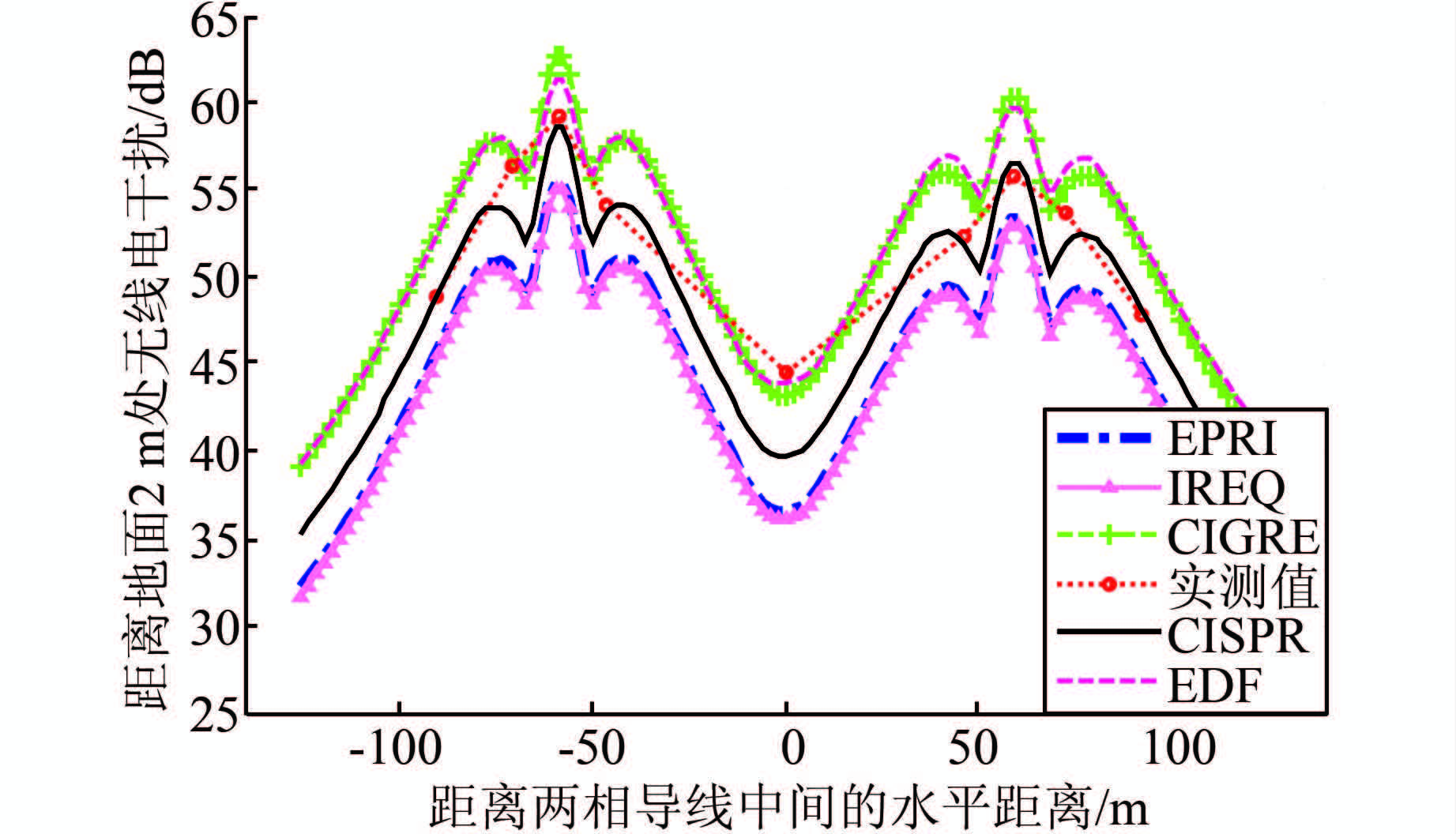
当线路采用多分裂导线时，经验公式法的计算偏差较大.根据美国EPRI公司、加拿大魁北克电力研究所(IREQ)、国际大电网(CIGRE)、法国(EDF)和CISPR18-3/1996(我国电力行业标准DL/T 691-1999)推荐的激发函数分别对实际线路无线电干扰情况进行仿真计算，以实测值为基准，将大雨值修正为好天气下的无线电干扰值，与实测值对比如图 4所示.计算时假设各相导线按正相序排列，土壤电阻率取100 Ω·m，海拔高度为0 m，大气温度为20 ℃，大气压强为101.325 kPa.

图 4 不同激发函数的计算结果与实测值对比 Figure 4 Comparison between different excitation function calculation results and measured values
图选项

从图 4中可以看出EPRI、IREQ的计算结果非常接近且较实测值偏小，EDF与CIGRE结果接近且比实测值较大，CISPR(DL/T 691-1999推荐)的激发函数计算结果与实测值最为接近.

表 3数据显示利用CISPR激发函数计算值与实测值除了线路中心线处有最大偏差4.7 dB，其他测量点的计算值与实际值比较吻合，即利用我国电力行业标准推荐的激发函数相比于经验公式法更能较为准确地评价该线路无线电干扰实际情况.

表 3 CISPR激发函数与实测值对比 Table 3 Comparison between CISPR excitation function calculation results and measured values
dB
测点计算值实测值误差
a48.748.50.2
b53.456.43.0
c58.859.30.5
d53.554.20.7
e39.844.54.7
f51.952.40.5
g56.755.80.9
h51.853.71.9
i48.247.80.4
表选项

激发函数是在模拟大雨条件下试验笼内的导线或试验线路得到的.在雨天的电晕放电强度比晴天时大得多，线路的无线电干扰最为严重，但经雨水冲洗后，空气污染状况、导线表面清洁程度等随机因素对无线电干扰的影响大为减小[19, 20]，使得无线电干扰趋于稳定.因此，大雨条件下激发函数法的计算结果与好天气条件下的方法相比更为理想.

同时，从距线路中心线左右140 m范围内的无线电干扰的分布情况可以看出，实测线路和普通同塔双回线路的无线电干扰分布情况有所区别.实测的两回并行线路左右两回之间的距离较同塔双回线路远得多，无线电干扰随相序、对地高度、分裂半径、子导线截面等因素的变化情况也会有所不同.

3.3 无线电干扰影响因素分析 3.3.1 相序

不同的导线排布方式会影响各导线间的电压叠加效果，引起导线表面的电场强度不同，从而产生不同的无线电干扰.保持左边回路的相序为A/B/C不变，改变右边回路的相序，一共有6种排列情况，如表 4所示.

表 4 同塔双回线路 6 种不同的相序 Table 4 6 different phase sequences of double-circuit transmission line
相序
123456
1aAAAAAA
1bBBBBBB
1cCCCCCC
2aAABBCC
2bBCACAB
2cCBCABA
表选项

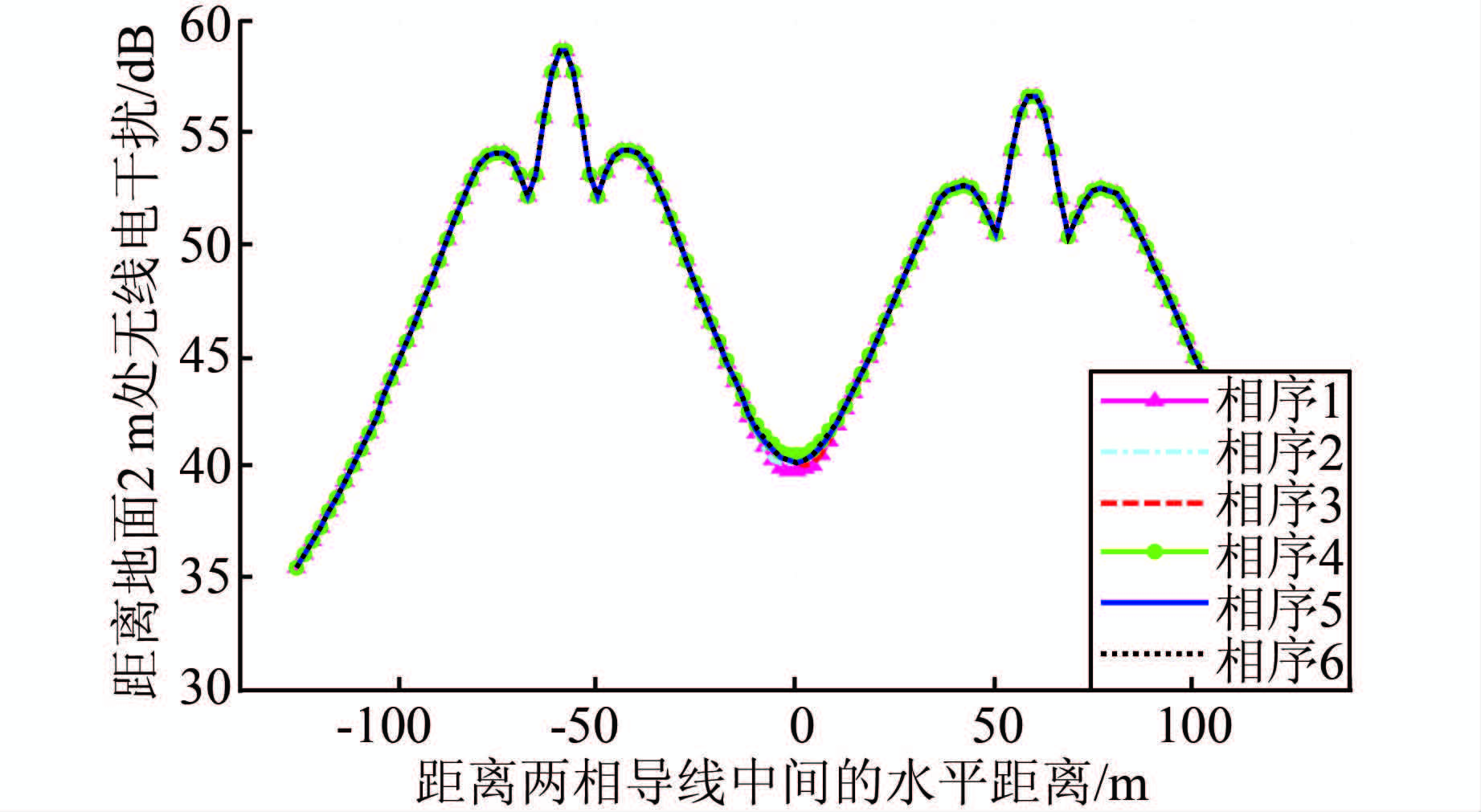
根据图 5中无线电干扰的分布，导线不同相序排列时在线路中心线两侧120 m范围内的无线电干扰变化很小.在线路中心线处不同相序产生的无线电干扰相差最大；在线路中心线两侧20 m范围内，相序4的无线电干扰最大；不同相序产生的无线电干扰相差在0.7 dB以内.

图 5 不同相序下无线电干扰横向分布 Figure 5 Transverse distribution of radio interference with different phase sequences
图选项
3.3.2 对地高度

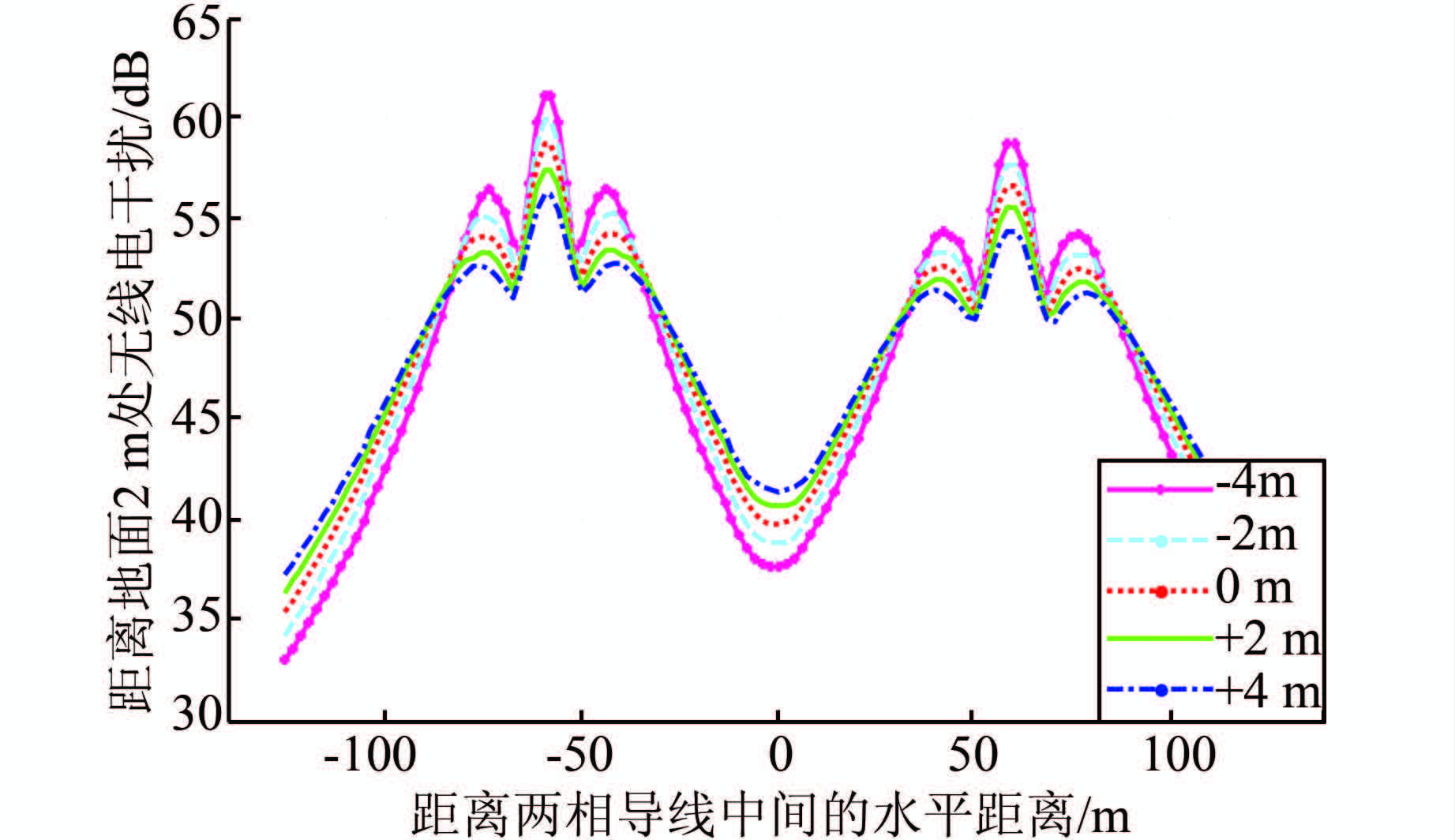
定义实际双回线路的导线对地的高度为参考标准0 m，假设双回线路按照相序1排列，保持线路中心线两侧各回相导线和地线的相对位置不变的基础上改变相导线及地线的对地高度，研究线路实测点位置的无线电干扰，如图 6所示.

图 6 不同对地高度无线电干扰横向分布 Figure 6 Transverse distribution of the radio interference with different ground height
图选项

由图 6分析可知，随着导线对地高度的增加，在测点b~d和f~h范围内，距地面2 m高处无线电干扰逐渐减小，且随着导线高度的增加无线电干扰强度减小的程度逐渐缓慢；在线路中心线处的测点附近及距左右回路外边相导线30 m之外的空间内无线电干扰随着对地高度的增加呈上升趋势；距边相导线20 m处的无线电干扰值随着导线对地高度的增加变化不明显.因此，增加导线对地高度不是减小这条线路下方无线电干扰的有效措施.

3.3.3 分裂间距

导线的分裂间距即子导线间的距离，增大导线的分裂间距则子导线间的相互作用减弱，导线表面场强也随之减小；另一方面增大分裂间距会增大等值半径，导线电荷量增加，导线表面场强逐渐增加.分裂间距对无线电干扰的影响跟线路的具体参数有关.

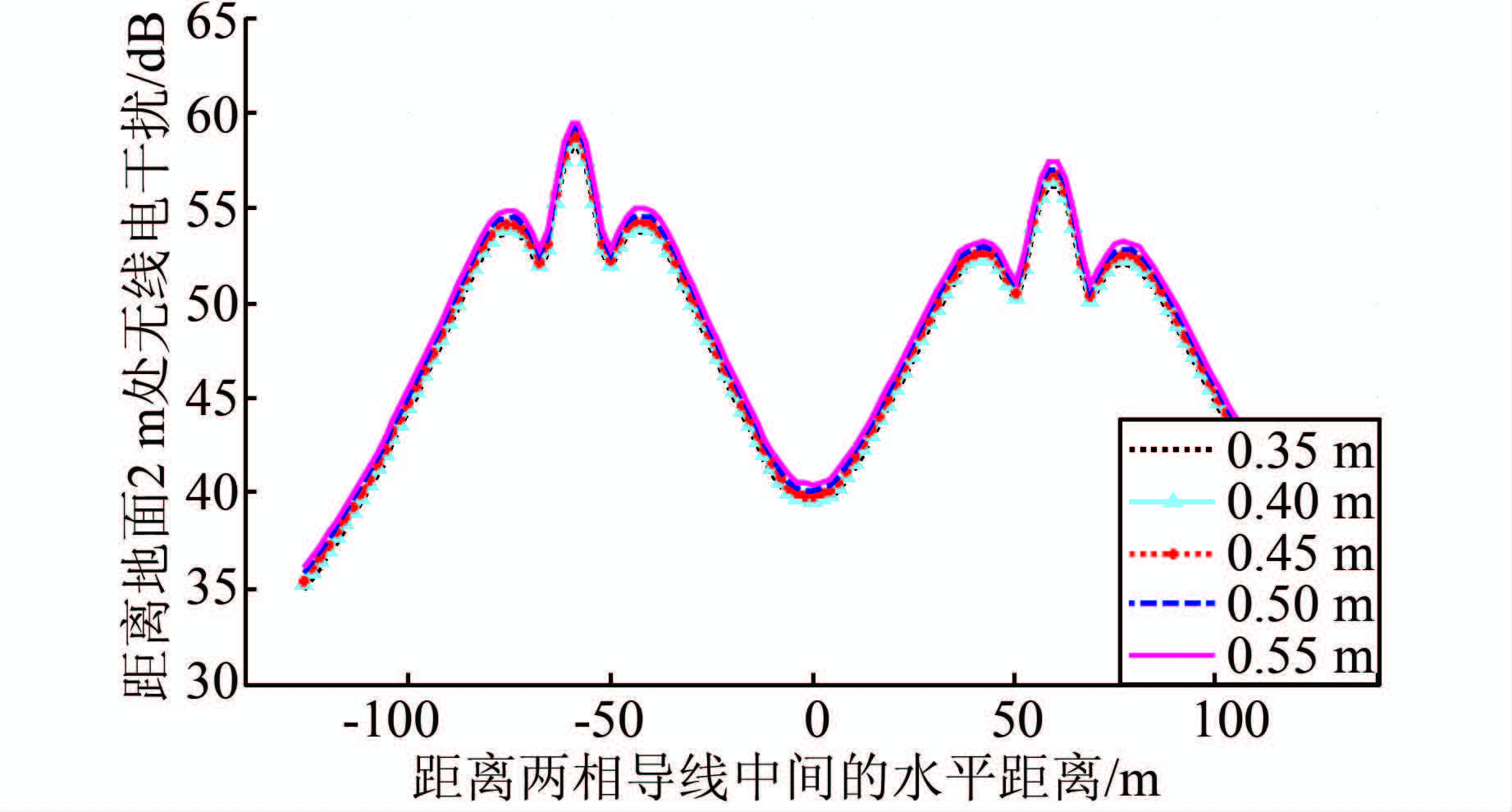
保持相导线的排列顺序及对地高度不变，考虑当导线的分裂间距分别为0.35、0.40、0.45、0.50、0.55 m时，线路下方距线路中心线140 m范围内的无线电干扰横向分布情况见图 7.

图 7 不同分裂间距无线电干扰横向分布 Figure 7 Transverse distribution of radio interference with different bundle spacing
图选项

图 7显示当导线的分裂间距在35~55 mm之间变化时其无线电干扰场强会随着分裂间距的增大而加强；分裂间距每增大5 mm，无线电干扰增大0.2~0.4 dB.因此，适当的减小分裂间距能减弱线路无线电干扰情况，但不能作为减小无线电干扰的有效措施.

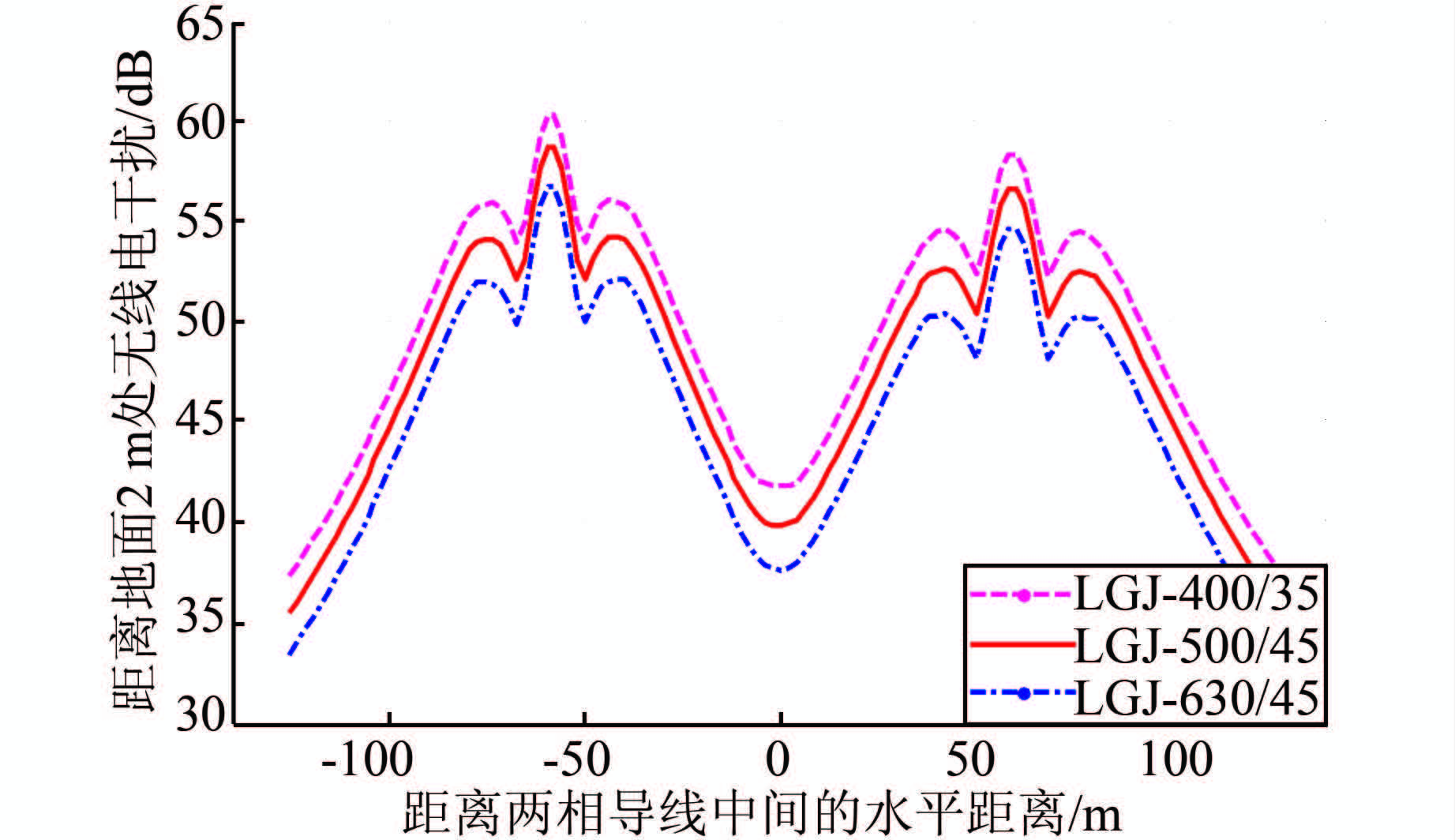
3.3.4 子导线直径

子导线直径分别为26.8(LGJ-400/35)、30(LGJ-500/45)、33.6 mm(LGJ-630/45)时，地面上方2 m测量点处无线电干扰的横向分布如图 8所示.

图 8 不同子导线直径无线电干扰横向分布 Figure 8 Transverse distribution of radio interferencewith different sub-conductor diameters
图选项

由图 8中可以发现子导线直径越大，输电线路下方的无线电干扰值越小；导线直径由26.8 mm增加33.6 mm时，左边相导线20 m处的无线电干扰值减小3.8 dB，右边相导线减小3.95 dB.因此，增加子导线直径是减小输电线路下方无线电干扰的一个措施.

4 结论

1) 在使用国际上各个机构推荐方法中，要注意适用范围和导线表面电场强度的参数正确选取.马克特-门德尔法和逐次镜像法计算实测线路的导线表面电场强度结果均能达到工程要求的精度.逐次镜像法能够计算子导线表面电场强度，更适合计算多分裂导线线路的无线电干扰，计算结果更接近于测量值.

2) 比较经验公式法和激发函数法对实测线路的计算结果，发现激发函数法的准确度优于经验公式法，其中我国电力行业标准(DL/T 691-1999)推荐的激发函数更适合我国线路情况，对于并行双回超高压输电线路，其计算结果最接近于测量值.

3) 改变实测线路模型的相序、对地高度、导线分裂间距时，距边相导线20 m处的无线电干扰值无明显变化；子导线直径在26.8~33.6 mm变化时，无线电干扰场强随着子导线直径的增大而明显减小.增加子导线直径是减小输电线路下方无线电干扰的一个措施.

参考文献
[1] Juette G W. Comparison of radio noise prediction methods with CIGRE/IEEE survey results[J]. IEEE Transactions on Power Apparatus and Systems, 1973, 92(3): 1029–1042.
[2] Olsen R G, Schennum S D, Chartier V L. Comparison of several methods for calculating power line electromagnetic interference levels and calibration with long term data[J]. IEEE Transactions on Power Delivery, 1992, 7(2): 903–913. DOI:10.1109/61.127097
[3] DL/T691-1999高压架空送电线路无线电干扰计算方法[S].北京：中国电力出版社，1999.
DL/T691-1999 Method of calculation of radio interference from high voltage overhead power transmission lines[S].Beijing:China Electric Power,1999.
[4] CISPR18-3 Radio interference characteristics of overhead power lines and high-voltage equipment—part 3[S],1996.
[5] 李俊杰, 邹军, 李本良, 等. 采用激发函数法计算分析不同相序排列下双回交流高压输电线路的无线电干扰[J]. 电网技术, 2010, 34(6): 14–18.
Li Junjie, Zou Jun, Li Benniang, et al. Analysis of radio interference from double-circuit of high voltage AC power transmission line under different arrangement of phase sequence by excitation function method[J]. Power System Technology, 2010, 34(6): 14–18.
[6] 庄池杰, 曾嵘, 龚有军, 等. 交流输电线路的无线电干扰计算方法[J]. 电网技术, 2008, 32(2): 56–60.
Zhuang Chijie, Zeng Rong, Gong Youjun, et al. Calculation methods of radio interference caused by AC transmission Lines[J]. Power System Technology, 2008, 32(2): 56–60.
[7] 姚丽娜.高压交流输电线路无线电干扰数值方法的研究[D].保定：华北电力大学,2012.
Yao Lina.Research on numerical method of radio interference of HVAC transmission lines[D].Baoding:North China Electric Power University,2012. http://cn.bing.com/academic/profile?id=fc52350f9e1d37651ac491a92630a21d&encoded=0&v=paper_preview&mkt=zh-cn
[8] 邬雄, 万保权. 输变电工程的电磁环境[M]. 2009.
Wu Xiong, Wan Baoquan. Power Transmission Project Electromagnetic Environment[M]. Beijing: China Electric Power Press, 2009.
[9] GB15707-1995高压交流架空送电线无线电干扰限值[S]，1995.
GB15707-1995 Limits of radio interference from AC high voltage overhead power transmisson lines[S],1995. http://cn.bing.com/academic/profile?id=76ff5116020af07e26f7f6d61d7df57f&encoded=0&v=paper_preview&mkt=zh-cn
[10] 万保权, 邬雄, 路遥, 等. 交流同塔双回特高压输电线路 无线电干扰研究[J]. 高电压技术, 2006, 32(12): 59–61.
Wan Baoquan, Wu Xiong, Lu Yao, et al. Study on radio interference of AC UHV double circuit transmission lines on the same tower[J]. High Voltage Engineering, 2006, 32(12): 59–61.
[11] IEEE Corona and Field Effects Subcommittee Report Radio Noise Working Group. A survey of methods for calculating transmission line conductor surface voltage gradients[J]. IEEE Transactions on Power Apparatus and Systems, 1979, 98(6): 1996–2014.
[12] 01工作组. 输电系统产生的电场和磁场[M]. 北京: 水利电力出版社, 1984.
Working Group 36. 01 CIGRE[M]. 1984.
[13] 李亚莎, 殷明. 500kV超高压输电线下工频电场分析[J]. 陕西电力, 2012, 40(2): 32–38.
Li Yasha, Ying Ming. Analysis of power frequency electric field generated by the 500kV high voltage transmission lines[J]. Shanxi Electric Power, 2012, 40(2): 32–38.
[14] 黄道春, 阮江军, 余世峰, 等. 特高压紧凑型输电线路 工频电场强度计算[J]. 高电压技术, 2006, 32(7): 69–71.
Huang Daochun, Ruan Jiangjun, Yu Shifeng, et al. Calculation of the power frequency electric field intensity of UHV compact transmission lines[J]. High Voltage Engineering, 2006, 32(7): 69–71.
[15] 甘艳, 阮江军, 邬雄. 有限元法分析高压架空线路附近电场分布[J]. 高电压技术, 2006, 32(8): 52–55.
Gan Yan, Ruan Jiangjun, Wu Xiong. Analysis of the electric field intensity nearby high voltage transmissionline by FEM[J]. High Voltage Engineering, 2006, 32(8): 52–55.
[16] 张宇, 郑伟, 文武, 等. 架空线路分裂导线表面电位梯度的数值计算[J]. 高电压技术, 2005, 31(1): 23–24.
Zhang Yu, Zheng Wei, Wen Wu, et al. Numerical calculation of electric field intensity on the surface of bundle conductors of overhead transmission lines[J]. High Voltage Engineering, 2005, 31(1): 23–24.
[17] 毛建伟, 史巍, 许刚. 基于有限元的输电线路附近建筑物内电磁屏蔽研究[J]. 华东电力, 2013, 41(4): 755–761.
Mao Jianwei, Shi Wei, Xu Gang. FEM-based electromagnetic shielding inside buildings near transmission line[J]. East China Electric Power, 2013, 41(4): 755–761.
[18] 牛林, 杜至刚, 赵建国. 特高压输电线路分裂导线表面电位梯度的计算及其特分析[J]. 电力自动化设备, 2007, 27(10): 5–9.
Niu Lin, Du Zhigang, Zhao Jianguo. Calculation and characteristic analysis of electric field intensity on the surface of bundle conductors of UHV transmission lines[J]. Electric Power Automation Equipment, 2007, 27(10): 5–9.
[19] 侯锐.基于激发函数法的有限长交流线路无线电干扰计算[D].保定：华北电力大学, 2009.
HouRui.Calculation of the radio interference of finite AC transmission lines based on excitation function[D]. Baoding: North China Electric Power University, 2009.
[20] 周益峰.特高压交流输电线路的无线电干扰研究[D].武汉：华中科技大学, 2011.
Zhou Yifeng.Study on radio interference of AC ultra high voltage transmission lines[D].Wuhan: Huazhong University of Science and Technology, 2011. http://cn.bing.com/academic/profile?id=ae89a5f858facd6ab87b88f7b488f4e3&encoded=0&v=paper_preview&mkt=zh-cn