武汉大学学报(工学版)   2016, Vol. 49 Issue (3): 441-445

文章信息

邓其军, 王慧琴
DENG Qijun, WANG Huiqin
频率匹配对谐振无线电能传输效率的影响
Efficiency of frequency matching for resonant wireless power transmission system
武汉大学学报(工学版), 2016, 49(3): 441-445
Engineering Journal of Wuhan University, 2016, 49(3): 441-445
http://dx.doi.org/10.14188/j.1671-8844.2016-03-021

文章历史

收稿日期: 2015-12-28
 Abstract              PDF               Figures               Tables
引用本文 0
邓其军, 王慧琴. 频率匹配对谐振无线电能传输效率的影响[J]. 武汉大学学报(工学版), 2016, 49(3): 441-445.
DENG Qijun, WANG Huiqin. Efficiency of frequency matching for resonant wireless power transmission system[J]. Engineering Journal of Wuhan University, 2016, 49(3): 441-445.
频率匹配对谐振无线电能传输效率的影响
邓其军, 王慧琴     
武汉大学动力与机械学院，湖北 武汉430072
收稿日期: 2015-12-28
作者简介: 邓其军(1975-)，男，博士，副教授，研究领域包括微网发电控制及优化、电力系统计算机控制技术、配电网GIS、配电网自动化、火电厂程控、嵌入式工作流管理系统等,E-mail:dqj@whu.edu.cn..
基金项目: 国家科技支撑计划资助(编号:2013BAA01B01.
摘要: 基于共振耦合式无线电能传输机理和数学模型，对无线电能传输发送端与接收端谐振频率的测量与调整进行了研究，结合Matlab仿真和实际实验操作，研究了在固定距离下两线圈组成的系统电能传输效率与工作频率的关系，研究并比较在不同耦合系数k值条件下两端谐振点频率未匹配和匹配情况下电能传输效率.研究表明不同k值情况下电能传输效率与工作频率的关系曲线存在差异，在相同的k值条件下两端谐振点频率匹配时比两端谐振点频率不匹配时表现出更高的电能传输效率.对于远距离电能传输，即在k值较小的情况下，调节两端谐振点至频率匹配时将有效提高传输效率.
关键词： 无线电能传输谐振     谐振频率     传输效率     Matlab    
Efficiency of frequency matching for resonant wireless power transmission system
DENG Qijun, WANG Huiqin     
School of Power and Mechanical Engineering, Wuhan University, Wuhan,430072,China
Abstract: Based on the theory and mathematical model of magnetic resonant coupled wireless power transmission, this paper studies the measuring and adjusting of the sending coil’s and receiving coil’s resonant frequencies of wireless power transmission. Combining simulation in Matlab and experiments, the article discusses the system’s transmission efficiency at a certain distance and the efficiency at different k values under the condition of whether the resonance point is frequency matching or not. The study results indicate that different values of k have different effects on the relation curve of transmission efficiency and operating frequency. The frequency matching system shows higher efficiency than the unmatching system under the same value of k. And for the remote wireless power transmission, the value of k is very small; so the transmission efficiency will be greatly improved when the resonance point is frequency matching.
Key words: wireless power transmission     frequency matching     resonant frequency     transmission efficiency     Matlab    

随着科技的发展和生活水平的提高，手机、笔记本等移动电器越来越多地走进了居民日常生活，而这些设备的有线充电给人们造成了诸多不便.在石油和采矿等工业生产领域，由于特殊的现场作业条件难以依靠架设电线的传统方式来供电.在电力输送方面，山顶的基站、孤立的岛屿等特殊的地段，传统的输电方式已经很难满足其供电需求[1].因此更为灵活、方便的无线能量传输方式已成为一种趋势需求.无线电能传输(Wireless Power Transmission,WPT)是借助于电磁场或电磁波进行能量传递的一种技术[2].无线输电大致可分为电磁感应式、电磁辐射式和电磁共振式.电磁感应式传输距离近、效率低，发电机、电动机的定转子之间的能量传递就是利用此原理，传输距离为毫米级；电磁辐射式传输距离远，但如果是全方向性辐射，传输电能的效率低，而如果是定向辐射，要具有不间断可视的方位和十分复杂的追踪仪器设备，其研制难度大；电磁共振式，即本文主要研究的磁耦合谐振式输能技术，在继承了可近距离传输的电磁感应式和远距离传输的电磁辐射式无线电能传输技术优点的同时，又克服了其不足[3]，可以在几米的范围内实现高效能量传输，该技术将改变人们的用电方式[4].

本文研究了无线电能传输发送端与接收端谐振频率的测量与调整方法，对不同耦合系数k 值下两线圈的谐振频率测量与调整以及电能的传输效率进行了理论分析，并进行了实验验证.

1 发射端与接收端谐振频率的计算与影响因素 1.1 共振耦合式无线能量传输的技术原理概述

无线电能传输系统如图 1 所示，包括高频信号发生器、高频功率放大电路、发射线圈、接收线圈、整流电路和负载.其中，发生耦合谐振的只有发射线圈和接收线圈.发射电路由高频逆变环节激发发射端线圈产生交变磁场,接受端的感应线圈拥有相同的频率[5]，进入交变磁场的范围后发生自激振荡，信号增强，发射端自激振荡频率与接受端自激振荡频率一致，发射端与接受端产生共振，成为一对共振偶极子，二者产生谐振耦合，而其他未达到谐振频率的物体则不能感应磁场能量，接收线圈将耦合得到的电能供给负载[6, 7].

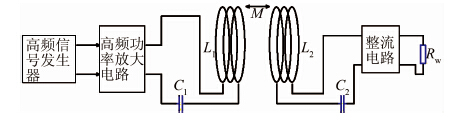
图 1 无线电能传输系统示意图 Figure 1 Schematic diagram of wireless power transmission system
图选项
1.2 共振耦合式无线能量传输模型建立与求解

基于磁场谐振的无线能量传输的工作示意图如图 2所示.图 2中，信号发生器电源为AC，发送和接受线圈内阻分别为Rs和Rd，发送端和接收端电感分别为Ls和Ld,发送端和接收端电容分别为Cs和Cd.

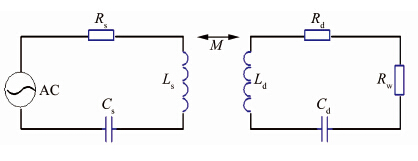
图 2 无线能量传输电路模型 Figure 2 英文The circuit model of wireless power transmission标题
图选项

根据图 2，使用相量法，建立系统的频域方程.令${{Z}_{s}}={{R}_{s}}+j\omega {{L}_{s}}+\frac{1}{j\omega {{C}_{s}}}$，${{Z}_{d}}={{R}_{w}}+{{R}_{d}}+j\omega {{L}_{d}}+\frac{1}{j\omega {{C}_{d}}}$，发射端线圈电流为Is，接收端线圈电流为Id.据KVL得到：

${{I}_{s}}\times {{Z}_{s}}+{{I}_{d}}\times j\omega M={{V}_{s}}$    (1)
${{I}_{s}}\times j\omega M+{{I}_{d}}\times {{Z}_{d}}=0$    (2)

式中:M 为线圈之间的互感.式(1)、(2)联立解出：

${{I}_{d}}=\frac{-j\omega M{{V}_{s}}}{{{\left( M\omega \right)}^{2}}+{{Z}_{d}}\times {{Z}_{s}}}$    (3)
${{I}_{s}}=\frac{{{V}_{s}}\times {{Z}_{d}}}{{{\left( M\omega \right)}^{2}}+{{Z}_{d}}\times {{Z}_{s}}}\le \frac{{{V}_{s}}\times {{Z}_{d}}}{{{Z}_{d}}\times {{Z}_{s}}}\text{=}\frac{{{V}_{s}}}{{{Z}_{s}}}$    (4)

令发射端的输入功率为Ps，接收端负载消耗功率为Pd，则

${{P}_{s}}=\left| \frac{V_{s}^{2}\times {{Z}_{d}}}{{{\left( M\omega \right)}^{2}}+{{Z}_{d}}\times {{Z}_{s}}} \right|$    (5)
${{P}_{d}}=\left| \frac{V_{s}^{2}\times {{\left( M\omega \right)}^{2}}\times {{R}_{w}}}{{{\left[ {{\left( M\omega \right)}^{2}}+{{Z}_{d}}\times {{Z}_{s}} \right]}^{2}}} \right|$    (6)

因此可以得出传输效率：

$\eta =\frac{{{P}_{d}}}{Ps}=\left| \frac{{{\left( M\omega \right)}^{2}}\times {{R}_{w}}}{\left[ {{\left( M\omega \right)}^{2}}+{{Z}_{d}}\times {{Z}_{s}} \right]\times {{Z}_{d}}} \right|\times 100%$    (7)

通过对线圈的适当处理使得发送端线圈和接收端线圈的谐振频率值相等，令此时的系统谐振频率为ω0，由谐振的定义，有：

$j{{\omega }_{0}}L+\frac{1}{j{{\omega }_{0}}C}=0$    (8)

即

${{\omega }_{0}}=\sqrt{1/(LC)}$    (9)

当系统的工作频率处于谐振频率时，即ω=ω0，此时$j\omega {{L}_{S}}+\frac{1}{j\omega {{C}_{S}}}=0$且$j\omega {{L}_{d}}+\frac{1}{j\omega {{C}_{d}}}=0$，对应的Zs和Zd模值最小.由直观分析，处在谐振频率下式(3)、(4)的分母较小，Id、Is较大.由此可以得出，发射端和接收端谐振点的寻找可转化成寻找发射端线圈和接收端线圈的电流最大点.

而互感M的计算比较复杂，可以近似为

$M\approx \frac{\pi {{\mu }_{0}}{{r}^{4}}{{N}^{2}}}{2{{d}^{3}}}$    (10)

式中：μ0为空间磁导率;r为线圈半径，mm;N为线圈匝数;d为传输距离,dm.由式(10)知，共振耦合式无线电能传输的互感值与传输距离的三次方成反比，即传输距离越远，互感值M 越小.

由式(7)、(10)可知，当系统确定之后，传输效率η就只与工作频率ω和传输距离d有关.

2 实验验证方案

实验中选用的发射端与接收端线圈各参数一致，线圈采用多股的漆包线进行制作，为保证实验效果，每圈的均半径20 cm，导线截面半径为1 mm.发射端和接收端线圈的匝数设定为19 匝，电容选择300 pF.

上述参数设定后均不变.具体接线如图 3实验接线示意图所示.

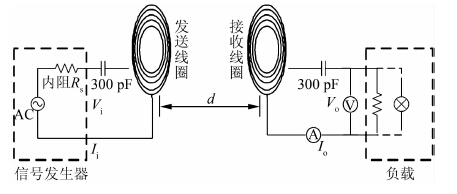
图 3 实验接线示意图 Figure 3 Schematic diagram of circuit connection
图选项

如图 3，实验电路中发射端电压源采用实验用信号发生器，型号为EE1642B1，从信号发生器的显示器上直接读出发送端的电压Vi和电流Ii；接收端选用高灵敏度的电压表和电流表，分别测量接收端负载两端的电压Vo和电流Io.

发送端的输入功率为

${{P}_{i}}={{V}_{i}}\cdot {{I}_{i}}$    (11)

接收端负载的消耗功率为

${{P}_{o}}={{V}_{o}}\cdot {{I}_{o}}$    (12)

无线传输效率为

$\eta =\frac{{{P}_{o}}}{{{P}_{i}}}\times 100%=\frac{{{V}_{o}}\cdot {{I}_{o}}}{{{V}_{i}}\cdot {{I}_{i}}}\times 100%$    (13)

由实验测得电压Vi、Vo和电流Ii、Io，再根据式(13)可计算出效率的变化.

3 实验步骤及数据分析 3.1 发射端与接收端谐振频率的测量

将信号发生器、电容和发送线圈串联连接，并将接收线圈移至较远处，以防止接收线圈对发送线圈的影响.本实验中，电路各参数为：发送端电感Ls=300 μH、电容Cs=300 pF、电阻Rs=7.736 Ω，接收端电感Ld=283 μH、电容Cd=300 pF、电阻Rd=5.956 Ω，负载电阻Rw=9 Ω.

接通电源后将信号发射器的电压调至20 V，在信号发生装置的面板上通过键盘来调节频率，当工作频率发生变化时信号发生器上电流显示的值也会跟着变化.记录下每次调节频率后电流的变化情况，运用 Matlab的画图功能，作出发送端电流随工作频率变化的变化情况的图.将发送线圈换成接收线圈，按相同的接线方式和同样的实验方法作出接收端电流随工作频率变化的变化情况的图.本实验实得电流I和工作频率ω的关系如图 4.

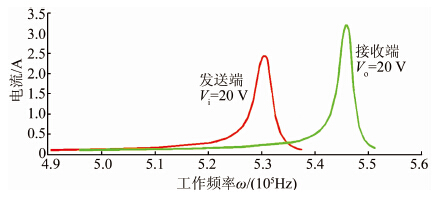
图 4 发送端与接收端电流随频率的变化关系 Figure 4 Diagram of sending coil’s and receiving coil’s currents varying with frequency
图选项

当电流出现峰值时，此时对应的工作频率ω即是单端谐振频率ωr.由图 4知，在现有的条件下，发送端线圈的谐振频率ωr发在530 580 Hz附近，接收端线圈的谐振频率ωr收在545 900 Hz附近.

3.2 接收端谐振频率的调整

一般来说，两个有一定距离的电磁系统，相互之间是弱耦合，但若两个系统的固有谐振频率相同，则会产生强磁谐振，如果一方不断为系统提供能量，而另一方消耗能量，则实现了能量的传输[2, 8-9].

在3.1中测得发射端谐振频率的基础上固定发射端谐振频率，通过增加绕制线圈的方法调节接收端谐振频率使其与发射端谐振频率接近或者相等.绕制线圈的增加改变了线圈的电感L值，由此使得线圈的谐振频率变小.增加不同匝数绕制线圈对电感L的改变程度不同，匝数越多对电感L的改变量越大，从而对线圈谐振频率ωr的改变量越大.本实验中，通过给接收端添加不同匝数的绕制线圈，经过反复实验使接收端线圈的谐振频率ωr收与发送端线圈的谐振频率ωr发接近或者相等.

3.3 不同距离下工作频率的调节及调整前后传输效率的仿真与实验

高频条件下,空心线圈寄生电阻主要包括线圈的损耗电阻R0和辐射损耗电阻Rr:

${{R}_{_{0}}}=\sqrt{\frac{{{\mu }_{_{0}}}\omega }{2\sigma }}\frac{l}{2\pi a}=\sqrt{\frac{{{\mu }_{_{0}}}\omega }{2\sigma }}\frac{Nr}{a}$    (14)
${{R}_{r}}=320{{\pi }^{4}}{{N}^{2}}r\cdot \ln {{\left( \frac{\pi {{r}^{2}}}{{{\lambda }^{2}}} \right)}^{2}}$    (15)

式中：α为线圈导线截面半径;l为导线长度;σ为电导率(本实验中线圈材料为铜，其电导率σ=5.8×107 S/m);λ为电磁波的波长[10].

在本实验中，系统的谐振频率一般为4.5×105到6×105 Hz，此时${{R}_{0}}\gg {{R}_{r}}$，即进行仿真时可以忽略辐射损耗，则有R≈R0.

当发送端线圈与接收端线圈组成一个系统且两线圈间距离确定时，由于两线圈间存在互感M，使得此时实际意义上的两线圈电感值L为原来的两线圈单独的电感值减去该距离下两线圈间的互感值，这样由式(9)知两线圈的谐振频率发生了变化.当发送端线圈与接收端线圈间垂直距离发生变化时，距离的变化导致了耦合系数的变化使得M值不同，从而不同距离下系统的谐振频率会有差异.

3.3.1 仿真结果

用Matlab编程对系统进行仿真，通过改变仿真时的k值，可分别得到在未调整两端至谐振点频率匹配和调整两端至谐振点频率匹配两种情况下，系统在不同距离下电能的传输效率与工作频率的关系曲线.仿真设定参数如表 1，距离分别调整为49、39、31 cm.由$M=k\sqrt{{{L}_{s}}{{L}_{d}}}$和式(10)从而得到k值分别约为0.02、0.04、0.08，则仿真结果如图 5所示.图 5中实线表示的是Matlab仿真所得的关系曲线，圆点表示的是实际测得的在不同k值下电能传输效率η与工作频率ω的关系.

表 1 仿真参数设定 Table 1 Setting of simulation parameters
Ls/μHLd/μHCs/pFCd/pFRs/ΩRd/ΩRw/Ω
3002833003007.7365.9569
表选项
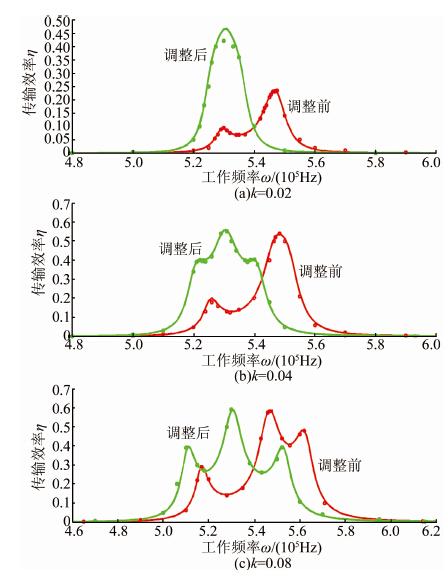
图 5 k=0.02,0.04,0.08时传输效率η随工作频率ω的关系曲线 Figure 5 Diagram of transfer efficiency ηvarying with working frequency ω when k=0.02, 0.04, 0.08
图选项

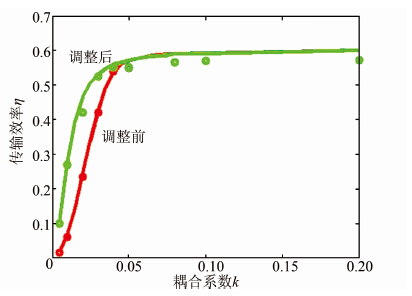
将k值在0.005~0.150内细分，分别找出对应的电能传输效率，再运用Matlab画图功能作出调整前后电能传输效率η随耦合系数k的关系曲线，如图 6所示.图 6中实线表示的是Matlab仿真所得的关系曲线，圆点表示的是实际测得的在不同k值下电能传输效率η与两线圈间耦合系数k的关系.

图 6 传输效率η与耦合系数k的关系曲线 Figure 6 Diagram of transfer efficiency η varying with coupling coefficient k
图选项

如图 5，在不同的k值条件下，传输效率η随工作频率ω的关系曲线存在着一定的差异,具体为:1)最大传输效率与k值有关，随着k值的增加而变大；2)曲线的走向不同，调整前的曲线随着k的增大由2个波峰1个波谷逐渐转变为3个波峰2个波谷，调整后的曲线随着k值的增大由1个波峰无波谷逐渐转变为3个波峰2个波谷；3)随着k值的增加，调整前后最大效率的差值逐渐变小.

如图 6，随着k值的增加，调整前后最大效率的差值逐渐变小，甚至趋向于0.但是在相同的k值条件下，调整后的最大效率值始终大于调整前的最大效率值.具体来讲，当k<0.06时调整后的最大传输效率大于调整前的最大传输效率；当k≥0.06时调整前后的最大传输效率几乎相等.在实际的电能传输中，对于远距离电能输送，由于距离较远导致k值比较小，通常k值小于0.02，在这样的情况下，发送端线圈与接收端线圈谐振点频率匹配时的传输效率是不匹配时传输效率的2倍以上.所以，对于远距离电能传输，需要调整两端谐振点至频率匹配才能保证较大的传输效率.

3.3.2 实验验证

按图 3的接线方式搭建该系统，保持信号发生器的输出电压为20 V.调整发送端线圈与接收端线圈间的距离分别为49、39、31 cm，从而使两线圈间的耦合系数k分别约为0.02、0.04、0.08.在每个固定的耦合系数k下，首先测量未调整发送端与接收端至谐振点频率匹配时发送端信号发生器显示器上电压值Vi和电流值Ii以及接收端电压表读数Vo和电流表读数Io，由式(13)计算出调整前电能传输效率η，利用Matlab的画图功能绘出调整前电能传输效率η随工作频率ω的关系曲线；再调整发送端与接收端至谐振点频率匹配，按相同的方法测量并计算调整后电能传输效率η并绘图.图 5中的圆点是根据实际测量并计算得出的电能传输效率η与工作频率ω之间的关系.

再分别调整发送端线圈与接收端线圈的垂直距离分别为78、62、49、43、39、36、31、29、23 cm，使得两线圈间耦合系数k值分别约为0.005、0.010、0.020、0.030、0.040、0.050、0.080、0.100、0.200，分别测量各组的电能传输效率.运用Matlab作图功能，作出调整前后电能传输效率η随发送端线圈与接收端线圈间耦合系数k的关系曲线.图 6中的圆点是根据实际测量并计算得出的电能传输效率η与耦合系数k之间的关系.

如图 6 中所示，实际测得的关系曲线与仿真结果大体趋势相同，仿真实验所得结论基本符合实际情况.

4 结语

本文研究了共振耦合式无线电能传输发送端与接收端谐振频率的测量与调整方法，研究了无线电能传输的传输效率，在简单的理论分析与推导之后又进行了实验分析，得出结论.

在固定距离下系统的电能传输效率随着系统的工作频率的变化而变化，并且存在一个最大传输效率点.不同耦合系数k情况下电能的传输效率与工作频率的关系曲线存在差异，随着k值的增加，调整前后最大效率的差值逐渐变小，甚至趋向于0.结果显示在相同的k值条件下两端谐振点频率匹配时电能传输效率比两端谐振点不匹配时高.由于远距离电能传输时k值较小，当调节发送端线圈与接收端线圈谐振点至频率匹配时电能传输效率大大提高.

参考文献
[1] DeJean G.Wireless Evanescent Coupling and its Connection to the Latest Developments Presented by Researchers at MIT[R]. Microsoft Research. September 27, 2007:2-4.
[2] Tak Y, Park J, Nam S. Mode-based analysis of resonant characteristics for near-field coupled small antennas[J]. IEEE Antennas and Wireless Propagation Letters, 2009, 8(4): 1238–1241.
[3] 汪强, 李宏, 陈东旭. 磁耦合谐振式无线电能传输系统的分析与设计[J]. 电源技术, 2012(11): 1741–1744.
Wang Qiang, Li Hong, Chen Dongxu. Analysis and design of magnetically coupled resonant wireless power transmission system[J]. Power Technology, 2012(11): 1741–1744.
[4] 吴嘉迅, 吴俊勇, 张宁, 等. 基于磁耦合谐振的无线能量传输的实验研究[J]. 现代电力, 2012, 29: 24–28.
Wu Jiaxun, Wu Junyong, Zhang Ning, et al. Experimental study of magnetic coupling resonant wireless power transmission[J]. Modern Electric Power, 2012, 29: 24–28.
[5] Kurs A, Karalis A, Moffatt R, et al. Wireless power transfer via strongly coupled magnetic resonances[J]. Science, 2007, 317(5834): 83–86. DOI:10.1126/science.1143254
[6] Rangelov A A, Suchowski H, Silberberg Y, et al. Wireless adiabatic power transfer[J]. Annals of Physics, 2011, 326(3): 626–633. DOI:10.1016/j.aop.2010.11.008
[7] Mazlouman S J, Mahanfar A, Kaminska B. Mid-range wireless energy transfer using inductive resonance for wireless sensors[C]// Computer Design, 2009， IEEE International Conference on, 2009:517-522. http://www.oalib.com/references/16579667
[8] Kumar A, Mirabbasi S, Chiao M. Resonance-based wireless power delivery for implantable devices [C]// 2009 IEEE Biomedical Circuits and Systems Conference, 2009: 25-28. http://www.oalib.com/references/9253673
[9] 刘宿城, 周雒维. 近场磁谐振耦合能量传输系统的建模与分析[J]. 电源学报, 2011, 33(1): 51–55.
Liu Sucheng, Zhou Luowei. Modeling and analysis of near-field magnetic resonance coupling energy transmission system[J]. Power Technology, 2011, 33(1): 51–55.
[10] 黄辉, 黄学良, 谭林林, 丁晓辰. 基于磁场谐振耦合的无线电力传输发射及接收装置的研究[J]. 电工电能新技术, 2011, 30(1).
Huang Hui, Huang Xueliang, Tan Linlin, Ding Xiaochen. Studies of transmitting and receiving device based on magnetic resonance coupling wireless power transmission[J]. Advanced Technology of Electrical Engineering and Energy, 2011, 30(1).