武汉大学学报(工学版)   2016, Vol. 49 Issue (5): 683-689

文章信息

肖志鹏, 吕庆, 赵宇, 刘琪
XIAO Zhipeng, LV Qing, ZHAO Yu, LIU Qi
基于移动最小二乘法的隧道支护稳定可靠度分析
Reliability analysis of tunnel support stability based on moving least squares method
武汉大学学报(工学版), 2016, 49(5): 683-689
Engineering Journal of Wuhan University, 2016, 49(5): 683-689
http://dx.doi.org/10.14188/j.1671-8844.2016-05-007

文章历史

收稿日期: 2016-04-01
 Abstract              PDF               Figures               Tables
引用本文 0
肖志鹏, 吕庆, 赵宇, 刘琪. 基于移动最小二乘法的隧道支护稳定可靠度分析[J]. 武汉大学学报(工学版), 2016, 49(5): 683-689.
XIAO Zhipeng, LV Qing, ZHAO Yu, LIU Qi. Reliability analysis of tunnel support stability based on moving least squares method[J]. Engineering Journal of Wuhan University, 2016, 49(5): 683-689.
基于移动最小二乘法的隧道支护稳定可靠度分析
肖志鹏, 吕庆, 赵宇, 刘琪     
浙江大学建筑工程学院，浙江 杭州 310058
收稿日期: 2016-04-01
作者简介: 肖志鹏（1990-），男，博士研究生，主要从事岩石开挖的不确定性分析方法研究，E-mail：xiaozhipeng@zju.edu.cn.
通讯作者: 吕庆（1978-），男，博士，副教授，主要从事岩石开挖的不确定性分析方法研究，E-mail：lvqing@zju.edu.cn
基金项目: 国家自然科学基金资助项目（编号：41202216）; 中央高校基本科研业务费专项资金项目（编号：2014QNA4020）; 浙江省交通厅科研计划项目（编号：2014H21）.
摘要: 提出了一种基于移动最小二乘法（MLSM）的隧道开挖可靠度分析方法，该方法利用MLSM构建功能函数的代理模型，解决了实际工程中功能函数需借助数值方法求解的问题; 通过均匀设计构造MLSM函数，在此基础上，采用一阶可靠度方法（FORM）计算不同极限状态的可靠度指标和失效概率.以一个存在3种不同失效模式的隧道开挖支护稳定问题为例，通过与多项式响应面法和直接FORM法比较，验证了该方法的精度和效率.讨论了不同失效模式下参数的敏感性以及隧道支护安装位置和参数相关性对不同模式下隧道失效概率的影响规律.
关键词： 隧道开挖     可靠度分析     移动最小二乘法     一阶可靠度方法     均匀    
Reliability analysis of tunnel support stability based on moving least squares method
XIAO Zhipeng, LV Qing, ZHAO Yu, LIU Qi     
College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China
Abstract: A reliability analysis procedure is proposed for tunnel excavation problems based on the moving least squares method (MLSM). The MLSM is employed herein as a surrogate model to approximate the actual performance functions which are always of implicit form in most of the practical applications. The MLSM function is constructed using sampling points generated via the uniform design method. Based on the obtained MLSM model, the reliability index and its corresponding failure probability are calculated with first-order reliability method (FORM). The accuracy and efficiency of the proposed approach are illustrated with an illustrative example of three different failure modes. The results are also compared with the polynomial response surface method (RSM) and the direct FORM. Sensitivity analysis and the influence of the support installation position and the correlation of random variables on the generated failure probabilities of different failure modes are investigated.
Key words: tunneling     reliability analysis     moving least square method     first-order reliability method (FORM)     uniform design    

各种确定性方法(包括数值法和解析法)是目前隧道受力和变形分析的主要方法.然而，隧道工程中存在着大量不确定性，包括岩体参数变异性、衬砌材料随机性等.相比于确定性方法，可靠度方法可以考虑各种不确定性对支护-围岩相互作用的综合影响，近年来被逐渐应用到隧道分析中[1-8].例如，曾杰等[1]运用蒙特卡罗模拟(Monte Carlo simulation,简称MCS)分析了深埋隧道初期支护的可靠性；Li和Low[2]利用一阶可靠度算法(first-order reliability method,简称FORM)，对一承受静水压力的圆形隧道的稳定性进行了可靠度分析.

实际工程中，支护-围岩相互作用分析常涉及数值计算，采用MCS进行可靠度分析，需要大量重复计算，效率低，在工程中难以应用.另外，复杂问题的功能函数常缺乏显式表达，不能直接应用FORM等现有方法进行分析.为此，许多学者提出基于各种响应面模型(也称为代理模型)的地下开挖的可靠度计算方法[4, 6-8].通过构造不同的响应面模型来代替复杂的数值计算，在已有的确定性方法和可靠度方法之间架起“桥梁”，为实际隧道工程问题的可靠度分析提供了新的思路.

响应面模型众多，常用的有多项式响应面[4]、人工神经网络[5]、支持向量机[7]等，其中，多项式响应面表达简单，构建容易，应用最广.但构建多项式响应面所需样本数会因随机变量数增加而显著增加，且拟合精度受多项式阶数和有无交叉项影响，某些情况下，甚至会出现“伪响应面”问题[5].人工神经网络和支持向量机具有很好的非线性函数拟合精度，可弥补多项式响应面的不足，但函数结构复杂，内部参数选择不易.

移动最小二乘法(moving least square method，简称MLSM)是一种高效的函数和曲面拟合方法，克服了传统最小二乘法用简单多项式函数拟合整个变量空间、局部精度难以保证的问题.相比于全局最小二乘法，MLSM是一种局部最小二乘法，因而具有更高的函数拟合精度.

本文将MLSM引入可靠度分析，运用均匀设计法确定样本点，构建MLSM响应面模型，再通过FORM计算可靠度指标和失效概率.通过一个隧道围岩-支护相互作用可靠度分析的算例，说明了本文方法的效率和精度，为隧道开挖不确定性的定量分析和风险评价提供参考.

1 可靠度方法

FORM因为只需要随机变量的一次二阶矩信息就可求解可靠度指标和失效概率，简单易用，是目前最常用的可靠度分析方法.

FORM算法的核心是在标准正态空间(U空间)中寻找极限状态面上距离坐标原点最近的点，称为验算点，记作u*.而验算点u*到U空间原点的距离即为一阶可靠度指标β：

$\beta =\underset{g\left( x \right)\le 0}{\mathop{\min }}\,\sqrt{{{u}^{T}}u}$    (1)

传统的FORM算法，需将相关非正态分布的随机变量x通过相关矩阵分解和Rosenblatt变换[9]，从原始变量空间(X空间)转换到标准正态空间(U空间)，获得独立的标准正态分布向量u.

Low和Tang[10]用膨胀椭球体的观点重新阐述了β的几何意义，建立了原始变量空间中FORM算法[11]，定义β为

$\beta =\underset{x\in F}{\mathop{\min }}\,\sqrt{{{\mathbf{n}}^{T}}{{\mathbf{R}}^{-1}}\mathbf{n}}$    (2)

式中：F表示失效域；R为相关矩阵；n为相关等效标准正态分布向量.

原始变量xi可通过下式获得：

${{x}_{i}}={{F}^{-1}}\left[ \Phi \left( {{n}_{i}} \right) \right]$    (3)

式中:Φ(·)为标准正态分布累计概率分布函数(CDF)；F-1(x)为原始非正态分布累计概率分布的反函数.

为计算方便，一般在U空间中构造响应面.为此，需建立X空间中的变量x和U空间中的变量u之间的关系.由式(1)、(2)可知，变量n和变量u具有如下关系[12]：

$n=Lu$    (4)

式中：L为相关矩阵R分解获得的下三角阵，即满足R=LLT，可由Cholesky分解方法实现.显然，若不考虑变量间的相关性，n和u相同.通过式(3)、(4)的转换，很容易用式(1)、(2)计算β.

一旦有了可靠度指标β，失效概率可由下式计算：

${{P}_{f}}\cong 1-\Phi \left( \beta \right)$    (5)

同前，式中Φ·为标准正态分布CDF.

2 基于移动最小二乘法的可靠度分析 2.1 移动最小二乘法(MLSM)

根据移动最小二乘法，功能函数可以近似表示为

$\overline{G}\left( x \right)=p{{\left( x \right)}^{T}}a\left( x \right)$    (6)

式中：ax=a1x,a2x,…,amxT，为待求系数向量，传统最小二乘法中，a是常数，而在MLSM中，系数ax是坐标x的函数，这是MLSM拟合精度提高的一个重要改进；

p(x)=p1x,p2x,…,pmxT，称为基函数，一般情况下是一个含有m项的多项式.

以二维问题为例，线性基函数为

$\mathbf{p}(\mathbf{x})={{\left[ 1,{{x}_{1}},{{x}_{2}} \right]}^{T}},m=3$    (7)

二次基函数为

$\mathbf{p}(\mathbf{x})={{\left[ 1,{{x}_{1}},{{x}_{2}},{{x}_{1}}{{x}_{2}},x_{1}^{2},x_{2}^{2} \right]}^{T}},m=6$    (8)

二次基函数也可不包括交叉项.

待求的系数向量ax可以通过使样本点处近似功能函数值和真实功能函数值误差最小来求得，其误差定义为

$\begin{align} & E\left( \mathbf{x} \right)=\sum\limits_{i=1}^{N}{\omega (x-{{x}_{i}})}{{\left( \bar{G}\left( {{x}_{i}} \right)-G\left( {{x}_{i}} \right) \right)}^{2}} \\ & =\sum\limits_{i=1}^{N}{\omega (x-{{x}_{i}})}{{\left( \mathbf{p}{{\left( {{\mathbf{x}}_{i}} \right)}^{T}}a\left( x \right)-G\left( {{x}_{i}} \right) \right)}^{2}} \\ \end{align}$    (9)

式中：N为样本点的个数；ω(x-xi)为样本点xi的权函数；Gxi为样本点xi的真实功能函数值.

式(9)可重新写成矩阵形式如下：

$E\left( \mathbf{x} \right)={{(\mathbf{Pa}(\mathbf{x})-\mathbf{G})}^{T}}\mathbf{W}\left( \mathbf{x} \right)\left( \mathbf{Pa}(\mathbf{x})-\mathbf{G} \right)$    (10)

其中：

$\mathbf{G}={{\left[ G\left( {{\mathbf{x}}_{1}} \right),G\left( {{\mathbf{x}}_{2}} \right),...,G\left( {{\mathbf{x}}_{N}} \right) \right]}^{T}}$    (11)
$\mathbf{P}={{\left[ {{\mathbf{p}}^{T}}\left( {{\mathbf{x}}_{1}} \right),{{\mathbf{p}}^{T}}\left( {{\mathbf{x}}_{2}} \right),...,{{\mathbf{p}}^{T}}\left( {{\mathbf{x}}_{N}} \right) \right]}^{T}}$    (12)
$\mathbf{W}\left( \mathbf{x} \right)= \left[ \begin{align} & \omega \left( {{\mathbf{x}}_{1}}-\mathbf{x} \right) 0 \cdots 0 \\ & 0 \omega \left( {{\mathbf{x}}_{2}}-\mathbf{x} \right) 0 \\ & \vdots \ddots \vdots \\ & 0 0 \cdots \omega \left( {{\mathbf{x}}_{N}}-\mathbf{x} \right) \\ \end{align} \right]$    (13)

为了使误差Ex最小，对系数ax求偏导，得

$\frac{\partial E\left( x \right)}{\partial \mathbf{a}}=\mathbf{A}\left( \mathbf{x} \right)\mathbf{a}\left( \mathbf{x} \right)-\mathbf{B}\left( \mathbf{x} \right)=0$    (14)

则

$\mathbf{a}\left( \mathbf{x} \right)={{\mathbf{A}}^{-1}}\left( \mathbf{x} \right)\mathbf{B}\left( \mathbf{x} \right)$    (15)

其中：

$\mathbf{A}\left( \mathbf{x} \right)={{\mathbf{P}}^{T}}\mathbf{W}\left( \mathbf{x} \right)\mathbf{P}$    (16)
$\mathbf{B}\left( \mathbf{x} \right)={{\mathbf{P}}^{T}}\mathbf{W}\left( \mathbf{x} \right)\mathbf{G}$    (17)

求得系数ax后，将系数代入式(6)即可得到近似功能函数x.

由于插值误差，在样本点处的估计值x和其真实值Gxi之间可能不完全相等，即xi≠Gxi.为此，Krishnamurthy[13]通过逆变换得到虚拟真实值G(xi)，使得近似功能函数x在样本点处的函数值和其真实功能函数值相等，并发现获得的MLSM模型具有更高的精度.本文采用该方法确定MLSM模型的系数向量.

为提高局部拟合精度，MLSM引入紧支(Compact Support)概念，认为插值点x处的函数值y只受x附近子域内节点影响，这个子域称作点x的支持域，支持域外的节点对y的取值没有影响.在支持域内定义一个权函数w(x)，以高斯函数为例，其表达式如下：

$\omega \left( \mathbf{x-}{{\mathbf{x}}_{\mathbf{I}}} \right)=\left\{ \begin{align} & \frac{{{e}^{-{{\left( {\alpha \left\| \mathbf{x-}{{\mathbf{x}}_{\mathbf{I}}} \right\|}/{D}\; \right)}^{2}}-{{e}^{-{{\alpha }^{2}}}}}}}{1-{{e}^{-{{\alpha }^{2}}}}} \left\| \mathbf{x-}{{\mathbf{x}}_{\mathbf{I}}} \right\|\le D\text{ } \\ & \text{ }0\text{ 其他} \\ \end{align} \right.$    (18)

其中：α为可选参数；D为支持域半径；‖x-xI‖为样本点与插值点之间的距离.本文采用α=3.0的高斯权函数，引入权函数概念是MLSM又一个重要改进，若权函数在整个区域取为常数，MLSM就退化为传统的全局最小二乘法.

在MLSM中，支持域半径D是一个重要的参数.若半径D太大，不能充分体现其局部拟合的优势；若半径D太小，会导致求解系数时式(15)中矩阵A(x)成为奇异矩阵.因此，为了A(x)正定可解，应选择合适的支持域半径D，使支持域范围内至少包括m个样本点(m为待定的系数向量个数，见式(7)、(8)).

本文采用如下方法确定支持域半径：首先，将插值点与样本点的距离按从小到大排序，获得处于第m位点的距离dm；然后，将支持域半径取为D=kdm，其中k为放大系数，本文取k=1.5.

2.2 均匀设计法

基于响应面模型进行可靠度分析，其计算精度不仅取决于响应面模型本身的拟合精度，而且受制于构造模型所用样本点的代表性.目前，样本点主要采用随机取样法和试验设计法两类方法确定.随机取样不能保证样本点在设计空间内均匀分布，特别在样本点较少时，取样不均会造成响应面模型不能准确反映整个域内系统的真实响应.均匀设计法(Uniform Design)是由我国数学家方开泰教授和王元院士[14]提出的一种保证样本点在整个设计空间内均匀分布的试验设计方法，均匀设计法取样得到的样本点能较均匀地分布在整个样本空间，而随机取样得到的样本点往往会在某些区域相对集中，而在另一些区域缺失.此外随机取样难以复制，每次获得的样本点不完全一致，计算结果稳定性难以保证.

采用均匀设计法处理多元函数拟合问题时，能在设计空间生成最具代表性的样本点，从而大幅减少试验次数，缩短试验周期.通过选择适当的均匀设计表很容易确定样本点.均匀设计表可从文献[14]或互联网上获得(http://uic.edu.hk/isci/UniformDesign/UD%20Tables.html).本文采用均匀设计法来选择样本点，构造MLSM函数.

2.3 基于移动最小二乘法的可靠度分析算法

为了用最少的确定性计算获得最优的计算精度，采用迭代算法构造MLSM模型，具体算法如下：

1) 通过均匀设计法在标准正态空间(U空间)中取样，通过式(3)、(4)转换获得原始空间(X空间)样本点.第一次迭代时，以各随机变量均值点为中心进行取样，取样范围[-2,2]；随后迭代中，以前次计算获得的临时验算点ut*为中心进行取样，取样范围逐次减半.

2) 通过确定性计算不同功能函数在样本点处的系统响应.确定性计算可以是解析方法也可以是有限元等数值方法.获得样本点u及其对应功能函数值G(u)，建立样本集.

3) 利用样本集中u和G(u)的对应关系，构建MLSM来拟合功能函数，获得MLSM响应面模型.

4) 用获得的MLSM响应面模型代替实际功能函数，采用FORM算法[11]进行可靠度分析，获得临时可靠度指标βt和临时验算点ut*.

5) 重复步骤1~4，直到可靠度指标βt收敛.即两次迭代获得的可靠度指标β值的变化小于容许误差,容许误差可根据计算精度要求设定，本文取为0.001.

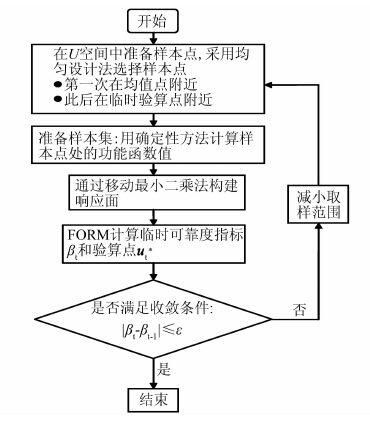
本文算法的计算流程图见图 1.

图 1 基于MLSM的可靠度计算流程图 Figure 1 Proposed procedures for reliability analysis using MLSM
图选项
2.4 算例验证

采用一具有高度非线性的假想功能函数[15]验证上述算法的准确性：

$G\left( x \right)=-0.16{{\left( {{x}_{1}}-1 \right)}^{3}}-{{x}_{2}}+4-0.04cos\left( {{x}_{1}}\cdot {{x}_{2}} \right)$    (19)

式中，x1和x2均服从标准正态分布.

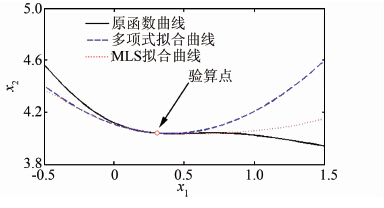
采用本文算法，经过6次迭代获得最终收敛的可靠度指标和验算点，表 1对比了MLSM、多项式响应面法和FORM的结果.可见本文提出的MLSM可获得与多项式响应面法及FORM一致的结果，且本文构造MLS响应面模型所需的样本数更少，得到的验算点和FORM结果更接近.图 2对比了MLSM和多项式响应面法在验算点附近的函数拟合效果，由图可见，MLSM比多项式响应面法具有更高的拟合精度，说明基于MLSM的可靠度分析是一种准确、高效、实用的方法.

表 1 不同方法的结果比较 Table 1 Comparison of reliability results using different methods
MLSM 多项式响应面 FORM
可靠度指标β 4.052 4.052 4.052
验算点 x1 0.307 5 0.311 3 0.309 3
x2 4.040 4 4.040 0 4.040 1
样本点数 22 24 -
表选项
图 2 不同方法在验算点附近的拟合精度对比 Figure 2 Comparison of fitting accuracy of MLSM and polynomial RSM in vicinity of the design point
图选项
3 基于MLSM的隧道支护稳定可靠度分析 3.1 隧道分析模型

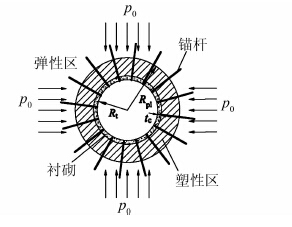
以一个受静水压力圆形隧道的例子来说明本文方法在隧道开挖不确定性分析中的应用.如图 3所示，圆形隧道半径3 m，承受3 MPa均匀围岩压力，采用混凝土衬砌加锚杆支护，支护位置离掌子面2 m.假定围岩为均质、各向同性弹塑性材料.

图 3 均匀围压作用的圆形隧道 Figure 3 A circular tunnel under a hydrostatic in situ stress
图选项

对于圆形隧道的弹塑性分析目前已有很多解，最具代表性的是假定围岩服从Mohr-Coulomb准则的Duncan-Fama解[16]和服从Hoek-Brown准则的Carranza-Torres解[17].为反映岩体非线性力学行为，本文采用基于Hoek-Brown准则的Carranza-Torres解来计算隧道开挖过程中支护-围岩的相互作用.

考虑3种破坏模式，对应的功能函数定义如下：

${{g}_{1}}\left( \mathbf{x} \right)={{p}_{s}}^{max}-{{p}_{s}}^{D}$    (20)
${{g}_{2}}\left( \mathbf{x} \right)=\varepsilon _{u}^{max}-\frac{u_{r}^{D}}{{{R}_{t}}}$    (21)
${{g}_{3}}\left( \mathbf{x} \right)={{L}_{\text{bolt}}}-({{R}_{pl}}-R+\text{1}\text{.2})$    (22)

其中：x为随机变量；psmax为隧道衬砌结构的承载力；psD是作用于衬砌上的围岩压力；Rt是隧道半径；uD是隧道径向位移；Rpl是塑性区半径；εumax是相对应urD/Rt的最大容许值；Lbolt是锚杆长度.

式(20)反映的是支护结构承载力极限状态，即认为当隧道衬砌承载力psmax小于围岩压力pusD时，发生承载力不足破坏；式(21)反映的是由于围岩变形过大引起的围岩失稳破坏，即认为当径向位移与隧道半径的比值urD/Rt大于收敛容许值εmax时发生破坏，不同工程的εumax不同，一般在1%～5%之间，本文取εumax=2%；式(22)反映的是隧道塑性区域范围过大引起的锚杆破坏，即认为当锚杆长度小于塑性区大小与锚杆锚固长度之和时发生破坏，锚固长度本文取1.2 m.上述3个功能函数反映了两类极限状态，其中式(20)属于承载能力极限状态，式(21)、(22)属于正常使用极限状态.支护-围岩的相互作用分析采用收敛约束法[4].

隧道围岩和混凝土衬砌、锚杆等支护参数见表 2.选择其中7个参数作为随机变量，包括岩体参数、衬砌参数，其概率统计分布和统计特征参数见表 3.

表 2 围岩和支护结构参数 Table 2 Properties of rock mass and support system
参数名称 取值
围岩 岩体的地质强度指标 GSI=30
完整岩石材料常数 mi=10
完整岩石单轴抗压强度 σci=20 MPa
弹性模量 Erm=1.185 GPa
岩石泊松比 v=0.3
支护结构 喷射混凝土厚度 tc=0.1 m
无侧限抗压强度 σcc=15 MPa
弹性模量 Ec=20 GPa
泊松比 v=0.2
锚杆 长度 Lbolt=4 m
直径 Db=0.025 m
间距 1 m
表选项
3.2 可靠度计算结果

采用MLSM对3个功能函数分别进行可靠度分析，经过6次迭代，通过48个样本点的确定性计算，可获得收敛的可靠度指标β以及相应的失效概率Pf.

表 3 随机变量的概率分布及统计参数 Table 3 Statistical properties of random variables for tunnel
变量 分布 μ σ COV
GSI 正态 30 7.5 0.25
mi 正态 10 2.0 0.2
σci/MPa 对数正态 20.0 6.0 0.3
Erm/GPa 对数正态 1.185 0.332 0.28
P0/MPa 正态 3.0 0.45 0.15
ks/MPa 对数正态 251.9 50.4 0.2
psmax/MPa 对数正态 0.52 0.13 0.25
表选项

表 4比较了MLSM与FORM、多项式响应面法的计算结果，包括一阶多项式、二阶无交叉和有交叉项多项式，由表 4可见，本文方法能够获得和FORM一致的计算结果，且相比于多项式响应面法所需的样本计算量更少，有力地说明了基于MLSM的可靠度计算方法是一种准确、高效的方法.

表 4 不同方法的可靠度计算结果比较 Table 4 Comparison of reliability results using different methods the circular tunnel
本文MLSM FORM RSM-1 RSM-2 RSM-3
g1 β 3.550 3.549 3.549 3.549 3.549
Pf/% 0.019 0.019 0.019 0.019 0.019
样本数 48 56 60 180
g2 β 2.243 2.244 2.245 - 2.244
Pf /% 1.245 1.241 1.239 - 1.241
样本数 48 64 - 144
g3 β 1.535 1.536 1.536 1.536 1.536
Pf /% 6.236 6.222 6.221 6.225 6.222
样本数 48 56 75 144
注：RSM-1、2、3分别为一阶、无交叉项和有交叉项的二阶多项式响应面.
表选项
3.3 参数间相关性对可靠度结果的影响

和传统的确定性方法相比，可靠度方法的一个重要优势在于能够考虑参数的相关性及其对结果的影响.例如，在上述圆形隧道的可靠度分析中，考虑变量GSI、σci、Erm正相关，ks与psmax正相关，假定其他参数不变，只改变参数间的相关性，计算结果见表 5.可见，参数相关性对隧道开挖可靠度具有显著影响.特别对围岩收敛值过大的破坏模式(式(21))影响最明显.不考虑相关性时(即相关性系数ρ为0)，其失效概率为0.315%；当考虑GSI和Erm、GSI和σci、ks与psmax间的相关性系数分别为0.6、0.6、0.2时，其失效概率为1.245%，提高了将近4倍.这在传统的确定性分析中是无法考虑的.

表 5 参数相关性对可靠度分析结果的影响 Table 5 Influence of correlation coefficients of random parameters on reliability results
相关性系数 g1(x) g2(x) g3(x)
ρGE ρσE ρkp β Pf/% Error/% β Pf/% Error/% β Pf/% Error/%
1 0 0 0 3.281 0.052 - 2.731 0.315 - 1.523 6.387 -
2 0.6 0 0 3.431 0.030 42.3 2.367 0.897 184.8 1.531 6.286 1.6
3 0 0.6 0 3.366 0.038 26.9 2.550 0.539 71.1 1.528 6.326 1.0
4 0 0 0.2 3.359 0.039 25.0 2.731 0.315 0 1.523 6.387 0
5 0.6 0.6 0.2 3.550 0.019 63.5 2.243 1.245 295.2 1.535 6.236 2.4
表选项
3.4 参数敏感性分析

此外，可靠度分析不仅能获得失效概率，而且从验算点数值大小可以直接反映参数敏感性，这构成了可靠度方法另一个重要优势.以功能函数g1为例，在U空间中的验算点us*为(0.5，-0.52，-0.13，-0.27，1.5，-0.25，-3.11)，其中参数P0和pmax对应的数值较大，而以psmax对应的数值最大，说明计算结果对参数psmax最敏感，P0次之.而对功能函数g2，U空间中验算点us*为(-1.75，-0.51，-1.06，-0.38，0.66，0.03，0.03)，从数值大小可以看出，参数GSI和σci 最敏感，参数ks和pmax影响较小.同样对功能函数g3，验算点us*为(-1.2，-0.57，-0.69，0.01，0.34，0.006，0.009)，说明参数GSI最敏感，而参数ks和pmax不敏感.对比发现，对g1影响最大的参数psmax,对g2、g3影响却较小，说明通过提高衬砌的承载力能显著提高功能函数g1的可靠度，但对功能函数g2、g3的影响却不大.

3.5 支撑位置对隧道稳定性的影响

根据支护-围岩相互作用原理，隧道支护安装位置距掌子面的距离对最终围岩变形和支护受力有很大影响.若支护安装距离掌子面过近，围岩前期变形释放较少，最终作用在支护上的围岩压力较大，将造成衬砌结构受力过大而引起的承载力不足破坏.相反，支护安装距离掌子面过远，围岩前期变形得不到有效抑制，在围岩条件较差时，可能造成由于围岩变形过大而诱发围岩失稳问题.因此，安装位置对支护-围岩系统的破坏模式影响巨大.这与新奥法隧道施工原理是一致的.

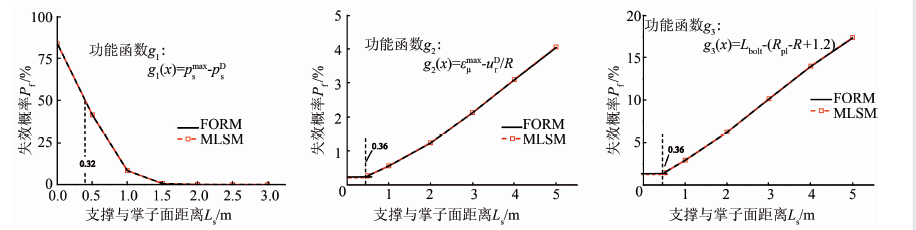
图 4为支护安装位置对不同破坏模式失效概率的影响规律.由图可见，衬砌结构承载力破坏概率随着支护安装位置距掌子面距离增大而减小；而过大围岩收敛变形和过大塑性区范围的失效概率，随着支护安装位置距掌子面距离增大而增大，这与前述支护-围岩相互作用规律的基本认识一致.采用可靠度分析，可明确量化支护安装位置与隧道支护系统破坏模式之间的对应关系，为选择最优支护时间提供参考.而不同破坏模式之间存在着内在的串联关系，可采用系统可靠度方法对其进行详细分析.

图 4 支撑位置对隧道3种失效模式的失效概率的影响 Figure 4 Influence of the support installation position on the failure probability with respect to three failure modes
图选项
4 结语

本文提出了一种基于移动最小二乘法(MLSM)的可靠度分析方法.采用均匀设计选取样本点，利用MLSM构造功能函数的代理函数，并在生成的MLSM函数基础上采用一阶可靠度方法(FORM)计算可靠度指标和失效概率.主要结论总结如下：

1) MLSM能够准确地拟合功能函数，与多项式响应面等其他方法相比，具有高效、实用的特点.

2) 采用均匀设计法选取样本点，能够保证样本点在参数设计空间中具有代表性，克服随机取样中样本点离散不均问题，有利于提高MLSM函数的拟合精度.

3) 隧道开挖算例表明，本文方法可获得与FORM一致的结果，相比多项式响应面方法所需计算量更少，显示了该方法的准确性和高效性.

4) 参数相关性和支护安装位置对隧道-围岩系统的失效概率和破坏模式有显著影响.可靠度分析为量化上述影响提供了有力工具，体现了可靠度方法相比确定性方法的优势.

参考文献
[1] 曾杰, 靳晓光, 张永兴, 等. 公路隧道初期支护可靠度分析[J]. 重庆建筑大学学报, 2008, 30(4): 78–81.
Zeng Jie, Jin Xiaoguang, Zhang Yongxing, et al. Reliability analysis of initial support in a highway tunnel based on the Monte Carlo method[J]. Journal of Chongqing Jianzhu University, 2008, 30(4): 78–81.
[2] Li H Z, Low B K. Reliability analysis of circular tunnel under hydrostatic stress field[J]. Computers and Geotechnics, 2010, 37(1): 50–58.
[3] Li D Q, Jiang S H, Chen Y F, et al. Reliability analysis of serviceability performance for an underground cavern using a non-intrusive stochastic method[J]. Environmental Earth Sciences, 2014, 71(3): 1169–1182. DOI:10.1007/s12665-013-2521-x
[4] Lü Q, Sun H Y, Low B K. Reliability analysis of ground-support interaction in circular tunnels using the response surface method[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(8): 1329–1343. DOI:10.1016/j.ijrmms.2011.09.020
[5] Lü Q, Chan C L, Low B K. Probabilistic evaluation of ground-support interaction for deep rock excavation using artificial neural network and uniform design[J]. Tunnelling and Underground Space Technology, 2012, 32(0): 1–18.
[6] 陈建康, 朱殿芳, 赵文谦, 等. 基于响应面法的地下洞室结构可靠度分析[J]. 岩石力学与工程学报, 2005, 24(2): 351–356.
Chen Jiankang, Zhu Dianfang, Zhao Wenqian, et al. Structure reliability analysis of underground cavern based on response surface method[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(2): 351–356.
[7] 赵洪波. 支持向量机在隧道围岩变形预测中的应用[J]. 岩石力学与工程学报, 2005, 24(4): 649–652.
Zhao Hongbo. Predicting the surrounding deformations of tunnel using support vector machine[J[J]. ] Chinese Journal of Rock Mechanics and Engineering, 2005, 24(4): 649–652.
[8] 赵旭峰, 严松宏. 响应面法在隧道衬砌结构可靠度分析中的应用[J]. 岩石力学与工程学报, 2003, 22(S2): 2853–2856.
Zhao Xufeng, Yan Songhong. Reliability analysis of tunnel lining structure by response surface method[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(S2): 2853–2856.
[9] Rosenblatt M. Remarks on a multivariate transformation[J]. Annals of Mathematical Statistics, 1952, 23(3): 470–472. DOI:10.1214/aoms/1177729394
[10] Low B K, Tang W H. Efficient reliability evaluation using spreadsheet[J]. Journal of Engineering Mechanics-Asce, 1997, 123(7): 749–752. DOI:10.1061/(ASCE)0733-9399(1997)123:7(749)
[11] Low B K, Tang W H. Efficient spreadsheet algorithm for first-order reliability method[J]. Journal of Engineering Mechanics-Asce, 2007, 133(12): 1378–1387. DOI:10.1061/(ASCE)0733-9399(2007)133:12(1378)
[12] Low B K, Zhang J, Tang W H. Efficient system reliability analysis illustrated for a retaining wall and a soil slope[J]. Computers and Geotechnics, 2011, 38(2): 196–204. DOI:10.1016/j.compgeo.2010.11.005
[13] Krishnamurthy T. Comparison of response surface construction methods for derivative estimation using moving least squares, kriging and radial basis functions[C]// 46 th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2005: 1-28.
[14] 方开泰. 均匀设计与均匀设计表[M]. 北京: 科学出版社, 1994.
Fang Kaitai. Uniform Design and Uniform Design Table[M]. Beijing: Science Press, 1994.
[15] Gavin H P, Yau S C. High-order limit state functions in the response surface method for structural reliability analysis[J]. Structural Safety, 2008, 30(2): 162–179. DOI:10.1016/j.strusafe.2006.10.003
[16] Fama M E D. Numerical modelling of yield zones in weak rocks[J]. Comprehensive Rock Engineering, 1993, 2: 49–75.
[17] Carranza-torres C. Elasto-plastic solution of tunnel problems using the generalized form of the hoek-brown failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(3): 480–481. DOI:10.1016/j.ijrmms.2003.12.014