武汉大学学报(工学版)   2016, Vol. 49 Issue (3): 417-422

文章信息

韦自强, 鲁海亮, 蓝磊, 韩翔宇, 岳云峰, 谭可立
WEI Ziqiang, LU Hailiang, LAN Lei, HAN Xiangyu, YUE Yunfeng, TAN Keli
有限长交流输电线路电晕的无线电干扰
Radio interference caused by corona on finite-length AC transmission line
武汉大学学报(工学版), 2016, 49(3): 417-422
Engineering Journal of Wuhan University, 2016, 49(3): 417-422
http://dx.doi.org/10.14188/j.1671-8844.2016-03-017

文章历史

收稿日期: 2015-12-09
 Abstract              PDF               Figures               Tables
引用本文 0
韦自强, 鲁海亮, 蓝磊, 韩翔宇, 岳云峰, 谭可立. 有限长交流输电线路电晕的无线电干扰[J]. 武汉大学学报(工学版), 2016, 49(3): 417-422.
WEI Ziqiang, LU Hailiang, LAN Lei, HAN Xiangyu, YUE Yunfeng, TAN Keli. Radio interference caused by corona on finite-length AC transmission line[J]. Engineering Journal of Wuhan University, 2016, 49(3): 417-422.
有限长交流输电线路电晕的无线电干扰
韦自强1, 鲁海亮1, 蓝磊1, 韩翔宇1, 岳云峰2, 谭可立2     
1. 武汉大学电气工程学院，湖北 武汉 430072;
 2. 广东省电力设计研究院，广东 广州 510600
收稿日期: 2015-12-09
作者简介: 韦自强(1990-)，男，硕士研究生，从事输电线路无线电干扰、配电线路雷击跳闸率计算及防雷评估技术等方面的研究，E-mail：1041189392@qq.com..
摘要: 电力系统运行过程中产生的无线电干扰会影响周边环境和设备运行，进而影响电力行业的进一步发展.因此有必要对线路无线电干扰水平进行计算研究.为此提出了一种以变电站出线端为代表的有限长交流输电线路电晕的无线电干扰计算方法.根据输电线路的空间排列、材料参数，采用激发函数法，得出当三相线路发生均匀电晕时产生的电晕电流.然后利用相模变换和行波在变电站入口处发生反射的原理，建立了体现电晕电流在有限长导线端部反射特性的传播模型，计算出电晕电流在空间任意点产生的电场强度，进而得到无线电干扰值.以变电站出线端的有限长输电线路模型为例，对单回和双回线路的无线电干扰进行了计算，并研究了不同空间位置无线电干扰值的规律.实地测量值验证了计算方法的准确性，对后续研究和工程实践提供了参考和指导.
关键词： 有限长     无线电干扰     激发函数法     电场强度     电晕电流    
Radio interference caused by corona on finite-length AC transmission line
WEI Ziqiang1, LU Hailiang1, LAN Lei1, HAN Xiangyu1, YUE Yunfeng2, TAN Keli2     
1. School of Electrical Engineering, Wuhan University ,Wuhan 430072;
 2. China;Guangdong Electric Power Design Institute, Guangzhou 510600, China
Abstract: Radio interference caused during the operation of the power system would affect the surrounding environment，which links closely with the health of living creatures including human beings. It also cause problems in equipment operation, which in turn affect the further development of the power industry. All these issues make it necessary to implement a deep research into the calculation of radio interference. A method to calculate the value of radio interference caused by finite-length AC transmission lines is proposed. Based on the excitation function, when corona occurs evenly in the three-phase lines, corona currents are calculated according to the spatial arrangement and material parameters of the transmission lines. By considering phase-mode transformation and how corona currents transmit in the case of reflection and refraction，a transmission model which reflects the reflection characteristics of corona currents in finite-length transmission lines is established. And then the electric intensity caused by corona currents and the value of radio interference are obtained. Taking the model of finite-length AC transmission lines of the substation outlet side for example, the radio interferences caused by single-circuit transmission lines and double-circuit transmission lines are calculated. Besides, the relationship between radio interference and spatial location is also studied. By adopting rational material parameters and setting the structures and spatial arrangement legitimately, the radio interference can be limited into a reasonable range. Field measurements have proved the accuracy of the calculating method, which would provide useful references and guidance to further researches and engineering practices.
Key words: finite-length     radio interference     excitation function method     electric field strength     corona current    

随着经济社会和电力系统的发展，输电线路电晕对周围环境产生的无线电干扰问题日益受到社会的关注.当干扰水平达到一定程度时可能会影响周围生物的健康状况和无线电设施的正常工作[1]，对无线电干扰的研究具有越来越重要的意义.

有限长输电线路是指一端连接变电站、换流站或者发电厂的输电线路.其中变电站是输配电过程中非常重要的一部分，也是产生无线电干扰的重要来源[2-3].当输电线路进出变电站时，无线电干扰对周围电磁环境产生的影响会更加特殊、复杂，因此对变电站附近的电磁环境进行研究无疑具有重要的理论和实践意义.

目前国内外对无限长输电线路的无线电干扰问题已经有了较深入的研究，包括产生无线电干扰的原因、影响、理论计算与测量方法、防护措施等[4-9].其中在理论计算方面，国内外学者和机构提出了多种不同的方法.其中包括国际无线电干扰特别委员会(CISPR)和我国电力行业标准DL/T 691-1999等提出了经验公式法[10-11]，但仅适用于导线分裂数较少的三相单回和双回线路，也没有考虑电晕电流的传播过程，且经验公式法的计算准确度值得商榷；我国电力行业标准DL/T 691-1999同时提出了激发函数法，但是仅简单给出了三相单回线路的计算方法[11]；国际上重要的研究机构如美国电力研究协会(EPRI)和国际大电网会议(CIGRE)等也都提出了基于激发函数法的无限长输电线路无线电干扰计算理论[12-14].

上述计算方法均只是针对无限长输电线路，缺少对于以变电站出线端为代表的有限长输电线路的无线电干扰问题的研究.近年来才有侯锐对有限长输电线路的电晕无线电干扰进行了研究[15]，但是其研究电晕电流的传播过程采用的贝瑞隆法过于复杂，而且也没有对变电站周围电磁环境的规律性进行研究.本文针对上述问题，以变电站出线端模型为例，提出了一种有限长输电线路无线电干扰值的计算方法，综合考虑了影响无线电干扰值的各种因素，且适用于不同回路的计算[16-17].通过建立模型和实际计算，得出了无线电干扰值的最终结果.研究了有限长输电线路附近不同位置无线电干扰值的变化规律，有助于变电站附近的电磁环境的深入研究，也为输电线路的工程实践中有关无线电干扰的设计和运行提供了依据和约束条件.

1 有限长输电线路无线电干扰计算理论

激发函数法假设导线在单位长度上均匀地发生相同程度的电晕，表征电晕产生的带电粒子及其运动特性，是导线表面最大场强与导线半径的函数[18].

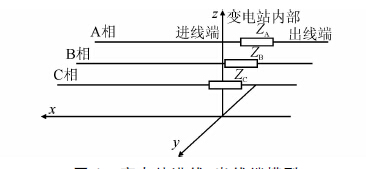
本文以三相单回输电线路为例，详细叙述了变电站出线端的有限长交流输电线路电晕产生的无线电干扰值的计算方法.变电站进出线端的空间三维简化模型以及空间坐标系如图 1所示，将变电站简化成三相阻ZA、ZB、ZC.

图 1 变电站进线、出线端模型 Figure 1 Model of input and output transmission lines for substation
图选项
1.1 求取导线表面最大场强

采用镜像法[19]，求出三相导线的电位系数矩阵P.然后利用下列公式可以计算出三相导线的表面最大场强[20]：

$Q={{P}^{-1}}U=CU$    (1)
$\begin{align} & {{E}_{i\max }}=\frac{{{q}_{i}}}{2n\pi {{\varepsilon }_{0}}r}[1+(n-1)\frac{r}{R}] \\ & (iabc\text{A,B,C)} \\ \end{align}$    (2)

式中：Q为线路表面电荷矩阵，C/m;U为线路电压矩阵,kV；n为导线分裂数；r为子导线半径，m；R为导线分裂半径,m.

1.2 选取激发函数

国内外不同的机构发布的激发函数不尽相同，比较常用的有如下几种[21]：

$\left. \begin{matrix} {{\Gamma }_{\text{CISPR}}}=-121+120\lg {{E}_{\max }}+401\text{g}(2r) \\ {{\Gamma }_{\text{EPRI}}}=76.62-580/lg{{E}_{\max }}+381\text{g(2}r\text{/3}\text{.8)} \\ {{\Gamma }_{\text{CIGRE}}}=-40.69+3.5{{E}_{\max }}+12r \\ {{\Gamma }_{\text{IREQ}}}=-93.03+92.42lg{{E}_{\max }}+43.021\text{g}(2r)+5.1-B(n) \\ \end{matrix} \right\}$    (3)

激发函数是通过试验和实地测量的数据进行统计归纳得到的，环境因素的影响很大.为保证计算准确性，本文选取我国电力行业标准DL/T691-1999[11] 推荐的激发函数，较为符合我国特殊的地理环境：

${{\Gamma }_{\text{DL}}}=70-585/{{E}_{\max }}+35\lg (2r)-10\lg n$    (4)
1.3 求取导线电晕电流

单位长度导线发生均匀电晕时产生的电晕电流按下式计算[22]：

$I=\frac{1}{2\pi {{\varepsilon }_{0}}}C\Gamma $    (5)
1.4 电晕电流在导线上的传播过程

由于导线之间有电磁联系，电晕电流在多根导线上的传播过程不能视为各自互相独立，而且电晕电流行波在端口处会发生折反射.贝瑞隆法将上述分布参数电路转化为集中参数电路，利用各物理量之间的关系列出微分方程组，然后求解，较为复杂.而本文则将互相影响的导线电晕电流进行相模变换，在经过相模变换之后，可以按互相独立的单根导线的波过程求解[23]，然后利用波的折反射原理描述出电晕电流在变电站出线端的模型.

求取线路的模转换矩阵Tu、Ti,通过相模变换矩阵Ti将求得的电晕电流转化为模电流矩阵Im：

$T_{n}^{-1}LC{{T}_{n}}={{L}^{m}}{{C}^{m}}=T_{i}^{-1}CL{{T}_{i}}={{C}^{m}}{{L}^{m}}=\text{diag}({{D}_{1}},{{D}_{2}},{{D}_{3}})={{D}^{M}}$    (6)
$I={{T}_{i}}{{I}^{m}}$    (7)

利用Ti和Tu将线路参数矩阵L、C、R变换为模量下的参数矩阵：

${{L}^{m}}=\text{diag}[L_{1}^{m},L_{2}^{m},L_{3}^{m}]$    (8)
${{C}^{m}}=\text{diag}[C_{1}^{m},C_{2}^{m},C_{3}^{m}]$    (9)
${{R}^{m}}=\text{diag}[R_{1}^{m},R_{2}^{m},R_{3}^{m}]$    (10)

线路上的模电流传播系数为[24]

${{\gamma }_{i}}={{\alpha }_{i}}+\text{j}{{\beta }_{i}}=\sqrt{-{{\omega }^{2}}R_{i}^{m}L_{i}^{m}+\text{j}\omega R_{i}^{m}C_{i}^{m}}$    (11)

式中：αi为衰减系数；βi为畸变系数.

有限长输电线路模型与无限长模型的最大不同在于电晕电流会在线路端口处发生折反射，对这一过程的处理是无限长输电线路无线电干扰的关键.以变压器绕组的阻抗作为变电站模型，相对于线路阻抗来说变压器绕组的阻抗非常大，故可认为电晕电流传播到变电站出线端会发生全反射.如果A相线路上距离变电站出线端s0点发生电晕，A相中的电晕电流分布如下[25]：

${I_A}(x) = \left\{ {\begin{array}{*{20}{c}} {0,x ＜ 0}\\ {\frac{{{I_A}}}{2}\left[ {exp[{\alpha _A}(x - {s_0})] + exp[ - {\alpha _A}(x + {s_0})],0 ＜ x ＜ {s_0}} \right.}\\ {\frac{{{I_A}}}{2}\left[ {exp[{\alpha _A}(x - {s_0})] - {\kern 1pt} exp[ - {\alpha _A}(x + {s_0})],x > {s_0}} \right.} \end{array}} \right.$    (12)
1.5 求取线路均匀电晕时某点的无线电干扰值

第i相x点处发生电晕时，对空间坐标为(x0，y0，z0)处的N点产生的电场强度为[26]

${{E}_{iN(x)}}=60\sum\limits_{i为A,B,C}{{{I}_{i}}(x)}[\frac{{{z}_{i}}-{{z}_{0}}}{{{({{z}_{i}}-{{z}_{0}})}^{2}}+{{({{y}_{i}}-{{y}_{0}})}^{2}}}+\frac{{{z}_{i}}+2p+{{z}_{0}}}{{{({{z}_{i}}+2p+{{z}_{0}})}^{2}}+{{({{y}_{i}}-{{y}_{0}})}^{2}}}]$    (13)

其中：

$p=\sqrt{\rho /(\pi {{\mu }_{0}}f)}$    (14)

式中：ρ为土壤电阻率，Ωm； f为电晕电流频率，MHz.

当第i相全长发生均匀电晕时，对N点产生的场强按以下积分计算[27]：

${{E}_{i(N)}}=\sqrt{\int_{0}^{{{x}_{0}}}{{{\left| {{E}_{iN(x)}} \right|}^{2}}dx+\int_{{{x}_{0}}}^{\infty }{{{\left| {{E}_{iN(x)}} \right|}^{2}}dx}}}~$    (15)

化为分贝值：

${{E}_{i}}=20\lg {{E}_{iN}}$    (16)

上式中，EiN的单位为μV/m.用上述方法可以得到A、B、C相单独发生电晕时的无线电干扰值EA、EB、EC.取最大的两个值，设为E1、E2[28].

$\left. \begin{matrix} {{E}_{1}}\ge {{E}_{2}}+3\text{dB}时,取无限电干扰值E={{E}_{1}} \\ 否则取:E=\frac{1}{2}\left( {{E}_{1}}+{{E}_{2}} \right)+1.5\text{dB} \\ \end{matrix} \right\}$    (17)
1.6 多回输电线路无线电干扰计算

在多回线路中，对每回线路都进行式(1)~(16)的运算，将会得到一系列Emi,m是回路数，m=1,2,3,…；i是相代号，i为A,B,C.然后对同相电晕产生的无线电干扰值进行如下计算[29]：

${{E}_{i}}=10lg\sum{{{(1{{0}^{(\frac{{{E}_{mi}}}{20})}})}^{2}}}$    (18)

上述EA、EB、EC中，取较大的两个值，设为E1,E2，进行式(17)的逻辑运算.

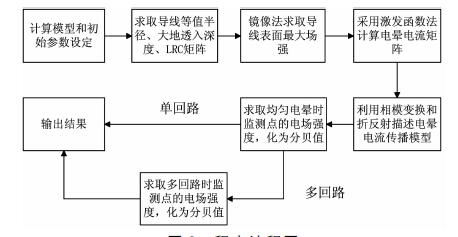
2 算例分析和讨论 2.1 单回与双回输电线路算例

根据上节推导的理论计算过程，本文用C#语言进行了程序编写，程序流程图如图 2所示.

图 2 程序流程图 Figure 2 Program flow diagram
图选项

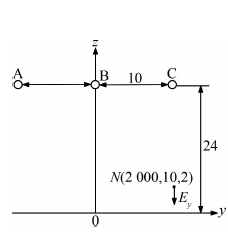
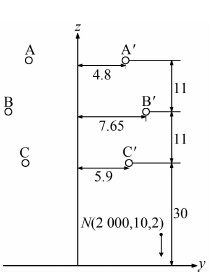
以变电站出线端三相单回和双回输电线路为例，运用激发函数法，计算无线电干扰值.单回路和双回路输电线路空间排列模型及坐标如图 3和图 4所示(已考虑垂弧等因素),图中N点为计算点.线路及变电站参数如表 1.

表 1 线路及变电站参数 Table 1 The parameters of transmission lines and transformer substation
项目单回线路双回线路
导线分裂数44
子导线半径/cm1.341.34
分裂间距/cm45.0045.00
电压等级/kV500750
电晕电流频率/MHz0.50.5
土壤电阻率/(Ωm)1 0001 000
变压器等效电阻/Ω0.3120.089
变压器等效电感/H0.5090.416
表选项
图 3 单回路输电线路空间排列(单位：m) Figure 3 Spatial distribution of single-circuit transmission lines(unit:m)
图选项
图 4 双回路输电线路空间排列(单位：m) Figure 4 Spatial distribution of double-circuit transmission lines(unit:m)
图选项

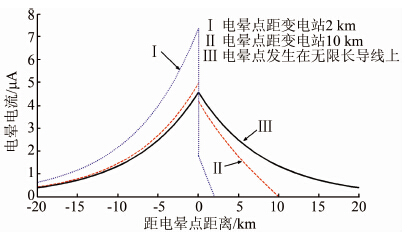
采用激发函数ГDL，单回线路A相某点发生电晕时，以电晕点为横坐标零点，电晕电流在输电线路中的分布情况如图 5所示.

图 5 电晕电流沿线分布情况 Figure 5 Distribution of corona current along transmission line
图选项

由图 5可知，电晕发生在无限长导线上时，电晕电流向两侧无限对称传播；电晕发生在变电站附近时，电晕电流沿远离变电站方向无限传播，沿变电站方向快速衰减.

按照图 3和图 4中的导线的空间排列模型以及表 1中的初始参数，计算均匀电晕下坐标为(2 000,10,2)的N点无线电干扰值，结果如表 2所示.

表 2 5种激发函数计算出的无线电干扰值 dB(μV/m) Table 2 Calculated values based on five excitation functions
线路ГCISPRГEPRIГCIGREГIREQГDL
单回59.1360.5459.6261.0159.75
双回64.6366.2764.4868.9565.87
表选项

由表 2可以看出，采用不同激发函数的计算值非常接近,均处在国家标准发布的合理范围内[30].

2.2 无线电干扰值随空间坐标变化的规律

采用激发函数ГDL，对单回线路和双回线路空间不同点处无线电干扰值的变化规律进行了计算研究.由于单回线路和双回线路的规律较为相似，因此以图 3所示500 kV变电站出线端三相单回输电线路为例，对具体规律的现象和原因探究进行阐述.

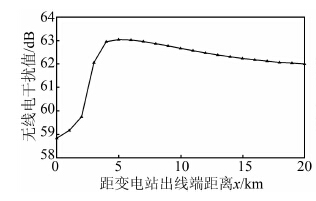
2.2.1 距离变电站位置不同

当监测点距地面高度2 m，距导线中心位置10 m，但距变电站出线端位置不同时，无线电干扰值变化规律如图 6所示.

图 6 无线电干扰值与距变电站距离的关系 Figure 6 Relationship between ratio interference and distance to transformation station
图选项

由图 6可以看出，随着监测点距变电站出线端距离的增加，无线电干扰值先增大，大约在5 km出现最大值，随后开始减小，最终趋近于一个确定值.

影响其变化规律的是监测点和变电站之间的电晕.当距变电站较近时，电晕较少，随着距离的增加，电晕增多，故无线电干扰值先增大；距离继续增加，电晕继续增多，但是由于距离较长，经折射返回的电晕电流大幅衰减，因此无线电干扰值在达到一个最大值后开始减小；最终趋近于一个稳定值，即无限长导线电晕时的干扰值.

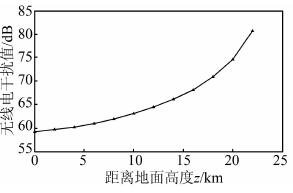
2.2.2 距离地面高度不同

当监测点距变电站出线端2 km，距导线中心位置10 m，但距地面高度不同时，无线电干扰值变化规律如图 7所示.

图 7 无线电干扰值与高度的关系 Figure 7 Relationship between ratio interference and distance to the ground
图选项

由图 7可知，随着监测点高度的增加，无线电干扰值增大.原因显而易见，即监测点距离导线越近，电晕电流在这点感应出的电场强度越大，无线电干扰值也就越大.

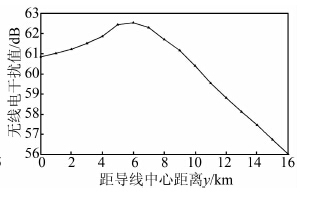
2.2.3 距离导线中心距离不同

当监测点距地面高度2 m，距变电站出线端2 km，但距三相导线中心位置不同时，无线电干扰值变化规律如图 8所示.

图 8 无线电干扰值与距三相导线中心距离的关系 Figure 8 Relationship between ratio interference and distance to the center oftransmission lines
图选项

由图 8可以看到，随着监测点距三相导线中心距离的增加，无线电干扰值先增大，大约在6 m处出现最大值，随后开始减小，最终将趋近0.

当监测点位于三相导线正下方时，距中相导线最近，但是距两条边相导线太远，干扰值不大；随着监测点向一条边相导线移动，干扰值增加；监测点继续移动，距离边相越来越近，但是距中相越来越远，故干扰值在达到一个最大值后开始减小；监测点继续远离三相导线，干扰值越来越小，最终趋近于0.

3 结论

基于变电站出线端输电线路的模型，采用激发函数法，详细分析了有限长输电线路无线电干扰理论计算步骤，并通过对单回路和多回路模型的实际计算，总结了无线电干扰值随监测点空间位置变化而变化的规律，得出以下结论：

1) 在无线电干扰计算中，无限长输电线路模型不同于有限长输电线路模型的关键和难点在于电晕电流行波在线路端点处的折反射过程；

2) 在变电站出线端的有限长输电线路模型中，随着监测点距变电站出线端距离的增加，无线电干扰值先增大，再减小，最终将趋近于一个无限长线路电晕产生的无线电干扰值；

3) 测试点距离导线越近，无线电干扰值越大；

4) 在不同地域的工程应用中，可根据具体环境选择合适的激发函数.

本文的相关研究，提供了有限长输电线路无线电干扰强度的通用计算方法，通过建立相关模型，利用设计参数，可以检验现有的输电线路设计是否符合相关要求，同时也可以为新的输电线路和变电站的设计施工提供约束和指导.

参考文献
[1] 粟福珩. 高压输电的环境保护[M]. 1989: 83.
Su Fuheng. Environmental Protection of High-voltage Transmission[M]. Beijing: Water Power Press, 1989: 83.
[2] 万保权, 谢晖春, 樊亮, 等. 特高压变电站的电磁环境及电晕控制措施[J]. 高电压技术, 2010.
Wan Baoquan, Xie Huichun, Fan Liang, et al. Electromagnetic environment and corona control measures of UHV substation[J]. High Voltage Engineering, 2010.
[3] 唐和香. 变电站无线电干扰预测计算方法研究[D]. 北京: 华北电力大学，2009.
Tang Hexiang. Study on the prediction method for radio interference of substations[D]. Beijing: North China Electric Power University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-11412-2010106359.htm
[4] Maruvada P Sarma. Corona Performance of High Voltage Transmission Lines[M]. London, UK: Research Studies Press Ltd, 1996: 256-260.
[5] 庄池杰, 曾嵘, 龚有军, 等. 交流输电线路的无线电干扰计算方法[J]. 电网技术, 2008.
Zhuang Chijie, Zeng Rong, Gong Youjun, et al. Calculation methods of radio interference caused by AC transmission lines[J]. Power System Technology, 2008.
[6] 杨彬, 张波. 试验线段无线电干扰测量方法仿真分析[J]. 高电压技术, 2011, 37(12): 2978–2983.
Yang Bin, Zhang Bo. Simulation analysis of effectiveness of radio interference measurement on test line[J]. High Voltage Engineering, 2011, 37(12): 2978–2983.
[7] 牛慧. 高压输电线路无线电干扰精确测量系统设计[D]. 郑州大学，2011.
Niu Hui. A system design for accurate measurement of radio interference from high voltage transmission lines[D]. Zhengzhou: Zhengzhou University,2011. http://cdmd.cnki.com.cn/Article/CDMD-10459-1011215619.htm
[8] 陈国庆, 张志劲, 孙才新, 等. 500 kV同塔双回输电线路导线排列方式对电气特性的影响[J]. 重庆大学学报, 2003, 26(6): 60.
Chen Guoqing, Zhang Zhijin, Sun Caixin, et al. Impact of line arrangement of 500 kV double-circuit transmission line on the electrical characteristics[J]. Journal of Chongqing University, 2003, 26(6): 60.
[9] 陈稼苗. 500 kV同塔四回输电线路电磁环境问题研究[D]. 北京: 华北电力大学, 2010.
Chen Jiamiao. Research on the electromagnetic environment of 500 kV quadruple-circuit transmission line on the same tower[D].Beijing:North China Electric Power University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-11412-2010105944.htm
[10] CISPR 18-2: 1982 Radio Interference Characteristics of Overhead Power Lines and High-voltage Equipment, Part 2; Method of Measurement and Procedure for Determining Limits[S]. Geneva, Switzerland: International Electrotechnical Commission, 1986.
[11] DL/T 691-1999 高压架空线路无线电干扰计算方法[S]. 北京：中国电力出版社，2000.
DL/T 691-1999 Calculation Methods of Radio Interference in High Voltage Transmission Lines[S]. Beijing: China Electric Power Press, 2000.
[12] 颜天佑, 黄业同. 110 kV同塔六回输电线路电磁环境研究[J]. 电力学报, 2012, 27(2): 92.
Yan Tianyou, Huang Yetong. Research on the electromagnetic environment of 110 kV six-circuit transmission line on the same tower[J]. Journal of Electric Power, 2012, 27(2): 92.
[13] Anderson J G. Transmission Line reference Book: 345 kV and Above[M]. USA: Fred Weidner&son Printers, INC, 1982: 217-224.
[14] Bd Haussmann. Interference produced by corona effect of electric systems[C]// International Conference on Large High Voltage Electric Systems, Paris: CIGRE Committee Report,1974.
[15] 侯锐. 基于激发函数法的有限长交流线路无线电干扰计算[D]. 北京: 华北电力大学, 2009.
Hou Rui. Calculation of the radio interference of finite AC transmission lines based on excitation function[D]. Beijing: North China Electric Power University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-11412-2010105701.htm
[16] Gary C H. The theory of the excitation function: A demonstration of its physical meaning[J]. IEEE Transactions on Power Apparatus and Systems, 1972, 91: 305–310.
[17] 万保权, 蒋虹, 张广州, 等. 三峡500 kV同塔双回线路无线电干扰预测[J]. 高电压技术, 2002.
Wan Baoquan, Jiang Hong, Zhang Guangzhou, et al. A prediction on the radio interference of 500 kV SanXia double circuit transmission lines[J]. High Voltage Engineering, 2002.
[18] Trinh N G, Maruvada P S, Poirier B. A comparative study of the corona performance of conductor bundles for 1 200 kV transmission lines[J]. IEEE Trans on Power Apparatus and Systems, 1974, 93(3): 940–949.
[19] 杨宪章. 工程电磁场[M]. 2002.
Yang Xianzhang. Engineering Electromagnetic Field[M]. Beijing: China Electric Power Press, 2002.
[20] 王泽忠, 全玉生, 卢斌先. 工程电磁场[M]. 1994.
Wang Zezhong, Quan Yusheng, Lu Binxian. Engineering Electromagnetic Field[M]. Beijing: Tsinghua University Press, 1994.
[21] 袁建生，邹军.计算架空线路无线电干扰的激发函数法分析[C]//无线电干扰和变电站电磁兼容研讨会论文集，珠海，中国，2008：17-23.
Yuan Jiansheng, Zou Jun. Analysis of the excitation function method for calculating the radio interference of transmission lines[C].//Research Papers of Radio Interference and Electromagnetic Compatibility of Substation, Zhuhai, China，2008：17-23.
[22] Tejada C, Gomez P, Escmilla J C. Computation of radio interference levels in high voltage transmission lines with corona[J]. Latin America Transactions, 2009, 7(1): 54–61. DOI:10.1109/TLA.2009.5173465
[23] 陈维贤. 超高压电网稳态计算[M]. 1993: 5-10.
Chen Weixian. Steady Calculation in UHV Network[M]. Beijing: China Water Power Press, 1993: 5-10.
[24] 西洛琴斯基ЛИ. 高压工程：电力系统波过程和内部过电压[M]. 1964: 12-13.
Ciro Censky. High Voltage Engineering:The Wave Process of Power System and Internal Overvoltage[M]. Beijing: China Industry Press, 1964: 12-13.
[25] 关根志. 高电压工程基础[M]. 北京: 中国电力出版社, 2003.
Guan Genzhi. High Voltage Engineering Fundamentals[M]. Beijing: China Electric Power Press, 2003.
[26] 邬雄, 万保权. 输变电工程的电磁研究[M]. 2009: 107.
Wu Xiong, Wan Baoquan. Electromagnetic Research on Power Transmission and Transformation[M]. Beijing: China Electric Power Press, 2009: 107.
[27] Juette G W, Roe G M. Modal components in multiphase transmission live radio noise analysis[J]. IEEE Trans on Power Apparatus and Systems, 1971, 90(2): 808–813.
[28] GB/T 7349-2002高压架空送电线、变电站无线电干扰测量方法[S].北京：中国标准出版社，2002.
GB/T 7349-2002 Methods of Measurement of Radio Interference on High Voltage Overhead Transmission Lines and Substation[S]. Beijing: China Standard Press, 2002.
[29] 张殿生. 电力工程高压送电线路设计手册[M]. 1991: 44.
Zhang Diansheng. Electric Power Engineering Design Manual of High Voltage Transmission Lines[M]. Beijing: China Water Power Press, 1991: 44.
[30] GB 15707-1995高压交流架空送电线无线电干扰限值[S].
GB 15707-1995 Limits of Radio Interference in High Voltage AC Overhead Transmission Lines[S]. http://www.cnki.com.cn/Article/CJFDTotal-DLBZ199704009.htm