文章信息
- 王涛, 周炜波, 徐大朋, 曾俊
- WANG Tao, ZHOU Weibo, XU Dapeng, ZENG Jun
- 基于光滑节理模型的岩体水力压裂数值模拟
- Numerical simulation of hydraulic fracturing of rock mass based on smooth joint model
- 武汉大学学报(工学版), 2016, 49(4): 500-508
- Engineering Journal of Wuhan University, 2016, 49(4): 500-508
- http://dx.doi.org/10.14188/j.1671-8844.2016-04-004
-
文章历史
- 收稿日期: 2015-09-18
2. 中国矿业大学(北京)煤炭资源与安全开采国家重点实验室,北京 100083;
3. 中国电建西北勘测设计研究院有限公司,陕西 西安 710065
2. State Key Laboratory of Coal Resources and Safe Mining, China University of Mining and Technology Beijing, Beijing 100083, China;
3. Northwest Engineering Corporation Limited, Power China, Xi’an 710065, China
水力压裂是因水压力的抬高而在岩体或土体中引起裂缝产生与扩展的一种物理现象,是高压水流或其他液体将岩体内已有的裂纹、孔隙等驱动、扩展、贯通等物理现象的统称[1].水力压裂作为一种破裂岩体的有效技术在石油、页岩气、煤层气等资源的开采方面发挥着重要的作用.我国页岩气资源丰富、勘探开发潜力巨大,但许多页岩气井存在低渗透性等特点,都需要进行水力压裂施工加以改善方能开采利用[2].利用水力压裂技术进行煤层气资源开发,一方面可以消除矿井瓦斯灾害隐患,另一方面将抽放的瓦斯加以利用可以变废为宝.所以,水力压裂一直以来都是研究的热点问题.
在水力压裂的数值模拟方面,传统的有限单元法(FEM)和边界元法(BEM)是广泛应用于水力压裂研究的常用数值方法. Papanastasiou等[3]基于有限元方法提出了一个完全耦合的弹塑性水力压裂模型.朱宝存等[4]采用有限元软件进行了煤岩的水力压裂数值模拟,研究了不同地应力及煤岩天然裂缝对破裂压力大小的影响. 连志龙等[5]利用有限元软件ABAQUS构建了一个三维非线性有限元水力耦合有限元模型,并使用此模型对大庆油田一个水平井的分段压裂过程进行了模拟. Aghighi等[6]采用有限元数值模型模拟了完全的气液耦合并研究了重复压裂的致密气储层的应力变化. Zhang等[7]利用二维边界元模型模拟了近井筒的裂缝迂曲问题. 刘伟[8]在考虑导流能力沿裂缝方向变化的条件下,在Laplace空间对有限导流垂直裂缝压力动态分布进行了详细讨论,同时应用边界元方法进行了数值求解.
在利用有限元法进行岩体裂纹扩展模拟时需要不断进行单元重新剖分,以反映裂纹在域内的扩展,网格重构极大地增加了计算工作量,影响了有限元计算的效率,而且由于裂缝的扩展主要由裂缝尖端奇异点的应力状态控制,所以只需考虑断裂边界上的问题而不必包括整个模型区域,因此边界元被认为比有限元更适合用于水力压裂的数值模拟. 岩体是由大量的完整岩石块体和不连续结构面组合而成的集合体. Fairhurst等[9]指出完整岩石与不连续面之间裂缝形成过程是非常复杂的,很难用连续介质的观点去考虑.非连续变形数值方法能够抓住完整岩石破裂以及不连续面滑动的本质,可以提高对岩体各种力学行为的理解.离散元方法作为其中的一个典型代表是研究岩体水力压裂的有效方法.
离散元方法最早由Cundall[10]提出,1979年Cundall[11]运用离散元方法开发了颗粒离散元数值计算程序,并将其用于模拟圆形颗粒的相对运动及相互作用.该方法非常具有吸引力,它不需要非常复杂的本构方程,无需像连续介质模型那样需要作一定的理论假设,且不受宏观材料力学行为的限制. 颗粒离散元方法不需要屈服函数或是塑性势函数,而只需要选择基本的细观力学参数来描述被模拟材料的宏观力学本构特性.另外,颗粒离散元方法能够考虑块体的破坏及节理对块体强度及变形的影响.
许多学者利用颗粒离散元方法进行了水力压裂研究,Al-Busaidi等[12]进行了花岗岩水力压裂的数值模拟并将结果与实验获得的声发射数据进行了对比分析.Shimizu等[13]进行了一系列完整岩石的水力压裂数值模拟,研究了液体粘度及颗粒粒径分布与水力压裂效果之间的相关关系.Wang等[14]研究了岩石力学性质以及注水参数对水力压裂裂缝扩展规律的影响,并对实际工程的水力压裂过程进行模拟.除了采用离散元,有些学者也尝试采用其他非连续分析方法进行压裂的计算[15, 16].文章利用二维颗粒离散元程序(PFC2D)中的颗粒粘结模型及光滑节理模型来分别表征完整岩块及节理面,对完整岩石及裂隙岩体进行水力压裂数值模拟并作对比分析.
1 接触模型及颗粒离散元流固耦合原理在颗粒离散元中颗粒视为刚性球体,每个刚球通过有限刚度的弹簧连接,颗粒之间允许相互嵌入,颗粒集合体的本构行为通过接触模型及接触特性获得[17].引入颗粒粘结模型形成颗粒集合体以此来表征完整的岩石块体,在颗粒集合体中加入光滑节理模型来表征含有节理的裂隙岩体.
1.1 颗粒粘结模型及光滑节理模型1) 完整岩石的表征
Potyondy等[18]采用BPM模型(Bonded-Particle Model)模拟了Lac du Bonnet花岗岩的力学行为.BPM模型是通过平行粘结(用来表征粘结物)将相互接触的颗粒粘结起来形成集合体,以此来表征完整的岩石,如图 1所示.平行粘结可以想象为一系列具有恒定法向刚度与切向刚度的弹簧并作用于颗粒接触点处,并假设这些弹簧有一定的抗拉强度与抗剪强度,平行粘结可以传递颗粒间的力和力矩.BPM模型的细观力学参数如表 1所示.

|
| 图 1 颗粒粘结模型示意图 Figure 1 Diagram of bonded-particle model |
| 参数符号 | 含义 |
| Rmin | 颗粒最小粒径 |
| Rmax/Rmin | 颗粒粒径比 |
| ρ | 颗粒密度 |
| μ | 颗粒内摩擦系数 |
| Ec | 颗粒接触杨氏模量 |
| kn/ks | 颗粒接触法向与切向刚度比 |
| λ pb | 平行粘结半径扩大系数 |
| Ec | 平行粘结杨氏模量 |
| σc | 平行粘结法向粘结强度 |
| τc | 平行粘结切向粘结强度 |
| kn/ks | 平行粘结法向与切向刚度比 |
BPM模型中平行粘结是一个具有一定大小的弹性梁,其所承受的力${{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}}}_{i}}$与力矩${{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {M}}}_{\mathbf{i}}}$可以沿着接触平面分解成法向与切向方向的分量:
式中:Fn,Fs,Mn,Ms分别代表法向与切向方向上的力与力矩的分量,对于PFC2D程序,扭矩Mn=0,弯矩Ms≠0,${{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n}}}_{\mathbf{i}}}$和${{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {t}}}_{\mathbf{i}}}$分别表示颗粒接触处法向与切向单位向量.
每一个计算步中,颗粒间的相对位移及转动会产生弹性力与力矩增量,产生的增量将累加到当前值进行计算,力与力矩增量计算式:
式中:A为平行粘结截面面积;kn和ks为平行粘结法向与切向刚度;I为平行粘结截面的惯性矩:
对于PFC2D程序,式中t=1.0,R=λpbmin(RA,RA),RA,RA是2个接触颗粒的半径,λpb是平行粘结半径扩大系数.
2)节理的表征
利用BPM模型可以对完整岩石的力学行为进行模拟,但是却不能很好地反映岩体的非连续特性,而天然岩体存在许多诸如节理等的不连续结构面.Kulatilake[19],Park[20]等通过降低节理面上颗粒的粘结强度及刚度来模拟岩体中的节理,但是这种方法存在一些问题,比如这种节理模型往往由于颗粒的粗糙度过大或者颠簸效应而影响模拟的效果.虽然可以通过引入小颗粒减少粗糙度来表征软弱带以模拟节理,但是如果岩体中存在许多节理时,其模拟的工作量是相当大的.为克服这些问题,Cundalll21]提出了光滑节理模型(Smooth Joint Model(SJM))的概念,Mas Ivars等[22]通过引入SJM模型模拟了复杂节理岩体的力学行为.
光滑节理模型可以模拟节理的力学行为而无需考虑颗粒接触的方向,通过将节理两侧所有颗粒间的接触设置为光滑节理模型,可以用它来模拟有摩擦或者粘结作用的节理.如图 2所示,节理接触部位是光滑的,因此被设置为光滑节理接触的颗粒可以相互覆盖或是“滑过”对方,而不是在力的作用下一个颗粒绕着另外一个颗粒转动.光滑节理模型包含2个平行且最初重合的平面(面1和面2),2个接触颗粒(球1和球2)分别属于2个平面.光滑节理模型相关的细观参数如表 2所示.
| 符号参数 | 含义 |
| θp | 节理倾角 |
| kn & ks | 节理法向与切向刚度 |
| λ | 半径扩大系数 |
| μ | 内摩擦系数 |
| ψ | 剪胀角 |
| M | $粘结状态\left\{ \begin{array}{*{35}{l}} 0,无粘结且从不破坏 \\ 1,无粘结且张拉破坏 \\ 2,无粘结且剪切破坏 \\ 3,粘结 \\ \end{array} \right.$ |
| σc | 节理法向粘结强度 |
| cb | 粘结系统粘聚力 |
| φb | 粘结系统内摩擦角 |
光滑节理可以视为一系列均匀分布在矩形截面上的弹簧,它的中心位于接触点上,方向与节理面平行,其横截面面积:
式中:t=1.0;R=λmin(RA,RB),RA,RB是2个接触颗粒的半径,是半径扩大系数.
在每一个计算步中,2个颗粒上的相对平移位移增量可以分解为沿着节理面的法向与切向的分量:
将这些分量分别与节理面法向与切向刚度相乘即可算得节理面上力的增量,力的更新计算:
式中:ΔUn和ΔUs分别为沿节理面法向与切向位移增量;kn和ks分别为节理面法向与切向刚度;Fn和Fs为节理面上法向与切向力的分量;A为节理横截面面积.
1.2 颗粒离散元流固耦合原理在颗粒离散元程序中通过引入流体“域”和流体“管道”来模拟渗流作用,如图 3所示.流体“域”相当于用于储水的“水库”,是由接触颗粒的接触连接线(图中绿色直线所示)所围成的多边形封闭区域,通过链表可以将这些颗粒连接起来,域中的颗粒通过指针相互连接.同样每个“域”都有一个域指针,通过该指针可以将模型中所有的“域”联系起来.“管道”是固体中流体的流动通道,也是连接“域”的通道,在颗粒接触的地方用平行板模型来模拟,这个通道间隙的大小与颗粒间相互接触的法向位移成正比例,特别是当材料的初始状态为相互粘结时,这个通道间隙只有在粘结破坏或颗粒发生位移时才会变化.
1) 流量方程
如图 3所示,每一个流体“管道”实际上是一个具有一定长度及开度的平行板,流体在平行板中的流动满足立方定律,其中fc为作用在平行板上的作用力,因而单位厚度上(在垂直平面方向上)流过平行板的流量为
式中:μ为流体粘度;(p2-p1)为2个相邻域的压力差,正值使第2个流体“域”的流体流入第1个流体“域”,负值相反;L为“管道”长度,其大小为“管道”两侧的颗粒半径之和;a为“管道”孔径,通常情况下孔径的大小可以认为是裂缝的张开度,但是在流固耦合计算之前首先要假定一个很小的初始孔径a0,该孔径两侧颗粒保持粘结,但是没有外荷载作用,孔径大小计算:
式中:F为“管道”处的法向压力;F0为当“管道”孔径减少至初始孔径一半时的法向压力.当“管道”两侧的作用力为0或拉力时,“管道”的孔径与初始孔径a0及“管道”两侧颗粒的法向位移相关:
式中:g为“管道”两侧颗粒的法向位移;m为无量纲的位移比例乘子.
2) 压力方程
每个“域”从周围“管道”获得流量,“域”中的水压力随着耦合计算的进行不断变换,并且不断地以体积力的形式施加到“域”中各个颗粒上去.在一个时间步长Δt内,流体压力增量Δp(流入为正)为[17]
式中:Kf为流体的体积模量;Vd为“域”的表观体积;ΔVd为一个时间步长Δt内“域”表观体积的增量;∑q为从周围“管道”获得的流量总和.
3) 求解方法
在每一个计算步内,力学计算决定了“域”几何形状的变化,“域”的变化导致了“管道”的开度变化,进而影响到“管道”内的流量,而后“域”内压力得到更新.应用显式求解方法,将流量方程应用于所有的“管道”,并将压力方程应用于所有的“域”进行交替求解,从而实现耦合计算[17].计算中需要求出稳定的临界时间步长.假设某个“域”存在扰动压力Δpp,由于扰动而流入“域”内的流量:
式中:R为“域”周围颗粒的平均半径;N为连接“域”的所有“管道”的数量.
利用压力方程可以得到由于水流入而引起的响应压力变化Δpr:
保持稳定的条件就是水流入引起的压力变化必须小于扰动压力,即Δpr<Δpp,当两者相等时可求出临界时间步长Δt:
在计算中必须保证模型内每2个颗粒之间的接触都不小于2个,以确保在渗流过程中所有的“管道”都保持畅通.通过PFC的内置函数库函数扫描模型内所有颗粒,将任一颗粒的接触点都调整为大于或等于2个,然后用特定函数为模型定义一系列完整的“域”,创建相应的链接链表,任意2个相邻的“域”都有流动路径,以保证计算中流动的连续性.
4) PFC中裂纹扩展理论
在BPM模型中,平行粘结用来模拟完整岩石的粘结物,接触颗粒在发生相对运动或转动时,作用在平行粘结截面上的最大正应力与剪应力计算:
由于在设置平行粘结时指定了材料强度,所以,当最大正应力超过平行粘结法向粘结强度(σmax≥σc)或最大剪应力超过平行粘结切向粘结强度(ττmax≥τc)时,平行粘结就会发生破坏,那么在相应位置就会产生裂缝.对于有设置节理粘结强度的SJM模型,如果节理力沿法向的分量满足Fn≤-σcA,则意味着粘结在受拉方向发生破坏,即在节理面裂缝张开;否则,粘结依然存在,保持不变.如果节理力沿切向的分量满足|Fs|≥τcA,则粘结在剪切方向发生断裂;否则,粘结保持不变.
2 水力压裂数值模拟 2.1 模型建立采用二维颗粒离散元程序(PFC2D)对某高埋深页岩气储层进行水力压裂数值模拟,模型的尺寸为50 m×50 m.模型中的颗粒半径R的分布采用从Rmin到Rmax的均匀分布,取颗粒最小半径Rmin=0.19 m,颗粒最大半径与最小半径之比为r=1.66,最终生成颗粒11 710个.注意到文中所选颗粒的尺寸偏大,主要是因为若采用实际的岩石矿物尺度构建数值模型,那么颗粒数目将会非常庞大,需要极长的计算时间,考虑到所选颗粒相较于整个模型的尺寸还是较小,故可认为这样的选取是合理的.
颗粒集合体由四面墙围成,计算中通过伺服机制调整墙的加载速度来等效施加地应力,其中上下两道墙施加竖直向主应力,左右两道墙施加水平向主应力.分别构建2种计算模型,如图 4~6所示,图 4所示为完整岩石模型(模型Ⅰ),采用BPM模型来模拟;图 5所示为包含一系列相互平行节理的页岩岩体模型(模型Ⅱ);图 6所示为由一系列相互正交节理及岩块所组成的岩体(模型Ⅲ),其中完整岩块和节理分别采用BPM模型和SJM模型来模拟.

|
| 图 4 完整岩石模型示意图 Figure 4 Diagram of intact rock model |

|
| 图 5 包含平行节理的模型示意图 Figure 5 Diagram of model with parallel joints |

|
| 图 6 包含正交节理的模型示意图 Figure 6 Diagram of model with quadrature joints |
水力压裂模拟时在模型下方中心部位取一点(如图 4中蓝色的点所示)作为注水孔,初始时施加初始孔压p0,随后以定流量的方式向注水孔中不断注水加压.进行模拟之前需要指定相关BPM及SJM模型参数,模型细观参数主要采用数值试验标定获取,即不断调整细观参数的取值进行单轴压缩试验,直至试验所获宏观力学参数与实际工程所测参数接近为止,相关的研究思路见文献[14].具体标定后的模型细观参数、宏观参数及选取的地应力及注水参数如表 3~5所示.
| BPM模型 | SJM模型 | ||
| 参数 | 数值 | 参数 | 数值 |
| Rmin /m | 0.19 | kn/(GPa·m-1) | 66 |
| Rmax/Rmin | 1.66 | ks /(GPa·m-1) | 66 |
| ρ /(kg·m-3) | 3 169 | λ | 1.0 |
| μ | 0.5 | μ | 0.5 |
| Ec /GPa | 28 | ψ/(°) | 10 |
| kn/ks | 2.5 | M | 3 |
| λpb | 1.0 | σc /MPa | 22.4 |
| Ec /GPa | 28 | cb /MPa | 22.4 |
| σc/MPa | 56 | φb/(°) | 0 |
| τc /MPa | 56 | ||
| kn/s | 2.5 | ||
| 参数 | 模型Ⅰ | 模型Ⅱ | 模型Ⅲ |
| UCS/MPa | 75.8 | 52.56 | 44.63 |
| 弹性模量/GPa | 33.48 | 20.54 | 19.26 |
| 泊松比 | 0.24 | 0.19 | 0.15 |
|
竖直向主
应力/MPa |
水平向主应
力/MPa |
注水时
间/s |
注水流量/
(m3·s-1· m-1) |
初始孔
压/MPa |
| 93 | 80 | 320 | 1.77×10-3 | 74.8 |
运用PFC2D软件分别对上述3种模型进行水力压裂数值模拟,模拟过程中记录了不同时间裂纹分布、裂纹累计数目过程,并统计压裂过程中裂纹的扩展半径、注水孔周边孔隙度的变化情况,各模型水力压裂结果如图 7~15所示.对均质、无节理的完整岩石进行水力压裂模拟,最终会获得一条较为完整、连续且没有分叉的裂纹.如图 7所示,在水力压裂过程中,裂纹均匀扩展,裂纹累积数目基本上呈现出线性变化,并且裂纹大致沿着平行于竖直向主应力的方向扩展,其与大多数水力压裂物理试验结果以及经典的弹性力学理论所反映的规律是一致的[23, 24].在裂纹的扩展过程中,压裂半径及注水孔附近的孔隙度也基本上随之呈现出均匀线性递增的变化规律(图 8、9).

|
| 图 7 完整岩石裂纹扩展及分布 Figure 7 Cracks distribution of the intact rock model |

|
| 图 8 完整岩石压裂半径-时间曲线 Figure 8 Fracture radius vs. time for intact rock model |

|
| 图 9 完整岩石孔隙度变化量-时间曲线 Figure 9 Porosity variation vs. time for intact rock model |

|
| 图 10 含平行节理的岩体裂纹扩展及分布 Figure 10 Cracks distribution of model with parallel joints |
|
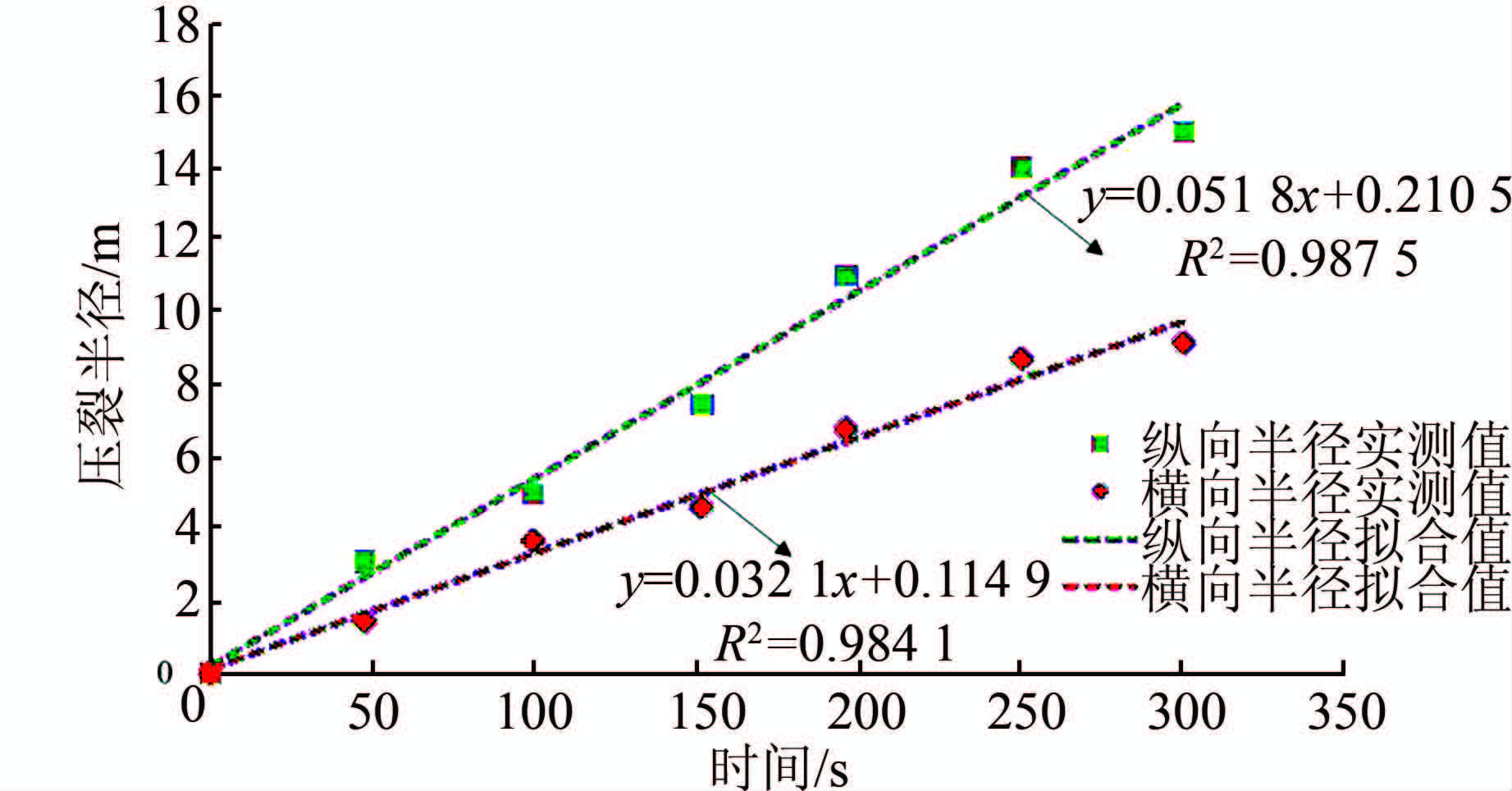
| 图 11 含平行节理的岩体压裂半径-时间曲线 Figure 11 Fracture radius vs. time for model with parallel joints |
|
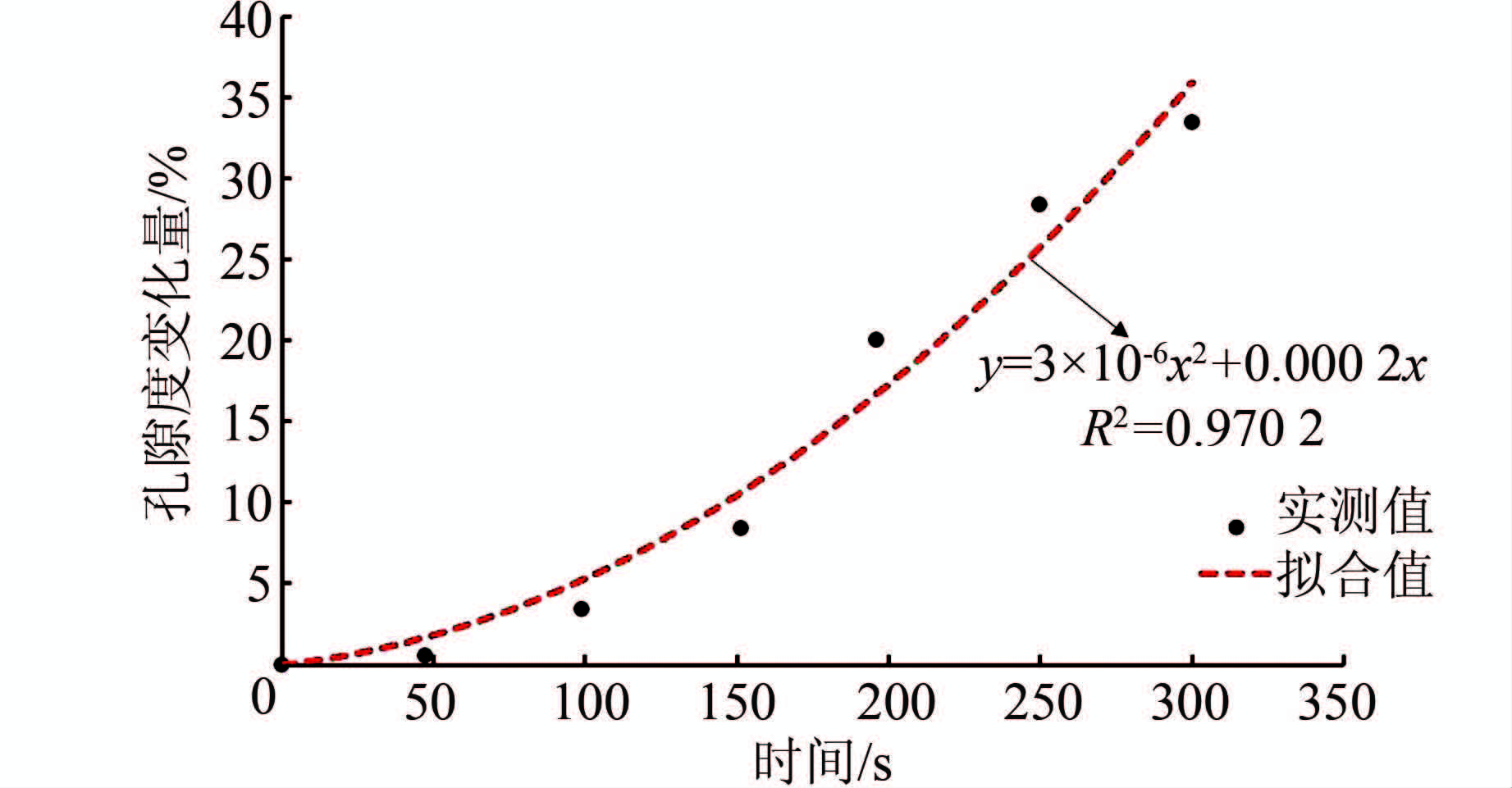
| 图 12 含平行节理的岩体孔隙度变化量-时间曲线 Figure 12 Porosity variation vs. time for model with parallel joints |
|
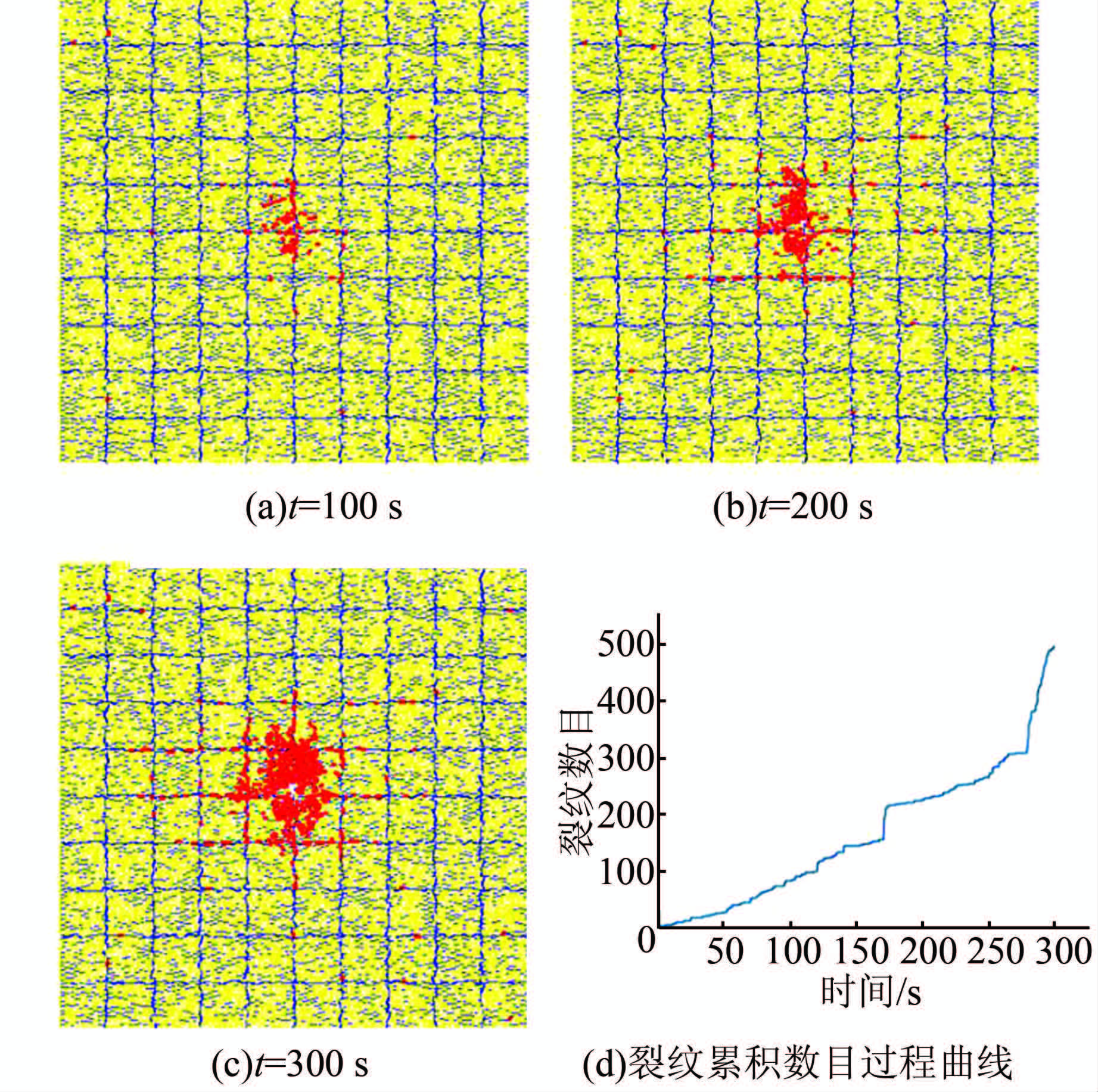
| 图 13 含正交节理的岩体裂纹扩展及分布 Figure 13 Cracks distribution of model with quadrature joints |
|
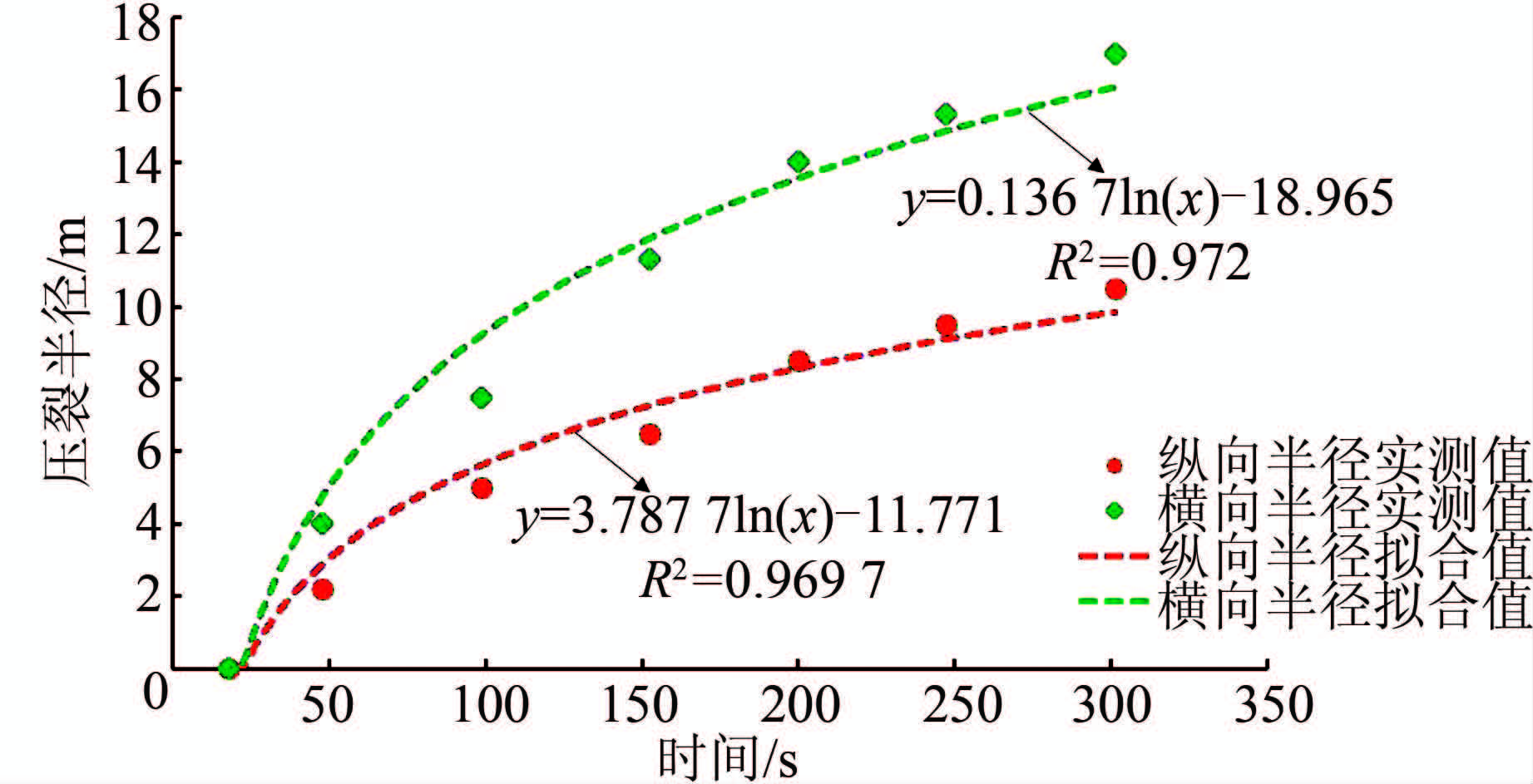
| 图 14 含正交节理的岩体压裂半径-时间曲线 Figure 14 Fracture radius vs. time for model with quadrature joints |
|
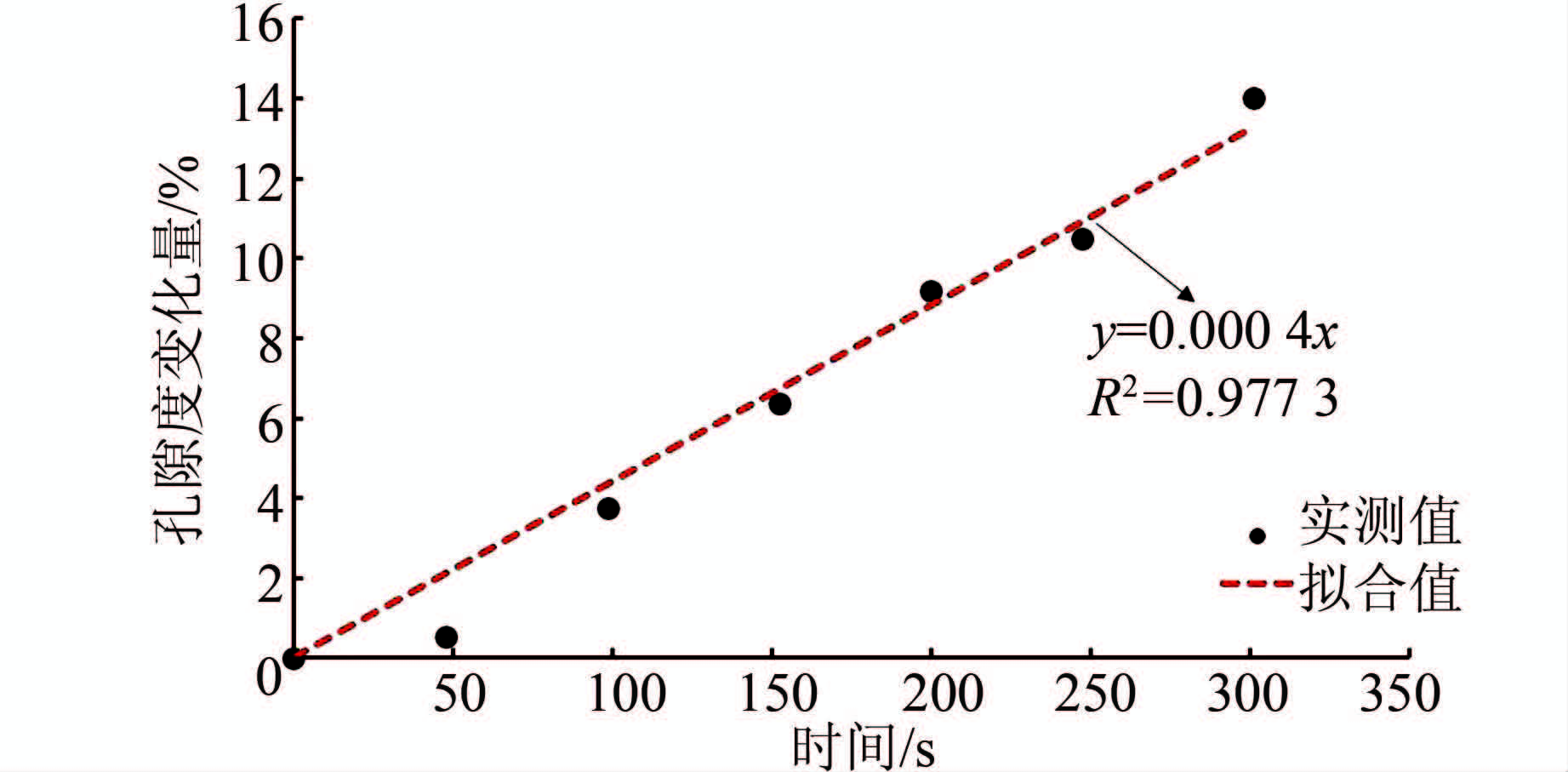
| 图 15 含正交节理的岩体孔隙度变化量-时间曲线 Figure 15 Porosity variation vs. time for model with quadrature joints |
节理的存在对水力压裂裂纹的扩展与分布具有很大影响,图 10所示为一系列遍布平行节理的岩体水力压裂裂纹分布图,可以看出,在初始阶段裂纹主要分布在注水孔附近且裂纹向四周不断萌生、扩展,没有出现与完整岩石相类似的一整条连续裂纹.其主要原因是注水孔附近存在较多的零散节理,这些结构面的存在构成一系列裂隙通道,其作用相当于“支流”,将注水孔附近的水流分散开来,所以在沿着竖直向应力的方向上流量急剧减少,孔压也相应降低,因而在此方向上难以较快形成较为完整且扩展方向明确的裂纹,但是随着流体的不断补充注入,裂纹的扩展发生了一定的变化,从t=100 s开始裂纹除了沿注水孔附近径向扩展,同时开始向着平行于竖直向主应力的方向不断发展,从图 11所示的压裂半径-时间过程曲线可以看出,纵向与横向裂纹的半径基本上随时间线性增加,并且纵向裂纹的扩展速度快于横向裂纹,与此同时,注水孔周边的孔隙度也有了较大幅度的提高(图 12).最后,在注水孔附近可以形成一片近似于椭圆形式的压裂区(图 10).因此,该模型的初始应力与节理分布对其裂纹的发展均有重要影响.
在BPM模型上设置一系列相互正交的SJM模型可以形成如图 13所示的模型,从水力压裂计算的裂纹分布结果可以看出,与之前的2个模型不同,在初始阶段裂纹主要沿着最靠近注水孔的节理面上萌生、扩展,在t=100 s时注水孔附近的横向与纵向节理面上已经形成“十字形”的完整连续裂纹,随着流体的不断注入,裂纹数目不断增加,节理的存在对水力压裂裂缝的形成不断发挥着“引导”作用.与此同时,在水压力的作用下节理面上的裂纹向节理面两侧发展,节理面两侧的完整岩体逐渐开始发生破裂,当注水时间t=200 s时,注水孔附近的完整岩体已经产生大量的裂纹,且沿着横向节理面上已经形成数条连续裂纹.在水压力的持续作用下裂纹数目快速增长,裂纹在注水孔附近不断径向扩展,同时在附近的节理面上不断向外延伸,裂纹大致上呈现出一种对称式的发展.当注水时间t=300 s时,可以看出在整个模型的中心区域形成了一个相对对称而完整的压裂区,裂纹沿注水孔周边、横向与纵向节理面上连续分布.从图 14所示的压裂半径时间过程曲线可以看出,整个模型中纵向与横向压裂区的半径基本上符合对数式的增长规律,横向裂纹增长的速度快于纵向裂纹.压裂过程中随着裂纹的不断张开及向外延伸,注水孔周边的孔隙度有了一定的提高,并且随时间呈线性增长(图 15).综合水力压裂模拟结果,可以得出结论:节理对水力压裂裂纹的萌生、扩展以及最终压裂区裂纹的分布形态具有非常重要的作用.
3 结语采用颗粒离散元方法,利用颗粒粘结模型及光滑节理模型分别模拟了深埋页岩气储层完整岩块及节理面,并构建了完整岩石以及包含节理的岩体的水力压裂数值模型,研究并对比分析了不同模型的水力压裂裂纹扩展及分布规律.
1) 采用颗粒离散元方法对较完整的岩石进行水力压裂模拟时,能够形成基本与最大主应力相平行的完整裂纹,其模拟结果与实验室水力压裂物理试验及理论分析的结论相一致,说明了基于颗粒离散元方法利用颗粒粘结模型模拟完整岩石,并进行水力压裂研究的可行性.
2) 实际工程中的岩体大多数包含大量不规则的节理,节理的存在极大影响了水力压裂及其裂纹扩展分布规律.其主要表现为节理的存在会对裂纹的扩展产生诱导作用,当裂纹扩展至节理面附近时,节理会“引导”裂纹的扩展,使裂纹沿着节理面产生扩展.
3) 光滑节理模型可以较好地反映节理的存在对实际岩体水力压裂现象的影响,尤其是在研究具有大量节理的岩体水力压裂问题时,其具有突出的优势.文章所述只是对采用颗粒离散元方法进行岩体水力压裂研究的初步探索,更深层次的内容(比如考虑随机节理的影响;考虑压裂的时间效应等)有待于进一步的研究.
| [1] |
黄文熙. 对土石坝科研工作的几点看法[J].
水利水电技术, 1982(4): 23–28.
Huang Wenxi. Some views on the scientific research of earth-rock dam[J]. Water Resources and Hydropower Engineering, 1982(4): 23–28. |
| [2] |
伊向艺, 雷群, 丁云宏.
煤层气压裂技术及应用[M]. 北京: 石油工业出版社, 2012.
Yin Xiangyi, Lei Qun, Ding Yunhong. CBM Fracturing Technology and Its Application[M]. Beijing: Petroleum Industry Press, 2012. |
| [3] | Papanastasiou P C. A coupled elastoplastic hydraulic fracturing model[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(3-4): 240–241. |
| [4] |
朱宝存, 唐书恒, 颜志丰, 等. 地应力与天然裂缝对煤储层破裂压力的影响[J].
煤炭学报, 2009, 34(9): 1199–1202.
Zhu Baocun, Tang Shuheng, Yan Zhifeng, et al. Effects of crustal stresses and natural fractures on fracture pressure of coal reservoirs[J]. Journal of China Coal Society, 2009, 34(9): 1199–1202. |
| [5] |
连志龙, 张劲, 王秀喜, 等. 水力压裂扩展特性的数值模拟研究[J].
岩土力学, 2009, 30(1): 169–174.
Lian Zhilong, Zhang Jin, Wang Xiuxi, et al. Simulation study of characteristics of hydraulic fracturing propagation[J]. Rock and Soil Mechanics, 2009, 30(1): 169–174. |
| [6] | Aghighi M A, Rahman S S. Horizontal permeability anisotropy: effect upon the evaluation and design of primary and secondary hydraulic fracture treatments in tight gas reservoirs[J]. Journal of Petroleum Science and Engineering, 2010, 74(1-2): 4–13. DOI:10.1016/j.petrol.2010.03.029 |
| [7] | Zhang X, Jeffrey R G, Bunger A P, et al. Initiation and growth of a hydraulic fracture from a circular wellbore[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(6): 984–995. DOI:10.1016/j.ijrmms.2011.06.005 |
| [8] |
刘伟.水力压裂压力动态试井分析与增产效果提高方法研究[D].北京: 中国地质大学, 2005.
Liu Wei.A study on the hydraulic fracturing pressure behavior well-testing analysis and stimulation effect improvement method [D].Beijing: China University of Geosciences, 2005. |
| [9] | Fairhurst C, Damjanac B, Brandshaug T.Rock mass strength and numerical experiments[C]// Proceedings of 35th Geomechanics Colloquium, Technical University Freiberg, Germany, 2007:1-20. |
| [10] | Cundall P A.A computer model for simulating progressive large scale movements in blocky rock systems[C]//Proceedings of Symposium Rock Fracture (ISRM), Nancy, France, 1971: Ⅱ-8. |
| [11] | Cundall P A, Strack O D L. A discrete numerical model for granular assemblies[J]. Geotechnique, 1979, 29(1): 47–65. DOI:10.1680/geot.1979.29.1.47 |
| [12] | Al-Busaidi A. Distinct element modeling of hydraulically fractured Lac du Bonnet granite[J]. Journal of Geophysical Research., 2005, 110(B6): 1–14. |
| [13] | Shimizu H, Koyama T, Ishida T, et al. Distinct element analysis for Class II behavior of rocks under uniaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(2): 323–333. DOI:10.1016/j.ijrmms.2009.09.012 |
| [14] | Wang T, Zhou W, Chen J, et al. Simulation of hydraulic fracturing using particle flow method and application in a coal mine[J]. International Journal of Coal Geology, 2014, 121: 1–13. DOI:10.1016/j.coal.2013.10.012 |
| [15] |
严成增, 郑宏, 孙冠华, 等. 模拟水压致裂的二维FDEM-flow方法[J].
岩石力学与工程学报, 2015(1): 67–75.
Yan Chengzeng, Zheng Hong, Sun Guanhua, et al. A 2D FDEM-Flow method for simulating hydraulic fracturing[J]. Chinese Journal of Rock Mechanics and Engineering, 2015(1): 67–75. |
| [16] | Zhang G, Li X, Li H. Simulation of hydraulic fracture utilizing numerical manifold method[J]. Science China Technological Sciences, 2015, 58(9): 1542–1557. DOI:10.1007/s11431-015-5901-5 |
| [17] | Itasca Consulting Group Inc.PFC2D-Particle Flow Code Two Dimensions.Ver.4.0 User’s Manual [M].USA: Minneapolis, 2010. |
| [18] | Potyondy D O, Cundall P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329–1364. DOI:10.1016/j.ijrmms.2004.09.011 |
| [19] | Kulatilake P H S W, Malama B, Wang J. Physical and particle flow modeling of jointed rock block behavior under uniaxial loading[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(5): 641–657. DOI:10.1016/S1365-1609(01)00025-9 |
| [20] | Park E-S, Martin C D, Christiansson R.Simulation of the mechanical behavior of discontinuous rock masses using a bonded-particle model[C]//Proceedings of the 6th North American Rock Mechanics Symposium, Houston, Yale D, et al, eds.; 2004, ARMA/NARMS 04-480. |
| [21] | Mas Ivars D, Potyondy D O, Pierce M, et al.The smooth-joint contact model[C]//Proceedings of the 8th World Congress on Computational Mechanics/ 5th European Congress on Computational Methanics and Applied Science and Engineering, Venice, Italy, 2008: 2735. |
| [22] | Mas Ivars D, Pierce M E, Darcel C, et al. The synthetic rock mass approach for jointed rock mass modelling[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(2): 219–244. DOI:10.1016/j.ijrmms.2010.11.014 |
| [23] |
蔺海晓, 杜春志. 煤岩拟三轴水力压裂实验研究[J].
煤炭学报, 2011, 36(11): 1801–1805.
Lin Haixiao, Du Chunzhi. Experimental research on the quasi three-axis hydraulic fracturing of coal[J]. Journal of China Coal Society, 2011, 36(11): 1801–1805. |
| [24] |
张旭, 蒋廷学, 贾长贵, 等. 页岩气储层水力压裂物理模拟试验研究[J].
石油钻探技术, 2013, 41(2): 70–74.
Zhang Xu, Jiang Tingxue, Jia Changgui, et al. Physical simulation of hydraulic fracturing of shale gas reservoir[J]. Petroleum Drilling Techniques, 2013, 41(2): 70–74. |
 2016, Vol. 49
2016, Vol. 49





