武汉大学学报(工学版)   2016, Vol. 49 Issue (6): 866-870

文章信息

吕大刚, 乔雨蒙, 贾明明, 米莹
LU Dagang, QIAO Yumeng, JIA Mingming, MI Ying
基于地震易损性分析的非延性RC框架黏滞阻尼器加固方案决策
Decision of retrofit schemes with viscous dampers for non-ductile RC frames based on seismic fragility
武汉大学学报(工学版), 2016, 49(6): 866-870
Engineering Journal of Wuhan University, 2016, 49(6): 866-870
http://dx.doi.org/10.14188/j.1671-8844.2016-06-012

文章历史

收稿日期: 2016-04-01
 Abstract              PDF               Figures               Tables
引用本文 0
吕大刚, 乔雨蒙, 贾明明, 米莹. 基于地震易损性分析的非延性RC框架黏滞阻尼器加固方案决策[J]. 武汉大学学报(工学版), 2016, 49(6): 866-870.
LU Dagang, QIAO Yumeng, JIA Mingming, MI Ying. Decision of retrofit schemes with viscous dampers for non-ductile RC frames based on seismic fragility[J]. Engineering Journal of Wuhan University, 2016, 49(6): 866-870.
基于地震易损性分析的非延性RC框架黏滞阻尼器加固方案决策
吕大刚1,2,3, 乔雨蒙1,2, 贾明明1,2, 米莹1,2     
1. 哈尔滨工业大学结构工程灾变与控制教育部重点实验室,黑龙江 哈尔滨 150090;
 2. 哈尔滨工业大学土木工程学院，黑龙江 哈尔滨 150090;
 3. 同济大学土木工程防灾国家重点实验室, 上海 200092
收稿日期: 2016-04-01
作者简介: 吕大刚 (1970-)，男，教授，博士，主要从事结构可靠度、工程风险分析、随机动力学、地震工程等研究，E-mail: ludagang@hit.edu.cn.
基金项目: 国家自然科学基金项目(编号：51378162,51408155);科技支撑计划(编号：2013BAJ08B01);土木工程防灾国家重点实验室开放基金(编号：SLDRCE12-MB-04).
摘要: 通过基于云图法的概率地震易损性分析对黏滞阻尼器加固的非延性RC框架结构的抗震性能进行评价.以黏滞阻尼器的速度系数和加固后结构的等效阻尼比为设计变量，设计了9种不同的黏滞阻尼器加固方案.基于地震易损性分析对不同方案的加固效果进行了评价，发现采用黏滞阻尼器加固后，非延性RC框架结构的地震易损性降低，抗震性能得到较大的提高，并基于易损性曲线分析给出了非延性RC框架黏滞阻尼器加固的最佳方案决策.
关键词： 地震易损性     抗震加固     黏滞阻尼器     非延性RC框架结构     评价     决策    
Decision of retrofit schemes with viscous dampers for non-ductile RC frames based on seismic fragility
LU Dagang1,2,3, QIAO Yumeng1,2, JIA Mingming1,2, MI Ying1,2     
1. Key Laboratory of Structures Dynamic Behavior and Control of Ministry of Education, Harbin Institute of Technology, Harbin 150090, China;
 2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China;
 3. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China
Abstract: The seismic performance of non-ductile RC frame retrofitted by viscous dampers are assessed by the probabilistic seismic fragility analysis based on cloud method. Taking the global damping ratio of the retrofitted frame and the velocity exponent of the viscous dampers as the design variables, 9 different retrofit schemes are obtained. Above retrofit schemes are assessed by the probabilistic seismic fragility analysis and conclude that the non-ductile RC frame’s fragility decreased while seismic performance improved after retrofit. And the optimal retrofit scheme of the non-ductile RC frame using the viscous dampers is decided according to the results of fragility curves.
Key words: seismic fragility     seismic retrofit     viscous dampers     non-ductile RC frame     assessment     decision making    

近年来，黏滞阻尼器作为一种重要的结构被动控制元件，逐渐应用到实际建筑结构的加固中，众多研究者使用黏滞阻尼器对RC框架结构、桥梁结构进行抗震加固，并开展了大量的理论与试验研究[1-5].由于不确定性广泛地存在于地震输入和结构本身中，一些学者也开始采用概率手段研究了加固结构的抗震性能[6-9]，并对加固效果进行了初步评价[10-12].然而，采用地震易损性分析系统性地评价结构的抗震加固效果的研究尚处于起步阶段.本文采用概率地震易损性分析来评价不同黏滞阻尼器加固方案的效果，并基于易损性曲线分析给出了非延性RC框架黏滞阻尼器加固的最佳方案.在进行最优加固方案决策时，本文选取加固后结构的抗震性能作为优化目标，尚未考虑加固成本与加固效率之间的平衡，基于抗震性能和加固成本的多目标优化问题，将成为进一步研究的方向之一.

本文建立了6层非延性RC框架结构模型，采用基于Maxwell模型的液缸式黏滞阻尼器对上述结构进行加固.在加固设计中，将黏滞阻尼器速度指数α和加固后结构整体阻尼比ξeff作为设计变量，分别取α=0.25、0.5、0.75，ξeff =0.1、0.15、0.2，设计了9种不同的黏滞阻尼器加固方案[13]，通过概率地震易损性分析以及整体概率抗倒塌能力分析对上述加固方案进行了评价并决策出最佳方案.

1 加固结构的地震易损性分析 1.1 基于云图法的概率地震需求分析

概率地震易损性分析包括概率地震需求分析和概率抗震能力分析两部分研究内容.从不确定性传递的角度，概率地震需求分析体现了不确定性从地震动到结构的传递过程，其分析结果表征了地震动强度与结构反应之间的概率关系.概率地震需求分析的核心内容是建立概率地震需求模型，基于时程分析的结果统计获得地震反应与地震动强度参数之间的关系.若采用若干实际地震动的时程分析结果进行统计，由于结果呈云图状，称之为云图法.云图法运算次数较少，计算效率较高，特别是对于复杂结构，能够有效节省计算资源，利于其在实际工程中的应用.

本文选取20条真实地震动作为输入[14]，基于Opensees平台，对黏滞阻尼器加固非延性RC框架结构进行时程分析.通过对时程分析结果进行统计回归，建立结构的概率地震需求模型.本文采用云图法建立结构的概率地震需求模型，假设结构概率地震需求中位值mD|IM与地震动强度参数IM服从对数线性关系[15]:

$ln{{m}_{D|IM}}={{\beta }_{0}}+{{\beta }_{1}}lnIM$    (1)

式中: β0=lna，β1=b.地震需求的对数标准差βD|IM的计算公式为

${{\beta }_{D|IM}}=\sqrt{\frac{\sum\limits_{i=1}^{N}{{{\left( ln(Di)-ln\left( {{m}_{D|IM}} \right) \right)}^{2}}}}{N-2}\text{ }}$    (2)

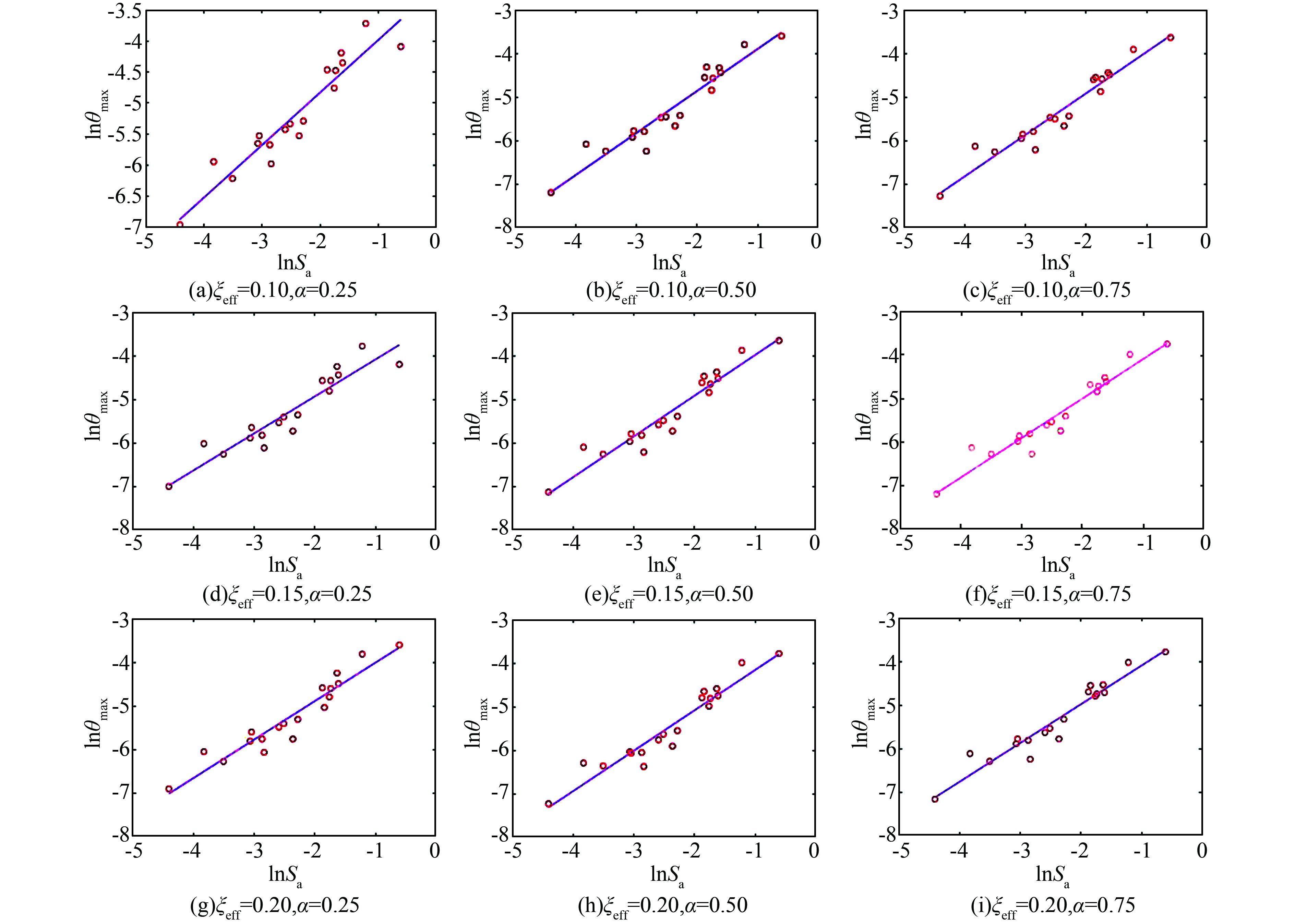
式中，Di(i=1, 2, …, N)为第i条地震动对应的结构非线性反应.本文采用结构在地震作用下的最大层间位移角θmax作为地震需求参数，采用谱加速度Sa作为地震动强度参数，应用云图法对地震需求模型进行拟合(如图 1所示)，进而获得不同的黏滞阻尼器加固方案对应的非延性钢筋混凝土框架结构的概率地震需求参数(如表 1所示)，其中α表示不同加固方案中黏滞阻尼器的速度指数，ξeff表示黏滞阻尼器加固后结构的整体阻尼比，R2为线性拟合优度，其值>0且＜1，R2值越大表明线性拟合效果越好.

表 1 各加固方案云图法概率地震需求拟合结果 Table 1 Fitting results of the probabilistic seismic demand about every retrofit schemes based on cloud method
ξeff= 0.10ξeff= 0.15ξeff= 0.20
αβ0β1βD|IMR2αβ0β1βD|IMR2αβ0β1βD|IMR2
0.25-3.142 80.842 60.284 30.895 80.25-3.236 10.850 90.305 90.882 50.25-3.124 70.884 80.266 40.911 4
0.50-2.932 40.966 80.280 30.917 30.50-3.048 20.936 80.261 30.923 90.50-3.230 00.928 80.259 00.923 0
0.75-2.773 81.028 70.370 50.878 20.75-3.190 60.906 20.240 20.923 50.75-3.124 70.884 80.266 40.911 4
表选项
1.2 黏滞阻尼器加固非延性RC框架结构的概率抗震能力分析

在地震易损性分析中通常假定结构的能力C服从对数正态分布，该模型的数学表达式[16]如下所示:

${{F}_{C}}\left( d \right)=P\left[ D>C|D=d \right]=\Phi [\frac{ln(d/{{m}_{C}})}{{{\beta }_{C}}}]$    (3)

式中:mC为结构极限状态抗震能力中位值；βC为结构极限状态抗震能力对数标准差，取值参考FEMA350[17]的建议值，即βC =0.25.结构的破坏状态应用FEMA273[18]中定义的破坏状态: 立即居住(IO)、生命安全(LS)及倒塌预防(CP).对于立即居住状态层间位移角限值取1/100；对于生命安全层间位移角限值取2/100；对于倒塌预防状态层间位移角限值取为4/100.

1.3 黏滞阻尼器加固非延性RC框架结构的概率地震易损性分析

结构的地震易损性(Seismic Fragility)可以定义为结构各个地震强度水准下结构达到或超过某种极限状态的条件概率.地震易损性函数FR(·)可定义为[16]

图 1 各加固方案云图法概率地震需求拟合图 Figure 1 Fitting lines of probabilistic seismic demand about rarious retrofit schemes based on cloud method
图选项
${{F}_{R}}\left( x \right)=\Phi \left[ \frac{ln{{m}_{D|IM}}-ln{{m}_{C}}}{\sqrt{{{\beta }_{C}}^{2}+{{\beta }_{D|IM}}^{2}}} \right]~$    (4)

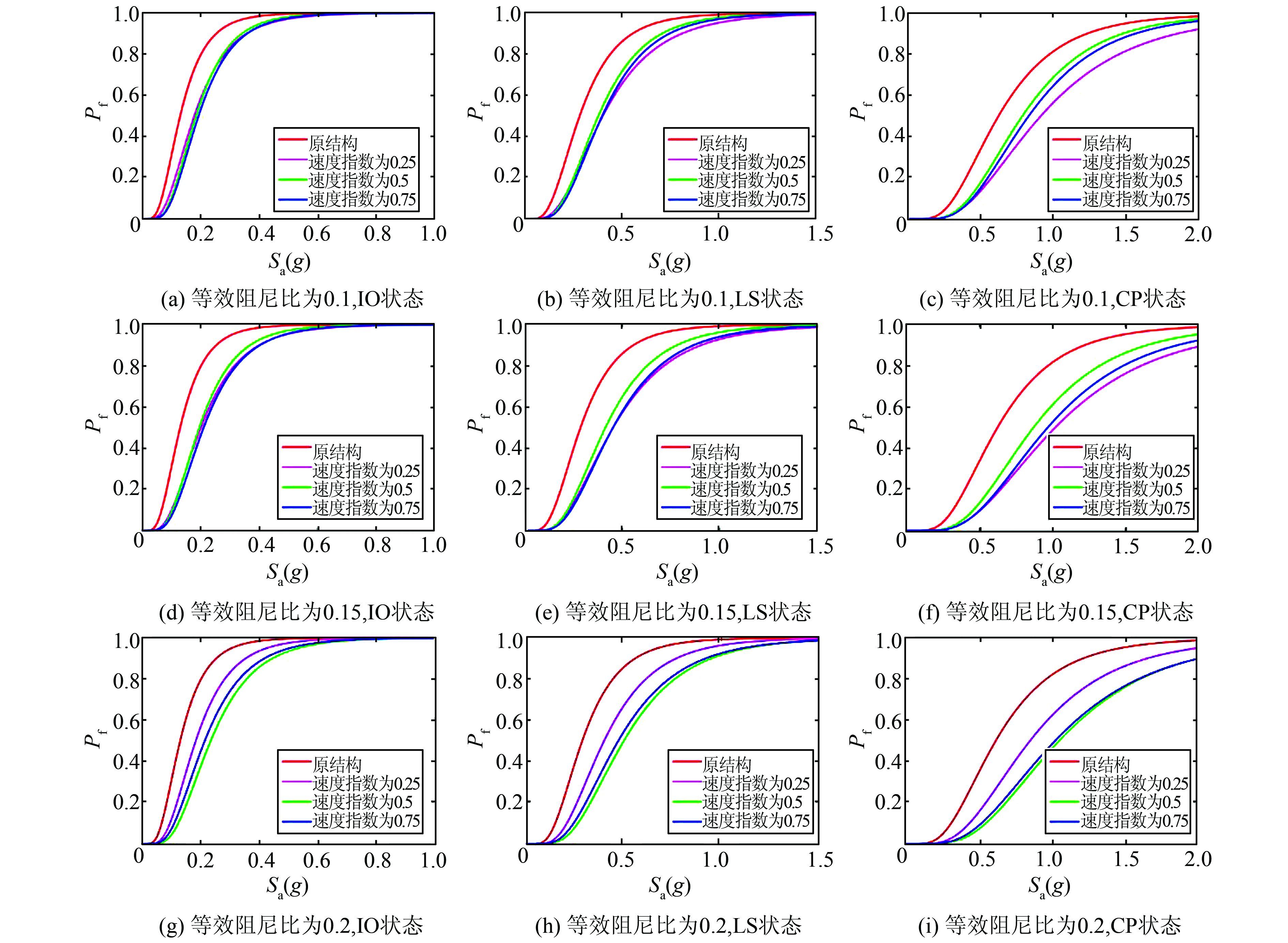
采用式(4) 可计算不同极限状态下的失效概率.图 2为使用不同的黏滞阻尼器加固前后结构在IO、LS、CP三种极限状态下的地震易损性曲线.

由图 2可知，采用黏滞阻尼器加固后，均能不同程度地提高原非延性RC框架的抗震性能.在IO极限状态下，当结构整体等效阻尼比相同时，不同速度指数的黏滞阻尼器加固方案间并未表现出明显的不同，这是由于在IO状态下层间位移角限值仅为1/100，不能充分发挥黏滞阻尼器的滞回性能，因而不同速度指数的黏滞阻尼器加固方案间没有明显差距.当结构整体阻尼比ξeff=0.2，在LS和CP极限状态下，通过比较结构不同加固方案的易损性曲线发现，黏滞阻尼器速度指数α=0.25时，结构易损性曲线在α=0.5和α=0.75的结构方案的上方，且随着层间位移角限值的增大曲线间的间距加大，说明黏滞阻尼器速度指数较小时加固效果较差.通过对比不同极限状态下的易损性曲线，可以发现随着极限状态的发展，加固黏滞阻尼器降低非延性RC框架结构易损性的效果越来越显著，这也是因为随着层间位移角增大，黏滞阻尼器的滞回耗能效果愈发显著，耗散地震动能量，降低结构的地震响应和失效概率.从结构整体概率抗震性能角度可以发现黏滞阻尼器加固后对结构易损性的降低效果是非常明显的.

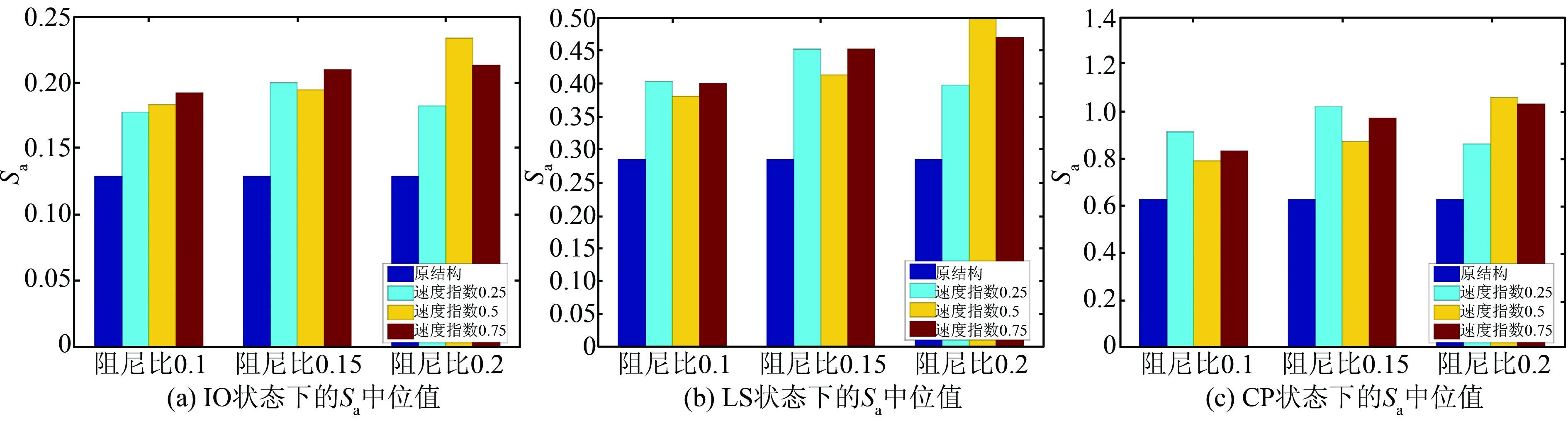
2 基于地震易损性曲线的加固方案决策

为了更直观地比较结构加固方案的优劣，取上述易损性曲线中失效概率为50%(即中位值)时对应的谱加速度Sa，并绘制出柱状图 3.

对于云图法得到的易损性曲线，在IO和CP极限状态下，对于不同的加固方案，不同结构整体阻尼比对中位值对应的Sa稍有影响，但其中的差异并不大，虽然结构整体阻尼比提高到20%时能在一定程度上进一步提升结构的抗震能力，但综合考虑对于该结构的分析结构可以看出只有α=0.5、ξeff=0.15及α=0.75、ξeff=0.15的加固方案较为符合提高结构抗震性能的预期，在易损性分析中黏滞阻尼器速度指数为0.75的加固方案稍稍优于速度指数为0.5的加固方案，但是从安全性的角度来说，速度指数达到0.75时阻尼器的力与速度关系接近于线性增长，当结构经受大地震时阻尼器可能会产生非常大的阻尼力，进而造成阻尼器自身的破坏，从而带来潜在的危害.综上所述，从最优加固方案决策的角度建议取α=0.5、ξeff=0.15，该加固方案便于设计前期预结构性能，安全合理，且阻尼器耗能减震作用发挥较好，对提高结构抗震性能的作用也非常显著.

图 2 原结构及不同加固方案结构的地震易损性曲线 Figure 2 Fragility curves of initial structure and structure retrofitted by different schemes
图选项
图 3 不同状态下谱加速度Sa的中位值比较 Figure 3 Comparison of medians of spectral acceleration between different statuses
图选项
3 结语

本文基于OpenSees平台，采用云图法对黏滞阻尼器加固非延性RC框架结构进行了研究，采用多输入IDA对加固后结构的地震易损性进行了分析，对不同方案加固的结构抗震性能进行了系统的对比分析，并对最优的加固方案进行了决策，得到以下结论:

1) 采用黏滞阻尼器加固后，非延性RC框架结构的地震易损性降低，抗震性能得到较大的提高；

2) 当加固后结构整体阻尼比ξeff的取值小于0.15时，其值越大，黏滞阻尼器的加固效果越好；

3) 当黏滞阻尼器速度指数α取值在0.25和0.75之间时，其值越大，黏滞阻尼器的加固效果越好；

4) 对于本文研究的结构，最优的黏滞阻尼器加固方案为黏滞阻尼器速度指数α取0.5，加固后结构整体阻尼比ξeff为0.15.

参考文献
[1] 王健. 黏滞阻尼器在框架结构抗震加固中的应用[D]. 北京: 北京交通大学, 2015.
Wang Jian. Application of viscous fluid damper in seismic retrofit of frame structures [D]. Beijing: Beijing Jiaotong University, 2015.
[2] 赵志刚. 桥梁黏滞阻尼器关键参数研究与优化设计[D]. 成都: 西南交通大学, 2015.
Zhao Zhigang. Research on the key parameter and optimization of bridge’s viscous damper [D].Chengdu: Southwest Jiaotong University, 2015.
[3] 杨小锋. 基于黏滞阻尼器的低层房屋减震优化设计[D]. 大连: 大连理工大学, 2015.
Yang Xiaofeng. Optimal design for seismic response reduction of low-rise buildings based on viscous dampers [D].Dalian: Dalian University of Technology, 2015.
[4] 聂利英, 郭其远, 李建中. 设置纵向大型液体黏滞阻尼器的大跨斜拉桥主梁纵向运动阻尼水平研究[J]. 工程力学, 2015, 32(9): 141–148.
Nie Liying, Guo Qiyuan, Li Jianzhong. Longitudinal damping level of girder motion of long-span cable stayed bridge with large longitudinal fluid viscous dampers[J]. Engineering Mechanics, 2015, 32(9): 141–148.
[5] 焦驰宇, 孙广龙, 陈永祁, 等. 液体黏滞阻尼器在市政桥梁抗震加固中的应用[J]. 工程力学, 2014, 31(S1): 177–181.
Jiao Chiyu, Sun Guanglong, Chen Yongqi, et al. Application of fluid viscous damper to seismic strengthening of municipal bridges[J]. Engineering Mechanics, 2014, 31(S1): 177–181.
[6] 王忱. 基于性能的RCS组合框架减震结构设计方法和易损性分析[D]. 西安: 西安建筑科技大学, 2015.
Wang Chen. Performance-based seismic design and study on seismic fragility analysis for RCS composite structure [D].Xi’an: Xi`an University of Architecture and Technology, 2015.
[7] 李宁. FRP加固非延性钢筋混凝土框架结构地震易损性分析[D]. 哈尔滨: 哈尔滨工业大学, 2014.
Li Ning. Seismic fragility analysis of non-ductile RC frame structures retrofitted with FRP [D].Harbin: Harbin Institute of Technology, 2014.
[8] 缪志伟, 宋前恩, 裘赵云. 强震作用下附设黏滞阻尼器RC框架结构的耗能机制与抗倒塌性能研究[J]. 工程力学, 2014, 31(7): 36–44.
Miao Zhiwei, Song Qian’en, Qiu Zhaoyun. Study on energy distribution and collapse-resistant capacity of RC frames with nonlinear viscous dampers under strong earthquakes[J]. Engineering Mechanics, 2014, 31(7): 36–44.
[9] 赵熹. 基于IDA方法的黏滞阻尼消能框架抗倒塌性能分析[D]. 昆明: 昆明理工大学, 2014.
Zhao Xi.Anti-collapse performance analysis of viscous damper in RC frame structure based on incremental dynamic analysis [D]. Kunming: Kunming University of Science and Technology, 2014.
[10] 陈静. 钢筋混凝土空心高墩桥梁地震易损性分析及抗震加固研究[D]. 北京: 北京交通大学, 2014.
Chen Jing.Seismic vulnerability analysis and strengthening of reinforced concrete hollow high-pier bridges [D]. Beijing: Beijing Jiaotong University, 2014.
[11] 叶生. 基于地震易损性的桥梁抗震加固优先级评定方法研究[J]. 合肥工业大学学报:自然科学版, 2013, 36(6): 733–736.
Ye Sheng. Prioritization method for seismic retrofitting of bridges based on seismic fragility curves[J]. Journal of Hefei University of Technology, 2013, 36(6): 733–736.
[12] 唐代远, 陆新征, 马玉虎, 等. 汶川地震典型教学楼附加BRB支撑防倒塌加固效果分析[J]. 灾害学, 2010, 25(S0): 157–160.
Tang Daiyuan, Lu Xinzheng, Ma Yuhu, et al. Study on the effect of strengthening a typical RC frame in Wenchuan earthquake with BRB brace[J]. Journal of Catastrophology, 2010, 25(S0): 157–160.
[13] 米莹. 基于地震易损性的非延性RC框架黏滞阻尼器加固方案决策[D]. 哈尔滨: 哈尔滨工业大学, 2014.
Mi Ying. Decision of retrofit schemes with viscous dampers for non-ductile RC frames based on seismic fragility [D].Harbin: Harbin Institute of Technology, 2014.
[14] 于晓辉, 吕大刚. 考虑结构不确定性的地震倒塌易损性分析[J]. 建筑结构学报, 2012, 33(10): 8–14.
Yu Xiaohui, Lü Dagang. Seismic collapse fragility analysis considering structural uncertainties[J]. Journal of Building Structures, 2012, 33(10): 8–14.
[15] 于晓辉, 吕大刚, 王光远. 关于概率地震需求模型的讨论[J]. 工程力学, 2013, 30(8): 172–179.
Yu Xiaohui, Lü Dagang, Wang Guangyuan. Discussions on probabilistic seismic demand models[J]. Engineering Mechanics, 2013, 30(8): 172–179.
[16] 于晓辉, 李雁军, 吕大刚, 等. 基于易损性的RC框架填充墙结构概率地震安全评估[J]. 土木工程学报, 2014, 47(S2): 260–265.
Yu Xiaohui, Li Yanjun, Lü Dagang, et al. Fragility-based probabilistic seismic safety assessment of RC frame structures with infilled masonry walls[J]. China Civil Engineering Journal, 2014, 47(S2): 260–265.
[17] Federal Emergency Management Agency (FEMA). Recommended seismic criteria for new steel moment frame buildings [R]. FEMA Publication 350, 2000.
[18] Federal Emergency Management Agency (FEMA). NEHRP guidelines for the seismic rehabilitation of buildings [R]. FEMA Publication 273, 1997.