武汉大学学报(工学版)   2016, Vol. 49 Issue (2): 212-217

文章信息

陈捷平, 杨建东, 郭文成, 滕毅
CHEN Jieping, YANG Jiandong, GUO Wencheng, TENG Yi
超长引水隧洞水电站调压室水力设计的探讨
Hydraulic design of surge tank in hydropower station with long-distance diversion tunnel
武汉大学学报(工学版), 2016, 49(2): 212-217
Engineering Journal of Wuhan University, 2016, 49(2): 212-217
http://dx.doi.org/10.14188/j.1671-8844.2016-02-009

文章历史

收稿日期: 2014-11-06
 Abstract              PDF               Figures               Tables
引用本文 0
陈捷平, 杨建东, 郭文成, 滕毅. 超长引水隧洞水电站调压室水力设计的探讨[J]. 武汉大学学报(工学版), 2016, 49(2): 212-217.
CHEN Jieping, YANG Jiandong, GUO Wencheng, TENG Yi. Hydraulic design of surge tank in hydropower station with long-distance diversion tunnel[J]. Engineering Journal of Wuhan University, 2016, 49(2): 212-217.
超长引水隧洞水电站调压室水力设计的探讨
陈捷平, 杨建东, 郭文成, 滕毅     
武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072
收稿日期: 2014-11-06
作者简介: 陈捷平(1991-)，女，硕士研究生,研究方向为水电工程，E-mail: chenjp090102@163.com.
基金项目: 国家自然科学基金资助项目(编号：51379158).
摘要: 基于超长引水隧洞水电站调压室最高涌浪限制值取决于蜗壳压力控制值这一前提，根据阻抗式、阻抗上室式和简单上室式调压室在机组甩负荷时水位波动的显示计算公式，分别推导了这3种型式调压室水力设计相关参数之间的关联表达式，同时引入临界值的概念，明确了上述3种型式调压室的适用条件.且将关联表达式应用于工程实例，进行了调压室型式的选择与水力设计参数的优化选取，探讨了超长引水隧洞水电站调压室水力设计的方法，得到了不同调压室在满足最高涌浪限制值要求时各自体型参数的选取依据.
关键词： 超长引水隧洞     调压室     最高涌浪     水力设计    
Hydraulic design of surge tank in hydropower station with long-distance diversion tunnel
CHEN Jieping, YANG Jiandong, GUO Wencheng, TENG Yi     
State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China
Abstract: Based on the premise that the highest surge limit value of surge tank in hydropower station with long-distance diversion tunnel is determined by the value of spiral case pressure, the explicit formula for calculating surges in throttled surge tank, throttled upper chamber surge tank and simple surge tank following load rejection, were combined to deduce their relevance expressions of shape parameters when restricting the highest surge, then the application condition of those three surge tanks were given. By using those expressions, the type of the surge tank in an engineering project is selected and optimized, and the hydraulic design procedures of surge tank in this kind of hydropower station are presented.
Key words: long-distance diversion tunnel     surge tank     the highest surge     hydraulic design    

随着水电事业的蓬勃发展，有的水电站由于受到地形地质条件的限制，不得不修建超长的引水隧洞.而对于西藏大拐弯水电开发，引水隧洞长度甚至达到了30 km以上.对于超长引水隧洞的界定，目前学术界和工程界尚无严格定义，在实际应用时通常将长度大于5 km的隧洞称为超长引水隧洞[1-2].

水电站引水隧洞越长，水流惯性越大，调压室涌浪的幅度越大.该类电站调节保证计算的结果往往是调压室最高涌浪水位决定了蜗壳最大动水压力，而不取决于常见的机组甩负荷时采用的导叶关闭规律[1] .为进一步说明该现象，以3个电站的实际计算结果为例进行验证，计算结果见图 1、表 1.所以设计中需要对调压室最高涌浪水位进行限制，不能超过蜗壳最大测压管水头.

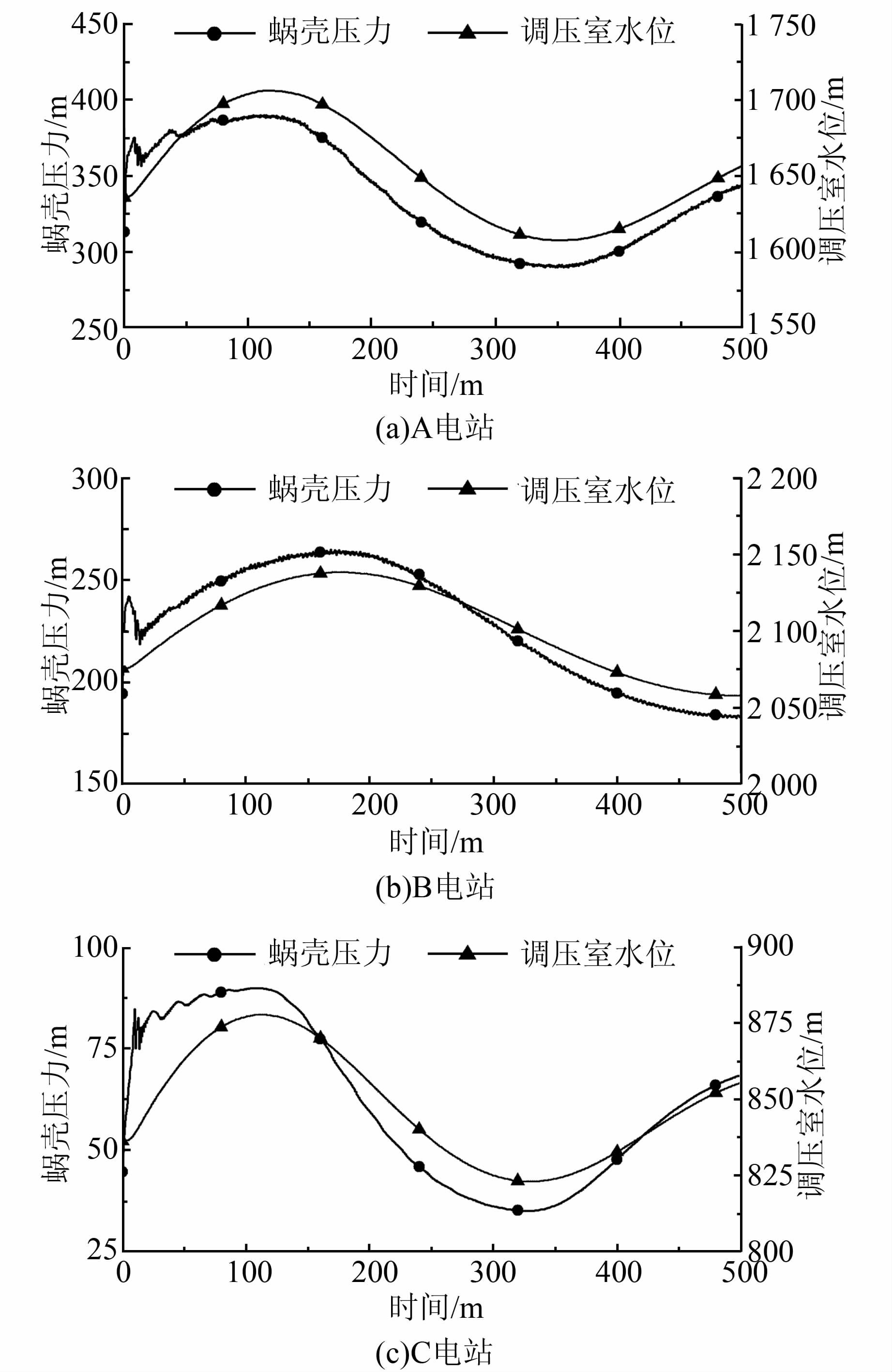
图 1 A、B、C电站蜗壳压力及调压室涌浪与时间关系图 Figure 1 Time charts about spiral case pressure and the surge of surge tank in Power Station A、B、C
图选项
表 1 电站参数及极值表 Table 1 The parameters and the extremums of power station
电站 引水隧洞长/m 蜗壳最大压力/m(发生时间/s) 调压室最高涌浪/m(发生时间/s)
A 16737.0 390.77(107.56) 1705.98(115.98)
B 16562.2 265.25(174.3) 2138.32(175.7)
C 10037.8 89.82(106.5) 877.74(111.42)
表选项

那么，采用何种型式的调压室可以减小超长引水隧洞调压室涌浪的幅度？其水力设计参数如何选取？是超长引水隧洞水电站调压室水力设计面临的关键问题.陈祥荣[2]采用仿真模拟技术，以满足调节系统稳定为取舍条件，对上调断面积作了敏感性分析；彭天枚[3]通过计算穿井压力给出了最优阻抗孔口确定的方法；高志芹[4]研究了调压室水位波动周期和导叶关闭规律对底板压差的影响；付亮[1]得到以下结论：超长引水隧洞水电站由于调压室波动周期长、衰减慢、振幅大，一般情况下其上游管线最大、最小压力分布均受到上游调压室最高、最低涌浪的控制.

尽管人们持续地关注超长引水隧洞调压室的研究，但至今仍然缺少调压室型式选择的依据以及水力设计参数的选取标准.本文根据阻抗式、阻抗上室式、简单上室式3种调压室型式的涌浪显示计算公式[5-9]，推导了调压室水力设计相关参数之间的关联表达式，提出了上述3种型式调压室的适用条件，且应用于工程实例.

1 基本方程

对超长引水隧洞水电站，采用简化的超长引水隧洞-调压室系统进行研究，示意图如图 2~4，分别表示阻抗式、阻抗上室式和简单上室式调压室.

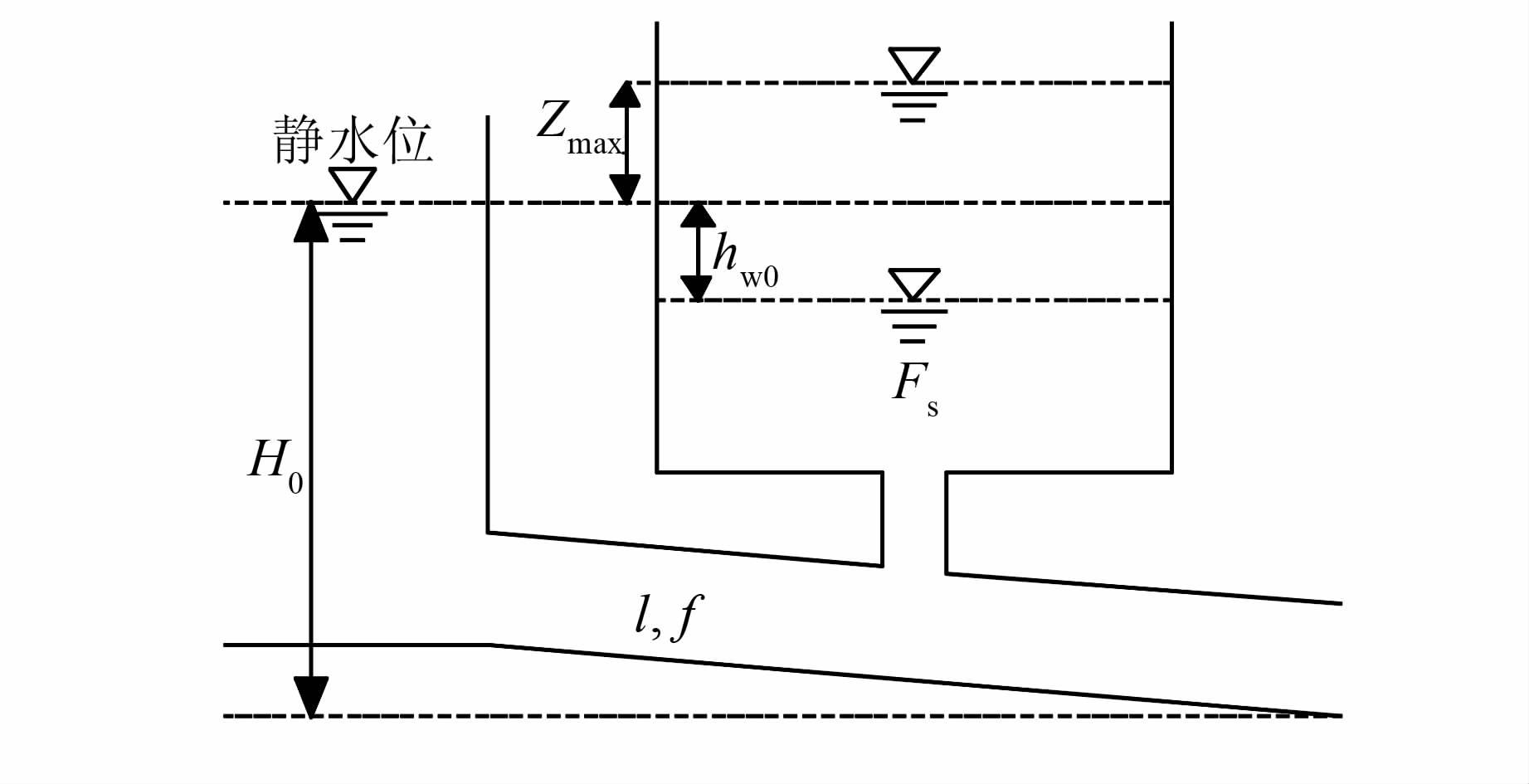
图 2 阻抗式系统示意图 Figure 2 Sketch map of throttled surge tank
图选项
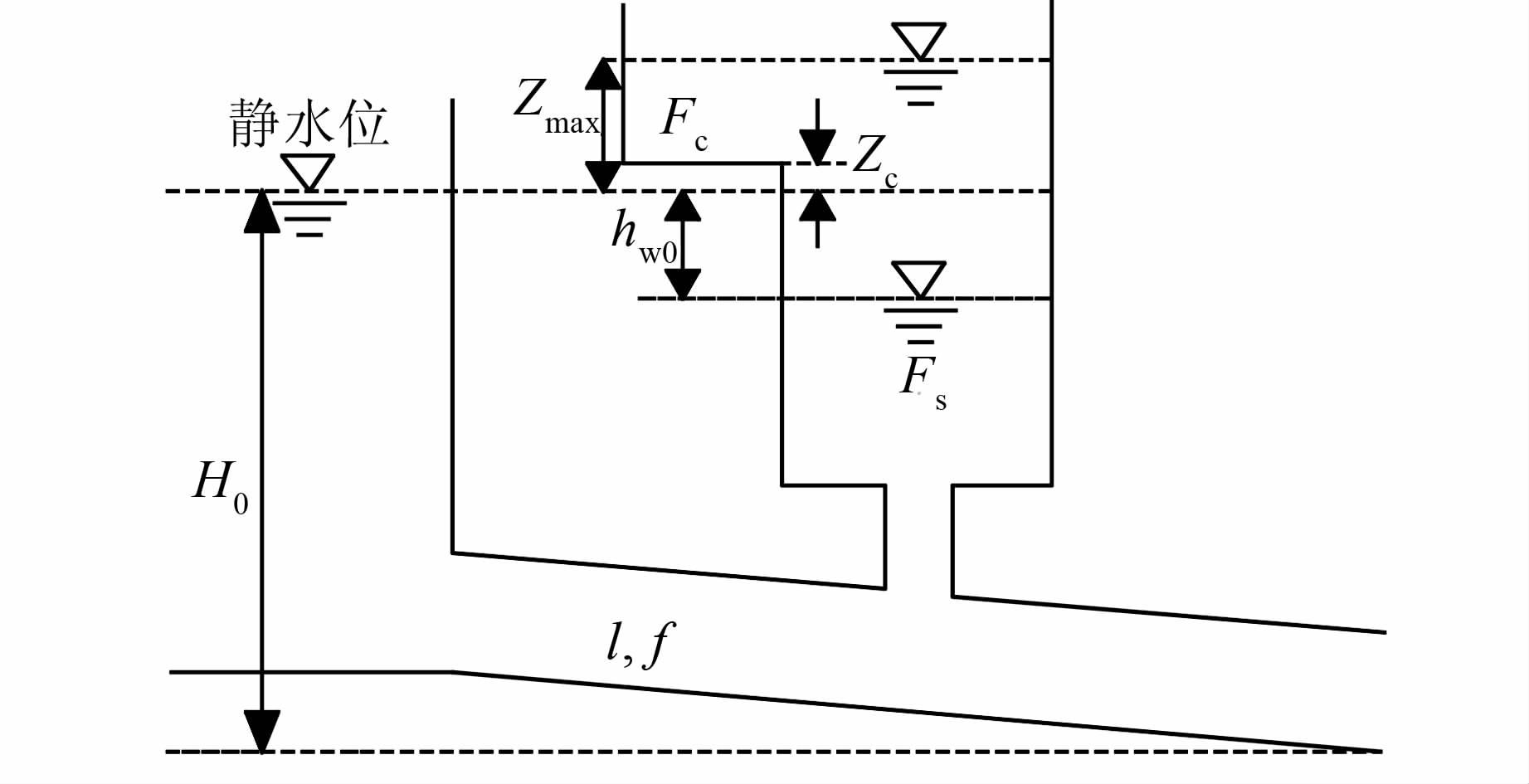
图 3 阻抗上室式系统示意图 Figure 3 Sketch map of throttled upper chamber surge
图选项
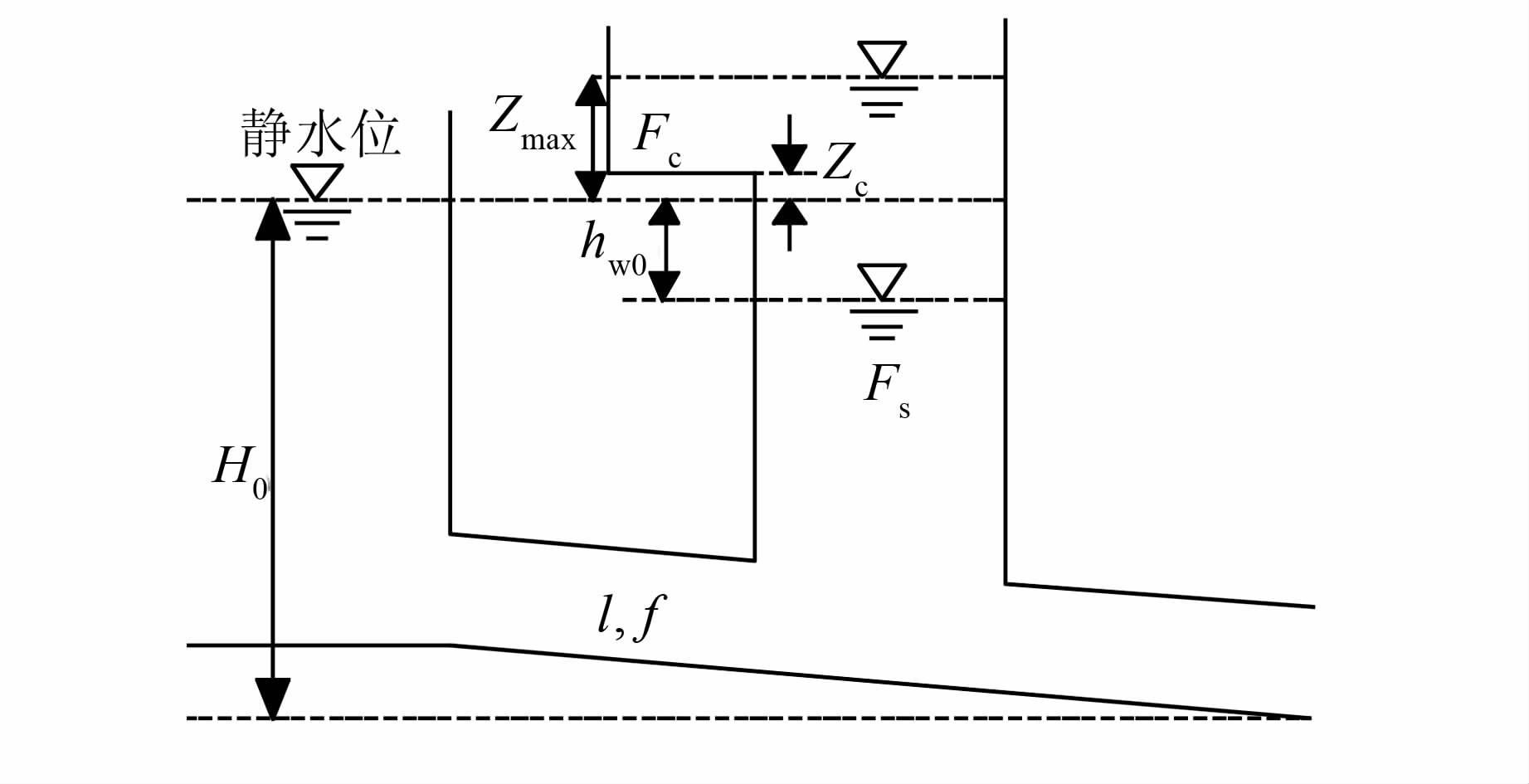
图 4 简单上室式系统示意图 Figure 4 Sketch map of simple upper chamber surge tank
图选项

1) 机组甩负荷时阻抗式调压室最高涌浪显示计算公式如下[5, 8-9]：

${Z_{\max }} = \frac{{ - {a_0}}}{{1 + \frac{{2{a_0}(\eta + 1)}}{{3\pi s}}(\pi - {\psi _0})}}$    (1)

式中：水位Z以水库静水位为基准，取向下为正；${{a}_{0}}=\sqrt{h_{w0}^{2}+{{({{{v}_{0}}f}/{{{F}_{s}}\omega }\;)}^{2}}}$；ψ0=arccos(hw0/a0)； ω02=gf/(lFs)；s=lfv2/(2gFshw0)， 表示“引水隧洞-调压室”系统特性，具有长度因次；η=hc0/hw0，称为阻抗系数,hw0和hc0分别为流量Q流经引水道和进入调压室所引起的水头损失，l、f、v0为引水道的长度、断面积、水体流速，Fs为调压室断面积.

2) 机组甩负荷时阻抗上室式调压室最高涌浪(发生在上室)计算公式同式(1)[6-7]，式中：${{a}_{0}}=\sqrt{Z_{c}^{2}+{{({{{Q}_{t={{t}_{c}}}}}/{{{F}_{c}}{{\omega }_{2}}}\;)}^{2}}}$；${{Q}_{t={{t}_{c}}}}={\sqrt{2}{{\omega }_{1}}{{F}_{s}}\sqrt{1+{{P}_{1}}{{Z}_{c}}-{{A}_{1}}{{e}^{{{P}_{1}}{{Z}_{c}}}}}}/{{{P}_{1}}}\;$(tc时刻，涌浪Z=Zc时，流入调压室的流量)；A1=(1-ηP1hw0)e-P1hw0/；s=lfv2/(2gFchw0)；ψ0=arccos(Zc/a0)；ω12=gf/(lFs)；ω22=gf/(lFc)；P1=2αgFs(1+η)/lf，Zc为上室底板相对于静水位的距离，Fs为竖井断面积，Fc为上室断面积，α为引水隧洞的水头损失系数.

3) 简单上室式调压室即为η=0时，计算公式仍然同式(1).

2 调压室水力设计相关参数的关联表达式

调压室水力设计相关参数包括阻抗孔面积S、调压室段面积Fs和Fc、调压室最高涌浪Zmax1以及上室底板位置Zc等.

对调压室最高涌浪计算公式(1)进行无量纲化处理，即令β=S/f、ns=Fs/Fth、nc=Fc/Fth、m=|Zmax|/H0、p=Zc/H0、γ=l/H0，可推导上述3种型式调压室水力设计相关参数之间的关联表达式. 其中Fth为调压室托马断面积，Fth=lf/(2αg(H0-hw0))；

由于甩负荷时调压室最高涌浪的控制工况为额定工况，故H0取为额定工况下电站静水头.

2.1 阻抗式

对于阻抗式调压室，有ψ0=arccos(hw0/a0)=π/2-hw0/a0(泰勒展开取前两项)，代入式(1)进行无量纲化，可得到

$\beta ={{\left\{ {{k}_{1}}\gamma \cdot \left[ \frac{3(1-{{k}_{2}}\gamma )}{{{n}_{s}}m}(1-\frac{\pi m+2{{k}_{2}}\gamma }{\pi \sqrt{{{{\left( {{k}_{2}}\gamma \right)}^{2}}+2{{k}_{2}}\gamma (1-{{k}_{2}}\gamma )}/{{{n}_{s}}}\;}+2{{k}_{2}}\gamma })-1 \right] \right\}}^{-{1}/{2}\;}}$    (2)

式中：k1=2gH0φ02n2/R4/3，k2=n2v2/R4/3;n为管道糙率;R为引水隧洞水力半径;φ为阻抗孔口流量系数，取0.6~0.8[10-11].

2.2 阻抗上室式

对于阻抗上室式调压室，将式中eP1(Zc-hw0) 及ψ0均进行泰勒展开，得到：

$\begin{align} & {{e}^{{{P}_{1}}({{Z}_{c}}-{{h}_{w0}})}}=1+{{P}_{1}}({{Z}_{c}}-{{h}_{w0}})+{{{\left[ {{P}_{1}}({{Z}_{c}}-{{h}_{w0}}) \right]}^{2}}}/{2}\;, \\ & {{\psi }_{0}}=\arccos \frac{{{Z}_{c}}}{{{a}_{0}}}=\frac{\pi }{2}-\frac{{{Z}_{c}}}{{{a}_{0}}} \\ \end{align}$

代入式(1)，则有：

$\left( 1-Dm \right)\sqrt{A{{p}^{2}}+Bp+C}=m\left( 1+\frac{2D}{\pi }p \right)$    (3)

式中：

$\begin{array}{l} A = 1 + \frac{{{n_s}}}{{{n_c}}}\left[ {\frac{{\eta \left( {1 + \eta } \right){n_s}{k_2}\gamma }}{{1 - {k_2}\gamma }} - 1} \right]\\ B = 2{k_2}\gamma \frac{{{n_s}}}{{{n_c}}}\left[ {1 + \eta - \frac{{\eta \left( {1 + \eta } \right){n_s}{k_2}\gamma }}{{1 - {k_2}\gamma }}} \right]\\ C = \frac{{{n_s}}}{{{n_c}}}\left[ \begin{array}{l} \frac{{\eta \left( {1 + \eta } \right){n_s}k_2^3{\gamma ^3}}}{{1 - {k_2}\gamma }} - (1 + 2\eta )k_2^2{\gamma ^2}\\ + \frac{{2{k_2}\gamma \left( {1 - {k_2}\gamma } \right)}}{{{n_s}}} \end{array} \right]\\ D = \frac{{\left( {1 + \eta } \right){n_c}}}{{3\left( {1 - {k_2}\gamma } \right)}},\eta = \frac{{{h_{c0}}}}{{{h_{w0}}}} = \frac{1}{{{\beta ^2}{k_1}\gamma }} \end{array}$
2.3 简单上室式

对于简单上室式调压室，同式(3)，大井不设阻抗孔，则有阻抗系数η=0. 式中：$A=1-\frac{{{n}_{s}}}{{{n}_{c}}}$，$B=2{{k}_{2}}\gamma \frac{{{n}_{s}}}{{{n}_{c}}}$， $C=\frac{{{n}_{s}}}{{{n}_{c}}}\left[ -k_{2}^{2}{{\gamma }^{2}}+\frac{2{{k}_{2}}\gamma \left( 1-{{k}_{2}}\gamma \right)}{{{n}_{s}}} \right]$，$D=\frac{{{n}_{c}}}{3\left( 1-{{k}_{2}}\gamma \right)}$ .

3 对比分析及适用条件 3.1 对比分析

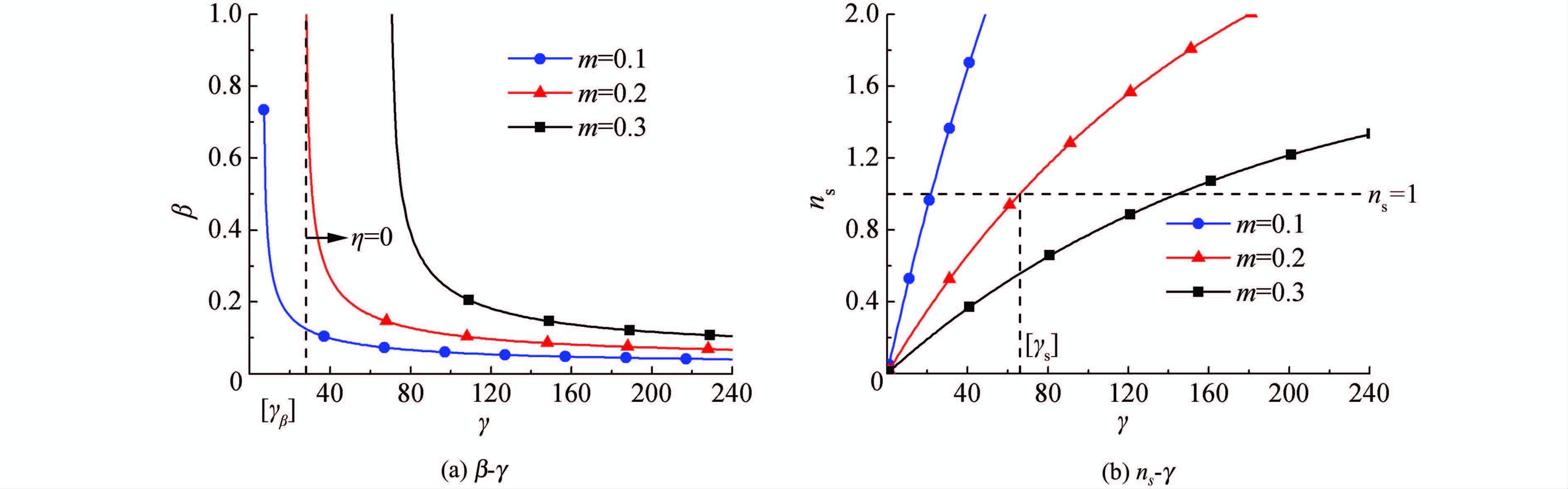
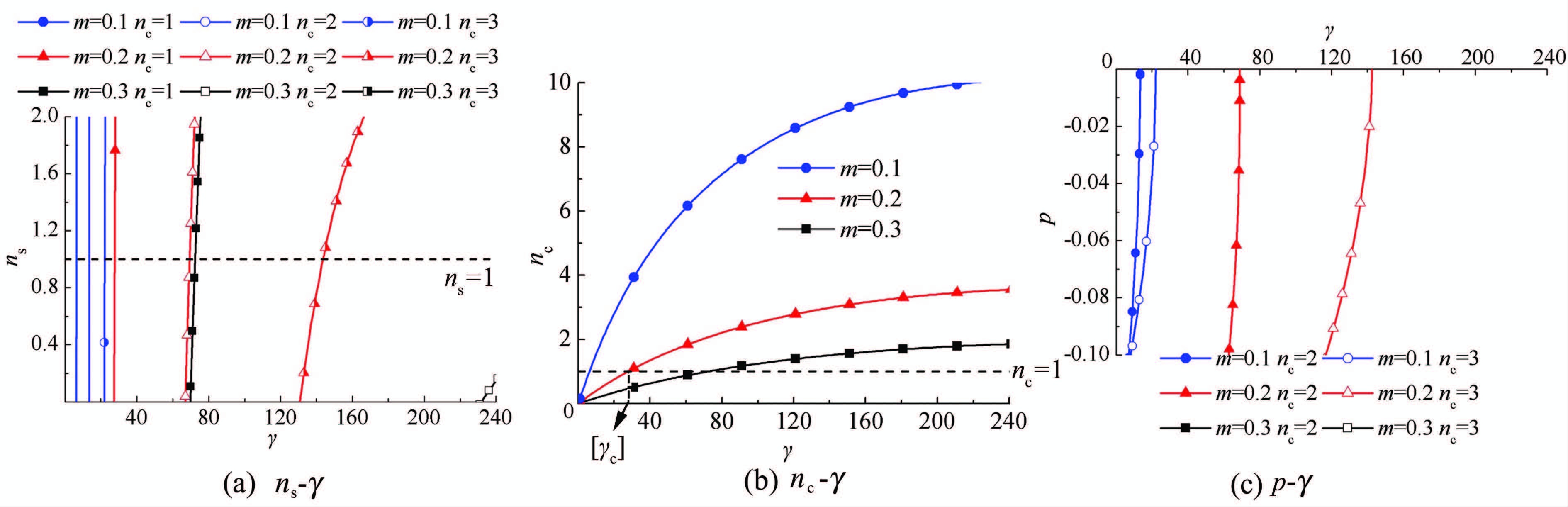
采用控制变量法分析上述3种型式调压室水力设计相关参数之间的关联，统一以γ为横坐标，绘制γ与其他参数之间的关系曲线.绘制中，设基准值：k1=0.145，k2=7.635×10-4；默认变量：ns=1，β=0.15，p=0.由于调压室最高涌浪限制值取决于蜗壳压力控制值，m一般在0.2~0.3之间，故m依次取0.1、0.2、0.3绘图，以便分析.

绘制结果如图 5~7所示，分别表示阻抗式、阻抗上室式和简单上室式.对比分析如下：

图 5 阻抗式调压室 Figure 5 Throttled surge tank
图选项
图 6 阻抗上室式调压室 Figure 6 Throttled upper chamber surge tank
图选项
图 7 简单上室式调压室 Figure 7 Simple upper chamber surge tank
图选项

1) 相同条件下，随着γ的增大或m的减小或nc的减小，β逐渐减小.该结果说明当其他条件不变时，引水隧洞长度的增长、调压室最高涌浪控制标准的提高以及上室面积的减小(当减小至与大井相同nc=ns=1时，即无上室)，都需减小阻抗孔面积.在此须指出：随着γ的增大会使得沿程水头损失增大，当水头损失超过水头(hw0/H0>1)修建水电站则毫无意义，故必须对γ进行限制.一般情况下k2γ=hw0/H0<0.2，即γ=0.2/k2时，可得到β的最小值.β值太小有可能产生“水击穿井”问题，本文暂不考虑该问题，在后续研究中进一步论证.

2) 相同条件下，随着γ的增大或m的减小，ns逐渐增大.该结果表明当其他参数不变时，引水隧洞的增长以及调压室最高涌浪控制标准的提高都要求调压室大井面积适当增大；而对于带上室的调压室，nc增大也可起到同样的作用.但m和nc较小时，ns变化相当敏感，接近垂直直线，见图 6(b)和图 7(a).随着m和nc增大，ns曲线表现出了一定的抛物线弧度.对于最高涌浪发生在上室的调压室，大井的作用相对上室是较弱的，增加大井面积作用不大，一般取ns=1~1.2即可.

3) 对于上室nc，相同条件下γ增大或者m减小，所需nc也增大.对于上室底板位置p(p<0表示在静水位以上，不考虑设置在静水位以下的位置)，可看到p较小时曲线是接近垂直的，逐渐增大时，曲线末端开始弯曲，见图 6(d)和图 7(c).当m不变时，垂直段p可以有多种取值，且均不影响对最高涌浪的控制.于是当γ较小时，p值不宜过大，故选取时应取垂直段的p值，即在0~-0.02范围内即可.

4) 临界值的确定

(a) η=0时，调压室即无阻抗孔，代入式(2)及式(3)，解记为γβ.γ=γβ即为β-γ曲线的竖直渐近线，见图 5(a)和图 6(a).当引水隧洞γ≤γβ时，可不设阻抗孔.

(b) ns=1时，代入式(2)及式(3)，解记为γs.当γ≤γs时，调压室断面积应取ns=1；当γ>γs时，一般取ns=1~1.2.

(c) nc=1时，应有ns=1，即无上室，代入式(2)，解记为γc.当引水隧洞γ≤γc时，应取nc=1，此时可不设上室；当γ>γc时，nc根据计算取值.可发现阻抗上室式的γc大于阻抗式的γs，是由阻抗和上室共同作用的结果.

3.2 3种型式调压室的适用条件

由上述的临界值可以得到阻抗式、阻抗上室式、简单上室式3种型式调压室的适用条件，如表 2所示.

表 2 3种型式调压室的适用条件 Table 2 The application conditions of three types of surge tank
前提假设 判别条件 推荐的调压室类型
式(2) ns=1 γ≤[γs]
γ>[γs]		 阻抗式、简单式
阻抗上室式、简单上室式
式(3) η=0 γ≤[γβ]
γ>[γβ]		 简单上室式、简单式
阻抗式、阻抗上室式
注：① 通常情况下k2γ=hw0/H0<0.2；② 一般情况下ns取1~1.2；p取0~-0.02.
表选项
4 工程实例

已知某超长引水隧洞-调压室系统：H0=300 m，Q0=90 m3/s，f=30 m2，φ=0.7，n=0.014，γ=100.控制调压室最高涌浪m=0.2时调压室如何选取？

首先计算临界值：

令式(2)ns=1(β=0.2)：[γs]=36，γ>[γs]，故需设置上室.

令式(3)η=0(ns=1，nc=2，p=0)：[γβ]=60.35，γ>[γβ]，需设置阻抗孔，故选择阻抗上室式调压室.

若令式(3)η=0(ns=1，nc=3，p=0)：[γβ]=125.33，γ<[γβ]，则不需设置阻抗孔，为简单上室式调压室.

其次，比较阻抗上室式和简单上室式，在考虑经济因素及地质条件下选择上室面积较小的阻抗上室式.

由于大井面积与上室底板高程影响较小，故设初始时ns=1，p=0，则绘制β~nc曲线，如图 8所示.最后，选取符合要求的调压室水力设计参数：nc=2，β=0.2可满足m=0.2的要求.

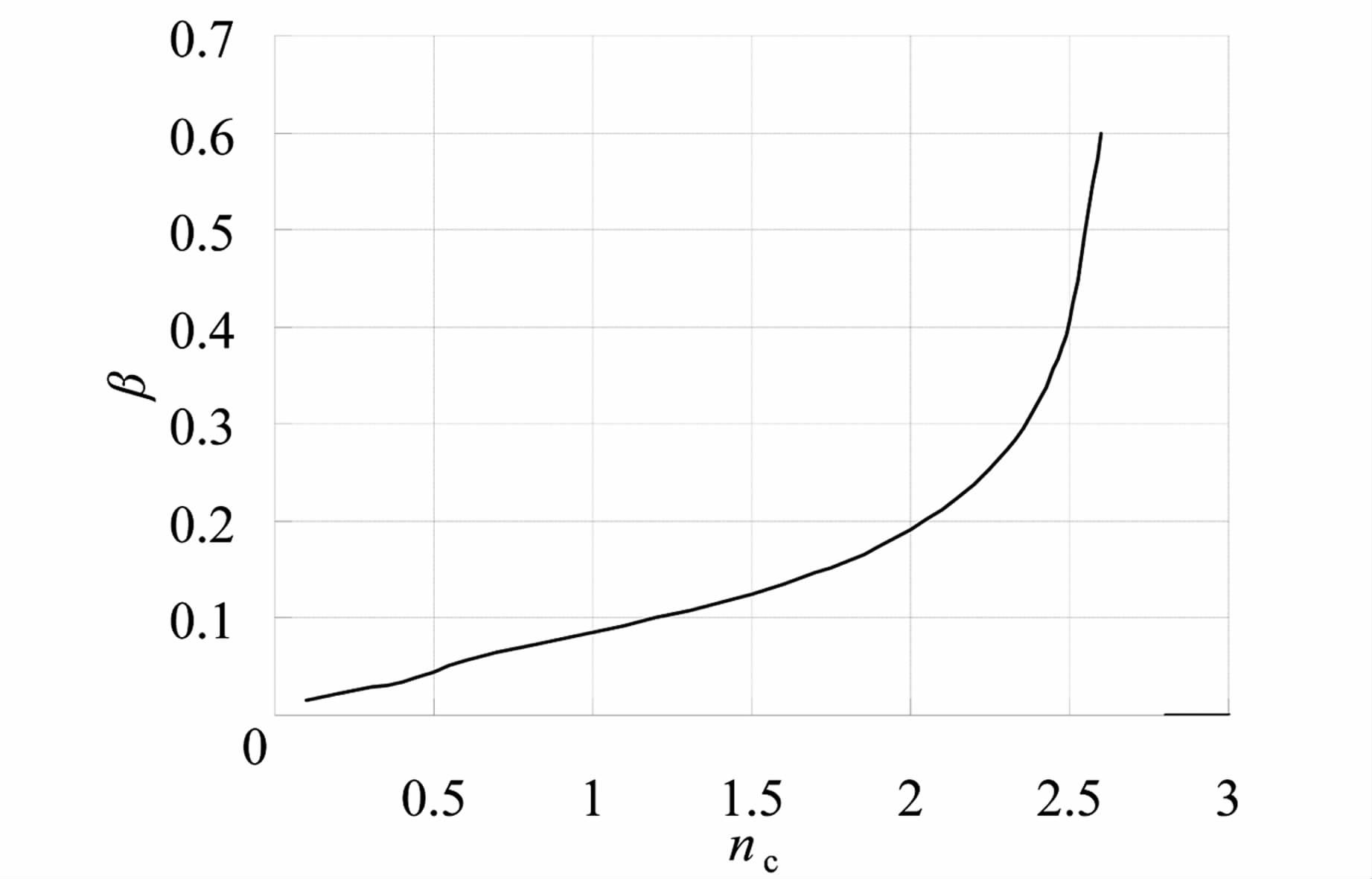
图 8 阻抗上室式β-nc关系曲线 Figure 8 The relation curve about β and nc
图选项

综上所述，该工程调压室型式为阻抗上室式，其主要的水力设计参数β=0.2，ns=1，nc=2，p=0.

5 结论

本文通过对阻抗式、阻抗上室式及简单上室式调压室甩负荷时限制最高涌浪计算的显示公式进行了无量纲处理，得到了调压室水力设计相关参数之间的关联表达式 (2)及式(3)，通过对该关系式的分析计算，得到了如下结论：

1) 采用临界值并结合地形地质及经济因素，可选取超长引水隧洞水电站应使用的调压室类型；

2) 若超长引水隧洞水电站采用阻抗式调压室，与较短引水隧洞水电站(β=0.3~0.4)相比，其阻抗面积要偏小，通常β=0.2左右，为规范规定的偏小值(规范规定的β的范围为0.15~0.5[15])；

3) 设有上室的调压室，其大井面积及上室底板位置相对于阻抗面积及上室面积的作用小得多，故可以直接假定初始值ns=1~1.2，p=0~-0.02，再根据关联表达式(2)及式(3)计算确定调压室其他水力设计参数.

参考文献
[1] 付亮, 杨建东, 王建伟. 超长引水隧洞水电站大波动过渡过程特殊问题[J]. 中国农村水利水电, 2006(9): 112–114.
Fu Liang, Yang Jiandong, Wang Jianwei. Special problems of large oscillation transient process of hydropower station with long-distance diversion tunnel[J]. China Rural Water and Hydropower, 2006(9): 112–114.
[2] 陈祥荣. 长引水洞电站系统调节稳定性分析计算[J]. 红水河, 1998(1): 45–49.
Chen Xiangrong. Stability analysis and caculation of long water diverting tunnel for hydropower system regulation[J]. Hongshui River, 1998(1): 45–49.
[3] 彭天玫, 杨效亮. 阻抗式调压井穿井压力计算及最优阻抗孔口的研究[J]. 水力发电学报, 1986(3): 61–76.
Peng Tianmei, Yang Xiaoliang. Calculation of water-hammer transmission of throttled surge chamber and study on its optimum size of orifice[J]. Journal of Hydroelectric Engineering, 1986(3): 61–76.
[4] 高志芹, 吴余生. 阻抗式调压室底板压差的影响因素分析[J]. 云南水力发电, 2008(2): 25–28.
Gao Zhiqin, Wu Yusheng. Influence factor analysis of throttled surge chamber bottom plate pressure difference[J]. Yunnan Water Power, 2008(2): 25–28.
[5] 张健, 索丽生. 阻抗式调压室甩负荷涌浪计算显式公式[J]. 水力发电学报, 1999(2): 70–74.
Zhang Jian, Suo Lisheng. Explicit formula for calculating surges in throttled surge tank following load rejection[J]. Journal of Hydroelectric Engineering, 1999(2): 70–74.
[6] 李高会, 张健, 齐央央, 等. 阻抗上室调压室突弃全负荷时涌浪的解析解[J]. 水电能源科学, 2009, 27(3): 56–57.
Li Gaohui, Zhang Jian, Qi Yangyang. Analytical solution for surges in throttled upper chamber surge tank following load rejection[J]. Water Resources and Power, 2009, 27(3): 56–57.
[7] Li Gaohui, Jiang Hongjun, Zhang Jian, Chen sheng. The explicit solution to calculate maximum upsurge in water chamber surge tank under superposed condition[C]// 2013 2nd International Conference on Mechanical Engineering, Industrial Electronics and Informatization (MEIEI 2013). Chongqing: Atlantis Press, 2013:392-395.
[8] 张永良, 缪明非. 组合工况下阻抗式调压室涌浪计算的显式公式[J]. 水利学报, 2012(4): 467–472.
Zhang Yongliang, Miu mingfei. Experimental investigation on pressure fluctuations in suction chamber and volute of a double-suction centrifugal pump[J]. Journal of Hydraulic Engineering, 2012(4): 467–472.
[9] 张志昌, 刘松舰, 刘亚菲. 阻抗式和简单调压室甩负荷时水位波动的显示计算方法[J]. 应用力学学报, 2004, 21(1): 50–55.
Zhang Zhichang, Liu Songjian, Liu Yafei. Explicit formula for calculating surges in throttled and simple surge tank following load rejection[J]. Chinese Jounal of Applied Mechanics, 2004, 21(1): 50–55.
[10] 刘启钊, 彭守拙. 水电站调压室[M]. 北京: 水利电力出版社, 1995.
Liu Qizhao, Peng Shouzhuo. Surge Chamber for Hydropower Station[M]. Beijing: China Hydro&Power Press, 1995.
[11] 刘启钊. 水电站(第3版)[M]. 北京: 中国水利水电出版社, 2007.
Liu Qizhao. Hydropower Station (the third edition)[M]. Beijing: China Water Power Press, 2007.
[12] 季奎, 马跃先, 王世强, 等. 调压室大波动稳定断面研究[J]. 水利学报, 1990(5): 45–51.
Ji Kui, Ma Yuexian, Wang Shiqiang. Study on the large surge wave stability area of surge tank[J]. Journal of Hydraulic Engineering, 1990(5): 45–51.
[13] 董兴林. 水电站调压井稳定断面问题的研究[J]. 水利学报, 1980(4): 37–48.
Dong Xinglin. Study on the stable cross-sectional area of surge tank[J]. Journal of Hydraulic Engineering, 1980(4): 37–48.
[14] 洪振国. 水电站调压井形式比选研究[J]. 中国农村水利水电, 2013(4): 113–115.
Hong Zhenguo. Research on comparison and selection of hydropower station shaft types[J]. China Rural Water and Hydropower, 2013(4): 113–115.
[15] 中华人民共和国电力工业部. Specifications for Design of Surge Chamber of Hydropower Stations[M]. Beijing: China Power Press, 1997.