武汉大学学报(工学版)   2016, Vol. 49 Issue (5): 648-653

文章信息

张洁, 胡金政, 马建增, 王贺, 丁金伟
ZHANG Jie, HU Jinzheng, MA Jianzeng, WANG He, DING Jinwei
基于多元分析的花岗岩残积土物理力学性质概率分布模型
Probabilistic model for mechanical properties of completely decomposed granite based on multivariate analysis
武汉大学学报(工学版), 2016, 49(5): 648-653
Engineering Journal of Wuhan University, 2016, 49(5): 648-653
http://dx.doi.org/10.14188/j.1671-8844.2016-05-002

文章历史

收稿日期: 2016-05-16
 Abstract              PDF               Figures               Tables
引用本文 0
张洁, 胡金政, 马建增, 王贺, 丁金伟. 基于多元分析的花岗岩残积土物理力学性质概率分布模型[J]. 武汉大学学报(工学版), 2016, 49(5): 648-653.
ZHANG Jie, HU Jinzheng, MA Jianzeng, WANG He, DING Jinwei. Probabilistic model for mechanical properties of completely decomposed granite based on multivariate analysis[J]. Engineering Journal of Wuhan University, 2016, 49(5): 648-653.
基于多元分析的花岗岩残积土物理力学性质概率分布模型
张洁1, 胡金政1, 马建增1, 王贺1, 丁金伟2     
1. 同济大学地下建筑与工程系，上海 200092;
 2. 中国能源建设集团广东省电力设计研究院，广东 广州 510663
收稿日期: 2016-05-16
作者简介: 张洁(1980-)，男，副教授，博士生导师，研究方向为岩土和地下工程灾害和风险分析及控制，E-mail：cezhangjie@tongji.edu.cn.
基金项目: 国家自然科学基金（编号：41372275）.
摘要: 基于533组花岗岩残积土土样的土工试验数据，研究了花岗岩残积土黏聚力、内摩擦角、压缩系数与常见物理指标之间的相关关系，分别采用经验方法和主成分分析方法建立了花岗岩残积土力学性质的联合概率密度函数.研究表明，花岗岩残积土黏聚力的离散性很大，难以准确预测.和黏聚力相比，内摩擦角和压缩系数的可预测性更强，内摩擦角和压缩系数之间存在一定的负相关性，黏聚力和内摩擦角、压缩系数的相关性较弱.采用经验法和主成分分析法建立的联合概率密度函数类似，验证了所提出的概率模型的可靠性.
关键词： 花岗岩残积土     土体参数     多元分析     概率统计分析    
Probabilistic model for mechanical properties of completely decomposed granite based on multivariate analysis
ZHANG Jie1, HU Jinzheng1, MA Jianzeng1, WANG He1, DING Jinwei2     
1. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China;
 2. Guangdong Electric Power Design Institute, China Energy Engineering Group Co., Ltd., Guangzhou 510663, China
Abstract: Based on 533 sets of laboratory test data, this paper studies the relationship between the total cohesion, friction angle, and the coefficient of compressibility and physical parameters of the completely decomposed granite. Probabilistic models are then constructed based on an empirical method and the principal component analysis method. It is found that the apparent cohesion is very difficult to predict. Compared with the total cohesion, the friction angle and the coefficient of compressibility is easier to predict. The friction angle is negatively correlated with the coefficient of compressibility. The correlation between the total cohesion and the friction angle as well as the correlation between the total cohesion and the coefficient of compressibility are quite weak. The probabilistic models constructed based on the empirical method and the principle component analysis method are quite similar, so as to verify the reliability of the constructed models.
Key words: completely decomposed granite     soil parameters     multivariate analysis     probabilistic assessment    

花岗岩残积土广泛分布于我国的东部沿海地区.在福建、广东等省份，花岗岩残积土层厚度最大可达40 m[1].由于风化条件和风化程度的不同，花岗岩残积土表现出较强的变异性.在这些地区，花岗岩残积土的性质对岩土工程设计和施工有重要影响.

Lumb[2]分析研究了香港地区花岗岩残积土的性质；戴继等[1]比较了中国多个地区的花岗岩残积土性质之间的差异性；杨树俊等[3]基于深圳地铁工程的勘察数据，分析了深圳地区花岗岩残积土物理力学参数的统计特性；梁仕华等[4]对广州东部地区花岗岩残积土物理力学指标进行了统计分析，建立了花岗岩残积土力学性质的一元回归公式；陈洪江等[5]对我国东南沿海地区花岗岩残积土的九项指标进行了统计分析，获得了部分参数的一元回归方程；Hu等[6]采用单因素分析方法研究了花岗岩残积土常见物理力学性质之间的相关性.

上述研究为增进对花岗岩残积土物理力学性质的理解起到了重要的作用.由于花岗岩残积土变异性强，非常适合采用可靠度理论对其进行分析.陈洪江等[7]根据我国东南沿海地区花岗岩残积土的土工试验资料，进行了内摩擦角、黏聚力等8项指标的概率分布检验，得出各项指标大都可用对数正态或正态分布函数拟合的结论.不足的是，该文没有考虑花岗岩残积土力学性质与其他参数之间的相关性，也没有考虑不同力学参数之间的相关性.目前，花岗岩残积土力学参数概率模型方面的研究还较为少见.

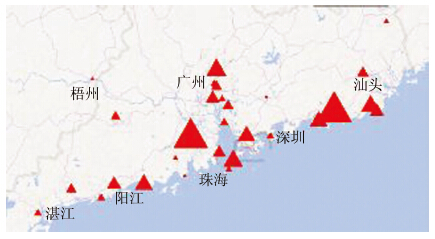
1 花岗岩残积土土样数据库

为系统建立花岗岩残积土力学参数的概率分布模型，本文搜集了总计533个花岗岩残积土土样的土工试验数据，数据包括土的颗粒级配数据、含水率、饱和度、界限含水率等物理指标参数，以及压缩系数、黏聚力、内摩擦角等力学指标参数，其中，黏聚力和内摩擦角由室内直剪试验得出.土样的取土地点大部分位于广东省，取土地点的分布如图 1所示.其中三角形的大小标志了样本数量的大小.

图 1 数据库土样取土地点分布 Figure 1 The places where soil samples were taken
图选项

数据库中各指标的统计参数如表 1、2所示.本文的回归分析中，均采用如表 1、2所示的量纲.可知，对于颗粒比重、天然密度、干密度等指标，变异性都不大，变异系数在10%以内.其他指标的变异性相对较大.本文获得的花岗岩残积土变异性较Lan等[8]报道的花岗岩残积土变异性更大，这可能是因为Lan等[8]数据主要来自深圳地区的花岗岩残积土，而本文使用的数据涵盖地区更广.

表 1 各指标统计参数 Table 1 Basic descriptive statistics of soil samples
指标 含水率w/% 颗粒比重Gs 天然密度ρ/ (g·cm-3) 干密度ρd/(g·cm-3) 饱和度Sr/% 孔隙比e0 液限wL/% 塑限wP/% 塑性指数IP /% 液性指数IL 压缩系数a/MPa-1 压缩模量Es/MPa 黏聚力c/kPa 内摩擦角 φ/(°)
范围 10.4~52.5 2.66~2.76 1.41~2.12 1.11~1.83 40~100 0.47~1.48 22~65.6 12.4~44.36.9~28.8 -1.72~1.35 0.157~1.223 1.94~10.31 1.6~89.7 4.9~43.1
均值 26.18 2.72 1.84 1.46 81.99 0.88 39.77 26.3913.38 -0.02 0.44 4.54 14.59 29.54
变异系数/% 24.4 0.6 5.6 8.4 13.9 18.6 18.3 18.9 26.4 2023.0 29.5 25.9 77.9 17.1
表选项
表 2 颗粒级配统计参数 Table 2 Basic descriptive statistics of particle gradation
颗粒 砾石及更大S1/%>2 mm 粗砂S2/%0.5~2 mm 中砂S3/%0.25~0.5 mm 细砂S4/%0.075~0.25 mm 粉土及黏土S5/% <0.075 mm
范围 0~66.2 1.3~36.2 2.2~32.6 1.9~36.4 3.8~88.9
均值 20.89 16.45 9.73 9.41 43.49
变异系数/% 65.4 37.7 55.3 57.4 29.2
表选项
2 基于经验方法的花岗岩残积土力学参数概率分布模型 2.1 基本变量的选取

颗粒组成往往对土的内部结构的形成起到重要作用，从而对花岗岩残积土的性质产生影响.赵建军等[9]的花岗岩残积土土样数据取自香港地区，发现内摩擦角与颗粒组成具有显著的相关关系.本文选取了表 2中颗粒级配指标作为回归分析的基本变量.由于5个颗粒级配分数之和为100%，5个参数是线性相关的，因此在做线性回归分析时，只取用其中4个，本文取用前4个，即S1、S2、S3及S4.

在界限含水率指标中,塑性指数是土的一项重要综合指标，特别是对于黏性土.例如，Ibrahim等[10]基于取自马来西亚玻璃市州的红土层的土样数据，发现塑性指数和压缩系数之间存在较强的相关关系.Jaie等[11]基于取自印度多个河谷的土样，发现塑性指数和土样的压缩性之间也具有强相关性.本文也选取塑性指数作为一项基本变量.

此外，水对土体的物理力学性质具有较大的影响，本文也选取含水率w作为一项基本变量.土样的干密度往往也会反映出土样的压密状态，对土体的力学性能也有重要影响.本文也将干密度ρd作为一项基本变量，基于以上分析，经验分析方法中选择w、ρd、IP、S1、S2、S3以及S4为基本变量.基于来自伊朗西部哈马丹省的200份包括表层覆土、次深层覆土的土样土工试验数据，Khanlari等[12]将颗粒级配组成、塑性指数、天然密度作为基本变量，进行了多元线性回归分析，直接对黏聚力和内摩擦角进行预测.本文也做了类似的分析.

在分析中发现，使用天然密度和干密度的结果差别不大.主要是由于二者具有较高的相关性，二者的相关系数为0.84.表 3为使用本文介绍的经验选取基本变量方法，分别取用天然密度和干密度分析的结果对比，其中r为回归相关系数，σ为回归残余误差的标准差.在下文的分析中，使用干密度作为基本变量.

表 3 分别使用干密度和天然密度分析结果对比 Table 3 Comparison between results from dry density and wet density
预测变量 干密度ρd 天然密度ρ
r σ r σ
黏聚力c 0.27 0.71 0.27 0.71
内摩擦角φ 0.52 0.18 0.52 0.18
压缩系数a 0.72 0.20 0.72 0.21
表选项
2.2 力学指标的回归预测模型

为方便表述，令δ={c,φ,a},θ=lnd={θ1,θ2,θ3}={lnc,lnφ,lna}.采用线性回归方法建立了黏聚力与基本变量的关系如下：

$\begin{align} & {{{\hat{\theta }}}_{1}}=\text{ }5.1802-0.0432w-1.4168{{\rho }_{\text{d}}}+0.0248{{I}_{\text{P}}} \\ & +0.01(2.3206{{S}_{1}}-0.9483{{S}_{2}}+2.5960{{S}_{3}}+0.1418{{S}_{4}}) \\ \end{align}$    (1)

其中：1为θ1的回归方程预测值.

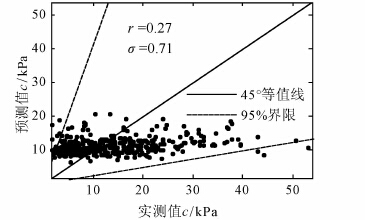
图 2给出了黏聚力预测值与试验值对比散点图以及公式(1)中相关系数r和标准差σ，由图可知，预测值与实测值之间的相关性较弱.Wesley[13]指出，相比较沉积土，花岗岩残积土复杂的结构对其性质影响更大.戴继等[1]也指出，花岗岩残积土在各向异性、扰动性等方面具有与一般黏性土不同的性质.图 2中实测值与回归方程预测值相关性较弱，这可能是因为黏聚力受到结构性等其他因素的影响较大，但这些因素无法纳入回归方程考虑的缘故.

图 2 黏聚力预测值与试验值对比散点图 Figure 2 Relationship between predicted and observed values of cohesion
图选项

采用多元回归分析，获得内摩擦角与基本变量的关系如下所示：

$\begin{align} & {{{\hat{\theta }}}_{2}}=\text{ }4.0956-0.0160w-0.1539{{\rho }_{\text{d}}}-0.0066{{I}_{\text{P}}} \\ & +0.01(-1.3319{{S}_{1}}+0.1611{{S}_{2}}+0.2702{{S}_{3}}-0.3969{{S}_{4}}) \\ \end{align}$    (2)

其中:${\hat{\theta }}$2为θ2的回归方程预测值.

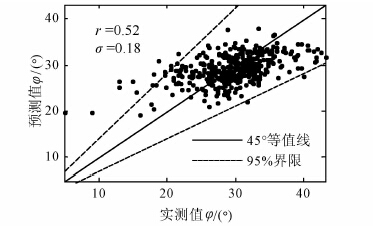
图 3给出了内摩擦角实测值与回复方程预测值之间的散点图，以及回归方程(2)的相关系数及残余误差的标准差.由图可知，内摩擦角与基本变量的相关性较黏聚力与基本变量的相关性要强，说明内摩擦角具有更强的可预测性.

图 3 内摩擦角预测值与试验值对比散点图 Figure 3 Relationship between predicted and observed values of friction angle
图选项

基于多元回归分析，获得压缩系数与基本变量的关系如下：

$\begin{align} & {{{\hat{\theta }}}_{3}}=\text{ }1.5597-0.0022w-1.6942{{\rho }_{\text{d}}}-0.0091{{I}_{\text{P}}} \\ & +0.01(0.3268{{S}_{1}}+0.0731{{S}_{2}}-0.1057{{S}_{3}}-0.1500{{S}_{4}}) \\ \end{align}$    (3)

其中:3为θ3的回归方程预测值.

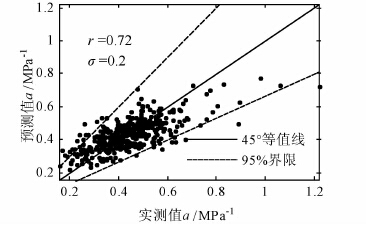
压缩系数预测值与试验值对比散点图如图 4所示.图 4还给出了回归方程(3)的相关系数和回归误差.与黏聚力和内摩擦角相比，压缩系数回归方程的相关性最强，说明其可预测性最强.

图 4 压缩系数预测值与试验值对比散点图 Figure 4 Relationship between predicted and observed values of coefficient of compressibility
图选项

Khanlari等[12]研究中关于黏聚力和内摩擦角的回归方程的相关系数分别为0.818和0.890.而本文获得的黏聚力和摩擦角的回归方程的相关系数分别为0.27和0.52.本文结果相关系数较低，一方面这体现了花岗岩残积土相比较一般黏性土具有一定的特殊性；另一方面，本文数据库样本数较多对此也有影响.黏聚力的相关性较低，这可能是因为花岗岩残积土因其原址风化成因,内部结构具有不均匀性、各向异性等特殊性[1]，而黏聚力受内部结构性因素影响比较大，这一因素常常难以定量描述.

戴继等[14]通过压缩试验推断，花岗岩残积土的结构性强弱与其粗颗粒(粒径> 0.5 mm，即本文中S1和S2)含量有关.从本文获得的压缩系数的回归分析来看，粗颗粒含量高则压缩系数更大，与戴继等[14]得出的结论一致.

2.3 不同力学指标之间的相关性分析

令ei=θi-${\hat{\theta }}$i代表实测值与回归方程预测值之间的残差，利用εik代表对应于θi的第k项残差.θi、θj回归方程残差之间的相关系数可按下式计算：

${{r}_{ij}}=\left( \sum\limits_{k=1}^{n}{{{\varepsilon }_{ik}}{{\varepsilon }_{ik}}} \right)/\left( \sqrt{\sum\limits_{k=1}^{n}{\varepsilon _{\text{ik}}^{2}}}\sqrt{\sum\limits_{k=1}^{n}{\varepsilon _{\text{jk}}^{2}}} \right)$    (4)

其中:n为样本容量，即本文数据库中的土样数.

令r12、r13、r23分别代表回归方程(1)和(2)、(1)和(3)以及(2)和(3)残差之间的相关性.这3个系数分别代表了黏聚力与内摩擦角、黏聚力与压缩系数以及内摩擦角与压缩系数之间的相关性.基于方程(4)，可得：r12=-0.14,r13=-0.31,r23=-0.15.相关性分析显示，黏聚力与压缩系数之间存在较强的相关性，而黏聚力与其他两个强度参数之间的相关性较弱.

2.4 花岗岩残积土力学参数概率分布模型

建立力学指标随机分布模型，可为岩土工程可靠度分析提供依据.陈洪江等[7]根据我国东南沿海地区花岗岩残积土的土工试验资料，进行了内摩擦角、黏聚力等8项指标的概率分布检验，得出各项指标大都可用对数正态或正态分布函数拟合的结论.在岩土工程中，常假设力学参数服从多元对数正态分布.基于这一假设，θ服从多元正态分布，即δ～LN3(μθ,Cθ).θ的均值和标准差可由回归分析方程确定，即μθ = $\left\{ \ln \hat{c},\ln \hat{\varphi },\ln \hat{a} \right\}$，σθ = {0.71,0.18,0.2}.基于不同力学指标之间的相关性分析，θ的相关系数矩阵为

${{\mathbf{R}}_{\text{ }\!\!\theta\!\!\text{ }}}\text{ }=\left( \begin{matrix} 1 & \text{-0}\text{.14} & \text{-0}\text{.31} \\ \text{-0}\text{.14} & 1 & \text{-0}\text{.15} \\ \text{-0}\text{.31} & \text{-0}\text{.15} & 1 \\ \end{matrix} \right)$    (5)

对数值回归残差的样本协方差矩阵可作为θ的协方差的预测估计值，即

${{\mathbf{C}}_{\text{ }\!\!\theta\!\!\text{ }}}\mathbf{ }=\left( \begin{matrix} 0.493 & -0.018 & -0.044 \\ -0.018 & \text{0}\text{.030} & -0.005 \\ -0.044 & -0.005 & \text{0}\text{.041} \\ \end{matrix} \right)$    (6)

基于多元正态分布特性，θ={lnc,lnφ,lna}的联合概率密度函数为

$f(\mathbf{\theta })={{\left( 2\pi \right)}^{-\frac{3}{2}}}{{\left| {{\mathbf{C}}_{\text{ }\!\!\theta\!\!\text{ }}} \right|}^{-\frac{1}{2}}}\exp \left[ -\frac{1}{2}{{\left( \mathbf{\theta }-{{\mathbf{\mu }}_{\text{ }\!\!\theta\!\!\text{ }}} \right)}^{T}}\mathbf{C}_{\theta }^{-1}\left( \mathbf{\theta }-{{\mathbf{\mu }}_{\text{ }\!\!\theta\!\!\text{ }}} \right) \right]$    (7)

在获得θ的联合概率密度函数后，通过变换，即可获得δ= {c,f,a}的概率密度函数.设由θ对δ的雅可比行列式为J(θ→δ)，则可得

$\mathbf{J}(\mathbf{\theta }\to \mathbf{\delta })=\left| \begin{matrix} \frac{\partial (\ln c)}{\partial c} & \frac{\partial (\ln c)}{\partial \phi } & \frac{\partial (\ln c)}{\partial a} \\ \frac{\partial (\ln \phi )}{\partial c} & \frac{\partial (\ln \phi )}{\partial \phi } & \frac{\partial (\ln \phi )}{\partial a} \\ \frac{\partial (\ln a)}{\partial c} & \frac{\partial (\ln a)}{\partial \phi } & \frac{\partial (\ln a)}{\partial a} \\ \end{matrix} \right|={{\left( c\phi a \right)}^{-1}}$    (8)

进而可得δ= {c,φ,a}的概率密度函数为

$\begin{align} & g(\mathbf{\delta })=f(\mathbf{\theta })\cdot \left| \mathbf{J}(\mathbf{\theta }\to \mathbf{\delta }) \right|= \\ & {{\left( 2\pi \right)}^{-\frac{3}{2}}}{{\left| {{\mathbf{C}}_{\text{ }\!\!\theta\!\!\text{ }}} \right|}^{-\frac{1}{2}}}{{\left( c\phi a \right)}^{-1}}\exp \left[ -\frac{1}{2}{{\left( \ln \mathbf{\delta }-{{\mathbf{\mu }}_{\text{ }\!\!\theta\!\!\text{ }}} \right)}^{T}}\mathbf{C}_{\theta }^{-1}\left( \ln \mathbf{\delta }-{{\mathbf{\mu }}_{\text{ }\!\!\theta\!\!\text{ }}} \right) \right] \\ \end{align}$    (9)
3 基于主成分分析的花岗岩残积土力学参数分布模型 3.1 主成分的获取

在上面的分析中，采用经验判别法选择了回归分析的基本变量.花岗岩残积土各物理指标之间常存在一定的相关关系(梁仕华等[4]，Hu等[6]).对于相关性数据，也可用主成分分析方法选取基本变量，减少基本变量选取过程中的主观性.此外，主成分分析可以综合考虑各个参数，并对变量进行降维，从而实现对数据的简化.主成分分析方法的原理是将数据按一定规则线性变换，通过削弱各个量之间相关性的影响，使得主成分之间相关性最小，并尽可能携带更多的样本信息.

对于颗粒级配分数，由于各个量存在制约关系，因此不对其进行主成分分析，直接选取S1、S2、S3、S4作为基本变量.塑性指数与塑限和液限线性相关，在分析时，只选取塑限与塑性指数.因此，将表 1中w、Gs、ρ、ρd、Sr、e0、wP、IP各个物理试验指标进行主成分分析.分析表明，第1主成分至第4主成分X1、X2、X3及X4的样本方差累计贡献率为99.999%.X1、X2、X3及X4与w、Gs、ρ、ρd、Sr、e0、wP、IP各个物理试验指标的变换关系如下式：

$\left\{ {\matrix{ \matrix{ {X_1} = 0.4298w + 0.0003{G_S} + 0.0023\rho - 0.0029{\rho _d} \hfill \cr + 0.8888{S_r} + 0.0043{e_0} + 0.1398{w_p} + 0.076{I_p} \hfill \cr} \cr \matrix{ {X_2} = {\rm{0}}{\rm{.5212}}w + {\rm{0}}{\rm{.0016}}{G_S} - {\rm{0}}{\rm{.0123}}\rho - {\rm{0}}{\rm{.0157}}{\rho _d} \hfill \cr - 0.{\rm{0}}{\rm{.3880}}{S_r} + {\rm{0}}{\rm{.0211}}{e_0} + {\rm{0}}{\rm{.6824}}{w_p} + {\rm{0}}{\rm{.3335}}{I_p} \hfill \cr} \cr \matrix{ {X_3} = {\rm{0}}{\rm{.7361}}w - {\rm{0}}{\rm{.001}}{G_S} - {\rm{0}}{\rm{.0139}}\rho - {\rm{0}}{\rm{.0185}}{\rho _d} \hfill \cr - {\rm{0}}{\rm{.2433}}{S_r} + {\rm{0}}{\rm{.0249}}{e_0} - {\rm{0}}{\rm{.5677}}{w_p} - {\rm{0}}{\rm{.2749}}{I_p} \hfill \cr} \cr \matrix{ {X_4} = - {\rm{0}}{\rm{.0046}}w + {\rm{0}}{\rm{.0036}}{G_S} + {\rm{0}}{\rm{.0021}}\rho + {\rm{0}}{\rm{.0021}}{\rho _d} \hfill \cr - {\rm{0}}{\rm{.0056}}{S_r} + {\rm{0}}{\rm{.0006}}{e_0}{\rm{0}}{\rm{.4388}}{w_p} + {\rm{0}}{\rm{.8986}}{I_p} \hfill \cr} \cr } } \right.$    (10)

由于主成分分析方法获得的综合指标X1、X2、X3、X4自身已经覆盖了w、Gs、ρ、ρd、Sr、e0、wP、IP各指标的影响，故回归分析中不需再重复考虑w、Gs、ρ、ρd、Sr、e0、wP、IP等指标.在下面的回归分析中，将采用X1、X2、X3、X4、S1、S2、S3、S4作为基本变量.

3.2 回归分析结果

基于上述基本变量，采用多元回归分析方法建立了lnc、lnφ、lna的回归方程如下：

$\left\{ {\matrix{ \matrix{ {{\hat \theta }_1} = 3.5574 - 0.0138{X_1} + 0.0044{X_2} - 0.0043{X_3} + 0.0234{X_4} \hfill \cr + 0.01\left( { - 0.1437{S_1} - 1.1890{S_2} + 2.3527{S_3} - 0.2519{S_4}} \right) \hfill \cr} \cr \matrix{ {{\hat \theta }_2} = 3.3087 - 0.0049{X_1} - 0.0040{X_2} - 0.0153{X_3} - 0.0101{X_4} \hfill \cr + 0.01\left( {0.4017{S_1} + 0.2338{S_2} + 0.8650{S_3} + 0.1758{S_4}} \right) \hfill \cr} \cr \matrix{ {{\hat \theta }_3} = - 0.6627 + 0.0036{X_1} + 0.0276{X_2} + 0.0272{X_3} + 0.0042{X_4} \hfill \cr + 0.01\left( { - 0.2013{S_1} - 0.1356{S_2} - 0.1834{S_3} - 0.4186{S_4}} \right) \hfill \cr} \cr } } \right.$    (11)

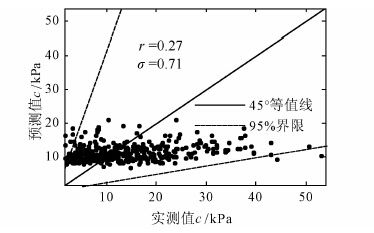
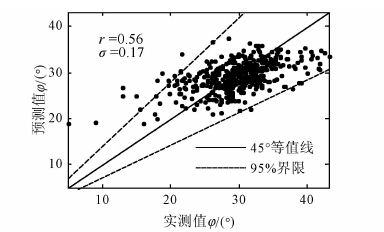
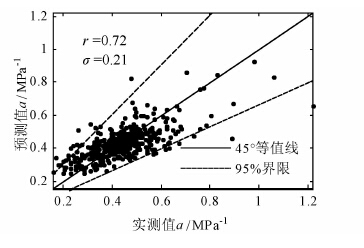
图 5~7分别给出了上述回归方程对黏聚力、内摩擦角和压缩系数的预测值和实测值的对比，图中也给出了回归方程的相关系数及残余误差的标准差.

图 5 黏聚力预测值与试验值对比散点图 Figure 5 Relationship between predicted and observed values of coefficient of cohesion
图选项
图 6 内摩擦角预测值与试验值对比散点图 Figure 6 Relationship between predicted and observed values of coefficient of friction angle
图选项
图 7 压缩系数预测值与试验值对比散点图 Figure 7 Relationship between predicted and observed values of coefficient of compressibility
图选项

从相关系数来看，基于主成分分析获得回归方程的相关系数与基于经验法获得的回归方程类似，说明采用更复杂的方法选择基本变量并不能显著提高回归效果，验证了基于经验法选择基本变量的合理性.

3.3 概率分布模型

采用岩土工程中常用的多元正态假设，假定δ= {c,φ,a}服从对数正态分布.此时，θ服从多元正态分布，θ的均值和标准差可由回归分析方程确定，即μθ = $\left\{ \ln \hat{c},\ln \hat{\varphi },\ln \hat{a} \right\}$，σθ = {0.71,0.18,0.2}.采用与经验法相同的步骤可获得θ的相关系数矩阵：

${{\mathbf{R}}_{\text{ }\!\!\theta\!\!\text{ }}}\text{ }=\left( \begin{matrix} 1 & \text{-0}\text{.13} & \text{-0}\text{.3} \\ \text{-0}\text{.13} & 1 & \text{-0}\text{.11} \\ \text{-0}\text{.3} & \text{-0}\text{.11} & 1 \\ \end{matrix} \right)$    (12)

相应地，θ的协方差矩阵为

${{\mathbf{C}}_{\text{ }\!\!\theta\!\!\text{ }}}\mathbf{ }=\left( \begin{matrix} \text{0}\text{.493} & \text{-0}\text{.016} & \text{-0}\text{.043} \\ \text{-0}\text{.016} & \text{0}\text{.028} & \text{-0}\text{.004} \\ \text{-0}\text{.043} & \text{-0}\text{.004} & \text{0}\text{.042} \\ \end{matrix} \right)$    (13)

将μθ和Cθ代入式(8)，即可获得θ的概率密度函数.将μθ和Cθ代入式(9)，即可获得δ的概率密度函数.

比较由经验法获得的θ的协方差矩阵和由主成分分析方法获得的协方差矩阵，两者非常类似.采用不同方法建立的概率模型较为接近，这进一步验证了本文提出的概率模型的可靠性.

4 结论

基于533组花岗岩残积土土样的土工试验数据，本文研究了花岗岩残积土黏聚力、内摩擦角、压缩系数与常见物理指标之间的相关关系，分别采用经验方法和主成分分析方法建立了花岗岩残积土力学性质的联合概率密度函数.研究表明，花岗岩残积土黏聚力的离散型很大，难以准确预测，这可能是因为黏聚力的影响因素复杂，没有在回归分析中充分考虑的缘故.和黏聚力相比，内摩擦角和压缩系数的可预测性更强，内摩擦角和压缩系数之间存在一定的负相关性.黏聚力和内摩擦角、压缩系数的相关性较弱.采用经验法和主成分分析法建立的联合概率密度函数类似，验证了本文提出的概率模型的可靠性.

参考文献
[1] 戴继, 高广运, 王铁宏. 花岗岩残积土的地区差异及对其工程特性的研究[J]. 港工技术, 2009, 46(1): 56–59.
Dai Ji, Gao Guangyun, Wang Tiehong. Regional differences of granitic residual soil and research on its engineering characteristics[J]. Port Engineering Technology, 2009, 46(1): 56–59.
[2] Lumb P. The properties of decomposed granite[J]. Géotechnique, 1962, 12(3): 226–243. DOI:10.1680/geot.1962.12.3.226
[3] 杨树俊, 陈明星. 浅析花岗岩残积土的物理力学性质[J]. 科技情报开发与经济, 2010, 20(6): 161–163.
Yang Shujun, Chen Mingxing. Analysis of the physico-mechanical properties of granite residual soil[J]. Sci-Tech Information Development & Economy, 2010, 20(6): 161–163.
[4] 梁仕华, 周世宗, 张朗, 等. 广州东部地区花岗岩残积土物理力学指标统计分析[J]. 广东工业大学学报, 2015(01): 29–33.
Liang Shihua, Zhou Shizong, Zhang Lang, et al. Statistical analysis of physical and mechanical indexes of granite residual soil in eastern Guangzhou[J]. Journal of Guangdong University of Technology, 2015(01): 29–33.
[5] 陈洪江, 崔冠英. 花岗岩残积土物理力学指标的概率统计分析[J]. 华中科技大学学报:自然科学版, 2001, 29(5): 95–97.
Chen Hongjiang, Cui Guanying. Probability statistic analysis of physical mechanical parameters of granite eluvial soil[J]. Journal of Huazhong Univ. of Sci. & Tech., 2001, 29(5): 95–97.
[6] Hu J Z, Wang H, Ma J Z, et al. Probabilistic assessment of the properties of completely decomposed granite[C]// 6th Asian-Pacific Symposium on Structural Reliability and its Applications (APSSRA6), Shanghai, China.
[7] 陈洪江, 崔冠英. 花岗岩残积土物理力学指标的概型分布检验[J]. 华中科技大学学报:自然科学版, 2001, 29(5): 92–94.
Chen Hongjiang, Cui Guanying. Probability type testing of the distribution on the granite eluvial soil mechanical parameters[J]. Journal of Huazhong Univ. of Sci. & Tech., 2001, 29(5): 92–94.
[8] Lan H X, Hu R L, Yue Z Q, et al. Engineering and geological characteristics of granite weathering profiles in South China[J]. Journal of Asian Earth Sciences, 2003, 21(4): 353–364. DOI:10.1016/S1367-9120(02)00020-2
[9] 赵建军, 王思敬, 尚彦军, 等. 全风化花岗岩抗剪强度影响因素分析[J]. 岩土力学, 2005, 26(4): 624–628.
Zhao Jianjun, Wang Sijing, Shang Yanjun, et al. Control factors on shear strength of completely decomposed granite[J]. Rock and Soil Mechanics, 2005, 26(4): 624–628.
[10] Ibrahim N M, Rahim N L, Amat R C, et al. Determination of plasticity index and compression index of soil at perlis[J]. Apcbee Procedia, 2012, 4: 94–98. DOI:10.1016/j.apcbee.2012.11.016
[11] Jain V K, Dixit M, Chitra R. Correlation of plasticity index and compression index of soil[J]. International Journal of Innovations in Engineering and Technology (IJIET), 2015, 5(3): 263–270.
[12] Khanlari G R, Heidari M, Momeni A A, et al. Prediction of shear strength parameters of soils using artificial neural networks and multivariate regression methods[J]. Engineering Geology, 2012.
[13] Wesley L D. Influence of structure and composition on residual soils[J]. Journal of Geotechnical Engineering, 1990, 116(4): 589–601. DOI:10.1061/(ASCE)0733-9410(1990)116:4(589)
[14] 戴继, 王铁宏, 高广运, 等. 由压缩试验分析砾质花岗岩残积土的结构特性[J]. 地下空间与工程学报, 2009, 5(4): 675–679.
Dai Ji, Wang Tiehong, Gao Guangyun, et al. Analysis for structural character of gravelly granitic residual soil by compression test[J]. Chinese Journal of Underground Space and Engineering, 2009, 5(4): 675–679.