武汉大学学报(工学版)   2016, Vol. 49 Issue (4): 610-615

文章信息

孙小庆, 石端伟
SUN Xiaoqing, SHI Duanwei
垂直升船机传动系统动力学仿真及疲劳寿命预测
Dynamics simulation and fatigue life prediction of drive system of vertical shiplift
武汉大学学报(工学版), 2016, 49(4): 610-615
Engineering Journal of Wuhan University, 2016, 49(4): 610-615
http://dx.doi.org/10.14188/j.1671-8844.2016-04-021

文章历史

收稿日期: 2015-09-20
 Abstract              PDF               Figures               Tables
引用本文 0
孙小庆, 石端伟. 垂直升船机传动系统动力学仿真及疲劳寿命预测[J]. 武汉大学学报(工学版), 2016, 49(4): 610-615.
SUN Xiaoqing, SHI Duanwei. Dynamics simulation and fatigue life prediction of drive system of vertical shiplift[J]. Engineering Journal of Wuhan University, 2016, 49(4): 610-615.
垂直升船机传动系统动力学仿真及疲劳寿命预测
孙小庆1, 石端伟2     
1. 上海交通大学机械系统与振动国家重点实验室，上海 200240;
 2. 武汉大学动力与机械学院，湖北 武汉 430072
收稿日期: 2015-09-20
作者简介: 孙小庆(1987-)，男，博士，研究方向为振动控制、机械系统动力学仿真，E-mail：sxq5656@163.com.
通讯作者: 石端伟(1963-)，男，教授， 博士生导师，研究方向为机械系统动力学、虚拟样机技术，E-mail：dwshi@whu.edu.cn
基金项目: 湖北省水电机械设备设计与维护重点实验室基金(编号：2012KJX01).
摘要: 针对垂直升船机传动系统大模数齿轮的疲劳寿命问题，提出一种联合虚拟仿真技术.运用SolidWorks及其插件GearTrax建立传动齿轮齿条机构的三维模型，在ADAMS中进行齿轮齿条机构动态啮合力仿真，并研究了传动速度对啮合力的影响.基于有限元软件ANSYS分析了传动机构大模数齿轮的弯曲应力，与理论计算值相比误差为1.6%，误差较小，可以作为齿轮疲劳寿命预测的依据.利用获得的载荷历程和弯曲应力结果，基于名义应力法对该大模数齿轮进行疲劳寿命预测，结果表明该大模数齿轮能很好地满足设计使用要求，联合虚拟仿真技术能有效地研究大模数齿轮的疲劳寿命问题.
关键词： 垂直升船机     齿轮齿条     动力学仿真     有限元分析     疲劳寿命预测    
Dynamics simulation and fatigue life prediction of drive system of vertical shiplift
SUN Xiaoqing1, SHI Duanwei2     
1. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiaotong University, Shanghai 200240, China;
 2. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China
Abstract: A virtual combined simulation method is proposed for predicting the fatigue life of vertical shiplift's big modulus gear. First, a three-dimensional assembly model of rack and pinion mechanism is built by using SolidWorks. Then in order to discuss the dynamic responses of the system, combined simulation is conducted based on ADAMS; besides the effects between transmission speed and meshing force are studied. After that, bending stress of the gear is calculated by ANSYS; and the error is 1.6%, compared with the theoretical value. Finally, based on nominal stress method, the fatigue life of the gear is estimated; the results show that the gear could well meet the design requirements.
Key words: vertical shiplift     drive gear and rack     dynamics simulation     finite element alalysis(FEA)     fatigue life prediction    

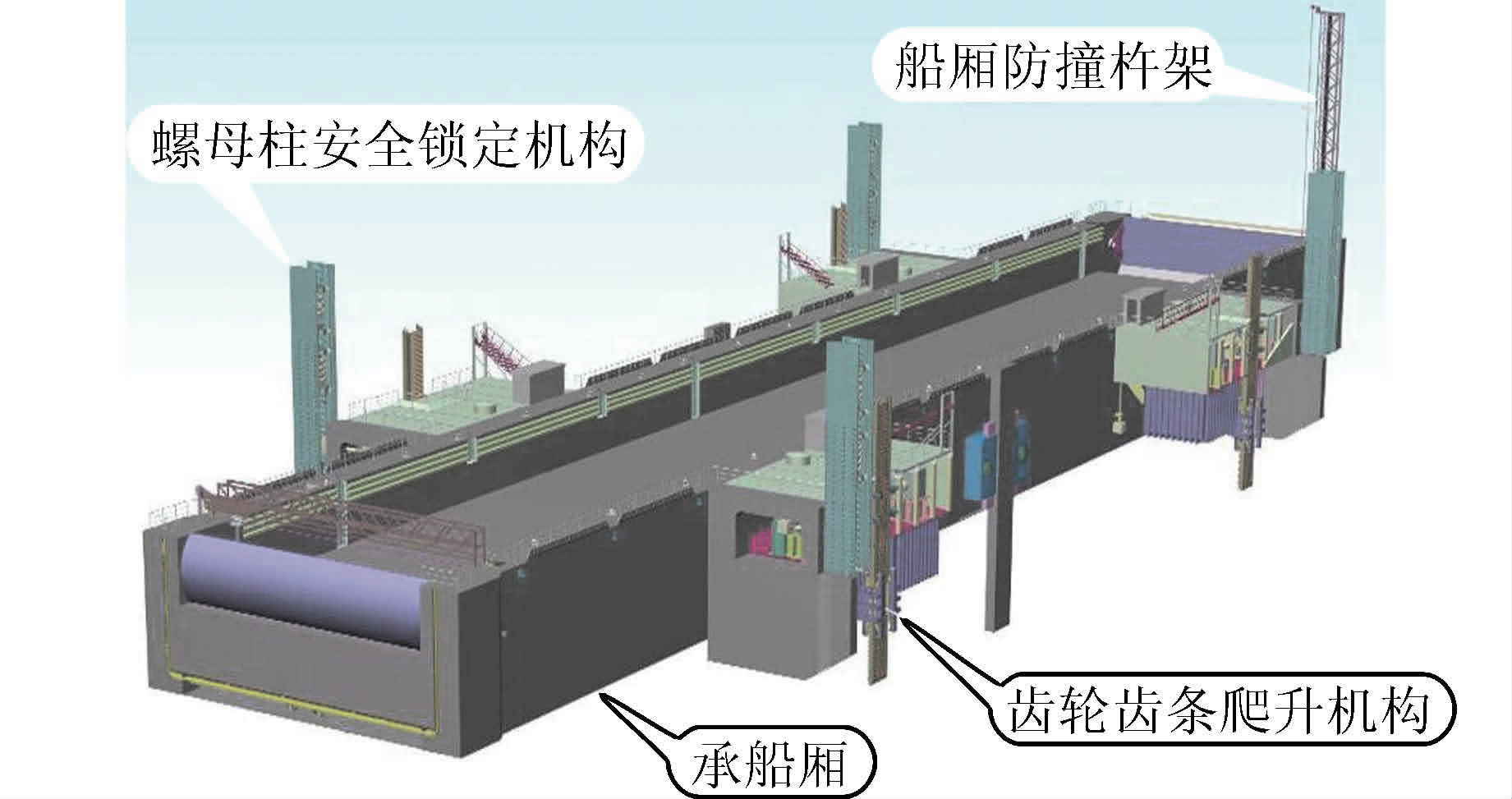
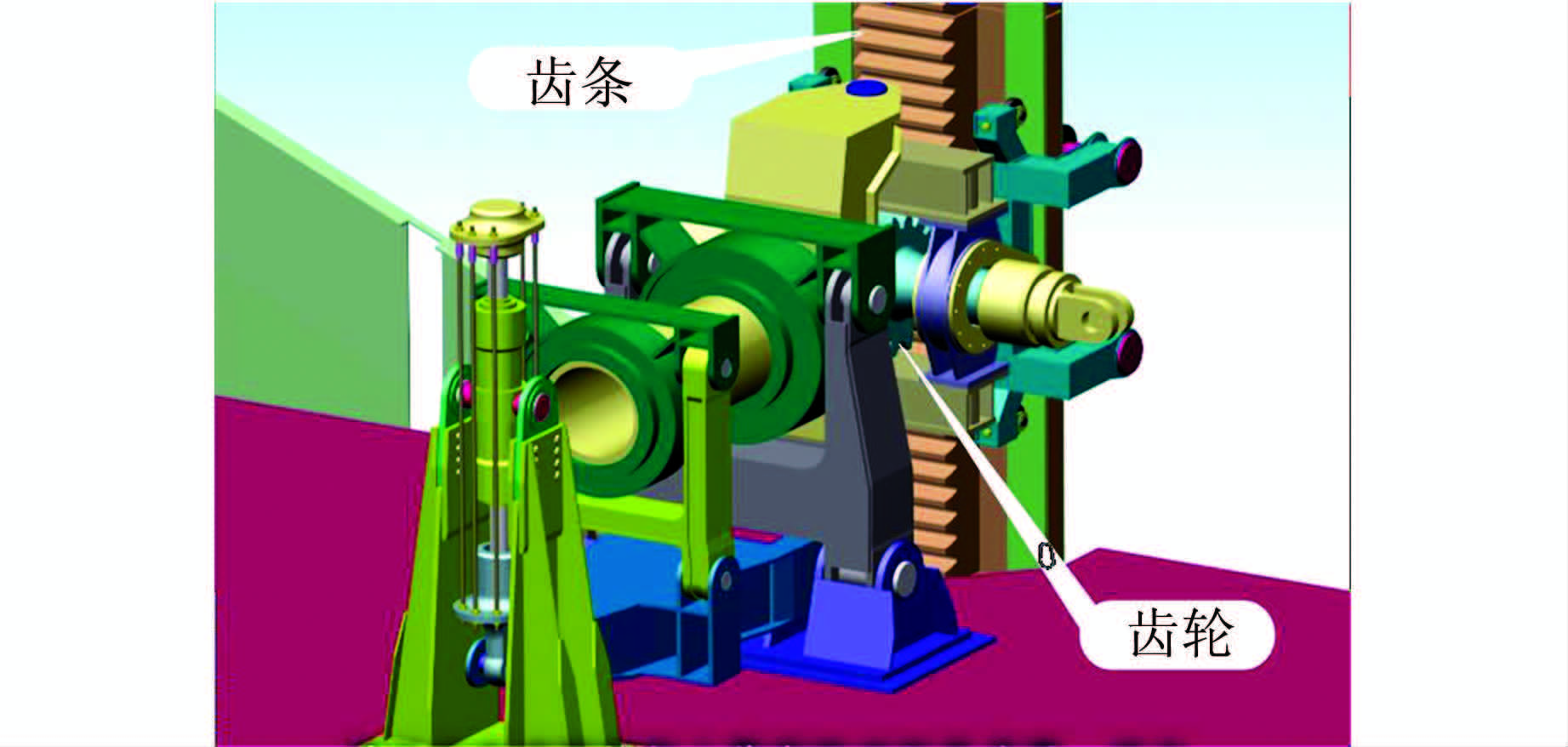
齿轮传动广泛应用于现代大型机械设备上，如矿山机械、石油机械、建筑机械、升船机械、海洋平台等.由于大型设备尺寸及传递荷载的需要，齿轮模数不断增大.文章研究的齿轮齿条爬升式垂直升船机传动机构的齿轮模数达到62.67 mm，该升船机模型如图 1所示，齿轮齿条传动机构如图 2所示.

图 1 垂直升船机模型 Figure 1 Graphic model of shiplift
图选项
图 2 垂直升船机齿轮齿条传动机构 Figure 2 Graphic model of transmission system
图选项

针对升船机大模数齿轮疲劳寿命问题研究相对薄弱的现状，提出基于联合虚拟仿真的方法研究传动齿轮的疲劳寿命.相关结论不仅为大模数齿轮的前期设计、寿命验证提供一种新的途径，同时为齿轮后期的安全运行提供指导依据，并且也可为其他机械大模数齿轮的疲劳寿命研究提供借鉴.

文章对该型号垂直升船机传动机构进行动力学仿真，重点研究影响疲劳寿命的2种主要工况下的啮合力时域曲线，进而分析不同传动速度对齿轮啮合力的影响.其次，利用有限元法和国标法研究传动机构大模数齿轮的疲劳弯曲应力.最后，联合动力学仿真获得的载荷谱与有限元分析获得的应力谱，基于名义应力法通过疲劳仿真分析软件DesignLife对齿轮的疲劳寿命进行预测.

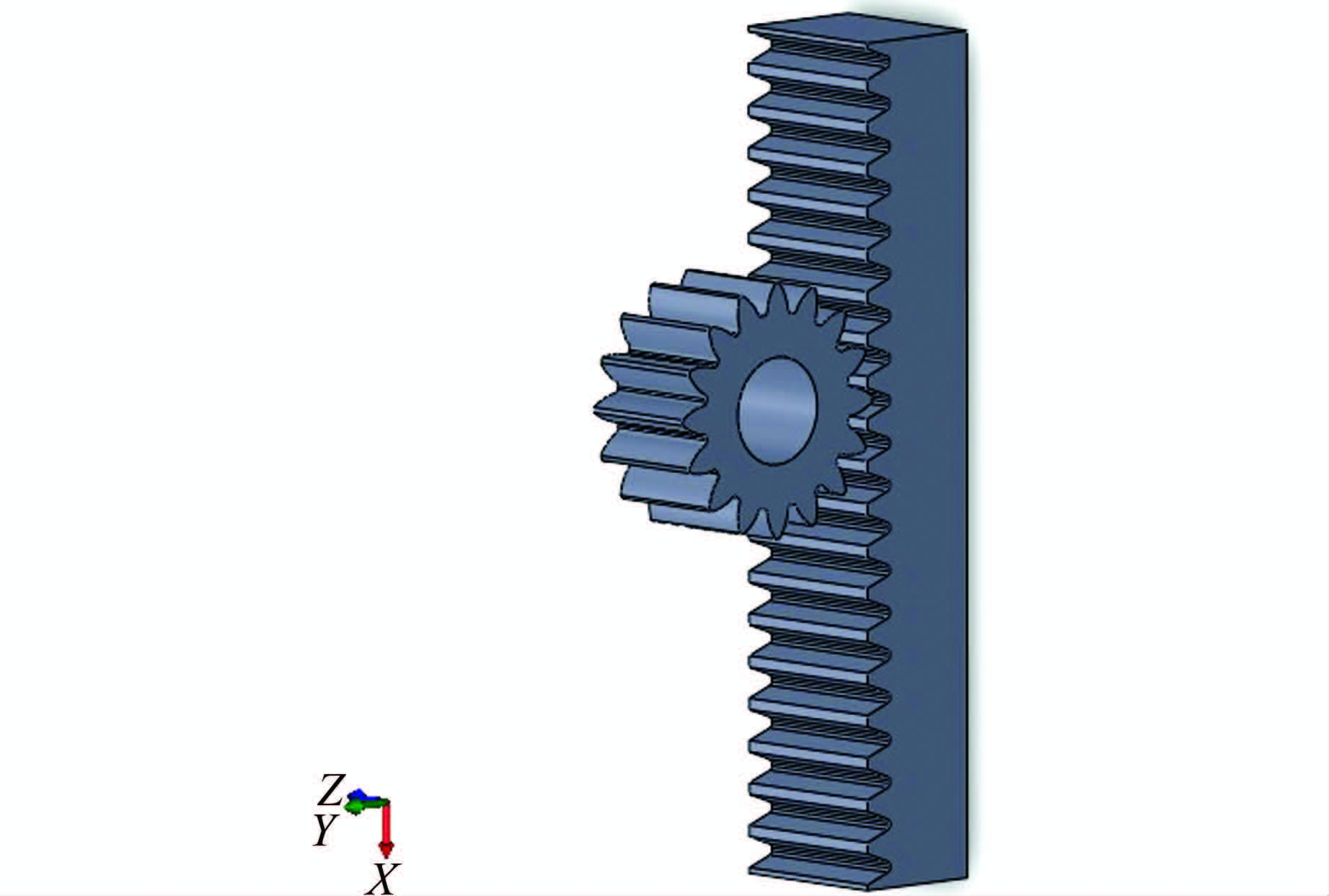
1 传动机构三维建模、装配

精确的三维实体模型是仿真分析结果具有高可信度的保证，通过SolidWorks结合专业插件GearTrax创建系统实体模型.该大型垂直升船机传动机构的齿轮齿条基本参数如表 1所示.虚拟装配后的传动机构如图 3所示.

表 1 齿轮齿条基本参数 Table 1 Basic parameters of gear and rack
齿轮 齿条
模数/mm 齿/mm 分度圆直径/mm 齿数 齿宽/mm 槽宽、齿厚/mm 每节长度/mm 总长度/mm
62.67 600 1 002.72 16 800 98.391 9 4 725 113
表选项
图 3 齿轮齿条装配体 Figure 3 Three-dimensional model
图选项

在SolidWorks中将装配体模型文件另存为Parasolid格式，在ADAMS中选择输入xmt_txt格式的Parasolid文件，将模型导入ADAMS.

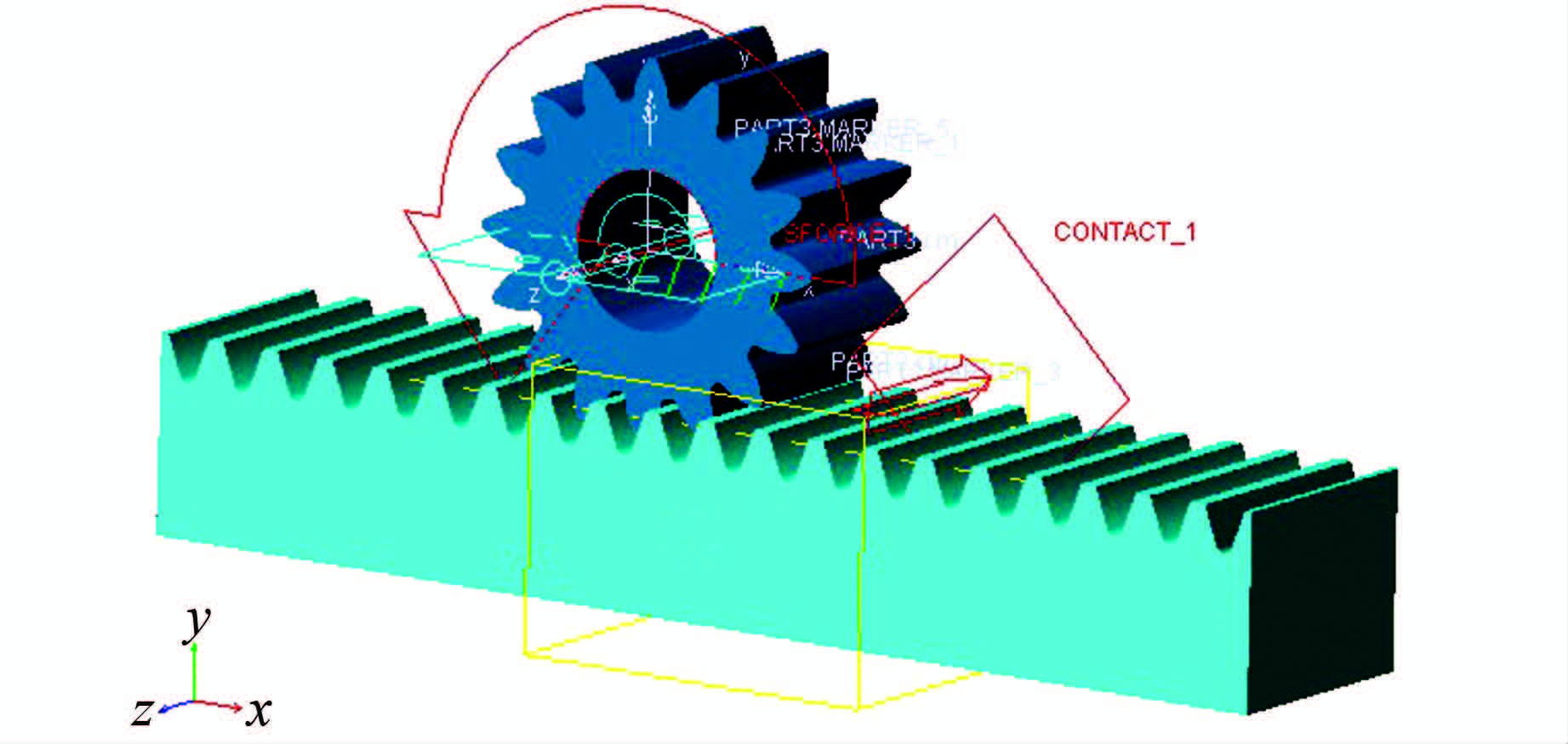
2 基于ADAMS的刚体动力学分析 2.1 仿真参数设置及分析

根据传动系统运动规律定义各构件间的约束关系，齿轮齿条之间添加接触模拟接触面啮合力，齿轮与机架(地面)之间添加旋转副，齿条与机架(地面)之间建立滑移副，确保齿条只能沿轴线方向运动.ADAMS提供2种计算接触力的方法：1)补偿函数法(Restitution)；2)冲击函数法(Impact).基于冲击函数法模拟齿轮齿条间的动态啮合力.ADAMS接触力定义：

$F\_{\rm{impact}} = \left\{ {\matrix{ {{\rm{ }}} \cr {{\rm{ }}} \cr } } \right.\matrix{ {\rm{0}} & {{\rm{q}} \ge {{\rm{q}}_{\rm{0}}}} \cr {{\rm{K}}{{\left( {{{\rm{q}}_{\rm{0}}}{\rm{ - q}}} \right)}^{\rm{e}}}{\rm{0}}C*{{{\rm{dq}}} \over {{\rm{dt}}}}*STEP\left( {{\rm{q,}}{{\rm{q}}_{\rm{0}}} - d,1,{q_0},0} \right)} & {{\rm{q ＜ }}{{\rm{q}}_{\rm{0}}}} \cr } $    (1)

式中：q0为两物体间初始距离；q为物体碰撞过程中实际距离；STEP为阶跃函数；q0-q为碰撞过程中的变形量.

上式表示，当q≥q0时，接触力为0，两物体不发生碰撞；当q＜q0时，两物体发生碰撞并相互穿透，其接触力的大小与变形量q0-q、刚度系数K、碰撞指数e、阻尼系数C和阻尼完全作用时的变形距离d有关.刚度系数K根据文献[1, 2]计算,K由撞击物体结构形状及材料所决定：

$K=\frac{\text{4}}{\text{3}}{{R}^{\frac{\text{1}}{\text{2}}}}{{E}^{*}}$    (2)

式中：$\frac{\text{1}}{R}=\frac{\text{1}}{{{R}_{\text{1}}}}+\frac{\text{1}}{{{R}_{\text{2}}}};\frac{\text{1}}{{{E}^{*}}}=\frac{\left( \text{1}-\text{v}_{\text{1}}^{\text{2}} \right)}{{{E}_{\text{1}}}}+\frac{\left( \text{1}-\text{v}_{\text{2}}^{\text{2}} \right)}{{{E}_{\text{21}}}}$；R1、R2分别为相互啮合两齿轮在接触点处的当量半径(考虑到齿轮的齿高和分度圆半径相比较小的特点可近似以分度圆半径来代替齿轮接触点处的当量半径)；v1、v2分别为两齿轮材料的泊松比；E1、E2分别为两齿轮材料的杨氏模量.齿轮齿条材料均为42CrMo4V，弹性模量为2.06×105 MPa，泊松比为0.29，计算得到接触副刚度为3.37×106 N/mm3/2.参考文献[3]，碰撞系数取1.5，阻尼系数取50 N·s/mm，击穿深度为0.1 mm.设置完毕后传动机构虚拟样机模型如图 4所示.

图 4 齿轮齿条虚拟样机模型 Figure 4 Virtual prototype of transmission system
图选项
2.2 仿真条件及结果分析

根据传动机构进行疲劳强度校核的2种主要工况(工况1：80%的5 cm误载水深，齿轮轮齿所受扭矩为3.72×108 N/mm；工况2：20%的10 cm误载水深，齿轮轮齿所受扭矩为5.25×108 N/mm)，分别将扭矩施加在齿轮上，同时在齿条移动副上赋予齿条速度200 mm/s.参考文献[4]，为避免陡变，加载时均使用step函数.

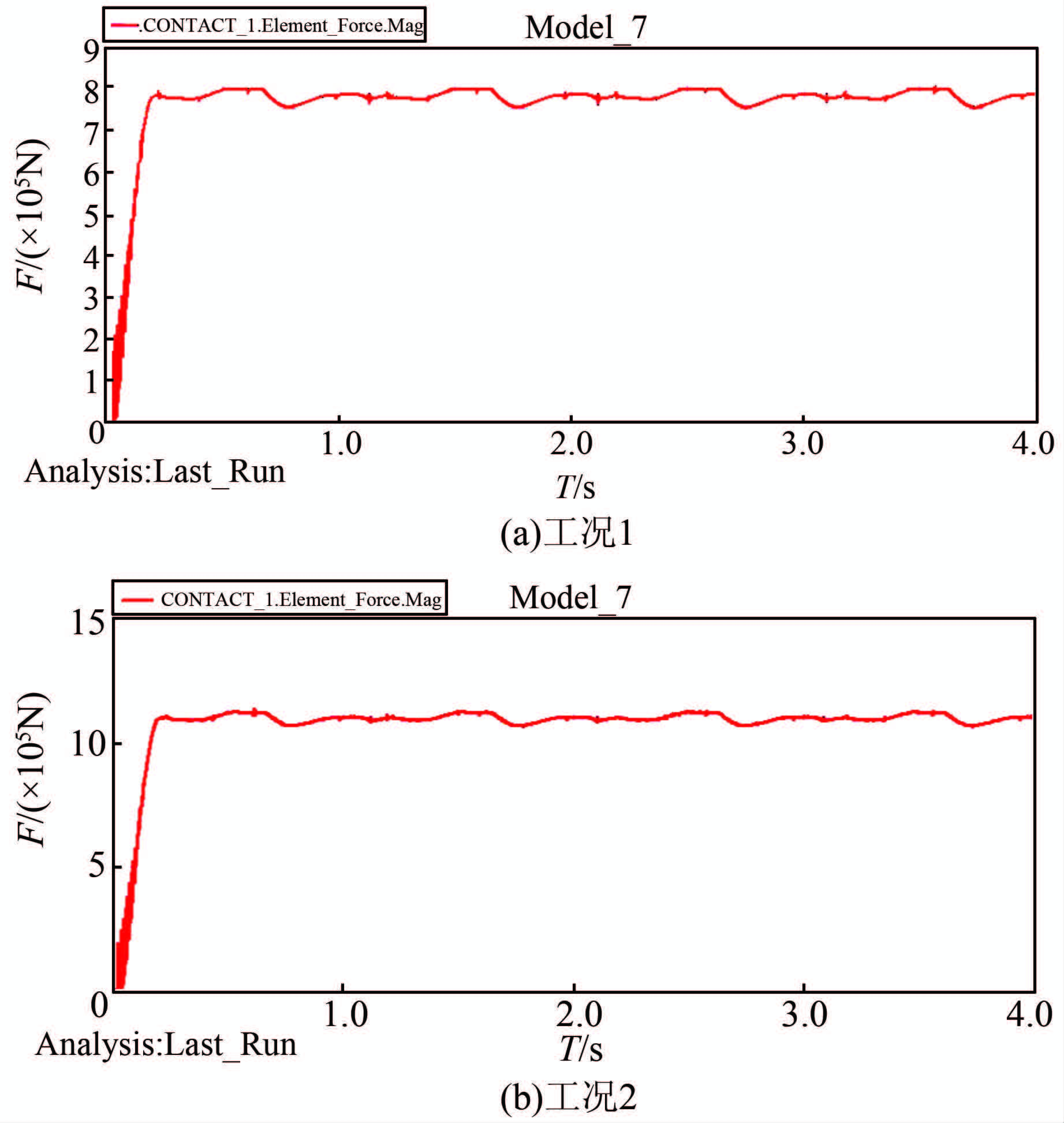
图 5是齿轮齿条啮合力在2种工况下的时域图.从图上看出：1)齿轮齿条的啮合力在某一均值(静载荷)附近上下波动，且呈周期性变化，啮合力大小的变化是因为齿轮在传动过程中齿轮齿条接触啮合造成的接触变形量的变化引起的；2)齿轮啮合力中含有动载荷成分，且动载荷非对称循环，齿轮齿条啮合传动过程中存在冲击振动，但作用时间占整个啮合时间的比例非常小.

图 5 齿轮齿条下啮合力时域图 Figure 5 Time domain results of meshing force
图选项

对于不同工况的啮合力数值分析见表 2.

表 2 齿轮啮合力数值分析 Table 2 Numerical analysis of meshing force
工况 F/N Fmax/N Fm/N 误差(Fm-F)/
F/%
1 7.42×105 8.03×105 7.58×105 2.2
2 1.048×106 1.142×106 1.065×106 1.6
表选项

表 2中，Fmax为最大值，Fm是平均值,F是作用在齿轮上的作用力.

分析数据：2种工况下，动力学仿真获得的啮合力均值与实际作用静载荷的误差分别是2.2%与1.6%，与作用静载比较吻合，验证了仿真模型的合理性.同时，动载荷幅值要稍大于静载荷.

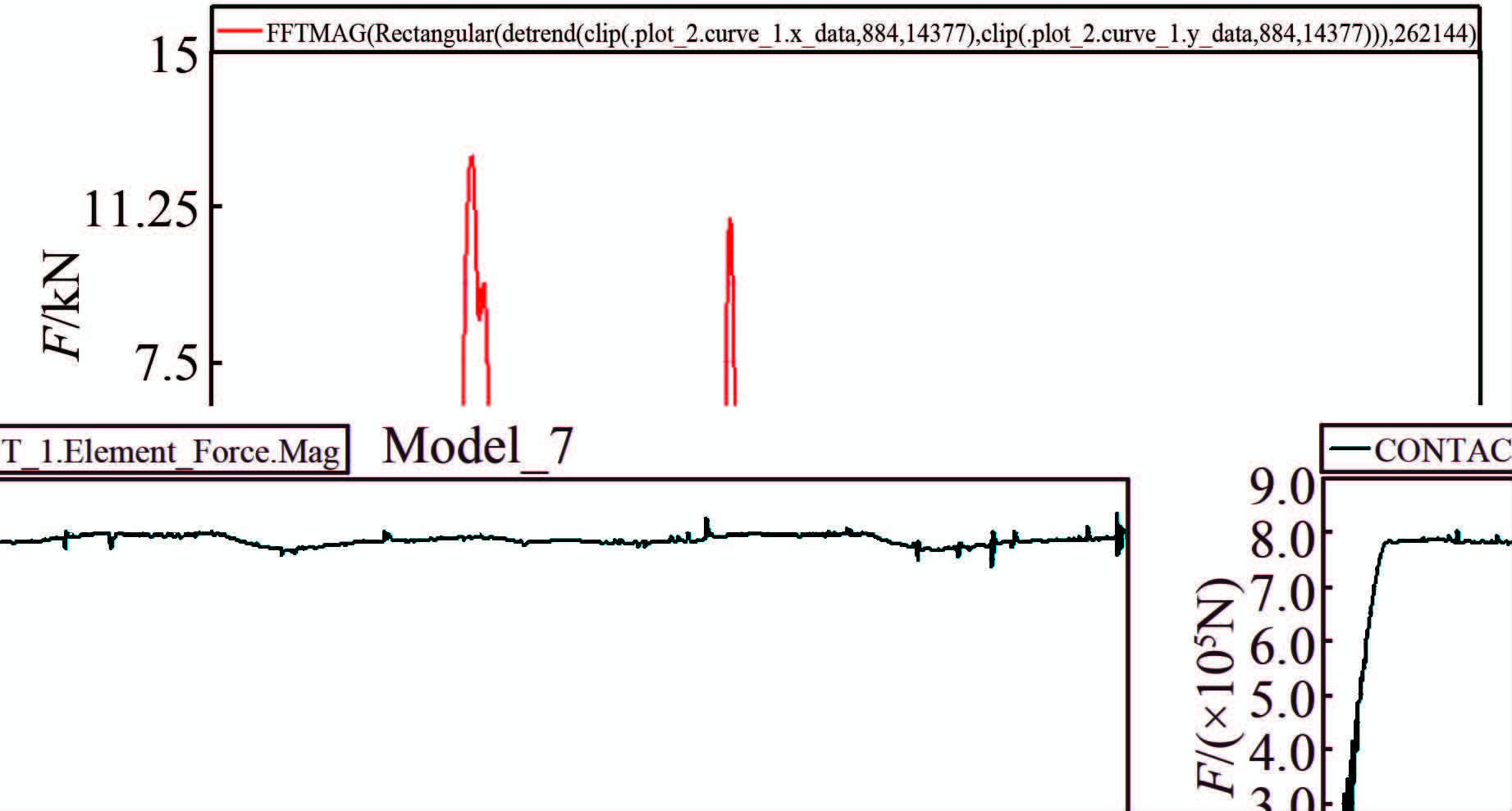
根据啮合齿轮的频率特性，分析齿轮齿条传动速度为200 mm/s时的啮合频率.参考文献[5]，齿轮啮合频率理论计算公式为fZ=Z×n/60,Z为齿数,n为转速，由ωr=v，ω=2πn得到转速n=v/2πr，代入得到啮合频率为0.96 Hz.对啮合力曲线做FFT变换，得到其频域图如图 6所示，证实齿轮啮合频率仿真结果与理论值较吻合，再次验证了仿真的可信度.

图 6 齿轮齿条在传动速度为200 mm/s时啮合力频域图 Figure 6 Frequency domain results of meshing force with 200 mm/s velocity
图选项

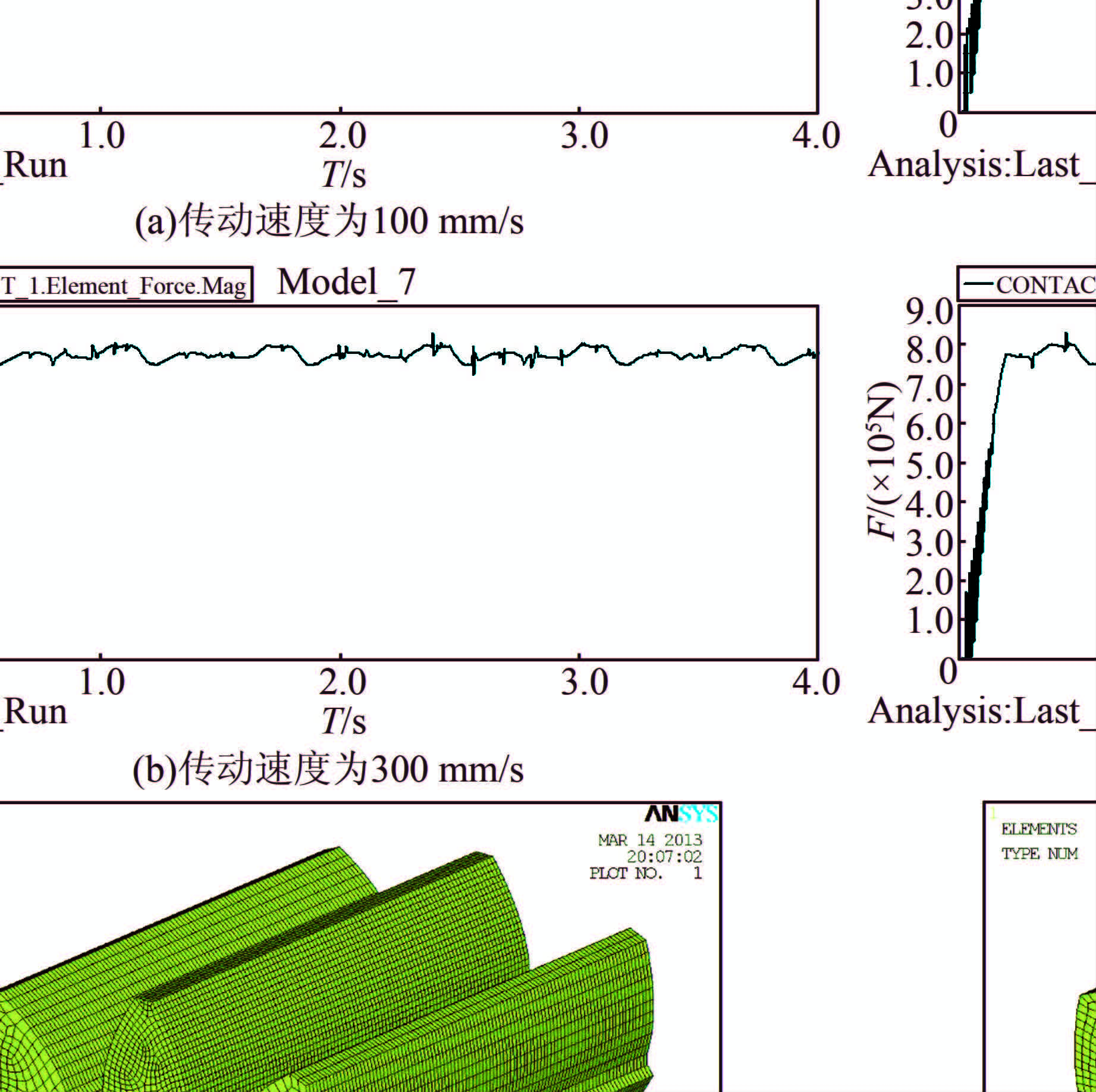
进一步研究齿轮齿条传动过程中，动态啮合力随传动速度变化的关系.在第1种工况下改变齿条速度，分别为100、300 mm/s，然后进行动力学分析，得到动态啮合力时域曲线如图 7所示.

图 7 齿轮齿条工况1下啮合力时域图 Figure 7 Time domain results of meshing force in first working condition
图选项

从传动速度分别为100、200与300 mm/s时啮合力时域曲线看出：1)随着传动速度的增加，齿轮齿条啮合力的波动程度随之增加，这表明在较低的传动速度下，有利于减小动载荷的波动程度；2)尽管传动速度发生了变化，但是齿轮动态啮合力仍然在7.58×105 N上下波动，表明传动速度对啮合力均值影响不大；3)随着传动速度的增加，随机产生的振动冲击载荷加剧.

根据相关结论，在升船机后期运行过程中应尽量避免齿轮齿条的高速运转，确保低速、匀速的工作环境对传动机构的平稳安全运行具有重要意义.

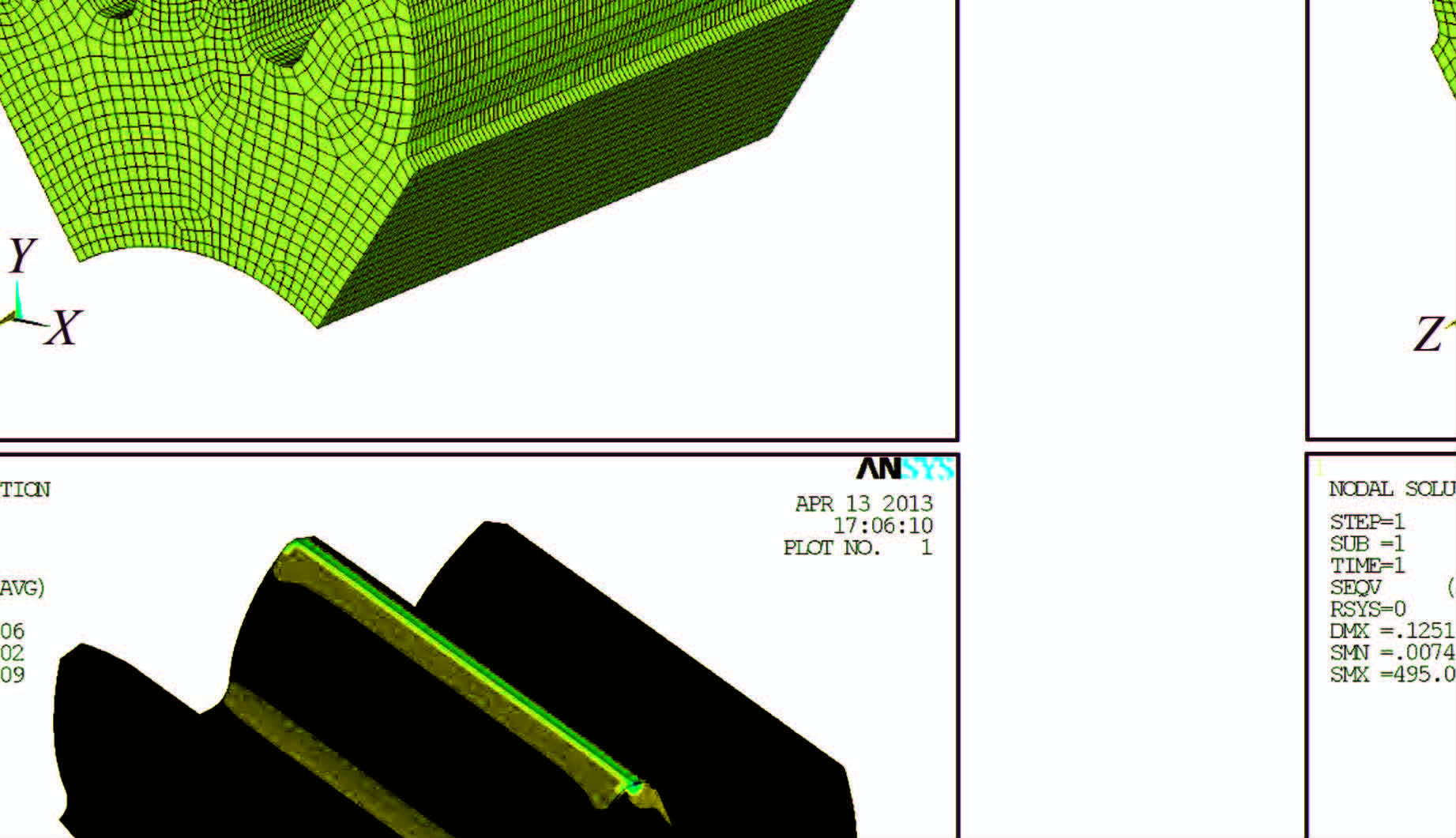
3 传动齿轮分析 3.1 弯曲应力有限元分析

将SolidWorks齿轮模型保存为.IGS格式并导入ANSYS.考虑到计算效率，取周向三齿计算应力应变.选择Solid45单元模拟齿轮，弹性模量、泊松比依据材料参数赋予.采用sweep网格划分，并对中间轮齿进行网格精细处理.有限元模型见图 8.参考文献[6]，根据该垂直升船机大模数齿轮的工作状况，在简化齿轮的两侧面和底面施加自由度约束，两端面不做约束.由于是一般中低速传动齿轮，考虑在单齿齿顶线位置承受全部载荷作用.研究工况1下齿轮的齿根弯曲应力，在齿顶施加7.89×105 N的力.

图 8 简化齿轮的有限元模型 Figure 8 Finite element model of gear
图选项

经有限元计算，相关结果从后处理查看.图 9为齿轮整体弯曲应力云图，图 10为齿轮齿根受拉侧和受压侧的弯曲应力分布云图.

图 9 齿轮整体应力云图 Figure 9 Stress nephogram of whole gear
图选项
图 10 齿根应力云图 Figure 10 Stress nephogram of tooth root
图选项

不考虑施加载荷位置处齿面的应力状况，两侧齿根处将产生较大弯曲应力，最大值为92.513 MPa.根据国标(GB/T3480-1997)，圆柱齿轮齿根弯曲应力为

${{\sigma }_{\text{f}}}=\frac{{{F}_{\text{t}}}}{\text{m}\times \text{b}}{{Y}_{F\alpha }}\text{ }\!\!\cdot\!\!\text{ }{{Y}_{\text{s}\alpha }}\text{ }\!\!\cdot\!\!\text{ }{{Y}_{\varepsilon \beta }}\text{ }\!\!\cdot\!\!\text{ }{{K}_{A}}\text{ }\!\!\cdot\!\!\text{ }{{K}_{V}}\text{ }\!\!\cdot\!\!\text{ }{{K}_{F\beta }}\text{ }\!\!\cdot\!\!\text{ }{{K}_{F\alpha }}$    (3)

式中：KA为使用系数;KV为动载系数;KFβ弯曲强度计算的齿向载荷系数;KFα为弯曲强度计算的齿间载荷系数;Yεβ为弯曲强度计算的重合度与螺旋角系数；YSα为作用于齿顶时的应力修正系数；YFα为作用于齿顶时的齿形系数.考虑到作用于齿顶圆上的名义切向力Ft为742 kN，齿宽b为600 mm，使用系数取1.25，动载系数为1，齿向载荷系数为1.42，齿间载荷系数为1，弯曲计算的重合度与螺旋角系数取0.68，YFS=YFα·YSα，YFS为复合齿形系数，取3.95.计算得到齿根弯曲应力σf为94.08 MPa.

对比有限元分析结果与国标法计算结果相对误差为1.6%，证明有限元仿真分析的结果是准确的，可以作为疲劳寿命预测的依据.

3.2 疲劳寿命分析

传动过程中，齿轮受动载作用易于发生疲劳破坏.参考文献[7-10]，基于名义应力法，利用动力学仿真得到的载荷谱以及有限元分析得到的应力谱，通过DesignLife14.0软件计算工况1下齿轮的疲劳寿命.

名义应力法是通过零部件危险点的名义应力为计算基准，利用载荷计数统计方法，在零部件材料的S-N曲线以及累计损伤理论的基础上估算零部件疲劳寿命的方法.描述材料S-N曲线常用的数学表达式为

${{S}_{m}}N=C$    (4)

式中：S为应力幅；N为达到疲劳断裂时的应力循环次数；m,C是与材料、应力比、加载方式等有关的参数.

疲劳累计损伤是疲劳问题的核心.选择Miner线性累计损伤理论，该理论认为各应力循环均对疲劳寿命产生一定影响，并造成损伤，总损伤可以通过线性叠加，即

$\sum{{{D}_{\text{i}}}=\sum{\frac{{{\text{n}}_{\text{i}}}}{{{N}_{\text{i}}}},\sum{N=\frac{\text{1}}{\sum{{{D}_{\text{i}}}}}}}}$    (5)

式中：Di为各级载荷产生的疲劳损伤；ni为各级载荷的循环次数；Ni为各级载荷对应的疲劳极限次数；∑N为总寿命.当损伤累计达到一定限度，构件将发生破坏.

疲劳分析基本流程如图 11所示.

图 11 疲劳分析基本流程图 Figure 11 Flowchart of fatigue life analysis
图选项

分别输入研究得到的第1种工况下的载荷时间历程和齿轮弯曲应力谱，并在S-N分析模块中设置相关参数.参考文献[11]，对齿轮材料42CrMo4的S-N曲线进行修正，修正后的材料S-N曲线如图 12所示.进行疲劳寿命计算，结果如图 13所示.

图 12 材料的S-N曲线 Figure 12 S-N curve of the material
图选项
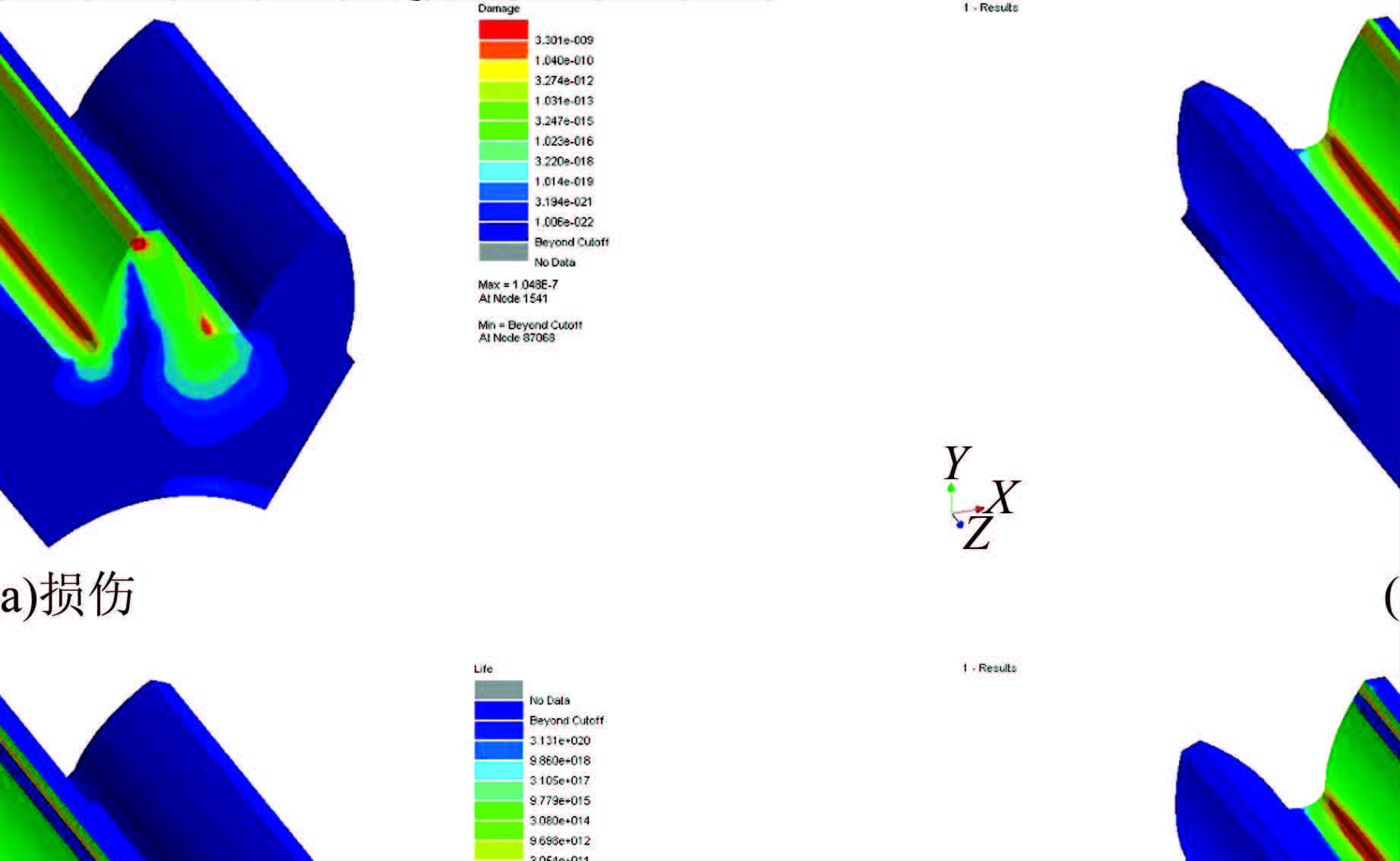
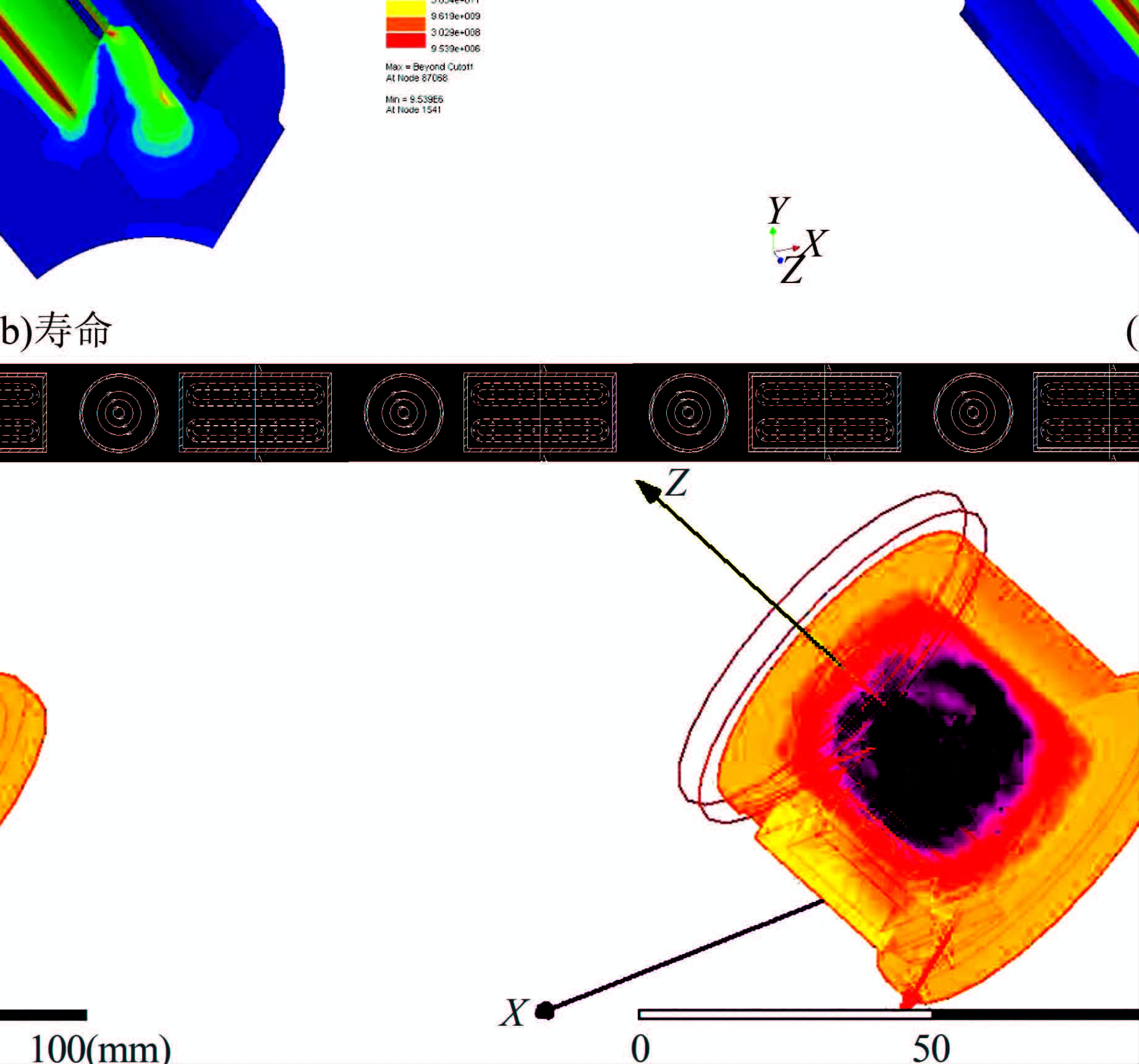
图 13 疲劳分布图 Figure 13 Distribution diagram of fatigue
图选项

据图 13分析，该工况下疲劳危险区域将集中在齿轮齿根过渡圆弧处，危险区域最小寿命为9.539×106次循环.由于4 s内齿轮转过4个齿，相当于单齿在4 s内啮合力加速4倍，相应的齿轮寿命计算结果就扩大4倍，故齿轮根部危险节点处的弯曲疲劳寿命为3.816×107次循环，即在第1种工况的动载荷作用下齿轮循环3.816×107次，将发生疲劳破坏.该研究得到的预测寿命能很好地满足齿轮设计应力循环寿命要求，不仅证明利用虚拟疲劳仿真技术研究大模数齿轮的疲劳寿命问题是相对可靠可行的，同时相关技术路线也可为其他大模数齿轮的疲劳寿命研究提供借鉴.

4 结论

1) 通过齿轮齿条传动机构动力学仿真，得到主要工况的啮合力时域曲线，为齿轮疲劳寿命预测提供载荷谱；研究不同传动速度对啮合力的影响，结果表明随着速度的增加，啮合力波动幅度变大，但均值不变，升船机运行过程中应尽量保持匀速平稳运行.

2) 利用有限元法与国标法对传动齿轮进行弯曲应力分析，得到齿根最大弯曲应力分别为92.513、94.08 MPa，相对误差为1.6%，表明有限元仿真的准确性，为齿轮疲劳寿命预测提供准确的应力谱.

3) 基于名义应力法研究得到传动齿轮的疲劳寿命为3.816×107次循环，满足齿轮实际循环寿命要求.证明基于联合虚拟仿真的方法研究大模数齿轮的疲劳寿命问题是可行的.

参考文献
[1] 黄中华, 张晓建, 周玉军. 渐开线齿轮啮合碰撞力仿真[J]. 中南大学学报, 2011, 42(2): 379–383.
Huang Z H, Zhang X J, Zhou Y J. Simulation of contact force of involute gear meshing[J]. Journal of Central South University, 2011, 42(2): 379–383.
[2] 龙凯, 程颖. 齿轮啮合力仿真计算的参数选取研究[J]. 计算机仿真, 2002, 19(6): 88–91.
Long K, Cheng Y. Research on the parameter selection of gear meshing force in simulation calculation[J]. Computer Simulation, 2002, 19(6): 88–91.
[3] 谢最伟,吴新跃.基于ADAMS的碰撞仿真分析[C]//第三届中国CAE工程分析技术年会论文集, 大连, 2007:347-350.
Xie Z W, Wu X Y. Crash simulation analysis based on ADAMS [C]// The Third China CAE Analysis Technology Annual Conference, Dalian, 2007:347-350.
[4] 徐方舟, 魏小辉, 张明, 等. 基于ADAMS的齿轮齿条刚柔耦合啮合分析[J]. 机械设计与制造, 2012, 7(2): 200–202.
Xu F Z, Wei X H, Zhang M, et al. Meshing analysis of rigid-flexible coupled model for rack and pinion based on ADAMS[J]. Machinery Design & Manufacture, 2012, 7(2): 200–202.
[5] Kahraman K. Planetary gear train dynamics[J]. Journal of Mechanical Design, 1994, 116(9): 712–720.
[6] 王建敏.大模数渐开线直齿圆柱齿轮弯曲强度研究[D].郑州:郑州机械研究所,2006.
Wang J M. Study on the bending strength of large module involute cylindrical spur gear [D]. Zhengzhou:Zhengzhou Mechanical Institute,2006.
[7] Hanumanna D, Krishnamurthy S, Narayanan S. Bending fatigue testing of gear teeth under random loading[J]. Proceedings of the Institution of Mechanical Engineers, 2001, 215(C): 773–784.
[8] Glodez S, Pehan S, Flasker J. Experimental results of the fatigue crack growth in a gear tooth root[J]. Int. J. Fatigue, 1998, 20(9): 669–675. DOI:10.1016/S0142-1123(98)00040-1
[9] James C, L i, Hyungdae Lee. Gear fatigue crack prognosis using embedded model,gear dynamic model and fracture mechanics[J]. Mechanical Systems and Signal Processing, 2005(19): 836–846.
[10] Belsak A, Flasker J. Method for detecting fatigue crack in gears[J]. Theoretical and Applied Fracture Mechanics, 2006(46): 105–113.
[11] 于世光.渐开线齿轮齿根疲劳断裂特性分析[D].南京:南京航空航天大学,2009.
Yu S G.Analysis of tooth root fatigue crack properties of involute gear [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009.