2. 成都理工大学油气藏地质及开发工程重点实验室, 四川成都 610059;
3. 中国地质大学构造与油气资源教育部重点实验室, 湖北武汉 430074
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu University of Technology, Chengdu 610059, China;
3. Key Laboratory of Tectonics and Petroleum Resources(China University of Geosciences), Ministry of Education, Wuhan 430074, China
地震数据中含有丰富的关于储层地层学、沉积学和岩石性质的信息, 地震反演是地质解释中挖掘上述信息的有效途径[1-2]。根据反演所利用的基础数据, 可将反演分为叠后反演和叠前反演。相对而言, 叠前反演信息量更丰富, 反演结果的分辨率更高。但叠后反演也有其自身的优势, 如可以相对快速地将地震波形信息转换为具有地质意义的波阻抗信息等, 指导储层的识别与刻画[3]。因此, 从反演技术的发展趋势来看, 叠后地震反演技术在油气勘探中仍然发挥着重要的作用。
在研究反演的过程中, 如何提高反演的精度一直都是国内外学者重点关注的问题, 比较常用的方法是增加先验信息。基于L2范数约束的Tikhonov正则化反演方法, 一定程度上提高了反演的精度。例如, 广义线性反演[4]和稀疏尖峰反演[5]。但是, 使用L2范数进行正则化约束会导致反演的结果过于光滑, 反射界面不明显。鉴于反射系数可看作由大量零值组成的稀疏信号, 可利用该稀疏性构造稀疏正则项, 进一步对反演结果进行约束[6]。
稀疏正则化的构建, 通常是采用L1范数进行正则化约束。在地球物理领域, 较早使用L1范数正则化的是在反褶积[7]和数据重构[8]等方面。但由于当时没有合适的算法对L1范数约束的优化问题进行准确求解, 使得L1范数正则化的反演算法未能得到进一步的推广。近十多年来, 压缩感知理论快速发展, 使得L1范数正则化再次引起了学者们的关注。
ZHANG等[9-10]使用基追踪算法求解L1范数约束问题, 通过对叠后地震数据反演得到反射系数, 为进一步增强横向连续性, 引入“Z型”空间导数进行多道反演。LIU等[11]使用L1范数正则化反演方法进行波阻抗反演, 并将该方法与阻尼最小二乘阻抗反演方法对比, 对比结果显示L1范数正则化反演方法具有更高的反演精度。张繁昌等[12]对基追踪反演算法进行改进, 将目标函数中保真项的L2范数约束替换为L1范数约束, 并使用对偶对数障碍规划算法进行反演, 反演精度相较于传统基追踪算法得到进一步提高。石战战等[13]为了增加在反演中噪声的鲁棒性, 在目标函数中引入L1范数拟合项, 提出一种L1-L1范数稀疏约束地震反演方法。ZHOU等[14]提出了一种多道基追踪叠后反演算法, 该算法在L1范数约束的基础上引入马尔可夫过程描述相邻地震道间的关系, 提高了对薄层的识别能力。WU等[15]将L1范数稀疏约束的拓展形式交叠组稀疏用于波阻抗反演, 通过交叠组稀疏的结构特性消除了局部异常值, 进一步提高反演精度。WANG等[16]提出了一种数据驱动的地震波阻抗反演方法, 该方法利用L1范数对地震空间连续信息进行约束并参与反演, 进一步提高反演精度。
上述算法大多是基于L1范数对地震数据的稀疏信息进行挖掘, 但是L1范数只是L0范数的凸松弛函数, 得到的稀疏先验信息有限, 于是直接使用L0范数进行反演[17-19]。L0范数虽然是最稀疏的范数, 但由于目前主流的求解算法是贪婪迭代策略方法[20], 这种方法容易在迭代时陷入局部极值。最近, 有学者提出Lp拟范数约束, 也就是范数的p次幂(0 < p < 1)。WOODWORTH等[21]指出Lp拟范数比L1范数更为逼近L0范数, 并提出一种求解Lp拟范数的迭代算法。之后Lp拟范数在一些领域得到应用。例如, ZHANG等[22]将Lp拟范数应用于红外目标检测中, 并与L1范数约束相比较, 证明Lp拟范数约束能够得到更准确的检测结果; CHEN等[23]将Lp拟范数约束与地震信号的时频分析结合, 提出一种稀疏时频分析方法, 得到较高精度的地震信号时频分布。总体而言, Lp拟范数相较于L1范数是一种更为稀疏的L0范数近似, 且易求解。基于以上所述, 本文提出了一种基于Lp拟范数稀疏约束的波阻抗反演方法。
选择比L1范数更为稀疏的Lp拟范数(0 < p < 1)作为稀疏约束, 为了对Lp拟范数这类非凸优化问题有效求解, 选择使用交替方向乘子算法[24], 对目标函数引入拉格朗日乘子项及对偶项, 将目标函数分解为多个可以求解的子函数, 交替求解。最后, 将该方法应用于理论模型数据和实际数据的反演, 证明该方法反演结果的精度更高。
1 基本原理 1.1 正演模型地震信号可以由反射系数与地震子波褶积表示:
| $ \boldsymbol{S}=w * \boldsymbol{R}+\bf{N} $ | (1) |
式中: S表示地震记录; R表示反射系数; w表示子波; N为随机噪声; “*”代表卷积运算符号。将卷积运算转化为矩阵相乘, 得到公式:
| $ \boldsymbol{S}=\boldsymbol{W R}+\bf{N} $ | (2) |
W的定义为:
| $ \boldsymbol{W}=\left[\begin{array}{cccc} w(1) & 0 & \cdots & 0 \\ \vdots & w(1) & \ddots & \vdots \\ w(m) & \vdots & \ddots & 0 \\ 0 & w(m) & \vdots & w(1) \\ \vdots & \ddots & \ddots & \vdots \\ 0 & \cdots & \ddots & w(m) \end{array}\right] $ | (3) |
当反射系数较小时, 反射系数与波阻抗之间存在以下关系:
| $ R_{i, j}=\frac{\boldsymbol{Z}_{i+1, j}-\boldsymbol{Z}_{i, j}}{\boldsymbol{Z}_{i+1, j}+\boldsymbol{Z}_{i, j}} \approx \frac{1}{2}\left(\ln \boldsymbol{Z}_{i+1, j}-\ln \boldsymbol{Z}_{i, j}\right) $ | (4) |
式中: Z为波阻抗; i为采样点序号; j为道数序号。假设L=lnZ, 反射系数与波阻抗之间的关系表示为:
| $ \boldsymbol{R}=\boldsymbol{D L} $ | (5) |
式中: D为差分矩阵。D定义为:
| $ \boldsymbol{D}=\left[\begin{array}{ccccc} -\frac{1}{2} & \frac{1}{2} & 0 & \cdots & 0 \\ 0 & -\frac{1}{2} & \frac{1}{2} & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & -\frac{1}{2} & \frac{1}{2} \end{array}\right] $ | (6) |
结合以上公式, 则公式可以表示为:
| $ \boldsymbol{S}=\boldsymbol{W D L}+ \boldsymbol{N} $ | (7) |
在上述正演模型基础上, 传统的目标函数可以表示为
| $ J(\boldsymbol{L})=\min\limits _{\boldsymbol{L}}\|\boldsymbol{S}-\boldsymbol{W D L}\|_F^2 $ | (8) |
为了得到更高精度反演结果, 采用Lp拟范数对反射系数进行稀疏约束。Lp拟范数的具体表达式为:
| $ \|X\|_p^p=\sum\limits_{i=1}^n \sum\limits_{j=1}^n\left|X_{i, j}\right|^p $ | (9) |
式中: 0 < p < 1。为了分析Lp拟范数的优势, 选择二维反射系数的优化问题比较其与L1范数的稀疏性, 该问题可以表示为:
| $ J(\boldsymbol{R})=\min\limits _r\|\boldsymbol{R}\|_1 \quad \text { s.t. } \quad\left\|\boldsymbol{R}-\boldsymbol{R}^{\prime}\right\|_F^2<\varepsilon^2 $ | (10) |
| $ J(\boldsymbol{R})=\min\limits _r\|\boldsymbol{R}\|_p^p \quad \text { s.t. } \quad\left\|\boldsymbol{R}-\boldsymbol{R}^{\prime}\right\|_F^2<\varepsilon^2 $ | (11) |
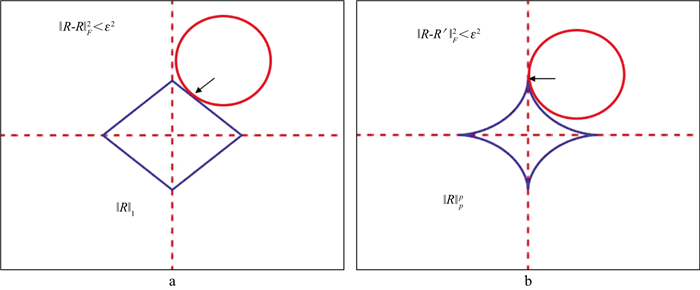
式中: R=[R1, R2]T为被估计参数; R′=[R′1, R′2]T为观测值; ε2为极小的正数。该优化问题的解如图 1所示。图 1中, 蓝色图形表示稀疏项; 红色图形表示‖R-R′‖F2 < ε2; 黑色箭头所指位置为两个图形的交点, 表示反射系数优化问题的解。由图 1可知, Lp拟范数优化问题的解能够在横坐标为0时取得, 而L1范数则无法得到。说明Lp拟范数具有更强的稀疏性。
|
图 1 反射系数优化问题 a L1范数; b Lp范数 |
结合(8)式, 并在目标函数中加入初始模型约束, 得到新的目标函数为:
| $ \begin{gathered} J(\boldsymbol{L})=\min\limits _L\|\boldsymbol{S}-\boldsymbol{W} \boldsymbol{DL}\|_F^2+\mu\left\|\boldsymbol{L}-\boldsymbol{L}_0\right\|_F^2+ \\ \lambda\|\boldsymbol{D} \boldsymbol{L}\|_p^p \end{gathered} $ | (12) |
式中: L0为初始模型; μ为初始模型约束参数; λ为正则项的约束参数。
1.3 反演方法在上述目标函数中, 不仅存在Frobenius范数, 而且还存在Lp拟范数。因此, 无法对该问题直接求解。在此引入交替方向乘子算法, 将目标函数中的不同范数约束转化为可以直接进行求解的多个子函数, 交替进行求解。具体过程为: 首先, 在(12)式中引入拉格朗日乘子项, 用R来代替DL, 即
| $ \begin{gathered} J(\boldsymbol{L})=\min\limits _{\boldsymbol{L}}\|\boldsymbol{S}-\boldsymbol{W D} \boldsymbol{L}\|_F^2+\mu\left\|\boldsymbol{L}-\boldsymbol{L}_0\right\|_F^2+ \\ \lambda\|\boldsymbol{R}\|_p^p \;\text { s.t. } \;\boldsymbol{R}=\boldsymbol{D} \boldsymbol{L} \end{gathered} $ | (13) |
引入对偶项将上述目标函数转化为无约束优化问题:
| $ \begin{gathered} J(\boldsymbol{L})=\min\limits _L\|\boldsymbol{S}-\boldsymbol{W} \boldsymbol{DL}\|_F^2+\mu\left\|\boldsymbol{L}-\boldsymbol{L}_0\right\|_F^2+ \\ \lambda\|\boldsymbol{R}\|_p^p+\eta\|\boldsymbol{R}-\boldsymbol{D} \boldsymbol{L}-\boldsymbol{C}\|_F^2 \end{gathered} $ | (14) |
式中: C表示R的对偶项; η为拉格朗日乘子的正则化参数项。
基于交替方向乘子算法(ADMM)流程, 将目标函数分解为分别与L, R, C有关的子函数。其中, 与L有关的目标函数为:
| $ \begin{gathered} J_1(\boldsymbol{L})=\min\limits _{\boldsymbol{L}}\|\boldsymbol{S}-\boldsymbol{W} \boldsymbol{DL}\|_F^2+\mu\left\|\boldsymbol{L}-\boldsymbol{L}_0\right\|_F^2+ \\ \eta\|\boldsymbol{R}-\boldsymbol{D} \boldsymbol{L}-\boldsymbol{C}\|_F^2 \end{gathered} $ | (15) |
(15) 式为常规的优化问题, 可直接采用凸优化算法的求解方法直接得到L的更新方式, 即
| $ \begin{gathered} \boldsymbol{L}^{i+1}=\left(\boldsymbol{D}^{\mathrm{T}} \boldsymbol{W}^{\mathrm{T}} \boldsymbol{W} \boldsymbol{D}+\mu \boldsymbol{E}+\eta \boldsymbol{D}^{\mathrm{T}} \boldsymbol{D}\right)^{-1} \cdot \\ \left(\boldsymbol{D}^{\mathrm{T}} \boldsymbol{W}^{\mathrm{T}} \boldsymbol{S}+\mu \boldsymbol{L}_0+\eta \boldsymbol{D}^{\mathrm{T}} \boldsymbol{R}^i-\eta \boldsymbol{D}^{\mathrm{T}} \boldsymbol{C}^i\right) \end{gathered} $ | (16) |
式中: E表示单位矩阵。在得到更新之后的L时, 则可以对R的子函数进行求解, 即
| $ J_2(\boldsymbol{R})=\min\limits _{\boldsymbol{R}} \lambda\|\boldsymbol{R}\|_p^p+\eta\|\boldsymbol{R}-\boldsymbol{D} \boldsymbol{L}-\boldsymbol{C}\|_F^2 $ | (17) |
由(17)式中可知, 该目标函数为一个基于Lp拟范数的优化问题, 在此引入软阈值收缩算法进行求解[25], 得到结果为:
| $ \begin{aligned} \boldsymbol{R}^{i+1}&=\max \left[\left|\boldsymbol{D} \boldsymbol{L}^{i+1}+\boldsymbol{C}^i\right|-\left(\frac{\eta}{\lambda}\right)^{p-2} \cdot\right. \\ &\left.\left|\boldsymbol{D} \boldsymbol{L}^{i+1}+\boldsymbol{C}^i\right|^{p-1}, 0\right] \cdot \operatorname{sign}\left(\boldsymbol{D} \boldsymbol{L}^{i+1}+\boldsymbol{C}^i\right) \end{aligned} $ | (18) |
其中, sign函数表示为:
| $ \operatorname{sign}(x)=\left\{\begin{array}{cc} 1 & x>0 \\ 0 & x=0 \\ -1 & x<0 \end{array}\right. $ | (19) |
而关于对偶项C的子函数可以表示为:
| $ J_3(\boldsymbol{C})=\min\limits _{\boldsymbol{C}} \eta\|\boldsymbol{R}-\boldsymbol{D} \boldsymbol{L}-\boldsymbol{C}\|_F^2 $ | (20) |
该问题也属于凸优化问题, 可利用其求梯度进行求解:
| $ \boldsymbol{C}^{i+1}=\boldsymbol{C}^i+\boldsymbol{D} \boldsymbol{L}^{i+1}-\boldsymbol{R}^{i+1} $ | (21) |
综合上述内容, 得到反演技术流程框架:
算法: 基于Lp稀疏约束和交替方向乘子算法的波阻抗反演
输入: 地震记录S, 初始模型L0, 地震子波w, 参数项μ, λ, η, p, 差分矩阵D, 收敛误差ε, 道数trace
输出: 地震波阻抗Z
初始化: i=0, t=0, L=L0, R=0, C=0
1. While t < trace
2. 输入单道地震数据S0, 单道初始模型L0
3. 利用(16)式计算L1
4. While ‖Li+1-Li‖2/‖Li‖2≥ε
5. i=i+1
6. 利用(18)式和(21)式计算Ri, Ci
7. 更新波阻抗对数Li+1
8. 更新乘子项及对偶项Ri+1, Ci+1
9. End While
10. 计算单道反演波阻抗Z=lg(Li+1)
11. t=t+1
12. End While
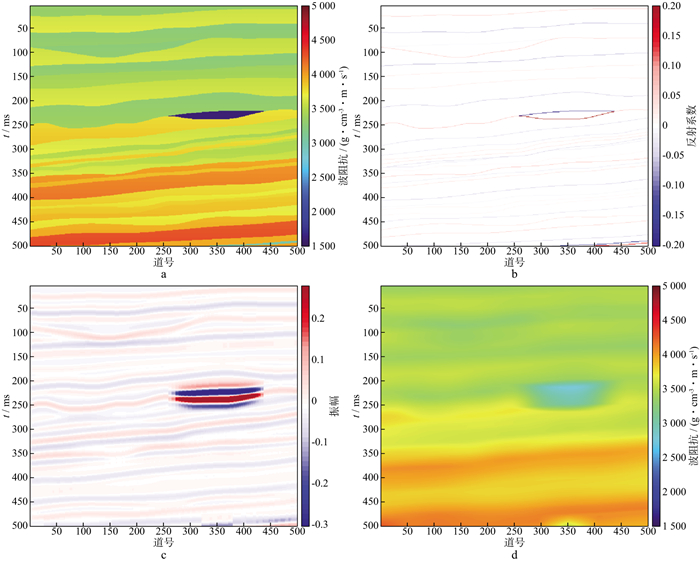
采用Marmousi2模型的部分数据构成理论模型(图 2), 对反演方法进行测试。图 2a为理论阻抗模型的二维剖面, 该模型共有500道地震数据, 每道共有450个采样点, 在采样点200至250, 道数250至450之间存在透镜体形状的含气储层。利用该波阻抗模型, 基于公式(4)得到反射系数(图 2b), 然后将得到的反射系数与30Hz的Ricker子波进行褶积得到地震记录(图 2c)。图 2d为使用高斯滤波器对原始波阻抗进行低通滤波得到的初始模型。
|
图 2 理论模型 a 理论阻抗模型; b 反射系数; c 合成地震记录; d 初始模型 |
为了验证新方法的可行性及优势, 使用基于L1范数约束的基追踪反演算法与Lp拟范数约束的反演算法对上述模型进行反演, 并比较两者与理论模型的差异。为了进一步验证新方法的抗噪性, 对合成地震记录分别加入20%和50%的高斯随机噪声后, 再次反演。
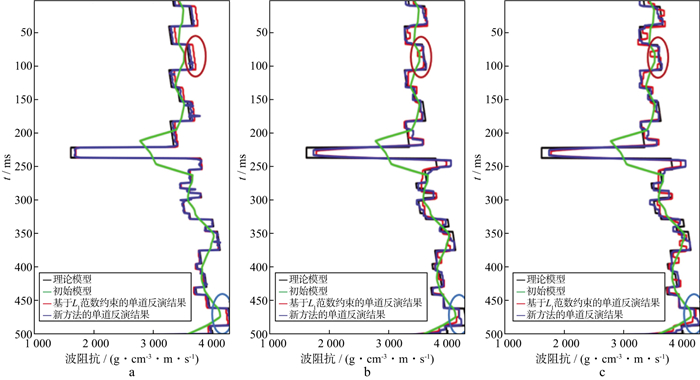
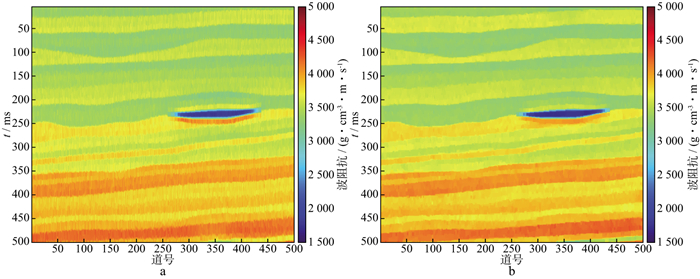
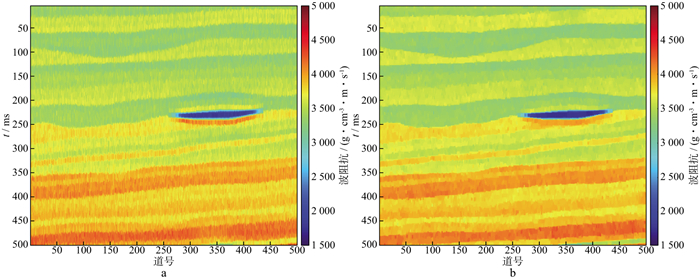
首先, 选择L1范数约束与Lp拟范数约束反演的第350道结果进行对比。不同噪声下单道反演结果对比如图 3所示, 黑色线条为理论阻抗模型; 绿色线条为初始模型; 红色线条为基于L1范数约束的单道反演结果; 蓝色线条为新方法的单道反演结果。由图 3可见, 在不同噪声情况下的单道反演结果对比中, 采用新方法得到的反演结果更接近理论模型, 该现象在红色和蓝色椭圆中较为明显。图 4, 图 5和图 6分别展示了不同噪声情况下的反演结果, 可以看出, Lp拟范数约束反演结果的横向连续性优于L1范数约束反演结果, 在纵向展布上的值也更接近理论模型。为了定量比较, 计算了两种反演结果与理论模型的信噪比(signal noise ratio, SNR)与均方误差(root mean square error, RMSE), 具体公式为:
| $ \mathrm{SNR}=10 \lg \frac{\sum\limits_{i=1}^M \sum\limits_{j=1}^N\left(L_{i, j}-\bar{L}\right)^2}{\sum\limits_{i=1}^M \sum\limits_{j=1}^N\left(\mathrm{~L}_{i, j}-\operatorname{inv} L_{i, j}\right)^2} $ | (22) |
| $ \mathrm{RMSE}=\sqrt{\frac{\sum\limits_{i=1}^M \sum\limits_{j=1}^N\left(\mathrm{~L}_{i, j}-\mathrm{inv} L_{i, j}\right)^2}{M \times N}} $ | (23) |
|
图 3 不同噪声下单道反演结果对比 a 无噪反演结果单道对比; b 含20%噪声单道反演结果对比; c 含50%噪声单道反演结果对比 |
|
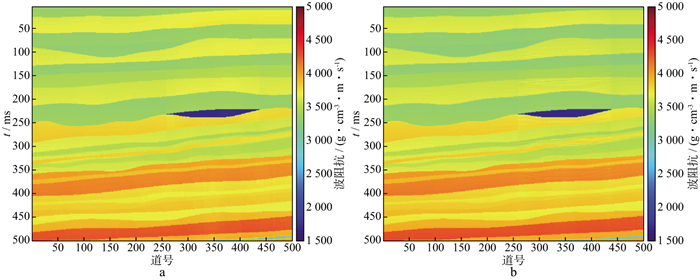
图 4 无噪声反演结果 a L1范数约束反演结果; b Lp拟范数约束反演结果 |
|
图 5 含20%噪声反演结果 a L1范数约束反演结果; b Lp拟范数约束反演结果 |
|
图 6 含50%噪声反演结果 a L1范数约束反演结果; b Lp拟范数约束反演结果 |
式中: L为理论阻抗值; L为理论阻抗的均值; invL为反演阻抗值; M和N分别为道数及采样点数。
表 1和表 2分别为两种约束条件下反演结果的信噪比与均方误差分析结果。由表 1可见, 新方法得到的反演结果的信噪比大于L1范数得到的反演结果, 而其均方误差小于L1范数的反演结果。由此证明了使用新方法得到的反演结果优于L1范数的反演结果。
| 表 1 基于理论模型的信噪比分析结果 |
| 表 2 基于理论模型的均方误差分析结果 |
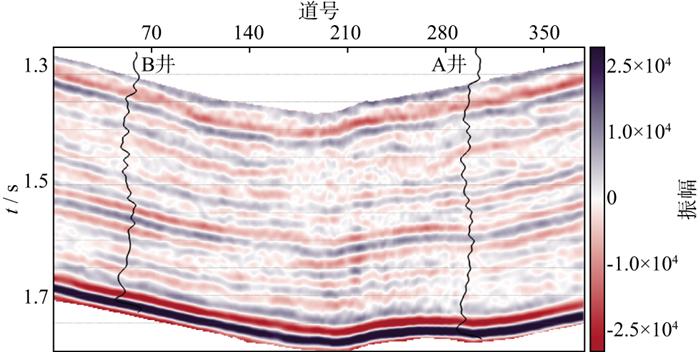
研究区位于四川盆地南缘, 目的层为志留系龙马溪组, 岩性为页岩。两口钻井(A井和B井)均钻遇优质页岩气储层, 但储层厚度较小(小于10m), 常规的阻抗反演方法由于受到精度和分辨率的限制, 很难对页岩气储层进行有效识别。为此, 选择该区域作为试验区, 验证新方法的有效性。图 7为过A井和B井的连井剖面。本次反演中, 在地震层位信息的指导下, 选择A井波阻抗数据进行外推插值并做低通滤波处理得到低频模型, 选择未进行反演的B井对反演结果进行验证。分别使用基于L1范数约束的反演方法与新方法进行反演, 得到的结果如图 8和图 9所示。
|
图 7 工区地震剖面 |
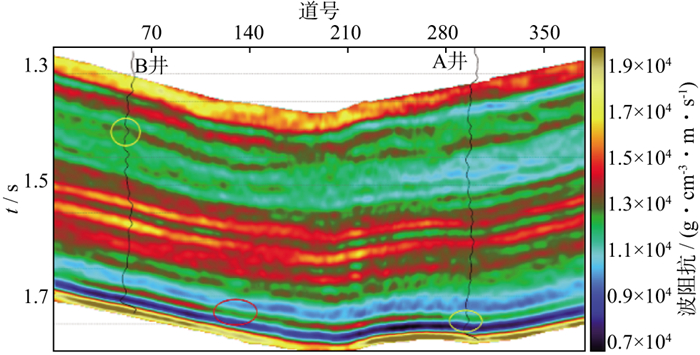
|
图 8 基于L1范数约束反演结果 |
|
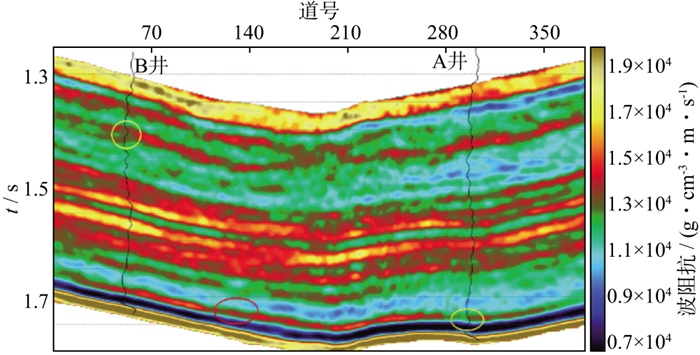
图 9 基于Lp拟范数约束反演结果 |
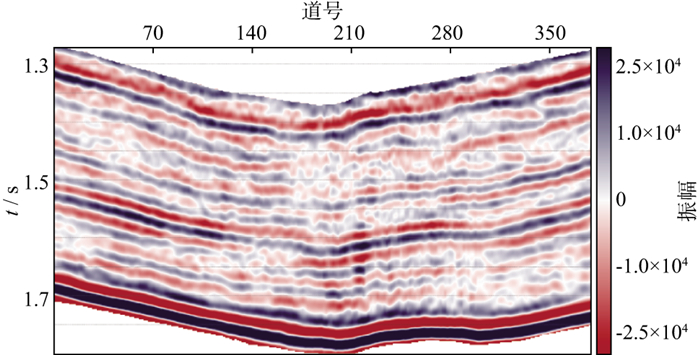
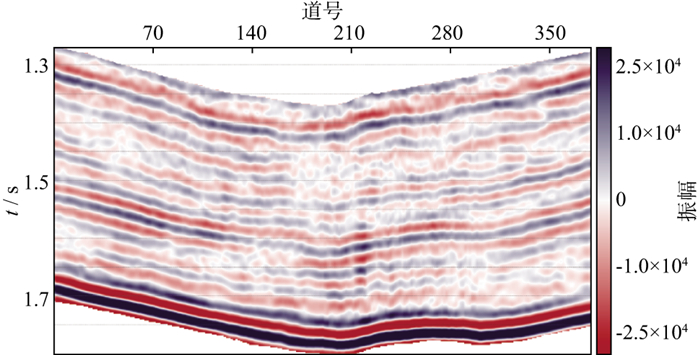
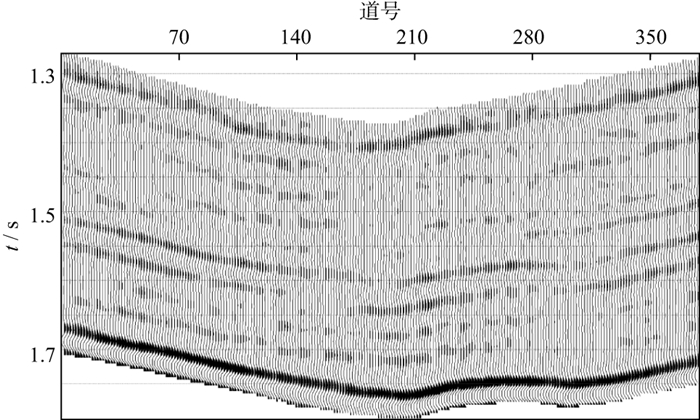
由图 8和图 9可以看到, 两种方法反演的纵波阻抗与A、B两井测井曲线吻合较好, 表明两种方法在野外资料应用中可行且有效。与基于L1范数约束反演方法的纵波阻抗剖面相比, 新方法能够反演出更多地层信息(图 8和图 9中的黄色圆圈)。同时, 新方法获得的阻抗信息具有更好的横向连续性(图 8和图 9中的红色圆圈)。为了进一步说明新方法的优越性, 利用两种方法的反演结果重新合成地震剖面(图 10和图 11), 再分别与实际地震剖面进行残差分析(图 12和图 13)。由图 12和图 13可见, 新方法的合成地震剖面与实际地震剖面残差更小, 即新方法反演结果与实际数据更吻合。
|
图 10 基于L1范数约束反演结果合成的地震剖面 |
|
图 11 基于Lp拟范数约束反演结果合成的地震剖面 |
|
图 12 基于L1范数约束反演结果合成的地震剖面与实际地震剖面的残差 |
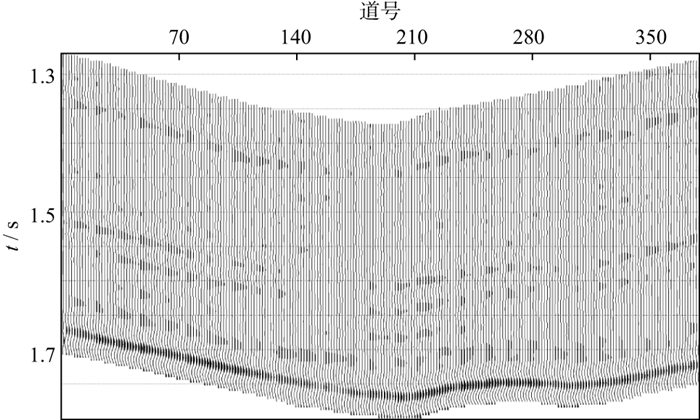
|
图 13 基于Lp拟范数约束反演结果合成的地震剖面与实际地震剖面的残差 |
为了提高反演结果的精度, 提出了一种基于Lp拟范数稀疏约束和交替方向乘子算法的波阻抗反演方法, 理论模型测试以及实际数据应用, 结果表明:
1) 针对传统L1范数挖掘地震数据的稀疏先验信息有限的问题, 引入了更为稀疏的Lp拟范数(0 < p < 1)参与反演, 该反演算法能够得到更高精度的反演结果。
2) 针对基于Lp拟范数稀疏约束的非凸优化问题, 采用交替方向乘子算法能够有效地进行求解。
新方法反演结果的精度相较于常规方法有较大提升, 但由于算法是针对单道数据的反演, 反演结果的横向连续性有待提高。下一步考虑引入全变分正则化, 对目标函数进行横向约束, 实现多道同时反演, 以提高反演结果的横向连续性。
| [1] |
高君, 黄捍东, 季敏, 等. 碳酸盐岩储层地震相控非线性反演技术及应用[J]. 石油物探, 2020, 59(3): 396-403. GAO J, HUANG H D, JI M, et al. Seismic phase-controlled nonlinear inversion of a carbonate reservoir[J]. Geophysical Prospecting for Petroleum, 2020, 59(3): 396-403. |
| [2] |
曹磊, 张达, 李宁, 等. 马尔可夫随机场反演在火山岩储层预测中的应用[J]. 石油物探, 2021, 60(1): 167-174. CAO L, ZHANG D, LI N, et al. Application of Markov random field inversion in the prediction of volcanic reservoirs[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 167-174. |
| [3] |
贾凌霄, 王彦春, 菅笑飞, 等. 叠后地震反演面临的问题与进展[J]. 地球物理学进展, 2016, 31(5): 2108-2115. JIA L X, WANG Y C, JIAN X F, et al. Problems and progress in post-stack seismic inversion[J]. Progress in Geophysics, 2016, 31(5): 2108-2115. |
| [4] |
COOKE D A, SCHNEIDER W A. Generalized linear inversion of reflection seismic data[J]. Geophysics, 1983, 48(6): 665-676. DOI:10.1190/1.1441497 |
| [5] |
VELIS D R. Parametric sparse-spike deconvolution and the recovery of the acoustic impedance[J]. Expanded Abstracts of 66th Annual Internat SEG Mtg, 2006, 2141-2146. |
| [6] |
GUITTO A, SYMES W W. Robust inversion of seismic data using the Huber norm[J]. Geophysics, 2003, 68(4): 1310-1319. DOI:10.1190/1.1598124 |
| [7] |
TAYLOR H L, BANKS S C, MCCOY J F. Deconvolution with the L1 norm[J]. Geophysics, 1979, 44(1): 39-52. DOI:10.1190/1.1440921 |
| [8] |
ZWARTJES P, GISOLF A. Fourier reconstruction with sparse inversion[J]. Geophysical Prospecting, 2007, 55(2): 199-221. DOI:10.1111/j.1365-2478.2006.00580.x |
| [9] |
ZHANG R, CASTAGNA J. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition[J]. Geophysics, 2011, 76(6): R147-R158. DOI:10.1190/geo2011-0103.1 |
| [10] |
ZHANG R, SEN M K, SRINIVASAN S. Multi-trace basis pursuit inversion with spatial regularization[J]. Journal of Geophysics and Engineering, 2013, 10(3): 035012. DOI:10.1088/1742-2132/10/3/035012 |
| [11] |
LIU C, SONG C, LU Q, et al. Impedance inversion based on L1 norm regularization[J]. Journal of Applied Geophysics, 2015, 120(9): 7-13. |
| [12] |
张繁昌, 彭德木, 张营革, 等. 基于对偶对数障碍规划算法的基追踪反演[J]. 石油物探, 2017, 56(2): 273-279. ZHANG F C, PENG D M, ZHANG Y G, et al. A basis pursuit inversion method based on the primal-dual log-barrier programming algorithm[J]. Geophysical Prospecting for Petroleum, 2017, 56(2): 273-279. |
| [13] |
石战战, 夏艳晴, 周怀来, 等. 一种基于L1-L1范数稀疏表示的地震反演方法[J]. 物探与化探, 2019, 43(4): 851-858. SHI Z Z, XIA Y Q, ZHOU H L, et al. Seismic reflectivity inversion based on L1-L1norm sparse representation[J]. Geophysics and Geochemical Exploration, 2019, 43(4): 851-858. |
| [14] |
ZHOU D Y, YIN X Y, ZONG Z Y. Multi-trace basis pursuit seismic inversion for resolution enhancement[J]. Geophysical Prospecting, 2019, 67(3): 519-531. DOI:10.1111/1365-2478.12752 |
| [15] |
WU H, LI S, CHEN Y P, et al. Seismic impedance inversion using second-order overlapping group sparsity with A-ADMM[J]. Journal of Geophysics & Engineering, 2020, 17(1): 97-116. |
| [16] |
WANG L, ZHOU H, LIU W, et al. Data-driven multichannel poststack seismic impedance inversion via patch-ordering regularization[J]. Geophysics, 2021, 86(2): R197-R210. |
| [17] |
周东勇, 文晓涛, 贺振华, 等. 双极子分解匹配追踪算法在薄层反演中的应用[J]. 石油地球物理勘探, 2014, 49(6): 1179-1183. ZHOU D Y, WEN X T, HE Z H, et al. Application of matching pursuit approach based on dipole decomposition algorithm in thin layer inversion[J]. Oil Geophysical Prospecting, 2014, 49(6): 1179-1183. |
| [18] |
刘晓晶, 印兴耀, 吴国忱, 等. 基于正交匹配追踪算法的叠前地震反演方法[J]. 石油地球物理勘探, 2015, 50(5): 925-935. LIU X J, YIN X Y, WU G Z, et al. Prestack seismic inversion method based on orthogonal matching pursuit algorithm[J]. Oil Geophysical Prospecting, 2015, 50(5): 925-935. |
| [19] |
印兴耀, 裴松, 李坤, 等. 多尺度快速匹配追踪多域联合地震反演方法[J]. 地球物理学报, 2020, 63(9): 3431-3441. YIN X Y, PEI S, LI K, et al. Seismic inversion in joint domain based on multi-scale fast matching pursuit[J]. Chinese Journal of Geophysics, 2020, 63(9): 3431-3441. |
| [20] |
张繁昌, 兰南英, 李传辉, 等. 地震匹配追踪技术与应用研究进展[J]. 石油物探, 2020, 59(4): 491-504. ZHANG F C, LAN N Y, LI C H, et al. A review on seismic matching pursuit[J]. Geophysical Prspecting for Petroleum, 2020, 59(4): 491-504. |
| [21] |
WOODWORTH J, CHARTRAND R. Compressed sensing recovery via nonconvex shrinkage penalties[J]. Inverse Problems, 2016, 32(7): 075004. |
| [22] |
ZHANG T F, WU H, LIU Y H, et al. Infrared small target detection based on non-convex optimization with Lp-Norm constraint[J]. Remote Sensing, 2019, 11(5): 559-590. |
| [23] |
CHEN Y P, PENG Z M, GHOLAMI A, et al. Seismic signal sparse time-frequency representation by Lp-quasinorm constraint[J]. Digital Signal Processing, 2019, 87(4): 43-59. |
| [24] |
BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations & Trends in Machine Learning, 2010, 3(1): 1-122. |
| [25] |
GLOWINSKI R, OSHER S J, YIN W. Splitting methods in communication, imaging, science and engineering[M]. Switzerland: Springer, 2017: 1-820.
|



