品质因子Q表征了介质本身固有的衰减特性[1], 近地表地层埋藏较浅, 压实作用较弱, 与地下地层相比, 其对地震波能量具有更强的吸收作用[2], 准确估算近地表Q值并补偿吸收衰减对高分辨地震勘探具有重要的现实意义。赵秋芳等[3]回顾并展望了常用的近地表吸收结构调查方法和手段, 指出微测井因其施工简单, 使用范围广, 是近地表吸收结构调查的主要方法。
国内外许多学者针对近地表Q值估算进行了诸多研究。HATHERLY[4]基于浅层折射波数据, 利用地震子波宽度随传播时间的变化测量浅层吸收衰减, 但测量结果精度较低; BADRI等[5]尝试在潜水面以下激发地震波, 以此来测量未完全固结地层的吸收参数, 但试验未取得稳定结果; 田钢等[6]利用微测井资料中有效直达波信息估计近地表Q值, 并通过最佳维纳滤波方法补偿吸收衰减; 宋智强等[7]在沙漠地区开展微测井实验, 基于谱比法估算Q值, 并补偿近地表吸收衰减; 宋桂桥[8]针对沙漠地区巨厚低速带地层表层结构调查难的问题, 基于超深微测井进行表层结构调查, 采用子波和Q值辅助分层的方法获得表层吸收结构; 李拥军等[9]根据微测井数据初至波能量最强的特点, 利用非零相位雷克子波匹配追踪自动提取用于Q值估算的初至波频谱和旅行时, 在谱比计算中引入整形正则化算子提高算法的稳定性, 通过深度学习算法获得准确的Q值模型; 宋吉杰等[10]针对常规衰减补偿处理中近地表Q模型建立方法存在的不足, 提出一种基于信息融合的近地表Q值估计方法以及稳定的反Q滤波处理技术, 运用信息融合策略, 利用调查点精细Q值约束相对Q值, 整合建立精确的近地表Q模型; 金子奇等[11]提出了一种改进的衰减旅行时层析方法, 在射线追踪衰减旅行时的过程中, 用方向速度梯度代替传统的速度梯度, 考虑不同射线在不同传播方向上的速度差异, 提高了衰减旅行时计算精度, 从而提高Q因子估算精度; 李伟娜等[12]鉴于旅行时间拾取误差或速度估算误差对Q因子估算的影响, 基于微测井分层速度回归分析思想, 提出了一种双线性回归品质因子Q估计算法, 同样没有考虑震源子波差异和检波器耦合响应差异对Q值估算的影响。
目前相关研究的重点主要集中在近地表Q值估算的算法上, 而实际资料对近地表Q值估算的影响却研究较少。蔡杰雄等[13]结合微测井资料分析影响近地表Q值建模的主要问题, 指出震源子波差异和检波器耦合响应差异对近地表Q值建模的影响不容忽视, 否则会影响近地表Q值模型精度; 丁冠东等[14]基于实际微测井资料研究了地震波主频变化特征, 认为不同深度激发获取的地震子波主频差异很大, 检波器耦合效应使地震子波严重缺失低频信息, 且高频部分出现类似“陷波”现象, 激发深度差异与检波器耦合差异会大幅度降低近地表Q值估算的精度; 李国发等[15]采用井地联合观测系统, 采用同一炮激发的地震记录估计Q值, 消除了震源子波差异的影响, 但并未完全消除检波器耦合响应差异对Q值估算的影响; 翟桐立等[16]基于井地一体化测井方法, 采用深井激发, 地面小排列接收的方式获得近地表Q值, 该方法较为稳定, 但并未考虑不同检波器耦合响应的差异。
本文采用四井微测井观测系统, 基于谱比法, 提出一种能同时消除震源子波差异和检波器耦合响应差异的近地表Q值估算方法。该方法通过运算, 增大了旅行时, 提高了Q值估算的稳定性, 并利用基于波场延拓反Q滤波技术补偿近地表吸收衰减, 提高了地震资料的分辨率。
1 技术方法 1.1 常规微测井Q估计及问题分析利用微测井资料不但能调查近地表速度结构, 也能调查近地表吸收结构。利用微测井资料调查近地表速度结构时主要利用的是地震波的走时信息, 受噪声干扰及波场干涉影响较少; 而调查近地表吸收结构时主要利用的是地震波的频率信息, 对噪声干扰及波场干涉十分敏感。常规微测井观测系统, 包括单井微测井和双井微测井, 通常采用地面激发、井中接收, 或者井中激发、地面接收的方式, 观测数据易受震源子波差异和检波器耦合响应差异的影响, 从而影响Q因子估算精度。
1.1.1 单井微测井图 1为单井微测井观测系统。距离激发井井口一定距离埋置一个检波器, 接收地震信号。理论上讲, 在激发井中不同深度激发两炮, 对接收到的两个直达波信号做谱比, 即可估算近地表Q因子。利用谱比法估算Q因子的前提是单炮震源子波响应一致, 并且检波器具有相同的耦合响应。该观测系统只有一个检波器, 可以不考虑检波器耦合响应的影响, 但如果单炮震源子波响应不一致, 可能会导致错误的估算结果。
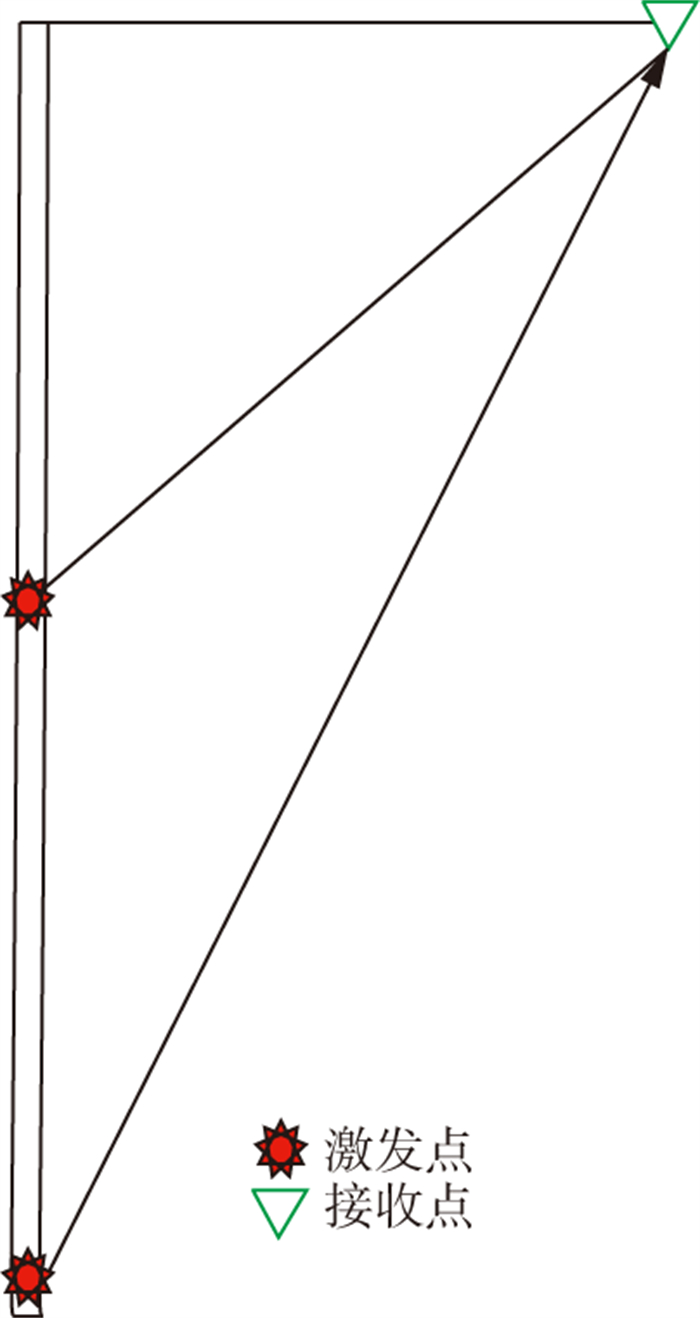
|
图 1 单井微测井观测系统示意 |
为了规避震源子波差异的影响, 采用双井微测井观测系统。如图 2所示, 在激发井中不同深度分别激发, 接收井井口和井底各埋置一个检波器接收地震信号。对同一炮激发的两个地震信号进行谱比来估算Q因子, 这样就规避了不同深度震源子波差异对Q因子估算的影响, 但双井微测井估算结果受不同检波器耦合响应差异影响。
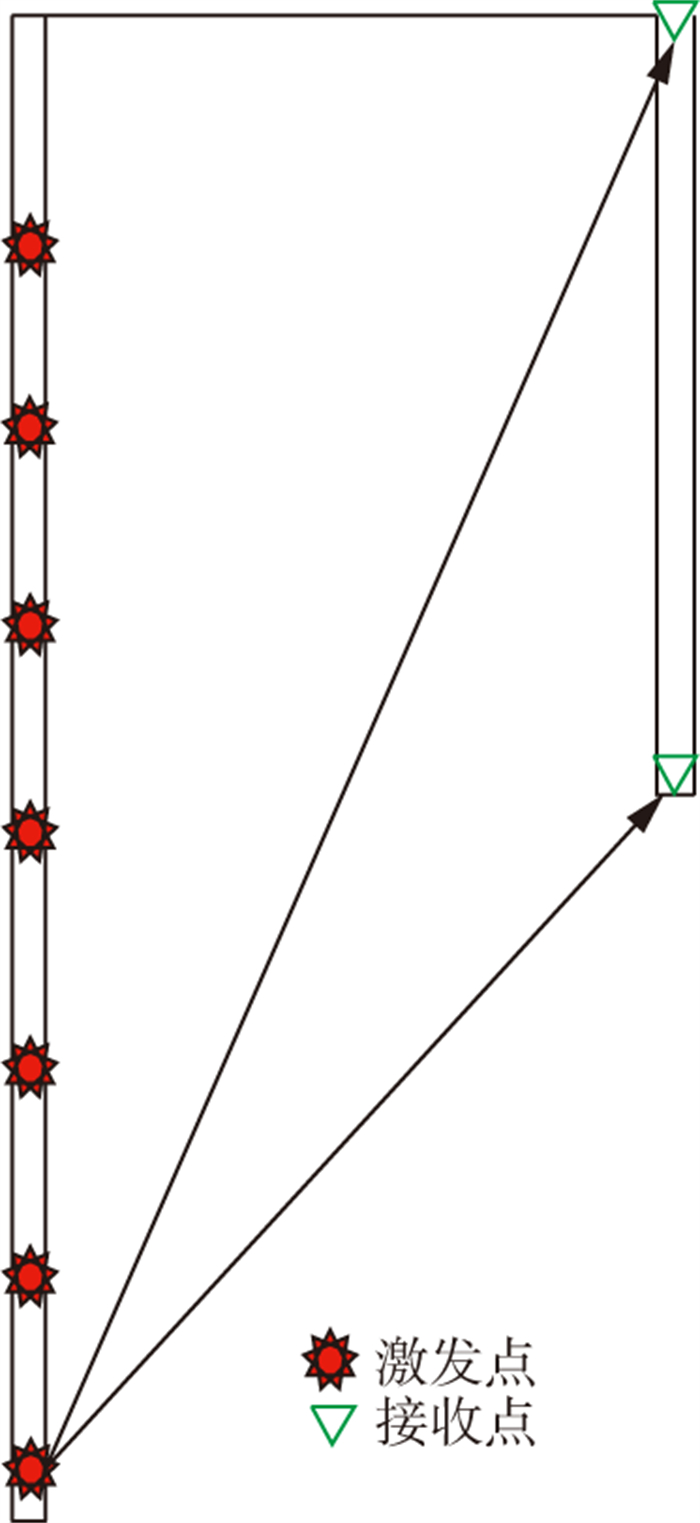
|
图 2 双井微测井观测系统示意 |
综上所述, 采用常规微测井观测系统实施Q因子估算, 单井微测井观测系统易受不同深度震源子波差异影响, 双井微测井观测系统易受检波器耦合响应差异影响。因此, 常规微测井观测数据所获得的调查结果可能存在很大的不确定性。
1.2 四井微测井观测系统图 3为四井微测井观测系统。相隔一定距离打4口井, 4口井在平面上排成一排直线, 中间两口井作为接收井, 两侧两口井作为激发井。S1和S2分别代表两口激发井中任意两炮, G1和G2分别代表埋置在接收井井底的两个检波器。
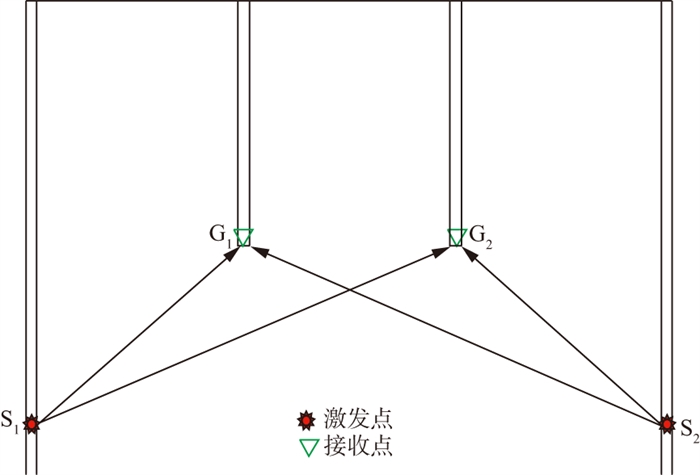
|
图 3 四井微测井观测系统示意 |
假设品质因子Q是一个与频率无关的常数, 地震波振幅谱在频率域可以用(1)式表示:
| $ x_{i j}(f)=p_{i j} \cdot s_{i}(f) \cdot g_{j}(f) \cdot \exp \left(-\pi f Q^{-1} t_{i j}\right) $ | (1) |
式中: f为频率; xij(f)表示第i炮激发, 第j个检波器接收信号的振幅谱; pij表示地震波从第i炮激发传播到第j个检波器过程中经历的与频率无关的衰减量, 例如几何扩散、透射损失等; si(f)表示第i炮激发震源子波影响因子; gj(f)表示第j个检波器耦合响应影响因子; tij代表地震波从第i炮激发传播到第j个检波器的旅行时, 例如, t11表示地震波从激发点S1处传播到接收点G1处的旅行时; Q代表地层品质因子。对公式(1)取自然对数有:
| $ X_{i j}(f)=P_{i j}+S_{i}(f)+G_{j}(f)-\pi f Q^{-1} t_{i j} $ | (2) |
式中: Xij(f)表示地震波从第i炮激发传播到第j个检波器接收信号的振幅谱的自然对数; Pij表示第i炮激发传播到第j个检波器过程中经历的与频率无关的衰减量的自然对数; Si(f)表示第i炮激发震源子波影响因子的自然对数; Gj(f)代表第j个检波器耦合响应影响因子的自然对数。
根据公式(2), 对于第一炮激发, 两个埋放在井底的检波器接收信号的自然对数谱可以用方程组(3)表示:
| $ \left\{\begin{array}{l} X_{11}(f)=P_{11}+S_{1}(f)+G_{1}(f)-\pi f Q^{-1} t_{11} \\ X_{12}(f)=P_{12}+S_{1}(f)+G_{2}(f)-\pi f Q^{-1} t_{12} \end{array}\right. $ | (3) |
用该方程组中的下式减去上式有:
| $ \begin{gathered} X_{12}(f)-X_{11}(f)=P_{12}-P_{11}+G_{2}(f)- \\ G_{1}(f)-\pi f Q^{-1}\left(t_{12}-t_{11}\right) \end{gathered} $ | (4) |
公式(4)表示消除第一炮激发因素影响, 残留检波器耦合影响的衰减曲线。
同理, 对于第2炮激发, 两个埋置在井底的检波器接收信号的自然对数谱可以表示为:
| $ \left\{\begin{array}{l} X_{21}(f)=P_{21}+S_{2}(f)+G_{1}(f)-\pi f Q^{-1} t_{21} \\ X_{22}(f)=P_{22}+S_{2}(f)+G_{2}(f)-\pi f Q^{-1} t_{22} \end{array}\right. $ | (5) |
用方程组(5)的上式减去下式有:
| $ \begin{gathered} X_{21}(f)-X_{22}(f)=P_{21}-P_{22}+G_{1}(f)- \\ G_{2}(f)-\pi f Q^{-1}\left(t_{21}-t_{22}\right) \end{gathered} $ | (6) |
将公式(4)和公式(6)相加, 有:
| $ X(f)=P-\pi f Q^{-1} t $ | (7) |
式中: t=t12-t11+t21-t22, 代表总旅行时; P代表与频率无关的总衰减量。公式(7)表示同时消除激发和接收因素影响的衰减曲线。衰减曲线表现为频率相关函数, 可以利用其斜率估算Q值:
| $ Q^{-1}=\frac{-M}{\pi t} $ | (8) |
式中: M为线性拟合斜率。
该方法联立两炮激发, 两道接收的4个直达波记录, 通过数学运算, 不但同时消除了震源子波差异和检波器耦合响应差异对Q因子估算的影响, 而且通过运算增大了旅行时, 进一步提高了Q因子估算的稳定性。
2 试验及分析为了验证和说明利用前述四井微测井观测系统实施近地表Q因子估算方法的可行性与稳定性, 在中国东部某油田开展了野外实际应用试验。为便于对比分析, 下面首先对常规微测井估算Q因子的局限性进行简要分析。
参考图 1所示的单井微测井观测系统, 采用电火花震源, 在激发井中9 m及5 m深度分别激发, 地面检波器接收的共检波点道集如图 4a所示。图 4a中第1道为9 m深度激发的地震信号, 第2道为5 m深度激发的地震信号。图 4b为两道直达波信号对应的振幅谱。理论上讲, 9 m深度激发的地震信号经历了更多的地层吸收衰减, 但其振幅谱主频却高于5 m深度激发的地震信号。出现这种现象的原因在于实际施工过程中难以保证单炮震源子波响应一致, 这样利用谱比法估算的Q因子为负值。
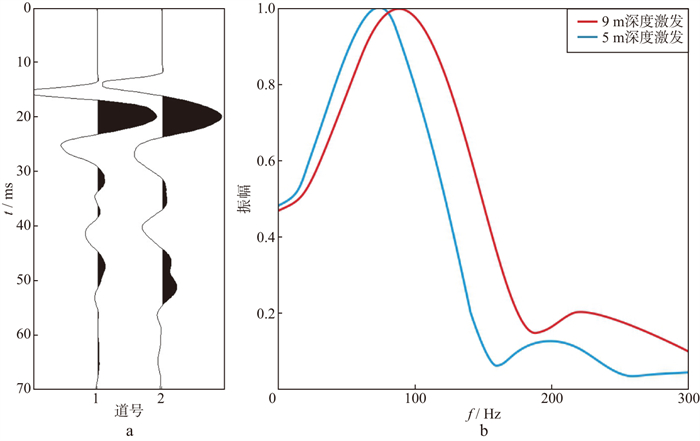
|
图 4 单井微测井共检波点道集(a)及其对应的振幅谱(b) |
基于图 2所示的双井微测井观测系统, 在激发井中18 m深度激发, 井口和井底检波器接收的共炮点道集如图 5所示。图 5中第1道为井底检波器接收的地震记录; 第2道为井口检波器接收的地震记录。由于井底检波器很难保证与井壁完全耦合, 因此井底检波器直达波信号尾部抖动十分明显, 导致难以分离出有效直达波信号, 双井微测井受不同检波器耦合响应差异影响, 难以准确估算近地表Q值。
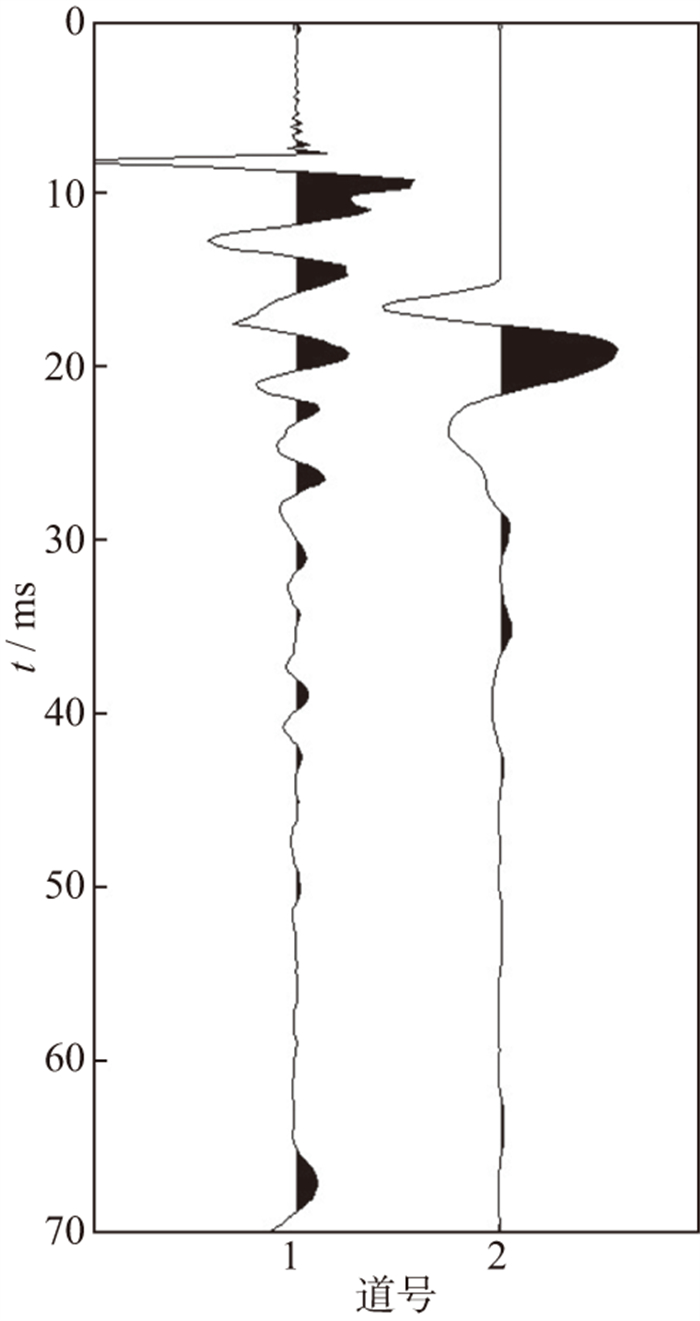
|
图 5 双井微测井共炮点道集 |
基于图 3所示四井微测井观测系统, 激发井井深均为18 m, 水平间隔为20 m。采用电火花震源, 由深至浅依次激发, 激发深度分别为18, 15, 12, 9, 6, 4, 2, 1 m, 共激发8炮。接收井井深均为9 m, 水平间隔为4 m。在接收井井底各埋置一个检波器接收地震信号。基于谱比法, 联立两炮激发、两个井底检波器分别接收的4个直达波信号的振幅谱, 通过计算得到图 6所示的衰减曲线, 同时消除了震源子波差异影响和检波器耦合响应差异影响。
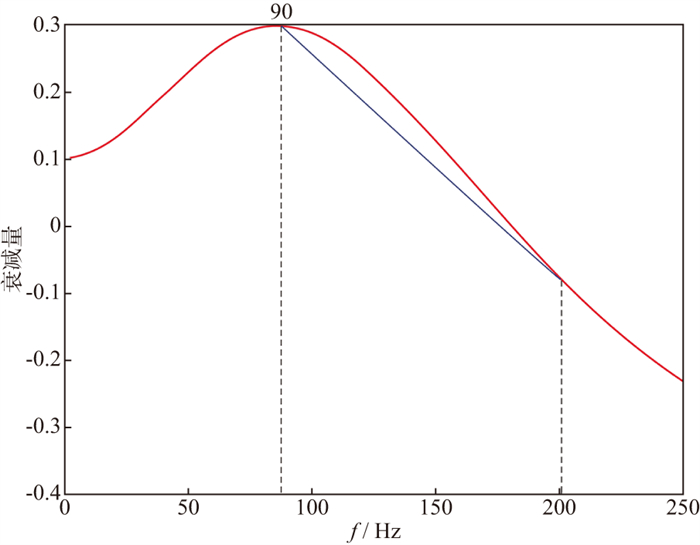
|
图 6 同时消除激发和接收因素影响的衰减曲线 |
在90 Hz之前的低频段, 观察到衰减量随频率的增大而增大的现象, 这是由于近场影响造成的。微测井观测和常规地震观测相比, 炮检距一般较小, 因此观测数据易受近场影响, 但近场对地震波频谱的影响通常表现在低频段。由于频谱低频段受近场效应影响明显, 高频段又易受噪声干扰, 因此, 我们优选90~200 Hz频带范围计算Q值, 基于谱比法, 估算出该试验点的近地表Q值约为12。
实际试验资料分析结果表明, 常规微测井观测数据受震源子波差异和检波器耦合响应差异影响, 近地表吸收结构调查结果存在很大的不确定性。利用四井微测井观测数据, 通过合理计算和优选频带规避了常规微测井缺陷, 获得较为稳定可靠的近地表Q值。
3 实际应用研究区位于中国东部某油田, 面积近150 km2, 地表主要是旱地农作物, 近地表为厚层胶泥夹少量薄层暗色泥沙。根据以往表层调查结果, 该地区地表高程起伏较小, 地层结构相对简单。近地表地层近乎为单层结构, 地层内部速度比较稳定, 层间散射较弱。采用四井微测井观测系统, 在研究区内以2 km×2 km网格, 共部署了48个四井微测井试验点, 基本实现了研究区均匀覆盖。
研究区近地表地层厚度分布较为稳定(图 7), 近地表地层厚度多集中在10~12 m, 局部厚度较大, 最大不超过18 m。综合经济成本和安全环保两方面考虑, 两口激发井井深为18 m, 水平间隔20 m。以电火花为震源, 激发深度分别为18, 15, 12, 9, 6, 4, 2, 1 m, 共激发8炮。两口接收井井深为9 m, 水平间隔4 m。井底埋置的两个检波器均经过严格检查, 利用井下助插器保障井底检波器耦合质量, 避免由于检波器与地层耦合不好造成接收信号尾部抖动现象。
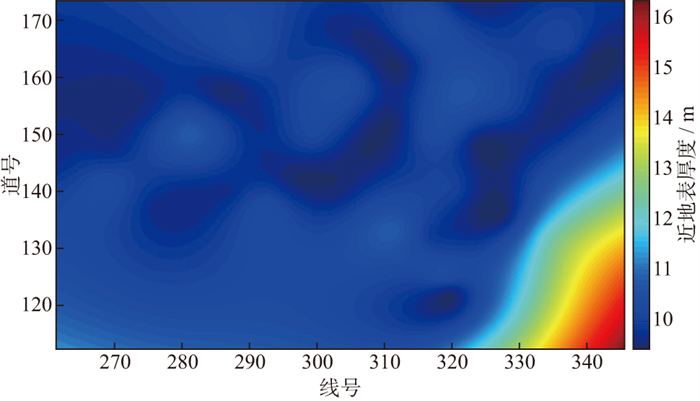
|
图 7 研究区近地表厚度平面分布 |
在每个四井微测井试验点处, 均选取两口激发井中较深的单炮数据估算近地表Q值。基于公式(8), 通过合理优选频带, 不但能有效规避近场和高频噪声的影响, 还能使旅行时增加, 计算的Q值结果更为稳定。基于每个试验点处四井微测井观测数据计算的Q值, 通过插值得到研究区近地表Q值平面分布(图 8)。研究区近地表局部存在Q值异常区, 但整体来看分布较为稳定, 多集中在8~15, 说明利用四井微测井观测系统能得到较为稳定可靠的近地表Q值。
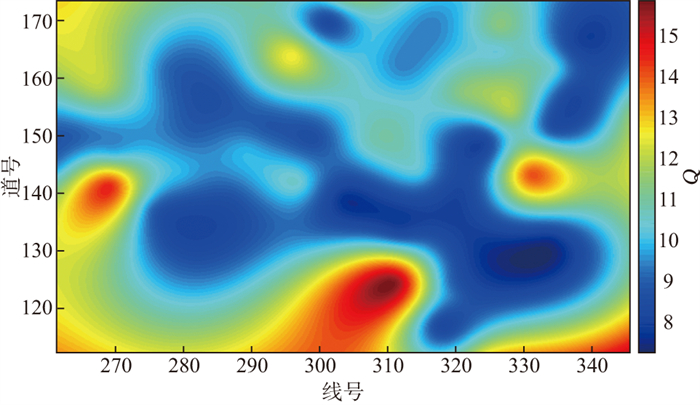
|
图 8 研究区近地表Q值平面分布 |
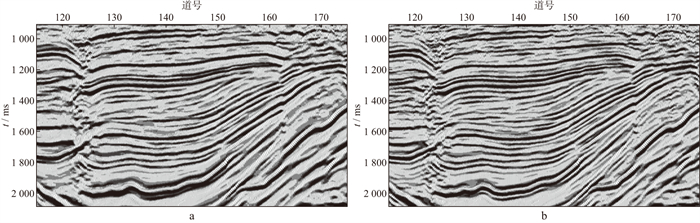
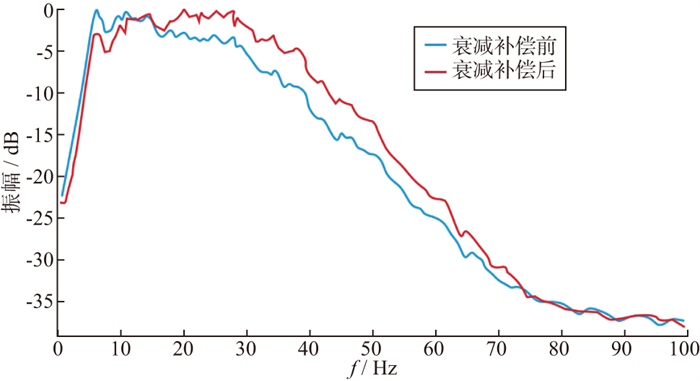
利用基于波场延拓的反Q滤波技术补偿近地表吸收衰减, 得到了补偿前、后的叠加剖面(图 9)及其频谱(图 10)。由图 9和图 10可见, 近地表吸收衰减补偿后地震资料高频成分得到合理恢复, 频谱主频明显向高频端移动。地震资料分辨率显著提高, 地震波组特征更加明显, 地质细节更加清晰。
|
图 9 近地表吸收衰减补偿前(a)、后(b)地震剖面 |
|
图 10 近地表吸收衰减补偿前、后振幅谱 |
本文采用四井微测井观测系统, 基于谱比法, 通过合理运算, 提出一种能同时消除震源子波差异和检波器耦合差异影响的近地表品质因子估算方法。工区实际应用结果表明, 该方法能获得较为稳定的近地表吸收Q参数。利用基于波场延拓的反Q滤波技术补偿近地表吸收衰减, 有效提高了地震资料的分辨率, 具有广阔的推广应用前景。
微测井观测和常规地震观测相比, 炮检距较小, 观测数据易受近场影响。但近场影响通常只在低频段, 而高频段又易受高频噪声的影响。因此, 利用微测井观测数据估算近地表Q因子时, 要优选频带, 尽量规避近场和高频噪声的影响。
本文方法在近地表地层近乎为单层结构时取得了较好的应用效果, 但当近地表为低速带和降速带两层结构时, 只能估算低速带之下降速带Q值, 无法估算低速带Q值。四井微测井观测系统有待进一步完善以适应多层Q模型地区, 下一步将尝试将四井微测井观测系统推广至近地表为两层结构地区, 届时将尝试基于完善后的观测系统建立更复杂的近地表Q值模型。
| [1] |
FUTTERMAN W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 67(13): 5279-5291. DOI:10.1029/JZ067i013p05279 |
| [2] |
李国发, 祝文亮, 翟桐立, 等. 低速带吸收补偿提高地震资料分辨率[J]. 石油学报, 2016, 37(增刊2): 64-70. LI G F, ZHU W L, ZHAI T L, et al. Enhancing seismic resolution via compensation for the weathering layer absorption[J]. Acta Petrolei Sinica, 2016, 37(S2): 64-70. |
| [3] |
赵秋芳, 云美厚, 朱丽波, 等. 近地表Q值测试方法研究进展与展望[J]. 石油地球物理勘探, 2019, 54(6): 1397-1418. ZHAO Q F, YUN M H, ZHU L B, et al. Progress and outlook of near-surfacquality factor Q measurement and inversion[J]. Oil Geophysical Prospecting, 2019, 54(6): 1397-1418. |
| [4] |
HATHERLY P J. Attenuation measurements on shallow seismic refraction data[J]. Geophysics, 1986, 51(2): 250-254. DOI:10.1190/1.1442084 |
| [5] |
BADRI M, MOONEY H M. Q measurements from compressional seismic waves in unconsolidated sediments[J]. Geophysics, 1987, 52(6): 772-784. DOI:10.1190/1.1442344 |
| [6] |
田钢, 石战结, 董世学, 等. 利用微测井资料补偿地震数据的高频成分[J]. 石油地球物理勘探, 2005, 40(5): 74-77. TIAN G, SHI Z J, DONG S X, et al. Using the uphole survey to compensate the high frequency components of seismic data[J]. Oil Geophysical Prospecting, 2005, 40(5): 74-77. |
| [7] |
宋智强, 刘斌, 陈吴金, 等. 沙漠区表层Q值求取及补偿方法研究[J]. 油气藏评价与开发, 2013, 3(4): 8-11. SONG Z Q, LIU B, CHEN W J, et al. Research on calculating and compensation methods of Q value in desert area surface[J]. Reservoir Evaluation and Development, 2013, 3(4): 8-11. DOI:10.3969/j.issn.2095-1426.2013.04.002 |
| [8] |
宋桂桥. 准噶尔盆地巨厚沙漠区地震勘探关键技术及其应用效果[J]. 石油物探, 2019, 58(4): 600-612. SONG G Q. Key techniques of seismic exploration in the desert area with very thick low-velocity layer of Junggar Basin, China[J]. Geophysical Prospecting for Petroleum, 2019, 58(4): 600-612. DOI:10.3969/j.issn.1000-1441.2019.04.015 |
| [9] |
李拥军, 宋炜, 唐传章, 等. 复数域匹配追踪近地表Q值估计及深度学习建模[J]. 石油物探, 2021, 60(1): 123-135. LI Y J, SONG W, TANG C Z, et al. Complex domain-matching pursuit for near-surface Q-estimate and deep learning modeling[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 123-135. DOI:10.3969/j.issn.1000-1441.2021.01.012 |
| [10] |
宋吉杰, 禹金营, 王成, 等. 近地表介质Q估计及其在塔河北部油田的应用[J]. 石油物探, 2018, 57(3): 436-442. SONG J J, YU J Y, WANG C, et al. Q estimation for near-surface media and its application in the Northern Tahe Oilfield, China[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 436-442. DOI:10.3969/j.issn.1000-1441.2018.03.013 |
| [11] |
金子奇, 孙赞东. 改进的衰减旅行时层析方法估计Q值[J]. 石油物探, 2018, 57(2): 222-230. JIN Z Q, SUN Z D. Improved attenuated traveltime tomography for Q estimation[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 222-230. DOI:10.3969/j.issn.1000-1441.2018.02.007 |
| [12] |
李伟娜, 云美厚, 党鹏飞, 等. 基于微测井资料的双线性回归稳定Q估计[J]. 石油物探, 2017, 56(4): 483-490. LI W N, YUN M H, DANG P F, et al. Stability Q estimation by dual linear regression based on uphole survey data[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 483-490. DOI:10.3969/j.issn.1000-1441.2017.04.003 |
| [13] |
蔡杰雄, 郑浩, 刘定进, 等. 近地表Q因子估算影响因素分析[J]. 地球物理学进展, 2018, 33(2): 547-553. CAI J X, ZHENG H, LIU D J, et al. Analysis of influencing factors of near surface Q estimation[J]. Progress in Geophysics, 2018, 33(2): 547-553. |
| [14] |
丁冠东, 张小明, 陈浩林, 等. 激发深度和检波器耦合对近地表Q值估算的影响分析[J]. 石油物探, 2018, 57(5): 678-684. DING G D, ZHANG X M, CHEN H L, et al. Effects of excitation depth and geophone coupling on near-surface Q value estimation[J]. Geophysical Prospecting for Petroleum, 2018, 57(5): 678-684. DOI:10.3969/j.issn.1000-1441.2018.05.006 |
| [15] |
李国发, 郑浩, 祝文亮, 等. 井地联合近地表Q因子层析反演[J]. 应用地球物理, 2016, 13(1): 93-102. LI G F, ZHENG H, ZHU W L, et al. Tomographic inversion of near-surface Q factor by combining surface and cross-hole seismic surveys[J]. Applied Geophysics, 2016, 13(1): 93-102. |
| [16] |
翟桐立, 马雄, 彭雪梅, 等. 基于井地一体化测量的近地表品质因子Q值估算与应用[J]. 石油物探, 2018, 57(5): 685-690. ZHAI T L, M X, PENG X M, et al. Near-surface Q factor measurements by combining surface and cross-hole seismic surveys[J]. Geophysical Prospecting for Petroleum, 2018, 57(5): 685-690. DOI:10.3969/j.issn.1000-1441.2018.05.007 |



