陆上勘探地震中, 初至波可以说是炮集中信噪比最高的波现象。初至波的识别及走时检测在表层及浅层的介质速度估计与建模中起着核心作用, 波动理论初至波走时层析速度反演及建模成为当今陆上地震波成像中关键步骤之一[1-2]。早期的初至走时大多由处理员依据经验人工拾取, 但这种可视化人工拾取过程十分繁琐耗时、效率低下, 并且过于依赖处理员的经验, 具有很强的主观性, 不同的处理员拾取的结果往往存在偏差或者不一致[3]。随着计算机技术和初至拾取算法的发展, 初至波全(半)自动化拾取方法逐渐普及[4-5], 目前的商业软件大都已具备自动拾取的功能。对于复杂地表条件下的工区, 如沙漠、戈壁、山区、盆地等, 复杂的近地表条件导致地震数据信噪比急剧降低, 道间时差变化剧烈[6-8], 此时常规的拾取方法难以满足需求, 同时随着“两宽一高”地震数据采集技术的逐渐普及[9], 地震数据量剧增, 随着人工智能技术在地球物理勘探领域的应用越来越广泛, 智能化初至拾取方法成为关注的重点。
传统的走时拾取算法主要基于单道和多道信息。基于单道的拾取算法主要依靠能量比[3, 10]、分形维数[11-12]、熵[3]、高阶统计量[13-15]等, 这类方法可以用于高信噪比数据中快速、稳定地拾取走时。基于多道的拾取算法主要有互相关方法[16-19]或模板匹配方法[20-21], 由于利用了多道之间的相关性信息, 该类方法可以在一定程度上识别低信噪比地震记录的初至, 但不能适应波形变化或存在坏道的情况。随着人工智能技术的发展与进步, 初至拾取成为人工智能算法在地震处理领域的成功应用之一。比如传统神经网络就已广泛应用于地震事件的自动分类识别[22-28], 但早期的网络结构泛化能力较差。卷积神经网络(CNN)是一种强大的深度学习算法, 具有自动提取特征或属性并同时对数据进行分类的优势, 此外, 还具有局部感知和权重共享的特性。YUAN等[29]将CNN直接应用于地震初至走时拾取中。LOGINOV等[30]以5000个训练样本训练包含4个隐藏层的CNN网络并用其完成了某3D地震数据(450×104道)的初至走时拾取工作, 正确率达到了95%。陈德武等[31]结合U-Net与SegNet深度学习网络的优点, 构建混合网络U-SegNet自动拾取初至, 网络结构更有利于分割背景噪声区域和含噪声信号区域, 提高了拾取精度。神经网络类方法属于有监督学习, 生成大量的标签样本不仅耗时, 同时也会引入人的先验认识。无监督学习算法(比如模糊聚类分析、支持向量机等)可以直接根据特征属性将地震信号自动分类, 同时也可以为有监督学习提供标签样本[32-33]。MA等[34]基于强化学习理论, 在能量比谱上自动化全局寻优实现初至走时拾取, 但该方法缺乏对模型参数的详细描述, 难以适应复杂波形; 罗飞等[35]在马尔可夫决策过程(Markov decision process, MDP)中进一步引入受空间几何信息约束的动作和转移概率, 降低了对起始状态和折扣因子选取的难度, 使地震数据初至走时拾取更加准确和自动化。总之, 初至拾取的基本思路是将地震信号的走时信息变换为某种特征属性, 从而凸显初至走时, 同时基于人工智能算法的初至拾取为地震数据处理带来了极大的便利。
在我国山前带等近地表复杂区域, 地震记录受各种近地表散射波以及面波的干扰, 信噪比低, 能量较弱。而传统的初至自动拾取方法, 普遍要求数据信噪比高, 且着重于单一属性, 此时依靠单一属性的初至拾取方法易受噪声以及地形变化剧烈的影响导致误拾。为此, 针对复杂地表地震数据, 将初至波识别与走时检测问题定位为弱初至掩埋在(较)强噪声中, 提出了一套初至波识别及走时检测智能化处理技术流程, 主要步骤包括炮集中与初至波相关的预处理、高维特征空间的构建、多属性加权K均值聚类划分初至波分布区域、多属性约束的马尔可夫决策过程初至走时检测等。实际资料应用结果表明了该方法流程的有效性和稳健性。
1 流程及关键技术 1.1 流程概述本文方法流程如图 1所示。
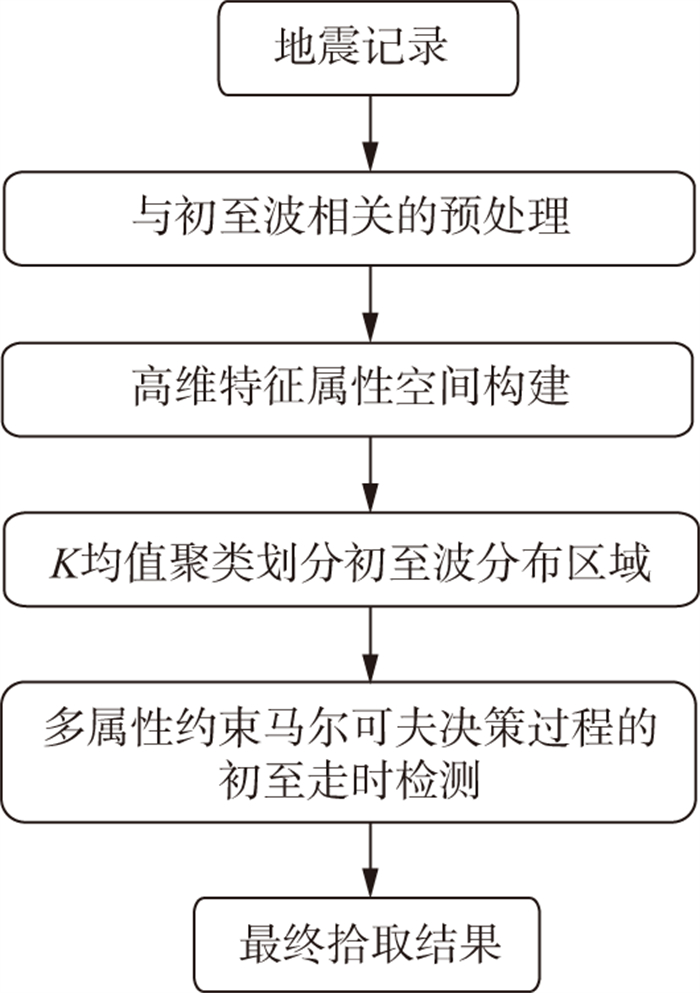
|
图 1 复杂地表区初至波识别及走时检测智能化流程 |
考虑到初至的空间连续性, 地表高程起伏会引起初至位置在相邻道之间发生跳跃, 导致初至拾取变得困难, 因此, 首先进行基于小平滑地表的道间时差跃变压制, 使其在后续拾取过程中满足更好的横向连续性。该方法首先统计地表高程, 并对其进行平滑, 获得平滑后的地表高程, 再利用(1)式计算地表高程起伏引起的道间时差校正量, 由此可以消除高波数(频)的道间时差抖动, 再将时差校正量反校回最终拾取的结果上。
| $ \Delta t=\frac{e_{1}-e_{2}}{v} $ | (1) |
式中: Δt为道间时差校正量; e1为平滑后的地表高程; e2为真实的地表高程; v为替换速度。
然后考虑高维空间中数据隐含的空间结构信息和多属性内在关系, 寻找合适的特征属性, 构建高维特征属性空间; 引入多属性加权K均值聚类划分出初至波分布区域, 缩小拾取范围, 降低拾取难度。
最后基于多属性约束马尔可夫最优决策理论框架下的走时检测技术, 将初至拾取问题看作高维特征属性空间内智能马尔可夫决策过程, 通过构建合适的模型参数, 在特定准则下进行全局寻优, 最终获得积累奖励值最大的路径, 从而智能化地拾取地震数据的初至信息。
1.2 高维特征属性空间构建一般地, 可将地震勘探中的数据认为是空间或/和时间有序的数据, 最通常的数据表达形式认为数据是多维(高维)随机向量。数据体可以定义为由源数据体生成的高维、多属性、多域特征数据体/集。初至拾取的基本思路是将地震信号的走时信息变换为某种特征属性, 在特征域中凸显差异, 从而拾取初至走时。常见的用于识别初至信息的属性从时间域看主要是利用能量变化、振幅变化、曲线长度变化、统计分布变化、信息量变化、曲线复杂度变化等[36]。现有的传统方法多着重于单一属性, 而依靠单一属性无法得到准确的拾取结果, 必须依靠多种属性相互约束。高维属性提取是高精度初至检测的基础, 其中能量属性对初至拾取较为敏感。本文采用长短时窗能量比、峰度和边缘强度这3种属性构建高维特征空间。
长短时窗均值比(STA/LTA)是信号在固定长度的短时窗和长时窗中特征函数平均值的比值。因为在地震记录中噪声的能量一般较弱, 当有效信号出现时, 信号的短时窗能量平均值(STA)会比信号的长时窗能量平均值(LTA)变化快, 从而比值增加, 当比值超过设定的阈值时, 便可用来确定初至位置。STA/LTA算法的基本公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathop{\rm LTA}\nolimits} (i) = \frac{1}{{{L_1}}}\sum\limits_{j = i}^{i + {L_1}} {{\mathop{\rm CF}\nolimits} } (j)}\\ {{\mathop{\rm STA}\nolimits} (i) = \frac{1}{{{L_\mathrm{s}}}}\sum\limits_{j = i + {L_1}}^{i + {L_1} + {L_\mathrm{s}}} {{\mathop{\rm CF}\nolimits} } (j)}\\ {\frac{{{\mathop{\rm STA}\nolimits} (i)}}{{{\mathop{\rm LTA}\nolimits} (i)}} \ge \lambda } \end{array}} \right. $ | (2) |
式中: i表示采样时刻; Ll代表长时窗长度; Ls代表短时窗长度; λ表示设定的阈值; CF(j)代表在j时刻的特征函数值。这里采用的特征函数为:
| $ \mathrm{CF}(j)=x^{2}(j) $ | (3) |
其中, x(j)表示振幅值。长、短时窗长度和阈值的选取会直接影响初至拾取的准确性。STA/LTA方法是目前应用最广泛的初至拾取方法, 计算效率较高, 但对于低信噪比数据, 存在拾取精度不足的问题[37-40]。
数据中信息的提取过程就是对数据中蕴含的结构信息进行感知和表达, 最基本的感知方法就是获取数据(随机过程)的各阶统计量。高阶统计量是描述随机过程高阶(二阶以上)统计特性的一种数学工具, 包括高阶矩、高阶累积量和高阶谱。相对于二阶统计量而言, 高阶统计量能够有效抑制高斯噪声, 并且对信号的异常更加敏感。地震数据中, 由于有效信号和噪声具有不同的统计性质, 峰度属性也可用于初至拾取[41]。峰度的表达式为:
| $ K^{\prime}=\frac{E\left[(x-E[x])^{4}\right]}{\left(E\left[(x-E[x])^{2}\right]\right)^{2}}-3 $ | (4) |
式中: E[·]表示求均值运算。在一般情况下, 地震信号中的随机噪声满足高斯分布, 而有效信号满足非高斯分布。具体计算时采用滑动窗口的方式进行, 当有效信号出现在时窗内时, 峰度值会出现明显的增大, 因此可将信号的峰度最大值对应的位置作为初至点。
图像边缘检测的目的是利用有关数学算子提取物体图像的边缘特征以确定物体的轮廓或细节。初至波一般具有能量强、起跳明显的特点, 与图形的边界特征很类似, 而预处理后的地震数据在横向上比较连续, 与边界特征相符, 因此可以将道集中各道初至时间的连线看作是初至前扰动与地震记录数据之间的边界[42]。在实际地震数据中, 首先将地震记录转化为灰度图, 这里采用取绝对值的方式。对于m道, 每道n个样点的单炮记录可以看作一幅m×n个像素的灰度图, 然后用小区域模板卷积来近似计算边缘强度。通常选用Sobel, Prewitt, Laplacian, Kirsch等微分算子进行识别, 这些算子都是以一个3×3的模板与图像中3×3的区域相乘, 得到的结果作为图像中这个区域中心位置的边缘强度[43-44], 本文选用Kirsch算子作为边缘检测算子。Kirsch算子模板(图 2)共有8个方向, 分别与地震图像中的各对应元素相乘后取计算结果的最大值作为中心点的边缘强度。例如在0°方向上, 设d(i, j)是(i, j)处的像素值, (i, j)位置处的边缘强度用其差分值来表示:
| $ \begin{aligned} &\Delta d_{0^{\circ}}=5 d(i-1, j-1)+5 d(i-1, j)+ \\ &5 d(i-1, j+1)-3 d(i, j-1)-3 d(i, j+1)- \\ &3 d(i+1, j-1)-3 d(i+1, j)-3 d(i+1, j+1) \end{aligned} $ | (5) |
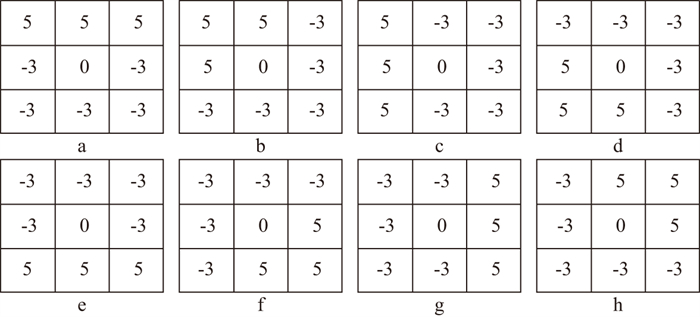
|
图 2 Kirsch算子模板 a至h方向依次为0°, 45°, 90°, 135°, 180°, 225°, 270°, 315° |
边缘强度的计算用到了高维空间中多道之间的信息, 充分利用了相邻地震道间的相关性。
1.3 K均值聚类算法确定初至波分布区域聚类方法以智能和数据驱动的方式收集类似的点归结为一类, 最终使得类内最相似、类间差异最大。K均值聚类算法是最常用的聚类方法之一, 该算法实现时简单快速, 可以用于较大的数据集, 其主要步骤是: 选择聚类数k, 随机生成k个聚类, 并确定聚类中心, 或者直接从原始数据点随机选择初始中心位置; 将每个点分配到离它最近的中心所对应的聚类, 然后重新计算新聚类的中心, 重复以上步骤, 直至中心点的变化很小或者达到指定的迭代次数。K均值聚类应用于初至拾取, 可以完成初至与非初至的二分问题[45]。考虑到不同属性对聚类和初至拾取结果的影响程度不同, 这里采用加权距离对不同的属性赋予不同的权重[46-47]:
| $ \operatorname{dist}\left(f_{i}, f_{j}\right)=\left\|\sum\limits_{k=1}^{m} w_{k}\left(f_{i k}-f_{j k}\right)\right\|_{2}^{2} $ | (6) |
式中: dist表示距离函数; wk≥0(k=1, 2, …, m)为权重系数, 表征不同属性的重要性; m为聚类属性个数; i, j为样本点(i, j=1, 2, …, n; n为样本个数); f表示特征属性值。权重系数的确定采用变异系数法。属性数据矩阵表示如下:
| $ \boldsymbol{F}=\left[\begin{array}{ccc} f_{11} & \cdots & f_{1 m} \\ \vdots & & \vdots \\ f_{n 1} & \cdots & f_{n m} \end{array}\right] $ | (7) |
首先计算样本各个属性的标准差σk:
| $ {\sigma _k} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{f_{ik}} - {{\bar f}_k}} \right)}^2}} }}{{n - 1}}} \quad k = 1, 2, \cdots , m $ | (8a) |
| $ {{\bar f}_k} = \frac{{\sum\limits_{i = 1}^n {{f_{ik}}} }}{n} $ | (8b) |
样本属性的标准差反映了各属性的绝对变异程度, 然后计算各个属性的变异系数ck:
| $ c_{k}=\frac{\sigma_{k}}{\bar{f}_{k}} \quad k=1, 2, \cdots, m $ | (9) |
变异系数反映了各个属性的相对变异程度, 属性的变异系数越大, 则属性变化越大。最后对各属性的变异系数进行归一化处理, 确定权重系数wk:
| $ {w_k} = \frac{{{c_k}}}{{\sum\limits_{i = 1}^m {{c_i}} }}\quad k = 1, 2, \cdots , m $ | (10) |
由于在实际数据中聚类结果并没有那么准确, 所以可以由聚类结果得到一条近似拟合初至的曲线, 然后将曲线上下平移得到初至波大致分布区域, 从而缩小拾取范围。
1.4 基于多属性马尔可夫决策过程的走时检测初至走时信息的拾取可以看作是处理人员在地震剖面(属性剖面)上从第一道的某点S0出发, 以经验认识为指导, 逐道挑选Sn, 最终寻找一系列满足经验认识和初至特征的点, 从而完成初至走时拾取任务的过程。这一过程可以抽象为序列决策问题, 而马尔可夫决策过程(MDP)就是一个典型的序列决策过程框架。
MDP通常用五元组〈S, A, P, R, γ〉来描述, 其中, S为有限状态集, A代表控制状态发生变化的所有可能动作的集合, P为状态转移概率(矩阵), R为奖励函数, γ代表用于计算累积收益的折扣因子。智能体从状态s通过动作a转移至s′的概率和期望奖励可分别表示为:
| $ P_{s s^{\prime}}^{a}=P\left(S_{t+1}=s^{\prime} \mid S_{t}=s, A_{t}=a\right) $ | (11) |
| $ R_{s}^{a}=E\left(R_{t+1} \mid S_{t}=s, A_{t}=a\right) $ | (12) |
MDP的本质是当前状态向下一状态转移的概率和奖赏值只取决于当前状态和选择的动作, 而与历史状态和历史动作无关, 即具有马尔可夫性。在MDP中目标是抵达目标状态的同时最大化累积收益的期望值, 价值函数是利用收益期望值评估当前状态或给定状态和动作下的智能体表现, 智能体期望未来得到的收益取决于智能体所选择的动作, 所以价值函数与特定的行为方式相关, 称之为策略。如果智能体在时刻t选择了策略π, 则π(a|s)就是当St=s时At=a的概率。vπ(s)为策略π下状态s的状态价值函数, 可表示为:
| $ \begin{aligned} &v_{\pi}(s)=E_{\pi}\left(G_{t} \mid S_{t}=s\right)=E_{\pi}\left(R_{t+1}+\gamma R_{t+2}+\right. \\ &\left.\gamma^{2} R_{t+3}+\cdots \mid S_{t}=s\right)=E_{\pi}\left(R_{t+1}+\gamma G_{t+1} \mid S_{t}=s\right)= \\ &E_{\pi}\left(R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s\right) \end{aligned} $ | (13) |
(13) 式称为vπ的贝尔曼方程, 其中, Gt表示从当前状态开始到终止状态结束整个过程所有收益按照一定比例衰减的总和, 数学表达式为:
| $ G_{t}=R_{t+1}+\gamma R_{t+2}+\cdots=\sum\limits_{k=0}^{\infty} \gamma^{k} R_{t+k+1} $ | (14) |
其中, γ为折扣因子, γ∈[0, 1], 用于削减远期决策对应的奖励权重。由上述公式可知, 价值函数由该状态的即时奖励期望和下一状态的价值期望与衰减系数的乘积两部分组成。同理可得, 在策略π下, 状态s采取动作a的动作价值函数, 表示为:
| $ \begin{gathered} q_{\pi}(s, a)=E_{\pi}\left(G_{t} \mid S_{t}=s, A_{t}=a\right)=E_{\pi}\left(R_{t+1}+\right. \\ \left.\left.\gamma q_{\pi}\left(S_{t+1}, A_{t+1}\right) \mid S_{t}=s\right), A_{t}=a\right) \end{gathered} $ | (15) |
(15) 式称为qπ的贝尔曼方程。
马尔可夫决策过程就是希望寻找一个合适的策略, 能够产生最大的累积收益。通常最优价值函数定义为所有策略下对应价值函数中的最大者, 对应的策略即为最优策略, 即:
| $ {v_*}(s) = \mathop {\max }\limits_\pi {v_\pi }(s) $ | (16) |
| $ q_{*}(s, a)=\mathop {\max }\limits_\pi q_{\pi}(s, a) $ | (17) |
式中: v*为最优状态价值函数; q*为最优动作价值函数。根据贝尔曼方程, 可以推导出价值迭代方法并求解出最优的策略[48]。
初至拾取问题可以看作是高维特征属性空间内智能马尔可夫决策过程, 模型构建如下所示。
S: 时空域地震数据的每一点位置sij=(ti, xj), i和j分别为时间和空间采样点;
A : 位移矢量, 具体为左移、右移、上移、下移;
R:
γ: γ∈[0, 1], 具体取值0.5。
2 实际数据应用为了验证本文方法的有效性, 选取复杂地表区实际数据进行测试。
2.1 西部地区可控震源数据测试图 3为西部地区某一测线的可控震源三维地震单炮记录, 共149道, 时间采样间隔为2 ms, 采样时长为1.8 s, 道间距为25 m。本数据高程起伏相对较小, 道间时差不存在跃变情况。
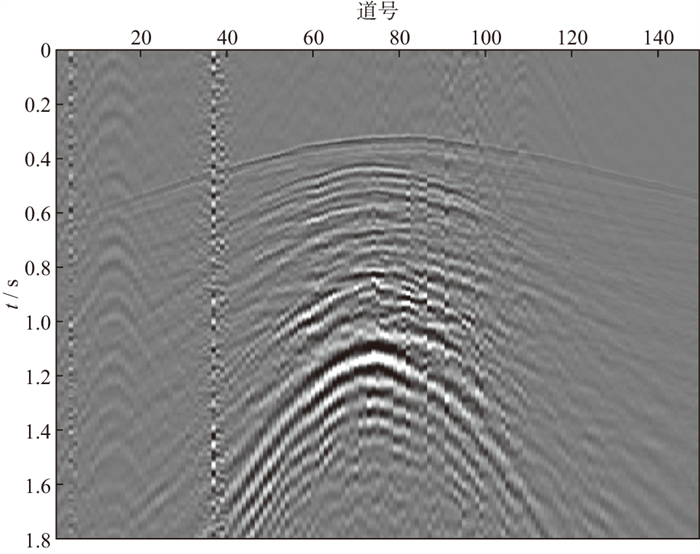
|
图 3 西部地区可控震源某一测线原始单炮记录 |
然后提取多属性构建特征空间, 能量比属性的长短时窗长度分别为100个网格点、30个网格点, 边缘属性选择Kirsch算子进行计算, 峰度属性的窗长为40个网格点。从图 4可以看出, 能量比属性和峰度属性存在初至错断、不连续的情况, 边缘强度属性在坏道部分对初至的刻画相对较差。
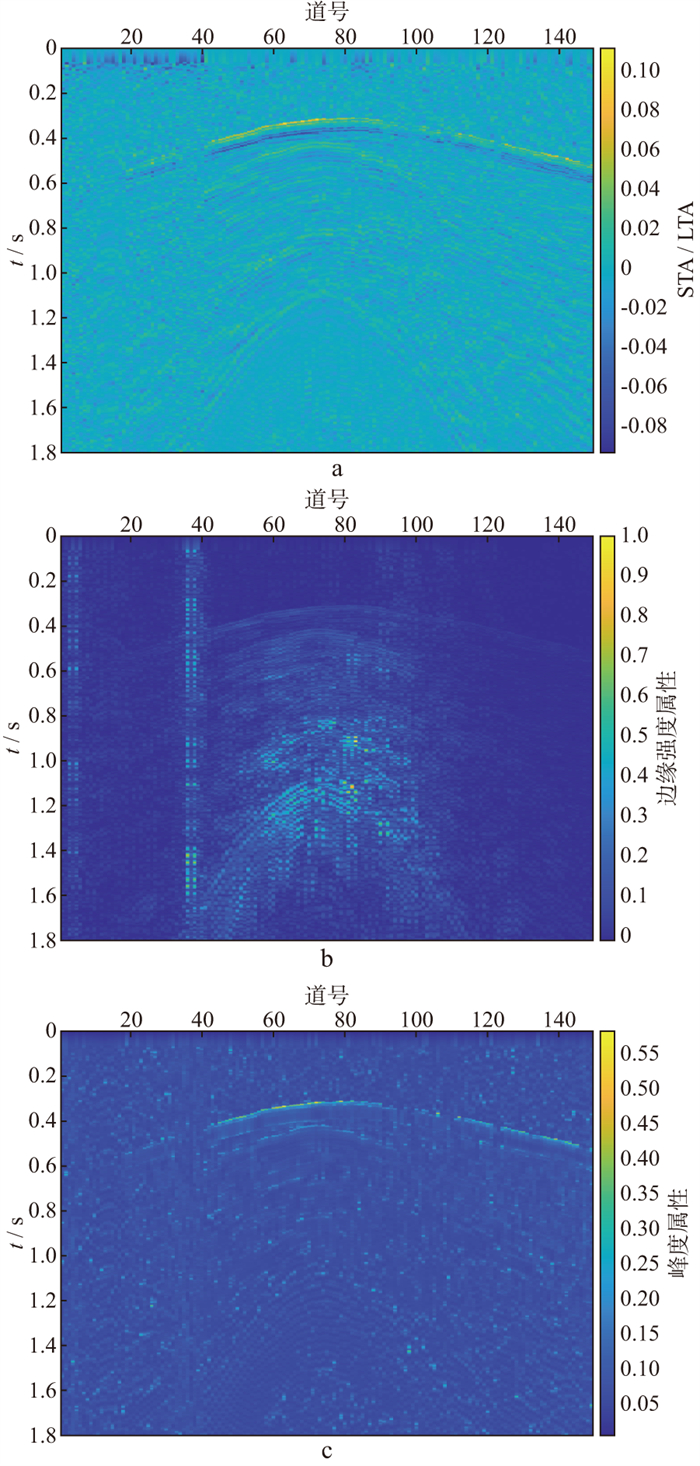
|
图 4 西部可控震源单炮记录属性 a 长短时窗能量比; b 边缘强度; c 峰度 |
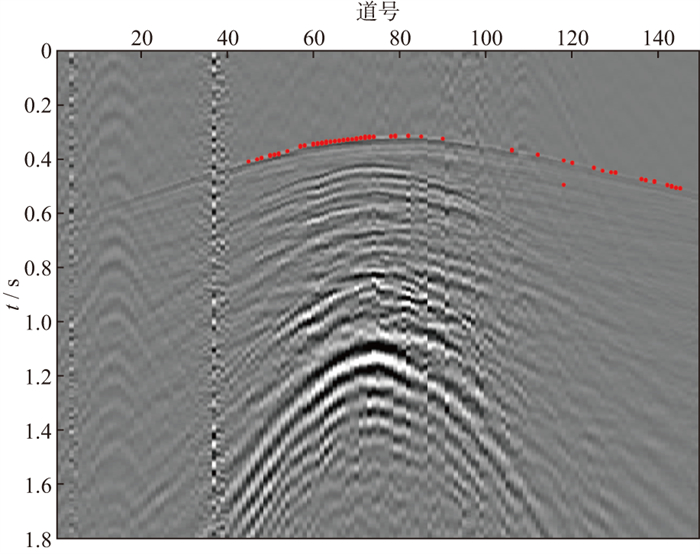
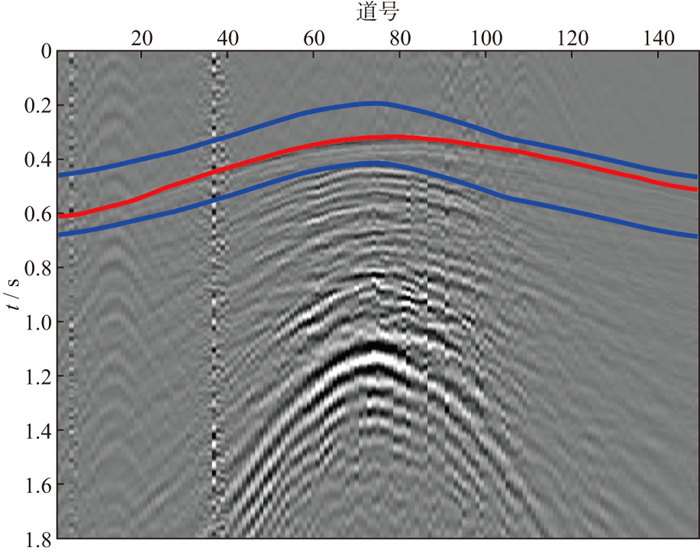
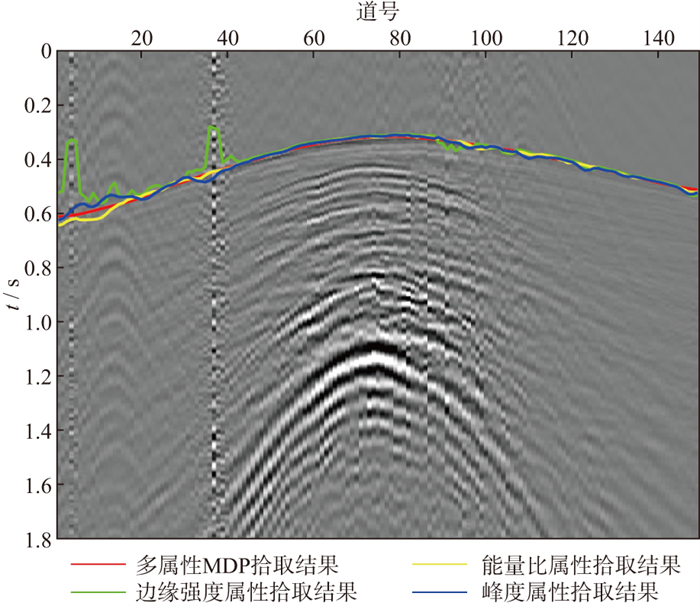
图 5为多属性加权K均值聚类结果, 由于本数据初至的能量相对较弱, 因此聚类结果为初至的点相对较少, 但是聚类结果基本为正确的初至位置。图 6为多属性加权K均值聚类得到的初至区域与最终拾取结果, 其中蓝线表示由多属性K均值聚类得到的初至区域, 红线表示拾取结果。图 7对比了基于多属性MDP拾取的结果与常规单属性拾取的结果, 可以看出, 基于多属性MDP的拾取结果稳定性较好, 基于峰度属性和能量比属性的拾取结果都存在跳跃现象, 基于边缘强度属性的拾取结果在坏道的部分相对较差, 基于本文方法的拾取结果在连续性和稳定性方面都存在较大优势。图 7证明了本文方法的有效性与稳定性。
|
图 5 西部可控震源单炮记录多属性加权K均值聚类结果(红点表示聚类结果为初至的点) |
|
图 6 西部可控震源单炮记录多属性加权K均值聚类得到的初至区域与最终拾取结果 (蓝线内为确定的初至区域, 红线为最终拾取结果) |
|
图 7 西部可控震源单炮记录多属性MDP拾取的结果与常规单属性拾取的结果对比 |
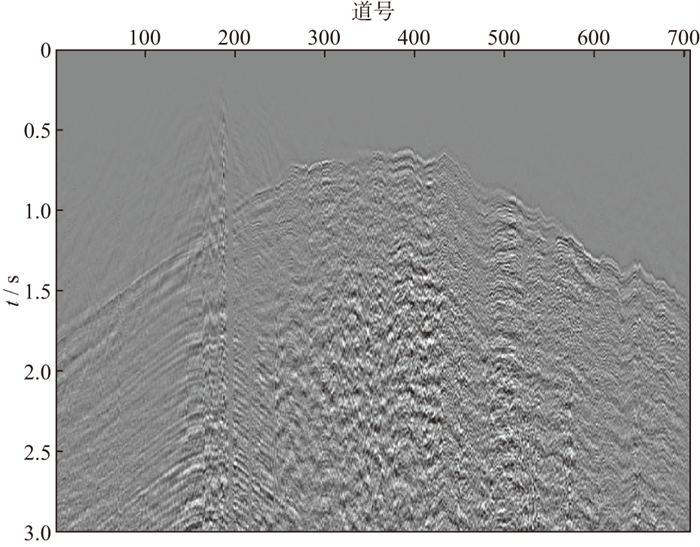
图 8为西部山地某测线的原始地震单炮记录, 共706道, 时间采样间隔为4 ms, 采样时长为3 s。该数据高程起伏较大, 首先对该地区进行高程统计, 然后通过道间时差跃变压制, 消除部分高频的道间时差, 校正后的地震单炮记录如图 9所示。
|
图 8 西部山地某测线的原始地震单炮记录 |
|
图 9 道间时差压制后的西部山地地震单炮记录 |
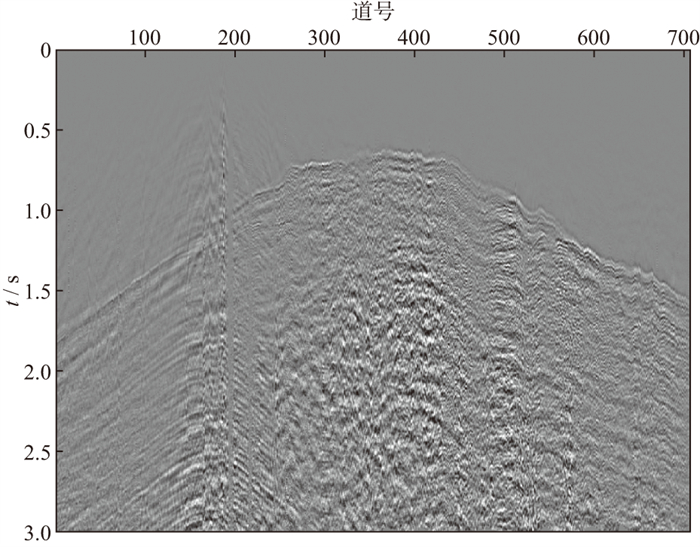
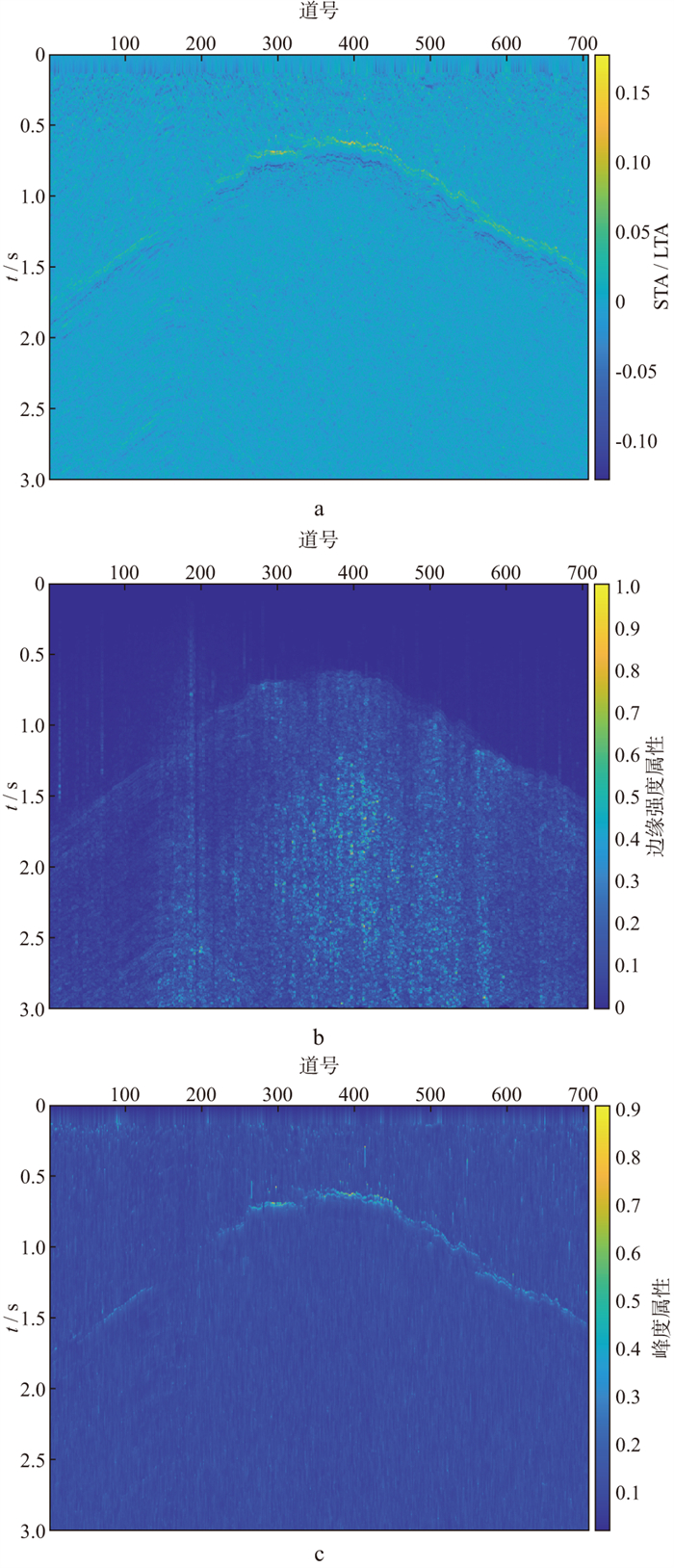
对高程平滑后的地震单炮记录进行多属性提取, 分别提取长短时窗能量比属性、边缘强度属性、峰度属性(图 10), 其中长、短时窗的长度分别为100个网格点、20个网格点, 边缘强度选取Kirsch算子, 峰度属性的窗长为30个网格点。由图 10可以看出, 在道号200附近, 由于强噪声和坏道的影响, 采用常规属性方法难以准确拾取。
|
图 10 西部山地地震单炮记录属性 a 长短时窗能量比; b 边缘强度; c 峰度 |
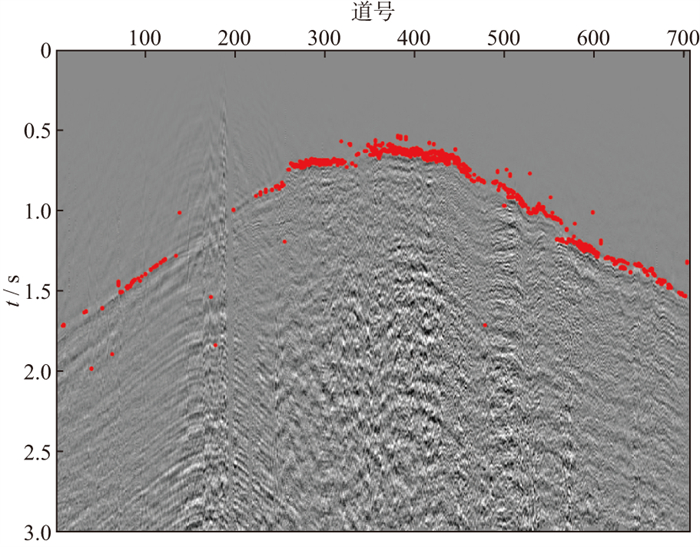
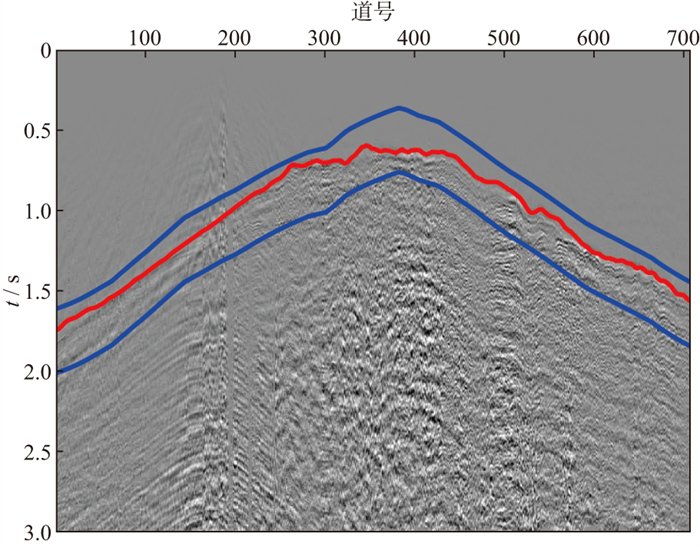
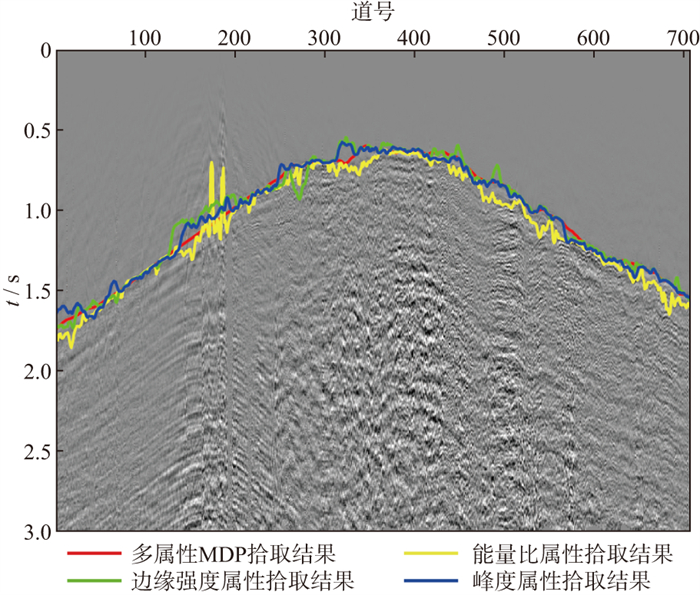
对3种属性进行多属性加权K均值聚类, 聚类结果如图 11所示, 大部分聚类为初至的点均分布在真实初至左右, 得到的初至分布范围如图 12蓝线所示, 然后在初至区域内通过多属性马尔可夫决策进行走时检测, 结果如图 12红线所示。图 13对比了基于多属性马尔可夫决策过程与常规单属性拾取的结果, 可以看出, 采用常规方法的拾取结果都存在不同程度的跳跃, 采用本文方法的拾取结果明显更加准确、连续性更好。
|
图 11 西部山地地震单炮记录多属性加权K均值聚类结果(红点表示聚类结果为初至的点) |
|
图 12 西部山地地震单炮记录多属性加权K均值聚类得到的初至区域及最终拾取结果 (蓝线内为确定的初至区域, 红线为拾取结果) |
|
图 13 西部山地地震单炮记录多属性MDP与常规单一属性拾取结果对比 |
初至拾取是地震数据处理中的重要一步, 复杂地表区的初至拾取问题可以看作是强噪声下的、存在道间时差的、近似线性信号(变化轨迹)的估计问题。本文方法的关键在于构建高维多属性特征空间, 并在MDP框架下, 利用多属性约束进行拾取。针对复杂地表地震数据, 采用小平滑地表进行时差跃变压制, 能够避免出现初至点跃变; 其次通过构建高维特征空间、进行高维多属性的提取, 在属性特征域中凸显初至的差异, 充分利用了地震数据的空间结构信息; 然后利用K均值聚类确定初至分布范围, 缩小了拾取范围, 降低了拾取难度; 最后利用多属性约束的马尔可夫决策过程拾取初至, 使得拾取结果具有更好的横向连续性。实际数据测试结果表明, 与常规单一属性相比, 采用本文方法能够自然回避由坏道、噪声产生的错误初至信息, 在一些信噪比较低、弱能量区域拾取效果更好。
在复杂地表区进行初至波的识别与走时检测面临的最主要问题是信噪比低, 因此要先通过预处理、去噪得到较为理想的、后续用于拾取的地震记录, 如何利用合适的去噪方法, 在去噪的同时保护好初至信息, 是需要进一步思考和研究的方向。包括属性数量在内的属性选取还需要做进一步的研究和测试。另外, 本文关于先验信息的利用还不充分, 在三维数据初至拾取中, 可以将震源附近较好的拾取结果作为先验约束应用到离震源较远的区域中。
| [1] |
冯波, WU Ru-Shan, 罗飞, 等. 广义Rytov近似有限频初至层析[J]. 石油地球物理勘探, 2021, 56(1): 92-99. FENG B, WU R S, LUO F, et al. Wave-equation traveltime tomography using the generalized Rytov approximation[J]. Oil Geophysical Prospecting, 2021, 56(1): 92-99. |
| [2] |
王华忠, 冯波, 王雄文, 等. 特征波反演成像理论框架[J]. 石油物探, 2017, 56(1): 38-49. WANG H Z, FENG B, WANG X W, et al. The theoretical framework of characteristic wave inversion imaging[J]. Geophysical Prospecting for Petroleum, 2017, 56(1): 38-49. DOI:10.3969/j.issn.1000-1441.2017.01.005 |
| [3] |
SABBIONE J I, VELIS D. Automatic first-breaks picking: New strategies and algorithms[J]. Geophysics, 2010, 75(4): V67-V76. DOI:10.1190/1.3463703 |
| [4] |
VANDECAR J C, CROSSON R S. Determination of teleseismic relative phase arrival times using multi-channel cross-correlation and least squares[J]. Bulletin of the Seismological Society of America, 1990, 80(1): 150-169. |
| [5] |
LOU X, VAN DER LEE S, LLOYD S. AIMBAT: A python/matplotlib tool for measuring teleseismic arrival times[J]. Seismological Research Letters, 2013, 84(1): 85-93. DOI:10.1785/0220120033 |
| [6] |
蔡存军, 毛锐强, 彭志文, 等. 低信噪比地震资料初至自动拾取技术[J]. 石油物探, 2020, 59(4): 517-529. CAI C J, MAO R Q, PENG Z W, et al. Automatic first-arrival picking from seismic data with low signal-to-noise ratio[J]. Geophysical Prospecting for Petroleum, 2020, 59(4): 517-529. DOI:10.3969/j.issn.1000-1441.2020.04.003 |
| [7] |
王亚娟, 李怀良, 庹先国, 等. 一种强噪声微地震信号P震相初至拾取的新方法[J]. 石油物探, 2020, 59(3): 356-365. WANG Y J, LI H L, TUO X G, et al. Picking the P-phase first arrival of microseismic data with strong noise[J]. Geophysical Prospecting for Petroleum, 2020, 59(3): 356-365. DOI:10.3969/j.issn.1000-1441.2020.03.004 |
| [8] |
宋维琪, 喻志超, 杨勤勇, 等. 低信噪比微地震事件初至拾取方法研究[J]. 石油物探, 2013, 52(6): 596-601. SONG W Q, YU Z C, YANG Q Y. The first arrival picking method of microseismic events with low S/N[J]. Geophysical Prospecting for Petroleum, 2013, 52(6): 596-601. |
| [9] |
王华忠. "两宽一高"油气地震勘探中的关键问题分析[J]. 石油物探, 2019, 58(3): 313-324. WANG H Z. Key problem analysis in seismic exploration based on wide-azimuth, high-density, and broadband seismic data[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 313-324. DOI:10.3969/j.issn.1000-1441.2019.03.001 |
| [10] |
COPPENS F. First arrival picking on common-offset trace collections for automatic estimation of static corrections[J]. Geophysical Prospecting, 1985, 33(8): 1212-1231. DOI:10.1111/j.1365-2478.1985.tb01360.x |
| [11] |
BOSCHETTI F, DENTITH M D, LIST R. A fractal-based algorithm for detecting first arrivals on seismic traces[J]. Geophysics, 1996, 61(4): 1095-1102. DOI:10.1190/1.1444030 |
| [12] |
JIAO L X, MOON W M. Detection of seismic refraction signals using a variance fractal dimension technique[J]. Geophysics, 2000, 65(1): 286-292. DOI:10.1190/1.1444719 |
| [13] |
YUNG S K, IKELLE L T. An example of seismic time-picking by third-order bicoherence[J]. Geophysics, 1997, 62(6): 1947-1952. DOI:10.1190/1.1444295 |
| [14] |
SARAGIOTIS C D, HADJILEONTIADIS L J, REKANOS I T, et al. Automatic P phase picking using maximum kurtosis and k-statistics criteria[J]. IEEE Geosci Remote Sens Letters, 2004, 1(3): 147-151. DOI:10.1109/LGRS.2004.828915 |
| [15] |
TSELENTIS G A, MARTAKIS N, PARASKEVOPOULOS P, et al. Strategy for automated analysis of passive microseismic data based on S-transform, Otsu's thresholding, and higher order statistics[J]. Geophysics, 2012, 77(6): KS43-KS54. DOI:10.1190/geo2011-0301.1 |
| [16] |
PERALDI R, CLEMENT A. Digital processing of refraction data study of first arrivals[J]. Geophysical Prospecting, 1972, 20(3): 529-548. DOI:10.1111/j.1365-2478.1972.tb00653.x |
| [17] |
GELCHINSKY B, SHTIVELMAN V. Automatic picking of first arrivals and parameterization of traveltime curves[J]. Geophysical Prospecting, 1983, 31(6): 915-928. DOI:10.1111/j.1365-2478.1983.tb01097.x |
| [18] |
MOLYNEUX J B, SCHMITT D R. First-break timing: Arrival onset times by direct correlation[J]. Geophysics, 1999, 64(5): 1492-1501. DOI:10.1190/1.1444653 |
| [19] |
喻志超, 谭玉阳, 翟尚, 等. 基于波形相似特征的微地震事件初至拾取及全局校正[J]. 地球物理学报, 2019, 62(12): 4782-4793. YU Z C, TAN Y Y, ZHAI S, et al. Arrival picking and global refinement for microseismic events based on waveform similarity[J]. Chinese Journal of Geophysics, 2019, 62(12): 4782-4793. DOI:10.6038/cjg2019M0296 |
| [20] |
PLENKERS K J, RITTER R R, SCHINDLER M. Low signal-to-noise event detection based on waveform stacking and cross-correlation: Application to a stimulation experiment[J]. Journal of Seismology, 2013, 17(1): 27-49. DOI:10.1007/s10950-012-9284-9 |
| [21] |
CAFFAGNI E, EATON D W, JONES J P, et al. Detection and analysis of microseismic events using a Matched Filtering Algorithm (MFA)[J]. Geophysical Journal International, 2016, 206(1): 644-658. |
| [22] |
YUAN S Y, ZHAO Y, XIE T, et al. SegNet-based first-break picking via seismic waveform classification directly from shot gathers with sparsely distributed traces[J]. Petroleum Science, 2022, 19(1): 162-179. DOI:10.1016/j.petsci.2021.10.010 |
| [23] |
周创, 居兴国, 李子昂, 等. 基于深度卷积生成对抗网络的地震初至拾取[J]. 石油物探, 2020, 59(5): 795-803. ZHOU C, JU X G, LI Z A, et al. A deep convolutional generative adversarial network for first-arrival pickup from seismic data[J]. Geophysical Prospecting for Petroleum, 2020, 59(5): 795-803. |
| [24] |
MURAT M E, RUDMAN A J. Automated first arrival picking: A neural network approach[J]. Geophysical Prospecting, 1992, 40(6): 587-604. DOI:10.1111/j.1365-2478.1992.tb00543.x |
| [25] |
MCCORMACK M D, ZAUCHA D E, DUSHEK D W. First-break refraction event picking and seismic data trace editing using neural networks[J]. Geophysics, 1993, 58(1): 67-78. DOI:10.1190/1.1443352 |
| [26] |
LANGER H, FALSAPERLA S, POWELL T, et al. Automatic classification and a-posteriori analysis of seismic event identification at Soufriere Hills volcano, Montserrat[J]. Journal of volcanology and geothermal research, 2006, 153(1/2): 1-10. |
| [27] |
MAITY D, AMINZADEH F, KARRENBACH M. Novel hybrid artificial neural network based autopicking workflow for passive seismic data[J]. Geophysical Prospecting, 2014, 62(4-Vertical Seismic Profiling and Microseismicity Frontiers): 834-847. |
| [28] |
MOUSAVI S M, LANGSTON C. Fast and novel microseismic detection using time-frequency analysis[C]//SEG Technical Program Expanded Abstracts 2016. USA: Society of Exploration Geophysicists, 2016: 2632-2636
|
| [29] |
YUAN S, LIU J, WANG S, et al. Seismic waveform classification and first-break picking using convolution neural networks[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(2): 272-276. DOI:10.1109/LGRS.2017.2785834 |
| [30] |
LOGINOV G, ANTON D, LITVICHENKO D, et al. The first-break detection for real seismic data with use of convolutional neural network[C]//81st EAGE Conference and Exhibition 2019. London: European Association of Geoscientists & Engineers, 2019: 1-5. https://doi.org/10.3997/2214-4609.201901614
|
| [31] |
陈德武, 杨午阳, 魏新建, 等. 基于混合网络U-SegNet的地震初至自动拾取[J]. 石油地球物理勘探, 2020, 55(6): 1188-1201. CHEN D W, YANG W Y, WEI X J, et al. Automatic picking of seismic first arrivals based on hybrid network U-SegNet[J]. Oil Geophysical Prospecting, 2020, 55(6): 1188-1201. |
| [32] |
CHEN Y. Automatic microseismic event picking via unsupervised machine learning[J]. Geophysical Journal International, 2020, 222(3): 1750-1764. DOI:10.1093/gji/ggaa186 |
| [33] |
蒋一然, 宁杰远. 基于支持向量机的地震体波震相自动识别及到时自动拾取[J]. 地球物理学报, 2019, 62(1): 361-373. JIANG Y R, NING J Y. Automatic detection of seismic body-wave phases and determination of their arrival times based on support vector machine[J]. Chinese Journal of Geophysics, 2019, 62(1): 361-373. |
| [34] |
MA Y, FEI T, LUO Y. A new insight into automatic first-arrival picking based on reinforcement learning[C]//81st EAGE Conference and Exhibition 2019. London: European Association of Geoscientists & Engineers, 2019: 1-5. https://doi.org/10.3997/2214-4609.201901615
|
| [35] |
罗飞, 王华忠. 基于约束Markov决策过程的初至自动识别技术[J]. 地球物理学报, 2021, 64(6): 2050-2060. LUO F, WANG H Z. Automatic first break picking based on Constrained Markov Decision Processes (CMDPs)[J]. Chinese Journal of Geophysics, 2021, 64(6): 2050-2060. |
| [36] |
杨培杰, 印兴耀, 张广智. 希尔伯特-黄变换地震信号时频分析与属性提取[J]. 地球物理学进展, 2007, 22(5): 1585-1590. YANG P J, YIN X Y, ZHANG G Z. Seismic signal time-frequency analysis and attributes extraction based on HHT[J]. Progress in Geophysics, 2007, 22(5): 1585-1590. DOI:10.3969/j.issn.1004-2903.2007.05.037 |
| [37] |
秦晅, 宋维琪. 基于时窗能量比与互信息量的微地震初至拾取方法[J]. 物探与化探, 2016, 40(2): 374-379. QIN X, SONG W Q. Automatic first arrival pickup method of microseismic event based on energy ratio and mutual information[J]. Geophysical & Geochemical Exploration, 2016, 40(2): 374-379. |
| [38] |
叶根喜, 姜福兴, 杨淑华. 时窗能量特征法拾取微地震波初始到时的可行性研究[J]. 地球物理学报, 2008, 51(5): 1574-1581. YE G X, JIANG F X, YANG S H. Possibility of automatically picking first arrival of microseismic wave by energy eigenvalue method[J]. Chinese Journal of Geophysics, 2008, 51(5): 1574-1581. DOI:10.3321/j.issn:0001-5733.2008.05.033 |
| [39] |
WONG J, HAN L, BANCROFT J, et al. Automatic time-picking of first arrivals on noisy microseismic data[J]. Canada Society of Exploration Geophysicists, 2009, 1(1/2): 1-4. |
| [40] |
吴治涛, 李仕雄. STA/LTA算法拾取微地震事件P波到时对比研究[J]. 地球物理学进展, 2010, 25(5): 1577-1582. WU Z T, LI S X. Comparison of STA/LTA P-pickers for micro seismic monitoring[J]. Progress in Geophysics, 2010, 25(5): 1577-1582. |
| [41] |
KHALAF A, CAMERLYNCK C, FLORSCH N, et al. Development of an adaptive multi-method algorithm for automatic picking of first arrival times: Application to near surface seismic data[J]. Near Surface Geophysics, 2018, 16(5): 507-526. DOI:10.1002/nsg.12014 |
| [42] |
潘树林, 高磊, 周熙襄, 等. 基于单道边界检测和样条插值的初至波自动拾取[J]. 石油物探, 2006, 45(3): 245-249. PAN S L, GAO L, ZHOU X X, et al. Automatic method of first break picking based on edge detection and spline interpolation[J]. Geophysical Prospecting for Petroleum, 2006, 45(3): 245-249. DOI:10.3969/j.issn.1000-1441.2006.03.007 |
| [43] |
李辉峰, 邹强, 金文昱. 基于边缘检测的初至波自动拾取方法[J]. 石油地球物理勘探, 2006, 41(2): 150-155. LI H F, ZOU Q, JIN W Y. Method of automatic first breaks pick-up based on edge detection[J]. Oil Geophysical Prospecting, 2006, 41(2): 150-155. DOI:10.3321/j.issn:1000-7210.2006.02.007 |
| [44] |
潘树林, 高磊, 邹强, 等. 一种实现初至波自动拾取的方法[J]. 石油物探, 2005, 44(2): 163-166. PAN S L, GAO L, ZOU Q, et al. An automatic method to pick up the first break time[J]. Geophysical Prospecting for Petroleum, 2005, 44(2): 163-166. DOI:10.3969/j.issn.1000-1441.2005.02.017 |
| [45] |
CHEN Y, ZHANG G, BAI M, et al. Automatic waveform classification and arrival picking based on convolutional neural network[J]. Earth and Space Science, 2019, 6(7): 1244-1261. DOI:10.1029/2018EA000466 |
| [46] |
周竹生, 曾维祖, 刘思琴, 等. 基于加权K均值聚类的多属性初至拾取方法[J]. 地震学报, 2020, 42(2): 177-186. ZHOU Z S, ZENG W Z, LIU S Q, et al. First arrival picking method by seismic multi-attribute based on weighted K-means clustering algorithm[J]. Acta Seismologica Sinica, 2020, 42(2): 177-186. |
| [47] |
陈东, 皮德常. 基于属性加权的改进K-Means算法[J]. 电脑知识与技术, 2009, 5(9): 2412-2413. CHEN D, PI D C. Improved K-means algorithm based on the attributes weighted[J]. Computer Knowledge and Technology, 2009, 5(9): 2412-2413. DOI:10.3969/j.issn.1009-3044.2009.09.190 |
| [48] |
SUTTON R S, BARTO A G. Reinforcement learning: An introduction[M]. Massachusetts: MIT Press, 2018: 1-342.
|



