传统偏移成像方法可以较好地处理地震波的运动学信息, 但大多采用线性正演算子的共轭转置, 而非逆算子作为其偏移算子[1-2]。因此得到的结果不能准确地反映真实的反射系数, 影响最终的成像质量。人们对由此引起的振幅不均、低频噪声、低信噪比等各种问题已进行过大量研究[3-5]。最小二乘偏移(least-squares migration, LSM)[6-8]通常基于梯度类的算法(如最速下降法等), 通过不断匹配观测数据和模拟数据之间的残差, 使残差最小化。该方法可以隐式消除Hessian效应[9], 有效压制噪声, 提升成像剖面的分辨率, 进而获得真振幅剖面。最小二乘偏移的计算成本高, 以射线类的方法为例, 虽然基于射线的偏移算法具有实现效率高的优势, 但是在最小二乘偏移的框架中, 每次迭代均需进行一次偏移和反偏移, 通常需要10次或更多的迭代次数, 这将产生至少20倍于传统偏移方法的计算成本[10]。与此同时, 不够准确的背景速度场、含噪数据、未知的震源子波等许多因素将导致数据空间最小二乘偏移的收敛速度缓慢, 甚至不收敛, 实际情况下, 计算成本将会更高。因此最小二乘偏移方法的实现效率成为了一个重要的研究方向。AOKI等[10]构建了一种去模糊化滤波器, 可以应用于最小二乘偏移中的预条件策略或正则化策略中, 相比传统算法, 该滤波器在保证高精度成像的情况下, 可以将计算效率提高约30%。KUEHL等[11]基于多平方根方程提出了最小二乘裂步偏移方法, 可以减小观测数据值和合成数据值之间的误差。YAO等[12]提出了一种非线性最小二乘逆时偏移算法, 该算法直接从反射率中生成预测数据, 无需假设它们之间存在线性关系。ZHANG等[13]提出了一种新的最小二乘逆时偏移方法, 通过观测数据和模拟数据之间的互相关最大化, 来计算最小二乘逆时偏移的最快收敛速度值。YU等[14]利用偏移解卷积滤波器处理局部偏移图像, 仅对关注的成像区域进行处理, 避免了全局计算, 该方法相当灵活。LECOMTE[15]使用基于射线的方法来估计Hessian的逆, 计算过程简洁。TANG[16]改进了原有的显式Hessian公式, 使Hessian算子的计算更加高效, 利用随机相位编码的Hessian算子可以得到振幅更为均衡的盐下成像。
反演理论证明, 常规偏移成像的结果是真实反射系数经模糊化算子卷积得到的退化结果[17], 该模糊化算子即Hessian算子, 许多学者进行过关于Hessian算子的讨论, XIE等[18]提出了照明矩阵、BOSCHI[19]提出了模型分辨率矩阵、YU等[14]提出了偏移解卷积滤波器、SCHUSTER等[20]提出了偏移格林函数、WANG等[21]提出了解卷积算子、FICHTNER等[22]提出了核函数, 以上概念实质上都是Hessian算子的不同称谓。在物理学意义上, Hessian算子包含了观测系统和速度模型的所有信息[23], 研究Hessian算子对于发展地震正、反演工作有着重要的启示作用。应用模型空间的最小二乘偏移方法是通过求取Hessian算子, 显式地压制Hessian效应。这种策略避免了在每一轮迭代中进行偏移和反偏移计算, 具有更高的实现效率, 但Hessian算子在线性化条件下是一个巨型的矩阵, 故实际运算中难以计算和保存。实际应用中需要引入Hessian近似, 在高频渐进条件下, Hessian矩阵可以看作对角矩阵[24-25], WANG等[26]利用对角Hessian的逆来重建地震反演中的深部结构, 可以平衡偏移图像振幅以及消除几何传播效应。点扩散函数(point spreading function, PSF)代表Hessian矩阵的一行元素, 通常将PSF元素投影在模型空间, 在二维情况下表现为目标点周围的一个椭圆型花样, 代表地下空间的一个单点对于观测系统的脉冲响应。通过求取地下空间的PSF, 可以得到Hessian算子的近似结果, 王雪君等[27]直接求取基于PSF的逆处理黏弹性介质逆时偏移成像成果, 有效均衡了成像振幅, 提高了分辨率。XU等[28]利用基于射线的方法生成PSF, 该方法在提高分辨率的同时, 兼具较高的灵活性。姚振岸等[29]构建了基于PSF的去模糊滤波器, 将其作为最小二乘逆时偏移迭代过程中的预条件化因子, 得到了高分辨率的偏移结果。
为了提升计算效率, 本文在两个方面进行了方法改进: ①建立散射点模型, 通过一次正演+偏移快速计算所有控制点点扩散函数, 并利用插值迅速得到全成像空间的点扩散函数, 进而得到近似Hessian算子; ②在模型空间展开反演。对于数据空间的反演而言, 每一次迭代都需要进行偏移和反偏移计算, 且输入庞大的地震数据集。模型空间的反演可转化为图像的去模糊化问题, 因其输入为小尺寸的偏移图像, 因此计算效率更高。本文采用模型空间反演的方法, 只需比数据空间小得多的计算量就可得到常规偏移成像去模糊化的反演结果。
1 方法原理 1.1 模型空间的最小二乘偏移成像理论在反演理论框架下, 利用最小二乘偏移方法将数据空间和模型空间之间的投影定义为如下线性问题:
| $ \boldsymbol{d}=\boldsymbol{L m} $ | (1) |
式中: d为Born近似下仅包含一次反射和散射的模拟数据; L为线性正演算子; m为地下模型的高频扰动项。传统的反演方法通过提出目标函数J(m)来实现模拟数据和观测数据之间残差的最小化。
| $ \boldsymbol{J}(\boldsymbol{m})=\left\|\boldsymbol{L} \boldsymbol{m}-\boldsymbol{d}^{2}\right\| $ | (2) |
最小二乘偏移时, m的计算式如下:
| $ \boldsymbol{m}=\left(\boldsymbol{L}^{*} \boldsymbol{L}\right)^{-1} \boldsymbol{L}^{*} \boldsymbol{d}=\boldsymbol{H}^{-1} \boldsymbol{L}^{*} \boldsymbol{d} $ | (3) |
式中: L*为伴随算子; H=L*L为Hessian算子。Hessian算子在数学上表示为目标函数对模型的二阶导数, 在物理上它代表观测系统对模型的分辨能力。mmig=L*d表示偏移成像的过程。(3)式可以改写为L*d=Hm, 观察等式两边可知, 偏移成像是特定观测系统下成像过程中对真实模型模糊化的结果, Hessian算子即模糊化算子。
在数据空间中进行最小二乘偏移需要在每次成像过程中, 将成像结果作为二次源生成模拟数据, 每次迭代均需要进行一次正演和偏移成像计算, 产生了巨大的计算量。模型空间的最小二乘偏移算法可以克服计算成本上的缺陷, 目标函数如下:
| $ \boldsymbol{J}(\boldsymbol{m})=\left\|\boldsymbol{H} \boldsymbol{m}-\boldsymbol{m}_{\text {mig }}\right\|^{2} $ | (4) |
无论是在数据空间还是模型空间中开展反演, 最小二乘偏移的核心都在于求解Hessian算子及其逆算子。基于波动方程得到的Hessian算子, 其逆可作为去卷积算子。使用梯度类方法解决该问题时, 该算子可作为步长。Hessian矩阵中对角元素的重要性已经得到了充分的证明[24-26], 忽略干扰项后, Hessian算子可写成如下格林函数表达式:
| $ \begin{gathered} \boldsymbol{H}(k, l)=\operatorname{Re}[\sum\limits_{\omega} \sum\limits_{k_{\mathrm{s}}} \sum\limits_{k_{\mathrm{r}}} \omega^{4}\left|f_{\mathrm{s}}(\omega)\right|^{2} \boldsymbol{G}\left(k_{\mathrm{s}}, k, \omega\right) \cdot \\ \boldsymbol{G}\left(k, k_{\mathrm{r}}, \omega\right) \boldsymbol{G}^{*}\left(l, k_{\mathrm{r}}, \omega\right) \boldsymbol{G}^{*}\left(k_{\mathrm{s}}, l, \omega\right)] \end{gathered} $ | (5) |
式中: G为格林函数; ks为震源; kr为检波点; fs(ω)为能量在圆频率ω上的谱; k和l为不同成像点, (1)式中的正演算子L可表示为:
| $ \begin{gathered} \left.\boldsymbol{L}\left(k_{\mathrm{s}}, k_{\mathrm{r}}, \omega\right)\right|_{x}=\omega^{2}\left|f_{\mathrm{s}}(\omega)\right| \boldsymbol{G}\left(k_{\mathrm{s}}, k, \omega\right) \cdot \\ \boldsymbol{G}\left(k, k_{\mathrm{r}}, \omega\right) \end{gathered} $ | (6) |
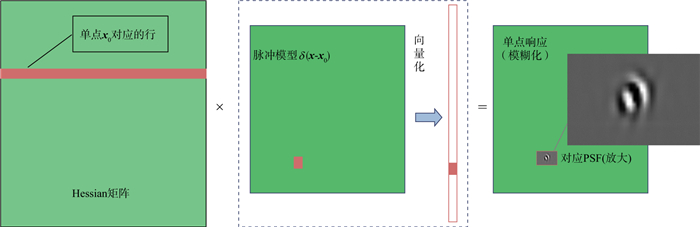
Hessian算子是一个巨型矩阵, 由(5)式可知, H(k, l)对应两组成像点k和l。如图 1所示, Hessian矩阵的每一行和每一列均对应于成像空间中的一个点。抽取线性Hessian矩阵中的一行数据即点扩散函数(PSF), 如下:
| $ \begin{gathered} \left.\boldsymbol{P}(l)\right|_{k}=\operatorname{Re}[\sum\limits_{\omega} \sum\limits_{k_{\mathrm{s}}} \sum\limits_{k_{\mathrm{r}}} \omega^{4}\left|f_{\mathrm{s}}(\omega)\right|^{2} \boldsymbol{G}\left(k_{\mathrm{s}}, k, \omega\right)\cdot \\ \boldsymbol{G}\left(k, k_{\mathrm{r}}, \omega\right) \boldsymbol{G}^{*}\left(l, k_{\mathrm{r}}, \omega\right) \boldsymbol{G}^{*}\left(k_{\mathrm{s}}, l, \omega\right)] \end{gathered} $ | (7) |
|
图 1 Hessian作用示意 |
通常在二维情况下, PSF在相应点周围展开为一个椭圆形的斑点。如图 2所示, 在反演框架下, 叠前偏移的结果为真实反射率被PSF模糊化后的结果, 因此PSF被视作构建Hessian算子近似的有力工具。PSF的精确求解需要大量的计算, 这里将(7)式分解为如下两个部分:
| $ \boldsymbol{P}_{1}\left(\omega, k_{\mathrm{s}}, k_{\mathrm{r}}, k\right)=\omega^{2} f_{\mathrm{s}}(\omega) \boldsymbol{G}\left(k_{\mathrm{s}}, k, \omega\right) \boldsymbol{G}\left(k, k_{\mathrm{r}}, \omega\right) $ | (8) |
| $ \boldsymbol{P}_{2}\left(\omega, k_{\mathrm{s}}, k_{\mathrm{r}}, l\right)=\omega^{2} f_{\mathrm{s}}(\omega) \boldsymbol{G}\left(k_{\mathrm{s}}, l, \omega\right) \boldsymbol{G}\left(l, k_{\mathrm{r}}, \omega\right) $ | (9) |

|
图 2 PSF模糊和去模糊化过程 |
对于一组震源ks和检波点kr, (8)式和(9)式中的P1和P2仅与k点和其周围的l点有关。如果给定一个参考点k, 那么只需要计算P1和其周围的P2, 并通过互相关得到PSF的图像。
为了得到(8)式和(9)式中格林函数的解, 我们在震源和检波点分别激发沿地下介质传播的波场, 并记录在时域或频域中, 然后通过频域正演得到精确的解。当模型空间较大时, 计算和存储的成本巨大。
由(6)式至(9)式可知, L=L(ks, kr, ω), 进而可得:
| $ \boldsymbol{P}_{1}=\boldsymbol{P}_{1}\left(\omega, k_{\mathrm{s}}, k_{\mathrm{r}}, k\right)=\left.\boldsymbol{L}\right|_{k} $ | (10) |
| $ \boldsymbol{P}_{2}=\boldsymbol{P}_{2}\left(\omega, k_{\mathrm{s}}, k_{\mathrm{r}}, l\right)=\left.\boldsymbol{L}\right|_{l} $ | (11) |
| $ \left.\boldsymbol{P}(l)\right|_{k}=\left.\left.\boldsymbol{L}\right|_{k} \cdot \boldsymbol{L}^{*}\right|_{l} $ | (12) |
只要在参考点k设置一个散射点(速度扰动), 就可以使用观测系统生成一组新的数据
| $ \tilde{\boldsymbol{d}}=\left.\boldsymbol{L}\right|_{k} $ | (13) |
PSF的计算过程为这组数据的成像过程:
| $ \left.\boldsymbol{P}(l)\right|_{k}=\left.\boldsymbol{L}^{*}\right|_{l} \tilde{\boldsymbol{d}} $ | (14) |
我们将PSF的计算过程转换为一次正演+偏移的过程, 因为该过程需要遍历所有的成像空间, 故仍存在巨大的计算量。从图 1可见, PSF在散射点周围扩散成一个斑点。因此, 我们首先可以选择一定间隔的离散点作为控制点, 并保证每个控制点生成的PSF斑点不会互相重合, 然后使用上述过程一次性计算所有控制点上的PSF, 最后在成像空间上对与控制点相邻的点进行空间插值, 快速获得全成像空间的PSF。插值方法采用反距离加权(inverse distance weight, IDW)插值:
| $ W_{i}=\frac{h_{i}^{-p}}{\sum\limits_{j=1}^{n} h_{i}^{-p}} $ | (15) |
式中: Wi表示权值, 反映插值点受周围控制点影响的程度; hi表示插值点到控制点的距离; p为任意一个正实数, p值越大, 则更强调邻近控制点的作用, 反之相反。
1.3 基于PSF的图像去模糊方法解决图像的去模糊问题, 关键在于模糊(卷积)算子的估计和卷积效应的消除, 利用1.2节的方法可以高效求取模糊算子。那么通过对常规偏移成像结果进行解卷积处理即可得到去模糊图像, 一个二维图像的模糊正过程可由下式描述:
| $ g(x, y)=f(x, y) \otimes k(x, y) $ | (16) |
式中: ⊗表示卷积运算; f(x, y)表示真实图像; k(x, y)表示模糊算子; g(x, y)表示模糊后的退化图像。(16)式在波数域有如下表达式:
| $ G(u, v)=F(u, v) \cdot K(u, v) $ | (17) |
空间域的卷积对应于波数域的乘积, 其中G(u, v)、F(u, v)、K(u, v)分别由g(x, y)、f(x, y)、k(x, y)经二维傅里叶变换得到, u和v分别代表横、纵方向上的频率, (17)式可改写为如下形式:
| $ \hat{F}(u, v)=\frac{G(u, v)}{K(u, v)} $ | (18) |
式中:
| $ \hat{f}(x, y)=\mathrm{FFT}_{2}^{-1}[\hat{F}(u, v)]=\mathrm{FFT}_{2}^{-1}\left[\frac{G(u, v)}{K(u, v)}\right] $ | (19) |
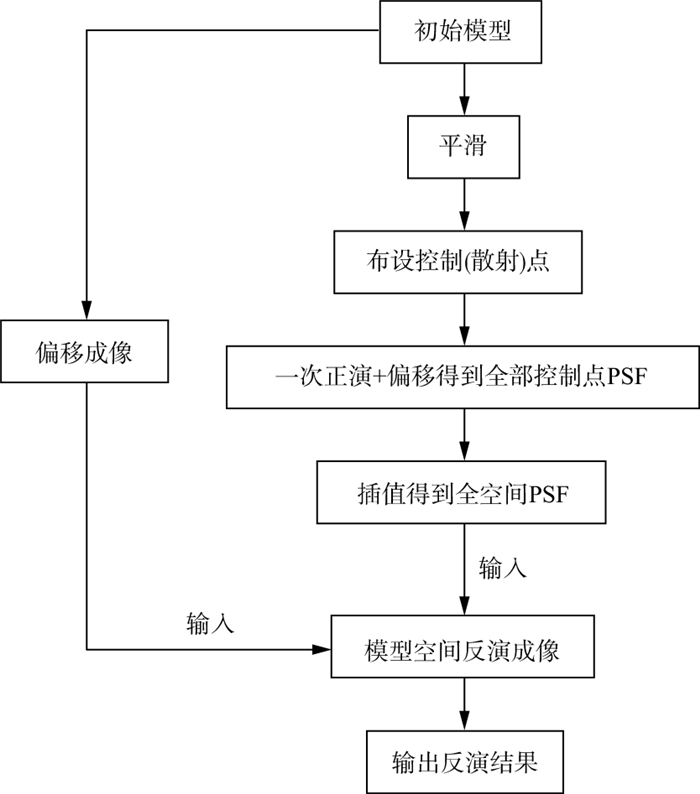
基于点扩散函数快速计算的模型空间反演成像流程如图 3所示。
|
图 3 基于点扩散函数快速计算的模型空间反演成像流程 |
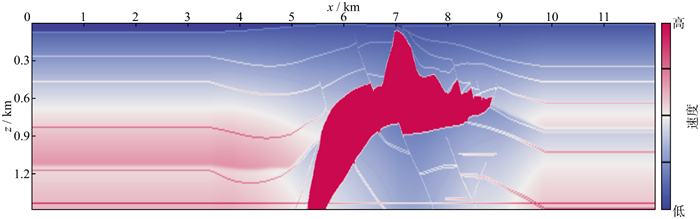
图 4为SEG/EAGE盐丘速度模型, 模型网格点数为1200×150, 两个方向的采样间隔均为10m, 速度为1500~4500m/s。合成地震数据的过程中炮间隔为100m, 共计80炮, 从地表2000m处开始均匀放炮。采集系统位于地表, 排列长度为整个模型的长度, 道间距为10m, 震源为主频为12.5Hz的雷克子波。计算时采用时间精度二阶, 空间精度十阶的时间域有限差分正演及完全匹配吸收边界条件。
|
图 4 SEG/EAGE盐丘速度模型 |
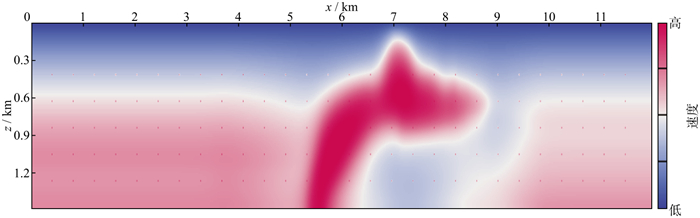
我们将Hessian近似的计算, 即PSF的计算转换为一次“正演+偏移+插值”过程, 目的是保证获得清晰的PSF斑点并且PSF斑点之间不互相重叠。对初始速度模型进行平滑处理后, 将控制点均匀分布在平滑后的速度模型上, 得到散射点模型(图 5), 控制点处速度为原速度的1.5倍。
|
图 5 图 4速度模型对应的散射点模型 |
利用散射点模型进行正演, 并对得到的地震数据进行逆时偏移(RTM)成像, 所得结果为控制点上的脉冲响应, 即PSF, 图 6展示了图 5散射点模型生成的PSF图像。对于控制点之外的点, 我们使用IDW插值生成其PSF, 图 7为幂值参数p在不同取值下的全成像点PSF图像(横向网格点数: 1200×41、纵向网格点数: 150×21)。当p值为1时, 所得的插值图像存在明显的网格状间断, 随着取值的增大, 图像更加平滑。在后续测试中我们将继续讨论不同p值对结果产生的影响。

|
图 6 图 5散射点模型生成的PSF图像 |

|
图 7 不同p值下的全成像点PSF图像 a p=1; b p=2; c p=3; d p=4 |
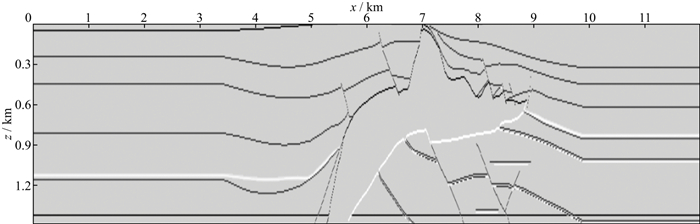
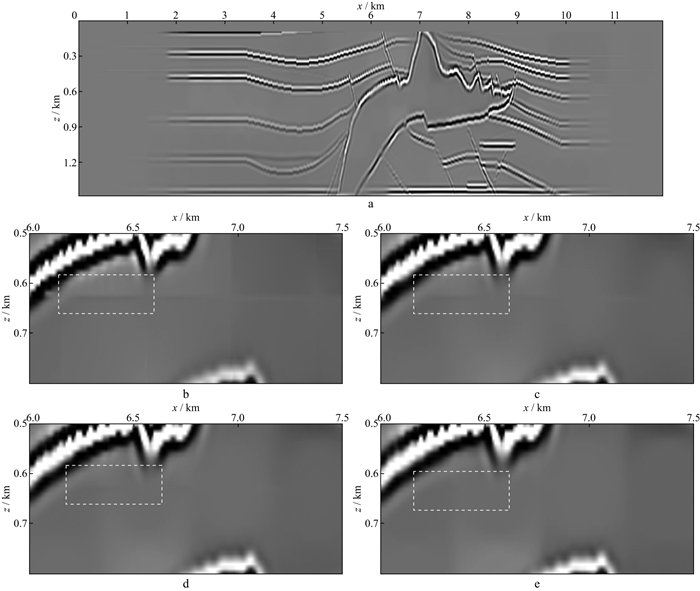
为了验证计算得到的PSF是否可以起到近似Hessian算子造成的模糊化效果, 首先从图 4的速度模型中计算反射率, 得到如图 8所示的盐丘反射率模型。我们将反射率模型与计算得到的PSF进行卷积, 得到如图 9a所示的图像(图像中空白为卷积运算无法覆盖区域, 显示时置零), 此时p取5, 可以看到图 9a的分辨率低于图 7, PSF的模糊化效应平滑了边界, 起到了模糊化的作用。观察图 9b至图 9e不同p值下的卷积局部放大结果, 可发现当插值幂次选取不当, 会在模糊化(卷积)的正过程中引入网格状间断, 而去模糊化问题的实现有赖于PSF的精度, 即正过程效果越好, 则去模糊化(解卷积)的效果越好, 这些间断会在后续反演过程中引入不必要的噪声, 图 9d的正过程效果最为理想, 故本实验选取p=5作为插值参数。
|
图 8 盐丘反射率模型 |
|
图 9 盐丘反射率模型卷积结果及不同p值下的卷积结果局部放大显示 a 反射率模型卷积结果(p=5); b p=1卷积结果局部放大; c p=3卷积结果局部放大; d p=5卷积结果局部放大; e p=8卷积结果局部放大 |
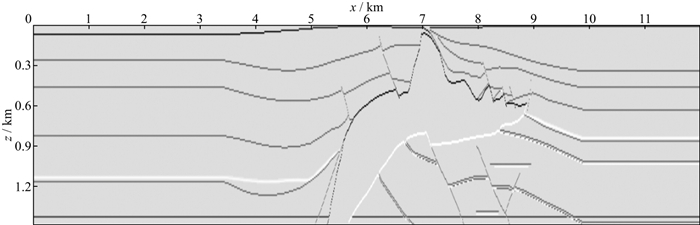
在对RTM成像结果去模糊化前, 可以先利用卷积模型验证波数域滤波方法的有效性, 将图 9a作为图像去模糊化问题的输入, 采用波数域滤波算法进行解卷积运算, 得到如图 10所示的去模糊化结果, 该模型与图 8中的原始反射率模型相似, 证明了当PSF模糊效应的正反过程匹配时, 波数域滤波算法有效。
|
图 10 盐丘反射率模型的去模糊化结果 |
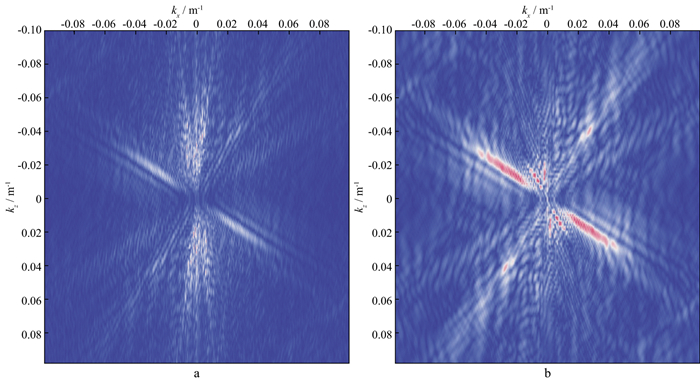
采用与计算PSF相同的观测系统和震源子波, 根据图 4的速度模型生成地震数据, 并进行RTM成像, 得到如图 11所示的结果。将波数域滤波方法应用于图 11的盐丘模型RTM成像结果, 得到的该模型RTM去模糊化结果如图 12所示, 可以看出, 处理后的结果中平层及盐丘顶部分辨率明显提升, 层位边界得到锐化。浅地表震源效应引起的线性噪声在滤波后得到了较好的压制, 同时深部层位的振幅能量一定程度上被抬高, 一些层位的连续性得到了提升。观察浅蓝线框可以发现, 滤波补齐了弱照明区域的层位(受观测孔径的影响, 补出的层位向上倾斜), 但会在盐丘内部引入噪声。图 13为盐丘模型波数域反演前、后的波数谱, 不难发现, 反演后的结果在波数域有着更宽的展布。

|
图 11 盐丘模型RTM成像结果 |

|
图 12 盐丘模型RTM成像去模糊化结果 |
|
图 13 盐丘模型波数域反演前(a)、后(b)的波数谱 |
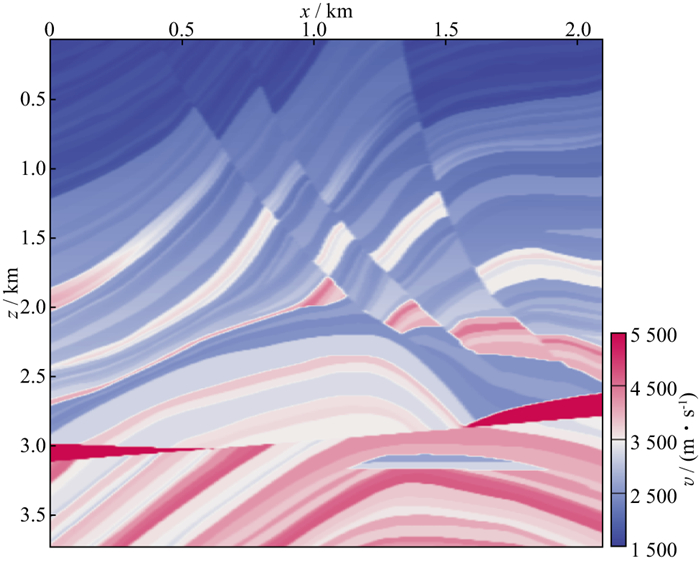
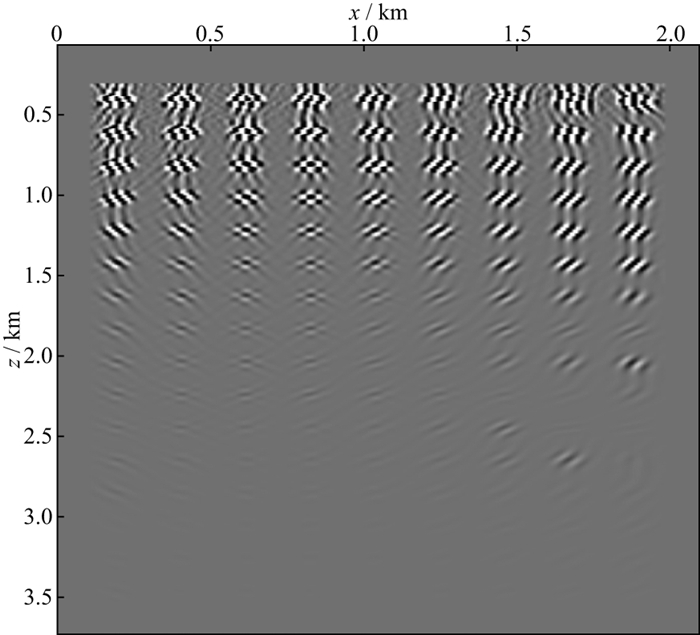
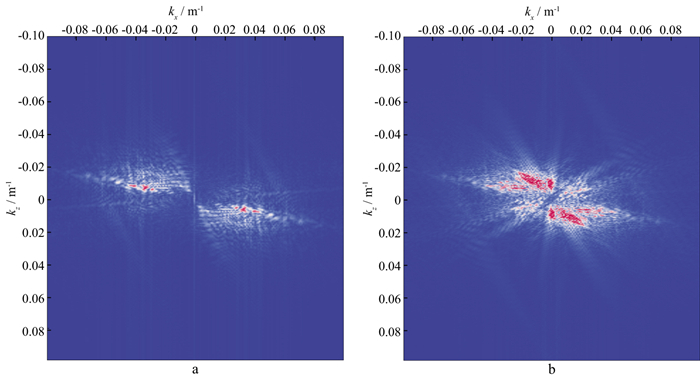
采用图 14的Marmousi速度模型进一步验证本文方法的有效性, Marmousi速度模型的RTM成像结果如图 15所示。采用本文方法计算得到的PSF图像如图 16所示, 应用波数域滤波算法处理图 15的RTM剖面, 得到如图 17所示的去模糊化结果, 图 18为Marmousi模型波数域反演前、后的波数谱。对比图 17和图 15可以发现, 本文方法可以锐化边界, 提高层位分辨率, 同时提高深部振幅能量, 相较于RTM成像结果, 采用本文方法得到的反演结果具有更加均衡的振幅。
|
图 14 Marmousi速度模型 |

|
图 15 Marmousi速度模型RTM成像结果 |
|
图 16 Marmousi散射点模型生成的PSF图像 |

|
图 17 Marmousi模型RTM成像去模糊化结果 |
|
图 18 Marmousi模型波数域反演前(a)、后(b)的波数谱 |
1) 正问题是反问题的基础, 图像去模糊化工作有赖于PSF的精度, 本文通过散射点模型一次“正演+偏移+插值”的过程获取PSF。在速度变化剧烈的区域, PSF的结果会有较大变动。因此, 控制点布设越密, 插值结果的准确性越高。控制点的疏密不会影响计算量, 但是布设过密时会导致PSF样式互相重叠, 影响精度。故在求取PSF时通常需要1~2次试验(正演+偏移)来获得最佳的散射点布设间隔。
2) 对于插值方法中的幂值参数选取, 以正过程(反射率模型同PSF卷积)结果不会引入额外噪声为原则。
3) 模型空间的反演基于偏移成像结果展开, 初始偏移成像结果的精度制约了最终的反演效果, 这个过程与数据空间一样需要相对精确的偏移速度。
4) 本文通过RTM的结果证明了方法的有效性, 该方法的核心在于PSF的求取和图像去模糊, 因此该策略同样适用于其它偏移算子方法进行求解。
4 结论本文分析了PSF和Hessian算子的数学物理性质, 提出了一种对散射点模型进行一次“正演+偏移+插值”获取点扩散函数的快速算法。控制点的PSF仅需要一次正演和偏移, 而后可以通过IDW插值快速获得全成像空间的PSF。该方法具有较高的计算效率和灵活性。与反射率模型的卷积结果对比发现, 该方法生成的PSF可以很好的起到模糊化作用。在得到模糊算子后, 将反演目标转化为模型空间下的图像去模糊化问题, 通过波数域反演算法一次运算就可以得到反演结果。反演过程仅需进行两组二维傅里叶正反变换和相应的矩阵运算, 具有较高的实现效率。模型测试结果表明, 本文方法可以提高常规偏移成像的分辨率, 均衡弱照明区域振幅。
致谢: 感谢中国石油化工股份有限公司石油物探技术研究院的资助。感谢同济大学波现象与智能反演成像研究组(WPI)徐鹏博士的有益讨论。| [1] |
CLAERBOUT J F. Earth soundings analysis: processing versus inversion[M]. Boston: Blackwell Scientific Publications, 1991: 1-334.
|
| [2] |
NEMETH T, WU C, SCHUSTER G. Least-squares migration of incomplete reflection data[J]. Geophysics, 1999, 64(1): 208-221. |
| [3] |
KUEHL H, SACCHI M. Least-squares split-step migration using the Hartley transform[J]. Expanded Abstract of 69th Annual Internat SEG Mtg, 1999, 1548-1551. |
| [4] |
DUQUET B, MARFURT K, DELLINGER J. Kirchhoff modeling, inversion for reflectivity and subsurface illumination[J]. Geophysics, 2000, 65(4): 1195-1209. |
| [5] |
RICKETT J. Illumination-based normalization for wave-equation depth migration[J]. Geophysics, 2003, 68(4): 1371-1379. |
| [6] |
LEBRAS R, CLAYTON R. An iterative inversion of back-scattered acoustic waves[J]. Geophysics, 1988, 53(4): 501-508. |
| [7] |
LAMBARE G, VIRIEUS J, MADARIAGA R, et al. Iterative asymptotic inversion in the acoustic approximation[J]. Geophysics, 1992, 57(9): 1138-1154. |
| [8] |
FOMEL S, BERRYMAN J, CLAPP R, et al. Iterative resolution estimation in least-squares Kirchhoff migration[J]. Geophysical Prospecting, 2002, 50(6): 577-588. |
| [9] |
李闯. 最小二乘逆时偏移优化方法及应用研究[D]. 青岛: 中国石油大学(华东), 2018 LI C. Research on the optimized algorithm and application of least-squares reverse time migration[D]. Qingdao: China University of Petrolem(East China), 2018 |
| [10] |
AOKI N, SCHUSTER G. Fast least squares migration with a deblurring filter[J]. Geophysics, 2009, 74(6): WCA83-WCA93. |
| [11] |
KUEHL H, SACCHI M. Least-squares split-step migration using the Hartley transform[J]. Expanded Abstracts of 69th Annual Internat SEG Mtg, 1999, 1548-1551. |
| [12] |
YAO G, JAKUBOWICZ H. Non-linear least-squares reverse-time migration[J]. Expanded Abstract of 82nd Annual Internat SEG Mtg, 2012, 4609-4612. |
| [13] |
ZHANG Y, DUAN L, XIE Y. A stable and practical implementation of least-squares reverse time migration[J]. Geophysics, 2015, 80(1): V23-V31. |
| [14] |
YU J, HU J, SCHUSTER G T, et al. Prestack migration deconvolution[J]. Geophysics, 2006, 71(2): S53-S62. |
| [15] |
LECOMTE I. Resolution and illumination analyses in PSDM: A ray-based approach[J]. The Leading Edge, 2008, 27(5): 650-663. |
| [16] |
TANG Y. Target-oriented wave-equation least-squares migration/inversion with phase-encoded Hessian[J]. Geophysics, 2009, 74(6): WCA95-WCA107. |
| [17] |
任浩然, 黄光辉, 王华忠, 等. 地震反演成像中的Hessian算子研究[J]. 地球物理学报, 2013, 56(7): 2429-2436. REN H R, HUANG G H, WANG H Z, et al. A research on the hessian operator in seismic inversion imaging[J]. Chinese Journal of Geophysics, 2013, 56(7): 2429-2436. |
| [18] |
XIE X B, JIN S, WU R S. Wave-equation based seismic illumination analysis[J]. Geophysics, 2006, 71(5): S169-S177. |
| [19] |
BOSCHI L. Measures of resolution in global body wave tomography[J]. Geophysical Research Letters, 2003, 30(19): 379-394. |
| [20] |
SCHUSTER G T, HU J. Green's function for migration: continuous recording geometry[J]. Geophysics, 2000, 65(1): 167-175. |
| [21] |
WANG Y, YANG C. Accelerating migration deconvolution using a nonmonotone gradient method[J]. Geophysics, 2010, 75(4): S131-S137. |
| [22] |
FICHTNER A, TRAMPERT J. Hessian kernels of seismic data functionals based upon adjoint techniques[J]. Geophysical Journal International, 2011, 185(2): 775-798. |
| [23] |
REN H, WU R S, WANG H. Wave equation least square imaging using the local angular Hessian for amplitude correction[J]. Geophysical Prospecting, 2011, 59(4): 651-661. |
| [24] |
BEYLKIN G. Imaging of discontinuities in the inverse scattering problem by inversion of a generalized Radon transform[J]. Journal of Mathematical Physics, 1985, 26(1): 99-108. |
| [25] |
BLEISTEIN G, NORMAN O. On the imaging of reflectors in the earth[J]. Geophysics, 1987, 52(7): 931-942. |
| [26] |
WANG Y, YING R. Reflection seismic waveform tomography[J]. Journal of Geophysical Research Solid Earth, 2009, 114(B3): B03304. |
| [27] |
王雪君, 任浩然, 江金生, 等. 基于点扩散函数的黏声介质反演成像[J]. 石油物探, 2019, 58(1): 82-91. WANG X J, REN H R, JIANG J S, et al. Inversion imaging based on point spreading function for visco-acoustic medium[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 82-91. |
| [28] |
XU P, WANG H, GUO S, et al. RTM deblurring with flexible WKBJ PSFs[J]. Expanded Abstract of 90th Annual Internat SEG Mtg, 2020, 3083-3087. |
| [29] |
姚振岸, 孙成禹, 喻志超, 等. 融合点扩散函数的预条件黏声最小二乘逆时偏移[J]. 石油地球物理勘探, 2019, 54(1): 73-83. YAO Z A, SUN C Y, YU Z C, et al. Preconditioned visco-acoustic least-squares reverse time migration integrated with point spread function[J]. Oil Geophysical Prospecting, 2019, 54(1): 73-83. |




