2. 成都理工大学油气藏地质及开发工程国家重点实验室, 四川成都 610059
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu University of Technology, Chengdu 610059, China
在储层评价中, 利用测井资料的分析解释成果可以对储层的岩性、物性以及含油气性做出综合评价。为了更好地建立油气藏模型, 降低地质解释的模糊性, 需要结合多种测井曲线与地震资料。但当测井仪器工作时出现故障、井壁遭到破坏并发生坍塌时, 会导致工区某些层段的测井曲线缺失[1]。因此, 利用已知层段的测井曲线补全未知层段的测井曲线, 对于后续的储层预测具有非常重要的意义[2-3]。
早期, 一些学者利用传统的统计和经验模型预测缺失的测井数据。SMITH[4]推导了电阻率测井和声波测井之间的关系。GARDNER等[5]利用Gardner方程表征岩石中声波和密度的关系。CASTAGNA等[6]提出了利用纵波速度计算横波速度的经验公式。此外, 还有一些岩石物理模型也可用于测井曲线预测[7-9]。因上述传统方法的预测效果受地层、岩性的影响, 故仍需专业人员人工干预其预测结果。
近年来, 深度学习的快速发展为测井曲线预测提供了新的研究思路, 深度学习方法通过学习可以掌握预测目标与输入变量之间隐含的非线性关系[10]。ROLON等[11]使用全连接神经网络(fully convolutional neural networks, FCNNs)通过现有的测井数据预测未知的测井数据, 但FCNNs生成的是输入数据到输出数据的点对点映射, 与测井曲线因不同深度岩层性质的差异所表现出的变化趋势不符。循环神经网络(recurrent neural network, RNN)具有一定的记忆功能, 对处理测井曲线类的序列数据非常有效。张东晓等[12]利用基于RNN改进的长短期记忆(long short-term memory, LSTM)网络和具有串级系统的长短期记忆(CLSTM)网络生成测井曲线, 王俊等[13-14]使用长短期记忆网络和门控循环单元(gated recurrent unit, GRU)神经网络较为准确地预测出了测井曲线的变化趋势。与基于全连接神经网络的方法相比, 基于循环神经网络的方法可在一定程度上改善测井曲线预测的效果, 但当测井曲线发生局部突变时, 其预测效果仍有待改进。
测井数据的数据结构具有序列性、特征性等特点, GRU神经网络能较好地预测出测井曲线的变化趋势。考虑到卷积神经网络(convolutional neural networks, CNN)具有良好的局部特性感知能力, 因此我们将CNN和GRU网络相结合, 提出基于CNN-GRU的测井曲线预测方法, 该方法在预测过程中可以兼顾测井数据的序列性与特征性, 最后我们将该方法应用于四川某地区A、B两个井区的测井数据进行预测, 并将预测结果与其它传统深度学习预测模型的应用结果进行对比, 以验证方法的有效性。
1 方法原理与模型构建 1.1 卷积神经网络模型卷积神经网络可以高效提取数据的局部特征, 主要由卷积层、池化层与全连接层组成。其中卷积层负责从输入的数据中提取特征, 并利用不同尺寸的卷积核对数据进行卷积运算, 一维卷积公式如下:
| $ y_{t}=\sum\limits_{k=1}^{K} w_{k} x_{t-k+1}+b $ | (1) |
式中: yt为输出的特征数据; wk为卷积核; xt-k+1为输入的数据; b为偏置; K为数据长度。
1.2 GRU循环神经网络循环神经网络能结合历史输入信息对与序列相关的任务进行处理, 其单元结构如图 1所示。
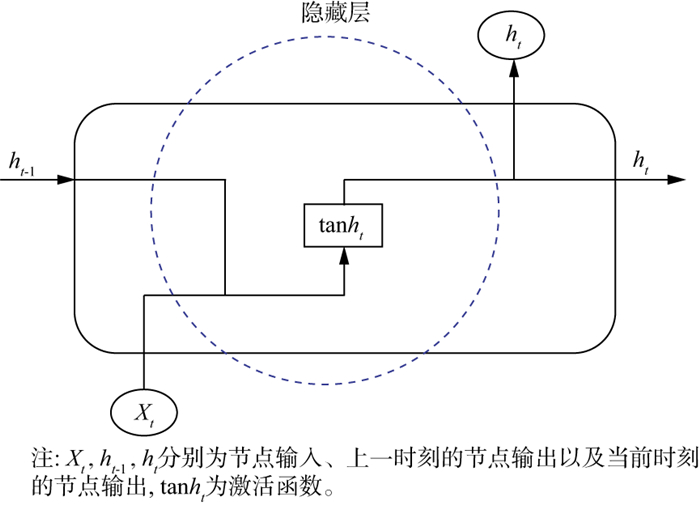
|
图 1 循环神经网络(RNN)单元结构 |
由图 1可知, RNN中隐藏层为循环体, 作用是对不同的输入数据执行相同的处理。RNN的不足在于只能记忆短期的历史输入信息, 当网络层数较深时可能出现梯度消失的现象, 导致无法解决输入信息的长期记忆问题。
长短期记忆网络实现了信息长期记忆的功能, 改进了传统循环神经网络, 适合对数据序列进行处理和预测。门控循环单元神经网络是对LSTM的改进, 其在保持LSTM长期记忆功能的情况下又简化了网络结构, 因此能更快地对数据序列进行处理和预测[15-17], 其结构如图 2所示。
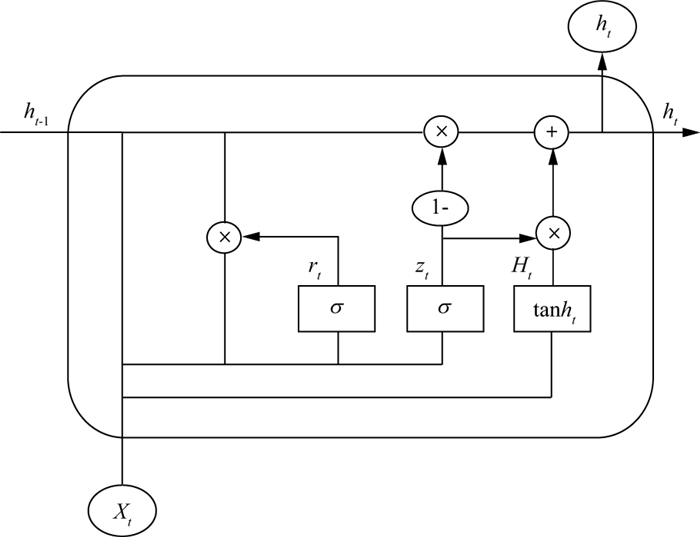
|
图 2 GRU神经网络结构 |
图中, Xt、ht-1、ht、rt、zt、Ht依次为节点输入信息、上一时刻的节点输出信息、当前时刻的节点输出信息、更新门的状态、重置门的状态、当前节点的状态; σ和tanh分别表示不同的激活函数。
由图 2可知, GRU神经网络的结构主要由重置门和更新门组成。重置门zt、更新门rt、节点状态Ht和节点输出ht的计算公式依次如下:
| $ z_{t}=\sigma\left(W_{z} \cdot\left[h_{t-1}, X_{t}\right]\right) $ | (2) |
| $ r_{t}=\sigma\left(W_{r} \cdot\left[h_{t-1}, X_{t}\right]\right) $ | (3) |
| $ H_{t}=\tan h\left(W \cdot\left[r_{t} \otimes h_{t-1}, X_{t}\right]\right) $ | (4) |
| $ h_{t}=\left(1-z_{t}\right) \otimes h_{t-1}+z_{t} \otimes \bar{h}_{t} $ | (5) |
式中: ⊗表示矩阵对应的元素相乘; Wz, Wr, W分别为GRU模型的不同共享参数; ht为ht的平均值。
1.3 CNN-GRU神经网络模型利用深度学习模型进行测井曲线预测时, 建立的预测模型大多只选取单一网络, 但单一网络模型不能兼顾测井曲线特征和测井深度域的变化趋势。本文提出的CNN-GRU神经网络既能高效地实现输入特征的提取, 又具备长期记忆测井曲线的功能, 因此利用CNN-GRU神经网络进行测井曲线预测是可行的。CNN-GRU神经网络模型的基本结构如图 3所示。
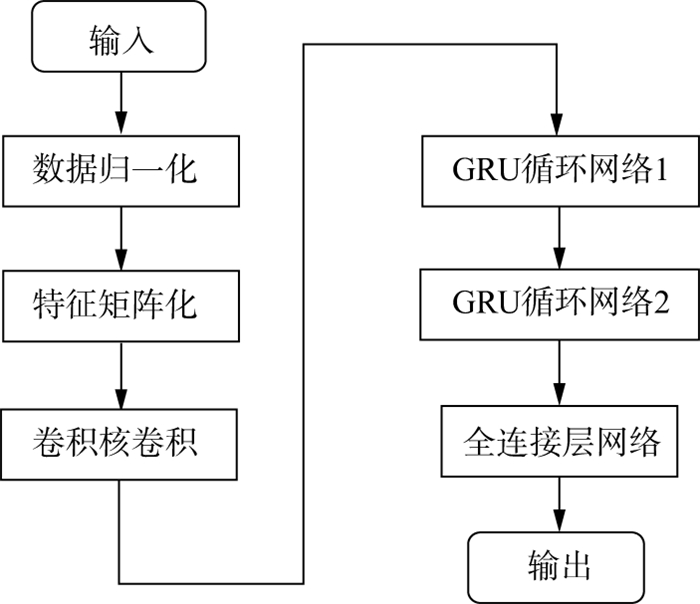
|
图 3 CNN-GRU神经网络模型的基本结构 |
由图 3可知, 输入数据在经归一化处理后, 先通过CNN网络提取数据的局部特征信息, 构建时序性的特征向量, 然后将结果输入两层方向相反的GRU模型中进行训练, 以提取数据在时间维度上的变化, 再通过全连接层网络输出数据。将CNN与GRU相结合可以实现对测井数据时空特征的完整学习。
本文将需要进行预测的井的已知层段以及从具有完整数据的邻井获得的测井曲线作为训练集, 将其输入到模型中进行训练, 然后由邻井对应深度的测井值预测该井未知层段的测井曲线。模型输出结果包括已知层段测井曲线的拟合值以及未知层段测井曲线的预测值。CNN-GRU神经网络模型对测井数据进行预测的技术流程如图 4所示。
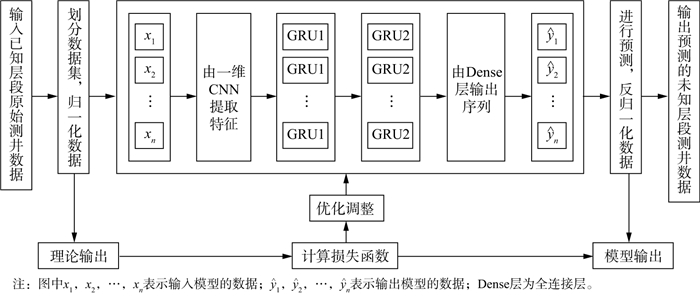
|
图 4 基于CNN-GRU神经网络模型的预测流程 |
该流程主要可分为以下4步:
1) 将输入的测井数据集划分为训练集和测试集, 并进行归一化处理;
2) 设置CNN-GRU模型的网络参数, 选用均方误差(mean-square error, MSE)为损失函数, 采用Adam优化算法来进行权重更新;
3) 利用训练集对模型进行训练, 并检验训练效果, 若模型对训练集的拟合效果满足要求, 则进入下一步, 否则回到第2)步, 调整网络参数及优化算法;
4) 利用训练好的模型对测试集进行测试, 并将测试结果反归一化, 得到测井曲线的预测值。
1.4 测井数据预处理与评价标准不同的测井曲线数据量纲不同且数值差异较大, 不利于模型参数优化。为了加速模型的训练和提高预测精度, 将测井数据进行归一化处理, 结果如下:
| $ X^{*}=\frac{X-X_{\min }}{X_{\max }-X_{\min }} $ | (6) |
式中: X*为归一化后的测井数据; X为原始测井数据; Xmax为训练集各维度中测井数据最大值; Xmin为训练集各维度中测井数据最小值。
为了综合评价模型对测井数据集的预测性能, 本文选用相关系数(R)、平均绝对误差(MAE)和均方根误差(RMSE)作为预测效果评价的标准, 其计算公式分别如下:
| $ R=\frac{\sum\nolimits_{i=1}^{N}\left(X_{i}-\bar{X}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\sum\nolimits_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{2}} \sqrt{\sum\nolimits_{i=1}^{N}\left(y_{i}-\bar{y}\right)^{2}}} $ | (7) |
| $ M_{\mathrm{AE}}=\frac{1}{N} \sum\nolimits_{i=1}^{N}\left|Y_{i}-\overset\frown{Y}_{i}\right| $ | (8) |
| $ R_{\mathrm{MSE}}=\sqrt{\frac{1}{N} \sum\nolimits_{i=1}^{N}\left(Y_{i}-\overset\frown{Y}_{i}\right)^{2}} $ | (9) |
式中: N为序列长度; Xi为预测值; X为Xi的平均值; yi为真实值; y为yi的平均值; Yi为预测值,
为了验证CNN-GRU神经网络模型对测井曲线预测的有效性, 选择四川某地区A、B两个井区的测井数据进行验证。此外, 还采用了单一的GRU神经网络、BP神经网络(BPNN)和随机森林(RF)作为基准模型与CNN-GRU神经网络模型预测结果进行对比。
2.1 实验设计实验数据为A井区的A1、A2井测井数据, 每口井的测井数据包括声波时差(AC)、自然伽马(GR)、密度(DEN)、孔隙度(POR)、电阻率(ILD)共5条曲线, 以及B井区的B1、B2、B3井, 每口井的测井数据包括声波时差(AC)、自然伽马(GR)、密度(DEN)、孔隙度(POR)、自然电位(SP)共5条曲线。
经过多次对比和测试, 最终搭建了4种测井曲线预测模型。CNN-GRU神经网络模型包括: 1层卷积层, 其神经元为128个, 卷积核尺寸为4, 序列长度为1;两层GRU层的神经元分别为124和64个; 1层Dense层(Dense层的作用是将数据转换维度后输出)。GRU神经网络模型包括: 两层GRU层, 其神经元分别为32和12个, 序列长度为1;1层Dense层。BPNN模型包括3层Dense层, 神经元分别为32, 12和1个; 1层Dropout层(Dropout层作用是防止预测结果过拟合)。RF模型中最大决策树个数为10, 随机种子数量为72。
2.2 实验结果及分析利用CNN-GRU神经网络、GRU神经网络、BPNN和RF 4种模型对B1井中AC曲线数据进行预测, 并将预测结果用于第一步验证。假设B1井2306~2356m的AC曲线缺失, B3井具有完整的AC曲线, 利用B1井2106~2306m的AC曲线以及B3井2106~2356m的AC曲线作为训练集, 对B1井缺失的AC曲线进行预测, 其中B1井训练集和测试集数据所在的层段为同一岩性。
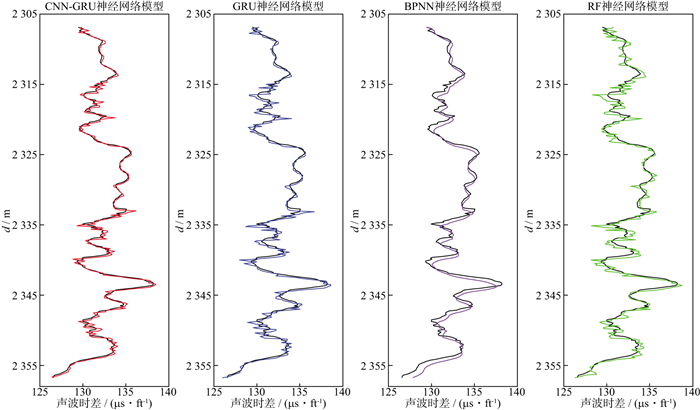
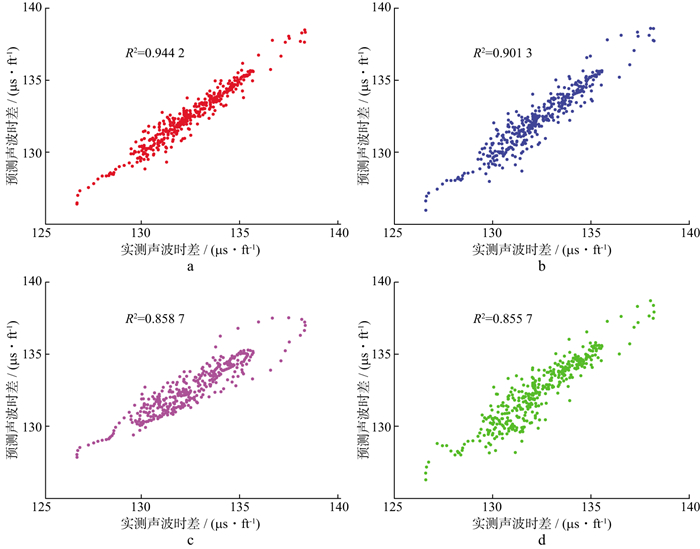
利用CNN-GRU神经网络、GRU神经网络、BPNN和RF 4种模型对B1井AC曲线进行预测, 结果如图 5所示。黑色曲线为实测AC值, 红色曲线为CNN-GRU神经网络模型预测结果, 蓝色曲线为GRU神经网络模型预测结果, 紫色曲线为BP神经网络模型预测结果, 绿色曲线为RF模型预测结果。4种模型的预测值与实测值的交会结果如图 6所示, 精度评价参数如表 1所示。
|
图 5 利用4种模型对B1井AC曲线进行预测的结果(1ft≈30.48cm) |
|
图 6 4种模型预测值与实测值的交会结果 a CNN-GRU神经网络模型交会结果; b GRU神经网络模型交会结果; c BPNN模型交会结果; d RF模型交会结果 |
从图 5可以看出, 4种模型对测井曲线的预测效果较好, 能够精确地预测出AC曲线随深度变化的趋势, 说明人工智能模型能有效地提取测井数据的时序性和非线性特征。通过观察可知, 模型预测结果与实测曲线存在微小的深度差, 这是因为原始测井数据包含噪声, 在预测过程中模型将包含噪声的真实数据视作异常数据, 导致输出的预测值相较于真实值在深度序列上存在一定的延后, 如果要消除这种误差, 就需要对原始数据进行去噪处理。
对比4种模型的预测效果, 发现BPNN模型预测结果较为平滑, 未能反应真实测井曲线的局部突变等细节。RF模型预测结果的精确度明显低于其它3种模型的预测结果。不难发现, CNN-GRU神经网络以及GRU神经网络模型可以精确地对测井曲线进行预测, 预测值的大小也与真实值更接近。
由图 6的交会结果可知, 根据CNN-GRU神经网络和GRU神经网络模型预测得到的声波时差值与真实的声波时差值具有较高的相关性。由表 1可知, CNN-GRU神经网络模型和GRU神经网络模型预测结果的平均绝对误差和均方根误差均较低, 而相关系数较高。由以上的分析可以证明, 相较于普通的机器学习模型, 具有长期记忆功能的CNN-GRU神经网络模型和GRU神经网络模型更适于对测井曲线进行预测。
| 表 1 4种模型的预测精度评价参数 |
将CNN-GRU神经网络模型和GRU神经网络模型用于A1、B2井中多条测井曲线的预测, 并将预测结果用来进一步验证模型效果。
以密度测井曲线为例, 假设A1井3640~3690m的密度测井曲线缺失, 并且A2井具有完整的密度测井曲线, 将A1井3440~3640m的密度测井曲线以及A2井3440~3690m的密度测井曲线作为训练集, 对A1井缺失的密度测井曲线进行预测, 其中A1井训练集和测试集数据所在的层段为同一岩性。
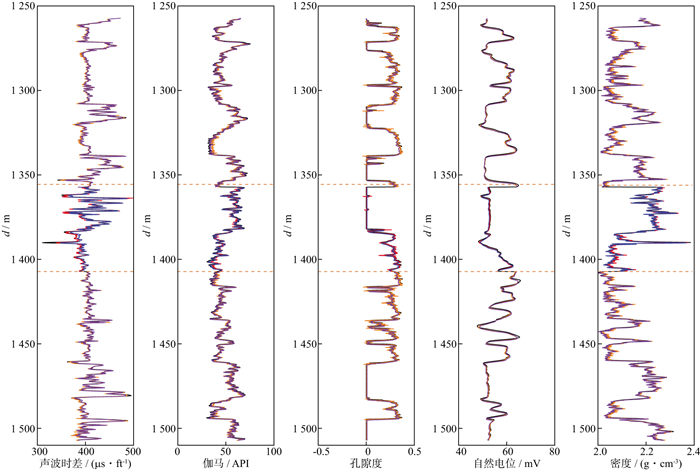
以声波时差测井曲线为例, 假设B2井1357~1407m的声波时差测井数据缺失, 并且B3井具有完整的声波时差测井数据, 将B2井1257~1357m、1407~1507m的声波时差测井数据以及B3井1257~1507m的声波时差测井数据作为训练集, 对B2井缺失的声波时差测井数据进行预测, 其中B2井训练集和测试集数据所在的层段为同一岩性。
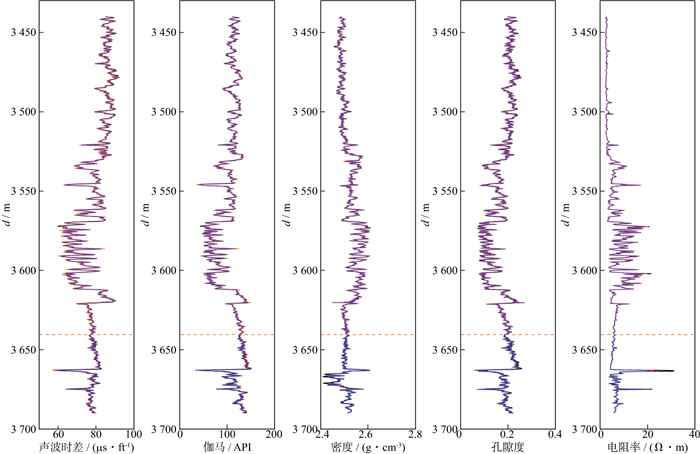
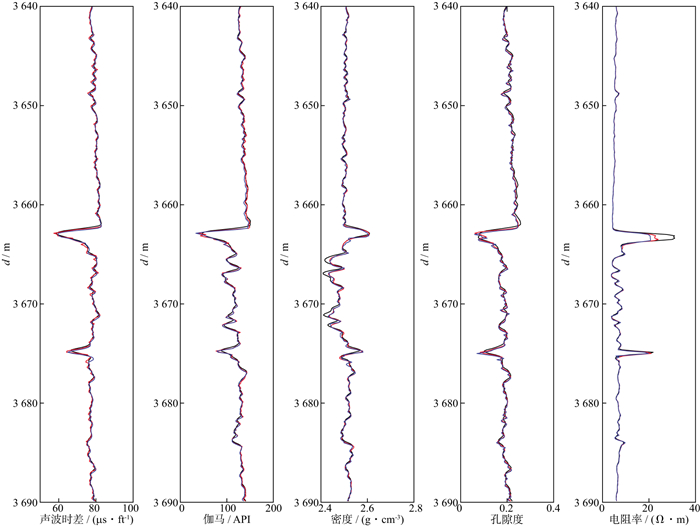
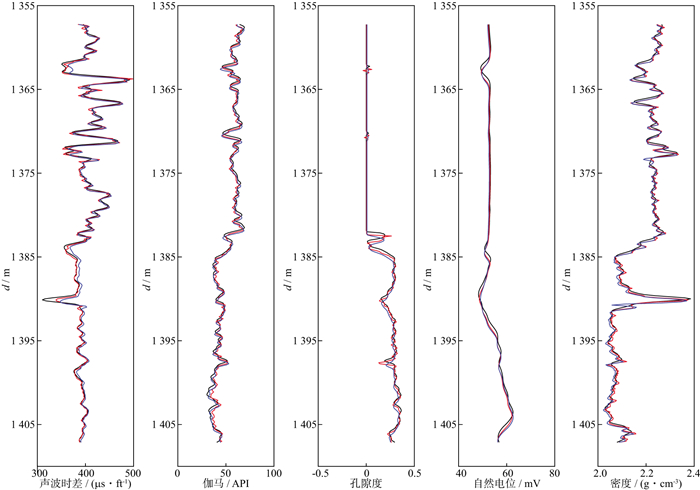
利用CNN-GRU神经网络模型和GRU神经网络模型对A1井的测井曲线进行预测的结果如图 7所示, 黄色虚线以上是对训练集的拟合结果, 以下是对测试集的预测结果, 图 8是对图 7测试集预测结果的局部放大显示。B2井的测井曲线预测结果如图 9所示, 两条黄色虚线的中间部分代表测试集的预测结果, 其余部分代表训练集的拟合结果, 图 10是对图 9测试集预测结果的局部放大显示。表 2和表 3分别为利用CNN-GRU神经网络模型和GRU神经网络模型对A1井和B2井的预测精度评价参数。图 7至图 10中, 黑色曲线为各条测井曲线对应的实测值, 黄色为CNN-GRU神经网络模型对训练集的拟合值, 紫色为GRU神经网络模型对训练集的拟合值, 红色为CNN-GRU神经网络模型对测试集的预测值, 蓝色为GRU神经网络模型对测试集的预测值。
|
图 7 A1井的测井曲线拟合与预测结果 |
|
图 8 A1井测井曲线预测结果的局部放大显示 |
|
图 9 B2井测井曲线拟合与预测结果 |
|
图 10 B2井测井曲线预测结果的局部放大显示 |
| 表 2 利用CNN-GRU神经网络模型与GRU神经网络模型得到的A1井预测精度评价参数 |
| 表 3 利用CNN-GRU神经网络模型与GRU神经网络模型得到的B2井预测精度评价参数 |
从图 7至图 10可以看出, 在训练集的拟合阶段, 利用CNN-GRU神经网络模型与GRU神经网络模型得到的拟合值与真实值基本重合, 证明模型训练效果较好。在测试集的预测阶段, 两种模型对各条测井曲线均取得较好的预测结果, 从整体上预测出了测井曲线的变化趋势。不难发现, CNN-GRU神经网络模型的预测精度高于GRU神经网络模型的预测精度。
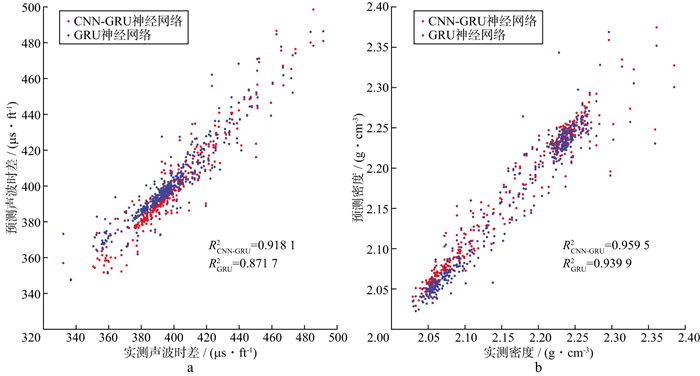
从全段预测范围对比CNN-GRU神经网络模型和GRU神经网络模型在局部细节的预测结果, 将B2井中声波时差和密度的模型预测值与实测值进行交会, 交会结果如图 11所示。
|
图 11 利用两种模型得到的预测值与实测值交会结果 a声波时差数据交会结果; b密度数据交会结果 |
从图 11的交会结果可知, CNN-GRU模型要比GRU模型更接近实测值, 并且CNN-GRU模型预测结果的R2值大于GRU模型的R2值, 说明CNN-GRU神经网络模型对测井数据多个局部细节的拟合结果均优于GRU神经网络模型。此外, 由表 2和表 3的评价参数可知, CNN-GRU神经网络模型相较于GRU神经网络模型的均方根误差较低, 而相关系数较高, 这也证明了CNN-GRU神经网络模型的预测精度高于GRU神经网络模型。
为了比较CNN-GRU神经网络模型和GRU神经网络模型在测井曲线局部发生突变时的预测能力, 对A1、B2井预测结果进行局部放大分析, 结果如图 12所示, 黑色曲线为实测值, 红色曲线为CNN-GRU神经网络模型预测结果, 蓝色曲线为GRU神经网络模型预测结果。
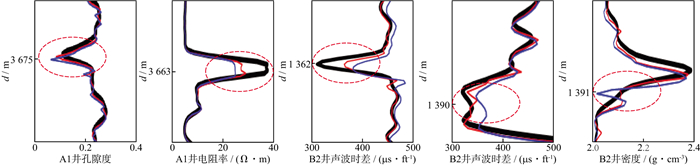
|
图 12 A1、B2井测井曲线预测结果局部放大显示 |
观察图 12可知, 当测井曲线变化较平稳时, CNN-GRU神经网络模型输出结果和GRU神经网络模型输出结果差别不大, 这是因为变化平稳时测井曲线没有明显的局部形状; 当测井曲线发生局部突变时(红色椭圆区域), CNN-GRU神经网络模型的预测结果比GRU神经网络模型更接近实测值(如图 12中孔隙度曲线3675m处、电阻率曲线3663m处, 声波时差曲线1390m处); 就曲线局部特征的重构结果而言, CNN-GRU神经网络模型的预测结果也优于普通的GRU神经网络模型(如图 12中声波时差曲线1362m处、密度曲线1391m处), 原因在于CNN-GRU神经网络模型中加入了卷积层, 可以充分提取测井曲线的空间特征。
由上述分析结果可知, CNN-GRU神经网络模型比单一的GRU神经网络模型对测井曲线的预测结果更优。CNN-GRU神经网络模型对测井曲线整体预测效果好, 同时对测井曲线局部的突变具有良好的预测能力, 充分表现出其预测测井曲线的优势。
3 结论本文将深度学习中特征表达能力较强的CNN和记忆能力较强的GRU神经网络相结合, 考虑到测井曲线的深度趋势和局部形态, 提出了针对测井数据的CNN-GRU神经网络预测模型。以四川某地区A、B两个井区的测井数据为样本, 将CNN-GRU神经网络模型与其它常用预测模型的预测结果进行对比, 得到了以下认识。
1) 本文方法的预测结果具有较高的精度, 更适合于测井曲线预测, 且对不同类型测井曲线均有较高的准确性, 适应性强。
2) 当测井曲线发生局部突变时, 本文方法对测井曲线多个局部细节的拟合结果要优于单一的模型, 对测井曲线的局部特征具有较强的重构能力。
需要指出的是, 本文方法虽取得了较好的效果, 但输入模型的特征集未考虑地层结构等因素, 不能完全反映真实的地下信息。下一步的研究会将地质背景输入到网络模型中, 进一步提高预测精度。
| [1] |
韩正波, 刘厚彬, 张靖涛, 等. 深层脆性页岩力学性能及井壁稳定性研究[J]. 特种油气藏, 2020, 27(5): 167-174. HAN Z B, LIU H B, ZHANG J T, et al. Study on the mechanical properties and wellbore stability of deep brittle shale[J]. Special Oil and Gas Reservoir, 2020, 27(5): 167-174. DOI:10.3969/j.issn.1006-6535.2020.05.026 |
| [2] |
陈云天. 基于机器学习的测井曲线补全与生成研究[D]. 北京: 北京大学, 2020 CHEN Y T. Research on well logging curve completion and generation based on machine learning[D]. Beijing: Peking University, 2020 |
| [3] |
孙宇航, 刘洋. 利用GRU神经网络预测横波速度[J]. 石油地球物理勘探, 2020, 55(3): 484-492, 503. SUN Y Y, LIU Y. Prediction of shear wave velocity using Gru neural network[J]. Oil Geophysical Prospecting, 2020, 55(3): 484-492, 503. |
| [4] |
SMITH J H. A method for calculating pseudo sonics from e-logs in a clastic geologic setting[J]. Gulf Coast Association of Geological Societies Transactions, 2007, 57(1): 675-678. |
| [5] |
GARDNER G, GARDNER L W, GREGORY A R. Formation velocity and density-the diagnostic basics for stratigraphic traps[J]. Geophysics, 1974, 39(6): 770-780. |
| [6] |
CASTAGNA J P, BATZLE M L, EASTWOOD R L. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks[J]. Geophysics, 1985, 50(4): 571-581. |
| [7] |
李雄炎, 秦瑞宝, 刘小梅, 等. 多方法对比分析及随钻声波测井曲线的预测[J]. 地球物理学进展, 2016, 31(3): 1131-1138. LI X Y, QIN R B, LIU X M, et al. Multi method comparative analysis and prediction of acoustic logging while drilling[J]. Progress in Geophysics, 2016, 31(3): 1131-1138. |
| [8] |
杜佳男. 基于曲线重构方法的水淹层测井评价技术研究[D]. 北京: 中国石油大学(北京), 2019 DU J N. A study on logging evaluation technology of flooded layer based on curve reconstruction method[D]. Beijing: University of Petroleum of China(Beijing), 2019 |
| [9] |
SENGUPTA S, BASAK S, SAIKIA P, et al. A review of deep learning with special emphasis on architectures, applications and recent trends[J]. Knowledge-Based Systems, 2020, 194(1): 112-120. |
| [10] |
杨静, 陈云天, 蒋春碧. 测井曲线生成问题的机器学习建模范式——以长宁威远地区页岩井为例[J]. 中国海上油气, 2021, 33(1): 76-84. YANG J, CHEN Y T, JIANG C B. Machine learning modeling paradigm for well logging curve generation: A case study of shale wells in Weiyuan area, Changning[J]. Offshore Oil and Gas of China, 2021, 33(1): 76-84. |
| [11] |
ROLON L, MOHAGHEGH S D, AMERI S, et al. Using artificial neural net works to generate synthetic well logs[J]. Journal of Natural Gas Science and Engineering, 2009, 1(4): 118-133. |
| [12] |
张东晓, 陈云天, 孟晋. 基于循环神经网络的测井曲线生成方法[J]. 石油勘探与开发, 2018, 45(4): 598-607. ZHANG D X, CHEN Y T, MENG J. Logging curve generation method based on recurrent neural network[J]. Petroleum Exploration and Development, 2018, 45(4): 598-607. |
| [13] |
王俊, 曹俊兴, 刘哲哿, 等. 基于长短期记忆网络的钻前测井曲线预测方法[J]. 成都理工大学学报(自然科学版), 2020, 47(2): 227-236. WANG J, CAO J X, LIU Z K, et al. Prediction method of pre drilling logging curve based on long-term and short-term memory network[J]. Journal of Chengdu University of Technology(Natural Science Edition), 2020, 47(2): 227-236. |
| [14] |
王俊, 曹俊兴, 尤加春, 等. 基于门控循环单元神经网络的储层孔渗饱参数预测[J]. 石油物探, 2020, 59(4): 616-627. WANG J, CAO J X, YOU J C, et al. Prediction of reservoir porosity and saturation parameters based on neural network of gate control cycle unit[J]. Geophysical Prospecting for Petroleum, 2020, 59(4): 616-627. |
| [15] |
SHEWALKAR A, NYAVANANDI D, LUDWIG S A. Performance evaluation of deep neural networks applied to speech recognition: RNN, LSTM and GRU[J]. Journal of Artificial Intelligence and Soft Computing Research, 2019, 9(4): 11. |
| [16] |
杨丽, 吴雨茜, 王俊丽, 等. 循环神经网络研究综述[J]. 计算机应用, 2018, 38(S2): 1-6, 26. YANG L, WU Y X, WANG J L, et al. Review of recurrent neural networks[J]. Computer Applications, 2018, 38(S2): 1-6, 26. |
| [17] |
QIN Z W, YU F X, LIU C C, et al. How convolutional neural networks see the world-A survey of convolutional neural network visualization methods[J]. Mathematical Foundations of Computing, 2018, 1(2): 32. |




